Exploring the Early Afterglow Polarization of GRB 190829A

GRBs (gamma-ray bursts) are among the brightest phenomena in the universe. They are originated when massive stars die (Woosley, 1993; Paczyński, 1998; Woosley & Bloom, 2006; Cano et al., 2017) or two compact objects, such as neutron stars (NSs; Duncan & Thompson, 1992; Usov, 1992; Thompson, 1994; Eichler et al., 1989; Metzger et al., 2011) and a NS - black hole (BH, Narayan et al., 1992), merge. Long GRBs (lGRBs) and short GRBs (sGRBs), usually associated with the dying of massive stars and a merging of compact objects, are commonly classified based on their duration:¹¹1For a debate of controversial situations, see Kann et al. (2011); Becerra et al. (2019). $T_{90}\leq 2\mathrm{\,s}$ or $T_{90}\geq 2\mathrm{\,s}$,²²2$T_{90}$ is the time over which a GRB releases from $5\%$ to $95\%$ of the total measured counts. respectively (Mazets et al., 1981; Kouveliotou et al., 1993). GRBs are studied according to their phenomenology detected during the early and late temporal phases. From hard X-rays to $\geq 100$ MeV $gamma$-rays, the early and main episode known as the “prompt emission" is detected and explained by interactions with internal shells of material launched by a central engine at varying velocities and therefore, at different Lorentz factors (Rees & Meszaros, 1994; Paczynski & Xu, 1994), the photospheric emission (Thompson et al., 2007; Mizuta et al., 2011; Lazzati et al., 2013) or discharges from a Poynting-flux dominated outflow (Giannios, 2008; Zhang & Yan, 2011; Kumar & Crumley, 2015; Beniamini & Granot, 2016). The long-lasting multi-wavelength emission observed in $\gamma$-rays, X-rays, optical, and radio is known as “afterglow" (e.g., Costa et al., 1997; van Paradijs et al., 1997; Piro et al., 1998; Sari et al., 1998; Granot & Sari, 2002; Gehrels et al., 2009; Wang et al., 2015). It is often modelled with synchrotron radiation occurring when the relativistic outflow is decelerated by an external medium, and a significant portion of its energy is transferred to it (e.g., see Sari et al., 1998).

The synchrotron radiation produced at the afterglow is typically explored in a forward-shock (FS) scenario, and this mechanism is contingent on the existence of magnetic fields in the emission zone. The origin of magnetic fields in GRBs is still a topic of discussion. Magnetic fields can be advected from the burst’s source (Lyutikov & Blandford, 2003; Sironi & Spitkovsky, 2011), be generated from compression of an existing interstellar medium (ISM) magnetic field (Laing, 1980; Teboul & Shaviv, 2021), from shock-generated plasma instabilities (Weibel, 1959; Medvedev & Loeb, 1999), and even by magnetic reconnection in Poyinting-flux dominated outflows (Zhang & Yan, 2011). Probing these fields, and their originating sources, alongside other properties of GRBs, is a challenging task that requires multiple directions of theoretical considerations and observational data. One way is exploring the polarization characteristics of an observed emission. As the polarization relies on the configuration of the magnetic field, it analysis allow us to look into their configurations and, therefore, their origins.

Several authors have implemented polarization models in order to acquire source-related information (e.g., see Granot & Königl, 2003; Lyutikov et al., 2003; Nakar et al., 2003; Rossi et al., 2004; Gill et al., 2020; Stringer & Lazzati, 2020; Teboul & Shaviv, 2021; Shrestha et al., 2022). Unfortunately, despite the number of GRB observations, collecting polarization data remains being a challenge. Nevertheless, afterglow polarization measurements have been obtained for several GRBs at this point: at the early afterglow phase, the observations of GRB 090102 ($\Pi=10.2\pm 1.3\%$, Steele et al. (2009)), GRB 120308A ($\Pi=28\pm 4\%$, Mundell et al. (2013)) and the upper limits of GRB 190829A ($\Pi<6\%$, Dichiara et al. (2022)) were obtained; examples at the late afterglow include GRB 191221B ($\Pi=1.2\%$; Buckley et al., 2021), GRB 190114C ($\Pi=0.8\pm 0.13\%$; Laskar et al., 2019) on the radio band, and the upper limits of GRB 991216 (with $\Pi<7\%$; Granot & Taylor, 2005) and GRB 170817A (with $\Pi<12\%$, on the 2.8 GHz radio band Corsi et al., 2018). Furthermore, several global collaborations like the POLAR project (Orsi & Polar Collaboration, 2011), the Multicolour OPTimised Optical Polarimeter (MOPTOP; Shrestha et al., 2020), and the MASTER project (Lipunov et al., 2019), which are underway, or in preparation phases, could provide future observations and the much-needed polarization data of different GRB epochs.

In this work, we calculate the temporal evolution of the expected polarization for GRB 190829A in a synchrotron FS scenario, proven to allow for analysis of GRB 190829A’s afterglow in terms of the physical parameters of the system. We use the available polarimetric upper limits from Dichiara et al. (2022) to test the parameters and models required to explain the multi-wavelength afterglow observations of GRB 190829A. The paper is structured as follows; In Section 2, we briefly introduce the polarization model used in this paper in the synchrotron FS framework during the off-axis phase. In Section 3, we apply as particular case our polarization model to GRB 190829A using the best-fit parameters obtained in different scenarios. In Section 4, we discuss the results. Finally, in Section 5, we offer a brief summary and our concluding remarks.

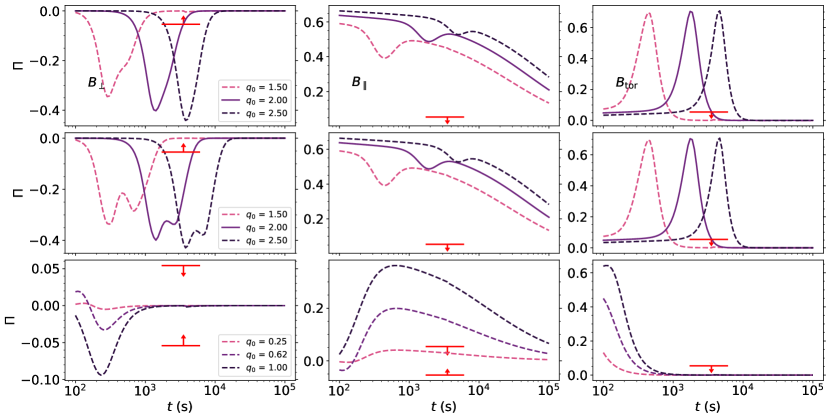
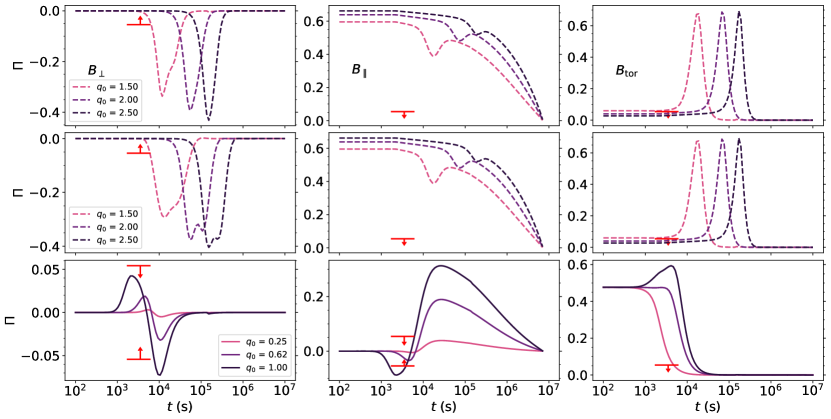
Figures 1, 3, 4, 5, 6 and 7 show the polarization degree for three magnetic field configurations, with each figure representing the parameters used by Sato et al. (2021), Sato et al. (2022), Salafia et al. (2022), Dichiara et al. (2022), Fraija et al. (2021) and Zhang et al. (2021a, b), respectively. The magnetic field configurations are arranged from left to right: $B_{\perp}$, $B_{\parallel}$, and $B_{\rm tor}$; and from top to bottom: a non-expanding jet configuration (i.e., homogeneous jet where $\theta_{\rm j}$ does not evolve) viewed off-axis, an expanding jet configuration³³3The choice to include both approaches to the homogeneous jet comes from the nearly identical flux light curves, but different polarizations (e.g. see Rossi et al., 2004) (i.e., homogeneous jet where $\theta_{\rm j}=\theta_{\rm j}(t)$, according to Huang et al. (2000) hydrodynamical equations) also viewed off-axis, and the same expanding jet viewed from within the jet’s beaming cone ($\theta_{\rm obs}<\theta_{\rm j}$). For all cases, we present the polarization for a range of initial values of $q_{0}=\frac{\theta_{\rm obs}}{\theta_{\rm j,0}}$, with solid lines as markers for the observation angle reported/assumed by the mentioned authors.

Sato et al. (2021, 2022) used a narrow jet FS synchrotron model to describe the early afterglow of GRB 190829A. They reported this model to be satisfactory in explaining the multi-wavelength observations in the range from $8\times 10^{2}$ to $2\times 10^{4}{\rm s}$. We use the most recent best-fit parameters reported in this work (see the first row of table 1), with the additional parameters of $\varepsilon_{e}=3.5\times 10^{-2}$, $\varepsilon_{B}=6\times 10^{-5}$, and $\zeta_{e}=0.2$ and a maximum flux at time $t_{\rm peak}=2\times 10^{3}{\rm s}$. We present in Figure 1 the polarization evolution considering these parameters. The solid line represents the values presented by Sato et al. (2022). Regardless of the choice of jet (expanding or not), the polarization values returned from these parameters break the upper limits of $\Pi(t\approx[1700-6000]{\rm s})\lesssim 6\%\$ imposed by Dichiara et al. (2022). For an expanding jet, the set of parameters presented by the authors return the following polarization values $\Pi(B_{\perp},t\approx 2000\,{\rm s})\approx 30\%$, $\Pi(B_{\perp},t\approx 4000\,{\rm s})\approx 22.2\%$ and $\Pi(B_{\perp},t\approx 6000\,{\rm s})\approx 0\%$. For a toroidal field, the polarization observed is $\Pi(B_{\rm tor},t\approx 2000{\rm s})\approx 63\%$, $\Pi(B_{\rm tor},t\approx 4000\,{\rm s})\approx 2\%$ and $\Pi(B_{\rm tor},t\approx 6000\,{\rm s})\approx 0\%$. At first glance, this should enough to exclude the possibility of a viewing angle this high ($\theta_{\rm obs}=2\theta_{\rm j}$). However, it is worth noting that polarization is highly dependent on the magnetic field anisotropy, and we only explore the extremely anisotropic cases ($b=0;b\rightarrow\infty$). A more isotropic field, where $b$ is closer to unity, would severely reduce the polarization degree (e.g., see Gill & Granot, 2018; Corsi et al., 2018; Gill & Granot, 2020; Teboul & Shaviv, 2021, for the case of GRB 170817A) without any interference on the flux light curves (which does not take into consideration the magnetic field’s geometry). Exploring this parameter set with a more isotropic configuration could amend the discrepancy between polarization and flux fitting.

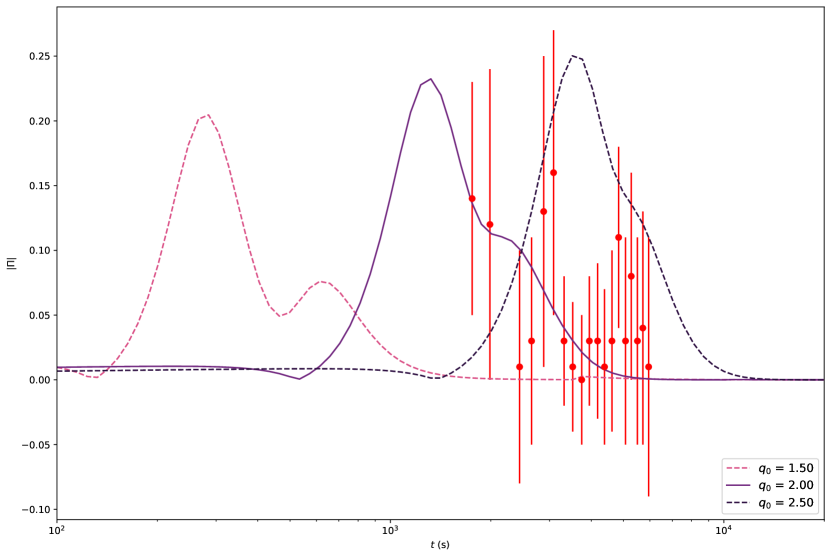
Figure 2 shows the polarization calculated for a less extreme anisotropy scenario. To obtain this polarization, we use Eq. 4 of Granot & Königl (2003) to sum the contributions of ordered and random components and take the absolute value:

This equation introduces two new parameters, $\eta$ and $\delta$, where $\eta=\frac{\expectationvalue{B_{\rm ord}^{2}}}{\expectationvalue{B_{\rm rnd}^{2}}}$ and $\delta$ is the angle between the ordered magnetic field and the jet axis (see Fig. 1 of the aforementioned paper). Information regarding these parameters cannot be obtained from Sato et al. (2021, 2022). We explore a possible case where $\eta=0.25$ and $\delta=\pi/2$. The change to a less extreme anisotropic scenario reduces the polarization significantly and, as is seen in Figure 2, allows to describe the polarization data observed by Dichiara et al. (2022). This implies the requirement of a sub-dominant ordered component a quarter as strong as the random one, perpendicular to the jet axis, to validate this parameter set.

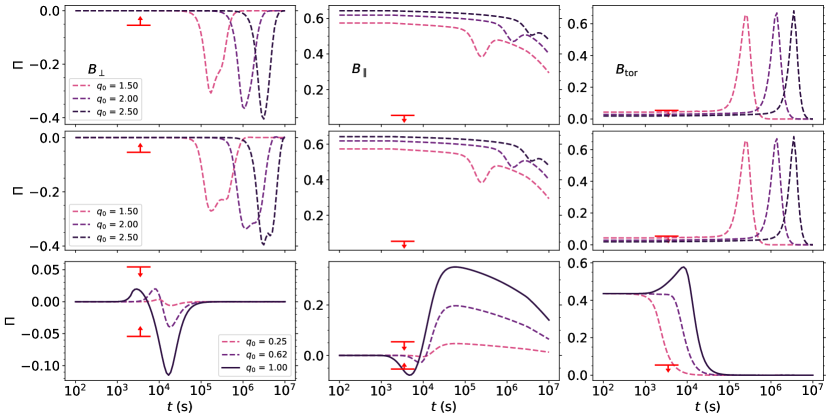
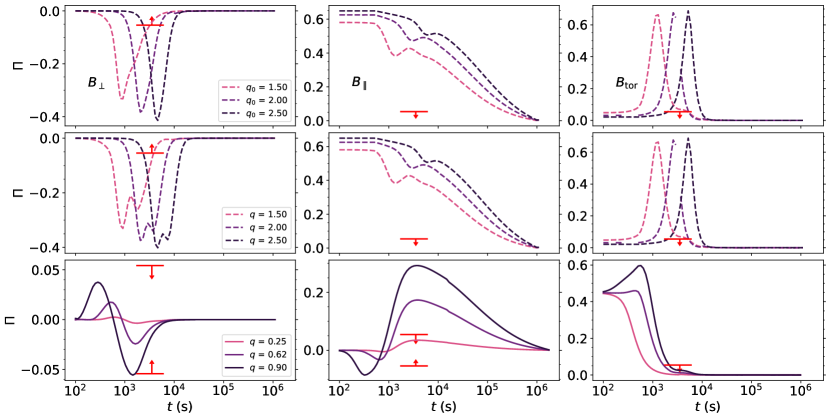
Salafia et al. (2022) described the afterglow of GRB 190829A with a dual component; a RS and FS emission. They proposed that the RS emission describes the early multiwavelength afterglow, while the FS emission dominates after $t>1{\rm day}$. The parameters reported by the authors for the FS emission are found in the second row of table 1, and additionally, $\varepsilon_{e}=3.0^{+2.9}_{-1.7}\times 10^{-2}$, $\varepsilon_{B}=2.5^{+3.5}_{-1.3}\times 10^{-5}$, and $\zeta_{e}=0.04$. The authors also constrained $\Delta\theta<2\,{\rm deg}$ based on a compactness argument and assumed an on-axis (i.e., the observation angle within the beaming cone of the jet) observation angle. For purposes of the calculation we take $\theta_{\rm obs}=\theta_{\rm j}$ as the authors’ choice, as indicated by Fig. 5 of their work, but also presented the values for $\theta_{\rm obs}=0.25\theta_{\rm j}$ and $\theta_{\rm obs}=0.62\theta_{\rm j}$. Figure 3 shows that the authors’ chosen values indicate a good fit for the polarization upper limits of $\Pi\lesssim 6\%$, with all values of on-axis $q_{0}$ returning polarization within the upper limits for the random magnetic field configuration $B_{\perp}$. We find a polarization degree of $\Pi(B_{\perp},t\approx 2000\,{\rm s})\approx 1.0\%$, $\Pi(B_{\perp},t\approx 4000\,{\rm s})\approx 1.2\%$, and $\Pi(B_{\perp},t\approx 6000\,{\rm s})\approx-1.4\%$, with $q_{0}\lesssim 0.62$ required to allow for a polarization originating from a $B_{\parallel}$ field and $B_{\rm tor}$ ruled out for $q_{0}\gtrsim 0.25$. While we limited ourselves to the forward shock synchrotron calculations in this dual component model, the polarization for iC has been explored before (Gill & Granot, 2020; Lazzati et al., 2004; Toma et al., 2009). These authors have found that polarization for iC is remarkably similar to the corresponding curves for synchrotron emission, with the caveat of a higher possible maximum polarization ($\Pi_{\rm max,syn}\simeq 75\%,\,\Pi_{\rm max,iC}\rightarrow 100\%$); however, the maximum polarization is directly linked to the spectral index $\alpha$ through $\Pi_{max}=(\alpha+1)/(\alpha+1.66)$. As such, with a known $\alpha$ (or $p$) and maximum polarization, the theoretical limit of maximum polarization is of little relevance. The polarization curves would be similar to the ones shown here, with the parameters used to calculate the RS emission.

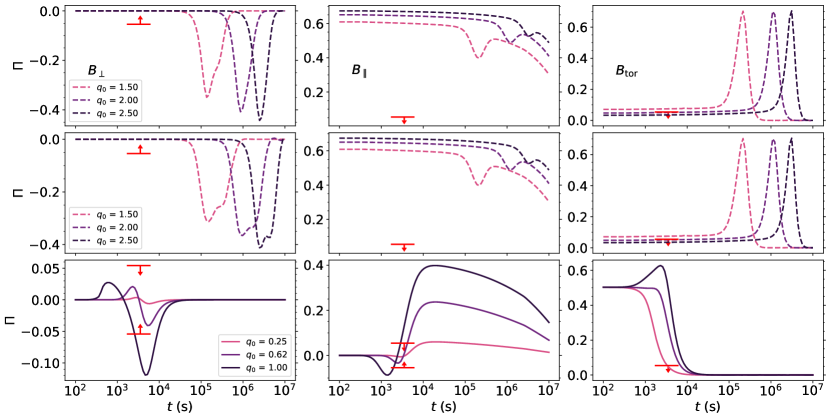
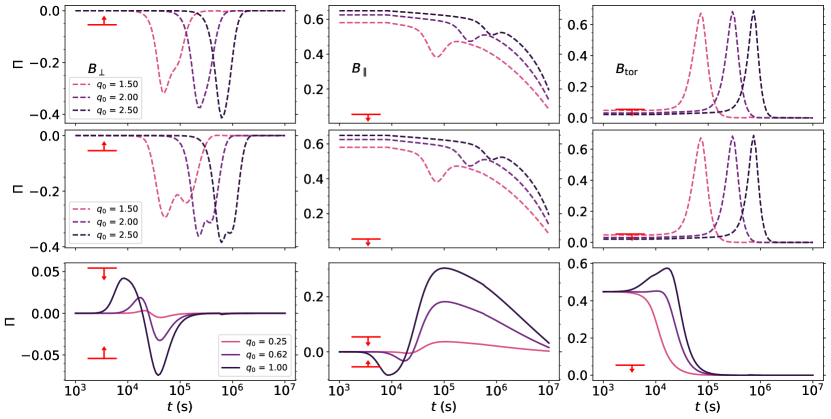
Dichiara et al. (2022) have also described the afterglow of GRB 190829A with dual component RS plus FS emission. The authors proposed that the rebrightening in the X-ray and optical observations is consistent with the RS component of the emission. The parameters reported by the authors are presented in the third row of table 1. Additionally, the authors expected $\varepsilon_{e}\approx 10^{-1}$ and $\varepsilon_{B}\approx 10^{-4}$. No fundamental assumptions were made on the observation angle for the emission. However, the authors used the polarization model presented by Rossi et al. (2004) to rule out a homogeneous jet viewed off-axis with a $90\%$ confidence. We then present the curves for $q_{0}\leq 1$ as the authors’ considered values and assume a value of $\Gamma_{0}=100$, between a minimal value for a typical off-axis jet and the typical values of $\Gamma_{0}$ for on-axis jets.⁴⁴4This value is also within the constrained values of Salafia et al. (2022), based on their compactness argument. The polarization results are presented in Figure 4. For all configurations, $q_{0}\geq 1$ is ruled out, while a value of $q_{0}=0.62$ returns the following polarizations $\Pi(B_{\perp},t\approx 2000{\rm s})\approx 1.8\%$, $\Pi(B_{\perp},t\approx 4000{\rm s})\approx-2.5\%$, and $\Pi(B_{\perp},t\approx 6000{\rm s})\approx-4.0\%$. For a parallel field configuration, we note that the upper limits rule out $q_{0}=1.0,0.62$, but a value of $q_{0}<0.62$ can still fit the polarization upper limits. This is in line with the conclusions reached by the authors, who expect that the low radiative efficiency ($<1\%$) could be explained by a jet viewed from $\theta_{\rm obs}<\theta_{\rm j}$. The considerations regarding iC done for Salafia et al. (2022) are the same for this model.

Fraija et al. (2021) proposed a synchrotron forward shock model originating from a spin-down millisecond magnetar source to describe the X-ray and optical observations of GRB 190829A, but expect an iC component as necessary to describe the high-energy and VHE photons observed. The parameters reported by the authors are found in the fourth row of table 1, with the additional parameters of $\varepsilon_{e}=0.8^{+0.1}_{-0.1}\times 10^{-1}$ and $\varepsilon_{B}=1.1^{+0.1}_{-0.1}\times 10^{-4}$. The authors also assume an on-axis emission to fit the light curves, and we present the polarization assuming $q_{0}\leq 1$ as the canonical choice. Figure 5 shows that, like the parameter set of Salafia et al. (2022), all choices of $q_{0}\leq 1$ are well poised to fit the set upper limits. The highest value of on-axis $q_{0}=1$, an observation angle set at the edge of the jet, returns polarization values of $\Pi(B_{\perp},t\approx 2000\,{\rm s})\approx 4.3\%$, $\Pi(B_{\perp},t\approx 4000\,{\rm s})\approx 2.1\%$, and $\Pi(B_{\perp},t\approx 6000\,{\rm s})\approx-1.9\%$. For a parallel field configuration, we note that the $q_{0}=1$ is ruled out, but a value of $q_{0}\lesssim 0.62$ can still fit the polarization upper limits. As such, a choice of $\theta_{\rm obs}=\theta_{\rm j}$ would make $B_{\perp}$ the sole possible configuration (assuming an extremely anisotropic configuration), while $\theta_{\rm obs}<\theta_{\rm j}$ would only rule out the globally ordered, toroidal field configuration.

Zhang et al. (2021a) proposed a paradigm to explain GRB 190829A. With the condition of a quasi-isotropic ejecta, the authors fit the X-ray, radio, and optical afterglow light curves with a forward shock model, where the afterglow emission is attributed to synchrotron and iC radiation. The parameters reported by the authors are found in the fifth row of table 1, with the additional parameters of $\log_{10}\varepsilon_{e}=-0.49^{+0.46}_{-0.22}$ and $\log_{10}\varepsilon_{B}=-3.22^{+1.21}_{-0.80}$. The authors assume an on-axis observation of the burst. As such, we take $q_{0}\lesssim 1$ as their canonical choice. We see from Figure 6 that for $q_{0}=1$ we find $\Pi(B_{\perp},t\approx 2000\,{\rm s})\approx-4.1\%$, $\Pi(B_{\perp},t\approx 4000\,{\rm s})\approx-1.0\%$, and $\Pi(B_{\perp},t\approx 6000\,{\rm s})\approx 0.0\%$. The values of $q_{0}=1.0,\,0.62$ rule out the globally ordered configurations, which require an $\theta_{\rm obs}\lesssim 0.25\theta_{\rm j}$ to fit the upper limits with these parameters.

Zhang et al. (2021b) proposed a combination of the external FS and a late prompt emission to describe the afterglow of GRB 190829A. The authors expected an eiC+SSC mechanism to describe the very-high-energy component by the High Energy Stereoscopic System (H.E.S.S.) observations and the typical FS model accounts for the lower-frequency emissions. The parameters reported by the authors are found in the sixth row of table 1, with the additional parameters of $\varepsilon_{e}=0.39$, $\varepsilon_{e}=8.7\times 10^{-5}$, and $\zeta_{e}=0.34$. The authors assumed an on-axis observation of the burst. As such we take $q_{0}\lesssim 1$ as their canonical choice. Figure 7 presents the polarization curves. We see that with this on-axis condition in mind, both a random ($B_{\perp}$) and ordered ($B_{\parallel}$) return a polarization within the upper limits of $<6\%$. Taking $q_{0}=1$, we find $\Pi(B_{\perp},t\approx 2000{\rm s})\approx 0.0\%$, $\Pi(B_{\perp},t\approx 4000{\rm s})\approx 0.5\%$, and $\Pi(B_{\perp},t\approx 6000{\rm s})\approx 3.4\%$ and $\Pi(B_{\parallel},t\approx 2000{\rm s})\approx 0.0\%$, $\Pi(B_{\parallel},t\approx 4000{\rm s})\approx-1.4\%$, and $\Pi(B_{\parallel},t\approx 6000{\rm s})\approx-5.0\%$. A globally ordered toroidal configuration is ruled out.

In this work, we have applied a semi-analytical FS synchrotron model, analogous with a homogeneous jet, to a polarization model and obtained a set of time-dependent polarization curves. This polarization depends on the parameters associated with the evolution of the bulk Lorentz factor and half-opening angle of synchrotron theory. Additionally, the polarization model depends on the geometry of the magnetic field, and we have explored the extremely anisotropic scenarios ($b=0,\,b\rightarrow\infty$) of a random and two ordered field configurations. We have used different parameter sets of previously published works capable of adequately describing the afterglow of GRB 190829A (e.g. see Sato et al., 2021, 2022; Salafia et al., 2022; Dichiara et al., 2022; Fraija et al., 2021; Zhang et al., 2021a, b) to fit the upper limits on polarization set by Dichiara et al. (2022).

The curves obtained favor the scenario where the observation angle is within the jet’s beaming cone ($\theta_{\rm obs}\lesssim\theta_{\rm j}$) while disfavoring an off-axis scenario. This result is in agreement with Salafia et al. (2022); Dichiara et al. (2022); Fraija et al. (2021); Zhang et al. (2021a, b) that predicted GRB 190829A to have been seen on-axis. However, the observations provided by Dichiara et al. (2022) cannot entirely exclude the off-axis scenario. This conclusion comes from the polarization’s dependency on magnetic field anisotropy. The presence of a subdominant field (i.e., $b\neq 0,\,b\nrightarrow\infty$) would decrease the observed polarization by a factor $>2$ (model dependent; see Gill & Granot, 2018; Corsi et al., 2018; Gill & Granot, 2020; Teboul & Shaviv, 2021), which is significant enough to reconcile the discrepancy between flux and polarization fitting.

While current evidence indicates that GRB 190829A was seen on-axis, more polarization data and deeper scrutiny of the afterglow fitting would be required to solve the degeneracy present between models properly.