Extension of the Asfgrid for correcting asteroseismic large frequency separations

The initial release of the Asfgrid by Sharma & Stello (2016) was published as part of an investigation of the Kepler red giant sample (Sharma et al., 2016). It was therefore made to cover the typical ranges in mass and [Fe/H] of those stars with most grid points concentrated in the parameter range where most Kepler giants were found. Because the community is increasingly studying oscillations in stars in the more extreme ends of the mass-[Fe/H] parameter space we have extended the Asfgrid from its initial 247 grid points in mass-[Fe/H] (see black points in Figure 1) to now having 632 points (black and red points). This extension was mainly made to cover the low-mass stars ($0.6<M/\mathrm{M}_{\odot}<0.8$) and to ensure that interpolations become more accurate at low metallicities ($-3<\mathrm{[Fe/H]}<-1.4$) where the initial grid was sparse. In addition, we have extended the grid to slightly higher mass ($M/\mathrm{M}_{\odot}\leq 5.5$) and higher metallicity ([Fe/H] $\leq 0.5$) relative to the initial release.

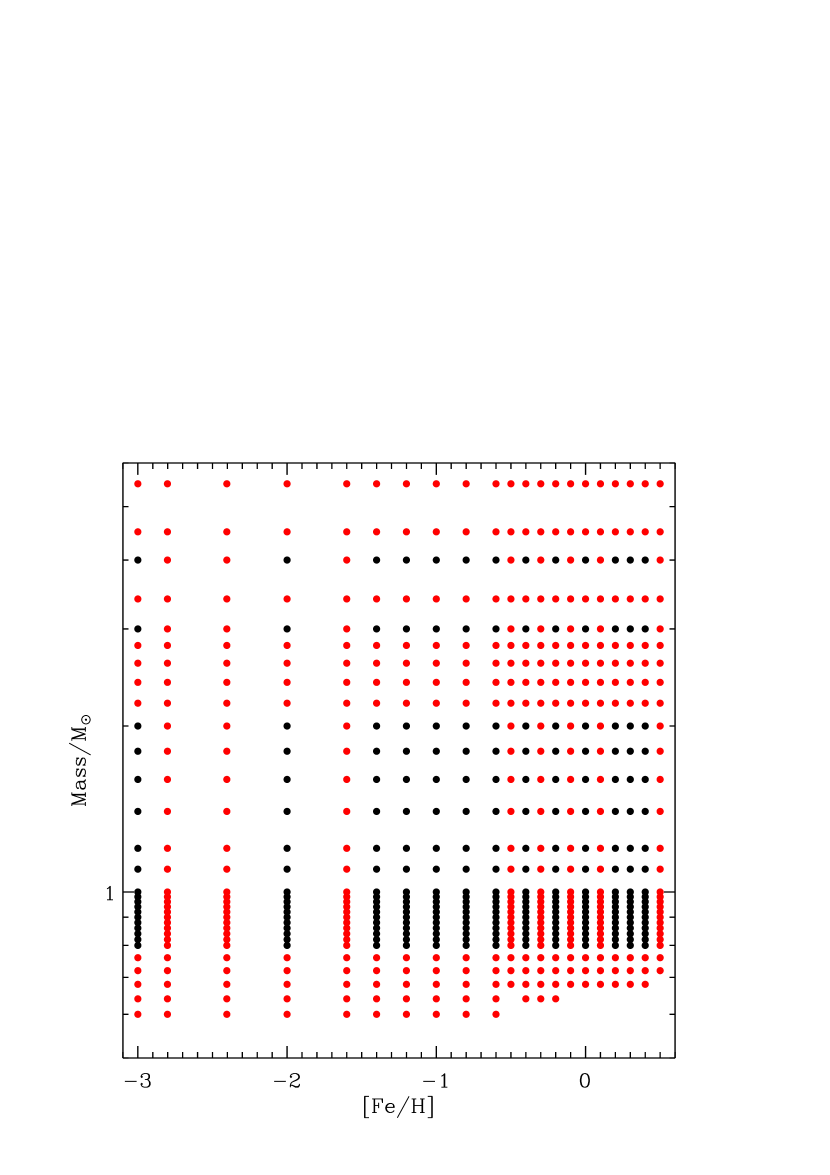
For the extension we used identical input physics and the same version of MESA (v6950) (Paxton et al., 2011, 2013, 2015) to calculate the stellar models ensuring consistency with the initial grid, which forms part of the final grid. The evolution was terminated at the tip of the asymptotic giant branch. We also used the same version of GYRE (v3.1) (Townsend & Teitler, 2013) with the same settings to calculate the adiabatic frequencies and the White et al. (2011) method to derive $\Delta\nu$ from those frequencies. Further details about the models are given in Sharma et al. (2016, section 2.3).

Like the initial release, the two main things that Asfgrid can estimate are:

• •

  Asteroseismic frequencies $\nu_{\mathrm{max}}$ and $\Delta\nu$ and the correction factor $f_{\Delta\nu}$: These are estimated from surface gravity ($\log g$), effective temperature ($T_{\mathrm{eff}}$), metallicity ($Z$), and mass ($M$). The interpolation is done over the model grid in $Z$, $M$, evolution state ($E_{\rm state}$), and $\gamma$, where

  $$\gamma=\log(T_{\rm eff})+0.01\log g\left[\tanh\left(\frac{\log g-4.5}{0.25}\right)+1\right]\frac{1}{2}.$$

  (1)

  We introduce $\gamma$ because we ideally want to interpolate the stellar properties over age. However, age is not an observable, while $T_{\rm eff}$ and $\log g$, which are observables, are not monotonic with age. Hence, $\gamma$ is designed to be roughly monotonic with age. The correction factor, $f_{\Delta\nu}$, is estimated alongside using the relation

  	$\displaystyle f_{\Delta\nu}$	$\displaystyle=$	$\displaystyle\frac{\Delta\nu}{135.1\ \mu{\rm Hz}}\left(\frac{\rho}{\rho_{\odot}}\right)^{-1/2}$		(2)
  		$\displaystyle=$	$\displaystyle\frac{\Delta\nu}{135.1\ \mu{\rm Hz}}\left(\frac{g}{g_{\odot}}\right)^{-3/4}\left(\frac{M}{{\rm M}_{\odot}}\right)^{1/4}$		(3)

• •

  Stellar mass $M$ and radius $R$: They are estimated from $T_{\mathrm{eff}}$, $Z$, $\nu_{\mathrm{max}}$, and $\Delta\nu$. The interpolation is done over the grid in $Z$, $M_{\rm seismic}$, $E_{\rm state}$, and $\gamma$, where

  	$\displaystyle M_{\rm seismic}$	$\displaystyle=$	$\displaystyle\left(\frac{g}{g_{\odot}}\right)^{3}\left(\frac{\Delta\nu}{\Delta\nu_{\odot}}\right)^{-4}{\rm M}_{\odot}\ {\rm with}$		(4)
  	$\displaystyle g$	$\displaystyle=$	$\displaystyle g_{\odot}\left(\frac{\nu_{\rm max}}{\nu_{{\rm max},\odot}}\right)\left(\frac{T_{\rm eff}}{T_{{\rm eff},\odot}}\right)^{1/2}$		(5)

  The following solar reference values are used, $g_{\odot}=4.43796\ {\rm cm\ s^{-2}}$, $T_{{\rm eff},\odot}=5777\ {\rm K}$, $\Delta\nu_{\odot}=135.1\ \mu{\rm Hz}$, $\nu_{{\rm max},\odot}=3090\ \mu{\rm Hz}$.

The new extended grid, along with the interpolation code, can be accessed at http://www.physics.usyd.edu.au/k2gap/Asfgrid/. If you use the extended Asfgrid (v0.0.6) for your research, we kindly ask you to cite both Sharma et al. (2016) and this Research Note.