122 \affiliation \institutionKyushu University, Fukuoka, Japan \city \country
Fairness and efficiency trade-off in two-sided matching
Abstract.
The theory of two-sided matching has been extensively developed and applied to many real-life application domains. As the theory has been applied to increasingly diverse types of environments, researchers and practitioners have encountered various forms of distributional constraints. As a mechanism can handle a more general class of constraints, we can assign students more flexibly to colleges to increase students’ welfare. However, it turns out that there exists a trade-off between students’ welfare (efficiency) and fairness (which means no student has justified envy). Furthermore, this trade-off becomes sharper as the class of constraints becomes more general. The first contribution of this paper is to clarify the boundary on whether a strategyproof and fair mechanism can satisfy certain efficiency properties for each class of constraints. Our second contribution is to establish a weaker fairness requirement called envy-freeness up to peers (EF-), which is inspired by a similar concept used in the fair division of indivisible items. EF- guarantees that each student has justified envy towards at most students. By varying , EF- can represent different levels of fairness. We investigate theoretical properties associated with EF-. Furthermore, we develop two contrasting strategyproof mechanisms that work for general hereditary constraints, i.e., one mechanism can guarantee a strong efficiency requirement, while the other can guarantee EF- for any fixed . We evaluate the performance of these mechanisms through computer simulation.
Key words and phrases:
two-sided matching, strategyproof mechanism, mechanism design1. Introduction
The theory of two-sided matching has been developed and has been applied to many real-life application domains (see Roth and Sotomayor (1990) for a comprehensive survey in this literature). It has attracted considerable attention from AI researchers Aziz et al. (2022c); Aziz et al. (2019); Hosseini et al. (2015); Ismaili et al. (2019); Kawase and Iwasaki (2017); Yahiro et al. (2020); Suzuki et al. (2023). As the theory has been applied to increasingly diverse types of environments, researchers and practitioners have encountered various forms of distributional constraints (see Aziz et al. (2022b) for a comprehensive survey on various distributional constraints). There exist three representative classes of constraints. First, the standard model of two-sided matching considers only the maximum quota of each individual college Roth and Sotomayor (1990), which we call maximum quotas constraints.111Although our paper is described in the context of a student-college matching problem, the obtained result is applicable to matching problems in general.
More general classes of constraints are hereditary constraints Aziz et al. (2022a); Goto et al. (2017); Kamada and Kojima (2017) and hereditary M♮-convex set constraints Kojima et al. (2018). An M♮-convex set is a discrete counterpart of a convex set in a continuous domain. Hereditary constraints require that if a matching between students and colleges is feasible, then any matching that places weakly fewer students at each college is also feasible.
As a mechanism can handle a more general class of constraints, we can incorporate more complex constraints required for real-life application domains. Also, we obtain more flexibility in assigning students to colleges. As a result, we can expect that students’ welfare can be increased in the obtained matching. Furthermore, maximum quotas constraints can be considered to be too restrictive. In a real-life situation, it is common that some flexibility exists in determining the capacity of each college, i.e., we can increase the maximum quota of a college if it turns out to be very popular (say, by assigning additional resources). Such flexibility can be modeled naturally using a more general class of constraints.
In this paper, we focus our attention on strategyproof mechanisms, which guarantee that students have no incentive to misreport their preference over colleges. From a theoretical standpoint, if we are interested in a property achieved in dominant strategies, strategyproof mechanisms can be exclusively considered without any loss of generality, as supported by the well-known revelation principle Gibbard (1973). This principle states that if a certain property is satisfied in a dominant strategy equilibrium using a mechanism, it can also be achieved through a strategyproof mechanism. Strategyproof mechanisms are not only theoretically significant but also practically beneficial, as students do not need to speculate about the actions of others to achieve desirable outcomes; they only need to report their preferences truthfully.
Most existing works in two-sided matching require that the obtained matching must be fair, i.e., no student has justified envy. However, just requiring fairness is not sufficient since the matching that no student is assigned to any college is fair; we should achieve some requirement on students’ welfare (which is referred to as efficiency in economics) in conjunction with fairness. In the standard maximum quotas model, the renowned Deferred Acceptance mechanism (DA) Gale and Shapley (1962) can achieve an efficiency property called nonwastefulness in conjunction with fairness. A matching satisfying fairness and nonwastefulness together is called stable.
However, when some distributional constraints are imposed, there exists a trade-off between fairness and efficiency/students’ welfare. In particular, Cho et al. (2022) show that no strategyproof mechanism satisfies fairness and a weaker efficiency property called weak nonwastefulness under hereditary constraints.
The first goal of this paper is to clarify the tight boundaries on whether a strategyproof and fair mechanism can satisfy certain efficiency properties for each class of constraints (see Table 1 in Section 4). In particular, we show that under hereditary constraints, no strategyproof mechanism can simultaneously satisfy fairness and a very weak efficiency requirement called no vacant college property.
This impossibility result illustrates a dilemma: we are expanding/generalizing the classes of constraints in the hope that we can improve students’ welfare. However, if we require strict fairness, we cannot guarantee a very weak requirement of students’ welfare under general hereditary constraints. Given this dilemma, our next goal is to establish a weaker fairness requirement. In this paper, we propose a novel concept called envy-freeness up to peers (EF-). This concept is inspired by a criterion called envy-freeness up to items, which is commonly used in the fair division of indivisible items Budish (2011). EF- guarantees that each student has justified envy towards at most students. By varying , EF- can represent different levels of fairness. On one hand, EF- is equivalent to standard fairness. On the other hand, any matching satisfies EF-(), where is the number of students. To the best of our knowledge, this paper is the first to address the relaxed notion of fairness in two-sided, many-to-one matching.
We show that there exists a case that no matching is nonwasteful and EF- for any , and checking whether a nonwasteful and EF- matching exists or not is NP-complete. Then, we develop two contrasting strategyproof mechanisms that work for general hereditary constraints. One is based on the Serial Dictatorship mechanism (SD) Goto et al. (2017), which utilizes an optimal master-list (where students are assigned in its order) that minimize based on colleges’ preferences, such that the obtained matching is guaranteed to satisfy EF-. Although holds in the worst case, we experimentally show that tends to be much smaller when colleges’ preferences are similar. The other one is based on the Sample and Deferred Acceptance mechanism (SDA) Liu et al. (2023), which is developed for a special case of hereditary constraints called student-project-resource matching-allocation problem. This mechanism satisfies EF- for any given . We extend SDA such that the obtained matching satisfies no vacant college property under a mild assumption. We experimentally show that this mechanism can significantly improve students’ welfare compared to a fair (EF-) mechanism even when is very small.
2. Model
A matching market under distributional constraints is given by . The meaning of each element is as follows.
-
•
is a finite set of students. Let denote
-
•
is a finite set of colleges. Let denote .
-
•
is a finite set of contracts. Contract represents the matching between student and college .
-
•
For any , let and denote the sets of contracts in that involve and , respectively.
-
•
is a profile of the students’ preferences. For each student , represents the preference of over , where represents an outcome such that is unmatched. We assume is strict for each . We say contract is acceptable for if holds. We sometimes use notations like instead of .
-
•
is a profile of the colleges’ preferences. For each college , represents the preference of over , where represents an outcome such that is unmatched. We assume is strict for each . We say contract is acceptable for if holds. We sometimes write instead of .
-
•
is a function that represents distributional constraints, where is the number of colleges and is the set of vectors of non-negative integers. For , we call a family of vectors induced vectors of .
We assume each contract in is acceptable for . This is without loss of generality because if some contract is unacceptable for a college, we can assume it is not included in .
We say is a matching, if for each , either (i) and is acceptable for , or (ii) holds.
For two -element vectors , we say if for all , holds. We say if and hold. Also, let denote the norm of , i.e., .
Definition \thetheorem (feasibility with distributional constraints).
Let be a vector of non-negative integers. We say is feasible in if . For , let us define as . We say is feasible (in ) if is feasible in .
We assume is bounded, i.e., is finite. This is without loss of generality because we can assume each college can accept at most students, i.e., holds when .
Let us first introduce a very general class of constraints called hereditary constraints. Intuitively, heredity means that if is feasible in , then any subset is also feasible in . Let denote an -element unit vector, where its -th element is and all other elements are . Let denote an -element zero vector .
Definition \thetheorem (heredity).
We say a family of -element vectors is hereditary if and for all , if and , then holds. We say is hereditary if its induced vectors are hereditary.
Kojima et al. (2018) show that when is hereditary, and its induced vectors satisfy one additional condition called M♮-convexity, there exists a general mechanism called Generalized Deferred Acceptance mechanism (GDA), which satisfies several desirable properties.222To be more precise, Kojima et al. (2018) show that to apply their framework, it is necessary that the family of feasible matchings forms a matroid. When distributional constraints are defined on rather than on contracts , the fact that the family of feasible contracts forms a matroid corresponds to the fact that (i) the family of feasible vectors forms an M♮-convex set, and (ii) it is hereditary Murota and Shioura (1999).
Let us formally define an M♮-convex set.
Definition \thetheorem (M♮-convex set).
We say a family of vectors forms an M♮-convex set, if for all , for all such that , there exists such that and hold. We say satisfies M♮-convexity if its induced vectors form an M♮-convex set.
An M♮-convex set can be considered as a discrete counterpart of a convex set in a continuous domain. Intuitively, Definition 2 means that for two feasible vectors and , there exists another feasible vector, which is one step closer starting from toward , and vice versa. An M♮-convex set has been studied extensively in discrete convex analysis, a branch of discrete mathematics. Recent advances in discrete convex analysis have found many applications in economics (see the survey paper by Murota (2016)). Note that heredity and M♮-convexity are independent properties.
Kojima et al. (2018) show that various real-life distributional constraints can be represented as a hereditary M♮-convex set. The list of applications includes matching markets with regional maximum quotas Kamada and Kojima (2015), individual/regional minimum quotas Fragiadakis et al. (2015); Goto et al. (2017), diversity requirements in school choice Ehlers et al. (2014); Kurata et al. (2017), distance constraints Kojima et al. (2018), and so on. However, M♮-convexity can be easily violated by introducing some additional constraints.
Let us introduce the most basic model where only distributional constraints are colleges’ maximum quotas.
Definition \thetheorem (maximum quotas).
We say a family of vectors is given as colleges’ maximum quotas, when for each college , its maximum quota is given, and iff , holds. We say is given as colleges’ maximum quotas if its induced vectors are given as colleges’ maximum quotas.
If is given as colleges’ maximum quotas, then is a hereditary M♮-convex set, but not vice versa.
With a slight abuse of notation, for two sets of contracts and , we denote if either (i) , , and for some , or (ii) for some that is acceptable for and . Furthermore, we denote if either or . Also, we use notations like or , where is a contract, is a matching, and is a college.
Let us introduce several desirable properties of a matching and a mechanism. We say a mechanism satisfies property A if the mechanism produces a matching that satisfies property A in every possible matching market.
First, we define fairness.
Definition \thetheorem (fairness).
In matching , student has justified envy toward another student if is acceptable for , , , and hold. We say matching is fair if no student has justified envy.
Fairness implies that if student is not assigned to college (although she hopes to be assigned), then prefers all students assigned to it over .
Next, we define a series of properties on students’ welfare (efficiency).
Definition \thetheorem (Pareto efficiency).
Matching is Pareto dominated by another matching if , , and , hold. Feasible matching is Pareto efficient if no other feasible matching Pareto dominates it.
In short, feasible matching is Pareto efficient if there exists no other feasible matching such that all students weakly prefer over , and at least one student strictly prefers over .
Definition \thetheorem (nonwastefulness).
In matching , student claims an empty seat of college if is acceptable for , , and is feasible. We say feasible matching is nonwasteful if no student claims an empty seat.
Intuitively, nonwastefulness means that we cannot improve the matching of one student without affecting other students.
When additional distributional constraints (besides colleges’ maximum quotas) are imposed, fairness and nonwastefulness become incompatible in general. One way to address the incompatibility is weakening the requirement of nonwastefulness. Aziz et al. (2022a) introduce a weaker efficiency concept called cut-off nonwastefulness.
Definition \thetheorem (cut-off nonwastefulness).
Feasible matching is cut-off nonwasteful if student claims an empty seat of college , then there exists another student such that , , and is infeasible.
Intuitively, we consider the claim of student to move her to college from her current match is not considered legitimate if by doing so, another student would have justified envy toward . Aziz et al. (2022a) show that a fair and cut-off nonwasteful matching always exists under hereditary constraints. This result carries over to less general hereditary and M♮-convex set constraints, as well as weaker efficiency requirements described below. Note that the existence of a fair and cut-off nonwasteful matching does not guarantee the existence of a strategyproof mechanism for obtaining it, as shown in Section 4.
Kamada and Kojima (2017) propose another weaker version of the nonwastefulness concept, which we refer to as weak nonwastefulness.
Definition \thetheorem (weak nonwastefulness).
In matching , student strongly claims an empty seat of if is acceptable for , , and is feasible. We say feasible matching is weakly nonwasteful if no student strongly claims an empty seat.
Student can strongly claim an empty seat of only when , i.e., the matching obtained by adding her to college (without removing her from her current college), is feasible.
Let us define two more weaker efficiency properties.
Definition \thetheorem (no vacant college).
We say feasible matching satisfies no vacant college property if student claims an empty seat of college , then or holds.
Intuitively, no vacant college property means that the claim of student to move her to college from her current match is considered legitimate only when is not matched to any college and no student is assigned to .
Definition \thetheorem (no empty matching).
In matching , student very strongly claims an empty seat of college , when , , , and is feasible. Feasible matching satisfies no empty matching property if no student very strongly claims an empty seat of any college.
Note that this series of efficiency properties becomes monotonically weaker in this order as long as distributional constraints are hereditary. More specifically, Pareto efficiency implies nonwastefulness, but not vice versa, nonwastefulness implies cut-off nonwastefulness, but not vice versa, and so on. Pareto efficiency means that we cannot improve the matching of a set of students without hurting other students, while nonwastefulness means that we cannot improve the matching of one student without affecting other students. Thus, Pareto efficiency implies nonwastefulness. If is nonwasteful, no student can claim an empty seat. If is cut-off nonwasteful, a student can claim an empty seat in some cases. Thus, cut-off nonwastefulness is weaker than nonwastefulness. Next, we show that cut-off nonwastefulness implies weak nonwastefulness by showing its contraposition. More specifically, we assume student strongly claims an empty seat of college in . Then, we show that cannot be cut-off nonwasteful. The fact that strongly claims an empty seat of implies that also claims an empty seat of since if is feasible, is also feasible. Assume there exists another student , where and hold. Then, since is feasible, is also feasible. Thus, cannot be cut-off nonwasteful.
Next, we show that weak nonwastefulness implies no vacant college property by showing its contraposition. More specifically, no vacant college property means that the claim of student to move her from the current matching to is considered legitimate only when is not matched to any college and no student is assigned to . Let us assume does not satisfy no vacant college property, i.e., there exists student who claims an empty seat of when and . Then, we show strongly claims an empty seat of in . Since , the fact that is feasible implies that is feasible. Thus, also strongly claims an empty seat of . Finally, we show that no vacant college property implies no empty matching property by showing its contraposition. More specifically, we assume student very strongly claims an empty seat of in matching . Then, we show that does not satisfy no vacant college property. The fact that student very strongly claims an empty seat of implies , , and hold. Thus, does not satisfy no vacant college property.
Next, we introduce strategyproofness.
Definition \thetheorem (strategyproofness).
We say a mechanism is strategyproof if no student ever has any incentive to misreport her preference no matter what the other students report. More specifically, let denote the matching obtained when declares her true preference , and denote the matching obtained when declare something else, then holds.
Here, we consider strategic manipulations only by students. It is well-known that even in the most basic model of one-to-one matching Gale and Shapley (1962), satisfying strategyproofness (as well as basic fairness and efficiency requirements) for both sides is impossible Roth (1982). One rationale for ignoring the college side would be that the preference of a college must be presented in an objective way and cannot be skewed arbitrarily.
3. Existing mechanism
In this section, we briefly introduce existing mechanisms, which are strategyproof for a given class of constraints. First, let us introduce Generalized Deferred Acceptance mechanism (GDA), which works under hereditary M♮-convex set constraints Hatfield and Milgrom (2005). As its name shows, it is a generalized version of the Deferred Acceptance mechanism Gale and Shapley (1962). To define GDA, we first introduce choice functions of students and colleges.
Definition \thetheorem (students’ choice function).
For each student , her choice function specifies her most preferred contract within each , i.e., , where is the most preferred acceptable contract in if one exists, and if no such contract exists. Then, the choice function of all students is defined as .
Definition \thetheorem (colleges’ choice function).
We assume each contract is associated with its unique strictly positive weight . We assume these weights respect each college’s preference , i.e., if , then holds. For , let denote . Then, the choice function of all colleges is defined as .
As long as induces a hereditary M♮-convex set, a unique subset exists that maximizes the above formula. Furthermore, such a subset can be efficiently computed in the following greedy way. Let denote the set of chosen contracts, which is initially . Then, sort in the decreasing order of their weights. Then, choose contract from one by one and add it to , as long as is feasible.
Using and , GDA is defined as Mechanism 1.
Note that we describe the mechanism using terms like ”student offers” to make the description more intuitive. In reality, GDA is a direct-revelation mechanism, where the mechanism first collects the preference of each student, and the mechanism chooses a contract on behalf of each student.
Kojima et al. (2018) show that when induces a hereditary M♮-convex set, GDA is strategyproof, the obtained matching satisfies a property called Hatfield-Milgrom stability (HM-stability), and is the student-optimal matching within all HM-stable matchings (i.e., all students weakly prefer over any other HM-stable matching).
Definition \thetheorem (HM-stability).
Matching is HM-stable if , and there exists no contract , such that and hold.
Intuitively, HM-stability means there exists no contract in that is mutually preferred by students and colleges. Note that HM-stability implies fairness. If student has justified envy in matching , there exists , , s.t. and holds. Then, and hold, i.e., is not HM-stable.
For standard maximum quotas constraints, the only distributional constraints are , i.e., iff for each , holds. Then, is defined as , where is the choice function of each college , which chooses top contracts from based on . When is defined this way, GDA becomes equivalent to the standard DA.
Next, we introduce two mechanisms that work for hereditary constraints. The Serial Dictatorship (SD) mechanism Goto et al. (2017) is parameterized by an exogenous serial order over the students called a master-list. We denote the fact that is placed in a higher/earlier position than student in master-list as . Students are assigned sequentially according to the master-list. In our context with constraints, student is assigned to her most preferred college , where considers her acceptable (i.e., holds) and assigning to does not cause any constraint violation. More specifically, assume the obtained matching for students placed higher than in is . Then, can be assigned to when holds. SD is strategyproof and achieves Pareto efficiency.
The Artificial Cap Deferred Acceptance mechanism (ACDA) is defined as follows. First, we choose one vector s.t. , and there exists no where , i.e., a maximal feasible vector. Note that must be chosen independently from students’ preferences to guarantee strategyproofness. Then, we apply standard DA, where maximum quota for each college is given as . Intuitively, in ACDA, the set of feasible vectors is artificially reduced to a hyper-rectangle, where is feasible iff . ACDA is strategyproof and fair, assuming is chosen independently from students’ preferences.
4. Existence of fair and strategyproof mechanism
| maximum | hereditary & | hereditary | |
| quotas | M♮-convex | ||
| set | |||
| Pareto efficiency | ✖ Roth (1982) | ✖ | ✖ |
| nonwastefulness | ✓ Roth (1985) | ✖ Kamada and Kojima (2017) | ✖ |
| cut-off nonwastefulness | ✓ | ✗ [Thm 4] | ✗ |
| weak nonwastefulness | ✓ | ✓ Kimura et al. (2023) | ✗ Cho et al. (2022) |
| no vacant college | ✓ | ✓ | ✗ [Thm 4] |
| no empty matching | ✓ | ✓ | ✓ [Thm 4] |
In this section, we examine whether a fair and strategyproof mechanism exists under a given class of distributional constraints in conjunction with some efficiency property. The classes of constraints we consider are: maximum quotas constraints, hereditary and M♮-convex set constraints, and hereditary constraints.
First, we list known results.
-
•
For maximum quotas constraints, fairness, nonwastefulness, and strategyproofness are compatible, i.e., the standard DA satisfies these properties Roth (1985). On the other hand, fairness and Pareto efficiency are incompatible, i.e., even without strategyproofness, a matching that satisfies Pareto efficiency and fairness may not exist Roth (1982).
- •
-
•
For hereditary constraints, fairness, weak nonwastefulness, and strategyproofness are incompatible Cho et al. (2022)
Given these known results, the remaining open questions are as follows.
-
(1)
Under hereditary and M♮-convex set constraints, does a strategyproof, fair, and cut-off nonwasteful mechanism exist?
-
(2)
Under hereditary constraints, can a strategyproof and fair mechanism satisfy any property weaker than weak nonwastefulness?
For question (1), we obtain a negative answer, as shown in Theorem 4. For question (2), we obtain a stronger result than Cho et al. (2022), i.e., Theorem 4 shows that no mechanism simultaneously satisfies strategyproofness, fairness, and no vacant college property. Then, we show a simple mechanism that satisfies strategyproofness, fairness, and no empty matching property (Theorem 4). In summary, we obtain tight boundaries (at least in the granularity of efficiency properties we consider in this paper) on whether a strategyproof and fair mechanism can satisfy certain efficiency properties for each class of constraints (Table 1).
No mechanism can simultaneously satisfy fairness, strategyproofness, and cut-off nonwastefulness under hereditary M♮-convex set constraints.
(Theorem 4)
| preference | possible | ||
|---|---|---|---|
| profile | matchings | ||
| [] | |||
| [] | |||
| ], [] |
Proof.
Consider a matching market with two students and two colleges . The colleges’ preference profile are as follows:
To make the description concise, we denote a preference of students by a sequence of acceptable colleges. For example, we denote as , and as . Furthermore, we denote a matching as a pair of colleges assigned to and . For example, we denote matching as .
Suppose if and only if for some . This setting reflects the situation where the regional quotas constraints are imposed, which form M♮-convex set constraints.
Assume, for the sake of contradiction, that there exists a fair, strategyproof, and cut-off nonwasteful mechanism. We examine three students’ preference profiles: , and . These preference profiles and possible matchings that satisfy fairness and cut-off nonwastefulness are summarized in Table 2. First, for , due to fairness, we cannot allocate to . Also, due to cut-off nonwastefulness, we cannot allocate to . Then, the mechanism must choose .
Next, for , due to fairness, we cannot allocate to . Also, due to cut-off nonwastefulness, we cannot allocate to . Then, the mechanism must choose .
Finally, for , due to cut-off nonwastefulness and distributional constraints, exactly one student must be assigned to her acceptable college. Thus, there exist two possible matchings: (a) or (b) . If (a) is chosen, then has an incentive to manipulate (to modify the profile to ) so that she is assigned to . If (b) is chosen, then has an incentive to manipulate (to modify the profile to ) so that she is assigned to . This fact violates our assumption that the mechanism is strategyproof. ∎
No mechanism can simultaneously satisfy fairness, strategyproofness, and no vacant college property under hereditary constraints.
(Theorem 4)
| preference | possible | ||
|---|---|---|---|
| profile | matchings | ||
| [] | |||
| [], [] | |||
| [], [] | |||
| [], [] | |||
| [], [] | |||
| [], [] | |||
| [] |
Proof.
Consider a matching market with two students and four colleges . The colleges’ preferences are as follows:
Suppose if and only if for some .
Assume, for the sake of contradiction, that there exists a mechanism that is fair, strategyproof, and satisfies no vacant college property.
Here, we examine seven possible students’ profiles described in Table 3. For each students’ profile, we also enumerate all matchings that are fair and satisfy no vacant college property. For , due to no vacant college property, both students must be assigned to their first choice colleges. Thus, the only possible matching is . For , another matching, [] is also possible. However, if the mechanism chooses [], student has an incentive to manipulate (to modify the profile to ) so that she is assigned to . Thus, the mechanism must choose . For , both students consider and acceptable. Due to fairness, only can be assigned to , and only can be assigned to . Also, if we assign to , due to no vacant college property, we need to assign to , However, this violates fairness. Thus, possible matchings are either [] or []. However, if the mechanism chooses [], student has an incentive to manipulate (to modify the profile to ) so that she is assigned to . Continuing a similar argument, we obtain that the mechanism must choose the matching colored in blue in Table 3. In particular, for , the mechanism must choose []. For , the only matching that satisfies no vacant college property is []. This implies that when the profile is , student has an incentive to manipulate (to modify the profile to ) so that she is assigned to . This violates our assumption that the mechanism is strategyproof. ∎
Next, we show that there exists a mechanism that satisfies fairness, strategyproofness, and no empty matching property under hereditary constraints. This mechanism utilizes GDA. More specifically, for given , which is hereditary, we construct a set of vectors such that , holds (i.e., is a subset of vectors induced by ), and is a hereditary M♮-convex set. Then, we apply GDA by using (where iff ) instead of . is constructed as follows. We initialize . Then, for each , if , we add to . Clearly, is an M♮-convex set; it contains only and ().
Under hereditary constraints, GDA using is fair, strategyproof, and satisfies no empty matching property.
Proof.
For the obtained matching by GDA, holds. Then, by way of constructing , holds, i.e., is feasible. Since induces a hereditary M♮-convex set, GDA is strategyproof and fair Kojima et al. (2018). Also, as long as there exists such that and hold, holds. This is because if , then and hold, which violates the fact that GDA obtains an HM-stable matching. ∎
5. New fairness concept: Envy-Free up to peers (EF-)
In this section, we introduce a weaker fairness concept called envy-free up to peers (EF-). For matching and student , let denote .
Definition \thetheorem (Envy-free up to peers).
Matching is envy-free up to peers (EF-) if , holds.
EF- is equivalent to fairness. Any matching is EF-, where .
There are other ways to relax fairness than EF-. One straightforward way is to minimize the total number of justified envies. However, this criterion can be unfair among students, e.g., one student has many envies while others have only a few. Our definition of EF- is more egalitarian; it minimizes the envies of the worst student. Other egalitarian criteria are also possible. For example, instead of counting the number of students to whom each student has envy, we can count the colleges at which each student has envy. Also, we can count the number of students by whom each student is envied. Which concept is socially acceptable is difficult to tell. This work is a first step that brings up new research directions in two-sided matching, i.e., how to relax the fairness concept in a socially acceptable way.
We use the following example to show that nonwastefulness and EF- are incompatible for any under hereditary M♮-convex set constraints.
Example \thetheorem
There are students and colleges. For each student , her preference is: . For each college , its preference is: . In short, for each student , her most preferred college considers her as the least preferred student, and her least preferred college considers her as the most preferred student. Distributional constraints is defined as: iff , and hold, i.e., each college can accept at most one student, and the total number of students accepted to all colleges is at most . Clearly, induces a hereditary M♮-convex set.
Under hereditary M♮-convex set constraints, there exists a case that no matching is nonwasteful and EF- for any .
Proof.
Consider the setting in Example 5. The total number of accepted students is at most . Also, due to nonwastefulness, exactly one student is unassigned to any college. By symmetry, without loss of generality, let us assume is unassigned. Then, there exists exactly one vacant college, i.e., a college to which no student is assigned. The vacant college must be , since if () is vacant, student claims an empty seat of . Also, must be assigned to . Otherwise, she is assigned to where ; she claims an empty seat of . Then, must be assigned to . Otherwise, she is assigned to where ; she claims an empty seat of . By repeating a similar argument, we obtain that each student () is assigned to her most preferred college . Then, has justified envy toward . Thus, holds. ∎
Given Theorem 5, a natural question is the complexity of checking the existence of a nonwasteful and EF- matching (for ). Let us assume can be computed in a constant time. To examine this complexity, we utilize the following lemma.
Lemma \thetheorem
Checking whether a fair and nonwasteful matching exists or not is NP-complete, even when distributional constraints form a hereditary M♮-convex set.
Proof.
Aziz et al. (2022a) show that checking the existence of a strongly stable matching is NP-complete for REG constraints. Strong stability is equivalent to fairness and nonwastefulness. REG constraints mean regional maximum quotas for mutually disjoint regions, which is a special case of hereditary M♮-convex set constraints. Thus, this complexity result carries over to hereditary M♮-convex constraints, which is more general than REG. ∎
Checking whether an EF- () and nonwasteful matching exists or not is NP-complete, even when distributional constraints form a hereditary M♮-convex set.
Proof.
First, for given matching , we can check whether is EF- and nonwasteful in polynomial time, so the problem is in NP. Next, we show a reduction from the problem of checking whether a fair and nonwasteful matching exists or not. Consider an original matching problem instance , where distributional constraints form a hereditary M♮-convex set. We create an instance of an extended market as follows.
-
•
For each college in , we create a corresponding college in . Let denote the set of these colleges in . The distributional constraints over are the same as the original instance .
-
•
For each student in , we create students , as well as additional colleges . These additional colleges for form a region with regional maximum quota . Each student in is a copy of student in the original instance .
-
•
The preference of additional college is defined in the same way as Example 5. More specifically, each additional college can accept only corresponding (copied) students , and most prefers and least prefers .
-
•
Each student prefers any of its additional colleges over any original college. The order of original colleges is the same as the original instance . The order of her additional colleges is defined in the same way as Example 5, i.e., most prefers .
-
•
The preference of each college is defined as follows. If holds in the original instance, holds for any . The preference over , i.e., the copied students of the same original student, can be decided arbitrarily.
We can observe the following facts. Matching in the extended instance is nonwasteful only when for each and copied students , exactly students are assigned to their additional colleges . Also, these students must be assigned to their first-choice colleges. Thus, the only student who is not assigned to her additional colleges has justified envy toward other copied students. Let denote the set of students who are not assigned to their additional colleges. will be assigned to . Assume is EF- and nonwasteful, then the matching between and within must be nonwasteful and fair; otherwise, at least one student in has justified envy toward more than students or is wasteful for the original instance (to obtain a matching in the original instance from , we replacing to and to ). Also, if there exists a fair and nonwasteful matching in the original instance , then there exists an EF- and nonwasteful matching in ; the assignment of is the same as , and the rest of the students are assigned to their favorite additional colleges. ∎
6. New mechanisms
In this section, we introduce two contrasting strategyproof mechanisms that work for general hereditary constraints. The first one (called SD∗) satisfies the strongest efficiency property, i.e., Pareto efficiency, while it cannot guarantee EF- for any fixed . The second one (called SDA with reserved quotas) satisfies EF- for any fixed , while it can only guarantee a rather weak efficiency property. In the next section, we experimentally show that SD∗ can guarantee EF- where is much smaller than when colleges’ preferences are similar. Furthermore, we experimentally show that SDA with reserved quotas can significantly improve students’ welfare compared to a fair (EF-) mechanism even when is very small.
6.1. Pareto efficient mechanism
First, we develop a strategyproof and Pareto efficient mechanism based on SD. For master-list , a pair of students , and college , we say disagrees with for if and holds. Otherwise, we say agrees with for . In short, disagrees with for , when is ranked higher than in , both and are acceptable for college , and prefers over . Assume we use SD based on . Then, in obtained matching , if disagrees with for , has a chance to have justified envy toward in , since is chosen before and can be allocated to , while might not be allocated to . On the other hand, if agrees with for , then never has justified envy toward in . This is because, the fact that agrees with for means: (i) is ranked higher than in , (ii) is ranked lower than in , or (iii) either or is unacceptable for . In each of the above three cases, cannot have justified envy toward in .
Let denote , i.e., counts the number of students such that for some college , a disagreement related to occurs.
The following theorem holds. {theorem} Assume for master-list , , holds. Then, SD using is EF-.
Proof.
Assume, for the sake of contradiction, that in obtained matching , there exists student with . Then, for each , we have (i) , and (ii) for , . Thus, disagrees for . This is true for each . Then, holds, a contradiction. ∎
Theorem 6.1 means that if we can choose a good master-list , such that is small, e.g. at most , the obtained matching is guaranteed to be EF-. Note that this guarantee holds independently from the actual distributional constraints and students’ preferences; can be computed using colleges’ preference profile only. Thus, for given students’ preference , the obtained matching can be EF- for that is much smaller than guaranteed by Theorem 6.1; see the experimental results that clarify this in the next section.
Let us examine the problem of finding an optimal master-list (in terms of minimizing ) for given colleges’ preference profile . {theorem} For given colleges’ preference profile , computing master-list , which minimizes can be done in polynomial time.
Proof.
Let us first introduce a graphical representation of the above optimization problem. Consider a directed graph , where each student is a vertex. For a pair of students and , if there exists college s.t. holds, we add a directed edge . This means that to make agree with the obtained master-list for , the master-list must rank higher than . Then, for and master-list , is equal to the number of outgoing edges from toward any of higher-ranked students than in . For , let denote the set of outgoing edges from . Clearly, for any , holds. Also, holds when is ranked lowest in . This implies holds, i.e., the optimal cannot be smaller than . This is because some student must be ranked lowest in , and holds. Then, when choosing the student who should be ranked lowest in , we can safely choose with the smallest to guarantee ’s optimality. Thus, the following greedy algorithm obtains an optimal master-list (as well as ).
-
(1)
For given graph (where ), set , and to an empty list.
-
(2)
If , return and .
-
(3)
Choose . Add to the top of . . Remove and all edges related to from . Go to (2).
Clearly, the complexity of this greedy algorithm is . ∎
Let us call SD mechanism using optimal as SD∗. SD∗ is strategyproof and Pareto efficient. When we apply SD∗ to the matching instance presented in Example 5, the above algorithm returns with and the obtained matching cannot be EF- for any . In the next section, we show that SD∗ can be EF- for smaller when colleges’ preferences are similar.
Let us examine situations where SD∗ can be used in practice. Assume there exists an authority who decides a matching based on colleges’/students’ preferences. The authority is allowed to override colleges’ preferences to some extent in order to improve students’ welfare. More specifically, the authority can use its own ordering among students to decide the matching, where the ordering is chosen such that it is as close as possible to colleges’ preferences. Our SD∗ is based on this idea, which uses ordering that minimizes . The obtained matching is guaranteed to be EF-. There can be alternative minimization criteria for choosing , e.g., minimizing the sum of Kendall tau distances (the number of pairwise disagreements). However, this optimization problem is computationally hard Bartholdi et al. (1989) and can be unfair among students.
6.2. EF- mechanism
Next, we develop a strategyproof and EF- mechanism for any given . First, let us define the standard Sample and Deferred Acceptance (SDA) mechanism. This mechanism is developed by Liu et al. (2023) for a special case for hereditary constraints where the maximum quota of each college is determined by allocating indivisible resources to each college. The basic idea of SDA is to combine SD and ACDA. One major limitation of ACDA is that we need to determine the maximal feasible vector (which determines the maximum quota of each college) independently from students’ preferences. As a result, the maximum quotas of popular colleges can be low, while those of unpopular colleges can be high. In the standard SDA, first, we choose a subset of students , where . We call sampled students, and regular students. We assign sampled students using SD. Assume the obtained matching for sampled students is . Then, we choose a maximal feasible vector based on the preferences of sampled students. Liu et al. (2023) present several alternative ways to choose . In this paper, as described later, we apply a simulation-based method using copies of sampled students, which is shown to be most effective in Liu et al. (2023). Then, we apply ACDA for regular students, where maximum quota for each college is given as .
The standard SDA is strategyproof. It is also EF-, since for each sampled student , she has justified envy only toward another sampled student assigned before her. Thus, holds. Also, since DA is fair, for regular student , she has justified envy only toward sampled students. Thus, holds.
However, if the preferences of sampled students are completely different from the preferences of regular students, obtained can be bad for regular students. As a result, even no vacant college property is not satisfied. We can assume SDA satisfies no empty matching property. No empty matching property is violated only in an exceptional case where all sampled students assume all colleges unacceptable. In such a case, we can choose additional sampled students until at least one student is assigned to some college.
We propose a generalized version of SDA, such that no vacant college property is satisfied under a mild assumption. The basic idea is that, since there exists a chance that the preferences of sampled students are completely different from those of regular students, we reserve some seats for each college even if the college seems unpopular based on the preferences of sampled students. Let be reserved quotas, where for each , and holds. The goal of the reserved quotas is to guarantee that each college is guaranteed to accept at least students, as long as enough students hope to be assigned to , even if seems unpopular among sampled students.
For two -element vectors and , let denote the element-wise maximum, i.e., .
First, let us define SD with reserved quotas . As standard SD, we assign students sequentially based on master-list . Let denote the assignment obtained so far. The current student can be assigned to , as long as holds. In short, the current student can be assigned to , if can still accept one more student, assuming each college will be assigned at least students.
Then, SDA with reserved quotas is defined as follows. Choose sampled students (the remaining students are regular students). They are assigned by SD with reserved quotas . Let denote the matching for sampled students. Then, obtain a matching , by further assigning multiple virtual students, each of which is a copy of sampled students by SD with reserved quotas, until no more student can be assigned. More specifically, let us assume sampled students are . We create virtual students , which are copies of each sampled student . Then, after sampled students are assigned. We assign these virtual students in a round-robin order, i.e., . Note that this procedure is just for choosing appropriate ; in reality, these virtual students are not allocated to any college. Then, we choose maximal feasible vector such that holds. For each college , we set its maximum quota as , and run ACDA for regular students.
Assume for , holds, and , such that holds, also holds. Then, SDA with reserved quotas and -sampled students is strategyproof, EF-, and satisfies no vacant college property.
Proof.
It is clear even after the above modifications, SDA with reserved quotas is still strategyproof and EF-.
We show that it also satisfies no vacant college property. Assume, for the sake of contradiction, that obtained matching does not satisfy no vacant college property, i.e., student strongly claims an empty seat of , while and . Since is obtained by SDA with reserved quotas , holds. Also, and holds. However, this fact means that if applies to , she must be accepted to (either in SD with reserved quotas or ACDA). This violates the fact that . ∎
Let us examine situations where SDA can be used in practice. Assume there exist distinguished students, e.g., they have excellent achievements in sports / volunteer works, etc., they are from financially difficult families / minority groups, or even chosen by lottery. If giving them priority in college administration is socially acceptable, we can use these distinguished students as sampled students in SDA. Then, the outcome is guaranteed to be EF-.
7. Experimental Evaluation
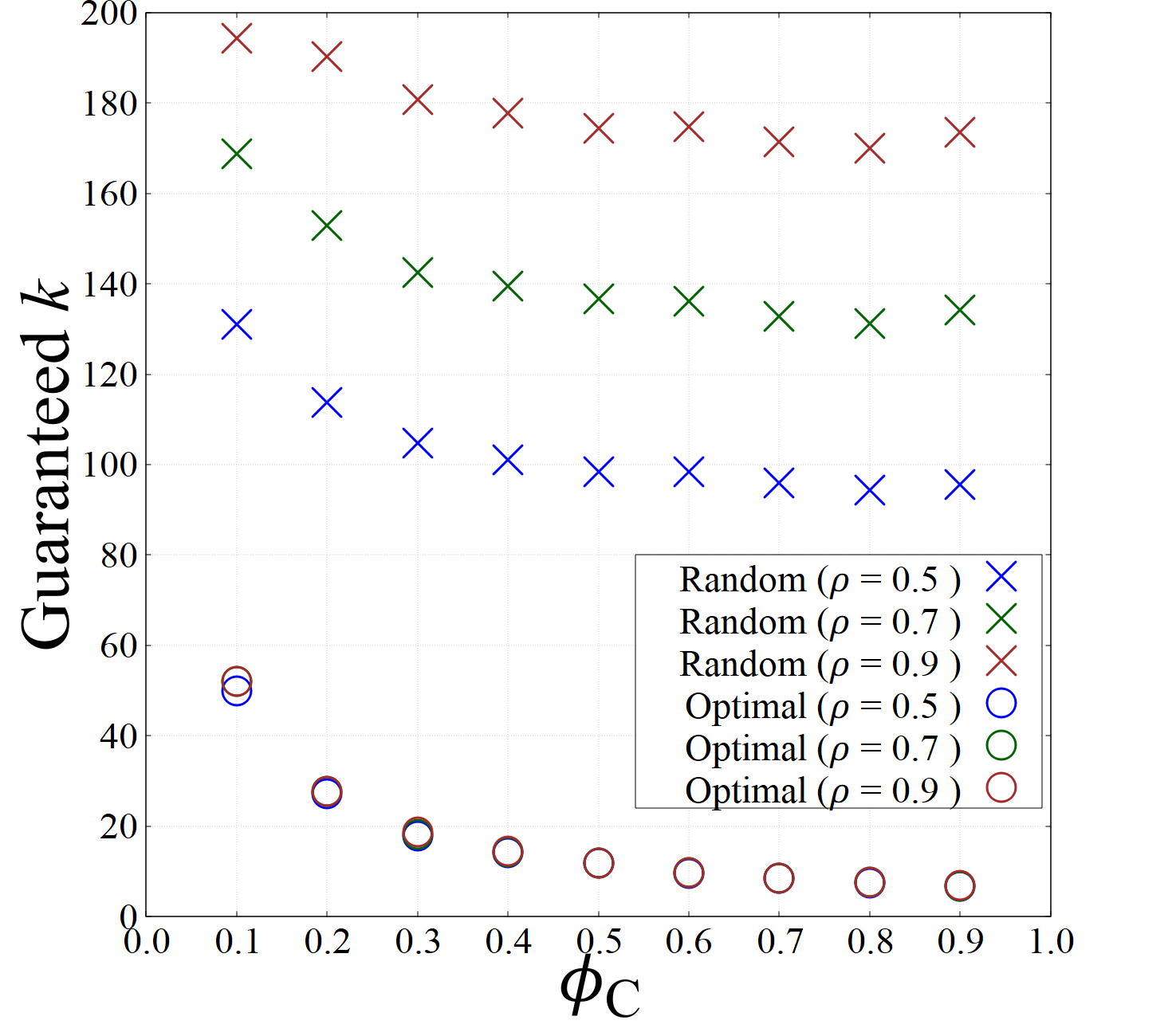
First, we show the level of that SD∗ can be guaranteed by using an optimal master-list. We set the number of students to 200 and the number of colleges to 20. We generate the preference of each college using the Mallows model Drummond and Boutilier (2013); Lu and Boutilier (2014); Mallows (1957); college preference is drawn with probability: Here denotes the spread parameter for colleges, is a central preference uniformly randomly chosen from all possible preferences, and represents the Kendall tau distance, which is the number of pairwise inversions between and . Intuitively, colleges’ preferences are distributed around a central preference with spread parameter . When , the Mallows model becomes identical to the uniform distribution, while increasing leads to convergence towards a constant distribution, yielding . Initially, each does not include . We insert at the position (where ).
Figure 3 shows the guaranteed when using an optimal master-list by varying the spread parameter and . Each data point is an average of 10 instances. We also show the result when the master-list is randomly chosen. We can see that when the spread parameter becomes larger (colleges’ preferences become more similar), SD∗ can guarantee EF- for smaller . For example, becomes less than 5% of when is 0.6. We can see has almost no effect on SD∗, while it significantly affects randomly selected master-lists.
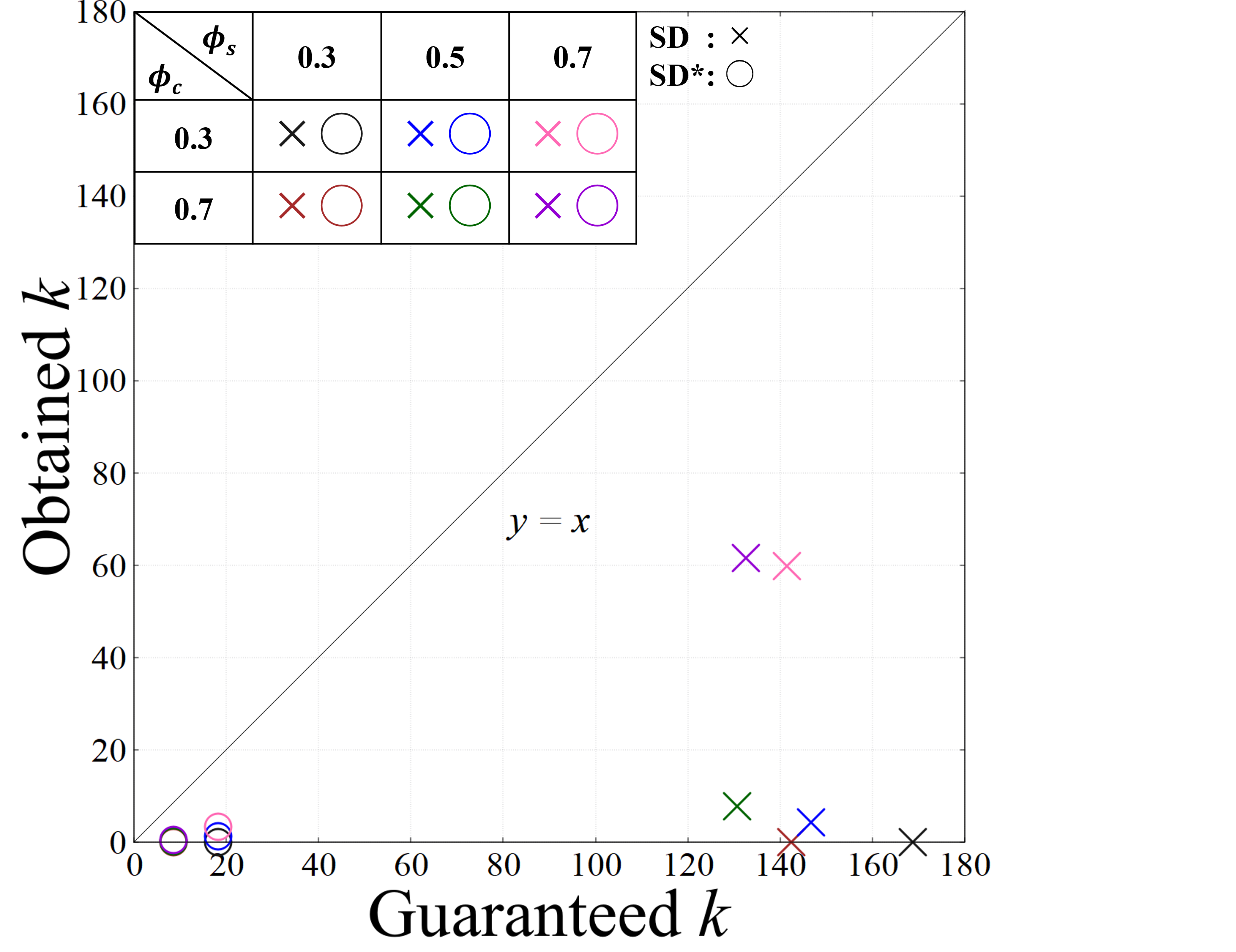
Next, we apply SD∗ to each matching market and measure the obtained level of that SD∗ achieves. We consider the following distributional constraints Liu et al. (2023). There exists a set of indivisible resources . Each resource has its capacity . For each resource , its college compatibility list is defined; resource can be allocated to exactly one college in . Mapping denotes one possible allocation of resources to colleges, i.e., maps each resource to a college . For given allocation , the maximum quota of college is given as , i.e., the maximum quota of each college is endogenously determined as the sum of the capacities of allocated resources. We assume if there exists s.t. holds for all . Each market has resources. For each resource , we generate such that each college is included in with probability . There are 40, 20, and 40 resources with capacity 1, 2, and 3, respectively; thus the total capacity of colleges is equal to . We generate each student’s preference in a similar way as a college’s preference, i.e., we utilize the Mallows model with spread parameter . We do not apply for students; each student considers all colleges acceptable.
Figure 3 shows the average of 10 instances. The -axis shows the guaranteed and the -axis shows the actually obtained . We set colleges’ spread parameter to and , and students’ spread parameter to , , and . is set to 0.7. By definition, each data point must be located in the lower-right half. The result shows the actually obtained is much smaller than the guaranteed . In particular, for SD∗, it is between 0 and 4. For SD, we can see that when becomes larger, the competition among students becomes more intense. As a result, more students tend to have justified envy.
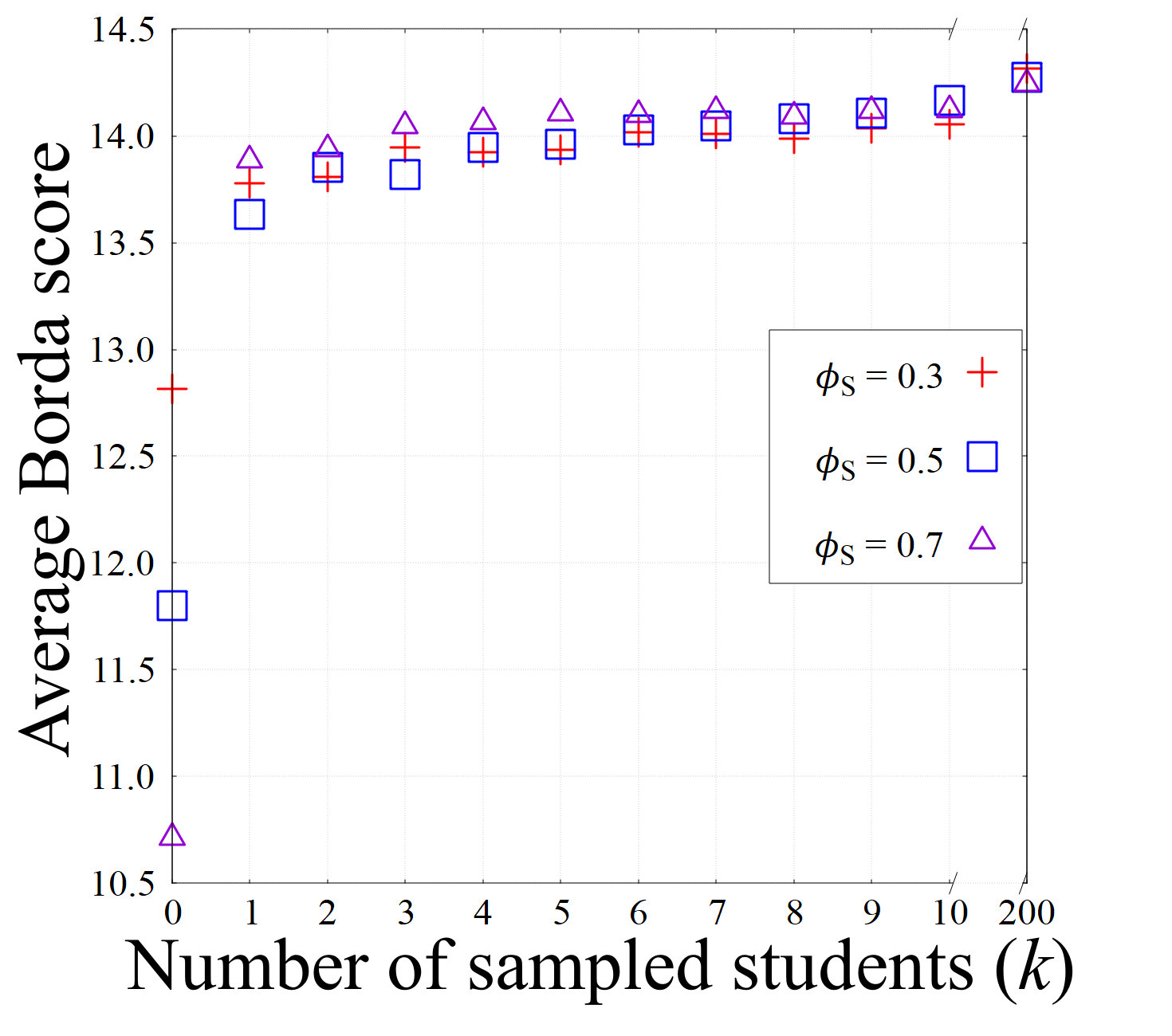
Next, we evaluate SDA with reserved quotas. By varying , it can be identical to ACDA (when ) and SD∗ (when ), assuming we use the same master-list as SD∗ and the same reserved quotas. Figure 3 shows the average Borda score of the students varying and the students’ spread parameter . If a student is assigned to her -th choice college, her Borda score is . We fix the colleges’ spread parameter to 0.7 and to 0.7. We set reserved quotas to . Each data point represents an average of 10 instances. In this setting, SDA with sampled students (which is identical to SD∗) guarantees EF- for in average. The average Borda score significantly improves as increases from the case where . Note that increasing the average Borda score by one is significant; each student must be assigned to a strictly better college. The difference between (where SDA is identical to ACDA) and becomes larger when becomes larger, i.e., when students’ preferences are similar. We can see that SDA achieves a high degree of fairness and efficiency with a few sampled students.
In summary, SD∗ is much fairer than SD with a randomly selected master-list, and can attain EF- for that is much smaller than guaranteed by Theorem 6.1. Also, SDA with reserved quotas is much more efficient than ACDA, and attains very good fairness at the expense of a little efficiency compared to SD*.
8. Conclusions and future works
When distributional constraints are imposed in two-sided matching, there exists a trade-off between fairness and efficiency. We clarified the tight boundaries on whether a strategyproof and fair mechanism can satisfy certain efficiency properties for each class of constraints. We also established a new fairness requirement called EF-. We examined theoretical properties related to EF-, and developed two contrasting strategyproof mechanisms that work for general hereditary constraints. We evaluated the performance of these mechanisms via computer simulation. We believe EF- is significant since it brings up many new research topics in constrained matching literature; there remain many open questions related to EF-. For example, can any strategyproof mechanism guarantee EF- for some fixed in conjunction with some efficiency property (which is stronger than no vacant college property, e.g., weak nonwastefulness)? Furthermore, there exists another mechanism called Adaptive DA Goto et al. (2017) that works for any hereditary constraints. Comparing this mechanism with our newly proposed mechanisms is our immediate future work.
We would like to thank anonymous reviewers for their valuable comments. This work was partially supported by JST ERATO Grant Number JPMJER2301, and JSPS KAKENHI Grant Numbers JP21H04979 and JP20H00609, Japan.
References
- (1)
- Aziz et al. (2022a) Haris Aziz, Anton Baychkov, and Peter Biró. 2022a. Cutoff stability under distributional constraints with an application to summer internship matching. Mathematical Programming (2022). https://doi.org/10.1007/s10107-022-01917-1
- Aziz et al. (2022c) Haris Aziz, Péter Biró, Tamás Fleiner, Serge Gaspers, Ronald de Haan, Nicholas Mattei, and Baharak Rastegari. 2022c. Stable matching with uncertain pairwise preferences. Theoretical Computer Science 909 (2022), 1–11. https://doi.org/10.1016/j.tcs.2022.01.028
- Aziz et al. (2022b) Haris Aziz, Peter Biró, and Makoto Yokoo. 2022b. Matching Market Design with Constraints. In Proceedings of the 36th AAAI Conference on Artificial Intelligence (AAAI-2022). 12308–12316. https://doi.org/10.1609/aaai.v36i11.21495
- Aziz et al. (2019) Haris Aziz, Serge Gaspers, Zhaohong Sun, and Toby Walsh. 2019. From Matching with Diversity Constraints to Matching with Regional Quotas. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems (AAMAS-2019). 377–385.
- Bartholdi et al. (1989) J. Bartholdi, C. A. Tovey, and M.A. Trick. 1989. Voting Schemes for which It Can Be Difficult to Tell Who Won the Election. Social Choice and Welfare 6 (1989), 157–165. https://doi.org/10.1007/BF00303169
- Budish (2011) Eric Budish. 2011. The combinatorial assignment problem: Approximate competitive equilibrium from equal incomes. Journal of Political Economy 119, 6 (2011), 1061–1103. https://doi.org/10.1086/664613
- Cho et al. (2022) Sung-Ho Cho, Miyuki Koshimura, Pinaki Mandal, Kentaro Yahiro, and Makoto Yokoo. 2022. Impossibility of weakly stable and strategy-proof mechanism. Economics Letters 217 (2022), 110675. https://doi.org/10.1016/j.econlet.2022.110675
- Drummond and Boutilier (2013) Joanna Drummond and Craig Boutilier. 2013. Elicitation and Approximately Stable Matching with Partial Preferences. In Proceedings of the 23rd International Joint Conference on Artificial Intelligence (IJCAI-2013). 97–105.
- Ehlers et al. (2014) Lars Ehlers, Isa E. Hafalir, M. Bumin Yenmez, and Muhammed A. Yildirim. 2014. School Choice with Controlled Choice Constraints: Hard Bounds versus Soft Bounds. Journal of Economic Theory 153 (2014), 648–683. https://doi.org/10.1016/j.jet.2014.03.004
- Fragiadakis et al. (2015) Daniel Fragiadakis, Atsushi Iwasaki, Peter Troyan, Suguru Ueda, and Makoto Yokoo. 2015. Strategyproof Matching with Minimum Quotas. ACM Transactions on Economics and Computation 4, 1 (2015), 6:1–6:40. https://doi.org/10.1145/2841226
- Gale and Shapley (1962) David Gale and Lloyd Stowell Shapley. 1962. College Admissions and the Stability of Marriage. The American Mathematical Monthly 69, 1 (1962), 9–15. https://doi.org/10.2307/2312726
- Gibbard (1973) Allan Gibbard. 1973. Manipulation of Voting Schemes: A General Result. Econometrica 41, 4 (1973), 587–601. https://doi.org/10.2307/1914083
- Goto et al. (2017) Masahiro Goto, Fuhito Kojima, Ryoji Kurata, Akihisa Tamura, and Makoto Yokoo. 2017. Designing Matching Mechanisms under General Distributional Constraints. American Economic Journal: Microeconomics 9, 2 (2017), 226–262. https://doi.org/10.1257/mic.20160124
- Hatfield and Milgrom (2005) John William Hatfield and Paul R. Milgrom. 2005. Matching with Contracts. American Economic Review 95, 4 (2005), 913–935. https://doi.org/10.1257/0002828054825466
- Hosseini et al. (2015) Hadi Hosseini, Kate Larson, and Robin Cohen. 2015. On Manipulablity of Random Serial Dictatorship in Sequential Matching with Dynamic Preferences. In Proceedings of the 29th AAAI Conference on Artificial Intelligence (AAAI-2015). 4168–4169. https://doi.org/10.1609/aaai.v29i1.9744
- Ismaili et al. (2019) Anisse Ismaili, Naoto Hamada, Yuzhe Zhang, Takamasa Suzuki, and Makoto Yokoo. 2019. Weighted Matching Markets with Budget Constraints. Journal of Artificial Intelligence Research 65 (2019), 393–421. https://doi.org/10.1613/jair.1.11582
- Kamada and Kojima (2015) Yuichiro Kamada and Fuhito Kojima. 2015. Efficient Matching under Distributional Constraints: Theory and Applications. American Economic Review 105, 1 (2015), 67–99. https://doi.org/10.1257/aer.20101552
- Kamada and Kojima (2017) Yuichiro Kamada and Fuhito Kojima. 2017. Stability Concepts in Matching under Distributional Constraints. Journal of Economic Theory 168 (2017), 107–142. https://doi.org/10.1016/j.jet.2016.12.006
- Kawase and Iwasaki (2017) Yasushi Kawase and Atsushi Iwasaki. 2017. Near-Feasible Stable Matchings with Budget Constraints. In Proceedings of the 26th International Joint Conference on Artificial Intelligence (IJCAI-2017). 242–248. https://doi.org/10.24963/ijcai.2017/35
- Kimura et al. (2023) Kei Kimura, Kwei guu Liu, Zhaohong Sun, Kentaro Yahiro, and Makoto Yokoo. 2023. Multi-Stage Generalized Deferred Acceptance Mechanism: Strategyproof Mechanism for Handling General Hereditary Constraints. arXiv: 2309.10968 (2023).
- Kojima et al. (2018) Fuhito Kojima, Akihisa Tamura, and Makoto Yokoo. 2018. Designing matching mechanisms under constraints: An approach from discrete convex analysis. Journal of Economic Theory 176 (2018), 803–833. https://doi.org/10.1016/j.jet.2018.05.004
- Kurata et al. (2017) Ryoji Kurata, Naoto Hamada, Atsushi Iwasaki, and Makoto Yokoo. 2017. Controlled School Choice with Soft Bounds and Overlapping Types. Journal of Artificial Intelligence Research 58 (2017), 153–184. https://doi.org/10.1613/jair.5297
- Liu et al. (2023) Kwei-guu Liu, Kentaro Yahiro, and Makoto Yokoo. 2023. Strategyproof Mechanism for Two-Sided Matching with Resource Allocation. Artificial Intelligence 316 (2023), 103855. https://doi.org/10.1016/j.artint.2023.103855
- Lu and Boutilier (2014) Tyler Lu and Craig Boutilier. 2014. Effective Sampling and Learning for Mallows Models with Pairwise-Preference Data. Journal of Machine Learning Research 15 (2014), 3963–4009.
- Mallows (1957) Colin L Mallows. 1957. Non-null ranking models. I. Biometrika 44, 1-2 (1957), 114–130. https://doi.org/10.2307/2333244
- Murota (2016) Kazuo Murota. 2016. Discrete Convex Analysis: A Tool for Economics and Game Theory. Journal of Mechanism and Institution Design 1 (2016), 151–273. https://doi.org/10.22574/jmid.2016.12.005
- Murota and Shioura (1999) Kazuo Murota and Akiyoshi Shioura. 1999. M-convex Function on Generalized Polymatroid. Mathematics of Operations Research 24, 1 (1999), 95–105. https://doi.org/10.1287/moor.24.1.95
- Roth (1982) Alvin E. Roth. 1982. The Economics of Matching: Stability and Incentives. Mathematics of Operations Research 7, 4 (1982), 617–628. https://doi.org/10.1287/moor.7.4.617
- Roth (1985) Alvin E. Roth. 1985. The College Admissions Problem is not Equivalent to the Marriage Problem. Journal of Economic Theory 36, 2 (1985), 277–288. https://doi.org/10.1016/0022-0531(85)90106-1
- Roth and Sotomayor (1990) Alvin E. Roth and Marilda A. Oliveira Sotomayor. 1990. Two-Sided Matching: A Study in Game-Theoretic Modeling and Analysis (Econometric Society Monographs). Cambridge University Press. https://doi.org/10.1017/CCOL052139015X
- Suzuki et al. (2023) Takamasa Suzuki, Akihisa Tamura, Kentaro Yahiro, Makoto Yokoo, and Yuzhe Zhang. 2023. Strategyproof Allocation Mechanisms with Endowments and M-convex Distributional Constraints. Artificial Intelligence 315 (2023), 103825. https://doi.org/10.1016/j.artint.2022.103825
- Yahiro et al. (2020) Kentaro Yahiro, Yuzhe Zhang, Nathanaël Barrot, and Makoto Yokoo. 2020. Strategyproof and Fair Matching Mechanism for Ratio Constraints. Autonomous Agents and Multi-Agent Systems 34 (2020), 1–29. https://doi.org/10.1007/s10458-020-09448-9