Fano resonances in dielectric, metallic and metamaterial photonic structures
Abstract
We investigate numerically Fano resonances excited in periodic arrays of dielectric, metallic and left-handed cylinders. Of particular interest are Fano resonances excited in the linear array of cylinders. We analyze spatial distribution and symmetry of electromagnetic field and discuss the relation between observed Fano resonances and frequency spectra of two-dimensional arrays of cylinders.
I Introduction
Fano resonance fano originates from the interference of an incident wave with excited eigenmode of the system. When electromagnetic (EM) wave propagates through photonic structure, Fano resonance manifests oneself as a resonance of scattering parameters (transmission or reflection coefficient) when the frequency of incident wave coincides with the resonant frequency of a leaky mode of the structure sfan ; fan ; astratov . Although Fano resonances excited in a linear array of dielectric cylinders has been observed numerically already in 1979 on , their systematic studies is rather new miro ; luk ; poddubny ; rybin-2013 . It has been observed that Fano resonances could strongly influence the EM response of the photonic system and the transmission of EM wave through the system. Even more, by proper design of the photonic system enables us to chose the position of Fano resonances which opens a possibility to construct a new class of dielectric metamaterials rybin-2015 .
Recently, pm-pra we have observed that frequency of Fano resonances excited in the linear array of dielectric cylinders coincides with position of flat frequency bands found in the spectrum of corresponding two-dimensional photonic crystals. Physically this coincidence means that, besides Bragg frequency bands which originate from the spatial periodicity of the permittivity sakoda , the spectrum of photonic crystal contains also another frequency bands in which the propagation of electromagnetic (EM) field is conveyed by subsequent excitation of Fano resonances, from one linear chain to the neighboring one. We call these bands Fano bands. The presence of Fano bands in the spectrum is well-known sakoda ; joan-pc , but their physical origin has not been completely discussed. In metallic photonic structures Fano resonances are associated with surface waves excited at the interface between metallic cylinder and dielectric embedding media. Their excitation is responsible for rather complicated frequency spectrum of two dimensional array of metallic rods ino ; moreno ; kuzmiak . Of special interest are cylinders made form left-handed material pm-oc which combines both properties of dielectrics (they are transparent) and feasibility to excite surface waves ruppin .
In this paper we present typical examples of Fano resonances excited in a systems composed from dielectric, metallic and left-handed cylinders. Numerical method is described in Sect. II. In Sect. III we presents Fano resonances excited in three photonic structures: isolated cylinder, linear array of cylinders and, finally, the photonic slab consisting from a finite number of rows of cylinders made from dielectric, metallic and left-handed material. Conclusion is given in Sect. IV.
II Model and Numerical method
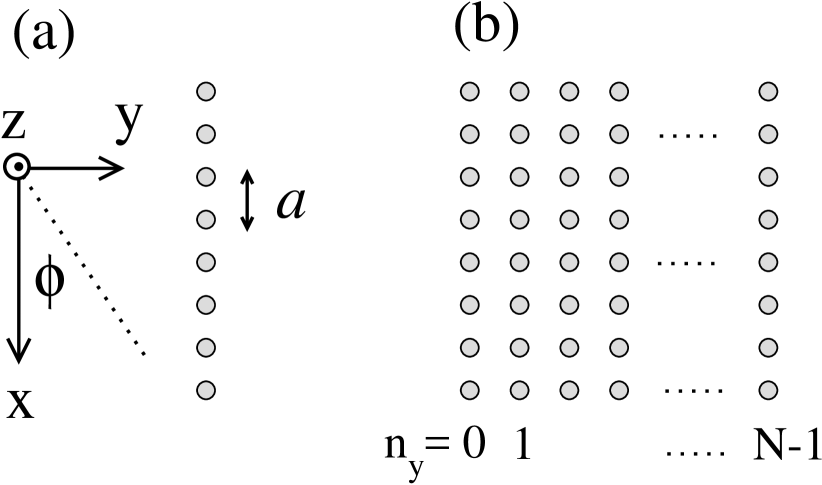
We are interested in photonic structures which consist from homogeneous cylinders made from material with permittivity and permeability embedded in vacuum. Cylinders are parallel with axis and arranged in periodic array in the plane with spatial period . We study a single cylinder, a linear array of cylinders (infinite in the direction) and the system consisting of chains arranged in planes , (Fig. 1). Radius of cylinders is . We calculate scattering parameters (transmission and reflection coefficients) of incident plane wave propagating in the plane with wavelength and dimensionless frequency . The direction of propagation with respect to the axis is defined by the incident angle which is zero when the EM wave propagates in the direction. Similarly to other methods natarov ; asa we expand the EM field inside the structure into the series of cylinder eigenfunctions. For instance, for the polarized wave, the electric field can be express in terms of cylinder functions stratton ; hulst : inside the cylinder centered in ()
| (1) |
and outside this cylinder ()
| (2) |
with
| (3) |
Here are Bessel functions and are Hankel functions of the first kind AS . Note that Hankel functions are normalized by a factor in order to eliminate numerical instabilities caused by very large values of Hankel functions of small arguments. The angle is defined in Fig. 1. The EM field in the vacuum has a wavelength and is the refractive index of material of cylinder.
The field scattered by other cylinders centered at can be expressed in the form of Eqs. (1) and (2) with a new set of coefficients and and cylindrical coordinates and corresponding to the position of each cylinder.
Two components of magentic fields, and , will be calculated from Maxwell’s equations:
| (4) |
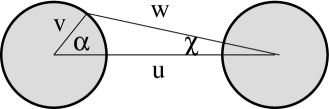
Requirements of continuity of tangential components of electric and magnetic fields at the interfaces of each cylinder give us a system of linear equations for coefficients and . This system can be considerably simplified in three steps: First, we can express all fields associated with various cylinders in terms of variables and associated with the cylinder located at the point , . This can be done with the use of the transformation formula for cylinder functions AS
| (5) |
for and its derivative (See Fig. 2 for definition used symbols).
Second, since the structure is periodic in the direction we use the Bloch theorem
| (6) | |||
| (7) |
to reduce considerably the number of unknown parameters. Third, coefficients could be easily expressed as a linear combination of coefficients . Finally, if is the highest order of the Bessel function used in Eqs. (1) and (2), we end up with linear equations for unknown coefficients (, )
| (8) |
The vector f the right hand side of Eq. (8) defines an incident EM wave.
In numerical simulations, we use typically . Then, in the case of linear array of cylinders, the program solves for each frequency the system of linear equations. For the photonic slab composed from chains, the number of equations increases to 600. The central point of the algorithm is the calculation of elements of the matrix C in Eq. 8. This task requires summation of contributions of field scattered on all cylinders in the structure. Explicit form of matrix C is given elsewhere pm-oc . We consider cylinders along the axis.
The transmission coefficient can be calculated as a ratio of Poynting vectors calculated on the opposite side of the structure to the incident Poynting vector .
III Fano resonances in various photonic structures
Numerical algorithm described in Section II can be used for the calculation of the frequency dependence of the transmission and reflection coefficient of any periodic structure composed from parallel cylinders. For the systems of rows of cylinders, considered in this paper, we expect that, owing to spatial periodicity, the frequency dependence of transmission coefficient would exhibit a series of Bragg transmission bands separated by gaps sakoda ; joan-pc . This idyllic picture is disturbed by excitation of Fano resonances fan ; pm-pra . While the eigenfrequency of Fano resonance is determined by the material parameters and shape of individual cylinder, the position of Bragg band is given by the spatial periodicity of the structure. Two bands of different origin – Bragg and Fano – can therefore overlap. Interference of two bands strongly influences resulting frequency bands observed in the spectrum. For instance, we will see below that Fano resonance can split an original Bragg band into two separated bands. For the qualitative understanding of frequency spectra and identification of the origin of individual frequency bands is useful to calculate the frequency dependence of all parameters and defined in Eqs. (1,2) and determine the order of Fano resonances from their resonant behavior.
We identify resonances excited in three photonic structures. We start with isolated cylinder stratton ; hulst ; pfeifer . The second structure of interest is a linear chain of cylinders. We show that each resonance excited in the cylinder is splitted into two resonances – even and odd – when incident wave scatters on an infinite array of cylinders. The third structure consists from linear rows of cylinders. If resonances observed in the linear chain, do not couple with Bragg transmission bands, they develop into separated transmission bands. Typically, these bands are very narrow (their width is determined by the overlap of fields excited at neighboring cylinders).
III.1 Dielectric cylinders with high permittivity
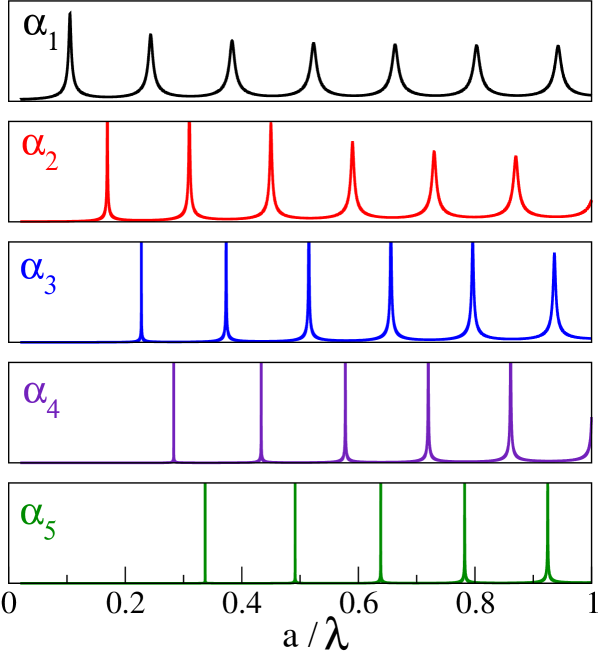
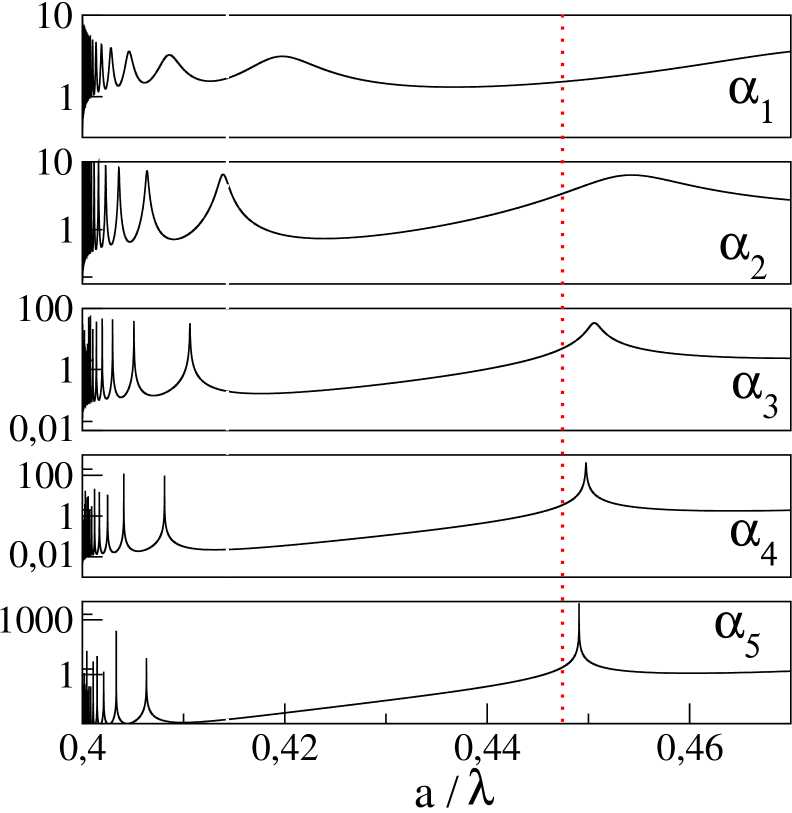
Periodic array of dielectric rods have been analyzed in rybin-2015 . In our work pm-pra we studied the formation of Fano bands and interaction between Bragg and Fano bands. in the array of dielectric cylinders of radius and permittivity and found five Fano bands in the frequency interval . The number of resonances increases when either cylinder radius pm-pra or the permittivity increases. While the increase of the radius is limited by the spatial period of the structure, the permittivity can possess, at least in theoretical model, rather high values. In this paper, we study dielectric cylinders of radius and permittivity . Incident EM wave is polarized with parallel to cylinders. Results are summarized in Figs. 3 and 4.
Left Fig. 3 shows the spectrum of resonances excited on an isolated cylinder. A series of resonances for each coefficient corresponds to oscillation of Bessel function inside the cylinder hulst . Right Fig. 3 shows how Fano resonances influence the transmission coefficient of plane wave propagating through linear chain of dielectric rods. For the sake of simplicity, the incident angle so that only even resonances are excited sak . Besides Fabry-Perot oscillations of transmission coefficient we identify irregularities in transmission when frequency of incident wave coincides with the eigenmode of the structure fan . To demonstrate the creation of Fano transmission bands, we add in panel (d) also the transmission coefficient for the finite photonic slab.
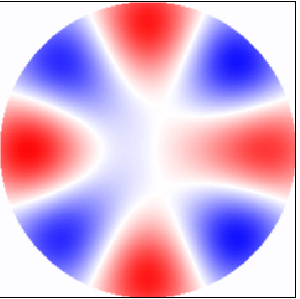
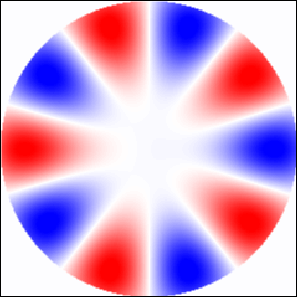
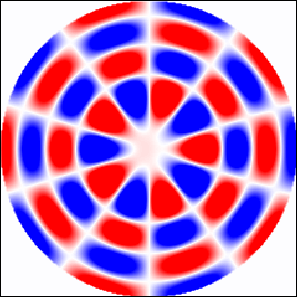
Spatial distribution of electric field for a few selected resonances is shown in Fig 4. The order of resonance is clearly visible, and can be confirmed by the frequency dependence of coefficients and (not shown). Since EM wave propagates along the axis (from the left to the right), all excited resonances are even (). Frequency corresponds to the first resonance of the 4th order. At frequency the second resonance of is excited. Two resonances of the 5th order, excited at frequencies and 0.7815, correspond to the 1st and the 4th resonance of , respectively. (Note that in accordance with notation used in Eq. (1), resonances of and are even, while resonances of and are odd with .)

III.2 Thin metallic rods
Frequency spectrum of periodic arrays of metallic rods have been investigated in ino ; moreno and recently in kuzmiak . It has been shown that Fano resonances could be associated with surface waves excited at the interface between cylinder and embedding media. To observe them, we consider the incident wave polarized with magentic intensity parallel to the cylinders.
We analyze resonant behavior of periodic arrays of thin metallic rods of radius . The permittivity of metal is given by Drude formula with plasma frequency
| (10) |
so that the wavelength corresponding to equals to the spatial periodicity .
Owing to dispersion relation of surface waves economou-surface ; WP , we expect a series of Fano bands in narrow frequency interval below the frequency .
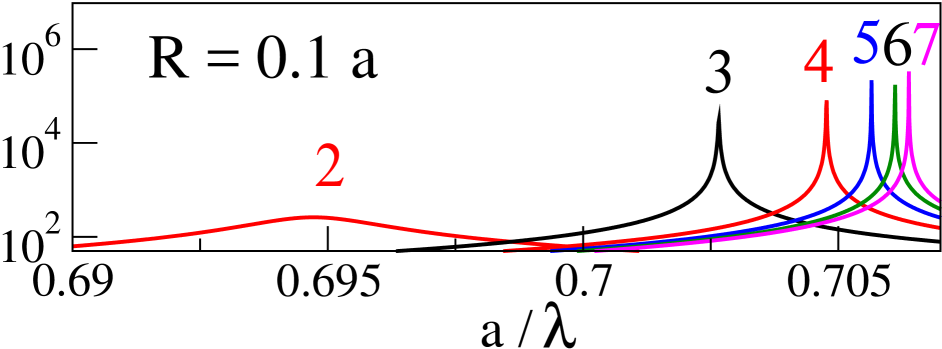
Figure 5 shows the resonances of coefficients for isolated metallic cylinder. Resonant frequencies converge to the limiting value when . This confirms that Fano resonances are associated with an excitation of surface waves. The th resonance is excited when the wavelength of surface wave fulfills the relation . With the use of the dispersion relation for surface waves,
| (11) |
it is easy to verify that observed resonant frequencies are identical with frequencies found from Eq. (11).
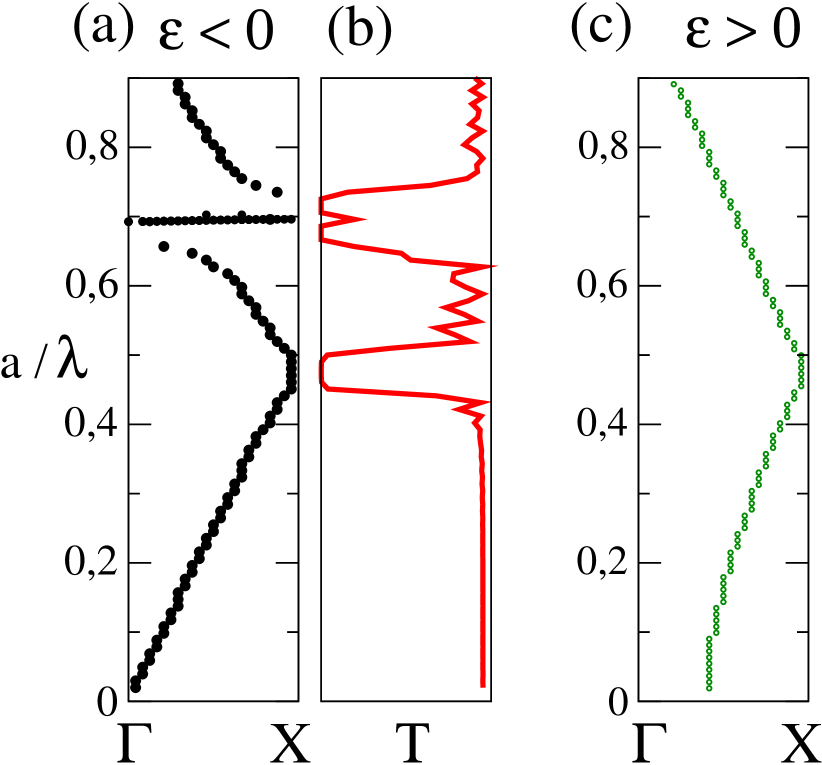
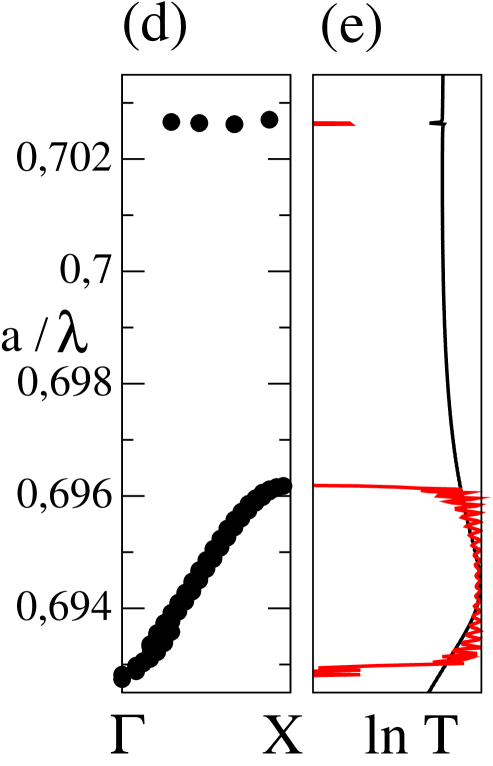
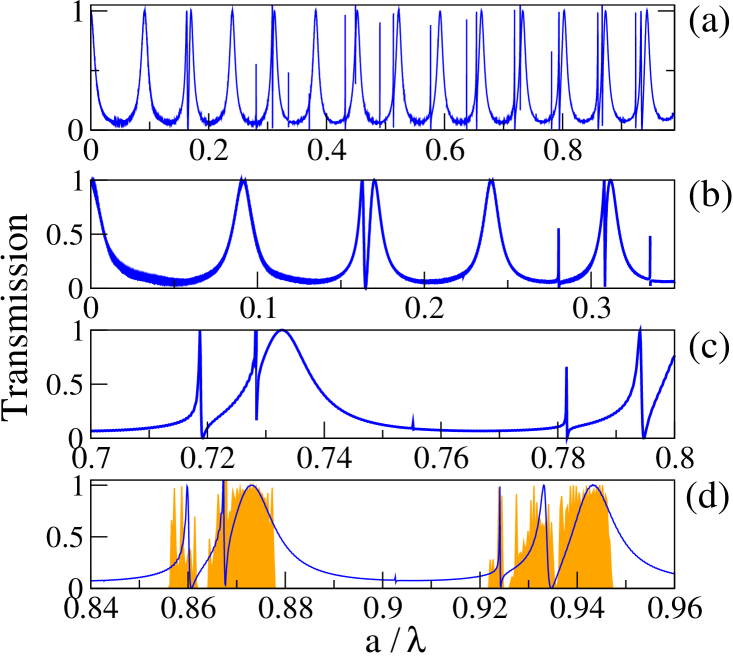
The band spectrum of periodic array of thin metallic cylinders is shown in Fig. 6(a). Since all Fano resonances are concentrated in a narrow frequency interval , it seems, on the eye, that three broad frequency bands shown in Fig. 6(a) are periodic Bragg bands. However, since both the 2nd and the 3rd bands have a minimum in the X point, we suppose that they originate from one Bragg band which is splitted into two bands by Fano resonances, Similar split of Bragg band has been described in dielectric photonic crystal in Ref. pm-pra . To support this conjecture, we shown in Fig. 6(a) the frequency spectrum of periodic array of cylinders with positive dispersive permittivity . Now, since the permittivity is positive, no surface modes could be excited and we indeed observe an unperturbed 2nd band for .
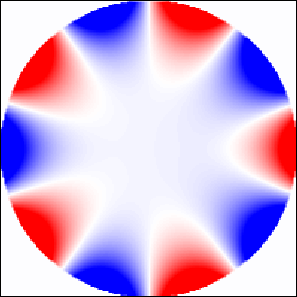
In the gap between two splitted Bragg bands, , we observe a series of very narrow Fano bands. Their frequency can be estimated approximately from resonances shown in Fig. 5. As an example, we show in Figure 6(d) the 2nd Fano band associated with the resonance of coefficient lying in the interval . Very narrow 3rd band is also identified at frequency . The width of higher Fano resonances decreases rapidly. For instance, the width of the 5th Fano bands located at is only . We have no ambition to analyze all these frequency bands numerically, only show in Fig. 7 the distribution of magnetic intensity calculated for the 5th resonance on an array of cylinders. As expected, the field is concentrated along the cylinder surfaces and is small in the center. Higher resonances at thicker metallic cylinders are discussed in kuzmiak .
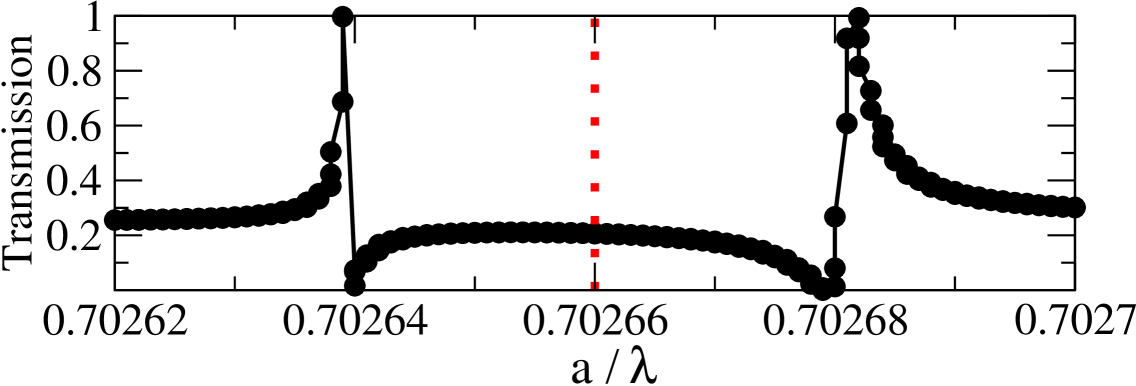


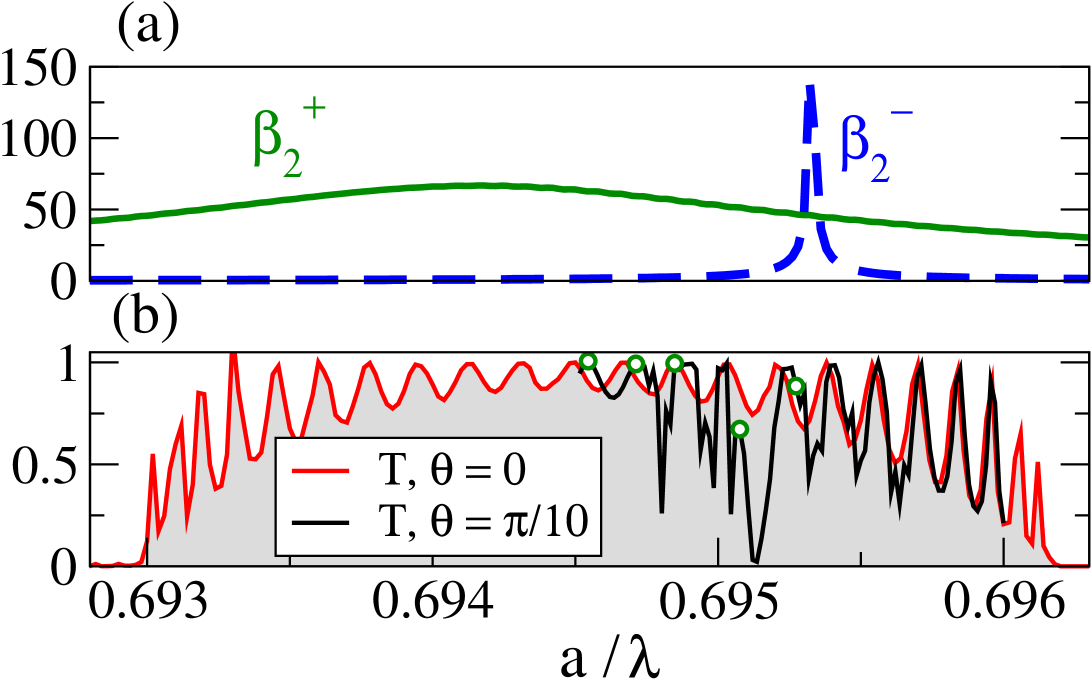



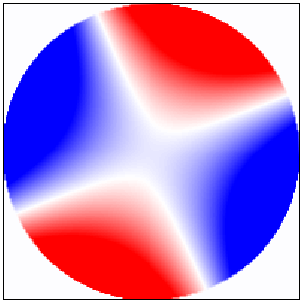

Figure 8 presents the transmission coefficient for the linear chain of cylinders in the vicinity of the third cylinder resonance . Figure confirms that single resonance observed at isolated cylinder splits to even and odd resonances in the linear chain of cylinders. Since each resonance corresponds to Fano band in 2D photonic crystal, we expect that Fano bands in photonic crystals appear always in pairs with even lower bands and odd higher band kuzmiak .
Of particular interest are interference effect caused by overlap of two Fano bands shown in Fig. 9. Since the even 2nd Fano ban is rather broad, it overlaps over narrow odd 2nd band. This can be seen in Fig. 9(a). For zero incident angle, odd resonance does not couple to the incident wave sak and the transmission coefficient exhibits regular frequency dependence typical for transmission band shown in Fig. 9(b). However, for non-zero incident angle, the transmission is influenced by both even and odd resonances. Irregular frequency dependence of the transmission coefficient is typical for interference of two overlapping transmission bands sakoda ; pm-pra . An overlap of two bands is confirmed also by the the change of the symmetry of electric field inside the cylinder when energy passes across the odd Fano band.
III.3 Thick Left-handed cylinders
Finally, we consider periodic array of cylinders made from left-handed material. with frequency dependent permittivity
| (12) |
and permeability
| (13) |
In the frequency interval cylinders behave as a left-handed material with both permittivity and permeability negative. In the analogy with theory of photonic crystals, one would expect that periodic array of such LH cylinders possesses standard band structure. However, negative values of permittivity and permeability allows also excitations of surface wave at the cylinder surface ruppin in a similar way than on metallic rods.
Consider the -polarized incident EM wave, with electric field parallel to the cylinder surface. It excites the TE polarized surface waves at the surface of the cylinder. The wavelength of surface wave is given by relation WP
| (14) |
Since must be real, surface waves can be excited only in frequency intervals and . Therefore, similarly to the case of metallic rods, higher order Fano resonances are concentrated in the narrow frequency region where is small, namely for frequencies where .
Figure 10 shows coefficient for resonances excited at isolated LH cylinder of radius . A series of resonances converging to the frequency can be easily identified. Since when , this series is equivalent to that discussed in ref. pm-oc . The structure of resonances in lower frequency interval reminds resonances on dielectric cylinders shown in Fig. 3. Note that the permeability diverges to negative infinite values when . Interestingly, Fano resonances appear in the reverse order: higher resonances are excited for lower frequency pm-oc .
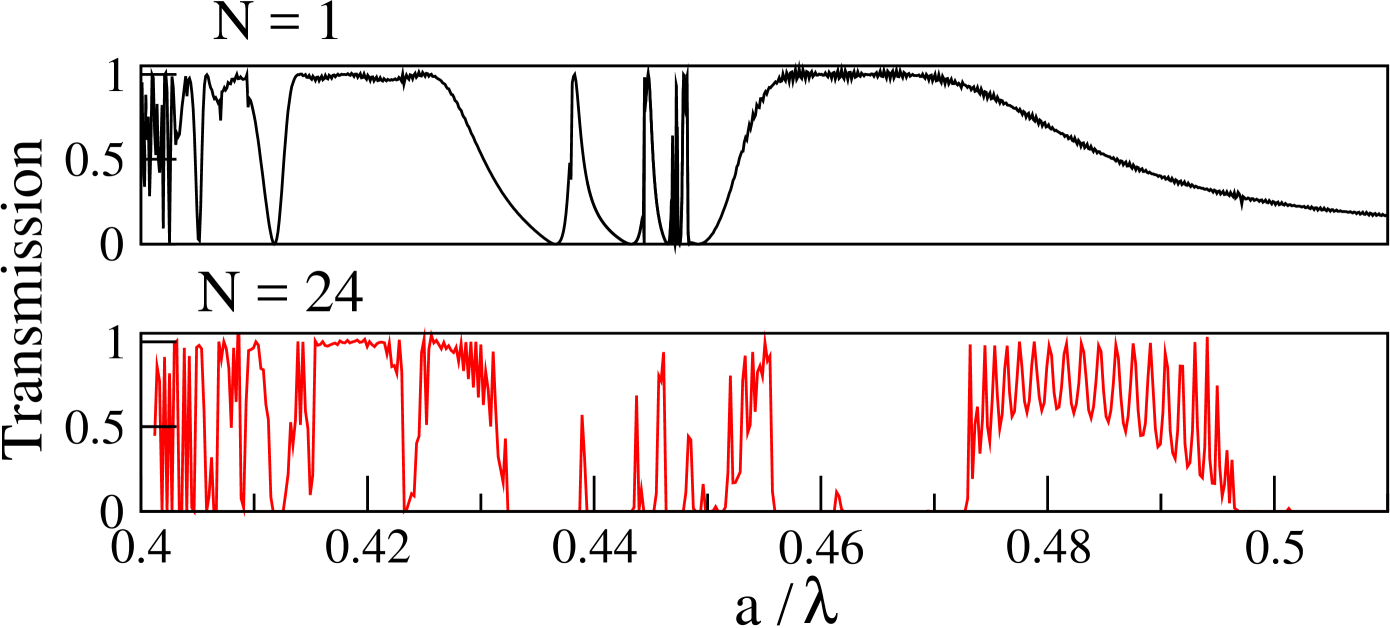
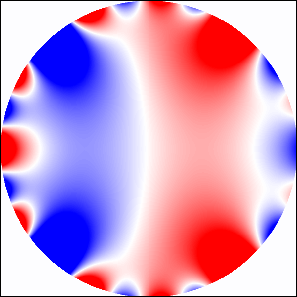
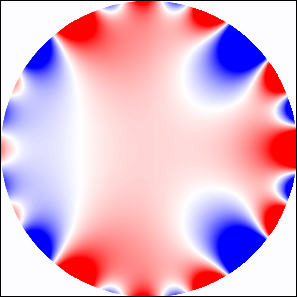
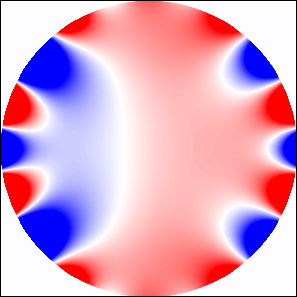

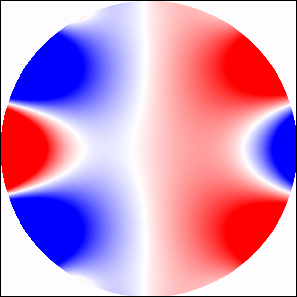
Figure 11 shows the transmission coefficient of -polarized wave propagating through linear array of LHM cylinders of radius and through a system of rows of cylinders. For higher frequencies as well as in the interval we observe transmission bands typical for dielectric photonic structures. In the frequency regions where Fano resonances are excited, we expect the existence of series of very narrow frequency bands. However, as shown in Fig. 12, identification of the order of the resonance is more difficult than in the case of metallic cylinders since the EM field inside the LH cylinder is given by a superposition of two or more overlapping resonant modes.
IV Conclusion
Detailed analysis of spectra of Fano resonances is necessary for complete understanding of the frequency and transmission spectra of photonic structures. Resonances excited in simple structures – single cylinder, linear array of cylinders – give rise to frequency bands in two dimensional structures. Such bands can overlap with periodic Bragg bands which causes various irregularities observed in the transmission spectra of photonic crystals.
The spectrum of Fano resonances can be rather complicated: in dielectric cylinders, incident electromagnetic wave can excited a series of resonances for each symmetry of EM field. In contrast to dielectrics, metallic cylinder allows resonances associated with surface states. The richest spectrum of Fano resonances can be found in structures made from cylinders made from the left-handed material which combines properties of both dielectrics and metals.
Excitation of Fano resonances is associated with strongly inhomogeneous spatial distribution of electromagnetic fields in the photonic structure, especially when higher-order surface modes are excited. Numerical algorithms based either on the discretization of the space pendry-1992 or on the expansion of EM field into Fourier series rcwa are therefore not appropriate for the analysis of such states. Our methods, based on the expansion of the electromagnetic field into cylinder eigenfunctions overcomes this difficulty and is suitable for qualitative and quantitative analysis of photonic structures composed from elements with cylindric symmetry.
Acknowledgment
This work was supported by the Slovak Research and Development Agency under the contract No. APVV-0108-11 and by the Agency VEGA under the contract No. 1/0372/13.
References
- (1) U. Fano, Effects of Configuration Interaction on Intensities and Phase Shifts, Phys. Rev. 124, 1866 (1961).
- (2) S. Fan, W. Suh and J. D. Joannopoulos, Temporal couple-mode theory for the Fano resonance in optical resonators, J. Opt. Soc. Amm. A 20 569 (2003).
- (3) S. Fan and J. D. Joannopoulos, Analysis of guided resonances in photonic crystal slabs, Phys. Rev. B 65 235112 (2002).
- (4) V. N. Astratov, I. S. Culshaw, R. M. Stevenson, D. M. Whittaker, M. S. Skolnick, T. F. Krauss and R. M. De La Rue, Resonant Coupling of Near-Infrared Radiation to Photonic Band Structure Waveguides, J. Light. Technol. 17, 2050 (1999).
- (5) K. Ohtaka, H. Numata, Multiple scattering effects in photon diffraction for an array of cylindrical dielectrics, Phys. Lett. 73A, 411 (1979).
- (6) A. E. Miroshnichenko et al., Fano resonances in nanoscale structures, Rev. Mod. Phys. 82, 2257 (2010).
- (7) B. Lukyanchuk et al., The Fano resonance in plasmonic nanostructures and metamaterials, Nature Mat. 9, 707 (2010).
- (8) A. N. Poddubny et al. Fano interference governs wave transport in disordered systems, Nat. Comm. 3, 914 (2012).
- (9) M. V. Rybin, et al., Mie scattering as a cascade of Fano resonances, Optics Express 21, 30107 (2013).
- (10) M. V. Rybin et al., Phase diagram for transition from photonic crystals to dielectric metamaterials, Nature Comm. 6, 10102(1-6) (2015).
- (11) P. Markoš, Fano resonances and bad structure of two dimensional photonic structures, Phys. Rev. A 92 043814 (2015).
- (12) K. Sakoda, Optical Properties of Photonic Crystals, Berlin, Heidelberg: Springer (2005).
- (13) J. D. Joannopoulos, S. G. Johnson, J. N. Winnand R. G. Meade, Photonic Crystals: Molding the Flow of Light 2nd edition. Princeton: Princeton University Press (2008).
-
(14)
K. Sakoda et al.,
Photonic bands of metallic systems. I. Principle of calculation and accuracy,
Phys. Rev. B 64, 045116 (2001);
T. Ito and K. Sakoda, Photonic bands of metallic systems. II. Features of surface plasmon polaritons Phys. Rev. B 64, 045117 (2001). - (15) E. Moreno et al., Band structure computations of metallic photonic crystals with the multiple multipole method, Phys. Rev. B 65, 155120 (2001).
- (16) P. Markoš and V. Kuzmiak, Coupling between Fano and Bragg bands in photonic band structure of two dimensional metallic photonic structures, submitted (2016).
- (17) P. Markoš, Guided modes in photonic structures with left-handed components, Opt. Comm. 361 65(2016).
- (18) R. Ruppin, Surface polaritons of a left-handed medium. Phys. Lett. A 277, 61 (2000).
- (19) D. N. Natarov et al. Effect of Periodicity in the Resonant Scattering of Light by Finite Sparse Configurations of Many Silver Nanowires, Plasmonics 9, 389 (2013).
-
(20)
A. A. Asatryan et al. ,
Two-dimensional Greenś function and local density of states in photonic crystals consisting of a finite number of cylinders of infinite length,
Phys. Rev. E 63, 046612 (2001);
A. A. Asatryan et al. Local density of states of metamaterial photonic crystals Australian Institute of Physics, 18th National Congress, (2008). - (21) J. A. Stratton, Electromagnetic Theory New York: Mc Graw-Hill Comp., 1941.
- (22) H. C. van de Hulst, Light scattering by small particles Dover Publ. Inc, NY (1981).
- (23) M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions Dover Publ. (1965).
- (24) C. A. Pfeiffer, E. N. Economou and K. L. Ngai, Surface polaritons in a circularly cylindrical interface: Surface plasmons Phys. Rev. B 10, 3038 (1974).
- (25) K. Sakoda, Symmetry, degeneracy, and uncoupled modes in two-dimensional photonic lattices, Phys. Rev. B 52, 7982 (1995).
- (26) E. N. Economou, Surface plasmons in thin films. Phys. Rev. 182, 539 (1969).
- (27) P. Markoš and Costas M. Soukoulis, Wave Propagation: From Electrons to Photonic Crystals and Left-Handed Materials, Princeton University Press, Princeton and Oxford, 2008.
- (28) Ali Soltani Vala et al. Detailed study of flat bands appearing in metallic photonic crystals Physica Status Solidi C 8, 2965 (2011).
-
(29)
J. B. Pendry and A. MacKinnon, Calculation of photon dispersion relations, Phys. Rev. Lett. 69, 2772 (1992).
P. Markoš and C. M. Soukoulis, Numerical studies of left-handed materials and arrays of split ring resonators, Physical Review E 65, 036622 (2002). -
(30)
J.J. Hench and Z. Strakoš, The RCWA method - a case study with open questions and perspectives of algebraic computations, Electron. Trans. Numer. Anal. 31, 331, (2008);
G. Kajtár, Electromagnetic properties of two dimensional periodic structures, PhD Thesis, Bratislava (2014).