D. LEMIRE, O. KASER, N. KURZ
*Daniel Lemire, 5800 Saint-Denis, Office 1105, Montreal, Quebec, H2S 3L5 Canada.
Faster Remainder by Direct Computation
\subtitlefontApplications to Compilers and Software Libraries
Abstract
[Summary]On common processors, integer multiplication is many times faster than integer division. Dividing a numerator by a divisor is mathematically equivalent to multiplication by the inverse of the divisor (). If the divisor is known in advance—or if repeated integer divisions will be performed with the same divisor—it can be beneficial to substitute a less costly multiplication for an expensive division.
Currently, the remainder of the division by a constant is computed from the quotient by a multiplication and a subtraction. But if just the remainder is desired and the quotient is unneeded, this may be suboptimal. We present a generally applicable algorithm to compute the remainder more directly. Specifically, we use the fractional portion of the product of the numerator and the inverse of the divisor. On this basis, we also present a new, simpler divisibility algorithm to detect nonzero remainders.
We also derive new tight bounds on the precision required when representing the inverse of the divisor. Furthermore, we present simple C implementations that beat the optimized code produced by state-of-art C compilers on recent x64 processors (e.g., Intel Skylake and AMD Ryzen), sometimes by more than 25%. On all tested platforms including 64-bit ARM and POWER8, our divisibility-test functions are faster than state-of-the-art Granlund-Montgomery divisibility-test functions, sometimes by more than 50%.
\jnlcitation\cname, , and , \ctitleFaster Remainder by Direct Computation, \cvol2018.
keywords:
Integer Division, Bit Manipulation, Divisibility1 Introduction
Integer division often refers to two closely related concepts, the actual division and the modulus. Given an integer numerator and a non-zero integer divisor , the integer division, written , gives the integer quotient (). The modulus, written , gives the integer remainder (). Given an integer numerator and an integer divisor , the quotient () and the remainder () are always integers even when the fraction is not an integer. It always holds that the quotient multiplied by the divisor plus the remainder gives back the numerator: .
Depending on the context, ‘integer division’ might refer solely to the computation of the quotient, but might also refer to the computation of both the integer quotient and the remainder. The integer division instructions on x64 processors compute both the quotient and the remainder.aaaWe use x64 to refer to the commodity Intel and AMD processors supporting the 64-bit version of the x86 instruction set. It is also known as x86-64, x86_64, AMD64 and Intel 64. In most programming languages, they are distinct operations: the C programming language uses / for division () and % for modulo ().
Let us work through a simple example to illustrate how we can replace an integer division by a multiplication. Assume we have a pile of 23 items, and we want to know how many piles of 4 items we can divide it into and how many will be left over (, ; find and ). Working in base 10, we can calculate the quotient and the remainder , which means that there will be 5 complete piles of 4 items with 3 items left over ().
If for some reason, we do not have a runtime integer division operator (or if it is too expensive for our purpose), we can instead precompute the multiplicative inverse of 4 once () and then calculate the same result using a multiplication (). The quotient is the integer portion of the product to the left of the decimal point (), and the remainder can be obtained by multiplying the fractional portion of the product by the divisor : .
The binary registers in our computers do not have a built-in concept of a fractional portion, but we can adopt a fixed-point convention. Assume we have chosen a convention where has 5 bits of whole integer value and 3 bits of ‘fraction’. The numerator 23 and divisor 4 would still be represented as standard 8-bit binary values (00010111 and 00000100, respectively), but would be 00000.010. From the processor’s viewpoint, the rules for arithmetic are still the same as if we did not have a binary point—it is only our interpretation of the units that has changed. Thus we can use the standard (fast) instructions for multiplication () and then mentally put the ‘binary point’ in the correct position, which in this case is 3 from the right: 00101.110. The quotient is the integer portion (leftmost 5 bits) of this result: 00101 in binary ( in decimal). In effect, we can compute the quotient with a multiplication (to get 00101.110) followed by a right shift (by three bits, to get 000101). To find the remainder, we can multiply the fractional portion (rightmost 3 bits) of the result by the divisor: ( in decimal). To quickly check whether a number is divisible by 4 (?) without computing the remainder it suffices to check whether the fractional portion of the product is zero.
But what if instead of dividing by 4, we wanted to divide by 6? While the reciprocal of 4 can be represented exactly with two digits of fixed-point fraction in both binary and decimal, cannot be exactly represented in either. As a decimal fraction, is equal to the repeating fraction 0.1666…(with a repeating 6), and in binary it is 0.0010101…(with a repeating 01). Can the same technique work if we have a sufficiently close approximation to the reciprocal for any divisor, using enough fractional bits? Yes!
For example, consider a convention where the approximate reciprocal has 8 bits, all of which are fractional. We can use the value 0.00101011 as our approximate reciprocal of 6. To divide by 6, we can multiply the numerator (10111 in binary) by the approximate reciprocal: . As before, the decimal point is merely a convention, the computer need only multiply fixed-bit integers. From the product, the quotient of the division is 11 in binary ( in decimal); and indeed . To get the remainder, we multiply the fractional portion of the product by the divisor (), and then right shift by 8 bits, to get 101 in binary ( in decimal). See Table 1 for other examples.
| numerator times the approx. reciprocal () | quotient | fractional portion divisor () | remainder | |
| bits bits bits | bits | bits bits bits | bits | |
| 0 | 0 | 0 | ||
| 1 | 0 | 1 | ||
| 2 | 0 | 2 | ||
| 3 | 0 | 3 | ||
| 4 | 0 | 4 | ||
| 5 | 0 | 5 | ||
| 6 | 1 | 0 | ||
| 17 | 2 | 5 | ||
| 18 | 3 | 0 | ||
| 19 | 3 | 1 | ||
| 20 | 3 | 2 | ||
| 21 | 3 | 3 | ||
| 22 | 3 | 4 | ||
| 23 | 3 | 5 | ||
| 24 | 4 | 0 | ||
| 63 | 10 | 3 |
While the use of the approximate reciprocal prevents us from confirming divisibility by 6 by checking whether the fractional portion is exactly zero, we can still quickly determine whether a number is divisible by 6 (?) by checking whether the fractional portion is less than the approximate reciprocal (?). Indeed, if then the fractional portion of the product of with the approximate reciprocal should be close to : it makes intuitive sense that comparing with determines whether the remainder is zero. For example, consider (101010 in binary). We have that our numerator times the approximate reciprocal of 6 is . We see that the quotient is 111 in binary ( in decimal), while the fractional portion is smaller than the approximate reciprocal (), indicating that 42 is a multiple of 6.
In our example with 6 as the divisor, we used 8 fractional bits. The more fractional bits we use, the larger the numerator we can handle. An insufficiency of fractional bits can lead to incorrect results when grows. For instance, with ( in binary) and only 8 fractional bits, times the approximate reciprocal of 6 is , or 22 in decimal. Yet in actuality, ; using an 8 bit approximation of the reciprocal was inadequate.
How close does the approximation need to be?—that is, what is the minimum number of fractional bits needed for the approximate reciprocal such that the remainder is exactly correct for all numerators? We derive the answer in § 3.
The scenario we describe with an expensive division applies to current processors. Indeed, integer division instructions on recent x64 processors have a latency of 26 cycles for 32-bit registers and at least 35 cycles for 64-bit registers 1. We find similar latencies in the popular ARM processors 2. Thus, most optimizing compilers replace integer divisions by constants that are known at compile time with the equivalent of a multiplication by a scaled approximate reciprocal followed by a shift. To compute the remainder by a constant (), an optimizing compiler might first compute the quotient as a multiplication by followed by a logical shift by bits , and then use the fact that the remainder can be derived using a multiplication and a subtraction as .
Current optimizing compilers discard the fractional portion of the multiplication (). Yet using the fractional bits to compute the remainder or test the divisibility in software has merit. It can be faster (e.g., by more than 25%) to compute the remainder using the fractional bits compared to the code produced for some processors (e.g., x64 processors) by a state-of-the-art optimizing compiler.
2 Related Work
Jacobsohn3 derives an integer division method for unsigned integers by constant divisors. After observing that any integer divisor can be written as an odd integer multiplied by a power of two, he focuses on the division by an odd divisor. He finds that we can divide by an odd integer by multiplying by a fractional inverse, followed by some rounding. He presents an implementation solely with full adders, suitable for hardware implementations. He observes that we can get the remainder from the fractional portion with rounding, but he does not specify the necessary rounding or the number of bits needed.
In the special case where we divide by 10, Vowels4 describes the computation of both the quotient and remainder. In contrast with other related work, Vowels presents the computation of the remainder directly from the fractional portion. Multiplications are replaced by additions and shifts. He does not extend the work beyond the division by 10.
Granlund and Montgomery5 present the first general-purpose algorithms to divide unsigned and signed integers by constants. Their approach relies on a multiplication followed by a division by a power of two which is implemented as an logical shift (). They implemented their approach in the GNU GCC compiler, where it can still be found today (e.g., up to GCC version 7). Given any non-zero 32-bit divisor known at compile time, the optimizing compiler can (and usually will) replace the division by a multiplication followed by a shift. Following Cavagnino and Werbrouck6, Warren7 finds that Granlund and Montgomery choose a slightly suboptimal number of fractional bits for some divisors. Warren’s slightly better approach is found in LLVM’s Clang compiler. See Algorithm 1.
Following Artzy et al.8, Granlund and Montgomery5 describe how to check that an integer is a multiple of a constant divisor more cheaply than by the computation of the remainder. Yet, to our knowledge, no compiler uses this optimization. Instead, all compilers that we tested compute the remainder by a constant using the formula and then compare against zero. That is, they use a constant to compute the quotient, multiply the quotient by the original divisor, subtract from the original numerator, and only finally check whether the remainder is zero.
In support of this approach, Granlund and Montgomery5 state that the remainder, if desired, can be computed by an additional multiplication and subtraction. Warren7 covers the computation of the remainder without computing the quotient, but only for divisors that are a power of two , or for small divisors that are nearly a power of two (, ).
In software, to our knowledge, no authors except Jacobsohn3 and Vowels4 described using the fractional portion to compute the remainder or test the divisibility, and neither of these considered the general case. In contrast, the computation of the remainder directly, without first computing the quotient, has received some attention in the hardware and circuit literature9, 10, 11. Moreover, many researchers12, 13 consider the computation of the remainder of unsigned division by a small divisor to be useful when working with big integers (e.g., in cryptography).
3 Computing the Remainder Directly
Instead of discarding the least significant bits resulting from the multiplication in the Granlund-Montgomery-Warren algorithm, we can use them to compute the remainder without ever computing the quotient. We formalize this observation by Theorem 3.3, which we believe to be a novel mathematical result.
In general, we expect that it takes at least fractional bits for the approximate reciprocal to provide exact computation of the remainder for all non-negative numerators less than . Let us say we use fractional bits for some non-negative integer value to be determined. We want to pick so that approximate reciprocal allows exact computation of the remainder as where .
We illustrate our notation using the division of by as in the last row of Table 1. We have that is 111111 in binary and that the approximate reciprocal of is in binary. We can compute the quotient as the integer part of the product of the reciprocal by
Taking the -bit fractional portion (), and multiplying it by the divisor (110 in binary), we get the remainder as the integer portion of the result:
The fractional portion given by 10010101 is relatively close to the product of the reciprocal by the remainder () given by 10000001: as we shall see, this is not an accident.
Indeed, we begin by showing that the least significant bits of the product () are approximately equal to the scaled approximate reciprocal times the remainder we seek (), in a way made precise by Lemma 3.1. Intuitively, this intermediate result is useful because we only need to multiply this product by and divide by to cancel out (since ) and get the remainder .
Lemma 3.1.
Given , and non-negative integers such that
then
for all .
Proof 3.2.
We can write uniquely as for some integers and where and . We assume that .
We begin by showing that . Because , we have that
Because and , we have that which shows that
| (1) |
We can rewrite our assumption as . Multiplying throughout by the non-negative integer , we get
After adding throughout, we get
where we used the fact that . So we have that . We already showed (see Equation 1) that is less than so that . Thus we have that because (in general and by definition) if for some , then . Hence, we have that . This completes the proof.
Lemma 3.1 tells us that is close to when is close to . Thus it should make intuitive sense that multiplied by should give us . The following theorem makes the result precise.
Theorem 3.3.
Given , and non-negative integers such that
then
for all .
Proof 3.4.
We can write uniquely as where and . By Lemma 3.1, we have that for all .
We want to show that if we multiply any value in by and divide it by , then we get . That is, if , then . We can check this inclusion using two inequalities:
-
•
() It is enough to show that which follows since by one of our assumptions.
-
•
() It is enough to show that . Using the assumption that , we have that . Since , we finally have as required.
This concludes the proof.
Consider the constraint given by Theorem 3.3.
-
•
We have that is the smallest value of satisfying .
-
•
Furthermore, when does not divide , we have that and so implies . See Lemma 3.5.
On this basis, Algorithm 2 gives the minimal number of fractional bits . It is sufficient to pick .
Lemma 3.5.
Given a divisor , if we set , then
-
•
when is not a power of two,
-
•
and when is a power of two.
Proof 3.6.
The case when is a power of two follows by inspection, so suppose that is not a power of two. We seek to round up to the next multiple of . The previous multiple of is smaller than by . Thus we need to add to to get the next multiple of .
Example 3.7.
Consider Table 1 where we divide by and we want to support the numerators between 0 and so that . It is enough to pick or but we can do better. According to Algorithm 2, the number of fractional bits must satisfy . Picking and does not work since . Picking also does not work since . Thus we need and , at least. So we can pick . In binary, representing 43 with 8 fractional bits gives , as in Table 1. Let us divide by . The quotient is . The remainder is .
It is not always best to use the smallest number of fractional bits. For example, we can always conveniently pick (meaning ) and , since clearly holds (given ).
3.1 Directly Computing Signed Remainders
Having established that we could compute the remainder in the unsigned case directly, without first computing the quotient, we proceed to establish the same in the signed integer case. We assume throughout that the processor represents signed integers in using the two’s complement notation. We assume that the integer .
Though the quotient and the remainder have a unique definition over positive integers, there are several valid ways to define them over signed integers. We adopt a convention regarding signed integer arithmetic that is widespread among modern computer languages, including C99, Java, C#, Swift, Go, and Rust. Following Granlund and Montgomery 5, we let be rounded towards zero: it is if and otherwise. We use “” to denote the signed integer division defined as and “” to denote the signed integer remainder defined by the identity . Changing the sign of the divisor changes the sign of the quotient but the remainder is insensitive to the sign of the divisor. Changing the sign of the numerator changes the sign of both the quotient and the remainder: and .
Let be the function that selects the least significant bits of an integer , zeroing others. The result is always non-negative (in ) in our work. Whenever divides , whether is positive or not, we have .
Remark 3.8.
Suppose does not divide , then when the integer is negative, and when it is positive. Thus we have whenever does not divide .
We establish a few technical results before proving Theorem 3.15. We believe it is novel.
Lemma 3.9.
Given , and non-negative integers such that
we have that cannot divide for any .
Proof 3.10.
First, we prove that cannot divide . When divides , setting for some integer , we have that , but there is no integer between and .
Next, suppose that and divides . Since divides , we know that the prime factorization of has at least copies of 2. Within the range of () at most copies of 2 can be provided. Obtaining the required copies of 2 is only possible when and provides the remaining copies—so divides . But that is impossible.
Lemma 3.11.
Given , and non-negative integers such that
for all integers and letting , we have that .
Proof 3.12.
Write where .
Since is positive we have that . (See Remark 3.8.)
Lemma 3.1 is applicable, replacing with . We have a stronger constraint on , but that is not harmful. Thus we have .
We proceed as in the proof of Theorem 3.3. We want to show that .
-
•
() We have . Multiplying throughout by , we get , where we used in the last inequality.
-
•
() We have . Multiplying throughout by , we get . Because , we have the result .
Thus we have , which shows that . This completes the proof.
Lemma 3.13.
Given positive integers , we have that if does not divide .
Proof 3.14.
Define . We have . We have that
Theorem 3.15.
Given , and non-negative integers such that
let then
-
•
for all
-
•
and for all .
Proof 3.16.
We do not need to be concerned with negative divisors since for all integers .
We can pick in a manner similar to the unsigned case. We can choose and let where is an integer such that . With this choice of , we have that . Thus we have the constraint on . Because , it suffices to pick large enough so that . Thus any would do, and hence is sufficient. It is not always best to pick to be minimal: it could be convenient to pick .
3.2 Fast Divisibility Check with a Single Multiplication
Following earlier work by Artzy et al.8, Granlund and Montgomery5 describe how we can check quickly whether an unsigned integer is divisible by a constant, without computing the remainder. We summarize their approach before providing an alternative. Given an odd divisor , we can find its (unique) multiplicative inverse defined as . The existence of a multiplicative inverse allows us to quickly divide an integer by when it is divisible by , if is odd. It suffices to multiply by : . When the divisor is for odd and is divisible by , then we can write . As pointed out by Granlund and Montgomery, this observation can also enable us to quickly check whether a number is divisible by . If is odd and is divisible by , then . Otherwise is not divisible by . Thus, when is odd, we can check whether any integer in is divisible by with a multiplication followed by a comparison. When the divisor is even (), then we have to check that and that is divisible by (i.e., ). We can achieve the desired result by computing , rotating the resulting word by bits and comparing the result with .
Granlund and Montgomery can check that an unsigned integer is divisible by another using as little as one multiplication and comparison when the divisor is odd, and a few more instructions when the divisor is even. Yet we can always check the divisibility with a single multiplication and a modulo reduction to a power of two—even when the divisor is even because of the following proposition. Moreover, a single precomputed constant () is required.
Proposition 3.17.
Given , and non-negative integers such that then given some , we have that divides if and only if .
Proof 3.18.
We have that divides if and only if . By Lemma 3.1, we have that . We want to show that is equivalent to .
Suppose that , then we have that . However, by our constraints on , we have that . Thus, if then .
Suppose that , then because , we have that which implies that . This completes the proof.
Thus if we have a reciprocal with large enough to compute the remainder exactly (see Algorithm 2), then if and only if is divisible by . We do not need to pick as small as possible. In particular, if we set , then if and only if is divisible by .
Remark 3.19.
We can extend our fast divisibility check to the signed case. Indeed, we have that divides if and only if divides . Moreover, the absolute value of any -bit negative integer can be represented as an -bit unsigned integer.
4 Software Implementation
Using the C language, we provide our implementations of the 32-bit remainder computation (i.e., a % d) in Figs. LABEL:fig:codemod and 1 for unsigned and signed integers. In both case, the programmer is expected to precompute the constant c. For simplicity, the code shown here explicitly does not handle the divisors .
For the x64 platforms, we provide the instruction sequences in assembly code produced by GCC and Clang for computing in Fig. 2; in the third column, we provide the x64 code produced with our approach after constant folding. Our approach generates about half as many instructions.
In Fig. 3, we make the same comparison on the 64-bit ARM platform, putting side-by-side compiler-generated code for the Granlund-Montgomery-Warren approach with code generated from our approach. As a RISC processor, ARM does not handle most large constants in a single machine instruction, but typically assembles them from 16-bit quantities. Since the Granlund-Montgomery-Warren algorithm requires only 32-bit constants, two 16-bit values are sufficient whereas our approach relies on 64-bit quantities and thus needs four 16-bit values. The ARM processor also has a “multiply-subtract” instruction that is particularly convenient for computing the remainder from the quotient. Unlike the case with x64, our approach does not translate into significantly fewer instructions on the ARM platform.
These code fragments show that a code-size saving is achieved by our approach on x64 processors, compared to the approach taken by the compilers. We verify in § 5 that there is also a runtime advantage.
|
// our fast version
// + GCC 6.2
movabs rax,
194176253407468965
mov edi, edi
imul rdi, rax
mov eax, 95
mul rdi
mov rax, rdx
//
//
//
//
|
|
// our version of a % 95 + GCC 6.2
mov x2, 7589
uxtw x0, w0
movk x2, 0x102b, lsl 16
mov x1, 95
movk x2, 0xda46, lsl 32
movk x2, 0x2b1, lsl 48
mul x0, x0, x2
umulh x0, x0, x1
//
|
4.1 Divisibility
We are interested in determining quickly whether a 32-bit integer divides a 32-bit integer —faster than by checking whether the remainder is zero. To the best of our knowledge, no compiler includes such an optimization, though some software libraries provide related fast functions.bbbhttps://gmplib.com We present the code for our approach (LKK) in Fig. 4, and our implementation of the Granlund-Montgomery approach (GM) in Fig. 5.
5 Experiments
Superiority over the Granlund-Montgomery-Warren approach might depend on such CPU characteristics as the relative speeds of instructions for integer division, 32-bit integer multiplication and 64-bit integer division. Therefore, we tested our software on several x64 platforms and on ARMccc With GCC 4.8 on the ARM platform we observed that, for many constant divisors, the compiler chose to generate a udiv instruction instead of using the Granlund-Montgomery code sequence. This is not seen for GCC 6.2. and POWER8 servers, and relevant details are given in Table 2. The choice of multiplication instructions and instruction scheduling can vary by compiler, and thus we tested using various versions of GNU GCC and LLVM’s Clang. For brevity we primarily report results from the Skylake platform, with comments on points where the other platforms were significantly different. For the Granlund-Montgomery-Warren approach with compile-time constants, we use the optimized divide and remainder operations built into GCC and Clang.
We sometimes need to repeatedly divide by a constant that is known only at runtime. In such instances, an optimizing compiler may not be helpful. Instead a programmer might rely on a library offering fast division functions. For runtime constants on x64 processors, we use the libdivide librarydddhttp://libdivide.com as it provides a well-tested and optimized implementation.
On x64 platforms, we use the compiler flags -O3 -march=native; on ARM we use -O3 -march=armv8-a and on POWER8 we use -O3 -mcpu=power8. Some tests have results reported in wall-clock time, whereas in other tests, the Linux perf stat command was used to obtain the total number of processor cycles spent doing an entire benchmark program. To ease reproducibility, we make our benchmarking software and scripts freely available.eeehttps://github.com/lemire/constantdivisionbenchmarks
| Processor | Microarchitecture | Compilers | |
| Intel i7-6700 | Skylake (x64) | GCC 6.2; Clang 4.0 | default platform |
| Intel i7-4770 | Haswell (x64) | GCC 5.4; Clang 3.8 | |
| AMD Ryzen 7 1700X | Zen (x64) | GCC 7.2; Clang 4.0 | |
| POWER8 | POWER8 Murano | GCC 5.4; Clang 3.8 | |
| AMD Opteron A1100 | ARM Cortex A57 (Aarch64) | GCC 6.2; Clang 4.0 |
5.1 Beating the Compiler
We implement a 32-bit linear congruential generator14 that generates random numbers according to the function , starting from a given seed . Somewhat arbitrarily, we set the seed to 1234, we use 31 as the multiplier () and the additive constant is set to 27961 (). We call the function 100 million times, thus generating 100 million random numbers. The divisor is set at compile time. See Fig. 6. In the signed case, we use a negative multiplier ().
Because the divisor is a constant, compilers can optimize the integer division using the Granlund-Montgomery approach. We refer to this scenario as the compiler case. To prevent the compiler from proceeding with such an optimization and force it to repeatedly use the division instruction, we can declare the variable holding the modulus to be volatile (as per the C standard). We refer to this scenario as the division instruction case. In such cases, the compiler is not allowed to assume that the modulus is constant—even though it is. We verified that the assembly generated by the compiler includes the division instruction and does not include expensive operations such as memory barriers or cache flushes. We verified that our wall-clock times are highly repeatablefffFor instance, we repeated tests 20 times for 9 divisors in Figs. 7abcd and 8ab, and we observed maximum differences among the 20 trials of 4.8 %, 0.3 %, 0.7 %, 0.0 %, 0.8 % and 0.9 %, respectively. .
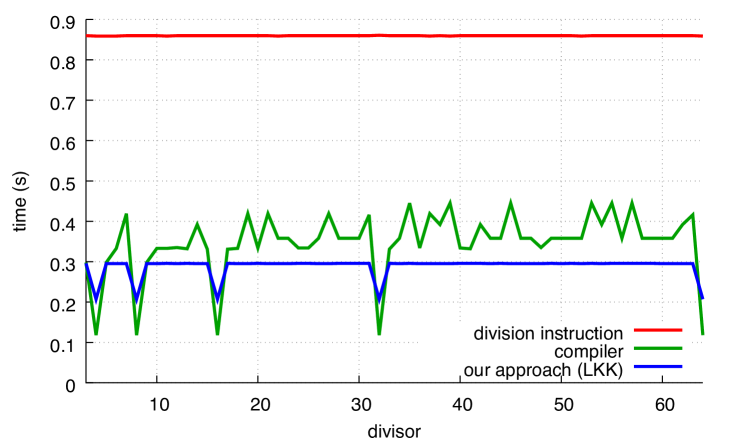
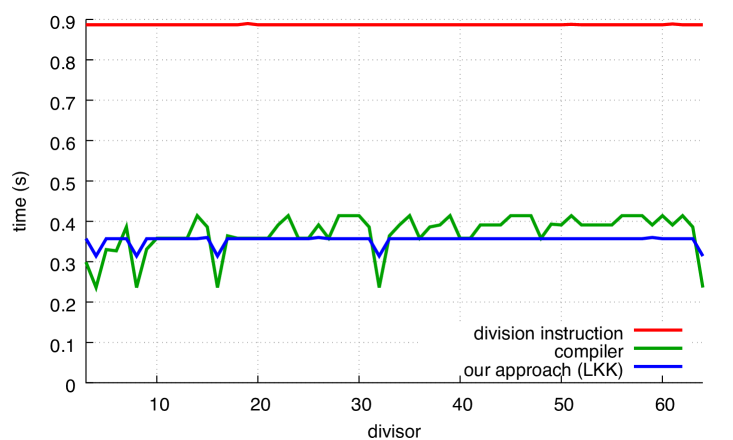
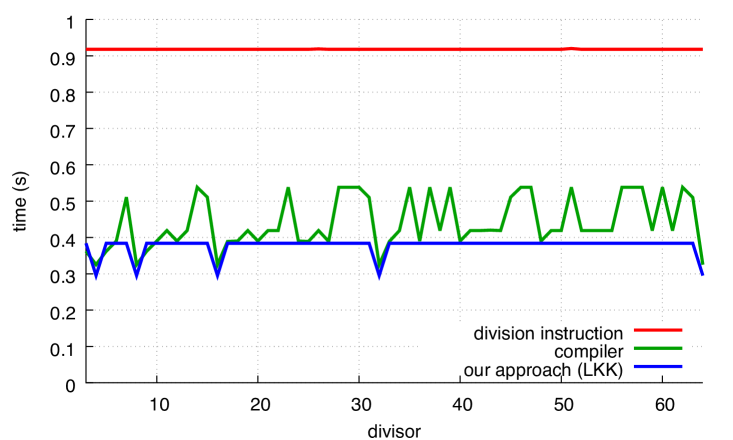
We present our results in Fig. 7 where we compare with our alternative. In all cases, our approach is superior to the code produced by the compiler, except for powers of two in the case of GCC. The benefit of our functions can reach 30%.
The performance of the compiler (labelled as compiler) depends on the divisor for both GCC and Clang, though Clang has greater variance. The performance of our approach is insensitive to the divisor, except when the divisor is a power of two.
We observe that in the unsigned case, Clang optimizes very effectively when the divisor is a small power of two. This remains true even when we disable loop unrolling (using the -fno-unroll-loops compiler flag). By inspecting the produced code, we find that Clang (but not GCC) optimizes away the multiplication entirely in the sense that, for example, is transformed into . We find it interesting that these optimizations are applied both in the compiler functions as well as in our functions. Continuing with the unsigned case, we find that Clang often produces slightly more efficient compiled code than GCC for our functions, even when the divisor is not a power of two: compare Fig. 7a with Fig. 7c. However, these small differences disappear if we disable loop unrolling.
Yet, GCC seems preferable in the signed benchmark: in Figs. 7b and 7d, Clang is slightly less efficient than GCC, sometimes requiring to complete the computation whereas GCC never noticeably exceeds .
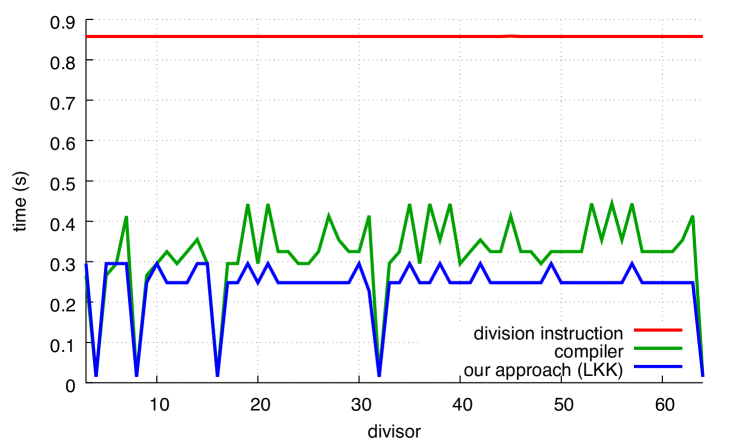
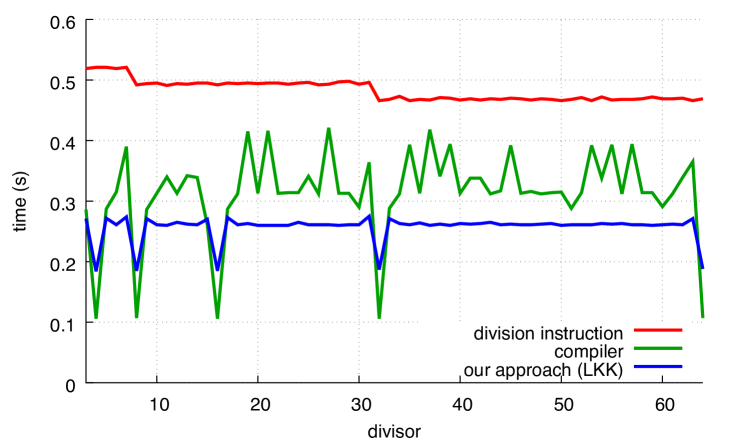
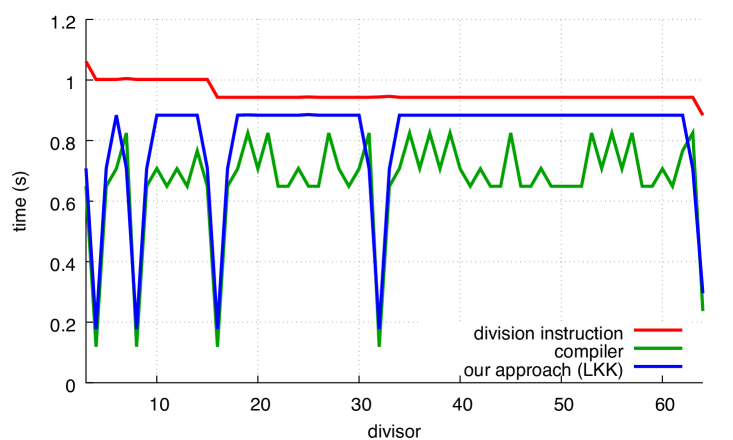

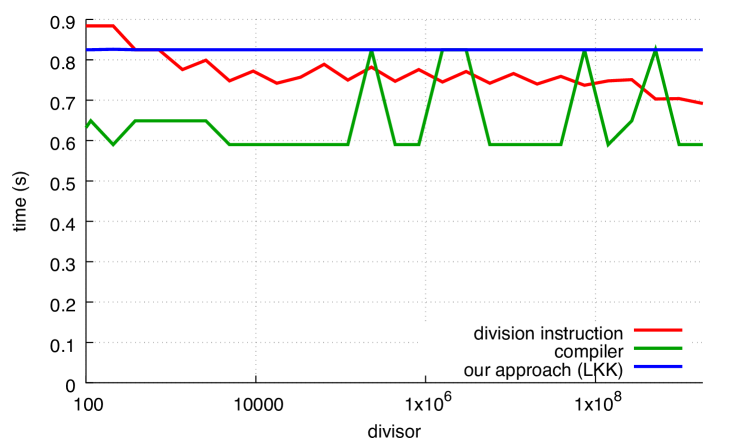
For comparison, Fig. 8 shows how the Ryzen, POWER8 and ARM processors perform on unsigned computations.The speed of the hardware integer-division instruction varies, speeding up at and again at for Ryzen and , 16, 64, 256 and 1024 for ARM. The gap between hardware integer division and Granlund-Montgomery (compiler) is less on Ryzen, POWER8 and ARM than on Skylake; for some divisors, there is little benefit to using compiler on POWER8 and ARM. On x64 platforms, our approach continues to be significantly faster than hardware integer division for all divisors.
On ARM, the performance is limited when computing remainders using our approach. Unlike x64 processors, ARM processors require more than one instruction to load a constant such as the reciprocal (), but that is not a concern in this instance since the compiler loads into a register outside of the loop. We believe that the reduced speed has to do with the performance of the multiplication instructions of our Cortex A57 processor 2. To compute the most significant 64 bits of a 64-bit product as needed by our functions, we must use the multiply-high instructions (umulh and smulh), but they require six cycles of latency and they prevent the execution of other multi-cycle instructions for an additional three cycles. In contrast, multiplication instructions on x64 Skylake processors produce the full 128-bit product in three cycles. Furthermore, our ARM processor has a multiply-and-subtract instruction with a latency of three cycles. Thus it is advantageous to rely on the multiply-and-subtract instruction instead of the multiply-high instruction. Hence, it is faster to compute the remainder from the quotient by multiplying and subtracting (). Furthermore, our ARM processor has fast division instructions: the ARM optimization manual for Cortex A57 processors indicates that both signed and unsigned division require between 4 and 20 cycles of latency 2 whereas integer division instructions on Skylake processors (idiv and div) have 26 cycles of latency for 32-bit registers 1. Even if we take into account that division instructions on ARM computes solely the quotient, as opposed to both the quotient and remainder on x64, it seems that the ARM platform has a competitive division latency. Empirically, the division instruction on ARM is often within 10% of the Granlund-Montgomery compiler optimization (Fig. 8b) whereas the compiler optimization is consistently more than twice as fast as the division instruction on a Skylake processor (see Fig. 7a).
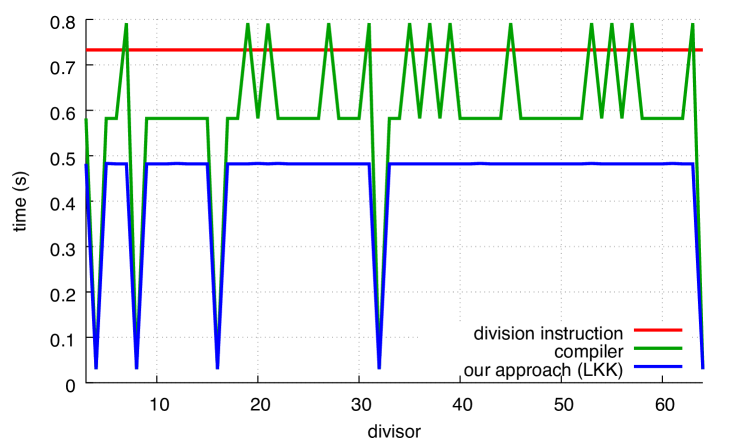
Results for POWER8 are shown in Figs. 8c and 8d. Our unsigned approach is better than the compiler’s; indeed the compiler would sometimes have done better to generate a divide instruction than use the Granlund-Montgomery approach. For our signed approach, both GCC and Clang had trouble generating efficient code for many divisors.
As with ARM, code generated for POWER8 also deals with 64-bit constants less directly than x64 processors. If not in registers, POWER8 code loads 64-bit constants from memory, using two operations to construct a 32-bit address that is then used with a load instruction. In this benchmark, however, the compiler keeps 64-bit constants in registers. Like ARM, POWER8 has instructions that compute the upper 64 bits of a 64-bit product. The POWER8 microarchitecture15 has good support for integer division: it has two fixed-point pipelines, each containing a multiplier unit and a divider unit. When the multi-cycle divider unit is operating, fixed-point operations can usually be issued to other units in its pipeline. In our benchmark, dependencies between successive division instructions prevent the processor from using more than one divider. Though we have not seen published data on the actual latency and throughput of division and multiplication on this processor, we did not observe the divisor affecting the division instruction’s speed, at least within the range of 3 to 4096.
Our results suggest that the gap between multiplication and division performance on the POWER8 lies between that of ARM and Intel; the fact that our approach (using 64-bit multiplications) outperforms the compiler’s approach (using 32-bit multiplications) seems to indicate that, unlike ARM, the instruction to compute the most significant bits of a 64-bit product is not much slower than the instruction to compute a 32-bit product.
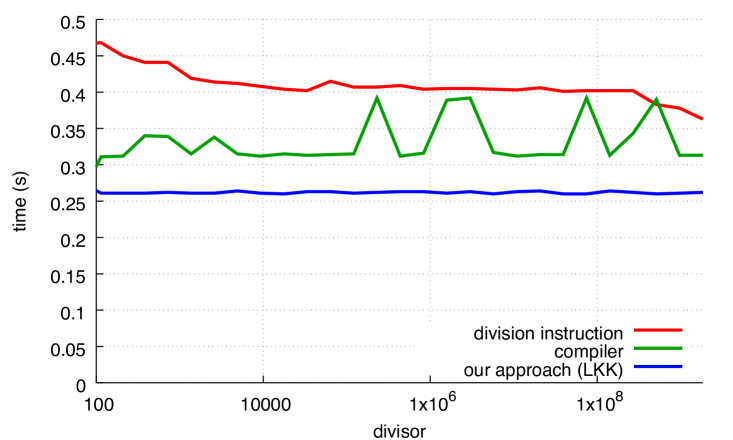
Looking at Fig. 9, we see how the approaches compare for larger divisors. The division instruction is sometimes the fastest approach on ARM, and sometimes it can be faster than the compiler approach on Ryzen. Overall, our approach is preferred on Ryzen (as well as Skylake and POWER8), but not on ARM.
5.2 Beating the libdivide Library
There are instances when the divisor might not be known at compile time. In such instances, we might use a library such as a libdivide. We once again use our benchmark based on a linear congruential generator using the algorithms, but this time, we provide the divisor as a program parameter.
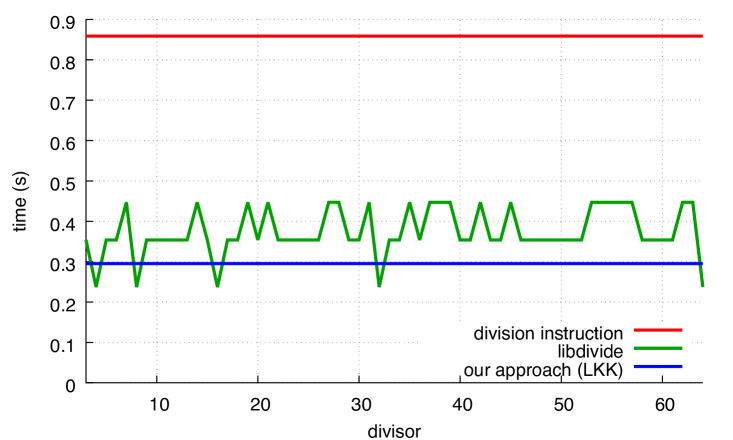
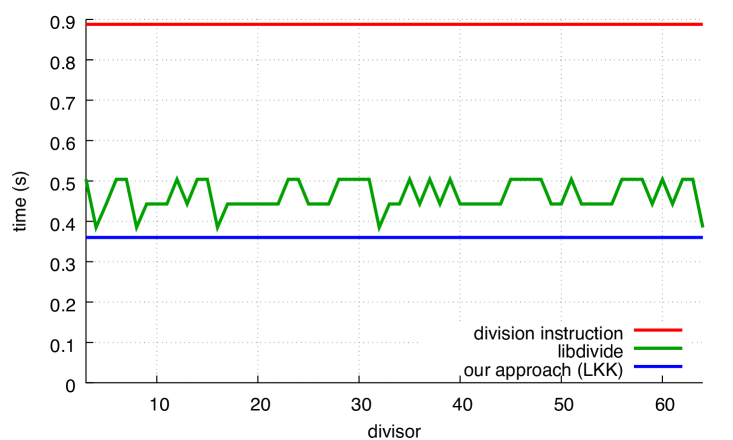
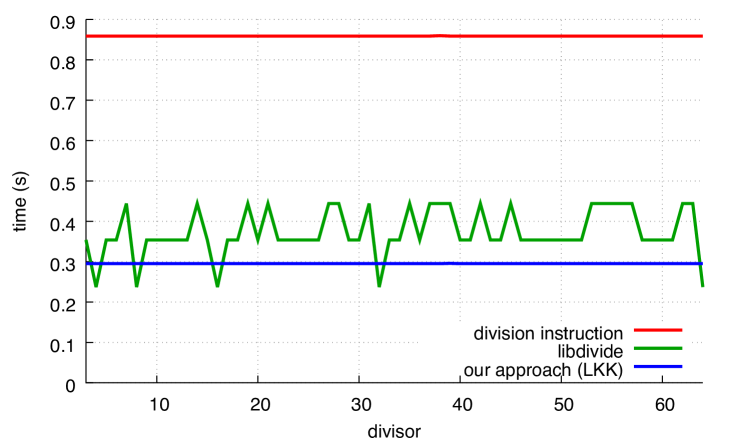
The libdivide library does not have functions to compute the remainder, so we use its functions to compute the quotient. It has two types of functions: regular "branchful" ones, those that include some branches that depend on the divisor, and branchless ones. In this benchmark, the invariant divisor makes the branches perfectly predictable, and thus the libdivide branchless functions were always slower. Consequently we omit the branchless results.
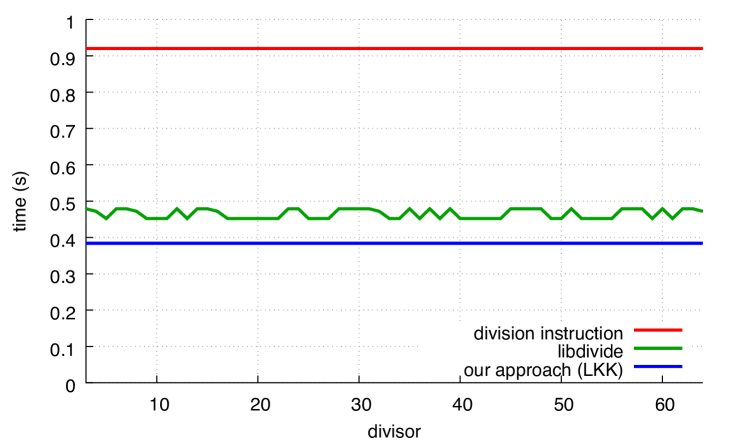
We present our results in Fig. 10. The performance levels of our functionsggg When 20 test runs were made for 9 divisors, timing results among the 20 never differed by more than 1%. are insensitive to the divisor, and our performance levels are always superior to those of the libdivide functions (by about 15%), except for powers of two in the unsigned case. In these cases, libdivide is faster, but this is explained by a fast conditional code path for powers of two.
5.3 Competing for Divisibility
We adapted a prime-counting benchmark distributed with libdivide, specialized to 32-bit operands. The code determines the number of primes in using a simplistic approach: odd numbers in this range are checked for divisibility by any smaller number that has already been determined to be prime. See Fig. 11. When a number is identified as a prime, we compute its scaled approximate reciprocal () value, which is repeatedly used in future iterations. In this manner, the computation of is only done once per prime, and not once per trial division by the prime. A major difference from the benchmark using the linear-congruential generator is that we cycle rapidly between different divisors, making it much more difficult to predict branches in the libdivide functions.
In these tests, we compare libdivide against LKK and GM, the fast divisibility tests whose implementations are shown in § 4.1; see Fig. 4 for LKK and Fig. 5 for GM. Divisibility of a candidate prime is checked either using
-
•
libdivide to divide, followed by multiplication and subtraction to determine whether the remainder is nonzero;
-
•
the Granlund-Montgomery (GM) divisibility check, as in Fig. 5;
-
•
the C % operation, which uses a division instruction;
-
•
our LKK divisibility check (Fig. 4).
LKK stores 64 bits for each prime; GM requires an additional 5-bit rotation amount. The division-instruction version of the benchmark only needs to store 32 bits per prime. The libdivide approach requires 72 bits per prime, because we explicitly store the primes.
Instruction counts and execution speed are both important. All else being equal, we would prefer that compilers emit smaller instruction sequences. Using a hardware integer division will yield the smallest code, but this might give up too much speed. In the unsigned case, our LKK has a significant code-size advantage over GM—approximately 3 arithmetic instructions to compute our versus about 11 to compute their required constant. Both fast approaches use a multiplication and comparison for each subsequent divisibility check. GM requires an additional instruction to rotate the result of the multiplication.
Performance results for the unsigned case are shown in Table 3, showing the total number of processor cycles on each platform from 1000 repetitions of the benchmark. On Skylake, 20 repeated computations yielded cycle-count results within 0.3% of each other. For ARM, results were always within 4%. Initially, Ryzen results would sometimes differ by up to 10% within 20 attempts, even after we attempted to control such factors as dynamic frequency scaling. Thus, rather than reporting the first measurement for each benchmark, the given Ryzen results are the average of 11 consecutive attempts (the basic benchmark was essentially executed 11 000 times). Our POWER8 results (except one outlier) were within 7% of one another over multiple trials and so we averaged several attempts (3 for GCC and 7 for Clang) to obtain each data point. Due to platform constraints, POWER8 results are user-CPU times that matched the wall-clock times.
LKK has a clear speed advantage in all cases, including the POWER8 and ARM platforms. LKK is between 15% to 80% faster than GM. Both GM and LKK always are much faster than using an integer division instruction (up to for Ryzen) and they also outperform the best algorithm in libdivide.
| Algorithm | Skylake | Haswell | Ryzen | ARM | POWER8 | |||||
| GCC | Clang | GCC | Clang | GCC | Clang | GCC | Clang | GCC | Clang | |
| division instruction | 72 | 72 | 107 | 107 | 131 | 131 | 65 | 65 | 18 | 17 |
| branchful | 46 | 88 | 56 | 98 | 59 | 71 | – | – | – | – |
| branchless | 35 | 35 | 36 | 37 | 34 | 37 | – | – | – | – |
| LKK | 18 | 18 | 18 | 18 | 17 | 18 | 27 | 27 | 8.7 | 8.0 |
| GM | 24 | 27 | 27 | 28 | 27 | 32 | 36 | 37 | 10 | 11 |
| GM/LKK | 1.33 | 1.50 | 1.50 | 1.55 | 1.59 | 1.77 | 1.33 | 1.37 | 1.15 | 1.38 |
6 Conclusion
To our knowledge, we present the first general-purpose algorithms to compute the remainder of the division by unsigned or signed constant divisors directly, using the fractional portion of the product of the numerator with the approximate reciprocal3, 4. On popular x64 processors (and to a lesser extent on POWER), we can produce code for the remainder of the integer division that is faster than the code produced by well regarded compilers (GNU GCC and LLVM’s Clang) when the divisor constant is known at compile time, using small C functions. Our functions are up to 30% faster and with only half the number of instructions for most divisors. Similarly, when the divisor is reused, but is not a compile-time constant, we can surpass a popular library (libdivide) by about 15% for most divisors.
We can also speed up a test for divisibility. Our approach (LKK) is several times faster than the code produced by popular compilers. It is faster than the Granlund-Montgomery divisibility check5, sometimes nearly twice as fast. It is advantageous on all tested platforms (x64, POWER8 and 64-bit ARM).
Though compilers already produce efficient code, we show that additional gains are possible. As future work, we could compare against more compilers and other libraries. Moreover, various additional optimizations are possible, such as for division by powers of two.
Acknowledgments
The work is supported by the Natural Sciences and Engineering Research Council of Canada under grant RGPIN-2017-03910. The authors are grateful to IBM’s Centre for Advanced Studies — Atlantic and Kenneth Kent for access to the POWER 8 system.
References
- 1 Fog A. Instruction tables: Lists of instruction latencies, throughputs and micro-operation breakdowns for Intel, AMD and VIA CPUs. Copenhagen University College of Engineering Copenhagen, Denmark; 2016. http://www.agner.org/optimize/instruction_tables.pdf. Accessed May 31, 2018.
- 2 Cortex-A57 Software Optimization Guide. ARM Holdings; 2016. http://infocenter.arm.com/help/topic/com.arm.doc.uan0015b/Cortex_A57_Software_Optimization_Guide_external.pdf. Accessed May 31, 2018.
- 3 Jacobsohn DH. A combinatoric division algorithm for fixed-integer divisors. IEEE T. Comput.. 1973;100(6):608–610.
- 4 Vowels RA. Division by 10. Aust. Comput. J.. 1992;24(3):81–85.
- 5 Granlund T, Montgomery PL. Division by invariant integers using multiplication. SIGPLAN Not.. 1994;29(6):61–72.
- 6 Cavagnino D, Werbrouck AE. Efficient algorithms for integer division by constants using multiplication. Comput. J.. 2008;51(4):470–480.
- 7 Warren HS. Hacker’s Delight. Boston: Addison-Wesley; 2nd ed.2013.
- 8 Artzy E, Hinds JA, Saal HJ. A fast division technique for constant divisors. Commun. ACM. 1976;19(2):98–101.
- 9 Raghuram PS, Petry FE. Constant-division algorithms. IEE P-Comput. Dig. T.. 1994;141(6):334-340.
- 10 Doran RW. Special cases of division. J. Univers. Comput. Sci.. 1995;1(3):176–194.
- 11 Ugurdag F, Dinechin F De, Gener YS, Gören S, Didier LS. Hardware division by small integer constants. IEEE T. Comput.. 2017;66(12):2097–2110.
- 12 Rutten L, Van Eekelen M. Efficient and formally proven reduction of large integers by small moduli. ACM Trans. Math. Softw.. 2010;37(2):16:1–16:21.
- 13 Moller N, Granlund T. Improved division by invariant integers. IEEE T. Comput.. 2011;60(2):165–175.
- 14 Knuth DE. Seminumerical Algorithms. The Art of Computer ProgrammingReading, MA: Addison-Wesley; 2nd ed.1981.
- 15 Sinharoy B, Van Norstrand J.A., Eickemeyer R.J., et al. IBM POWER8 processor core microarchitecture. IBM Journal of Research and Development. 2015;59.