Feedback-controlled solute transport through chemo-responsive polymer membranes

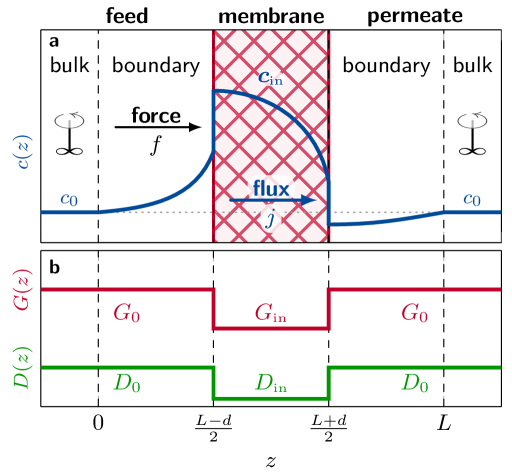
We consider the solute transport across a polymer membrane as a one-dimensional drift-diffusion process (in $z$-direction) of ideal solutes [see the system sketch in Fig. 2(a)]. The membrane has the width $d$, and is located in the center of the system of length $L$, yielding interfaces at $(L\pm d)/2$. It is in contact with two solute reservoirs of equal concentration $c_{0}$ via boundary layers on the feed and permeate sides. [66] The steady-state flux in the overdamped limit derived from the Smoluchowski equation, reads [67]

with the inverse temperature, $\beta=1/(k_{\text{\tiny B}}T)$, and the (external) driving force, $f$, which may result from various sources. We assume that the diffusion and energy landscapes, $D(z)$ and $G(z)$, are piecewise homogeneous, cf. Fig. 2(b), precisely

and

where the subscripts ‘$0$’ and ‘in’ refer to the regions outside and inside the membrane, respectively.

The quantities $D_{\text{\tiny in}}$ and $\Delta G=G_{\text{\tiny in}}-G_{0}$ define the membrane permeability in the solution–diffusion picture,[59, 60, 61, 62]

where $\mathcal{K}=\exp(-\beta\Delta G)$ is the equilibrium partitioning. The membrane permeability is a function of the polymer volume fraction, $\phi$, and depends on the solute–polymer interactions.

For not too attractive solute-polymer interactions, the solute diffusivity inside the membrane is well described by Yasuda’s free-volume theory,[60]

with $A$ a positive parameter accounting for steric solute–polymer effects. For dilute solute systems, the partitioning of the ideal solutes can be well approximated by[68]

where $B=2B_{2}v_{0}^{-1}$ is related to the second virial coefficient, $B_{2}$, rescaled by effective monomer volume $v_{0}$.

In fact, there exist many extended versions of scaling laws for $D_{\text{\tiny in}}$ and $\mathcal{K}$ which take into account further microscopic details, such as the chemistry, shape and size of the solutes, the solvent and the membrane types, and the architecture of the polymer network.[69, 70, 68, 71, 72, 61, 73, 74, 75] However, we use Eqs. 9 and 10 to explain the feedback effects of responsive polymers at the simplest level of detail.

Further, the presented framework assumes that the equilibrium findings for $\mathcal{K}$ and $D_{\text{\tiny in}}$ are also valid under moderate nonequilibrium conditions, i.e., they are independent of the flux or the force. The validity of this assumption was demonstrated in our preceding work with nonequilibrium coarse-grained simulations of membrane-bulk systems.[65]

With known $\mathcal{P}_{\text{\tiny mem}}$ and $c(0)=c_{0}$, we solve Eq. 1 to obtain the concentration profile, yielding

with

Using $c(L)=c_{0}$, the flux can be expressed as[65]

with $S(f)=\sinh(\beta fd/2)/\sinh(\beta fL/2)$, which determines the impact of $\mathcal{P}_{\text{\tiny mem}}/D_{0}$ in the low- and high-force limits (see Appendix A for further details).

By reinserting Eq. 13, one obtains the solute concentration profile throughout the system (see Appendix B for full expressions). We are particularly interested in the mean solute concentration inside the membrane, $c_{\text{\tiny in}}:=\langle c(z)\rangle_{\text{\tiny in}}=d^{-1}\int_{\text{\tiny in}}\mathrm{d}z\ c(z)$, with $z_{\text{\tiny in}}\in\mathopen{}\mathclose{{\left[(L-d)/2,(L+d)/2}}\right]$, because it is the key stimulus for our membrane response model. After integration, we obtain

The detailed behavior of Eq. 14 is described in the results section with an appropriate choice of the model parameters.

The above theoretical framework is straightforward for membranes with constant $\phi$. We now extend the model to membranes that are responsive (in $\phi$) to $c_{\text{\tiny in}}$. Motivated by experimental, theoretical, and computational findings, [46, 47, 48, 49, 50, 51, 36, 76, 77, 78] we consider that the polymer networks undergo a sigmoidal volume phase transition in the vicinity of a crossover concentration $c_{\text{\tiny c}}$. We assume the following form

where $\Delta\phi=(\phi_{\text{\tiny max}}-\phi_{\text{\tiny min}})$ is the maximum change, and $\phi_{\text{\tiny c}}=\phi(c_{\text{\tiny c}})=(\phi_{\text{\tiny min}}+\phi_{\text{\tiny max}})/{2}$ the polymer volume fraction at $c_{\text{\tiny c}}$. Hence, we call ($c_{\text{\tiny c}},\phi_{\text{\tiny c}}$) the crossover point. The transition may occur from a swollen state ($\phi_{\text{\tiny min}}$) to a collapsed state ($\phi_{\text{\tiny max}}$) or vice versa as $c_{\text{\tiny in}}$ increases (denoted by the ‘$\pm$’-symbol in Eq. 15), depending on the interactions between the solutes, the solvent, and the polymer. Effectively attractive solute-membrane interactions ($B<0$) are expected to cause a swollen-to-collapsed transition ($+$), while a transition from the collapsed to the swollen phase ($-$) is expected for repulsive interactions ($B>0$). Further, the parameter $\Delta c$ determines the sharpness of the transition, ranging from almost irresponsive ($\Delta c\gg c_{\text{\tiny c}}$) to very sharp transitions ($\Delta c\ll c_{\text{\tiny c}}$).

Note that Eq. 15 assumes continuous transitions although hysteresis has been reported in experimental studies.[49, 77, 79, 80] However, this work will demonstrate that hysteresis and bistability can result from the mutual dependencies of $\phi$ and $c_{\text{\tiny in}}$.

Furthermore, Eq. 15 is a mean-field approach as it does not resolve spatial inhomogeneities of $\phi$ and $c_{\text{\tiny in}}$ [cf. the example concentration profile in Fig. 2(a)]. We assume that the system is small and that the thin membranes do not change the width in the direction of the solute flux. Despite the multiple assumptions, our simplified model enables the investigation of the effect of a responsive membrane permeability on the transport.

All length scales are expressed in units of $\sigma$, the effective diameter of one monomer. We set the system size to $L=100\sigma$ and fix the membrane width to $d=90\sigma$, i.e., the boundary layers between the membrane and the two bulk reservoirs with concentration $c_{0}$ have the width $5\sigma$. The concentrations $c_{0}$, $c_{\text{\tiny in}}$ and the transition width $\Delta c$ are rescaled by the crossover concentration $c_{\text{\tiny c}}$ of the volume phase transition [Eq. 15]. We choose three different transition widths, $\Delta c/c_{\text{\tiny c}}\in\mathopen{}\mathclose{{\left\{0.1,1.0,10}}\right\}$. The force, $\beta f\sigma$, is rescaled by the thermal energy and the solute size. The solute diffusivity inside the membrane, $D_{\text{\tiny in}}$, and the permeability, $\mathcal{P}$, are expressed in units of the solute bulk diffusivity $D_{0}$. The parameters $A$ and $B$, which enter $D_{\text{\tiny in}}(\phi)$ [Eq. 9] and $\mathcal{K}(\phi)$ [Eq. 10], respectively, as well as the limits of the polymer volume fraction, $\phi_{\text{\tiny min}}=0.05$ and $\phi_{\text{\tiny max}}=0.35$, are based on our group’s coarse-grained simulations.[68, 70] We fix $A=5$, assuming that the diffusion is dominated by steric exclusion. The interaction parameter $B$ is chosen in a way to yield three different values for the equilibrium membrane permeability at $\phi_{\text{\tiny c}}=0.2$, and, hence, we denote the membranes as repulsive ($\mathcal{P}_{\text{\tiny mem}}(\phi_{\text{\tiny c}})/D_{0}=0.1$), neutral ($\mathcal{P}_{\text{\tiny mem}}(\phi_{\text{\tiny c}})/D_{0}=1.0$), and attractive ($\mathcal{P}_{\text{\tiny mem}}(\phi_{\text{\tiny c}})/D_{0}=10.0$). In fact, due to typical cancelling effects of $\mathcal{K}(\phi)$ and $D_{\text{\tiny in}}(\phi)$,[68, 70] we can safely assume that the permeability of our neutral membrane does not significantly deviate from unity throughout the range of $\phi$. In a system with Lennard-Jones (LJ) interactions between the solutes and the membrane monomers of equal size, the characteristic LJ interactions strengths would take the approximate values $\beta\varepsilon\approx 0.03$ (repulsive), $\beta\varepsilon\approx 0.55$ (weakly attractive), and $\beta\varepsilon\approx 0.9$ (attractive), respectively. All parameter values and relevant quantities are summarized in Table 1.

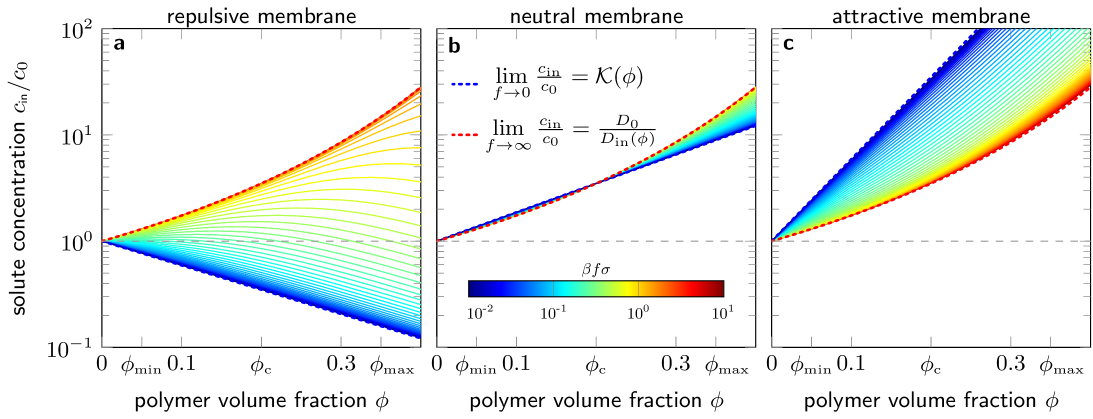
From Eq. 14, the low- and high-force limits for the mean solute concentration inside the membrane, $c_{\text{\tiny in}}$, can be deduced, which has been discussed and substantiated with concentration profiles from theory and coarse-grained simulations in our previous work.[65] Here, we recapture the main findings and discuss the results for the parameters used in this work.

In Fig. 3, we depict $c_{\text{\tiny in}}$ [Eq. 14] as a function of $\phi$ for different values of $\beta f\sigma\in\mathopen{}\mathclose{{\left[0.01,10}}\right]$ (color-coded) and for three different values of $\mathcal{P}_{\text{\tiny mem}}(\phi_{c})/D_{0}\in\mathopen{}\mathclose{{\left\{0.1,1.0,10.0}}\right\}$ (different panels). In the zero force limit, $c_{\text{\tiny in}}$ reduces to the expected equilibrium value, $\lim_{f\to 0}c_{\text{\tiny in}}=c_{0}\mathcal{K}(\phi)$, which monotonously decreases for the repulsive membrane [panel (a)] and increases otherwise [panels (b) and (c)]. The same limiting result is obtained, if $\mathcal{P}_{\text{\tiny mem}}(\phi)=D_{0}\ \forall\phi$, which applies approximately for the ‘neutral’ membrane [panel (b)]. In the high-force limit, the concentration profiles become piecewise constant with $\lim_{f\to\infty}c_{\text{\tiny in}}=c_{0}D_{0}D_{\text{\tiny in}}^{-1}(\phi)$, and one further finds $\lim_{f\to\infty}j=c_{0}\beta fD_{0}=c_{\text{\tiny in}}\beta fD_{\text{\tiny in}}$ for all membrane types, since it is independent of $\mathcal{K}$.

The solute uptake of the repulsive membrane at fixed $\phi$ increases with $f$, while it decreases in the attractive membrane [see Figs. 3(a) and 3(c) ]. For ‘neutral’ membrane [panel (b)], $c_{\text{\tiny in}}$ shows no significant force dependence.

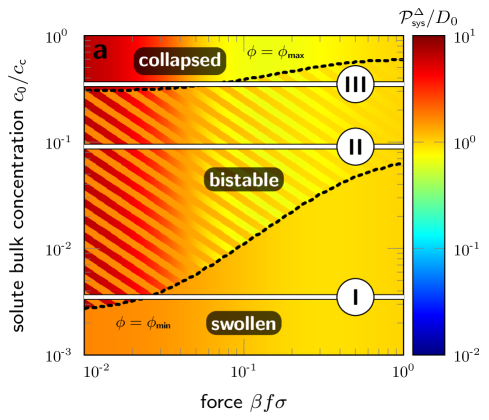
With Eqs. 15 and 14 the feedback loop depicted in Fig. 1 is closed. We obtain numerically the steady-state solutions, $(c_{\text{\tiny in}}^{*},\phi^{*},)$, by finding the intersection points of $c_{\text{\tiny in}}(\phi,f)$ and $\phi(c_{\text{\tiny in}})$ in the phase plane. In this section we show the results with the attractive membrane only and demonstrate the general procedure. (For the repulsive membrane, we show a representative phase plane in Fig. 7 in Appendix C.)

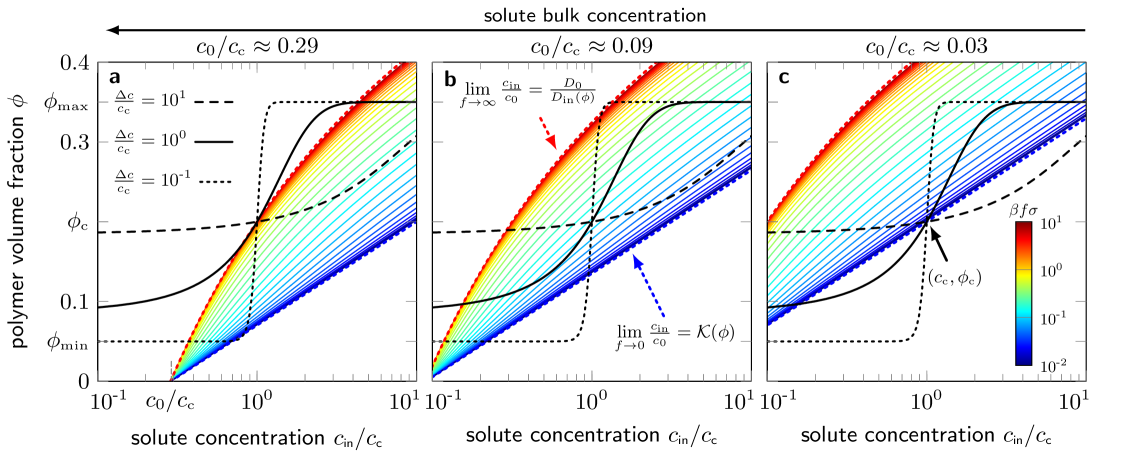
In Fig. 5, the black lines depict the polymer’s volume phase transition of $\phi(c_{\text{\tiny in}})$, Eq. 15, for three different values of $\Delta c/c_{\text{\tiny c}}\in\mathopen{}\mathclose{{\left\{0.1,1,10}}\right\}$. The colored lines, $c_{\text{\tiny in}}(c_{0},f,\phi)$, Eq. 14, are the inverted images of Fig. 3(c) and are plotted in Fig. 5 for three different bulk concentrations, $c_{0}$, from high [panel (a)] to low values [panel (c)]. As obvious, changing $c_{0}$ performs a shift of $c_{\text{\tiny in}}(c_{0},f,\phi)$ along the horizontal axis. In panel (a), we choose $c_{0}=c_{\text{\tiny c}}D_{\text{\tiny in}}(\phi_{c})/D_{0}\approx 0.29$ such that the high-force limit of $c_{\text{\tiny in}}$ intercepts with the crossover point $(c_{\text{\tiny c}},\phi_{\text{\tiny c}})$. In panel (c), we impose that the low-force limit intercepts with the crossover point, i.e., $c_{0}=c_{\text{\tiny c}}/(\mathcal{K}(\phi_{c})\approx 0.03$. In panel (b), the geometric mean, $c_{0}=c_{\text{\tiny c}}\sqrt{D_{\text{\tiny in}}(\phi_{c})/(D_{0}\mathcal{K}(\phi_{\text{\tiny c}}))}\approx 0.09$ is used as intermediate probe concentration.

For fixed $f$, $c_{0}$ and $\Delta c$, we find one or three interception points of $c_{\text{\tiny in}}(c_{0}f,\phi)$ and $\phi(c_{\text{\tiny in}})$, yielding the steady-state solutions, $\mathopen{}\mathclose{{\left(c_{\text{\tiny in}}^{*},\phi^{*}}}\right)$. In Fig. 5(b), for instance, the low-force limit (blue dotted line) intercepts with the black solid line ($\Delta c/c_{\text{\tiny c}}=1$) only once at $\phi^{*}\approx\phi_{\infty}$, while it has three interceptions with the black dotted line ($\Delta c/c_{\text{\tiny c}}=0.1$) at $\phi_{1}^{*}\approx\phi_{\text{\tiny min}}$, $\phi_{2}^{*}\approx 0.15$, and $\phi_{3}^{*}\approx\phi_{\text{\tiny max}}$. In the case of triple solutions, the intermediate one is an unstable solution, while the other two are stable solutions. Precisely, the latter correspond to asymptotically stable solutions of the time-dependent Smoluchowski equation, $\dot{c}(z,t)=-\partial j(z)/\partial z$, i.e., the steady-state solution, $c^{*}(z)$, is restored after a small perturbation. A more detailed discussion on the stability of multiple solutions and consequences for the bistable domains is provided in a separate section below.

We summarize the steady-state solutions for the attractive membrane by plotting $\phi^{*}(f)$ for different $c_{0}$, and $\Delta c$ in Fig. 5. We observe a swelling (decrease in $\phi$) with hysteresis due to an increase in $f$ [see panels (a), (b), and (e)]. In more detail, higher $c_{0}$ can shift the force-induced $\phi$-transition to higher force values [e.g., compare panels (a) and (b)] and whether transitions may occur at all. For instance, as in the case of low transition sharpness, $\Delta c/c_{\text{\tiny c}}=10$, and low solute concentration [panel (c)], there is no significant effect on $\phi^{*}$. Similarly for the moderate sharpness, $\Delta c/c_{\text{\tiny c}}=1$, no transition is induced if $c_{0}$ is too high [panel (d)].

Further, $\Delta c$, plays an important role as it tunes the width of the bistable domains, e.g., while only small force ranges with bistability are observed for weakly responsive membranes ($\Delta c/c_{\text{\tiny c}}=10$), see Figs. 5(a) and 5(b), it can exist in the entire force range for sufficiently sharp transitions ($\Delta c/c_{\text{\tiny c}}=0.1$), see Figs. 5(g) and 5(h).

We already conclude that the membrane’s feedback response can lead to large bistable domains in $\phi$ tuned by $f$ and $c_{0}$, which is characterized by drastic switching of the membrane properties, such as the permeability, due to the bifurcations at the critical values.

The flux $j(f)$, given by Eq. 13, is a nonlinear function of $f$ determined by two contributions: The change in the membrane permeability $\mathcal{P}_{\text{\tiny mem}}(\phi)$ (due to the change in $\phi$) and the spatial setup (see Appendix A and our previous work[65]). The nonlinear characteristics of $j(f)$ are quantified by the differential system permeability,[65] defined as

which describes the change in the steady-state flux induced by a change in the external driving force.

We make use of $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}(f)$ to highlight the novel nonlinear effects on $j(f)$ caused by the membrane’s feedback response. We limit ourselves to the very sharp membrane response ($\Delta c/c_{\text{\tiny c}}=0.1$), and point out the significant difference between the fluxes in attractive and repulsive membranes.

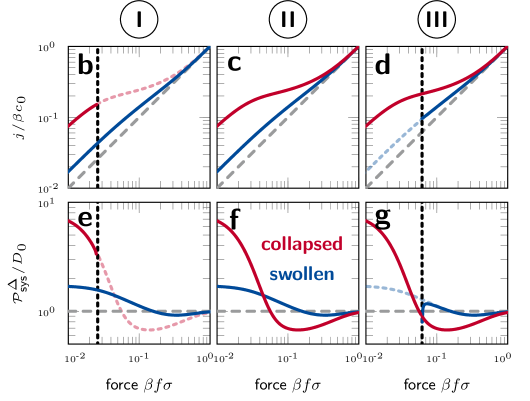
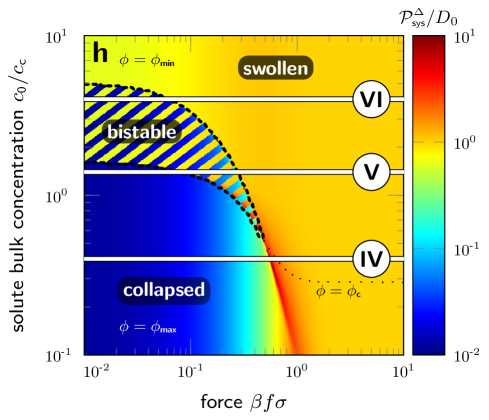
In Fig. 6, we present heatmaps of $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}$ in the $f$-$c_{0}$ plane for the attractive [panel (a)] and the repulsive membrane [panel (h)]. The white lines labeled with roman numerals depict selected values of $c_{0}$, and correspond to the panels below, showing $j$ and $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}$. The heatmaps share the same color-scale (see colorbars), allowing a direct comparison between the results of attractive and repulsive membranes.

The attractive membrane exhibits, in general, larger $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}$ values than the repulsive one, particularly in the low-force and collapsed regime ($\phi=\phi_{\text{\tiny max}}$), in which the influence of $\mathcal{P}_{\text{\tiny mem}}$ is the greatest. For $f\to 0$, we find $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}\approx 7D_{0}$ and $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}\approx 0.01D_{0}$ for the attractive and repulsive membrane in the collapsed state, respectively. In the high-force limit, the system permeability converges to $D_{0}$ irrespective of the volume phase. If the membrane is swollen ($\phi=\phi_{\text{\tiny min}}$), the permeability of the repulsive and the attractive membrane are of the same order of magnitude, i.e., $\mathcal{P}_{\text{\tiny mem}}(\phi_{\text{\tiny min}})\approx 0.6D_{0}$ and $\mathcal{P}_{\text{\tiny mem}}(\phi_{\text{\tiny min}})\approx 2D_{0}$, respectively, and $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}$ does not deviate significantly from bulk diffusivity $D_{0}$, even for low forces (compare blue lines in lower panels of Fig. 6).

Due to the sharp response with $\Delta c=0.1c_{c}$, the membrane is either fully swollen ($\phi_{\text{\tiny min}}$), or fully collapsed ($\phi_{\text{\tiny max}}$). Moreover, this also leads to large bistable domains in the $c_{0}$-$f$ plane, visualized as striped patterns in Figs. 6(a) and 6(h). Crossing the boundary of these domains leads to a discontinuous volume phase transitions accompanied with an order of magnitude change in the solute flux (examples I, III, V, and VI). In the case of the repulsive membrane, the flux can be switched even by two orders of magnitude, particularly for small $f$.

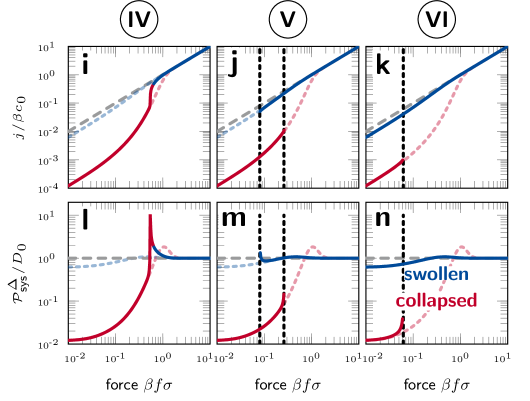
In examples I-VI [Figs. 6(b)–6(g), and 6(i)–6(n)], we also depict the results for nonresponsive membranes in the fully swollen and collapsed case for comparison. In the nonresponsive case, $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}$ can also be tuned in the same range by only controlling $f$. Nonetheless, the membrane’s responsiveness brings about more dramatic effects, such as bistability (I, III, V, VI) and hysteresis (V), yielding new control mechanisms to switch between two flux states. While nonresponsive membranes require large forces to exhibit bulk-like properties ($D_{0}$), a transition to this neutral state can be achieved in responsive membranes in a much sharper fashion and for lower force values, e.g., see Fig. 6 I, V, and VI. In V, for example, the crossover from the low- to the high-permeability state occurs abruptly around $\beta f\sigma\approx 0.2$ (red solid line), whereas for the collapsed, nonresponsive membrane a gradual change is observed in the range $\beta f\sigma\approx 0.1-1.0$.

Further, even if the polymer volume phase transition occurs without bifurcation, nonlinearities in the force–flux relations can be significantly enhanced. For instance, in panel (l) (example IV), we find a tenfold maximization of $\mathcal{P}^{\text{\tiny$\Delta$}}_{\text{\tiny sys}}\approx 12D_{0}$ at roughly $\beta f\sigma\approx 0.5$, which even exceeds the maximum differential system permeability measured for the attractive membrane.

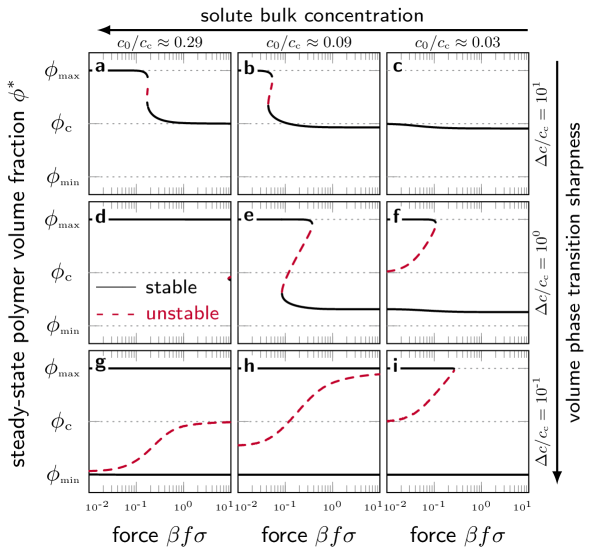
Our model results into well-defined force–flux relations in the domains with unique steady-state solutions. In the bistable domains, however, the question arises whether the states coexist or whether only one survives under real conditions. This far, the solutions were simply deduced from a deterministic interpretation of the macroscopic model equations, i.e., by evaluating the self-consistency equation $c_{\text{\tiny in}}=R(c_{\text{\tiny in}})$, with $R(c_{\text{\tiny in}})=d^{-1}\int_{\text{\tiny in}}c(z,\phi(c_{\text{\tiny in}}))\mathrm{d}z$. The steady state is asymptotically stable, if ${\mathrm{d}R(c_{\text{\tiny in}})}/{\mathrm{d}c_{\text{\tiny in}}}|_{c_{\text{\tiny in}}^{*}}<1$.[81] However, our approach neglects larger fluctuations in $\phi$ and $c_{\text{\tiny in}}$, and does not analyze further nonequilibrium extremum principles.[82] In the following, we first discuss the consequences of the deterministic perspective, and then briefly review alternative interpretations.

In the case of negligible fluctuations the (deterministic) transition between states can be either reversible or irreversible.[35] One reversible transition is example V [Figs. 6(j) and 6(m)]. Here, the membrane is in the collapsed state (red line) for small $f$. With increasing $f$, the membrane is driven into the bistable regime, yet remains in the collapsed state. Only if $f$ exceeds the second bifurcation line, the membrane swells. In the same example V, if $f$ is decreased from high force values, the membrane stays swollen in the bistable domain and returns to the collapsed state until the first bifurcation line is passed. Hence, we find a reversible transition with hysteresis between the two state in V.

In contrast, consider example I or VI, and assume that the membrane is in the collapsed state at $f=0$, an increase in $f$ leads to a swelling when the bifurcation line is crossed. Decreasing the force again, however, does not induce a collapse, and, hence, this transition can be termed irreversible in the deterministic interpretation. This is because only the swollen case survives once the threshold is surpassed. Analogously, see example III, a collapsed-to-swollen transition cannot be induced by increasing $f$.

Although two stable states may coexist in the deterministic model, one of them could be metastable and practically unoccupied under experimental conditions. In literature one finds nonequilibrium principles, e.g., based on the maximization of entropy, the minimization of entropy production (least dissipation), or the minimization of power, providing various possible routes.[83, 84, 85, 86, 31, 87, 88, 89, 82, 90] Such extremum principles may lead to unique solutions in the bistable regime, and to different values for $f$ and $c_{0}$, where the switching between the high and low flux states occurs. For example, it should be the minimum flux, if the least-dissipation principle applies. This has direct consequences on the flux–force relation and the critical transition values of $f$ and $c_{0}$, where the phase transition in V would occur always at the first bifurcation line, i.e., without bistability and hysteresis.

Furthermore, the presented diffusion process can also be modeled with the stochastic Smoluchowski equation,[91] and possibly further coarse-grained to a stochastic differential equation for $\dot{c}_{\text{\tiny in}}$.[92, 93] Hence, given the fluctuations are large enough, a stochastic switching between the two steady states may be observed in the bistable domains, and the effective force–flux relations are determined by the averaged values of $\phi$ and $c_{\text{\tiny in}}$. Consequently, changing $f$ results in a continuous transition between the two states, implying that example V does not exhibit hysteresis behavior, but is rather similar to the transition in example IV.

Ultimately, the appropriate stability interpretation remains to be verified, and is likely specific to the membrane material and the experimental nonequilibrium conditions. Nonetheless, a strong amplification of nonlinear characteristics and a critical switching in the force–flux relations can be expected due to the membrane’s responsiveness.

The authors have no conflicts to disclose.