11email: nidong@szu.edu.cn
Medical Ultrasound Image Computing (MUSIC) Lab, Shenzhen University, China
Marshall Laboratory of Biomedical Engineering, Shenzhen University, China
School of Biomedical Engineering and Informatics, Nanjing Medical University, China
Shenzhen RayShape Medical Technology Co., Ltd, China
Shenzhen People’s Hospital, Second Clinical Medical College of Jinan University, China
FFPN: Fourier Feature Pyramid Network for Ultrasound Image Segmentation
Abstract
Ultrasound (US) image segmentation is an active research area that requires real-time and highly accurate analysis in many scenarios. The detect-to-segment (DTS) frameworks have been recently proposed to balance accuracy and efficiency. However, existing approaches may suffer from inadequate contour encoding or fail to effectively leverage the encoded results. In this paper, we introduce a novel Fourier-anchor-based DTS framework called Fourier Feature Pyramid Network (FFPN) to address the aforementioned issues. The contributions of this paper are two fold. First, the FFPN utilizes Fourier Descriptors to adequately encode contours. Specifically, it maps Fourier series with similar amplitudes and frequencies into the same layer of the feature map, thereby effectively utilizing the encoded Fourier information. Second, we propose a Contour Sampling Refinement (CSR) module based on the contour proposals and refined features produced by the FFPN. This module extracts rich features around the predicted contours to further capture detailed information and refine the contours. Extensive experimental results on three large and challenging datasets demonstrate that our method outperforms other DTS methods in terms of accuracy and efficiency. Furthermore, our framework can generalize well to other detection or segmentation tasks.
1 Introduction
Recently, real-time, accurate and low-resource image segmentation methods have gained wide attention in the field of ultrasound (US) image analysis. These methods provide the basis for many clinical tasks, e.g. structure recognition [11], bio-metric measurement [13] and surgical navigation [2]. Fig. 1 illustrates the segmentation tasks we have accomplished in this paper, including the apical two-chambers heart(2CH) dataset, Camus dataset [8] and Fetal Head (FH) dataset.

Numerous segmentation methods based on deep learning have been proposed, most of which mainly rely on U-shaped networks, such as U-Net [12], nnU-Net [6], and SwinU-Net [1]. The excessive skip-connections and upsampling operations in these methods make the model sacrifices efficiency and resources to ensure accuracy. DeeplabV3 [3] is another commonly used segmentation framework, and it also sacrifices efficiency due to the design of multiscale embedding. In addition, these methods all face the issue of false positive segmentation due to the blurred boundaries in US images. Thus, Mask R-CNN [5] uses the bounding box (b-box) as a constraint on the segmentation region, which reduces the false positive. However, the serial scheme limits its efficiency and excessive reliance on the b-box’s output also affects its segmentation performance.
In order to balance resource consumption, efficiency and performance, detect-to-segment (DTS) framework has received significant attention in recent years. The core idea of DTS is to transform the pixel classification problem of an image into the regression and classification problem for each point on the feature map. By this way, each point on the feature map can predict multiple contour proposals. PolarMask [16] used a polar coordinate system for image segmentation, and it is difficult to process the situation that a ray intersects the object multiple times at a special direction. Point-Set [15] uniformly sampled several ordered points to represent the contour. PolySnake [4] designed a multiscale contour refinement module to refine the initial coarse contour. While these sample-based encoding methods are capable of representing contours, many of the points within them do not contain valid information and there is a lack of correlation between points. Consequently, these encoding methods may not be suitable for segmentation tasks. To enhance the encoding results of complex contours, Ellipse Fourier Description [7] (EFD) scheme (Fig. 2 (a)) entered the vision of many researchers [18, 17, 14]. FCENet [18] and FANet [17] represent the text instance in the Fourier domain, allowing for fast and accurate representation of complex contours. CPN [14] revisited the EFD scheme to represent cell instance segmentation and achieved promising results. Although these EFD-based methods achieves high performance comparable to Pixel-based methods, they only consider the scale characteristics but ignore the frequency characteristics of the Fourier expansion, as shown in Fig. 2 (b), resulting in sub-optimal performance.
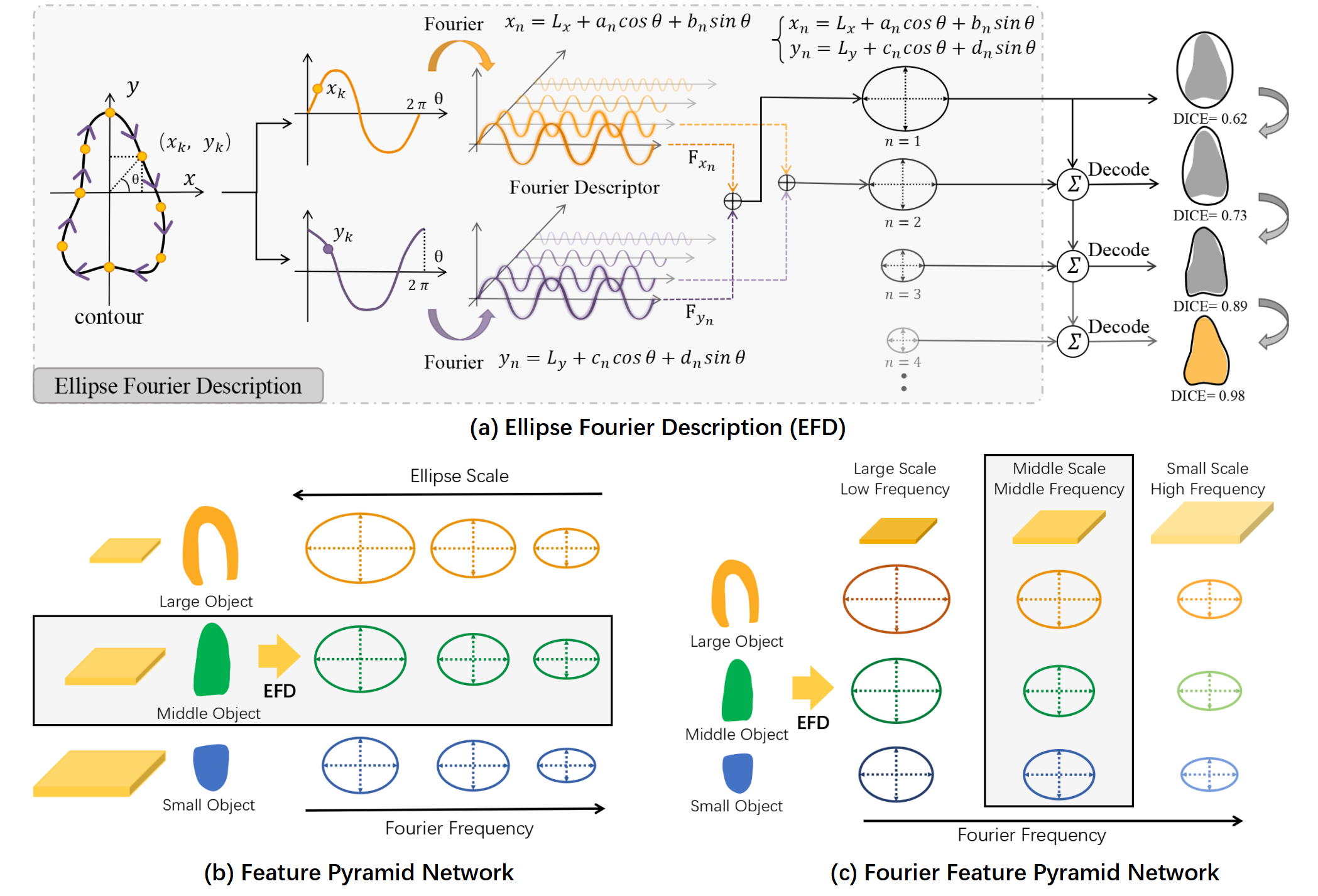
In this study, we revisited the EFD from another perspective, as shown in Fig. 2 (b) and (c). When the closed contour is expanded with Fourier, we focus on both the scale and frequency among different levels of Fourier series, and ingeniously incorporating it into the FPN [10] to devise a novel Fourier-anchor-based framework, named Fourier Feature Pyramid Network (FFPN). Our contributions are two fold. First, we design FFPN to assign Fourier series with similar informcation to the same feature map for collective learning (Fig. 2 (c)). This approach enhances the consistency of feature representation and improves the model’s ability to predict encoded results with better accuracy. Second, considering the complexity and blurring of object contours in US images, we propose a Contour Sampling Refinement (CSR) module to further improve the model’s ability to fit them. Specifically, we aggregate features at different scales in FFPN and extracted the relevant features around the contours on the feature map to rectify the original contour. Experimental results demonstrate that FFPN can stably outperform DTS competitors. Furthermore, our proposed FFPN is promising to generalize to more detection or segmentation tasks.
2 Methodology
Fig. 3 is the overview of our FFPN framework. Given an image, we first use the backbone with FPN to extract the pyramidal features. Then these features are unsampled to obtain Fourier pyramidal features. Next, we feed Fourier pyramidal features into different detector heads to generate different levels of Fourier series offsets, location offsets and classification scores. EFD decodes these predictions to the contour proposals. In CSR, the Fourier pyramid features are concatenated to generate the refinement features. Finally, the contour proposals and refinement features together are used to produce the final results.
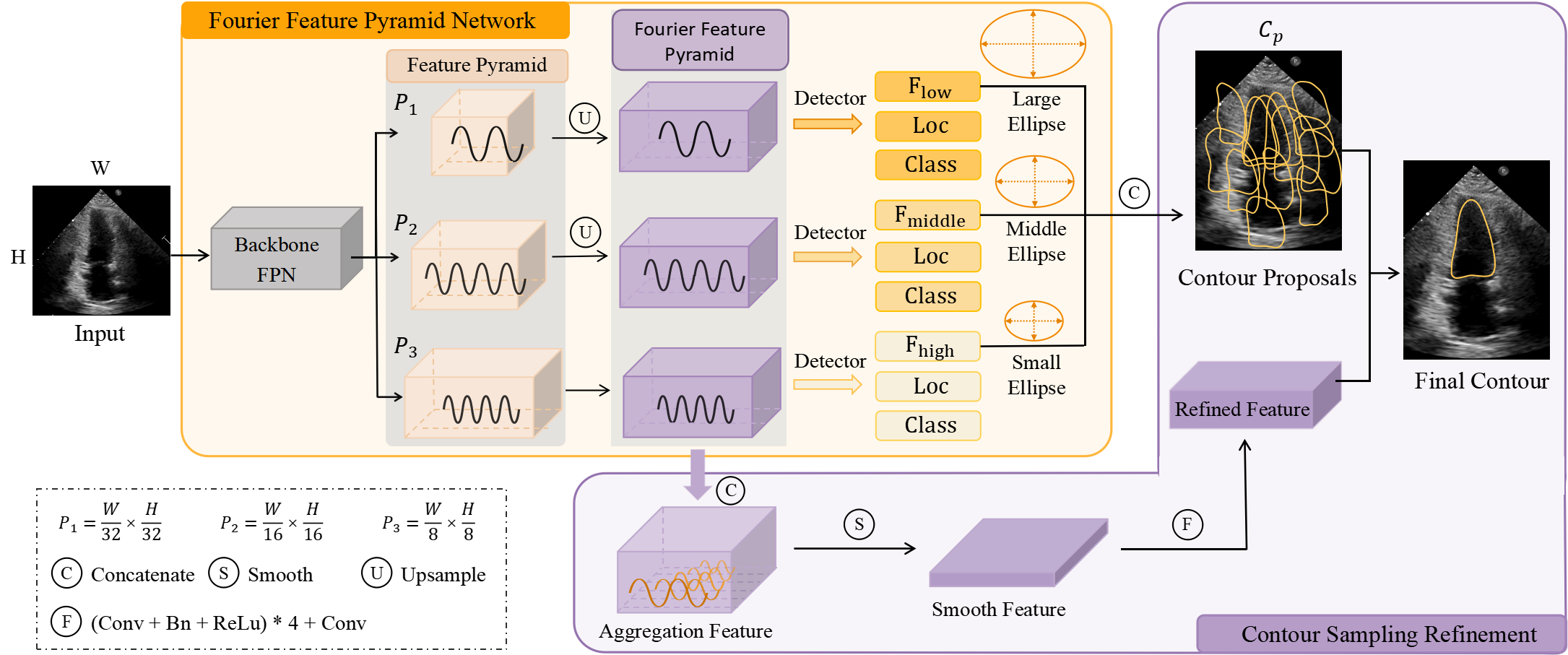
2.1 Fourier Feature Pyramid Network(FFPN)
Inspired by EFD (Fig. 2 (a)), the contour can be described as the Fourier series:
| (1) |
where is the -th sampled point on the contour, and the number of sampled points are set to , e.g. . is the number of Fourier series expansions. indicates the coordinates of the center point of the contour. denote the parameters obtained by Fourier coding of the x-coordinates of all contour points, and denote the corresponding parameters in the y-coordinates. Thus, the goal of FFPN is to accurately predict the parameters to represent the contour ( by default).
According to EFD (Fig. 2 (a)), the low-level Fourier series represent the contour’s low-frequency information and main scales, while the high-level Fourier series capture the contour’s high-frequency information and shape details. This is consistent with the extracted pyramidal features, where the low-level features contain more detailed information, while the high-level features capture semantics. Therefore, the proposed FFPN effectively aggregates Fourier series of similar scales and frequencies into the same feature map (as illustrated in Fig. 2 (c)). Then, different level features of feature pyramid are fed into different detector heads with the same architecture (three sibling 3x3 Conv-BN-ReLUs followed by a 3x3 Conv) to generate Fourier offsets, location offsets and classification scores (, and with yellow blocks in Fig. 3.). The up-sampling operations on the and features are only to align the scale and simplify subsequent operations. Next, the different level Fourier offsets are concatenated along the channel dimension to predict contour proposals. To simplify the calculation, location offsets and classification scores at different levels are averaged along the channel dimension. The learning objectives are as follows:
| (2) |
where the tuple represents the Ground truth(GT) of the Fourier series, and denotes the Fourier series of anchor. denotes the -th of the Fourier expansion. The Fourier expansion of each level can be expressed as an ellipse, as shown in Fig. 2 (a). and denote the width and height of the ellipse at level , respectively. is the center point coordinates of the GT contour, and is the center point coordinates of the anchor. are the learning objectives. Through the encoding operation of Eq. 2, we normalize the amplitude of Fourier series and center point coordinates to the same scale, simplifying the learning difficulty. The loss function is defined as follows:
| (3) |
The loss function about Location and Fourier are Smooth L1 Loss, and the classification loss is , where and . The contour loss is defined as , where the follows [16] and the is defined as the IoU between outline bounding boxes. The method to calculate IoU in this paper is defined as , which is a simple but effective way.
2.2 Contour Sampling Refinement (CSR) Module
Considering the complexity of contour representation, we adopt the two-stage strategy inspired from the detection frameworks [10, 5]. Unlike CPN [14] where the contour is directly optimized to destroy its smoothness or FANet [17] where the Fourier series of the contour needs to be refined iteratively, we refine once the Fourier series of the aggregation averaged contour. This strategy improves the model accuracy while ensures the boundary smoothness. Specifically, as shown in Fig. 3, we fuse pyramidal features as the refined-feature. And the top-n outputs of FFPN are the contour proposals to represent the same object. Thus, the refined-feature and the are the input of CSR module.
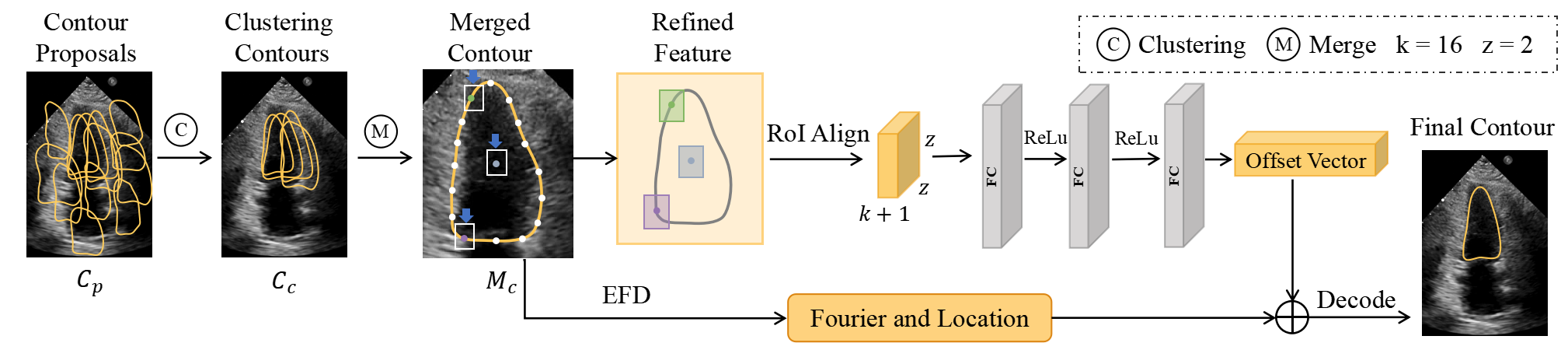
Fig. 4 demonstrates the workflow of CSR. First, we extract the closely clustered contours in . The definition of closely clustered is that: at least one contour exists, and the IoU of this contour with all the remaining contours is greater than a threshold . Second, we obtain the merged contour of the object by averaging the directly. We think that, as the network learns iteratively, has a high confidence in fitting the object. Thus, we extract the feature around to further refine . Concretely, we use the uniform point sampling approach to sample out sampling points, indicating the boundary points and one center point of the contour. To extract the features around the contour, we use the sampled points as center points to generate boxes to obtain rich information on refined-feature. RoI-Align module is used in this stage. Finally, these extracted features are passed through a three-layer Multi-Perceptron module to generate the Fourier and center point offsets. The losses used in CSR are same as FFPN, including , and . It is worth noting that the anchor information used at this stage is generated by , which draws on the common configuration of a two-stage detection framework.
3 Experimental Results
To validate the performance of our FFPN, we conducted comprehensive comparisons among our method and other segmentation methods, including DTS methods and Pixel-based methods. Additionally, we also compare FFPN with FFPNCSR (FFPN-R) to validate the effectiveness of CSR.
Datasets. We assess FFPN’s performance across three datasets (Fig. 1). Approved by local IRB, the 2CH dataset, comprising 1731 US images, is utilized for left ventricle (LV) segmentation, while the FH dataset, containing 2679 US images, is employed for fetal head segmentation. The Camus [8] dataset contains 700 US images and requires the segmentation of three structures, including the LV, left atrium (LA) and myocardium (MC). Both the 2CH dataset and the FH dataset have been manually annotated by experts using the Pair [9] annotation software package. Each dataset undergoes a random split into training (70%), validation (10%), and testing (20%) subsets.
Experimental Settings. To conduct a fair comparison, all methods implemented in Pytorch and under the same experiment settings, including learning rate (1e-3), input size (directly resized to 416x416), total epochs (200), one RTX 2080Ti GPU and so on. We evaluate the model performance using dice similarity coefficient (DICE), Hausdorff distance (HD), Intersection over Union (IoU) and Conformity (Conf) for all the experiments. Memory (Mem) and FPS are employed to evaluate the models’ memory usage and efficiency. As for the settings of FFPN, the Fourier-anchors are generated by contour clustering of the training set, each dataset has 9 base anchors. The IoU threshold for positive and negative samples are 0.25 and 0.10 respectively, and the others are ignored samples.
| DATASET | 2CH | FH | Model | ||||||
| DICE() | IoU() | HD(pixel) | Conf() | DICE() | HD(pixel) | Conf() | Mem(G) | FPS | |
| U-NET | 88.95(4.95) | 80.45(7.55) | 22.41(18.80) | 74.40(13.95) | 94.92(3.27) | 18.1(16.43) | 90.78(6.87) | 1.33 | 19.71 |
| DeepLabV3 | 88.92(5.06) | 80.40(7.69) | 19.98(12.14) | 74.26(14.55) | 95.89(2.56) | 16.63(22.59) | 91.27(6.33) | 0.49 | 15.83 |
| Swin U-NET | 88.83(4.63) | 80.21(7.21) | 20.25(10.28) | 74.20(12.67) | 95.81(1.38) | 15.30(5.67) | 91.21(3.10) | 2.27 | 9.81 |
| Mask RCNN | 79.50(6.71) | 66.48(9.04) | 47.53(13.87) | 46.51(22.90) | 82.60(2.33) | 58.24(6.73) | 57.64(7.10) | 0.43 | 20.33 |
| PolarMask | 84.54(14.65) | 77.42(13.15) | 34.13(25.81) | 58.96(78.22) | 94.25(5.31) | 25.96(15.12) | 64.28(489.90) | 0.52 | 15.43 |
| PolySnake | 86.50(6.05) | 76.67(8.73) | 22.75(13.05) | 67.48(18.82) | 92.11(4.39) | 22.95(11.46) | 82.32(11.43) | 0.17 | 14.73 |
| CPN | 87.62(6.23) | 78.47(9.02) | 23.81(15.81) | 72.61(15.30) | 94.00(5.93) | 22.73(22.89) | 86.17(16.83) | 0.20 | 27.20 |
| FFPN | 88.16(5.97) | 79.30(8.88) | 21.10(14.34) | 71.93(18.15) | 95.56(2.40) | 13.90(8.84) | 90.55(6.56) | 0.20 | 41.52 |
| FFPN-R | 89.08(5.24) | 80.70(8.10) | 19.76(12.52) | 74.64(14.55) | 96.73(1.11) | 10.24(4.13) | 93.21(2.43) | 0.23 | 33.52 |
Quantitative and Qualitative Analysis. As demonstrated in Table 1, FFPN exhibits superior performance compared to feasible DTS methods and achieves comparable performance when compared to effective Pixel-based methods in both the 2CH dataset and FH dataset. Specifically, comparing to the recently proposed method PolySnake, FFPN increases DICE by 1.66% and 3.45%, while simultaneously reducing HD by 1.65 pixels and 9.05 pixels on the 2CH dataset and FH dataset, respectively. This demonstrates the effectiveness of our encoding approach based on EFD. Moreover, in comparison to CPN, which follows the same encoding approach, FFPN improves DICE by 0.54% and 1.56%, and decreases HD by 2.71 pixels and 8.83 pixels on the two datasets, respectively. This fully proves that FFPN effectively utilizes Fourier information by mapping Fourier series with similar scales and frequencies into the same layer of the feature map. Furthermore, FFPN-R is capable of outperforming all methods in all metrics on the two datasets. This demonstrates the effectiveness of CSR, particularly in its ability to capture detailed information and refine contours.
Experimental results on computing resource consumption and efficiency are shown in the column of Table 1. FFPN achieves an impressive inference speed of 41.52 FPS with a memory consumption of only 0.2 GB, making it the fastest among all DTS and Pixel-based methods. Compared with PolySnake which has the smallest memory footprint, FFPN increases memory usage by only 17.6% while improving its speed by 182.0%. Furthermore, by incorporating CSR, FFPN-R achieves the best accuracy performance at a slight cost of increasing memory consumption by 15.0% and reducing inference speed by 19.5% FPS. Despite this minor trade-off, FFPN-R still exhibits superior resource consumption and efficiency compared to all Pixel-based and most DTS methods.
| LA | MC | LV | Mean | |||||
| DICE() | HD(pixel) | DICE() | HD(pixel) | DICE() | HD(pixel) | DICE() | HD(pixel) | |
| U-NET | 87.74(9.81) | 28.88(32.99) | 86.03(4.45) | 22.43(21.84) | 92.06(4.01) | 22.43(28.94) | 88.61(6.09) | 24.58(27.78) |
| DeepLabV3 | 88.93(6.34) | 22.84(21.91) | 87.84(4.04) | 17.49(13.05) | 92.79(4.02) | 16.51(9.36) | 89.85(4.80) | 18.69(18.80) |
| Swin U-NET | 87.28(9.47) | 26.39(24.97) | 86.38(4.32) | 19.31(8.60) | 91.73(4.71) | 18.68(11.69) | 88.46(6.17) | 21.46(15.10) |
| Mask RCNN | 76.83(18.61) | 43.38(40.57) | 55.99(26.54) | 66.78(84.70) | 75.16(16.99) | 53.95(32.10) | 69.33(20.71) | 54.70(52.46) |
| PolarMask | 81.56(20.44) | 40.91(16.25) | 27.28(21.16) | 59.92(12.98) | 81.56(20.44) | 42.67(37.64) | 65.75(16.23) | 47.83(22.29) |
| PolySnake | 83.77(17.23) | 22.99(19.92) | 43.65(32.27) | 21.82(11.43) | 89.58(9.80) | 19.72(11.30) | 72.33(19.77) | 21.51(14.21) |
| CPN | 87.11(13.68) | 27.35(37.09) | 69.17(25.75) | 41.58(58.22) | 92.08(5.06) | 19.26(13.62) | 82.79(14.83) | 29.40(36.31) |
| FFPN | 87.37(8.39) | 23.81(17.18) | 82.52(6.59) | 23.63(9.83) | 91.35(4.36) | 20.02(11.12) | 87.08(7.57) | 22.48(13.23) |
| FFPN-R | 88.76(7.85) | 21.10(17.65) | 85.03(4.54) | 20.25(7.43) | 92.39(4.08) | 16.97(9.36) | 88.72(6.48) | 19.44(12.43) |
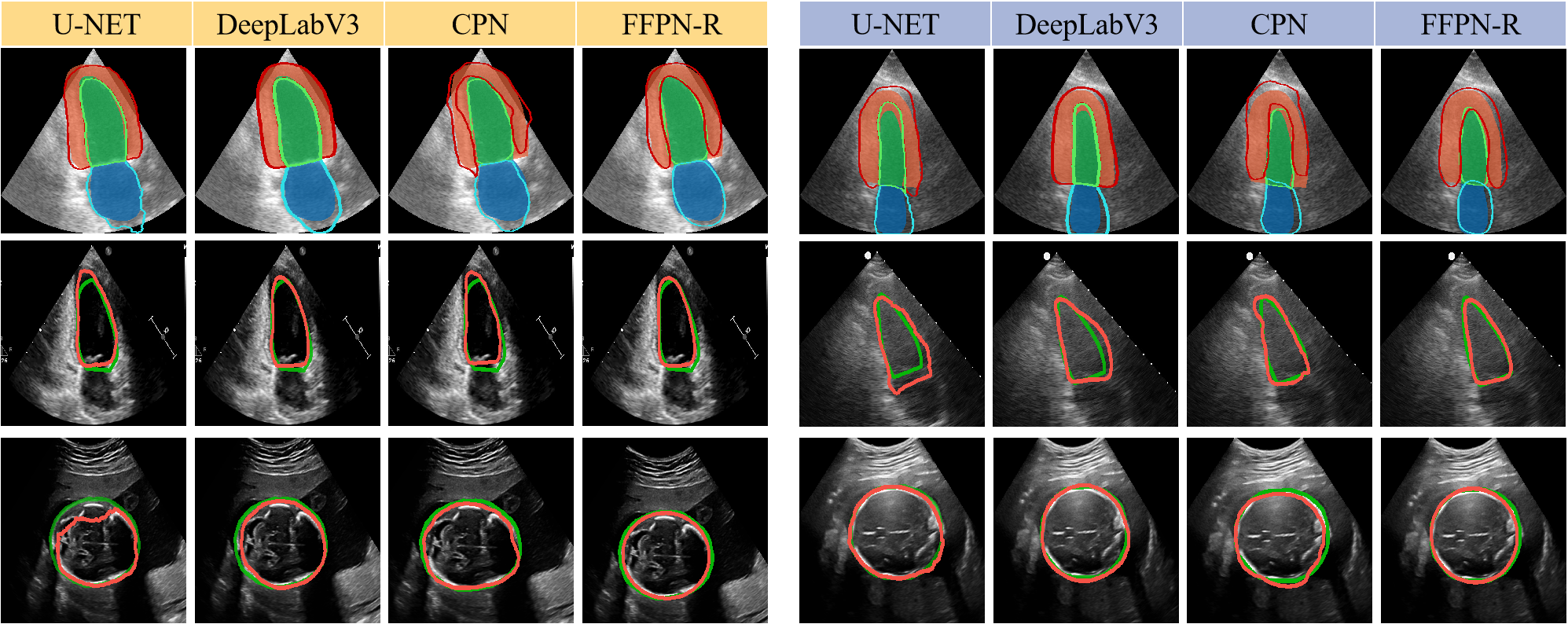
In addition, we have also validated the effectiveness of our framework in the multi-class segmentation task. As shown in Table 2, FFPN-R achieves a more significant improvement on the Camus dataset compared to other DTS approaches, as compared to the single-class segmentation tasks. This further illustrates the generalizability and scalability of our framework. On the Camus dataset, FFPN-R outperforms most Pixel-based methods. However, the wrapping of the myocardium around the left ventricle poses a challenge in accurately assigning positive and negative samples within the detection framework, resulting in our results being slightly inferior to DeeplabV3. Fig. 5 shows the segmentation results of U-NET, DeepLab V3, CPN and FFPN-R. It demonstrates the superior performance of FFPN-R on the segmentation task in US images.
4 Conclusion
In this study, we utilize the effectiveness of Fourier Descriptors to represent contours and propose Fourier Feature Pyramid Network (FFPN), a Fourier-anchor-based framework, to describe the segmentation region. It is found that FFPN achieves the best performance against other DTS methods. Moreover, we design a Contour Sampling Refinement (CSR) module to more accurately fit complex contours, which makes our method achieve further improvement and exhibit powerful capabilities on segmentation tasks. These experiments further demonstrate the well-balanced among performance, resource consumption and efficiency of our framework.
4.0.1 Acknowledge.
This work was supported by the grant from National Natural Science Foundation of China (Nos. 62171290, 62101343), Shenzhen-Hong Kong Joint Research Program (No. SGDX20201103095613036), and Shenzhen Science and Technology Innovations Committee (No. 20200812143441001).
References
- [1] Cao, H., Wang, Y., Chen, J., Jiang, D., Zhang, X., Tian, Q., Wang, M.: Swin-unet: Unet-like pure transformer for medical image segmentation. In: Computer Vision–ECCV 2022 Workshops: Tel Aviv, Israel, October 23–27, 2022, Proceedings, Part III. pp. 205–218. Springer (2023)
- [2] Chen, J., Lu, Y., Yu, Q., Luo, X., Adeli, E., Wang, Y., Lu, L., Yuille, A.L., Zhou, Y.: Transunet: Transformers make strong encoders for medical image segmentation. arXiv preprint arXiv:2102.04306 (2021)
- [3] Chen, L.C., Papandreou, G., Schroff, F., Adam, H.: Rethinking atrous convolution for semantic image segmentation. arXiv preprint arXiv:1706.05587 (2017)
- [4] Feng, H., Zhou, W., Yin, Y., Deng, J., Sun, Q., Li, H.: Recurrent contour-based instance segmentation with progressive learning. arXiv preprint arXiv:2301.08898 (2023)
- [5] He, K., Gkioxari, G., Dollár, P., Girshick, R.: Mask r-cnn. In: Proceedings of the IEEE International Conference on Computer Vision. pp. 2961–2969 (2017)
- [6] Isensee, F., Jaeger, P.F., Kohl, S.A., Petersen, J., Maier-Hein, K.H.: nnu-net: a self-configuring method for deep learning-based biomedical image segmentation. Nature methods 18(2), 203–211 (2021)
- [7] Kuhl, F.P., Giardina, C.R.: Elliptic fourier features of a closed contour. Computer graphics and image processing 18(3), 236–258 (1982)
- [8] Leclerc, S., Smistad, E., Pedrosa, J., Østvik, A., Cervenansky, F., Espinosa, F., Espeland, T., Berg, E.A.R., Jodoin, P.M., Grenier, T., et al.: Deep learning for segmentation using an open large-scale dataset in 2d echocardiography. IEEE Transactions on Medical Imaging 38(9), 2198–2210 (2019)
- [9] Liang, J., Yang, X., Huang, Y., Li, H., He, S., Hu, X., Chen, Z., Xue, W., Cheng, J., Ni, D.: Sketch guided and progressive growing gan for realistic and editable ultrasound image synthesis. Medical Image Analysis 79, 102461 (2022)
- [10] Lin, T.Y., Dollár, P., Girshick, R., He, K., Hariharan, B., Belongie, S.: Feature pyramid networks for object detection. In: Proceedings of the IEEE conference on Computer Vision and Pattern Recognition. pp. 2117–2125 (2017)
- [11] Painchaud, N., Duchateau, N., Bernard, O., Jodoin, P.M.: Echocardiography segmentation with enforced temporal consistency. IEEE Transactions on Medical Imaging 41(10), 2867–2878 (2022)
- [12] Ronneberger, O., Fischer, P., Brox, T.: U-net: Convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. pp. 234–241. Springer (2015)
- [13] Sobhaninia, Z., Rafiei, S., Emami, A., Karimi, N., Najarian, K., Samavi, S., Soroushmehr, S.R.: Fetal ultrasound image segmentation for measuring biometric parameters using multi-task deep learning. In: 2019 41st annual international conference of the IEEE Engineering in Medicine and Biology Society (EMBC). pp. 6545–6548. IEEE (2019)
- [14] Upschulte, E., Harmeling, S., Amunts, K., Dickscheid, T.: Contour proposal networks for biomedical instance segmentation. Medical Image Analysis 77, 102371 (2022)
- [15] Wei, F., Sun, X., Li, H., Wang, J., Lin, S.: Point-set anchors for object detection, instance segmentation and pose estimation. In: Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part X 16. pp. 527–544. Springer (2020)
- [16] Xie, E., Sun, P., Song, X., Wang, W., Liu, X., Liang, D., Shen, C., Luo, P.: Polarmask: Single shot instance segmentation with polar representation. In: Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition. pp. 12193–12202 (2020)
- [17] Zhao, Y., Cai, Y., Wu, W., Wang, W.: Explore faster localization learning for scene text detection. arXiv preprint arXiv:2207.01342 (2022)
- [18] Zhu, Y., Chen, J., Liang, L., Kuang, Z., Jin, L., Zhang, W.: Fourier contour embedding for arbitrary-shaped text detection. In: Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition. pp. 3123–3131 (2021)