Fiber Floer cohomology and conormal stops
Abstract.
Let be a closed orientable spin manifold. Let be a submanifold and denote its complement by . In this paper we prove that there exists an isomorphism between partially wrapped Floer cochains of a cotangent fiber stopped by the unit conormal and chains of a Morse theoretic model of the based loop space of , which intertwines the -structure with the Pontryagin product. As an application, we restrict to codimension 2 spheres where or . Then we show that there is a family of knots so that the partially wrapped Floer cohomology of a cotangent fiber is related to the Alexander invariant of . A consequence of this relation is that the link is not Legendrian isotopic to where .
1. Introduction
In this paper we consider the wrapped Floer cohomology of a cotangent fiber with wrapping stopped by a conormal. We relate it to chains of based loops on the complement of a submanifold. Then we show that the Legendrian conormal knows about the smooth topology of the submanifold beyond the fundamental group.
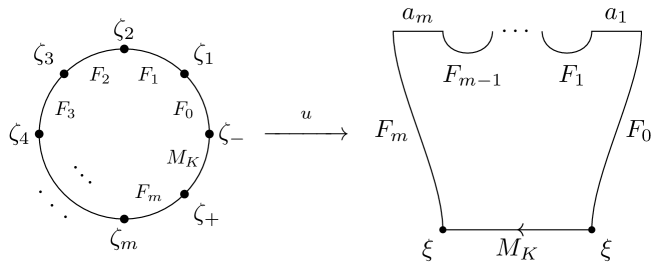
Let be a closed orientable spin manifold. Let be a submanifold and denote its complement by . Consider the disk cotangent bundle equipped with the canonical Liouville form . The ideal contact boundary of the Weinstein domain is the unit cotangent bundle . Associated to are the conormal bundle
and the unit conormal . Consider a cotangent fiber at and let be the partially wrapped Floer cochains on with wrapping stopped by . Let denote the space of piecewise geodesic loops in based at . Consider the space of cellular chains of equipped with the Pontryagin product. Then we have the following result:
Theorem 1.1 (4.12 and 5.3).
There exists a geometrically defined isomorphism of -algebras .
Moreover, induces an isomorphism of -modules.
We define using a surgery approach similar to [EL17, Appendix B] and [ENS16, Section 6] (see Section 3.1 for details). The outline of the surgery approach is the following. We attach a handle modeled on to along a neighborhood of . We denote the resulting Liouville sector by (with terminology as in [GPS20]). Then is the wrapped Floer cochain complex of in . The skeleton of is with clean intersection . By performing Lagrangian surgery along the clean intersection, we obtain an exact Lagrangian submanifold which is diffeomorphic to the complement (see Section 3.1 for details).
Let denote the space of loops in based at . Consider singular chains on the space of based loops . We give it the structure of an -algebra by equipping it with the Pontryagin product and all higher products equal to zero. See Section 3.2 and Section 4.2 for a more detailed discussion about the model of the based loop space we use.
In the spirit of Cieliebak–Latschev [CL09] and Abouzaid [Abo12b], we have a geometrically defined -homomorphism . By analyzing the action filtrations, we show that is diagonal with respect to the action filtrations. A key point in proving that is an isomorphism is showing that the disks contributing to the diagonal are transversely cut out. The solutions of the linearized Floer equation are precisely those vector fields along the disk that restricts to broken Jacobi fields along on which the Hessian of the energy functional is negative definite.
In the surgery approach we attach a handle modeled on , with skeleton . We consider a generic product metric on such that the metric on is scaled by a positive function with strictly negative derivative (warped product metric), see (A.1). By the genericity of the metric, there is a natural one-to-one correspondence between Reeb chords and geodesics, see 4.9 for details.
Since and are non-compact we use monotonicity of -holomorphic curves to prove that relevant moduli spaces of -holomorphic curves are compact, see Appendix A for details.
1.1. Applications
Let be a smooth manifold and let be a submanifold. Consider the cotangent bundle and the unit conormal bundle . It is known in certain cases that the symplectic topology of knows about the smooth topology of [Abo12a, ES16, EKS16]. In some cases the contact topology of knows about the smooth topology of . For instance, it is known that conormal tori of knots are complete knot invariants [She16, ENS16]. The results of Ekholm–Ng–Shende fit nicely into the broader picture of partially wrapped Floer cohomology that we consider in this paper, and is summarized in [ENS16, Section 1.3]. Specifically, in [ENS16] it is proven that there is a ring isomorphism
which is also obtained from 1.1 by restricting to degree 0. Furthermore there is a relation between the knot contact homology of and the Alexander polynomial of [Ng08, ENS16].
Let be a codimension 2 sphere. In this paper we show that the partially wrapped Floer cohomology of the fiber is related to the Alexander invariant. The Alexander invariant is regarded as a -module, where denotes the infinite cyclic cover of , see Section 5.4 for details. Denote by the unit conormal of the standard embedded . As an application of 1.1 we have the following theorem.
Theorem 1.2 (5.9).
Let or . Let be a point. Then there exists a codimension 2 knot with , such that is not Legendrian isotopic to .
1.2. Relation to other results
Let be a closed smooth manifold and consider the exact symplectic manifold where is the canonical Liouville form . Abbondandolo–Schwarz proved that the wrapped Floer cohomology of a cotangent fiber is isomorphic to the homology of the based loop space of [AS06]. Abouzaid extended this to an -quasi-isomorphism in [Abo12b] where the loop space is equipped with the Pontryagin product. Recently, Ganatra–Pardon–Shende proved that this result continues to hold even when is not assumed to be compact as a consequence of a deeper relationship between the wrapped Fukaya category of a Liouville sector and a certain category of sheaves [GPS18a].
In this paper, we consider a similar -holomorphic curve setup to the one used by Abouzaid in [Abo12b], but instead we work in the context of the partially wrapped Fukaya category of stopped by the unit conormal .
Remark 1.3.
Another interesting geometric point of view which motivates 1.1 is the following. Consider the wrapped Fukaya category of [GPS20, BKO19]. By [GPS18a, Corollary 6.1] we have an -quasi-isomorphism
where is the cotangent fiber at . We realize as the result of attaching a handle to as follows: Take a tubular neighborhood of and consider . Then remove and replace it with , identifying their common boundaries .
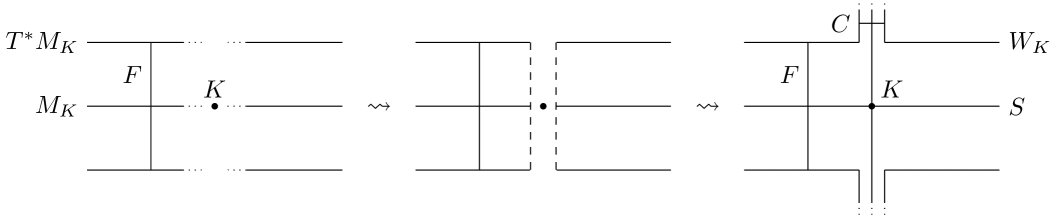
From the point of view of handle attachment, there is a new generator of the wrapped Fukaya category, namely the cocore disk . Because of this, the wrapped Floer cohomology of the fiber will change on the level of chains. However, if we push very far out in the punctured handle by a Lagrangian isotopy, we look at filtered -algebras and yield a chain isomorphism
where means we only consider generators of action less than . A standard filtration argument then shows that the wrapped Floer cohomology of is unaffected by this type of handle attachment and thus . Hence we obtain an indirect proof of the isomorphism
in 1.1.
1.3. Organization of the paper
In Section 2 we describe the version of wrapped Floer cohomology defined without Hamiltonian perturbations which we use in this paper. In Section 3 we first discuss the surgery approach to define partially wrapped Floer cohomology. Then we define the operations between and and show that is an -homomorphism. Section 4 is devoted to proving that is a isomorphism between and the Morse theoretic model of chains of based loops. Lastly, in Section 5 we equip and with -module structures relate to the Alexander invariant for certain families of codimension 2 knots . Then we show that this relation is used to show that is not Legendrian isotopic to , where is a point.
Acknowledgments
The author would like to thank his PhD advisor Tobias Ekholm for all his guidance and helpful discussions. He would also like to thank Georgios Dimitroglou Rizell for useful discussions regarding 1.3. Finally, the author would like to thank the anonymous referee whose many comments has improved the exposition of the paper. The author was supported by the Knut and Alice Wallenberg Foundation.
2. Wrapped Floer cohomology without Hamiltonian
In this paper, we consider a version of wrapped Floer cohomology defined without Hamiltonian perturbations. Wrapped Floer cohomology without Hamiltonian has been studied in e.g. [Ekh12, DR16, EL17] and in particular it is useful in proving various surgery formulas involving the wrapped Floer cohomology [BEE12, EL17, Ekh19]. It has also been used to study knots via knot contact homology from which there is a relationship to string topology and the cord algebra [ENS16, EENS13, CELN17].
Remark 2.1.
The relationship between wrapped Floer cohomology defined with and without Hamiltonians has also been studied. The version without Hamiltonian is known to be quasi-isomorphic to the version defined with Hamiltonians by counting strips with a Hamiltonian term that is turned on as one goes from the positive end to the negative end [EHK16, Theorem 7.2]. Such -holomorphic maps with a Hamiltonian term that turns on has been more systematically studied in [EO17] and it is proven in [EL17, Lemma 68, 69] that the two versions of wrapped Floer cohomology are -quasi-isomorphic.
When working with wrapped Floer cohomology without Hamiltonian we have a priori bubbling issues. This is circumvented by considering parallel copies, which also removes the possibility of having multiply covered curves, see [EL17, Section 3.3]. Furthermore we need to count anchored curves [BEE12, Section 2.2] [EL17, Section A.1]. A specific perturbation scheme involving anchored curves is constructed in [Ekh19], and we fix such perturbation scheme so that all relevant moduli spaces are transversely cut out.
We give a brief description of the wrapped Floer cohomology without Hamiltonian by following [EL17, Appendix A-B]. We consider a Weinstein domain together with a smooth exact Lagrangian submaniold . Let and be its Legendrian boundary. The boundary is a contact manifold. We consider the completion of and by attaching cylindrical ends to and to . Then we pick a system of parallel copies of as in [EL17, Section 3.3]. Consider a family of pairs of Morse functions, and . Let be the time-1 flow of of the Hamiltonian vector field , and let . Then we call a system of parallel copies of where . Let and .
Note that in this paper, is a cotangent fiber. Therefore we choose the Morse functions in such a way that all of them only have one minimum, since .
2.1. -structure and moduli space of disks
Let be a spin Weinstein domain. Let be an orientable exact Lagrangian with vanishing Maslov class (see [Arn67] for a definition of the Maslov class). Let be the corresponding system of parallel copies of as in the previous section.
First we define as a -graded module over . Note that, for each Reeb chord starting at and ending at , there is a unique Reeb chord of close to . Similarly, for each transverse intersection point in , there is a unique transverse intersection point . We implicitly fix an identification of with , and with . We then define to be the -graded module over , which is generated by Reeb chords of and intersection points . The grading is given by the Maslov index (see 2.3 below for a more precise definition).
We now describe how we equip with a -structure which is defined by -holomorphic curve counts. Let denote the positively oriented unit disk, with points along the boundary removed. We denote the boundary punctures in by , one of which is distinguished. These boundary punctures subdivide the boundary of into arcs. We enumerate these arcs by , according to the boundary orientation, starting from the distinguished boundary puncture. We call a boundary numbering of . If the sequence is decreasing (increasing), we say that the disk has decreasing (increasing) boundary numbering . If (), we say that the puncture is increasing (decreasing), and if we say that is a constant puncture.
We equip the boundary punctures with both a positive and a negative strip-like end. Namely, we pick biholomorphisms
where is a neighborhood of the boundary puncture .
Using notation as in [EL17], we are interested in the moduli spaces of -holomorphic disks which are denoted by , and . These moduli spaces consist of filling disks, symplectization disks and partial holomorphic buildings respectively, and we define them below.
- Filling disks:
-
Consider equipped with a strictly decreasing boundary numbering. Note that every puncture is strictly decreasing except for the distinguished puncture, which is strictly increasing. We let be a word of generators of . Then we define to be the moduli space of -holomorphic maps such that
-
•:
near the boundary puncture , is asymptotic to the generator , that is
The sign in the above formulas is equal to if , and otherwise.
-
•:
maps the boundary arc labeled by to the component of .
Figure 2. A -holomorphic disk in . The dot on the right hand side indicates that (near which, is asymptotic to ) is the distinguished puncture. -
•:
- Symplectization disks:
-
Consider equipped with a decreasing boundary numbering (not necessarily strictly decreasing). Let , where each is a point in the interior of . We equip each with a negative cylinder-like end. That is a biholomorphism
We let be a word of signed Reeb chord generators of , where for every . We also let be a word of Reeb orbits in , each of which is equipped with an asymptotic marker, i.e. a point . The distinguished boundary puncture induces an asymptotic marker for each interior puncture , which is a half-ray near [EO17, Section 2.1]. By abuse of notation we say that is the asymptotic marker of . Then we define to be the moduli space of -olomorphic maps such that
-
•:
near the boundary puncture , is asymptotic to the Reeb chord of at , depending on the sign , that is
-
•:
near the interior puncture , is asymptotic to the Reeb orbit in at respecting the asymptotic markers, that is
-
•:
maps the boundary arc labeled by to the component of , and
-
•:
if is a constant puncture, we require to be a negative puncture (i.e. asymptotic to a Reeb chord of at ).
Figure 3. A -holomorphic disk in . The dot on the right hand side indicates that the puncture is the distinguished puncture. The on the right hand side is the asymptotic marker . Let be a Reeb orbit in , equipped with the asymptotic marker . Let denote with one puncture , with a fixed choice of asymptotic marker at . Equip with a positive cylinder-like end
Let be the -perturbed moduli space of -holomorphic maps with notation as in [Ekh19, Theorem 1.1], satisfying
Then we define
See [Ekh19] and [EL17, Appendix A.1] for more deatils. Each curve in should be interpreted as curves shown in Fig. 3, but with all Reeb orbits capped off by punctured -holomorphic spheres.
Figure 4. A -holomorphic disk in . The dot on the right hand side indicates that the puncture is the distinguished puncture. The on the right hand side is the asymptotic marker . -
•:
- Partial holomorphic buildings:
-
The domain of a partial holomorphic building is a possibly broken disk with boundary punctures, see Fig. 5. We denote this (possibly broken) disk by and equip it with a decreasing boundary numbering . In the target, the partial holomorphic building consists of a two-level -holomorphic building, with exactly one symplectization disk (called the primary disk), and multiple filling disks (called secondary disks). We require that the distinguished puncture (which is the only increasing puncture), is a negative puncture of the primary disk. If the primary disk only has one negative puncture, the primary disk is the only component, and the disk is not broken. If the primary disk has more than 1 negative puncture, each additional negative puncture has a secondary disk attached to it, at the distinguished puncture of the secondary disks disk. If is a word of generators of , where is the generator to which the distinguished puncture is asymptotic to, we denote the moduli space of partial holomorphic buildings by .
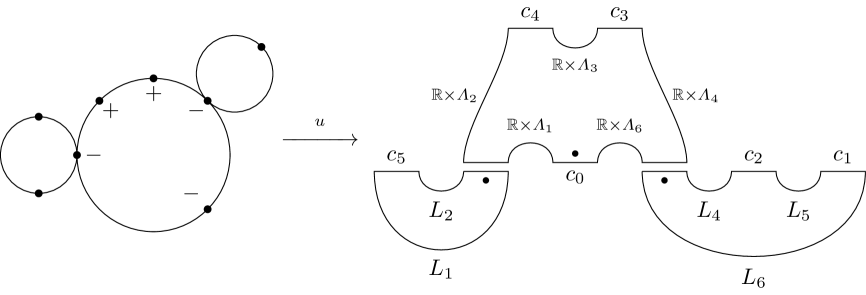
Figure 5. A partial holomorphic building in . The dots on the right hand side indicate the distinguished punctures of the corresponding disks. The signs on the left hand side indiciate the sign of the punctures of the primary disk. Remark 2.2.
Take note that we might have additional negative punctures of the symplectization disk, at which there are constant filling disks with only 1 positive puncture attached. We have not depicted these above, but they should nonetheless be taken into account.
By [EL17, Theorem 63,65] and [Ekh19, Theorem 1.1], and are transversely cut out smooth manifolds that are independent of the boundary numbering up to diffeomorphism. This follows from the observation that disks in or can not be multiply covered for topological reasons. Transversality is then proved using standard techniques as in [EES07]. Furthermore the moduli spaces admit compactifications that consists of -holomorphic buildings of several levels.
Remark 2.3.
For Reeb chord generators the grading is more explicitly described as follows. Suppose that , then we first define the Conley–Zehnder index by following [EES05, Section 2.2]. Namely, let and be the start and endpoints of the Reeb chord , respectively. Then pick a capping path so that , . Let and . Then is a Lagrangian submanifold. By parallel transport along and via the linearized Reeb flow we get a path of Lagrangian submanifolds in the contact planes . If we close this path up by positive close-up in the contact planes we obtain a loop of Lagrangian submanifolds in denoted by . We then define the Conley–Zehnder index of to be the Maslov index of (in the sense of [RS93]),
Then we define
For Lagrangian intersection generators we use the choice of graded lifts of and to obtain a path starting at and ending at . We close this path up in by a positive rotation. This gives a loop of Lagrangian submanifolds denoted by , which starts and ends at . Then define the grading of as the Maslov index of this loop [EL17, p. 89] [CEL10, Appendix A]
The dimension of the moduli space is dependent on whether the distinguished puncture is a Reeb chord or a Lagrangian intersection puncture. To emphasize the differences, we introduce some more notation.
-
•
If the distinguished puncture is a Reeb chord generator we denote it by , and
-
•
if the distinguished puncture is an intersection generator we denote it by .
Theorem 2.4.
Let be a word of generators of . Assume that is the distinguished puncture and that it is a Reeb chord generator. Then the dimension of the moduli space is
Let be a word of generators of . Assume that is the distinguished puncture and that it is a Lagrangian intersection generator. Then the dimension of the moduli space is
For any word of Reeb chord generators , the dimension of the moduli space is
For any word of Reeb chord generators , the dimension of the moduli space is
Proof.
The theorem follows from applying [CEL10, Theorem A.1], and the fact that the index of a several-level -holomorphic building is the sum of the indices of the disks at each level. Let be a word of generators of . Let either or . Let be the unit disk in together with regarded as marked points (and not punctures). The boundary of is equal to the union of closed boundary arcs such that the interiors of all the boundary arcs are pairwise disjoint, and only missing the marked points .
-
(T1)
For all Reeb chord generators , fix a complex trivialization of the contact structure along , such that the linearized Reeb flow along the chord expressed in is constantly equal to the identity.
-
(T2)
For each boundary arc in , fix a complex trivialization of (if ) or (if ) with the following properties:
-
(a)
If an endpoint of is a puncture asymptotic to a Reeb chord , then .
-
(b)
If an endpoint of is a puncture asymptotic to an intersection generator , then where is the common endpoint of the boundary arcs and .
-
(a)
Items (T1) and (T2) above give a complex trivialization of (or ) over the boundary arc of . For each boundary arc , let be the complement of its endpoints in . The tangent planes of along all expressed in the trivialization gives a collection of paths of Lagrangian subspaces in . We close up this path to a loop as follows. For each Reeb chord , denote its start and endpoints by respectively.
-
(C1)
For each positive puncture near which is asymptotic to the Reeb chord , the tangent planes of are connected by the product of the linearized Reeb flow along in , and the identity in the -factor, followed by negative close-up in the contact plane in (cf. 2.3). Denote this path of Lagrangian subspaces by .
-
(C2)
For each negative puncture near which is asymptotic to the Reeb chord , the tangent planes of are connected by the product of the backwards linearized Reeb flow along in , and the identity in the -factor, followed by negative close-up in the contact plane in (cf. 2.3). Denote this path of Lagrangian subspaces by .
- (C3)
Define to be the Maslov index of the loop of Lagrangian subspaces in which is constructed by closing up paths of Lagrangian subspaces as described in (C1), (C2) and (C3). For the moduli spaces of filling disks and symplectization disks, we then have by [CEL10, Theorem A.1.] that
Since is assumed to have vanishing Maslov class, the contribution to is equal to the sum of each contribution at every boundary puncture of . Next we describe each of these contributions in terms of the grading of each generator. First let .
-
(sy1)
If is a positive puncture near which is asymptotic to the Reeb chord then
-
(sy2)
If is a negative puncture near which is asymptotic to the Reeb chord then
Then let .
-
(fi1)
Let be a puncture near which is asymptotic to the Reeb chord .
-
(a)
If is the distinguished puncture then
-
(b)
If is not the distinguished puncture then
-
(a)
-
(fi2)
Let be a puncture near which is asymptotic to the intersection generator
-
(a)
If is the distinguished puncture then
-
(b)
If is not the distinguished puncture then
-
(a)
From (sy1) and (sy2) we obtain
From (fi1)(a), (fi1)(b) and (fi2)(b) we obtain
From (fi2)(a), (fi1)(b) and (fi2)(b) we obtain
For a partial holomorphic building, let be the positive punctures of the primary disk, let be the distinguished negative puncture of the primary disk and let be the remaining negative punctures. Let be all the non-distinguished punctures of all the secondary disks, see Fig. 6. Each secondary disk lies in . We may then compute the dimension by taking sums, that is
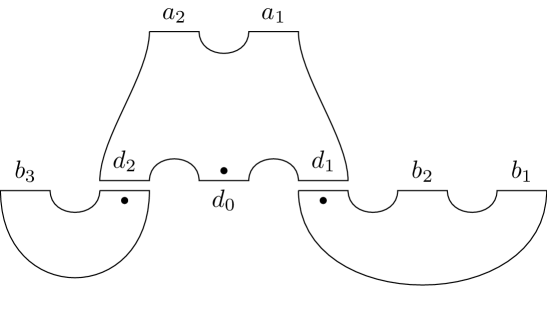
After canceling we get
Now let and let be the word of letters corresponding to all the generators in the appropriate order. Therefore
∎
We now define operations, one for each ,
that counts various -holomorphic disks discussed above. We split it as a sum , where takes values in Lagrangian intersection generators and takes values in Reeb chord generators.
First we consider . Let be a word of generators of . Then
The sum is taken over all Lagrangian intersection generators so that .
To define , consider a word of generators . Then
The sum is taken over all Reeb chords so that . The total operation is then defined as
| (2.1) |
where
Lemma 2.5.
Proof.
See [EL17, Lemma 67]. ∎
3. Partially wrapped Floer cohomology and chains of based loops
Let be any closed orientable spin manifold and any submanifold. The purpose of this section is to describe the surgery approach to compute the partially wrapped Floer cohomology of a cotangent fiber in the Weinstein domain stopped by the unit conormal . We then define a chain map relating the partially wrapped Floer cohomology of a fiber to chains of based loops on a Lagrangian submanifold that is diffeomorphic to the complement .
In Section 3 we describe the surgery approach in more detail, and also construct the Lagrangian . In Section 3.2 we describe the model we use for the chains of based loops on , and equip it with the Pontryagin product. Then in Section 3.3 we describe the moduli space of half strips which we need in order to to define an -homomorphism between the partially wrapped Floer cocomplex and the chains of based loops on . The construction of the -homomorphism is carried out in Section 3.4.
3.1. Partially wrapped Floer cohomology using a surgery approach
Following [EL17, Appendix B] and [ENS16, Section 6] we will now describe the surgery approach. We consider the disk cotangent bundle the conormal bundle of
Let be the unit conormal of . We take a tubular neighborhood of in and we attach a handle modeled on to . After handle attachment and after smoothing out corners, the Liouville vector field is equal to in (for large enough) for coordinates in the handle. We call the resulting manifold , see Fig. 7.
We then consider a cotangent fiber at in . Denote the wrapped Floer cochains of in as described in Section 2 by .
Remark 3.1.
In the language of Sylvan [Syl19], we obtain a stop from as follows. Pick a tubular neighborhood in , and a strict contactomorphism where is a tubular neighborhood of , viewed as the zero section. Then the Liouville hypersurface is a stop.
Another point of view, is to remove the tubular neighborhood from , and take the Liouville completion of to obtain a Liouville sector as defined [GPS20]. The wrapped Fukaya category of this Liouville sector coincides with the wrapped Fukaya category associated to the pair , and also with the Fukaya category associated to [EL17, GPS20, GPS18b].
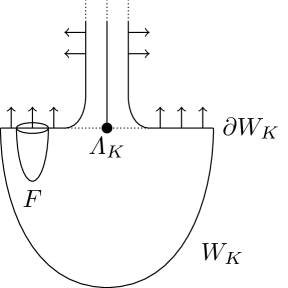
To construct the complement Lagrangian , we perform Lagrangian surgery of and which intersect cleanly along . Above each point of , the intersection looks like the transverse intersection of two Lagrangian disks of dimension . We perform Lagrangian surgery along as in [MW18, Section 2.2.2] [AENV14]. We denote the result of the surgery by (cf. [AENV14]).
Remark 3.2.
Note that the Maslov class of vanishes, because it is the result of surgery of and , both of which have vanishing Maslov class. In particular, consider the following model. We pick a -neighborhood around such that and . Following the discussion in [ES16, Section 2.2], we have a phase function which is unique up to an additive constant on the handle , so that and .
Any loop that is based at any point outside of the handle pass through the entire handle an even number of times, which means that the total Maslov index of the loop is zero.
3.2. Based loops on
Consider the Moore loop space of , based at
We use a cubical model for chains of based loops as in [Abo12b, EL17].
A singular -cube is a smooth map and it is called degenerate if is constant in at least one of the coordinates. We define the space of cubical -chains by
We equip with the differential
| (3.1) |
where
is the map that replaces the -th coordinate with .
The Pontryagin product is defined as the following composition:
| (3.2) |
The cross product of a singular -cube and a -cube is the -cube
The map is pointwise concatenation of loops where we first follow , and then . That is , where
From the definitions of and we see that for any two singular cubes and we have
This leads via (3.2) to
Hence is an -algebra with all higher operations being zero with sign conventions as in [AS10, Sei08].
3.3. Moduli space of half strips
Consider the cotangent fiber at defined in Section 3.1 and consider a system of parallel copies of as in Section 2. In this section we construct a moduli spaces of -holomorphic half strips similar to [Abo12b]. This moduli space is used to define a chain map between and . By non-compactness of in the horizontal direction, we use monotonicity for -holomorphic half strips to establish compactness of moduli spaces, see Appendix A for details.
Let be the positively oriented unit disk with three boundary punctures . Then is biholomorphic to
where and . The boundary segment between and is called the outgoing segment.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/48321ba7-28c9-4cd8-be91-fc4f33afc9f6/x8.png)
Define
equipped with the standard complex structure on . We pick a positive strip-like end near , and a negative strip-like end near . That is, are maps
defined in neighborhoods of and respectively. Fix a family of -compatible almost complex structures, parametrized by . Then consider a map
which satisfies
Given a generator we consider maps
that satisfies the following Floer equation:
| (3.3) |
where the boundary conditions on is indicated in Fig. 8 below.
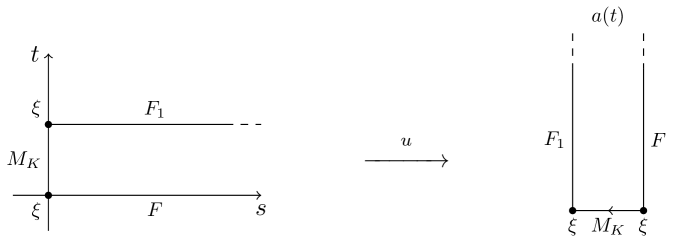
For a generator we define to be the moduli space of -holomorphic maps that satisfies (3.3).
Lemma 3.3.
For generic choices of almost complex structure , the moduli space is a smooth orientable manifold of dimension
Proof.
Let be the positively oriented unit disk with boundary punctures which we denote by . Let be the Deligne–Mumford space of unit disks in the complex plane with boundary punctures that are oriented counterclockwise. Let denote the Deligne–Mumford compactification of as in [Abo10, Section C.1] and [Sei08, Section (9f)]. Also define to be the Deligne–Mumford space of unit disks in the complex plane with boundary punctures that are oriented counterclockwise. Its Deligne–Mumford compactification is denoted by . The boundary of is obtained by adding broken disks and hence the codimension one boundary of is covered by the following spaces
| (3.4) | ||||
| (3.5) |
where we regard each stratum as being included in via the natural inclusion.
Consider a word of generators
Then we define the moduli space to be maps
where , and so that satisfies the following Floer equation
where and are strip-like ends near each puncture and for . The boundary conditions of is indicated in Fig. 9 below
Again, analogous to [EL17, Theorem 63] and [Abo12b, Lemma 4.7] we have the following standard transversality result.
Lemma 3.4.
For a generic choice of almost complex structure, is a smooth orientable manifold of dimension
Proof.
We first observe that disks in have switching boundary condition which implies that they can not be multiply covered for topological reasons. Then transversality is proved using standard techniques as in [EES07, EL17].
We now prove the statement about the dimension. The proof is similar to the proof of 2.4. By [CEL10, Theorem A.1.] we have
where is defined as in the proof of 2.4. There is a new type of contribution coming from the Lagrangian intersection punctures . By definition of we see that the sum of the contributions from both is equal to . The Maslov class of vanishes (see 3.2), so the only contributions to comes from the generators and the Lagrangian intersection pucntures . Therefore
Furthermore, by vanishing of the Maslov class of (see 3.2) it allows us to find a coherent orientation of the moduli spaces. See Appendix B for a more general discussion about orientations. ∎
Since is non-compact, we use monotonicity together with a generically chosen metric to make sure -holomorphic half strips do not escape to horizontal infinity, see Appendix A and in particular A.2. This gives that can be compactified by adding several-level curves and we denote the compactification by . Similar to [Abo12b, Lemma 4.9] and by (3.4), (3.5) the codimension one boundary of is stratified as
| (3.6) |
Note that we define to mean either or as in Section 2, depending on whether the breaking happens at a Reeb chord or a Lagrangian intersection generator.
To be more precise, (3.6) means that the codimension one boundary of is covered by images of the natural inclusions of products for subwords and for partitions
Note that is the word of generators obtained by starting with the word and replacing the subword with an auxiliary generator , see Fig. 10 and Fig. 11. If and then
| (3.7) |
In this case, where the auxiliary generator is placed at position in (3.7) we say that is a subword of at position .
We now have a lemma of how the orientation of the different strata compares to the boundary orientation. See Appendix B for a general discussion about orientations of moduli spaces.
Lemma 3.5.
The product orientation on differs from the boundary orientation on by where
| (3.8) |
while the product orientation on differs from the boundary orientation on by where
| (3.9) |
whenever is rigid. Here is a subword of at position as in (3.7).
Proof.
See Appendix B. ∎
Lemma 3.6.
Proof.
See [Abo12b, Lemma 4.11]. ∎
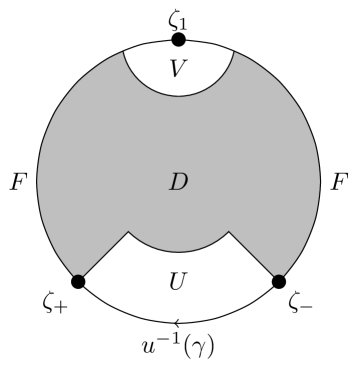
3.4. The evaluation map and construction of the -homomorphism
In this section we construct the evaluation map used to define the -homomorphism between and .
First pick any smooth, orientation reversing map which parametrizes the outgoing segment. (That is, the boundary arc of that lies between and .)
Pick two strip-like ends
where are neighborhoods of . We pick the strip-like ends so that are the parts of the boundary of that points towards (according to the boundary orientation on ), and are the parts of the boundary of that points away from .
Assume that satisfies the following
| (3.11) |
Then is a map so that . We reparametrize by arc length with respect to a Riemannian metric on (see (A.1)), and compactify the domain. In doing so, we get a smooth, orientation reversing map
that satisfies , which means . We then define the evaluation map as
| (3.12) | ||||
Lemma 3.7.
Let be a -holomorphic disk and take so that (3.11) holds. Then decays exponentially in the -topology.
Proof.
Pick strip-like ends
as above. By [RS01, Theorem A] we have that decays exponentially in the -topology. When we say that a function decays exponentially in the -toplogy we mean that there are constants so that and for every we have
| (3.13) |
Next consider which satisfies (3.11), where is large enough so that for . This also gives
where are maps so that
and
The previous lemma enables us to extend the evaluation map to the compactification of the moduli space of half strips.
Lemma 3.8.
Proof.
For this proof, we follow the idea outlined in [Abo12b, p. 37].
- Extension of to the compactification:
-
It is obvious how to extend it to the boundary strata ; we define the evaluation map of such broken disk to be the same as the evaluation map when we forget about the factor . However, if we have a sequence which Gromov converges to a broken disk in any of the boundary strata , then the Gromov limit is a stable -holomorphic map (a broken disk), consisting of two -holomorphic disks where , and two boundary punctures , so that we either have or [Fra08]. More precisely, it means that there are two families of Möbius transformations of the unit disk
so that
(3.14) and
Recall that convergence in means -convergence on every compact subset .
Define parametrizations
so that and satisfy (3.11). Then the two maps are smooth maps so that decay exponentially in the -topology by 3.7. Hence the composition of two smooth loops is again a smooth loop. There are two cases, depending on whether the two components of the broken disk have the puncture or in common. That is, we either have or . In the first case when , we define a map as
(3.15) In the second case when we swap places of and in the above definition of .
We then claim that this map is smooth and has exponentially decaying derivatives in the -topology as . Since and are smooth maps with exponentially decaying derivatives in the -topology as , it suffices to show that all derivatives of at exists. This follows from the exponential decay of every derivative of and in the -topology. We may then reparametrize by arc length and compactify the domain to obtain a map so that , that is , and we define .
- Commutativity of the diagram:
-
It follows almost immediately from the definition of the evaluation map
that the diagram
commutes, since in (3.15) is essentially defined as the concatenation of and . More precisely, we consider for as above. Then reparametrize and by arc length so that we obtain two maps
These maps are so that for , and the concatenation of these maps yields a map defined by
which coincides with the map obtained by parametrizing defined in (3.15) by arc length. The overall sign comes from 3.5, see Appendix B for a discussion about sign and orientations.
- Continuity of :
-
We claim that is a continuous map, meaning that if is a Gromov convergent sequence of -holomorphic disks, then the map defined in (3.15) is realized as a limit of loops in the compact-open topology of .
Pick a family of smooth maps which satisfies (3.11). Then we have that is a family of smooth maps with exponentially decaying derivatives as in the -topology by 3.7. From (3.14) we have two families of Möbius transformations and such that
for . We also have that preserves the boundary of and that preserves boundary marked points in the sense that . Then we have
(3.16) Hence for any multi-index and we have
(3.17) Let and define and . Inserting suprema over suitable compact sets and gives
(3.18) Here we have used that in and hence that is also bounded in this topology. Furthermore we have used that in by (3.16).
∎
The evaluation map
induces a map on chains . We then pick a fundamental chain by 3.6 so that (3.10) holds, and define a family of maps
| (3.19) | ||||
where
Note that means the grading of regarded as an intersection generator of as in Section 2.1.
Lemma 3.9.
The following diagram commutes,
and the following diagram commutes up to an overall sign of , where is defined in (3.8).
In the latter diagram we have the subdivision , and the map is the composition of the map induced by the inclusion
Proof.
That the first diagram commutes follows more or less by definition. Namely, let . Then , and by using the definition of in (3.1) and the definition of in (3.12) we get
The second diagram is split up into the following digram
The right square commutes, since the corresponding diagram before application of commutes, by 3.8, and the maps , and on chains are defined pointwise. The left square also commutes, because and act componentwise. Hence the outer square also commutes.
Lemma 3.10.
The maps form an -homomorphism. That is,
where
Proof.
From 3.4 it is clear that has degree .
We first ignore signs and prove the statement modulo 2. We look at the codimension one boundary of of dimension . It consists of two types of broken -holomorphic curves as in (3.10), and we analyze each boundary term separately.
-
(1)
The first boundary term is
where is a subword at position of .
-
(2)
The second boundary term is
and it consists of broken half strips that is broken at the Lagrangian intersection point .
In view of (3.10), we consider the fundamental chain of . Consider the natural inclusions of the boundary strata
We consider and use 3.9. Then
| (3.20) | ||||
We start by considering boundary terms of type (1). The evaluation applied to these terms is
because of the definition of on these boundary strata. Note that if is not rigid, then the image would be degenerate in , and hence does not contribute. In figures we illustrate this equality as follows
The word is the word obtained from , by replacing the word with . Therefore
| (3.21) |
where
This means that the broken disks of type (1) correspond to terms of the form where .
Similarly, for the first terms in (3.20) which correspond to broken disks of type (2) we apply 3.9 to get
| (3.22) |
so that the broken disks of type (2) correspond to terms of the form where .
Therefore via (3.21) and (3.22), equation (3.20) becomes
and these are precisely the -relations modulo 2. For confirmation of signs we refer the reader to Appendix B. ∎
4. The chain map is an isomorphism
This section is dedicated to the proof of 1.1.
Theorem 4.1 (1.1).
There exists a geometrically defined isomorphism of -algebras .
The first step is to replace the full Moore loop space with a Morse theoretic model of it. It is the space of piecewise geodesic loops and we denote it by (see Section 4.2). In the Morse theoretic model of the loop space, we have that the geodesics on are precisely critical points of the energy functional, with finite dimensional unstable manifolds, and infinite dimensional stable manifolds. There is a one-to-one correspondence between Reeb chords and oriented geodesics. Assuming that the metric is generic gives moreover that Reeb chords of degree are in one-to-one correspondence with geodesics of index (see 4.9). We will show that the evaluation map defined in Section 3.4 is transverse to the infinite dimensional stable manifolds, and that the kernel of the linearized operator has the same dimension as the unstable manifold.
In Section 4.1 we will define the action filtration on , followed by Section 4.2 where we first replace the full Moore loop space with the Morse theoretic model consisting of piecewise geodesic loops, and then we filter the space of loops by length. In Section 4.3 we prove that respects the action filtrations and in fact that is diagonal with respect to the action filtrations. In Section 4.5 we prove that is isomorphic to the Morse theoretic model of the loop space in each filtration level, which allows us to pass to colimits.
Consider and fix a generic Riemannian metric on such that in the handle of , the metric has the form
where is the coordinate in the -factor, and satisfies , and , see (A.1) for details.
4.1. Length filtration on
For a Reeb chord generator define its action by
In our case with for we only have a single Lagrangian intersection generator , whose action we define explicitly as . We then filter by this action, and use the notation
Now, by applying Stokes’ theorem to any -holomorphic disk which contributes to we get the following lemma. (Compare with e.g. [Ekh06, Lemma B.3].)
Lemma 4.2.
The differential does not increase the action of generators. That is,
for any .
4.2. Length filtration on
In this section we review basic material on the Morse theory of loop spaces from [Mil63].
One goal in this section is to replace the full Moore loop space with a homotopy equivalent Morse theoretic model by approximating Moore loops by piecewise geodesic loops. The second goal is to in detail define the filtration on the model of chains of based loops we use.
By abuse of notation, we denote by the space of continuous based loops with fixed domain . It is homotopy equivalent with the space of Moore loops as defined in Section 3.2. With respect to the generic Riemannian metric on as described in (A.1), equip with the supremum metric
The metric topology on induced by then agrees with the compact-open topology. Define as the space of piecewise smooth loops, and equip it with the metric
By [Mil63, Theorem 17.1], we have that the inclusion is a homotopy equivalence. We define the energy of by
| (4.1) |
Similarly we define the length of as
Define
Fix a subdivision of ,
Then define to be the set of loops in that are geodesic in the time interval for each . Let
Applying [Mil63, Lemma 16.1] then gives that for a sufficiently fine subdivision, is a smooth finite dimensional manifold which is a natural submanifold of . Moreover by [Mil63, Theorem 16.2], is a deformation retract of , and critical points of are the same as the critical points of , and is furthermore a Morse function.
We consider another increasing filtration on by filtering by length. Namely, define the length filtration of by
and correspondingly
By the same proof as [Mil63, Theorem 16.2], we construct an explicit deformation retract of onto (see 4.3 below).
If is a cubical -chain of piecewise geodesic loops, we define the action of as
We then define
which gives us an increasing filtration on . Futhermore, we see by definition that .
Lemma 4.3.
There is a deformation retract
which therefore induces a quasi-isomorphism
Proof.
From the proof of [Mil63, Theorem 16.2], we first define a retraction
as follows. Consider the closed ball with center and radius
For any , fix a fine enough subdivision of
so that for some small enough so that there is a unique geodesic between and . Because is contained in the ball , we have by [Mil63, Corollary 10.8] that there is a unique minimal geodesic between and of length less than . Define so that for each we have
Since geodesics are locally length minimizing, it is clear that and therefore that takes values in . For each we define
in such a way that for and any the map is so that
Then and it is continuous in both and . Hence it shows that is a deformation retract of .
It is now straightforward to see that this map is defined on singular chains. Namely, for any fixed , we pick a fine enough subdivision of
so that for every we have
Hence for any , there is a unique geodesic from to . Then induces a map
| (4.2) | ||||
∎
By [Mil63, Theorem 16.3], is a CW-complex with one cell of dimension for each closed geodesic on of index . We consider the cellular chain complex . We think of the generators of as the unstable manifolds of geodesics of index with respect to the energy functional on . We define the action of a -cell as
It is well known that singular chains and cellular chains on a CW-complex are homotopy equivalent. Denote the induced isomorphism on homology by
| (4.3) |
In particular by 4.3 the map in (4.2) induces an isomorphism
| (4.4) |
4.3. The chain map respects the filtration
The goal for this section is to prove that the chain map
respects the filtrations defined on and in Sections 4.1 and 4.2 respectively. The plan is to follow and adapt the proof of [CELN17, Proposition 8.9] to the current situation. The outline of the proof is to consider any -holomorphic disk contributing to and integrate the 2-form (defined in (4.7) below) over the disk. Using Stokes’ theorem we show that .
Consider a generator and pick some loop . Then pick a tubular neighborhood of in and a symplectomorphism
| (4.5) |
by the Lagrangian neighborhood theorem for some positive constant . By a similar argument to that of the proof of [Wei71, Theorem 7.1], we may assume that sends the fiber to a fiber of .
Recall that we use the metric on defined in (A.1). Pick coordinates in , and define the canonical 1-form . Then let be a -form on that is given by
When we restrict to , the Reeb vector field and the contact structure have the following expressions in these coordinates
Then we have the splitting . We have picked an almost complex structure on which is compatible with . The almost complex structure induces an almost complex structure on defined as
which satisfies the following:
-
(1)
is compatible with , and
-
(2)
preserves the splitting .
These two conditions ensure that the map
is -holomorphic.
By the proof of [CELN17, Lemma 8.8] we have that . However, if we integrate over the domain of we can not use Stokes’ theorem directly since is singular along the zero section, so we have to make some further modifications to get rid of this singularity.
Let
| (4.6) |
be a smooth function so that
-
•
near , and
-
•
for every ,
-
•
for for some small .
Then define
Lemma 4.4 ([CELN17, Lemma 8.8]).
For any outside of the zero section we have
For and equality holds if and only if , whereas at points where and equality holds if and only if is a linear combination of the Liouville vector field and the Reeb vector field .
Let be a generator and consider in . Denote by . Using the symplectomorphism in (4.5) we define an exact 2-form on . Define
| (4.7) |
on . We may extend to the whole of by defining it to be
Lemma 4.5.
The 2-form on defined above satisfies
Proof.
In we have , in which case the conclusion follows from 4.4. Otherwise we have which is non-negative on complex lines, because is -compatible. ∎
Lemma 4.6.
Consider the exact Lagrangian fiber . Its image under is exact with respect to .
Proof.
This follows immediately from the assumption that maps to a fiber of , say for . ∎
Proposition 4.7.
Let be any generator and be any -holomorphic half strip with positive puncture at . Letting we have
with equality if and only if is a branched covering of a half strip over a Reeb chord.
Proof.
Since by 4.5 we integrate it over the disk and use Stokes’ theorem:
| (4.8) |
For the remainder of this proof we follow the proof of [CELN17, Proposition 8.9]. We start by computing . To do this we consider . Then pick a biholomorphism
where is a neighborhood of the boundary arc between the boundary punctures both of which are mapped to , so that is a parametrization of the boundary arc between and . We choose small enough so that does not hit . Let
Since we have a non-flat metric on (see (A.1)) we consider the splitting and geodesic normal coordinates on . The almost complex structure then takes the vertical subspace to the horizontal and vice versa. Consider the Levi-Civita connection on , and denote its associated Christoffel symbols by . Recall that in geodesic normal coordinates, the metric tensor at has components , where is the Kronecker delta. In particular the Christoffel symbols vanish at . For any in a neighborhood of it follows that .
The almost complex structure in a neighborhood of is
Since is -holomorphic, we write
where
Recall that in our geodesic normal coordinates we have where is in a neighborhood of , and hence with we have
| (4.9) |
If we write we get from the the second equation in (4.9) that
where . We now have and hence . Setting in (4.9) gives . Next, from Taylor’s formula we get and . Then we get
| (4.10) | ||||
Next, pick so that it is smaller than the minimal norm of the -components of and pick a function as in (4.6). Namely, satisfies
Consider . By 4.4 we have , and also that agrees with in the set . Then we get
By 4.6 we have that is exact with respect to . Therefore we get
| (4.11) |
Finally, the integral in (4.3) is computed by using Stokes’ theorem and that outside of by definition.
| (4.12) |
By combining (4.12) with (4.3) we get
| (4.13) |
Note that along we have . Furthermore is an exact symplectomorphism so we have . Hence
and therefore (4.13) turns into
∎
Corollary 4.8.
Let be any generator and let . Then
Proof.
Fix a generator and consider the moduli space . The action of is
Note that the maximum is well-defined by the compactness of . Let be such that , and let . Since 4.7 holds for any , in particular it holds for . Therefore
Moreover, the inequality holds because does not increase filtration (see the proof of 4.3). ∎
4.4. The chain map is diagonal with respect to the action filtrations
In this section we prove that is diagonal with respect to the action filtrations, that is .
We first give a brief outline of the proof. We consider the trivial -holomorphic half strip whose image is the cone over the Reeb chord and whose tangent space at is spanned by and in geodesic normal coordinates. We show that is transversely cut out, and therefore by 4.4 together with the proof of 4.7 we get
To prove that is transversely cut out, we choose a generic Riemannian metric on (see (A.1)). Then we have a one-to-one correspondence between Reeb chords of degree and geodesics of index (see 4.9 below). We consider vector fields in the kernel of the linearized Cauchy–Riemann operator at . Then we show that restricts to broken Jacobi fields along for which the Hessian of the energy functional (4.1) is negative definite.
The following lemma is essentially found and proven in [RS95, Prop 6.38] and [Dui76]. Recall that the degree of Reeb chords is defined via the Conley–Zehnder index, see 2.3 for details.
Lemma 4.9.
Let be two real numbers. There is a one-to-one correspondence between Reeb chords of degree with action and geodesics in of index with length .
Proof.
It is a consequence of the first part of 4.11 and in particular (4.18) (which do not depend on the current lemma) that Reeb chords with action are in one-to-one correspondence with geodesics in with length . What is left to show is that this one-to-one correspondence also preserves degree/index.
Let be a (non-broken) geodesic. By Morse theory on the loop space, the index of is defined as the Morse index of the energy functional (4.1). Morse’s index theorem [Mil63, Theorem 15.1] says that the index of is equal to the number of points for , which is conjugate to along , counted with multiplicity. Recall that is conjugate to along by definition, if there is a Jacobi field along so that . A Jacobi field is a vector field along satisfying the Jacobi equation
where is the Levi-Civita connection on the bundle , and is the corresponding curvature tensor. The geodesic flow on lifts to the Reeb flow on . Therefore Jacobi fields — which are seen as linearizations of the geodesic flow — lift to the linearized Reeb flow.
Assume that so that is a point that is conjugate to . Then let be a parallel orthonormal frame of , and let be a Jacobi field so that . Defining we thus have that is a parallel orthonormal frame of along . Using the notation , we define . Then we have the system
By using and with , we get the system of differential equations
where is a symmetric matrix. This is equivalent to say that
An explicit fundamental solution to this system is
where
for . The fundamental solution satisfies and in particular
We use that the Jacobi field vanishes at . Then we plug in for which we also have . Thus
From this, we have that is conjugate to if and only if is singular at .
We consider , and using the metric isomorphism and scaling properly, we consider for . Since we assumed that (and hence ) was orthogonal to , we regard the lift as along the lifted geodesic. Since is symplectic with the standard symplectic form in these coordinates, we have that is Lagrangian. We then consider the path of Lagrangians
Whenever is conjugate to , the matrix is singular. Hence it has non-trivial kernel which contributes to the Maslov index exactly the dimension of the kernel. The dimension of the kernel also correspond to the multiplicity of as a conjugate point to . By closing up the loop positively, we find an extra contribution of . Hence
from which we conclude . ∎
Proposition 4.10.
Let be any generator. Let be a -holomorphic half strip as in Section 3.3, and let , where is the linearized Cauchy–Riemann operator at . Then consider the linearized solution
for any . Then we have
where .
Proof.
We modify the proof of 4.7. Since is not -holomorphic, we first prove that the estimate holds.
In a neighborhood of , we have a splitting
We pick a small ball of radius around . Let be the product almost complex structure on , which extends over , and let be the norm determined by and . Then we pick some coordinate in the domain of , and define
In the operator norm we have as . Then we have
| (4.14) |
Let be small enough so that . Then we have
Next we note that
and hence
In view of the definition of in (4.14), we have that .
Let be the projection onto the contact plane . By 4.4 the only contribution to comes from the restriction to . Summing over all balls covering the image of gives
| (4.15) |
The Taylor expansion of around is
where . Because is a non-zero solution of the linearized equation , we rescale in such a way that
| (4.16) |
where is the weighted Sobolev space with weight for some small and where is the coordinate in the -factor. Let for some . We use the Poincaré inequality , where (given that is small enough), together with (4.16). This gives that for some and some . Hence for some .
The same argument applied to and gives for some . Hence
for small enough . By (4.15) we therefore have .
Next, we show . The proof is similar to the computation in the proof of 4.7. The only difference is the computation of (with notation as in 4.7). Since , equation (4.9) becomes
| (4.17) |
where . Then from the second equation we get
Setting in (4.17) gives
and hence
By repeating the same calculation as in (4.10) we end up at
The rest of the proof of 4.7 (which does not require holomorphicity) gives us the result. ∎
Proposition 4.11.
Let be any generator and consider . Then
The same is also true for the chain map
Proof.
By 4.8 we have that
and to prove equality, it is enough to show that for any , there exists a transversely cut out -holomorphic disk with
We let
be the -holomorphic half strip that is the cone over the Reeb chord . In geodesic normal coordinates at , we have that the tangent space of at is which means that by 4.4 and hence by 4.7 we have
| (4.18) |
What is left to show is that is transversely cut out. Consider the following space of vector fields along
where is the projection along the Liouville flow, and is the index form (see (4.21) below for a definition). By 3.4 we have
That is, is equal to the dimension of the maximal subspace of the space of sections of on which is negative definite. The projection
is injective by unique continuation (cf. [Wen16, Corollary 2.27]), which implies that we have
| (4.19) |
For we have that is a disk that is near to for small . In particular, it is a solution of the Floer equation (3.3) up to the first order. By 4.10 and (4.18) we get
which in turn implies
| (4.20) |
where is the energy of the curve .
Now, by defining we compute
| (4.21) | ||||
where is the index form, see e.g. [Jos08, Section 4.1]. The Taylor expansion of around is
Hence for small enough , we obtain and consequently . Therefore we have
which concludes and therefore is transversely cut out.
The same proof shows that is diagonal with respect to the action and length filtrations of Reeb chords and chains of broken geodesic loops, respectively, because of [Mil63, Lemma 15.4]. Namely, the index of the Hessian is equal to the index of restricted to the tangent space . ∎
4.5. Isomorphism between and
The goal of this section is to show that there is a chain isomorphism between and . The outline of the proof is the following. Given a generator we consider the trivial -holomorphic half strip as in Section 4.4. By the genericity of the metric as in (A.1) we show that the evaluation map defined in Section 3.4 is transverse to the infinite dimensional stable manifold of the geodesic in . This gives a chain isomorphism between and by identifying a neighborhood of with the unstable manifold of the geodesic which correspnds to the generator .
We use the notation
and order the generators of by their action
Pick a strictly increasing sequence of numbers so that
and define
We extend the filtration to all of by letting for every .
Note that the ordering of the generators of gives an ordering of the generators of and by 4.11.
Recall the definition of the retraction
defined in the proof of 4.3: Let be any loop with . Pick a subdivision of the domain of
which is fine enough so that for some small enough. Then is defined so that
Then we define
Theorem 4.12.
The map
is an isomorphism
Proof.
We first show that for any the map
is an isomorphism.
By the definition of the numbers there is only one generator . Denote its degree by . By 4.9, there is exactly one generator that corresponds to . We think of as the unstable manifold of the geodesic corresponding to . Since both and only contains one generator each, we only need to show that
| (4.22) |
By 4.11 we already know that the trivial -holomorphic half strip over is so that . To prove that equation (4.22) holds it is enough to consider the map
and show that it is locally surjective at . We do this by showing that it is a submersion. That is, we consider
and we show that it is surjective onto the image of . As noted above, should be thought of as the unstable manifold of inside with respect to the energy functional . The following composition
is described as follows. Pick a subdivision of the domain of
for some . The tangent space of at has the following splitting
by [Mil63, Lemma 15.3, 15.4]. Here is the space of broken Jacobi fields vanishing at the endpoints, and is the space of all vector fields along so that for every (cf. [Mil63, Section 15]). Furthermore we write
where is the (maximal) subspace of on which the Hessian is negative definite, and is the subspace on which is positive semidefinite. We will show that for any non-zero , its image does not lie in , and that the image does not lie in .
- is transverse to :
-
Consider any non-zero , where
is the linearization of at . Here is the Sobolev space with weight for some small at the positive punctures in the domain . The differential of the evaluation map is a trace operator on , so is a vector field in along . Assume that is such that , that is for every . Since is a restriction to , we assume that is so that for every . We consider the subspace
It is closed and has codimension . The restricted linearized operator is therefore a Fredholm operator with index
If we pick large enough by making the subdivision of the domain of loops fine enough, the index is negative. Hence is empty for generic choices of almost complex structures on . This means that .
- is transverse to :
Therefore is an isomorphism.
The filtrations on and are both bounded from below which gives an isomorphism for every . Thus every square in the following diagram commutes.
We then pass to colimits to obtain the isomorphism
∎
5. Applications
The first goal of this section is to equip and with the structure of -modules. The second goal is then to consider the case when and exhibit examples of codimension 2 knots where the Alexander invariant is related to as -modules. From this we draw the conclusion that the unit conormal of knows about the smooth topology of beyond the fundamental group.
After we have discussed the -module structures in Section 5.1, we will provide background material surrounding the Alexander invariant in Sections 5.2 and 5.3. Then, in Section 5.4 we use the Leray–Serre spectral sequence associated with the path-loop fibration to relate the Alexander invariant to as a -module.
5.1. -module structures on and
Consider any homotopy class represented by the unique minimizing geodesic in the given homotopy class. Via the cell structure of , we associate to a generator . Then consider the map
where denotes the Pontryagin product as in (3.2).
Lemma 5.1.
The map defines a group action of on .
Proof.
Let . As above, we assign to and the cohomology classes . Assign to the composition the cohomology class
Since is associative up to a sign in cohomology we have
∎
By linearity we extend the action to a -module structure on .
Consider a generator , and denote by the geodesic that corresponds to. Via , we let be the cohomology class corresponding to . Then define
Lemma 5.2.
The map defines a group action of on .
Proof.
Let and be as in the proof of 5.1 above. Let be any generator. Because is associative up to a sign in cohomology we have
| (5.1) |
Because is an -homomorphism, we glue the two disks contributing to and to obtain
| (5.2) |
Hence there exists a -holomorphic disk in the symplectization of with two positive punctures and . Define . Then (5.2) says that
Thus is the generator corresponding to the concatenation . Combining this with (5.1) gives
Lastly, we need to prove that if is the constant loop, then . This follows from the definition of . The generator of which corresponds to the (0-chain of) the constant loop is the unique Lagrangian intersection generator in the compact part of which corresponds to the unique intersection point of with , call it . Therefore
∎
By linearity we extend the action to a -module structure on .
Theorem 5.3 (1.1).
The isomorphism
is an isomorphism of -modules.
Proof.
Let be a generator and let be a homotopy class represented by a unique minimizing geodesic . Then consider a generator so that , where is the cohomology class corresponding to . Then we have
∎
Remark 5.4.
Note that , and consider as an -algebra with operations where , is the Pontryagin product, and for . We observe that can be equipped with the structure of a left -module over . More precisely we define this left -module structure as a sequence of maps
defined by
where is the unique Reeb chord corresponding to via . Then by computation we have that satisfies the following equation for .
| (5.3) | ||||
Note that this means that there is a group action up to homotopy of on , but there are no higher coherent homotopies. However, this is enough to directly obtain 5.1 and 5.2.
Since is an -algebra, it can be regarded as a left -module over itself, and therefore also as a left -module over via the sequence of maps
defined by
By a computation we see that satisfies (5.3) for every . For the equation is trivial.
Furthermore we have that the -homomorphism induces an isomorphism of -modules over as follows. The isomorphism of -modules over is a sequence of maps
defined by
where is the unique generator corresponding to via . Then by computation we have that satisfies the following equation for .
The fact that this is an -module isomorphism directly implies 5.3.
5.2. Plumbings and infinite cyclic covers
In this section we review standard background material from [Rol76].
Let and . We consider the plumbing of with . That is, consider and . By identifying with the upper hemisphere of , we have
We then take the disjoint union of with and identify their common submanifolds via . We call the resulting space the plumbing of and , denoted by . In short we write
We note that is the deformation retract of . Let and note that it is a -dimensional sphere. Embed into and consider the complement of its boundary ; denote its infinite cyclic cover by .
Following [Rol76, Section 5.C] we find the simplicial structure of by cutting along . More precisely, let be an open bicollar of the interior of , and let
Consider infinitely many copies of each of , and . Denote the copies by , and for . Then consider the disjoint union of all the and glue them together by identifying with via the map
Define
| (5.4) |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/48321ba7-28c9-4cd8-be91-fc4f33afc9f6/x16.png)
5.3. The Alexander invariant
In this section we review standard material on the Alexander invariant from [Rol76].
Associated to the open cover of is the sequence of inclusions
from which we get a short exact sequence in singular chains (cf. [BT13, Section 8])
| (5.5) |
Let . Then
and for any we have
Since
the short exact sequence (5.5) induces a long exact sequence in homology
We have
where denotes reduced homology. Since , Alexander duality gives that
Since , we get
which means that unless .
Since the group of deck transformations of is infinite cyclic, we choose a generator which induces an automorphism
This gives a -module structure on as follows. Let , then for any let
where is the -fold composition power of . The Alexander invariant is then defined as considered as a -module.
Lemma 5.5 ([Rol76, Theorem 7.G.1]).
There exist non-trivial knots with infinite cyclic knot group, .
Proof.
Let and let . We then consider any obtained as , where
Now we have that is simply connected: Every loop in shrinks missing since is homotopy equivalent to . This is because and in . From the construction of in (5.4) we thus have . Hence, because the group of deck transformations of is , we have .
5.4. Using the Leray–Serre spectral sequence
Consider the knot with as in Section 5.2. We use the notation .
Associated to the path-loop fibration
is the Leray–Serre spectral sequence. It is first quadrant spectral sequence of -modules which converges:
Note that is Abelian and hence we can consider as a -module.
Since is only supported in degrees , and we have the following facts
- •
-
•
is only supported on the vertical lines .
-
•
The bottom row is , since .
Example 5.6.
Consider the case when is obtained as the boundary of where the core of the plumbing is depicted in Fig. 13. In this case, is only supported at the vertical lines . For this spectral sequence, the -th page is the first page after page 1 that has non-zero differentials. Namely, the -th page of this spectral sequence is
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/48321ba7-28c9-4cd8-be91-fc4f33afc9f6/x18.png)
Where and every tensor product is taken over . The differentials at every page succeeding the -th page is zero, so in particular we get
Example 5.7.
Suppose is obtained as the boundary of for where the core of the plumbing is depicted in Fig. 13. In this case the second page of the spectral sequence is only supported at the lines . The -th page of the spectral sequence is the first page after page 1 that has non-zero differentials and it looks as follows:
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/48321ba7-28c9-4cd8-be91-fc4f33afc9f6/x19.png)
Immediately from this page, we get an isomorphism of -modules
| (5.6) |
Furthermore, the next page with non-zero differentials is page , which looks as follows
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/48321ba7-28c9-4cd8-be91-fc4f33afc9f6/x20.png)
This is the last page with non-zero differentials, so and hence from page , we obtain an exact sequence
| (5.7) |
and for each we have an exact sequence
Furthermore, from page we get isomorphisms
for every . In particular, in view of (5.7), we have where
So if and is known, we compute by (5.6) but also a quotient of by exactness of (5.7)
Let us summarize what we have.
where
Example 5.8.
Let denote the unit conormal of the standard embedded . A consequence of these computations is the following theorem.
Theorem 5.9 (1.2).
Let or . Let be a point. Then there exists a codimension 2 knot with , such that is not Legendrian isotopic to .
Proof.
For the case , consider the knot where the core of the plumbing is depicted in Fig. 13. In the case we let and and consider , where the core of the plumbing is again depicted in Fig. 13.
We note that for dimensional reasons we have , but the Alexander invariant shows that is non-trivial [Rol76, Section 7.G] (see also 5.5).
The computations in 5.6 and 5.8 show that in particular
Since we use classical methods to show that is non-trivial (see 5.5, it follows that is non-trivial. Consider the unknot , then the complement is homotopy equivalent to a circle, which means that is only supported in degree 0. Therefore we have and so is not Legendrian isotopic to . ∎
Appendix A Monotonicity of -holomorphic half strips
To establish compactness of the moduli spaces in Section 3.3 we need to make sure that -holomorphic half strips in does not escape to horizontal infinity. Pick a tubular neighborhood of and call it . Then we decompose as
where we identify with . Pick a generic Riemannian metric on such that geodesics are non-degenerate critical points of the length and energy functionals. Define a function
so that
(A.1)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/48321ba7-28c9-4cd8-be91-fc4f33afc9f6/x21.png)
Define a metric on as
where is the coordinate in the -factor. Similar to the situation in [EL17, Appendix C], if are two points and a geodesic with and , then there is a unique geodesic so that
-
•
and , and
-
•
is a Morse function with a unique maximum at some interior point .
If we define
then
is an exhaustion of by compacts. Then given any geodesic , there exists some so that for every . In particular, if we restrict to the present situation in this paper, where every geodesic is a loop based at . To this end fix some constant and assume , that is is a piecewise geodesic loop based at with length bounded above by (for details see Section 4.2). Then there is some depending only on and the metric so that for every . We prove that there exists some (depending on and the metric ) so that the -holomorphic strips lie inside of by using the monotonicity lemma [Sik94, Proposition 4.7.2] (see also [CEL10, Lemma 3.4]).
Our metric defined in (A.1) extends to a metric on such that it has bounded geometry in the terminology of [Sik94, Section 4]. Furthermore, since is Lagrangian, the tuple is tame in the sense of [Sik94, Definition 4.1.1]. Let be constants so that for any
where and are the metrics induced by on and respectively. If we denote the lower bound on the injectivity radius by , we may assume .
Lemma A.1 ([Sik94, Proposition 4.7.2 (ii)]).
Let be tame. Then there exist a positive constant with the following property. Let be a -holomorphic curve so that where and . Then
We use this lemma with , and .
Theorem A.2.
Let be arbitrary and consider a generator . Then there exists so that for any .
Proof.
Consider a generator and pick some . Then by 4.11 we have
Because the -holomorphic disk has boundary on the Reeb chord , the exact Lagrangian for and the geodesic . Therefore there is some (depending only on ) so that for any . Then pick some (which a priori can be equal to ) and assume that . We consider and then we prove that is finite. Namely, fix some and let be the maximal number of points so that . Then we apply A.1 to each so that for each . Therefore
Since is bounded by , so is the area of . Hence
This shows that there is some finite such that for every . ∎
Appendix B Signs, gradings and orientations of moduli spaces
In this section, we use the same conventions and setup as in [Sei08, Section (11)] and [FOOO10, Section 8]. Pick some and consider the collection of Lagrangian branes of a cotangent fiber at and a system of parallel copies as in Section 3.3 and Section 2. Pick a word of generators where , and pick abstract perturbation data so that is regular. Then for some , denote the linearization of the operator at the -holomorphic disk by . Then we have the following:
Lemma B.1 ([Abo12b, Lemma 6.1]).
With the choice as above there is a canonical up to homotopy isomorphism
and in particular
Since the orientation lines are naturally graded by the indices of the linearized operators , we have a nautral isomorphism coming from reordering tensor products of orientation lines which produces a Koszul sign
Furthermore there are natural non-degnerate pairings
From now on we use the following abbreviation: For the word , we let
As in (3.4) and (3.5) denote by the moduli space of abstract -holomorphic disks with boundary punctures, and its Deligne–Mumford compactification by . Then the codimension one boundary is covered by the natural inclusions of the following strata
| (B.1) | ||||
| (B.2) |
Here is the Deligne–Mumford space of unit disks in the complex plane with boundary punctures that are oriented counterclockwise. We would like to compare the product orientation of each of the strata with the boundary orientation on . The orientation of the boundary is determined as follows. Any orientation on a manifold induces an orientation on its boundary via the outward normal first-rule. More precisely via the canonical isomorphism
where is the normal bundle of which is canonically trivialized by the outwards normal vector along the boundary. Following the conventions in [Sei08, Abo10, Abo12b] there is a choice of coherent orientations on such that the boundary strata (B.1) and (B.2) differs from the boundary orientation on by a sign and respectively where we have
| (B.3) | ||||
| (B.4) |
and is attached to the -th outgoing leaf of (cf. [Sei08, (12.22)]). The first sign is obtained from [Sei08, (12.22)] by using , and since is attached to at the last outgoing leaf.
The second sign is obtained from [Sei08, (12.22)] by using , and .
Proof of 3.5.
We consider the moduli space and the stratification of its codimension one boundary as in (3.6). We first consider the strata of the form where . Then, using B.1 we have
Reordering the factors so that becomes adjacent to introduces the Koszul sign where
since . Canceling the adjacent factors and then gives
Then by (B.3) we get a sign when comparing the product orientation of with the boundary orientation of . After these reorderings we arrive at
which is canonically isomorphic to . The total sign difference between the product orientation on and the boundary orientation on is therefore
Similarly, we compare the product orientation of with the boundary orientation on . Recall from (3.7) that if is a subword at position , then denotes the word with the subword replaced by an auxiliary generator . Again by B.1 we therefore have
Assuming that is rigid means especially that and so we move past without introducing any sign and arrive at
Because , moving to the front and adjacent to gives
with a sign difference of where
Recall from the assumptions in 3.5 that is a subword at position .
Then using and this collapses to
and using (B.4), with a sign difference of . The total sign difference between the product orientation of and the boundary orientation on is therefore
∎
Proof of 3.10 (continued).
To confirm that the signs match up in the -relation
we look at the terms one by one and compute the sign that is in front of each term. In the first term it is only the sign from that is taken into account, namely where
The second term has a sign coming from:
-
(1)
The definition of the Pontryagin product in (3.2) contributes with a sign where
-
(2)
the difference between the product orientation on and the boundary orientation on is , where and
as in 3.5,
- (3)
-
(4)
the definition of in (3.19) contributes with a sign where
Now it is straightforward to check that .
Next we consider the term in the right hand side. Let . This sum has a sign coming from:
-
(1)
The difference between the product orientation on and the boundary orientation on is where and
-
(2)
the definition of in (2.1) contributes with a sign where
-
(3)
the definition of in (3.19) contributes with a sign where
Note that since we assume that is rigid, we have
hence we get
It is then again a straightforward calculation to show that .
∎
References
- [Abo10] M. Abouzaid, A geometric criterion for generating the Fukaya category, Publications mathématiques de l’IHÉS, 112 (2010), pp. 191–240.
- [Abo12a] ———, Framed bordism and Lagrangian embeddings of exotic spheres, Annals of Mathematics, (2012), pp. 71–185.
- [Abo12b] ———, On the wrapped Fukaya category and based loops, Journal of Symplectic Geometry, 10 (2012), pp. 27–79.
- [AENV14] M. Aganagic, T. Ekholm, L. Ng, and C. Vafa, Topological strings, D-model, and knot contact homology, Advances in Theoretical and Mathematical Physics, 18 (2014), pp. 827–956.
- [Arn67] V. I. Arnol’d, Characteristic class entering in quantization conditions, Functional Analysis and its applications, 1 (1967), pp. 1–13.
- [AS06] A. Abbondandolo and M. Schwarz, On the Floer homology of cotangent bundles, Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences, 59 (2006), pp. 254–316.
- [AS10] M. Abouzaid and P. Seidel, An open string analogue of Viterbo functoriality, Geometry & Topology, 14 (2010), pp. 627–718.
- [BEE12] F. Bourgeois, T. Ekholm, and Y. Eliashberg, Effect of Legendrian surgery, Geometry & Topology, 16 (2012), pp. 301–389.
- [BKO19] Y. Bae, S. Kim, and Y.-G. Oh, A wrapped Fukaya category of knot complement, arXiv:1901.02239, (2019).
- [BT13] R. Bott and L. W. Tu, Differential forms in algebraic topology, volume 82, Springer Science & Business Media (2013).
- [CEL10] K. Cieliebak, T. Ekholm, and J. Latschev, Compactness for holomorphic curves with switching Lagrangian boundary conditions, Journal of Symplectic Geometry, 8 (2010), pp. 267–298.
- [CELN17] K. Cieliebak, T. Ekholm, J. Latschev, and L. Ng, Knot contact homology, string topology, and the cord algebra, J. Éc. polytech. Math, 4 (2017), pp. 661–780.
- [CL09] K. Cieliebak and J. Latschev, The role of string topology in symplectic field theory, New perspectives and challenges in symplectic field theory, CRM Proc. Lecture Notes, 49 (2009), pp. 113–146.
- [DR16] G. Dimitroglou Rizell, Lifting pseudo-holomorphic polygons to the symplectisation of and applications, Quantum Topology, 7 (2016), pp. 29–105.
- [Dui76] J. Duistermaat, On the Morse index in variational calculus, Advances in Mathematics, 21 (1976), pp. 173–195.
- [EENS13] T. Ekholm, J. B. Etnyre, L. Ng, and M. G. Sullivan, Knot contact homology, Geometry & Topology, 17 (2013), pp. 975–1112.
- [EES05] T. Ekholm, J. Etnyre, and M. Sullivan, The contact homology of Legendrian submanifolds in , Journal of Differential Geometry, 71 (2005), pp. 177–305.
- [EES07] ———, Legendrian contact homology in , Transactions of the American Mathematical Society, 359 (2007), pp. 3301–3335.
- [EHK16] T. Ekholm, K. Honda, and T. Kálmán, Legendrian knots and exact Lagrangian cobordisms, Journal of the European Mathematical Society, 18 (2016), pp. 2627–2689.
- [Ekh06] T. Ekholm, Rational symplectic field theory over for exact Lagrangian cobordisms, math/0612029, (2006).
- [Ekh12] ———, Rational SFT, linearized Legendrian contact homology, and Lagrangian Floer cohomology, in Perspectives in analysis, geometry, and topology, Springer (2012), pp. 109–145.
- [Ekh19] ———, Holomorphic curves for Legendrian surgery, arXiv:1906.07228, (2019).
- [EKS16] T. Ekholm, T. Kragh, and I. Smith, Lagrangian exotic spheres, Journal of Topology and Analysis, 8 (2016), pp. 375–397.
- [EL17] T. Ekholm and Y. Lekili, Duality between Lagrangian and Legendrian invariants, arXiv:1701.01284, (2017).
- [ENS16] T. Ekholm, L. Ng, and V. Shende, A complete knot invariant from contact homology, arXiv:1606.07050, (2016).
- [EO17] T. Ekholm and A. Oancea, Symplectic and contact differential graded algebras, Geometry & Topology, 21 (2017), pp. 2161–2230.
- [ES16] T. Ekholm and I. Smith, Exact Lagrangian immersions with a single double point, Journal of the American Mathematical Society, 29 (2016), pp. 1–59.
- [FOOO10] K. Fukaya, Y.-G. Oh, H. Ohta, and K. Ono, Lagrangian intersection Floer theory: anomaly and obstruction, Part II, volume 2, American Mathematical Soc. (2010).
- [Fra08] U. Frauenfelder, Gromov convergence of pseudoholomorphic disks, Journal of Fixed Point Theory and Applications, 3 (2008), pp. 215–271.
- [GPS18a] S. Ganatra, J. Pardon, and V. Shende, Microlocal Morse theory of wrapped Fukaya categories, arXiv:1809.08807, (2018).
- [GPS18b] ———, Sectorial descent for wrapped Fukaya categories, arXiv:1809.03427, (2018).
- [GPS20] ———, Covariantly functorial wrapped Floer theory on Liouville sectors, Publications mathématiques de l’IHÉS, 131 (2020), pp. 73–200.
- [Hat02] A. Hatcher, Algebraic Topology, Cambridge University Press (2002).
- [Jos08] J. Jost, Riemannian geometry and geometric analysis, Springer Science & Business Media (2008).
- [Mil63] J. Milnor, Morse Theory, Annals of Mathematic Studies, 51 (1963).
- [MW18] C. Y. Mak and W. Wu, Dehn twist exact sequences through Lagrangian cobordism, Compositio Mathematica, 154 (2018), pp. 2485–2533.
- [Ng08] L. Ng, Framed knot contact homology, Duke Mathematical Journal, 141 (2008), pp. 365–406.
- [Rol76] D. Rolfsen, Knots and links, volume 346, American Mathematical Soc. (1976).
- [RS93] J. Robbin and D. Salamon, The Maslov index for paths, Topology, 32 (1993), pp. 827–844.
- [RS95] ———, The spectral flow and the Maslov index, Bulletin of the London Mathematical Society, 27 (1995), pp. 1–33.
- [RS01] J. W. Robbin and D. A. Salamon, Asymptotic behaviour of holomorphic strips, in Annales de l’Institut Henri Poincare (C) Non Linear Analysis, volume 18(5), Elsevier Masson (2001), pp. 573–612.
- [Sei08] P. Seidel, Fukaya categories and Picard-Lefschetz theory, European Mathematical Society (2008).
- [She16] V. Shende, The conormal torus is a complete knot invariant, arXiv:1604.03520, (2016).
- [Shu10] M. G. Shulman, Equivariant spectral sequences for local coefficients, arXiv:1005.0379, (2010).
- [Sik94] J.-C. Sikorav, Some properties of holomorphic curves in almost complex manifolds, in Holomorphic curves in symplectic geometry, Springer (1994), pp. 165–189.
- [Syl19] Z. Sylvan, On partially wrapped Fukaya categories, Journal of Topology, 12 (2019), pp. 372–441.
- [Wei71] A. Weinstein, Symplectic manifolds and their Lagrangian submanifolds, Advances in mathematics, 6 (1971), pp. 329–346.
- [Wen16] C. Wendl, Lectures on Symplectic Field Theory, arXiv:1612.01009, (2016).