Fighting network space: it is time for an SQL-type language to filter phylogenetic networks

Rooted phylogenetic networks are extensions of rooted phylogenetic trees to explicitly incorporate reticulation events such as lateral gene transfer and hybridization, modelled as nodes with two or more parents (e.g. the network shown in Figure 1 has a reticulation $r_{1}$ with the three parents $p_{1}$, $p_{2}$, and $p_{3}$). While the potential of such networks for hypothesis generation and testing is increasingly recognised, a number of obstacles prevent their widespread use by evolutionary biologists. First, the space of rooted phylogenetic networks is vast, far larger than the space of rooted trees, and even heuristically navigating this space is a formidable computational challenge. Second, hypothesis-testing techniques that are standard in the tree literature, such as the ability to query whether there is support for a particular clade, are not yet well-developed. These two problems often coincide in the sense that, depending on the specific context, a large number of networks in the search space will be biologically irrelevant. For this reason it is both biologically and computationally attractive that biologists should be able to describe a priori, via a user-friendly SQL-style (Structured Query Language) modelling language, those networks which should (or should not) be taken into consideration. Such constraints can help biologists interpret the output of network-building software and, when incorporated into the search algorithms used by such software, potentially allow the search space to be dynamically pruned. Furthermore, they can equally be used a posteriori to filter an already given set of candidate networks for biological relevance. Historically, the idea of using constraints to reduce the search space of phylogenetic trees dates back to at least [1], who pointed out that a complete search of a smaller tree space could be better than a heuristic search of a larger space, in terms of finding the optimal tree. Inspired by this idea, we propose an outline for such a constraint-based framework for phylogenetic networks.

As indicated in Figure 1, a rooted phylogenetic network, henceforth simply network, is an extension of the rooted phylogenetic tree to the space of rooted directed acyclic graphs. For a technical description of their characteristics we refer the reader to [2]. Networks are often constructed as parsimonious summaries of incongruence within a set of trees. A common goal is to construct a network that is as parsimonious as possible, in terms of the number of reticulations, and which has all the input trees simultaneously embedded within it (e.g. the tree that is shown on the left-hand side of Figure 1 is embedded in the network that is shown on the right-hand side of the figure). Methods that work directly on sequence data are also emerging and show considerable promise, as well as approaches that model duplication, loss, transfer, and incomplete lineage sorting events by reconciling a gene tree with a species tree (e.g. [3]). However, severe computational intractability (NP-hardness or worse) is a recurring feature of almost all explicit network methodologies, greatly limiting the scope of their application. The core of the problem is that, even for a small number of taxa and reticulations, the space of networks is vast, and even heuristic traversal of this space is problematic. One way of trimming the space of networks is to heavily constrain the number of reticulations and/or their relative location in the network. Although beneficial from a tractability perspective such constraints should be first and foremost biologically well-motivated. Indeed, constraint-based pruning is a feature that one often encounters in tree-building software to test hypotheses (e.g. the SOWH test [4]). Software such as PAUP* [5] and RAxML [6], for example, allow the user to restrict the search of tree-space to trees that contain a certain clade or that are consistent with a given tree backbone (i.e. a constraint tree). Such restrictions allow the user to test support for competing clade hypotheses, an experimental technique that is used extensively in practice.

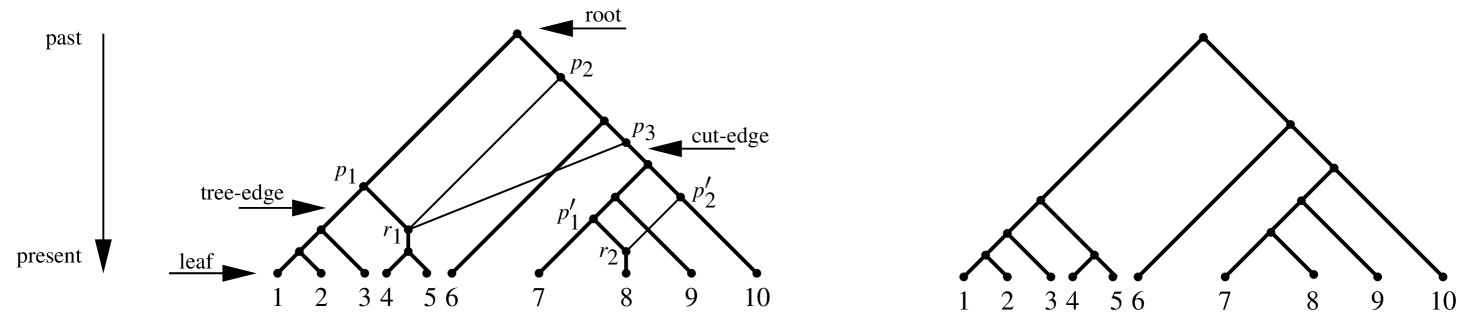
As Figure 1 suggests, networks have features that cannot be described simply in terms of clades. It is unlikely, and unreasonable to expect, that biologists will reach a single, unified consensus on which network features are meaningful and which are not. However, in a given experimental context, and guided by the data at hand, a biologist often already has some insight into which networks do, and do not, constitute plausible hypotheses. The challenge therefore is to provide biologists with an easy-to-use tool that allows them to formally articulate these insights. For maximum flexibility, such a tool should allow both certain natural atomic constraints and SQL-style compound constraints. We note here that SQL was originally developed for managing and retrieving database content by using complex queries, but the concept is now used widely in computational science. The atomic constraints should allow fundamental characteristics of the candidate network to be tested (and, ideally, should themselves be computationally tractable). Some examples include:

(a)

A given subset of taxa must be below a cut-edge, i.e. a locally isolated part of the network.

(b)

A given subset of taxa must be below a tree-edge, i.e. a purely tree-like part of the network.

(c)

A given taxon $x$ should be a hybrid of two other designated taxa $y$ and $z$.

(d)

A given tree should be embedded in the network.

To illustrate, taxa 7, 8, 9, and 10 are below a cut-edge and taxa 1, 2, and 3 are below a tree-edge in the network shown in Figure 1. Furthermore, taxon $r_{2}$ is a hybrid of the two taxa $p_{1}^{\prime}$ and $p_{2}^{\prime}$.

In addition to atomic constraints that describe certain topological characteristics of a network, one could also include statistically motivated constraints. For example, one may wish to consider only those networks whose probability of a given gene tree topology exceeds some user-defined value (for details, see [7]). Note, also, that constraints can be either positive (specifying characteristics that must appear in the final network) or negative (forbidding certain characteristics).

Lastly, as mentioned above, atomic constraints can be used as building blocks to design more powerful compound constraints. The next example combines three atomic constraints, and might be useful if one has more detailed information about the evolutionary history of a subset of the taxa under consideration. In such a case, one could build the following SQL-type query:

The purpose of SQL-style constraints in the construction and analysis of networks is twofold. First, they can be used a posteriori to filter a given set of candidate networks resulting from an analysis that reconstructs networks from a data set (e.g. characters, trees, clusters). Since many of these methods are based on combinatorial frameworks, the set of optimal candidate solutions can be quite large. For example, an analysis of a well-known grass data set that finds all networks containing two given trees, each on 40 taxa, and whose number of reticulations is minimized, results in a set of (at least) 2268 optimal solutions. Obviously, validating all optimal networks by hand becomes a tedious task. In order to support the biologist in this part of an analysis, [8] describes two constraints that are available as part of the Dendroscope program [9] and can be used to filter or rank a list of previously generated networks. Second, SQL-type constraints can also be defined before any analysis so that the search space of networks, which is vast, can be pruned dynamically. Since the space of networks is, in general, infinite for a fixed number of taxa, even a small number of constraints can greatly aid the computational process and significantly reduce its running time, so that instances of a larger input size can potentially be solved exactly. In the context of phylogenetic trees, [10] showed that the use of a constrained tree reduces the search space remarkably by calculating the difference between the number of trees of a fixed size that need to be considered in an unconstrained search and the number of trees of the same size that are compatible with a given constraint tree.

The technicalities involved in dynamic pruning will be nontrivial, but we draw inspiration from a number of “branch and bound”-style pruning techniques that are already being used, albeit in an ad hoc fashion, in the phylogenetic network literature. For example, algorithms that construct networks that contain embeddings of triplets (or clusters) will cease to explore a branch of the network search space if the partially constructed network already fails to contain a certain triplet, because adding more taxa to the network will never recover the missing triplet [11, 12]. Adding additional constraints should allow for even more aggressive pruning of the network search space. The step from high-level constraints to low-level pruning is a topic we hope to return to in a forthcoming article.

Furthermore, and perhaps most fundamentally, by using SQL-type constraints, biologists have more control on the output of programs that reconstruct networks. In fact, they can go beyond the widespread concept of regarding an algorithm as a black box, and actively engage in the construction of networks by adding extra biological information to it and, therefore, reduce the risk of misanalyses.

The space of phylogenetic networks is huge, and this is an obstacle from both a computational and interpretational viewpoint. We propose the development of an SQL-style constraint-based language that will allow the imposition of biologically relevant constraints on this space, thus enhancing the utility of phylogenetic networks for biologists, and potentially cutting down the search space of phylogenetic networks to a more reasonable size.

S.L. was supported by a Marie Curie International Outgoing Fellowship within the $7^{\textnormal{th}}$ European Community Framework Programme.