Finding Densest -Connected Subgraphs
Abstract
Dense subgraph discovery is an important graph-mining primitive with a variety of real-world applications. One of the most well-studied optimization problems for dense subgraph discovery is the densest subgraph problem, where given an edge-weighted undirected graph , we are asked to find that maximizes the density , i.e., half the weighted average degree of the induced subgraph . This problem can be solved exactly in polynomial time and well-approximately in almost linear time. However, a densest subgraph has a structural drawback, namely, the subgraph may not be robust to vertex/edge failure. Indeed, a densest subgraph may not be well-connected, which implies that the subgraph may be disconnected by removing only a few vertices/edges within it. In this paper, we provide an algorithmic framework to find a dense subgraph that is well-connected in terms of vertex/edge connectivity. Specifically, we introduce the following problems: given a graph and a positive integer/real , we are asked to find that maximizes the density under the constraint that is -vertex/edge-connected. For both problems, we propose polynomial-time (bicriteria and ordinary) approximation algorithms, using classic Mader’s theorem in graph theory and its extensions.
1 Introduction
Dense subgraph discovery is an important graph-mining primitive with a variety of real-world applications [20]. Examples include detecting communities and spam link farms in the Web graph [11, 19], extracting molecular complexes in protein–protein interaction networks [3, 45], finding experts in crowdsourcing systems [29], and real-time story identification from tweets [2].
One of the most well-studied optimization problems for dense subgraph discovery is the densest subgraph problem. Let be a simple undirected graph with edge weight , where is the set of positive reals. Throughout this paper, we assume that , edge-weighted graphs have only positive weights, and is connected. For , let denote the subgraph induced by , i.e., , where . The density of is defined as , where is the sum of edge weights of , i.e., . In the densest subgraph problem, given a graph , we are asked to find that maximizes . An optimal solution to this problem is referred to as a densest subgraph.
Unlike most optimization problems for dense subgraph discovery such as the maximum clique problem [18], the densest subgraph problem is polynomial-time solvable. Indeed, there are some polynomial-time exact algorithms such as Goldberg’s flow-based algorithm [21] and Charikar’s linear-programming-based algorithm [8]. Moreover, it was shown by Charikar [8] that a simple greedy algorithm admits -approximation in almost linear time. Partially due to its solvability, the densest subgraph problem has been employed in many real-world applications.
However, it can be seen that a densest subgraph has a structural drawback, that is, the subgraph may not be robust to vertex/edge failure. To see this, let us introduce some terminology. A vertex subset is called a vertex separator of if its removal disconnects , i.e., partitions into at least two non-empty graphs between which there are no edges. Note that no clique has a vertex separator. An edge subset is called a cut of if its removal disconnects . The weight of a cut is defined to be the sum of weights of edges within it. The vertex connectivity of , denoted by , is the smallest cardinality of a vertex separator of if is not a clique and otherwise. The edge connectivity of , denoted by , is the smallest weight of a cut of .
A densest subgraph does not necessarily have large vertex/edge connectivity, which means that the subgraph may be disconnected by removing only a few vertices/edges within it. For instance, consider an unweighted graph (i.e., for every ) consisting of two equally-sized large cliques that share only a few vertices or are connected by only a few edges. In both cases, the entire graph is a densest subgraph, but it is easily disconnected by removing the common vertices in the former case and the bridging edges in the latter case.


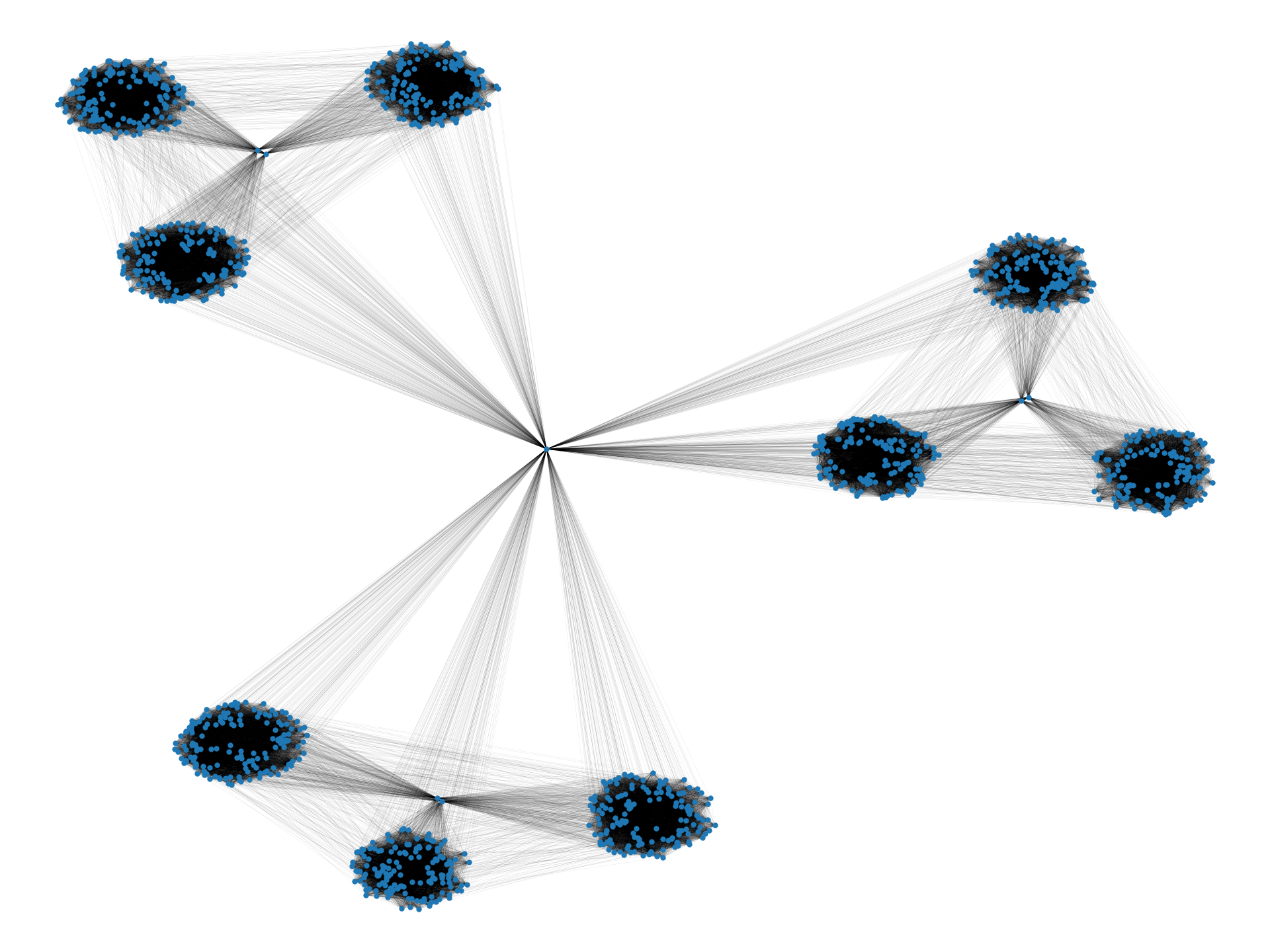
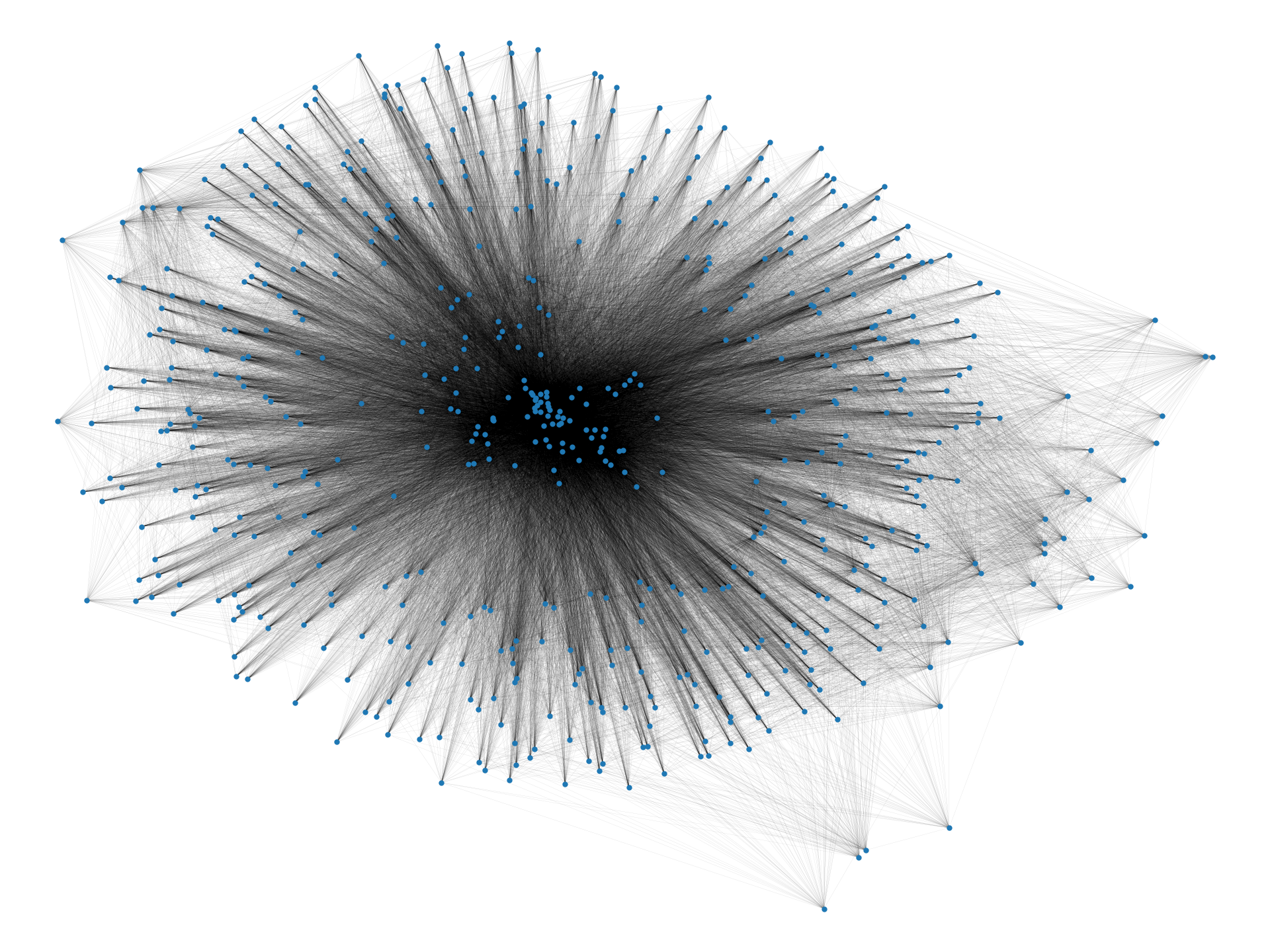
In this paper, we provide an algorithmic framework to find a dense subgraph that is well-connected in terms of vertex/edge connectivity. An (edge-weighted) graph is said to be -vertex-connected if is no less than . On the other hand, an edge-weighted graph is said to be -edge-connected if is no less than . Using these criteria, we introduce the following problems:
Problem 1 (Densest -vertex-connected subgraph).
Given an edge-weighted undirected graph , where , and a positive integer , the goal is to find that maximizes the density subject to the constraint that the induced subgraph is -vertex-connected.
Problem 2 (Densest -edge-connected subgraph).
Given an edge-weighted undirected graph , where , and a positive real , the goal is to find that maximizes the density subject to the constraint that the induced subgraph is -edge-connected.
In the two-cliques example we discussed earlier, an optimal solution to Problems 1 and 2 with a sufficiently large value for would be one of the cliques, which is robust to vertex/edge failure and nearly as dense as the densest subgraph (i.e., the entire graph). We observe that Problems 1 and 2 are meaningful for real-world data too; Figure 1 visualizes densest subgraphs of the four real-world Web graphs that are publicly available at SNAP (Stanford Network Analysis Project) [32] using a spring layout positioning.111Graphs have been made simple undirected by ignoring the direction of edges, and by removing self-loops and multiple edges. As we can visually observe, small separators may exist in real-world densest subgraphs. Table 1 summarizes the detailed statistics. As can be seen, the densest subgraphs in web-BerkStan and web-NotreDame have surprisingly small vertex connectivity; in fact, they have vertex connectivity of twelve and one, respectively. Note that for both densest subgraphs, vertex connectivity is much smaller than the minimum degree of vertices, a trivial upper bound on that.
| Graph | ||||||
|---|---|---|---|---|---|---|
| web-BerkStan | 392 | 40,535 | 103.41 | 12 | 201 | 201 |
| web-Google | 123 | 3,449 | 28.04 | 30 | 30 | 30 |
| web-NotreDame | 1,367 | 107,526 | 78.66 | 1 | 155 | 155 |
| web-Stanford | 597 | 35,456 | 59.39 | 60 | 60 | 60 |
For both problems, we propose polynomial-time (bicriteria and ordinary) approximation algorithms. Let and denote the maximum and minimum weights, respectively, over all edges in , i.e., and .
Our first result is polynomial-time -bicriteria approximation algorithms with parameter for Problems 1 and 2. That is, the algorithm for Problem 1/Problem 2 outputs having density at least the optimal value times but only satisfies a -vertex/edge-connectivity constraint (rather than the original -vertex/edge-connectivity constraint). Note that if we set , we can obtain -approximation algorithms. The design of our algorithms is based on an elegant theorem in graph theory, proved by Mader [34]. The theorem states that any (unweighted) dense graph contains a highly vertex-connected subgraph wherein the minimum degree of vertices is greater than the density of the entire vertex set. We refer to this subgraph as a Mader subgraph and our algorithm finds a Mader subgraph of a densest subgraph of each maximal -vertex-connected subgraph of . It should be noted that to deal with edge-weighted graphs, we generalize Mader’s theorem. Our generalized version cannot be directly obtained from the original statement of Mader’s theorem, and is essential to derive the bicriteria approximation ratio for edge-weighted graphs.
Our second result is polynomial-time -approximation algorithms for Problems 1 and 2, which improves the above approximation ratio of derived directly from the bicriteria approximation ratio. Our algorithm for Problem 1/Problem 2 computes the most highly connected subgraph in terms of vertex/edge connectivity, which can be done using the algorithms in Matula [38]. In the analysis of the approximation ratio, we use a useful variant of Mader’s theorem, recently proved by Bernshteyn and Kostochka [5].
Paper organization.
The remainder of this paper is organized as follows. In Section 2, we review related work. In Section 3, we extend Mader’s theorem to edge-weighted graphs and design an algorithm for finding a Mader subgraph. In Sections 4 and 5, we present our bicriteria and ordinary approximation algorithms, respectively. We conclude with some open problems in Section 6.
2 Related Work
Variations of the densest subgraph problem.
Wu et al. [52] consider the problem of detecting a dense and connected subgraph in dual networks. A dual network is a pair of graphs and defined on the same vertex set , which encode different types of connections using two edge sets and . Wu et al. [52] introduced the following problem: given a dual network , we are asked to find that maximizes in under the constraint that is connected (i.e., -edge-connected). They proved that the problem is NP-hard and devised a scalable heuristic. Problem 2 with , i.e., the densest -edge-connected subgraph, on unweighted graphs, can be seen as a special case of their problem wherein two graphs and are the same, i.e., . It is easy to see that unlike the general form of their problem, the densest -edge-connected subgraph problem (on unweighted graphs) is polynomial-time solvable.
Two closely related papers are due to Tsourakakis [48] and Kawase and Miyauchi [30]. They aim to find a near-clique (which is robust to vertex/edge failure) by extending the densest subgraph problem. Tsourakakis [48] introduced the problem called the -clique densest subgraph problem. In this problem, given an unweighted graph , we are asked to find that maximizes the -clique density , where is the number of -cliques (i.e., cliques with size ) in . Tsourakakis [48] showed that this problem (with constant ) remains polynomial-time solvable, and later, Mitzenmacher et al. [39] proposed a scalable algorithm that obtains a nearly-optimal solution. On the other hand, Kawase and Miyauchi [30] introduced the problem called the -densest subgraph problem with convex . In this problem, given an edge-weighted graph , we are asked to find that maximizes , where is a monotonically non-decreasing function that satisfies for any . This formulation generalizes the NP-hard optimal quasi-cliques problem due to Tsourakakis et al. [50, 49]. Kawase and Miyauchi [30] studied the hardness of the problem, and proposed a polynomial-time approximation algorithm. Although the above two problems contribute to computing a dense subgraph that is robust to vertex/edge failure, they cannot explicitly impose -vertex/edge connectivity.
There are also some variants that take into account the robustness to the uncertainty of input graphs. Zou [53] studied the densest subgraph problem on uncertain graphs. Uncertain graphs are a generalization of graphs, which can model the uncertainty of the existence of edges. More formally, an uncertain graph consists of an unweighted graph and a function , where is present with probability whereas is absent with probability . In the problem introduced by Zou [53], given an uncertain graph with , we are asked to find that maximizes the expected value of the density. Zou [53] observed that this problem can be reduced to the original densest subgraph problem, and designed polynomial-time exact algorithm using the reduction. Very recently, Tsourakakis et al. [51] introduced the problem called the risk-averse DSD. In this problem, given an uncertain graph with , we are asked to find that has a large expected density and at the same time has a small risk. The risk of is measured by the probability that is not dense on a given uncertain graph. They showed that the risk-averse DSD can be reduced to the densest subgraph problem with negative edge weights (which is NP-hard), and designed an efficient approximation algorithm based on the reduction.
Miyauchi and Takeda [41] considered the uncertainty of edge weights rather than the existence of edges. To model that, they assumed that they have an edge-weight space that contains the unknown true edge weight . To evaluate the performance of without any concrete edge weight, they employed a well-known measure in the field of robust optimization, called the robust ratio. In their scenario, the robust ratio of under is defined as the multiplicative gap between the density of in terms of edge weight and the density of in terms of edge weight under the worst-case edge weight , where is a densest subgraph of with . Intuitively, with a large robust ratio has a density close to the optimal value even on with the edge weight selected adversarially from . Using the robust ratio, they formulated the robust densest subgraph problem, where given an unweighted graph and an edge-weight space , we are asked to find that maximizes the robust ratio under . Miyauchi and Takeda [41] designed an algorithm that returns with a robust ratio of at least under some mild condition.
In addition to the above, there are many other problem variations. The most well-studied variants are size restricted ones [1, 6, 13, 31]. For example, in the densest -subgraph problem [13], given an edge-weighted graph and a positive integer , we are asked to find that maximizes subject to the constraint . It is known that such a restriction makes the problem much harder; indeed, the densest -subgraph problem is NP-hard and the best known approximation ratio is for any [6]. The densest subgraph problem has also been extended to more general computation models and graph structures. As for computation models, to cope with the dynamics of real-world graphs, some literature has considered dynamic settings [12, 26], and moreover, to model the limited computation resources in reality, some literature has considered streaming settings [2, 4, 7]. As for graph structures, the problem has been defined on hypergraphs [26, 40] and multilayer networks [17].
Vertex and edge connectivity.
In the vertex connectivity problem, we are asked to compute for a given graph . For this problem, Gabow [16] developed an -time algorithm, which also computes a corresponding minimum vertex separator . This is one of the current fastest deterministic algorithms for the problem, although there are various randomized algorithms (e.g., see [14, 24, 33, 43]). Note that there are linear-time algorithms that decide whether is 2-vertex-connected and 3-vertex-connected, respectively, due to Tarjan [47] and Hopcroft and Tarjan [25].
Another important problem related to vertex connectivity is to compute the family of maximal -vertex-connected subgraphs, which will be solved in our bicriteria approximation algorithm for Problem 1. For and , the induced subgraph is called a maximal -vertex-connected subgraph if is -vertex-connected and no superset of has this property. For this task, the first polynomial-time algorithm is given by Matula [37]. Note that maximal -vertex-connected subgraphs may overlap each other; the design of the algorithm by Matula [37] is based on the fact that the maximum total number of maximal -vertex-connected subgraphs is [37]. Later, Makino [36] designed an -time algorithm, where is the computation time required to find a vertex separator of size at most . Combined with the above vertex connectivity algorithm by Gabow [16], the algorithm by Makino [36] yields the running time of . For some special , there are some existing algorithms that have better running time. For and 3, there are linear-time algorithms by Tarjan [47] and Hopcroft and Tarjan [25], respectively. For any constant , Henzinger et al. [22] presented an -time algorithm.
In the (global) minimum cut problem, given an edge-weighted graph , we are asked to find the minimum weight cut . For this problem, Nagamochi and Ibaraki [42] designed an -time algorithm. Later, Stoer and Wagner [46] and Frank [15] independently presented a very simple algorithm that still has the same running time. For simple unweighted graphs, the seminal work by Karger [27] provides a randomized (Monte Carlo) algorithm that runs in nearly-linear, , time. As this algorithm does not necessarily return the right answer, Karger [27] posed an open question to find a nearly-linear-time deterministic algorithm. In a recent breakthrough, Kawarabayashi and Thorup [28] answered the question; they developed a deterministic algorithm for simple unweighted graphs that runs in time. Very recently, Henzinger et al. [23] improved the running time to time, which is better even than that of the randomized algorithm by Karger [27].
As in the vertex connectivity case, computing the family of maximal -edge-connected subgraphs is also an important problem, which will be solved in our bicriteria approximation algorithm for Problem 2. For and , the induced subgraph is called a maximal -edge-connected subgraph if is -edge-connected and no superset of has this property. The problem can be solved using any minimum cut algorithm as follows: if the weight of the minimum cut of the graph is less than , divide the graph into two subgraphs along with the cut and then repeat the procedure on the resulting subgraphs. For edge-weighted graphs, we can directly obtain an -time algorithm using one of the above minimum cut algorithms by Nagamochi and Ibaraki [42], Stoer and Wagner [46], and Frank [15]. To the best of our knowledge, there is no existing algorithm that has a better running time. For simple unweighted graphs, we can again directly obtain an -time algorithm using the above minimum cut algorithm by Henzinger et al. [23]. Unlike the weighted case, for some special , there are some existing algorithms that have a better running time. For , there is a linear-time algorithm by Tarjan [47]. For any constant , Henzinger et al. [22] presented an -time algorithm, and more recently, Chechik et al. [9] provided an -time algorithm. The latter algorithm is efficient particularly for sparse graphs; indeed, the latter is better than the former when . Very recently, for any , Forster et al. [14] developed a randomized (Las Vegas) algorithm that has expected running time , which is faster than the algorithm by Chechik et al. [9] (for general ).
3 Mader’s theorem and Mader subgraph
In this section, we extend Mader’s theorem to edge-weighted graphs and design an algorithm for finding a Mader subgraph.
3.1 Mader’s Theorem on Edge-Weighted Graphs
Mader’s theorem [34] is a foundational theorem in graph theory. The precise statement is as follows:
Theorem 1 (Mader [34]; see also Theorem 1.4.3 in Diestel [10]).
Let be an unweighted graph and let be a positive integer. If has density at least , then has a -vertex-connected subgraph wherein the minimum degree of vertices is greater than .
A straightforward application of Theorem 1 to edge-weighted graphs would yield the following result. Let be an edge-weighted graph, let be a positive real, and assume that has density at least . Now consider an unweighted graph defined on the same vertex set and edge set . As has the density of at least (i.e., at least ), by Theorem 1, we see that has a -vertex-connected subgraph wherein the minimum degree of vertices is greater than . Therefore, we can deduce that has a -vertex-connected subgraph wherein the minimum weighted degree of vertices is greater than . However, this is weaker than what we need to prove the approximation guarantee of our algorithms, as we discuss in Section 4.4.
Here we provide a stronger version for edge-weighted graphs. Specifically, we prove the following theorem:
Theorem 2.
Let be an edge-weighted graph and let be a positive real. If has density at least , then has a -vertex-connected subgraph wherein the minimum weighted degree of vertices is greater than .
Proof.
Let be a subgraph of with the minimum number of vertices that satisfies
| (1) |
There exists such a subgraph because itself satisfies the above condition. In fact, since holds, there exists a vertex with the weighted degree of at least , implying that the number of neighbors of such a vertex is at least , thus holds, and . Suppose that . Then we have
a contradiction. Therefore, we see that . Suppose also that there exists a vertex in whose weighted degree is at most in . Let be a subgraph constructed by removing from . Then we have
This means that also satisfies condition (1), which contradicts the minimality of . Therefore, we see that every vertex in has weighted degree greater than in .
From now on, we show that is -vertex-connected. Suppose, for contradiction, that there exists with whose removal separates into two non-empty subgraphs and so that there are no edges between them. For any vertex , its neighbors in are all contained in . As has weighted degree greater than in , the number of neighbors of in is at least , thus . From the minimality of , we see that the subgraph does not satisfy condition (1), which implies that
holds. Applying the same argument to , we also have
Combining these two inequalities, we have
which contradicts that satisfies condition (1). ∎
3.2 Algorithm for Finding a Mader Subgraph
We design an algorithm Mader_subgraph that extracts a Mader subgraph, i.e., the subgraph whose existence is guaranteed by Theorem 2. To this end, we first present a simple subprocedure, which we call Peel. For an edge-weighted graph and a positive real , the procedure Peel returns the maximal subgraph of wherein the minimum weighted degree of vertices is greater than if such a subgraph exists and Null otherwise. Specifically, Peel iteratively removes a vertex with the minimum weighted degree in the currently remaining graph while the minimum weighted degree is no greater than . Note that this procedure is similar to the procedure to find a -core. For reference, we describe the entire procedure in Algorithm 1, where for and denotes the weighted degree of in . This algorithm can be implemented to run in time, as mentioned in the literature [40].
Using Algorithm 1, we present Mader_subgraph in Algorithm 2, where the notation denotes the vertex set of subgraph of . Here we briefly explain the behavior of the algorithm. Let be a Mader subgraph of a given edge-weighted graph . The algorithm keeps a family of subgraphs in which exactly one subgraph contains as its subgraph. In each iteration, the algorithm tests whether a subgraph in is a Mader subgraph or not, and if not, the algorithm divides the subgraph into strictly smaller pieces and add (a part of) them to . The algorithm repeats this operation until it finds a Mader subgraph. It should be noted that our algorithm is based on Matula’s algorithm [38, Algorithm A], which finds the most highly connected subgraph in terms of vertex connectivity, i.e., .
The following theorem verifies the validity of Mader_subgraph. The proof strategy is similar to that for Matula [38, Theorem 3].
Theorem 3.
For a given edge-weighted graph , Algorithm 2 outputs a Mader subgraph of in time.
Proof.
It is easy to see that if the algorithm terminates, its output is a Mader subgraph of . Thus, in what follows, we analyze the time complexity of the algorithm.
Specifically, we prove that Algorithm 2 runs in time. The time complexity of the algorithm except for the while-loop is given by due to the time complexity of the procedure Peel. We can show that the time complexity of the while-loop is given by . To see this, we analyze the time complexity of each iteration and the number of iterations. The time complexity of each iteration is dominated by that required to compute the minimum vertex separator of . As reviewed in Section 2, the current best algorithm completes this task in time. Hence, the time complexity of each iteration is bounded by . Next we show that the number of iterations of the while-loop is bounded by . Let be a Mader subgraph of , that is, is a -vertex-connected subgraph of wherein the minimum weighted degree of vertices is greater than . It is easy to see that exactly one subgraph in contains as its subgraph in any iteration of the while-loop. Here we define the surplus of as
For the initial , we have . Note that holds in any iteration. Let us consider an arbitrary iteration in which the algorithm does not terminate. Let . If holds, then is simply deleted or replaced by a subgraph with at most vertices, in the updated . Thus, the surplus decreases by at least one in the iteration. Assume that . Then we have
where the last inequality follows from and . Note that holds because the algorithm has not yet terminated in the iteration. The above inequality implies that the surplus decreases by at least two in the iteration. Therefore, the number of iterations of the while-loop is bounded by . ∎
4 Bicriteria Approximation Algorithms
In this section, we first design a polynomial-time -bicriteria approximation algorithm with parameter for Problem 1, and then present a corresponding result for Problem 2.
4.1 Algorithm for Problem 1
For a given edge-weighted graph , our algorithm first finds the family of maximal -vertex-connected subgraphs using Makino’s algorithm [36] combined with Gabow’s vertex connectivity algorithm [16], which takes time. Note that if there is no -vertex-connected subgraph found, our algorithm returns INFEASIBLE because the instance is actually infeasible.
For each , the algorithm initializes as . Then the algorithm finds a densest subgraph (without any constraint) in . This can be done in polynomial time using Charikar’s linear-programming-based algorithm for the densest subgraph problem [8]. After that, if holds, then the algorithm employs as the vertex set of a Mader subgraph of , i.e., the vertex set of a -vertex-connected subgraph in wherein the minimum weighted degree of vertices is greater than , using the procedure Mader_subgraph (Algorithm 2). Here denotes the maximum weight of edges in . Note that holds. For , Mader_subgraph runs in time.
Finally, the algorithm outputs the densest subset among . For reference, we summarize the entire procedure in Algorithm 3. As the maximum total number of maximal -vertex-connected subgraphs is [37], the overall running time of Algorithm 3 is given by , where is the computation time required to find a densest subgraph in (any subgraph of) . Note that as mentioned above, is polynomial in and . Moreover, for unweighted graphs, Goldberg’s flow-based algorithm [21] gives , using Orlin’s maximum-flow algorithm [44].
4.2 Analysis
Using our generalized Mader’s theorem (Theorem 2), we provide the bicriteria approximation ratio of Algorithm 3:
Theorem 4.
Proof.
We first show that the output of Algorithm 3 is -vertex-connected. To this end, it suffices to confirm -vertex-connectivity of for each . Fix . If does not hold, we are done since is given by , which is -vertex-connected (thus -vertex-connected). Consider the case where holds. Applying Theorem 2 to with setting , we see that has a -vertex-connected subgraph, which is -vertex-connected. Algorithm 3 employs such a subset as .
We next analyze the first term of the bicriteria approximation ratio. It suffices to show that for each , the subset has density at least times the optimal value of Problem 1 on . Fix . Clearly, the optimal value of Problem 1 on , which we denote by , is at most .
We first consider the case where does not hold. In this case, Algorithm 3 just employs as . As is -vertex-connected, each vertex has weighted degree of at least ; thus, the density of is greater than
which means -approximation.
We next consider the case where holds. Applying Theorem 2 to with setting , we see that has a -vertex-connected subgraph wherein the minimum weighted degree of vertices is greater than . Algorithm 3 employs such a subset as . As each vertex has weighted degree greater than , the density of is greater than , which means -approximation (thus -approximation). ∎
From the proof, we see that if the if-condition of Algorithm 3 holds, the output admits -approximation, irrespective of edge weights. Moreover, it should be noted that setting in the theorem, we can obtain an ordinary -approximation algorithm for Problem 1. In Section 5, we present an algorithm with a better approximation ratio.
4.3 Algorithm for Problem 2 and Analysis
Here we present a bicriteria approximation algorithm for Problem 2, which is an edge-connectivity counterpart of Algorithm 3. For a given edge-weighted graph , our algorithm first finds the family of maximal -edge-connected subgraphs . As reviewed in Section 2, this can be done in time using one of the minimum cut algorithms by Nagamochi and Ibaraki [42], Stoer and Wagner [46], and Frank [15] as a subroutine. If is simple unweighted, the time complexity reduces to using the minimum cut algorithm by Henzinger et al. [23].
In the processing of for each , the algorithm computes a variant of a Mader subgraph of , i.e., a -edge-connected subgraph in wherein the minimum weighted degree of vertices is greater than . The existence of such a subgraph is guaranteed by a corollary of Theorem 2, which we will present later. Recall that Algorithm 3 uses the procedure Mader_subgraph. On the other hand, the above variant can be computed using the strategy employed by the algorithms for computing the family of maximal -edge-connected subgraphs, presented in Section 2. Specifically, the strategy in our scenario is as follows: if the weight of the minimum cut of is less than , divide the graph into two subgraphs along with the cut and then repeat the procedure on the resulting subgraphs (until it finds the variant of a Mader subgraph). It should be noted that in order to satisfy the minimum weighted degree condition, our algorithm needs to conduct the procedure Peel every time before it processes a new subgraph. For reference, the pseudocode of our algorithm is given in Algorithm 4.
Here we evaluate the running time of Algorithm 4. It is easy to see that the above algorithm for finding the variant of a Mader subgraph still has the same running time as that of algorithms for computing the family of maximal -edge-connected subgraphs. Therefore, the time complexity of the processing of each is bounded by , where is the computation time required to find a densest subgraph in . Recalling that maximal -edge-connected subgraphs do not overlap for any , we see that the time complexity of the entire for-loop is bounded by , which also bounds the overall running time of Algorithm 4. For simple unweighted graphs, we have the running time of .
Finally we analyze the theoretical performance guarantee of Algorithm 4. It is easy to see that any (edge-weighted) -vertex-connected graph is -edge-connected, which gives the following corollary to Theorem 2:
Corollary 1.
Let be an edge-weighted graph and let be a positive real. If has density at least , then has a -edge-connected subgraph wherein the minimum weighted degree of vertices is greater than .
Using this corollary, we can derive the bicriteria approximation ratio of Algorithm 4:
Theorem 5.
The proof is similar to that of Theorem 4, and is omitted.
4.4 Remarks on Theorem 2
Here we explain that our generalized Mader’s theorem (i.e., Theorem 2) is essential to derive the bicriteria approximation ratio given in Theorems 4 and 5. To this end, recall that the straightforward application of the original Mader’s theorem to edge-weighted graphs derives the following statement: Let be an edge-weighted graph and let be a positive real. If has density at least , then has a -vertex-connected subgraph wherein the minimum weighted degree of vertices is greater than .
Obviously, the above statement is weaker than Theorem 2. Indeed, vertex connectivity of in Theorem 2 has decreased to , which is only a slight deterioration, but the minimum weighted degree of in Theorem 2 has significantly decreased to . It is easy to see that to prove Theorems 4 and 5, vertex connectivity of is sufficient, but the minimum weighted degree of is insufficient. In fact, in the last paragraph of the proof of Theorem 4, by using the decreased minimum weighted degree, we can only guarantee that the density of is greater than (rather than in the proof). Note that may be less than , meaning that the decreased minimum weighted degree is insufficient to prove the theorem. We can see the same issue in the proof of Theorem 5.
5 Approximation Algorithms
In this section, we design a polynomial-time -approximation algorithm for Problem 1, which improves the approximation ratio of that is immediately derived by Algorithm 3. Then we present its counterpart result for Problem 2.
5.1 Algorithm for Problem 1
Our algorithm first computes the most highly connected subgraph in terms of vertex connectivity, i.e., . This can be done using Matula’s algorithm [38, Algorithm A]. Then our algorithm simply returns the subgraph if its vertex connectivity is no less than and INFEASIBLE otherwise. Our algorithm is described in pseudocode as Algorithm 5.
Matula [38] showed that the time complexity of the algorithm for computing the most highly connected subgraph in terms of vertex connectivity is given by , where is the computation time required to find a minimum vertex separator of . If we consider Gabow’s vertex connectivity algorithm [16], the time complexity becomes . Clearly, Algorithm 5 has the same time complexity.
5.2 Analysis
From now on, we analyze the theoretical performance guarantee of Algorithm 5. To this end, we use the following theorem, which is a useful variant of Mader’s theorem:
Theorem 6 (Bernshteyn and Kostochka [5]).
Let be an unweighted graph and let be an integer with . If satisfies and , then has a -vertex-connected subgraph.
We provide the approximation ratio of Algorithm 5 in the following theorem:
Proof.
Let be the output of Algorithm 5. Define
As we assumed that , we have . Recall that is a -vertex-connected subgraph. We denote by OPT the density of an optimal solution to Problem 1. Let be a densest subgraph (unconstrained) in . As , it suffices to show that holds. Let and denote the number of vertices and edges in , respectively.
Case I: . In this case, is a forest; therefore, using the fact that , we have . Any vertex subset (with size more than one) inducing a connected subgraph, including the output , has density of at least
Case II: . Let us define . As holds, we have , and thus . As for the value of , if , holds. Thus, by Theorem 6, if holds, then the subgraph has a -vertex-connected subgraph, which is also a subgraph of . Hence, we have . On the other hand, if holds, then . In either case, noticing that the output is -edge-connected, we see that has density at least
which completes the proof. ∎
5.3 Algorithm for Problem 2 and Analysis
Here we present an approximation algorithm for Problem 2, which is an edge-connectivity counterpart of Algorithm 5. Specifically, our algorithm first computes the most highly connected subgraph in terms of edge connectivity, i.e., . This can be done using a simple recursive algorithm mentioned by Matula [38], which is similar to the algorithms for computing the family of maximal -edge-connected subgraphs. Then our algorithm simply returns the subgraph if its edge connectivity is no less than and INFEASIBLE otherwise. For reference, we describe the entire procedure in Algorithm 6.
Matula [38] stated that the time complexity of the algorithm for computing the most highly connected subgraph in terms of edge connectivity is given by , where is the computation time required to find a minimum cut of . If we consider one of the minimum cut algorithms by Nagamochi and Ibaraki [42], Stoer and Wagner [46], and Frank [15], the time complexity becomes . If is simple unweighted, the time complexity reduces to using the minimum cut algorithm by Henzinger et al. [23]. Clearly, Algorithm 6 has the same time complexity.
Finally we analyze the theoretical performance guarantee of Algorithm 6. The following corollary is an edge-connectivity counterpart of Theorem 6:
Corollary 2.
Let be an edge-weighted graph and let be an integer with . If satisfies and , then has a -edge-connected subgraph.
Using this corollary, we can derive the approximation ratio of Algorithm 6:
The proof is similar to that of Theorem 7, and is omitted.
6 Open Problems
There are several directions for future research. The most interesting one is to design a polynomial-time algorithm that has a better (bicriteria or ordinary) approximation ratio. We wish to remark that assuming Mader’s conjecture [35], which is a stronger version of Theorem 6, we can improve the approximation ratio of Algorithms 5 and 6, i.e., , to . However, Mader [35] also conjectured that the statement is best possible, making it unlikely to obtain an approximation ratio better than via similar analysis. Another interesting direction is to investigate the computational complexity of Problems 1 and 2.
Acknowledgments
F.B., D.G-S., and C.T. acknowledge support from Intesa Sanpaolo Innovation Center, who had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. A.M. was supported by Grant-in-Aid for Research Activity Start-up (No. 17H07357) and Grant-in-Aid for Early-Career Scientists (No. 19K20218). This work was partially done while A.M. was at RIKEN AIP, Japan, and visitied ISI Foundation, Italy.
References
- [1] R. Andersen and K. Chellapilla. Finding dense subgraphs with size bounds. In WAW ’09: Proceedings of the 6th Workshop on Algorithms and Models for the Web Graph, pages 25–37, 2009.
- [2] A. Angel, N. Sarkas, N. Koudas, and D. Srivastava. Dense subgraph maintenance under streaming edge weight updates for real-time story identification. In VLDB ’12: Proceedings of the 38th International Conference on Very Large Data Bases, pages 574–585, 2012.
- [3] G. D. Bader and C. W. V. Hogue. An automated method for finding molecular complexes in large protein interaction networks. BMC Bioinformatics, 4(1):1–27, 2003.
- [4] B. Bahmani, R. Kumar, and S. Vassilvitskii. Densest subgraph in streaming and mapreduce. In VLDB ’12: Proceedings of the 38th International Conference on Very Large Data Bases, pages 454–465, 2012.
- [5] A. Bernshteyn and A. Kostochka. On the number of edges in a graph with no -connected subgraphs. Discrete Mathematics, 339(2):682–688, 2016.
- [6] A. Bhaskara, M. Charikar, E. Chlamtac, U. Feige, and A. Vijayaraghavan. Detecting high log-densities: An approximation for densest -subgraph. In STOC ’10: Proceedings of the 42nd ACM Symposium on Theory of Computing, pages 201–210, 2010.
- [7] S. Bhattacharya, M. Henzinger, D. Nanongkai, and C. E. Tsourakakis. Space- and time-efficient algorithm for maintaining dense subgraphs on one-pass dynamic streams. In STOC ’15: Proceedings of the 47th ACM Symposium on Theory of Computing, pages 173–182, 2015.
- [8] M. Charikar. Greedy approximation algorithms for finding dense components in a graph. In APPROX ’00: Proceedings of the 3rd International Workshop on Approximation Algorithms for Combinatorial Optimization, pages 84–95, 2000.
- [9] S. Chechik, T. D. Hansen, G. F. Italiano, V. Loitzenbauer, and N. Parotsidis. Faster algorithms for computing maximal 2-connected subgraphs in sparse directed graphs. In SODA ’17: Proceedings of the 28th Annual ACM-SIAM Symposium on Discrete Algorithms, pages 1900–1918, 2017.
- [10] R. Diestel. Graph Theory, volume 173 of Graduate Texts in Mathematics. Springer-Verlag Berlin Heidelberg, 5th edition, 2016.
- [11] Y. Dourisboure, F. Geraci, and M. Pellegrini. Extraction and classification of dense communities in the web. In WWW ’07: Proceedings of the 16th International Conference on World Wide Web, pages 461–470, 2007.
- [12] A. Epasto, S. Lattanzi, and M. Sozio. Efficient densest subgraph computation in evolving graphs. In WWW ’15: Proceedings of the 24th International Conference on World Wide Web, pages 300–310, 2015.
- [13] U. Feige, D. Peleg, and G. Kortsarz. The dense -subgraph problem. Algorithmica, 29(3):410–421, 2001.
- [14] S. Forster, D. Nanongkai, L. Yang, T. Saranurak, and S. Yingchareonthawornchai. Computing and testing small connectivity in near-linear time and queries via fast local cut algorithms. In SODA ’20: Proceedings of the 31st Annual ACM-SIAM Symposium on Discrete Algorithms, pages 2046–2065, 2020.
- [15] A. Frank. On the edge-connectivity algorithm of nagamochi and ibaraki. Laboratoire Artemis, IMAG, Universite J. Fourier, 1994.
- [16] H. N. Gabow. Using expander graphs to find vertex connectivity. Journal of the ACM, 53(5):800––844, 2006.
- [17] E. Galimberti, F. Bonchi, and F. Gullo. Core decomposition and densest subgraph in multilayer networks. In CIKM ’17: Proceedings of the 26th ACM International Conference on Information and Knowledge Management, pages 1807–1816, 2017.
- [18] M. R. Garey and D. S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman & Co., NY, 1979.
- [19] D. Gibson, R. Kumar, and A. Tomkins. Discovering large dense subgraphs in massive graphs. In VLDB ’05: Proceedings of the 31st International Conference on Very Large Data Bases, pages 721–732, 2005.
- [20] A. Gionis and C. E. Tsourakakis. Dense subgraph discovery: KDD 2015 Tutorial. In KDD ’15: Proceedings of the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 2313–2314, 2015.
- [21] A. V. Goldberg. Finding a maximum density subgraph. University of California Berkeley, 1984.
- [22] M. Henzinger, S. Krinninger, and V. Loitzenbauer. Finding 2-edge and 2-vertex strongly connected components in quadratic time. In ICALP ’15: Proceedings of the 42nd International Colloquium on Automata, Languages and Programming, pages 713–724, 2015.
- [23] M. Henzinger, S. Rao, and D. Wang. Local flow partitioning for faster edge connectivity. SIAM Journal on Computing, 49(1):1–36, 2020.
- [24] M. R. Henzinger, S. Rao, and H. N. Gabow. Computing vertex connectivity: New bounds from old techniques. Journal of Algorithms, 34(2):222–250, 2000.
- [25] J. E. Hopcroft and R. E. Tarjan. Dividing a graph into triconnected components. SIAM Journal on Computing, 2(3):135–158, 1973.
- [26] S. Hu, X. Wu, and T.-H. H. Chan. Maintaining densest subsets efficiently in evolving hypergraphs. In CIKM ’17: Proceedings of the 26th ACM International Conference on Information and Knowledge Management, pages 929–938, 2017.
- [27] D. R. Karger. Minimum cuts in near-linear time. Journal of the ACM, 47(1):46––76, 2000.
- [28] K.-I. Kawarabayashi and M. Thorup. Deterministic edge connectivity in near-linear time. Journal of the ACM, 66(1):Article No. 4, 2018.
- [29] Y. Kawase, Y. Kuroki, and A. Miyauchi. Graph mining meets crowdsourcing: Extracting experts for answer aggregation. In IJCAI ’19: Proceedings of the 28th International Joint Conference on Artificial Intelligence, pages 1272–1279, 2019.
- [30] Y. Kawase and A. Miyauchi. The densest subgraph problem with a convex/concave size function. Algorithmica, 80(12):3461–3480, 2018.
- [31] S. Khuller and B. Saha. On finding dense subgraphs. In ICALP ’09: Proceedings of the 36th International Colloquium on Automata, Languages and Programming, pages 597–608, 2009.
- [32] J. Leskovec and A. Krevl. SNAP Datasets: Stanford large network dataset collection. http://snap.stanford.edu/data, 2014.
- [33] N. Linial, L. Lovász, and A. Wigderson. Rubber bands, convex embeddings and graph connectivity. Combinatorica, 8(1):91–102, 1988.
- [34] W. Mader. Existenzn-fach zusammenhängender teilgraphen in graphen genügend großer kantendichte. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, 37(1):86–97, 1972.
- [35] W. Mader. Connectivity and edge-connectivity in finite graphs. In B. Bollobas, editor, Surveys in Combinatorics (Proceedings of the Seventh British Combinatorial Conference), volume 38 of London Mathematical Society Lecture Note Series, pages 66–95, 1979.
- [36] S. Makino. An algorithm for finding all the k-components of a digraph. International journal of computer mathematics, 24(3-4):213–221, 1988.
- [37] D. W. Matula. Graph theoretic techniques for cluster analysis algorithms. In J. V. Ryzin, editor, Classification and Clustering, pages 95–129. Academic Press, 1977.
- [38] D. W. Matula. -blocks and ultrablocks in graphs. Journal of Combinatorial Theory, Series B, 24(1):1–13, 1978.
- [39] M. Mitzenmacher, J. Pachocki, R. Peng, C. E. Tsourakakis, and S. C. Xu. Scalable large near-clique detection in large-scale networks via sampling. In KDD ’15: Proceedings of the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 815–824, 2015.
- [40] A. Miyauchi, Y. Iwamasa, T. Fukunaga, and N. Kakimura. Threshold influence model for allocating advertising budgets. In ICML ’15: Proceedings of the 32nd International Conference on Machine Learning, pages 1395–1404, 2015.
- [41] A. Miyauchi and A. Takeda. Robust densest subgraph discovery. In ICDM ’18: Proceedings of the 18th IEEE International Conference on Data Mining, pages 1188–1193, 2018.
- [42] H. Nagamochi and T. Ibaraki. Computing edge-connectivity in multigraphs and capacitated graphs. SIAM Journal on Discrete Mathematics, 5(1):54–66, 1992.
- [43] D. Nanongkai, T. Saranurak, and S. Yingchareonthawornchai. Breaking quadratic time for small vertex connectivity and an approximation scheme. In STOC ’19: Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, pages 241––252, 2019.
- [44] J. B. Orlin. Max flows in time, or better. In STOC ’13: Proceedings of the 45th Annual ACM Symposium on Theory of Computing, pages 765–774, 2013.
- [45] V. Spirin and L. A. Mirny. Protein complexes and functional modules in molecular networks. Proceedings of the National Academy of Sciences of the United States of America, 100(21):12123–12128, 2003.
- [46] M. Stoer and F. Wagner. A simple min-cut algorithm. Journal of the ACM, 44(4):585–591, 1997.
- [47] R. Tarjan. Depth-first search and linear graph algorithms. SIAM Journal on Computing, 1(2):146–160, 1972.
- [48] C. E. Tsourakakis. The k-clique densest subgraph problem. In WWW ’15: Proceedings of the 24th International Conference on World Wide Web, pages 1122–1132, 2015.
- [49] C. E. Tsourakakis. Streaming graph partitioning in the planted partition model. In COSN ’15: Proceedings of the 2015 ACM Conference on Online Social Networks, pages 27–35, 2015.
- [50] C. E. Tsourakakis, F. Bonchi, A. Gionis, F. Gullo, and M. Tsiarli. Denser than the densest subgraph: extracting optimal quasi-cliques with quality guarantees. In KDD ’13: Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 104–112, 2013.
- [51] C. E. Tsourakakis, T. Chen, N. Kakimura, and J. Pachocki. Novel dense subgraph discovery primitives: Risk aversion and exclusion queries. In ECML-PKDD ’19: Proceedings of the 2019 European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases, 2019. No page numbers.
- [52] Y. Wu, X. Zhu, L. Li, W. Fan, R. Jin, and X. Zhang. Mining dual networks: Models, algorithms, and applications. ACM Transactions on Knowledge Discovery from Data, 10(4):40:1–40:37, 2016.
- [53] Z. Zou. Polynomial-time algorithm for finding densest subgraphs in uncertain graphs. In MLG ’13: Proceedings of the 11th Workshop on Mining and Learning with Graphs, 2013. No page numbers.