Fingerprints of Mott and Slater gaps in the core-level photoemission spectra of antiferromagnetic iridates

Antiferromangetic (AFM) materials often exhibit gaps in their charge excitation spectra. Their origin can be traced either to strong electronic correlations present also in the paramagnetic (PM) phase, the Mott mechanism, or to the long-range AFM order and associated doubling of the unit cell, the Slater mechanism. Naively, the distinction between the two mechanisms is straightforward “Is there an intrinsic charge gap in the PM phase or not?”. The reality and its experimental determination are more complex. Detecting a gap using angle-resolved photoemission spectroscopy (ARPES) may prove difficult [1, 2]. Besides an instrumental resolution limitation, at higher Néel transition temperatures $T_{N}$ thermal broadening or possible coupling with bosonic excitations obscures small gaps. Moreover, changes in the ARPES spectra are very specific to the band structure of a given material, which makes identification of the Mott or Slater characteristics complicated.

Core-level photoemission spectroscopy, which measures the time evolution of the core hole left by the photoelectron, does not suffer from the above problems. On the other hand, the ability of a local probe to provide useful information about long-range AFM order is not obvious.

In this Letter, we show that it is possible to address the Mott vs Slater question using the core-level hard-x-ray photoemission spectroscopy (HAXPES). With Ruddlesden-Popper iridates Sr₂IrO₄ ($T_{N}\simeq$240 K) [3, 4] and Sr₃Ir₂O₇ ($\simeq$280 K) [5] serving as test materials, we observe a distinct signature of the Mott and Slater mechanisms at the AFM transition. The experimental spectra are well reproduced by theoretical calculations based on the local density approximation (LDA) + dynamical mean-field theory (DMFT), which provide an explanation for the observed behavior and link it to a dominant Mott or Slater mechanism.

Experiment. Single crystals of Sr₂IrO₄ and Sr₃Ir₂O₇ were grown by the flux method using SrCl₂ as the flux material, see Ref. 1 for the sample preparation and their characterization. The HAXPES data were collected at the beamline BL19LXU of SPring-8 [6]. The linearly polarized x-ray delivered by the 27m-long undulator was monochromized by the Si (111) double-crystal and Si (620) channel-cut monochromators, with the polarization vector set to be parallel to the photoelectron scattering plane [7]. The incident photon energy was set to 7.9 keV with the total energy resolution of $\Delta E=400$ meV as the full width at half maximum (FWHM). Clean (001) surfaces were obtained by cleaving the samples in situ in ultrahigh vacuum ($\leq 1\times 10^{-7}$ Pa).

Theory. The LDA+DMFT calculations are performed for the experimental crystal structures of Sr₂IrO₄ and Sr₃Ir₂O₇ with the implementation used in Refs. 8, 9, 10. The $dp$ tight-binding model spanning the Ir $5d$ and O 2$p$ bands derived from the LDA bands is augmented by the local electron-electron interaction on the Ir 5$d$ shell parameterized by Hubbard $U=4.5$ eV and Hund’s $J=0.8$ eV. These values are consistent with previous studies based on the density functional theory for iridates [11]. The double-counting correction $\mu_{\rm dc}$ is introduced in order to remove the interaction effects already present in the LDA description [12, 13]. The bare Ir $5d$ site energy $\varepsilon_{d}^{\rm LDA}$ is shifted by the $\mu_{\rm dc}$, which modifies the Ir $5d$–O 2$p$ splitting and, consequently, the Ir 5$d$ band width and the metal-insulator transition (MIT) [10]. This allows us to use $\mu_{\rm dc}$ as a tuning parameter to go between Slater and Mott-Hubbard regimes in the same material and thus demonstrate the impact on the core-level spectra. The realistic values of $\mu_{\rm dc}$ are obtained by comparison to the experimental core-level and valence-band HAXPES spectra. Continuous-time hybridization expansion Monte Carlo method [14] is employed as the DMFT impurity solver. The spectral functions and hybridization densities on the real-frequency axis are computed with the analytically continued self-energy $\Sigma(\omega)$ by the maximum entropy method [15]. The Ir $4f$ core-level photoemission spectra are calculated using the Anderson impurity model (AIM) with the DMFT hybridization densities where the core-valence interaction (core-hole potential) $U_{cd}$ is included explicitly in the photoemission final states [8, 16].

Figure 1(a) shows the core-level HAXPES spectrum of Sr₂IrO₄ in the vicinity of Ir $4f$ binding energy ($E_{B}$). Quasi-symmetric peaks corresponding to Ir $5s$ and $5p_{3/2}$ states are found around 100 eV and 50 eV, respectively. A complex spectral feature can be seen between them, which is attributed to Ir $4f$ and $5p_{1/2}$ states. According to previous studies of metallic Ir and IrO₂ [17], the Ir $5p_{1/2}$ state has the same $E_{B}$ as the Ir $4f$ states. Some spectral weights due to a Sr $4s$ plasmon satellite ($E_{B}\simeq 66$ eV) also contribute to form the complex Ir $4f$ spectral shape in strontium iridates. The $5p_{1/2}$ and plasmon contributions on the $4f$ states are quantitatively evaluated by a line-shape analysis shown in the Supplemental Material (SM) [18]. Unlike the $4f$ features, the $5p_{1/2}$ peak and plasmon satellite are essentially insensitive to the magnetic order and thus their contribution cancels out in the spectral difference $I_{\text{300 K}}-I_{\text{100 K}}$.

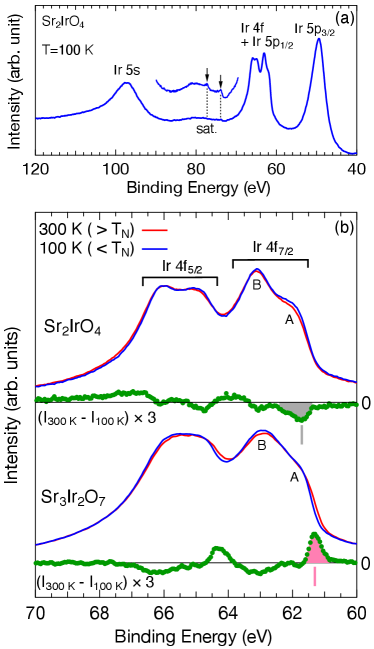
In both Sr₂IrO₄ and Sr₃Ir₂O₇, fine features labeled as $A$ and $B$ in the Ir $4f_{7/2}$ component can be identified, see Fig. 1(b). These features were reported in Sr₂IrO₄ and other Ir oxides. However, their interpretation has been controversial. In early studies [20, 21] the shoulder feature $A$ was attributed to a charge-transfer final state ($\underline{c}d^{6}\underline{L}$), while the feature $B$ was interpreted as (unscreened) ionic final states ($\underline{c}d^{5}$) along a textbook interpretation established for 3$d$ transition-metal oxides (TMOs). In contrast, a recent study [22] associated the two features with Ir³⁺ and Ir⁴⁺ valence states. The Ir $4f$ spectra in Sr₂IrO₄ and Sr₃Ir₂O₇ look rather similar and both exhibit a change upon cooling below $T_{N}$, as shown in Fig. 1(b). Remarkably, the change in the Ir $4f$ spectra is distinctly different in the two compounds with even opposite signs around the feature $A$. Importantly, the position of the distinct peak in $I_{\text{300 K}}-I_{\text{100 K}}$ of Sr₂IrO₄, indicated by the gray solid bar, is substantially higher ($\sim 1$ eV) than that of Sr₃Ir₂O₇, indicated by the pink solid bar. The observed qualitative difference arises from a disparate evolution of spectral intensities with temperature across $T_{N}$ in the two compounds. Specifically, the intensity of the feature $A$ is suppressed above $T_{N}$ in Sr₂IrO₄, while a tail ($\sim 61.3$ eV) associated with the feature $A$ emerges above $T_{N}$ in Sr₃Ir₂O₇.

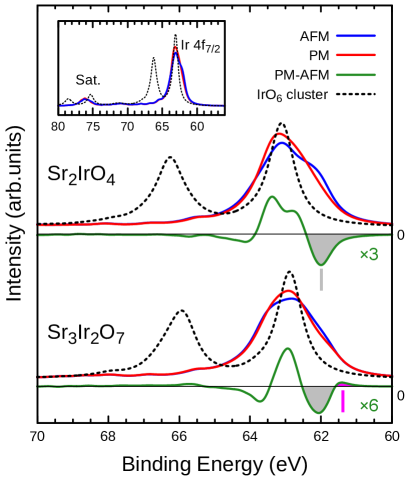
In the following we use numerical simulations to uncover the microscopic origin of this behavior. We start with analysis of the temperature and material dependence of Ir 4$f$ spectra of the IrO₆ cluster-model, dashed line in Fig. 2. The model includes the charge transfer from the nearest-neighboring ligands, the local valence-valence and core-valence interactions, and the spin-orbit coupling in the 4$f$ shell ¹¹1The one-particle Hamiltonian (including hopping integrals and crystal-field energies) in the IrO₆ cluster model are extracted from the LDA (tight-binding) Hamiltonian for the experimental crystal structures.. The cluster model yields sharp structureless 4$f_{7/2}$ and 4$f_{5/2}$ peaks and a weak satellite at high $E_{B}$ ($\sim 75$ eV), see the inset in Fig. 2. The satellite is observed in the experimental spectra as indicated by arrows in Fig. 1(a). Large splitting between the main line and the satellite is due to a strong Ir $5d\ e_{g}$ – O 2$p$ hybridization, similar to the origin of the satellite in 2$p$ core-level spectra of early 3$d$ TMOs [24, 25, 26]. The shoulder $A$ is missing in the cluster-model spectrum. No core-valence multiplet effects or interference between Ir 4$f_{7/2}$ and 4$f_{5/2}$ excitations are discernible in the cluster-model spectra. This allows us to neglect the orbital structure of the core states and compute the Ir 4$f_{7/2}$ and 4$f_{5/2}$ spectra separately, which reduces the computational effort of LDA+DMFT AIM simulations ²²2Note that in this approximation the Ir 4$f_{7/2}$ and 4$f_{5/2}$ are merely shifted and rescaled images of one another due to different energy and degeneracy of the 4$f_{7/2}$ and 4$f_{5/2}$ states..

Figure 2 also shows the Ir 4$f_{7/2}$ core-level spectra of Sr₂IrO₄ and Sr₃Ir₂O₇ obtained with LDA+DMFT AIM. The LDA+DMFT AIM treatment produces the shoulder $A$ in both Sr₂IrO₄ and Sr₃Ir₂O₇, in fair agreement with the experimental 4$f_{7/2}$ line. While LDA+DMFT AIM implements the same atomic Hamiltonian of the Ir 5$d$ shell as the cluster model [16, 8], it also includes the long-range hopping beyond the nearest-neighboring ligands. The fine structure of the 4$f_{7/2}$ peak can thus be attributed to a long-range charge-transfer effect, often referred to as non-local screening in the literature [28, 29, 30, 8, 31].

Next, we address the response of the spectra to the AFM ordering, characterized by the spectral difference, $I_{\text{PM}}-I_{\text{AFM}}$, and its relation to the insulating mechanism. We take advantage of the fact that, in a computer, we can tune between the Mott-Hubbard- and Slater-insulator regimes in both studied materials by changing the $E_{B}$ of the Ir $5d$ states away from its realistic value. In practice, this is achieved by varying $\mu_{\rm dc}$. The LDA+DMFT valence-band spectra for the two regimes are shown in Figs. 3(a)–(h). In the Mott-Hubbard regime for Sr₂IrO₄ [$\mu_{\rm dc}=19.4$ eV in (a)], the charge gap at the Fermi energy ($E_{F}$) survives in the PM insulating (PMI) solution. The gap size is slightly increased in the AFM insulating (AFI) solution compared with the PMI one, as in the single-band Hubbard model [32] and consistent with previous DMFT studies for Sr₂IrO₄ [33, 34, 35, 11, 36]. The charge gap collapses in the PM metallic (PMM) solution in the Slater-insulator regime for Sr₃Ir₂O₇ [$\mu_{\rm dc}=20.4$ eV in (g)]. The results for $I_{\text{PM}}-I_{\text{AFM}}$ in Figs. 3(i)–(p) show that the core-level HAXPES spectra reflects the insulating mechanism rather than a specific material. In particular, the spectral weight of the feature $A$ decreases in a Mott-Hubbard case upon the transition from AFI to PMI phase, indicated by the blue arrow in Fig. 3(i), resulting in a peak with negative sign in $I_{\text{PM}}-I_{\text{AFM}}$. In a Slater case, transitioning from AFI to PMM phase, the feature $A$ increases accompanied by the broad band feature extending to low $E_{B}$, indicated by the red arrow in Fig. 3(k), that produces a positive sign in $I_{\text{PM}}-I_{\text{AFM}}$. These behaviors in Fig. 3(i) for Sr₂IrO₄ and (o) for Sr₃Ir₂O₇ well reproduce the observed spectral changes shown in Fig. 1(b). The spectral evolution with the PMI to PMM transition can be found in Fig. S4 of SM [18]. Experimentally, the electrical resistivity of both compounds presents insulating behavior below $T_{N}$ [5, 37, 38, 4]. Near $T_{N}$ the resistivity of Sr₃Ir₂O₇ exhibits a sharp drop, whereas such a drop is not observed in Sr₂IrO₄, suggesting Slater-like and Mott-like character of the gap in the former and latter. Our HAXPES result, with the support of the LDA+DMFT simulations, is consistent with the resistivity measurement.

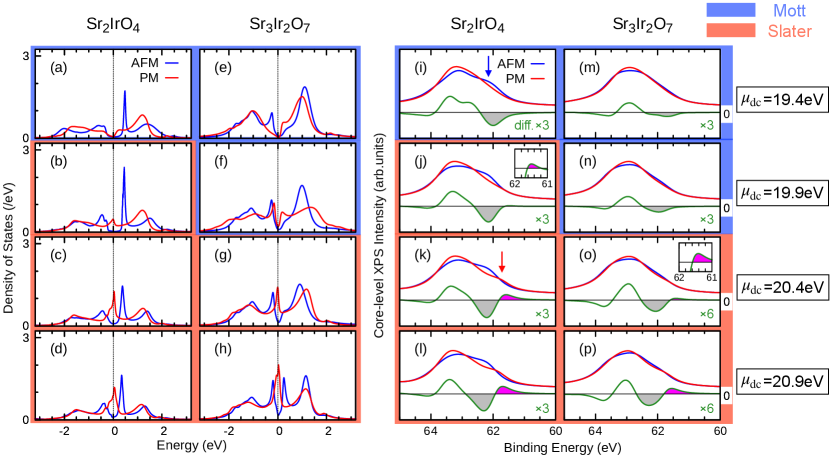
Why does the Ir $4f$ spectrum, in particular the feature $A$, respond differently to the AFM transition in the Mott-Hubbard and Slater insulators? The lower-energy shoulder feature $A$ is connected with non-local screening facilitated by the states just below $E_{F}$ [8, 10]. Two effects affect the non-local screening in the present context: (i) the non-local screening is more efficient in a metal than in an insulator due to the presence of states close to $E_{F}$ ³³3In order to assess whether such states can contribute to non-local screening one should look at hybridization function rather than an electronic spectral density., (ii) the non-local screening is more efficient in the AFM state than in the PM state since more Ir–Ir charge-transfer processes are prohibited by Pauli principle for parallel spin orientations, suppressed in the AFM state. Both (i) and (ii) are active in the Slater regime and the simulations for Sr₃Ir₂O₇ show that the dominant (i) leads to a larger weight of the feature $A$ in the PM state, in agreement with the experiment. In contrast, only (ii) is active in the Mott-Hubbard regime, resulting in the larger weight of the feature $A$ in the AFM state as seen in Sr₂IrO₄. Note that the sensitivity of the core-level photoemission spectroscopy to non-local spin-spin correlations or a long-range AFM ordering in a Mott insulator has been proposed theoretically for 3$d$ TMOs [40, 8, 41, 42], but has been escaping experimental detection so far, except in a recent report for MnO [43].

Finally we comment on the overestimation of the spectral changes in $I_{\rm PM}-I_{\rm AFM}$ in the LDA+DMFT result in Fig. 2. This stems primarily from a more pronounced suppression of the feature $A$ ($\sim 62$ eV) in the PM solution against the AF one, compared to the experiment below and above $T_{N}$, indicating that the deactivation of the non-local screening in the PM phase mentioned above is exaggerated in the theory. However, this behavior is not a surprising within the present theory neglecting the short-range AFM correlation. This approximation overcounts the Pauli blocking in the ferromagnetic spin configurations in the time propagation with a core hole and consequently underestimates the intensity of the feature $A$. This observation is consistent with the temperature evolution of the Mn 2$p_{3/2}$ line well above $T_{N}$ in MnO due to the short-range AFM correlation [43].

We have reported Ir $4f$ core-level HAXPES experiments across the AFM ordering transition in Sr₂IrO₄ and Sr₃Ir₂O₇. Using LDA+DMFT AIM simulations, we have explained the microscopic origin of the observed changes in the HAXPES spectra in response to the AFM order. We have shown that the spectral change reflects the Slater or Mott-Hubbard character of the AFM insulating state rather than material details. This broadens the applications of core-level HAXPES as a tool to study the magnetic and metal-to-insulator transitions in correlated systems.