Finite Abelian Groups with Toroidal Subgroup Lattices
Abstract.
In this paper, we determine the genus of the subgroup lattice of several families of abelian groups. In doing so, we classify all finite abelian groups whose subgroup lattices can be embedded into the torus.
1. Introduction
In every introductory abstract algebra course, students draw subgroup lattices, and they quickly learn that most subgroup lattices cannot be drawn without crossing edges. However, the groups whose subgroup lattice can be drawn on the plane without crossing edges were determined in [6] and [3]. Their results naturally lead us to the question of which groups have subgroup lattices that can be drawn on the -torus without crossing edges. In [2], the REU participants determined which cyclic groups have subgroup lattice that embed into the -torus. In this paper, we classify the abelian groups whose subgroup lattice graphs are genus one. Following the notation in [4], we formally define the subgroup lattice graph.
Definition 1.
The subgroup lattice graph of a finite group is a graph whose vertices are the subgroups of the group and two vertices, and are connected by an edge if an only if and there is no subgroup such that .
Definition 2.
The genus of a graph is the minimum such that there exists an embedding of into the orientable surface of genus .
Let denote the cyclic group of size . We now state the main result of this paper.
Theorem 1.
If is a finite abelian group, then if and only if
-
•
where where are distinct primes and , or
-
•
where where are distinct primes, or
-
•
where is prime, or
-
•
where is prime, or
-
•
.
2. Cyclic Groups
In [6], the authors determined all abelian groups whose subgroup lattice graphs are planar. For example, consider the subgroup lattice in Figure 1 of the cyclic group where are distinct primes. The lattice is simply the lattice of divisors where two divisors are connected if and only if their ratio is prime.
We readily see that the subgroup lattice of is simply the graph Cartesian product of the path graph on 3 vertices and the path graph on 4 vertices. This leads us to the following definition in which we follow the notation from [5].
Definition 3.
A -dimensional grid graph is the graph Cartesian product of paths, where the path has length .
From this definition, the following lemma follows immediately.
Lemma 1.
The subgroup lattice of the cyclic group where the are distinct primes and is precisely .
In [5], the authors prove many results about the genus of grid graphs . In particular, they prove the following result which lists all grid graphs with genus or . The first two bullet points of the below theorem had already been discovered by Starr and Turner [6] and the last two bullet points had been discovered by Berry, McGinnis, and Sanchez [2]. However, these earlier results used the language of subgroup lattice graphs of cyclic groups as opposed to grid graphs.
Proposition 1 ([2, 5, 6]).
A grid graph embeds on the torus if and only if
-
•
,
-
•
and at most one of is greater than 1,
-
•
and , or
-
•
and .
Thus, all cyclic groups whose subgroup lattice graphs are genus zero (the first two bullet points above) or one (the last two bullet points above) have been classified.
2.1. Tools for Finding the Genus of Subgroup Lattice Graphs of Cyclic Groups
Although Proposition 1 resolves the question of which cyclic groups have subgroup lattices of genus one, there are several results in [5] that let us determine the genus of the subgroup lattice of cyclic groups in other cases. One of the most useful results is the exact genus of grid graphs for which at least 3 of the are odd. Let and represent the number of edges and vertices respectively in a grid graph . The following result is due to White [8]; however, it has been rephrased in the language of [5].
Proposition 2 (Theorem 4,[8]).
Let be a -dimensional grid graph where and at least three are odd, for . Then is a lower-embeddable grid graph, i.e.
This leads to the immediate corollary.
Corollary 1.
If is a cyclic group with and odd for at least three , then:
| (1) |
Here is an easy consequence of the previous result.
Corollary 2.
Consider the subgroup lattice graph of the cyclic group where are distinct primes. Then
| (2) |
Another easy consequence is the genus of the -hypercube, which is the subgroup lattice graph of where are distinct primes.
Corollary 3.
Consider the subgroup lattice graph of the cyclic group where are distinct primes and . Then
| (3) |
Proposition 3 (Theorem 3, [5]).
For any , we have
| (4) |
Proposition 4 (Theorem 4, [5]).
For any , we have that
| (5) |
2.2. Lower and Upper Bounds on the Genus of a Grid Graph
While the previous section provided exact formulas for the genus of various grid graphs, there are several inequalities for the genus that will be useful. The first result is a lower bound for the genus of any grid graph.
Proposition 5 (Corollary 1, [5]).
Let be a grid graph with . Then
| (6) |
where and are the number of edges and vertices respectively in .
Proposition 6 (Proposition 3, [5]).
Let be a -dimensional grid with at least one even grid parameter.
-
(a)
If exactly one grid parameter is even (the third parameter), then
(7) -
(b)
If exactly two grid parameters are even (the second & third parameters), then
-
(c)
If all three grid parameters are even, then
While these formulas are useful, one sometimes needs to show that a graph has a lower bound for its genus by finding a graph minor with a particular genus. When one combines multiple copies of the same graph, e.g. one can use the block decomposition of a graph to compute its genus. We follow the discussion of block decompositions found in [5].
Definition 4.
A block of a graph is a maximal -connected subgraph of . Given a connected graph , there exists a unique collection of blocks such that , which is called the block decomposition of .
The following theorem connecting the genus of a graph to the genus of the blocks in its block decomposition is due to Battle, Harary, Kodama, and Youngs [1].
Theorem 2 (Theorem 1, [1]).
If is a graph with block decomposition , then .
Using these results, we can prove the following theorem.
Theorem 3.
Let be a cyclic group with subgroup lattice graph where with distinct primes. Then if and only if
-
•
and or
-
•
and .
We have if and only if
-
•
and or
-
•
and .
We have if
-
•
and
or
-
•
and .
Remark 1.
Proof.
Using equations (4), (5), and (2), we can easily show that all the subgroup lattice graphs above have the specified genus with the exception of where are distinct primes.
Using (7), we see that . Now, we must show it is at least four. Below, we have drawn a graph that is combination of four graphs.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/56f63e83-15df-472e-8651-2fc55733b343/x1.png)
Omit all the dotted edges and black vertices. Contract the blue, green, purple, brown, and orange paths to single vertices. Note that there are two separate blue paths, one with solid blue vertices and one with blue vertices outlined with a black circle. These paths are contracted to two different vertices. The same phenomenon occurs with the green, orange, and brown vertices. Doing so results in the following minor of .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/56f63e83-15df-472e-8651-2fc55733b343/x2.png)
Using Theorem 2 and the fact that we deduce that the genus of the above graph minor is . Hence, we have deduced that
Now, we must show that cyclic groups not appearing in the list above or in the list from Proposition 1 have genus at least 5 with the exception of . For the remainder of the proof, suppose that is a cyclic group not appearing in the list of groups in Proposition 1 or Theorem 3.
Suppose and .
If then . Since using (1), we deduce that .
Suppose and . If , then and thus by (2). If and then and thus by (6). If and then and by (6). If then and thus by (6).
Suppose and . Then we know since by (3). ∎
Thus, with the exception of , we have completed the classification of cyclic groups with subgroup lattice graphs of genus up to .
3. Non-Cyclic Abelian Groups
Now that we have classified all cyclic groups whose subgroup lattice graph has genus up to 4 with the exception of , we proceed with determining the non-cyclic abelian groups whose subgroup lattice has genus one. The following theorem classifies all non-cyclic abelian groups whose subgroup lattices have genus zero. The planar cyclic groups are described in the first two bullet points of Proposition 1.
Theorem 4 (Theorem 14, [6]).
Let be a finite abelian group. Then is planar if and only if is isomorphic to a planar cyclic group or to where is a prime and .
First, we examine a few families of graphs that will be needed to prove Theorem 1.
Lemma 2.
Let be the graph pictured below.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/56f63e83-15df-472e-8651-2fc55733b343/x3.png)
The genus of is .
Proof.
The graph has a clear minor and . Hence, . To demonstrate that can be drawn on a surface of genus , we will construct a set of cycles that traverse each edge in both directions (e.g. define the faces of the embedding of the graph on a surface). We will first consider the case when . The cycles are as follows:
-
•
, , , , ,
-
•
, , ,
-
•
, , ,
-
•
, , , ,
, ,
Using these cycles, observe that this embedding of the graph into some surface has faces, vertices, and edges. Using Euler’s formula, we deduce that This equation yields since . Observe that the fact that is used inherently in the definition of the -cycles in the fourth bullet point.
Thus we have proved our result in the case when . The other cases follow from the fact that is a subgraph of , and . If , there exists a unique integer satisfying with . ∎
We then use this result to prove the genus of .
Proposition 7.
For a prime , .
Proof.
The subgraph lattice graph of is pictured below in Figure 2.
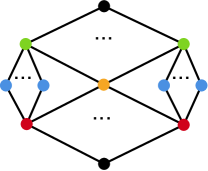
The red vertices represent the subgroups of size . The blue vertices represent the cyclic subgroups of size and the orange vertex represents the unique non-cyclic subgroup of size . The green vertices represent the subgroups of size .
It is easy to see that has a minor by merging all the blue vertices with the respective red vertex they connect to. Hence, . It is also relatively easy to see that since embeds onto a surface of genus , we can also embed on the same surface. This is because one can cut out a small neighborhood of the edges and replace it by the corresponding red vertex, green vertex, and blue vertices along with the edges that connect them. For example, see Figure 3.
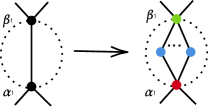
Hence, we have proven that . ∎
Lemma 3.
Let be the graph pictured below.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/56f63e83-15df-472e-8651-2fc55733b343/x6.png)
If is odd, the genus of is .
Proof.
Observe that contains two copies of . By deleting four of the red edges and using Theorem 2, one deduces that .
Now, we consider the case when . To demonstrate that can be drawn on a surface of genus , we will construct a set of cycles that traverse each edge in both directions exactly once. The cycles are as follows:
-
(a)
, , …, ,
-
(b)
, , …, ,
-
(c)
, , …, ,
-
(d)
, , …, ,
-
(e)
, , …,
, -
(f)
, , …,
, -
(g)
, , ,
-
(h)
Using these cycles, observe that this embedding of the graph into some surface has faces, vertices, and edges. Using Euler’s formula, we deduce that This equation yields since . Observe that we inherently used the fact that when we constructed the -cycles in bullets (e) and (f) since we need to be even to have an equal number of cycles beginning with versus (or versus ) in our list of -cycles.
Thus we have proved our result in the case when . The case when follows from the fact that is a subgraph of . ∎
Proposition 8.
For an odd prime , . When , .
Proof.
The subgroup lattice of is pictured below in Figure 4.
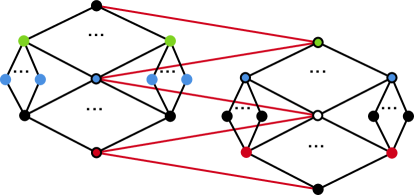
The red vertices represent the subgroups of size , and the red vertex with a black outline is the subgroup generated by . The black vertices in the third row from the bottom represent the cyclic subgroups of size , and the white vertex represents the unique non-cyclic subgroup of size . The blue vertices without a black outline represent the cyclic subgroups of size and the blue vertices with a black outline represent the non-cyclic subgroups of size . Lastly, the green vertices are the subgroups of size , and the green vertex outlined in black unique subgroup of size that is entirely torsion.
It is relatively easy to see that has a minor. Hence, . It is also relatively easy to see that since embeds onto a surface of genus , we can embed on the same surface. This is because one can cut out a small neighborhood of the edges and replace it by the corresponding black vertex, green vertex, and blue vertices along with the edges that connect them. For example, see Figure 5 below.

A similar operation allows one to cut out a small neighborhood of the edges and replace it by the corresponding red vertex, blue vertex, and black vertices along with the edges that connect them.
Now consider the case when . We know that by Theorem 4. To demonstrate that , we simply need to show that we can draw on the 1-torus which we do here in Figure 6.
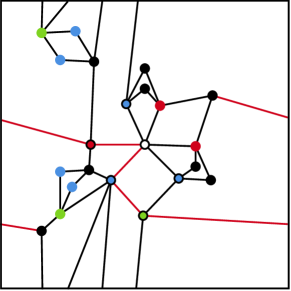
∎
Proposition 9.
The genus of for primes is .
Proof.
The subgroup lattice of is pictured below in Figure 7.
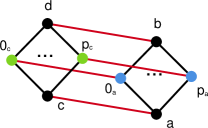
The blue vertices represent the subgroups of size , the vertex represents the trivial subgroup, the vertex represents the unique subgroup of size , the vertex represents the unique subgroup of size , the green vertices represent the subgroups of size and the vertex is the full group.
If one contracts the edges and deletes edges and , then one obtains a graph with genus . Hence, .
First, we will prove the case when is an prime. To show that we can embed the subgroup lattice on a surface of genus , we will exhibit a set of cycles that traverse each edge in both directions exactly once. The cycles are as follows:
-
•
, , ,
-
•
, , ,
-
•
,
-
•
,
-
•
, , ,
-
•
, , ,
Using these cycles, observe that this embedding of into some surface has faces, vertices, and edges. Using Euler’s formula, we deduce that . This equation yields since is an odd prime. Hence, we have shown that when is an odd prime.
When , we know that by Theorem 4. Since, is a subgraph of , we deduce that . ∎
Now, we compile our results to prove that all the graphs in the statement of Theorem 1 have genus one.
Proposition 10.
The following groups have subgroup lattices with genus one.
-
•
where is prime, or
-
•
where is prime, or
-
•
.
Proof.
All the groups listed in this proposition, with the exception of , have already been shown to have subgroup lattice graphs of genus one via Propositions 7, 8, and 9. Thus all that remains is to show the same result for . Since it does not appear in the list of planar groups in Theorem 4, it must have genus at least one. So all we must do is show that its subgroup lattice graph can be drawn on the -torus
The subgroup lattice of is below in Figure 8. The blue vertices represent the three cyclic subgroups of size and the blue vertex outlined in black is the subgroup generated by . The red vertex is the unique non-cyclic subgroup of size . The green vertices represent the three cyclic subgroups of size and the green vertex outlined in black is the subgroup generated by . The orange vertex is the unique non-cyclic subgroup of size .
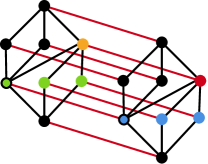
Figure 9 shows how can be drawn on the -torus.
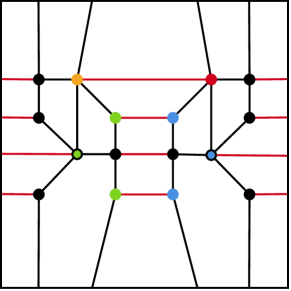
∎
3.1. Eliminating Graphs
In this subsection, we will determine why various families of graphs have genus at least two and thus cannot be embedded into the 1-torus. First, recall that the girth of a graph is the length of its shortest cycle. Now, we recall the following result.
Proposition 11 (Proposition 1, [5]).
Suppose is a connected graph whose girth is at least . Then .
Corollary 4.
If is a finite group whose subgroup lattice is not a tree then
| (8) |
Remark 2.
The only abelian groups whose subgroup lattice is a tree are .
Proof.
We proceed by showing that a subgroup lattice graph has girth at least . Clearly a subgroup lattice cannot have a cycle of length two since there is at most one edge between any two vertices. Could there be three subgroups that form the vertices of a -cycle in the subgroup lattice? If so, one deduces that one subgroup, say , is a subgroup of the other two. Furthermore, one of the remaining subgroups, say , is a subgroup of the last subgroup, . Hence . This is a contradiction with the fact that and are connected by an edge in the subgroup lattice graph. Hence, we conclude that a -cycle is impossible in a subgroup lattice graph. ∎
Lemma 4.
If is a prime, then .
Proof.
There are subgroups of size and subgroups of size . Since a subgroup of size contains elements of order , it thus contains subgroups of size . Thus, each subgroup of size connects to subgroups of size .
Using (8), the subgroup lattice graph has vertices and edges. Since the girth of the graph is ,
This is strictly bigger than since . ∎
Lemma 5.
The subgroup lattices of the groups below have genus at least .
-
•
-
•
for a prime
-
•
for distinct primes
-
•
for distinct primes
Proof.
The graph has 30 vertices and 76 edges. Using (8), one computes that
For a prime , the graph has 30 vertices and 63 edges. Using (8), one computes that
For distinct primes , the graph has 20 vertices and 44 edges. Using (8), one computes that
For distinct primes , the graph has 24 vertices and 56 edges. Using (8), one computes that ∎
Proposition 12.
The following groups have subgroup lattice graphs with genus at least .
-
•
For a prime ,
-
•
For a prime ,
-
•
-
•
-
•
For a prime , and
Proof.
To prove this proposition in every case except , we will display minors with genus of the subgroup lattice graphs of the groups listed above. The graphs with the identified minors are displayed below in Figures 10, 11, 12, 13, and 14.
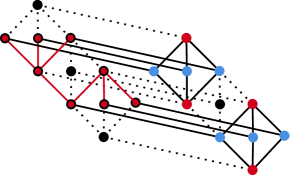
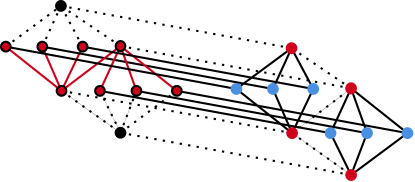
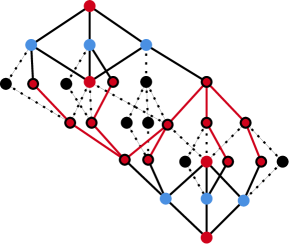
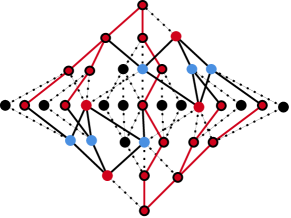
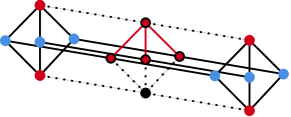
In all of the subgroup lattice graph diagrams in Figures 10, 11, 12, 13, and 14, merging all the red vertices with a black outline and deleting all the dotted edges results in the following graph minor.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/56f63e83-15df-472e-8651-2fc55733b343/x18.png)
By Theorem 2 and the fact that , we have shown that each of the above graphs have genus at least except in the case of . This result follows immediately from the fact that is a subgraph of . ∎
Lemma 6.
The genus of for primes is greater than or equal to .
Proof.
The subgroup lattice of is pictured below.
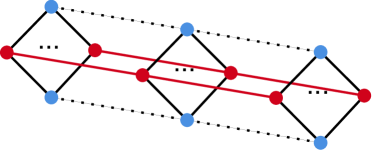
The vertices between each pair of red vertices represent subgroups, and there are red vertices total. If we merge the red vertices in groups of three as shown in the picture and remove the dotted edges, we obtain a graph which has genus .
∎
3.2. Proof of Theorem 1
Now, we can proceed with the proof of the main theorem.
Proof of Theorem 1.
Proposition 1 classifies all cyclic groups with subgroup lattice graphs of genus which are , , and where the are distinct primes.
We now turn to the non-cyclic abelian groups. Proposition 10 demonstrates that every non-cyclic abelian group listed in Theorem 1 has genus one.
Now, we must demonstrate that every non-cyclic abelian group not appearing in Theorem 1 or Theorem 4 has a subgroup lattice with genus at least two.
Let
| (9) |
be a non-cyclic abelian group with a subgroup lattice group with genus that does not appear in the list of Theorem 1 or Theorem 4. Since is not cyclic, for some in (9).
First, let’s consider the case where all the are the same in (9). Lemma 4 shows that necessarily. Because of Theorem 4, we only need to investigate the case . Proposition 7 shows us that when . Now, we need only consider the case where , , or and and . Proposition 8 shows us that when So, we are reduced to considering cases where and and or and . Proposition 12 shows that these groups have subgroup lattices with genus at least . Hence, Theorem 1 contains the complete classification of non-cyclic abelian group with subgroup lattice with genus equal to one in the case where all the are the same in (9).
Now, we consider the case where the collection of primes in (9) contains exactly two primes. Recall that at least one of the primes must be repeated in order for to be non-cyclic. Proposition 9 shows that if , then the prime repeated must be or .
Consider the case where . Proposition 12 forces . Since cannot appear in the list of Theorem 1, if , then necessarily. However, Lemma 6 rules out this case. Hence, we restrict ourselves to the case which implies necessarily. However, Lemma 5 rules out this possibility.
Now consider the case where . Proposition 12 forces either or . Since cannot appear in the list of Theorem 1, if , then necessarily. However, Proposition 12 rules out this case. Hence, we restrict ourselves to the case which implies necessarily. However, Lemma 5 rules out this possibility.
Hence, Theorem 1 contains the complete classification of non-cyclic abelian group with subgroup lattice with genus equal to one in the case that collection of primes in (9) contains exactly two distinct primes.
Lastly, we consider the case where the collection of primes in (9) contains at least three distinct primes. Proposition 9 shows that if , then the prime repeated must be or . However, Lemma 5 shows that in this case since our group would contain either or as a subgroup.
Hence, Theorem 1 contains the complete classification of non-cyclic abelian group with subgroup lattice with genus equal to one. ∎
4. Conclusion
The prospect of writing out explicit lists of abelian groups whose subgroup lattice graphs have genus for every seems daunting. However, there are various classes of abelian groups for which this task seems possible. In particular, the authors of [5] have a conjecture for the genus of the subgroup lattice graphs of cyclic groups with three distinct primes factors. In particular, they conjecture that the inequalities in Proposition 6 are actually equalities. Further investigation is warranted.
5. Acknowledgements
All the subgroup lattice graphs were constructed using SAGE [7]. The author would like to thank Colin Starr for introducing him to this problem in 2017 while the author was a Visiting Assistant Professor at Willamette University.
References
- [1] Joseph Battle, Frank Harary, Yukihiro Kodama, and J.W.T Youngs. Additivity of the genus of a graph. Bulletin of the American Mathematical Society, 68(6):565–568, 1962.
- [2] Jeremy Berry, Sarah McGinnis, and E. J. Sanchez. Subgroup graphs of non-orientable and oriented genus one. Missouri State REU, 2012.
- [3] Joseph P. Bohanon and Les Reid. Finite groups with planar subgroup lattices. Journal of Algebraic Combinatorics, 23(3):207–223, 2006.
- [4] Andrea Lucchini. The genus of the subgroup graph of a finite group. Bulletin of Mathematical Sciences, 11(01):2050010, 2020.
- [5] Christian Millichap and Fabian Salinas. Embedding grid graphs on surfaces. Graphs and Combinatorics, 38(3), 2022.
- [6] Colin L. Starr and Galen E. Turner III. Planar groups. Journal of Algebraic Combinatorics, 19(3):283–295, 2004.
- [7] The Sage Developers. SageMath, the Sage Mathematics Software System (Version 10.0), 2023. https://www.sagemath.org.
- [8] Arthur T. White. The genus of repeated cartesian products of bipartite graphs. Transactions of the American Mathematical Society, 151(2):393–393, 1970.