Finite Temperature Behavior in the Second Landau Level
of the Two-dimensional Electron Gas

The two-dimensional electron gas subjected to a perpendicular magnetic field is a model system that supports a large variety of electronic phases tsui ; jainBook ; willett ; fogler ; lilly99 ; du99 ; pan99 ; eisen02 ; xia04 ; kumar10 ; ethan15 . Many new phases were discovered in high quality GaAs/AlGaAs heterostructures and this system continues to play an important role in the study of these phases. Improvements in the material quality of bilayer graphene gr1 ; gr2 and ZnO zno offer a chance to study different realizations of these phases in alternative hosts.

The most fascinating region of current interest of the electron gas in GaAs/AlGaAs is the second orbital Landau level. Here we find numerous fractional quantum Hall states (FQHSs) willett ; pan99 ; eisen02 ; xia04 ; kumar10 ; ethan15 . Several of these FQHSs are thought to have topological order and exotic quasiparticle excitations which cannot be realized in the lowest Landau level tsui . The most well-known of these is the $\nu=5/2=2+1/2$ FQHS willett ; pan99 , which is believed to belong to the Pfaffian universality class and to host Majorana-like excitations mr ; zalat . The $\nu=2+2/5$ is another FQHS of interest xia04 as it is a candidate hosting Fibonacci anyons rr1 ; rr2 . In addition to FQHSs, the second Landau level also supports a set of traditional Landau phases with charge order. Examples are the electronic bubble phases fogler ; eisen02 ; deng12 , but under special circumstances the quantum Hall nematic may also develop nodar16 ; kate17 . The region of the second Landau level, therefore, stands out among other Landau levels in a prominent display of phase competition between two classes of different phases: FQHSs and charge ordered phases xia04 .

In most experiments, data in the second Landau level of the highest quality samples exhibit a consistent set of ground states: one typically observes fully developed FQHSs at $\nu=2+1/2$, $2+1/3$, $2+2/3$, $2+1/5$, $2+4/5$, and $2+2/5$ and up to four bubble phases. In addition, in setups reaching the lowest temperatures, several developing FQHSs are observed at $\nu=2+3/8$ xia04 ; kumar10 ; ethan15 ; pan12 ; qi17 ; choi08 ; deng12b ; pan08 ; nodar11 ; watson15 , $2+6/13$ kumar10 ; ethan15 ; pan12 ; qi17 ; deng12b ; watson15 , $2+2/9$ deng12b , $2+7/9$ ethan15 ; deng12b ; pan08 and $2+2/7$ xia04 ; dean08 ; choi08 ; pan12 . However, a careful inspection of the literature reveals that there are several additional magnetoresistance minima, such as the ones at $\nu=2+5/8$, $2+5/7$ in Ref.pan12 , $\nu=2+3/5$, $2+3/7$, $2+5/7$, $2+4/9$, $2+5/9$, $2+5/8$ in Ref.choi08 , and $\nu=2+4/9$, $2+5/9$, $2+5/7$ in Ref.ensslin14 . Even though these minima develop at filling factors compatible with FQHSs, they could not be associated with FQHSs either because of lack of Hall data choi08 ; pan12 or because the quantization of the Hall resistance was not consistent with that of a FQHS ensslin14 . Furthermore, with the exception of $\nu=2+5/8$, at the filling factors of these additional minima other experiments report bubble phases at either lower electron temperatures and/or in higher quality samples xia04 ; kumar10 ; ethan15 ; qi17 ; deng12b ; pan08 ; nodar11 .

There may be several reasons for the development of these additional local minima in $R_{xx}$ in certain experiments but of bubble phases in others. First, samples with different growth parameters have different electron-electron interaction that may result in a drastically different set of ground states. It is thus possible that, with improvement of sample quality, the signatures seen in Refspan12 ; choi08 ; ensslin14 develop into quantized FQHSs. Second, the available data may indicate a temperature-driven phase competition of FQHSs and bubble phases. Indeed, there are well-known FQHSs present at intermediate temperatures, which give way to a charge-ordered phase at the lowest accessible temperatures. Examples of such FQHSs are at $\nu=1/7$ hiB1 ; hiB2 and $2/11$ FQHSs hiB2 in the lowest Landau level, $\nu=4+1/5$ and $4+4/5$ in the third Landau level gervaisB , and $\nu=2+2/7$ in the second Landau level xia04 . Of these, the FQHSs observed at intermediate temperatures in the second and third Landau levels turn into bubble phases as the temperature is lowered.

Here we examine whether the earlier seen minima in $R_{xx}$ that could not be associated with a FQHS also develop in the second Landau level of a high quality GaAs/AlGaAs sample. We are interested in examining previously unavailable detailed temperature dependence to observe phases at intermediate temperatures. While in our sample we find peculiar features in the magnetoresistance in the vicinity of the filling factors of interest $\nu=2+3/5,2+3/7,2+4/9,2+5/9$, and $2+5/8$, we cannot associate FQHSs with these filling factors neither at the lowest nor at any finite temperatures. We show that these features arise from the development of the magnetoresistive fingerprints of the bubble phases. In contrast, at $\nu=2+2/7$ and $2+5/7$ we observe incipient FQHSs at intermediate temperatures, which yield to a bubble phase as the temperature is lowered further. Such a study is timely, because of the conflicting results reported in the second Landau level of the GaAs/AlGaAs system. Furthermore, our work is expected to be relevant for studies of bilayer graphene, in which an increasing number of FQHSs gr1 ; gr2 as well as of bubble phases have been recently reported cory .

Our sample is a symmetrically doped 30 nm quantum well sample with electron density $n=3.0\times 10^{11}$/cm² and mobility $\mu=32\times 10^{6}$cm²/Vs. Following the procedure described in the Supplement of Ref.dengAlloy , the sample state was prepared by a low temperature illumination with a red light emitting diode. Our sample is the same as the one used in Ref.kumar10 ; data presented in Figs.1-4 are, however, from a different sample state preparation than those from Ref.kumar10 . The sample is mounted in a He³ immersion cell which assures electron thermalization to the base temperature of our dilution refrigerator and enables a convenient temperature measurement through quartz tuning fork viscometry setup .

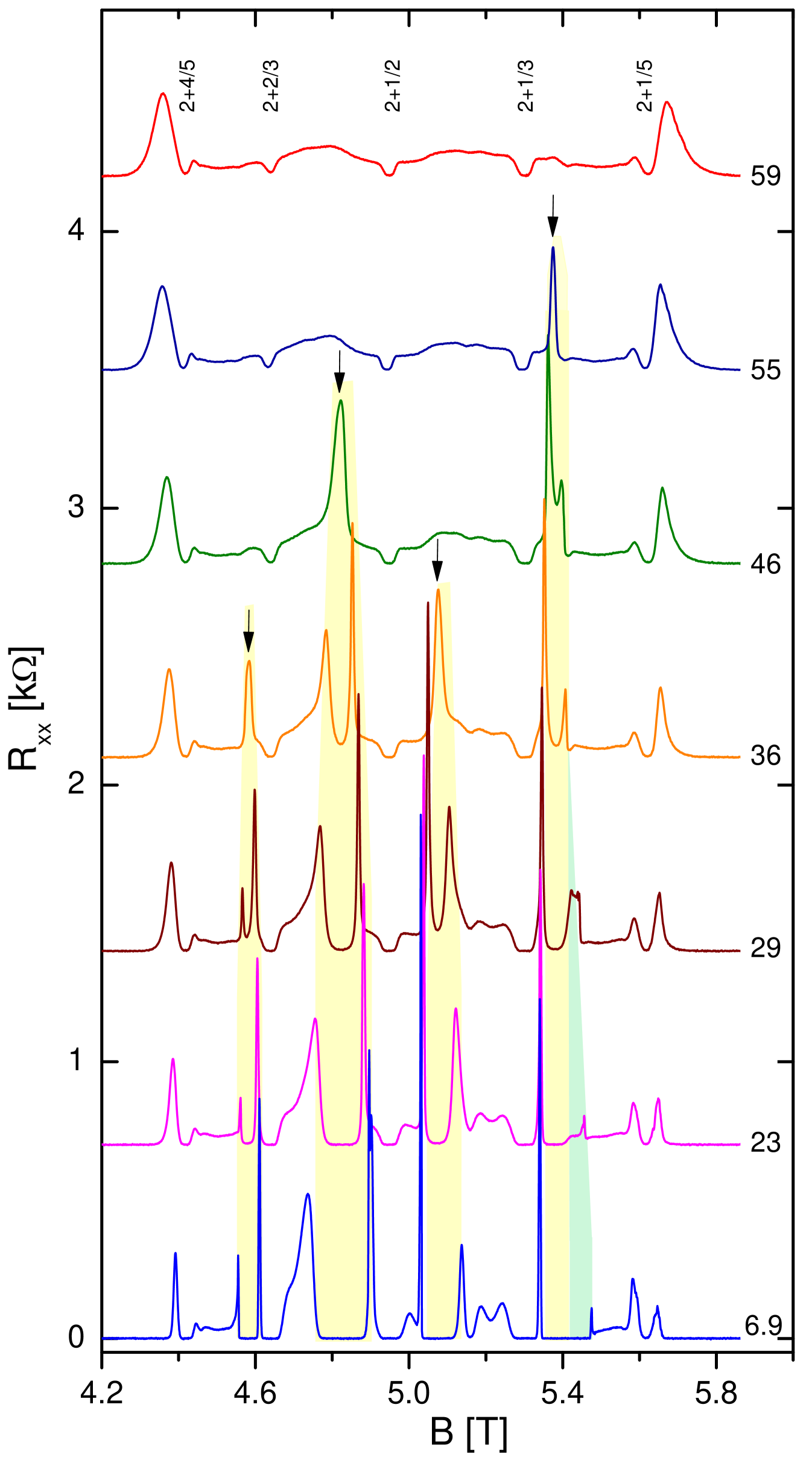
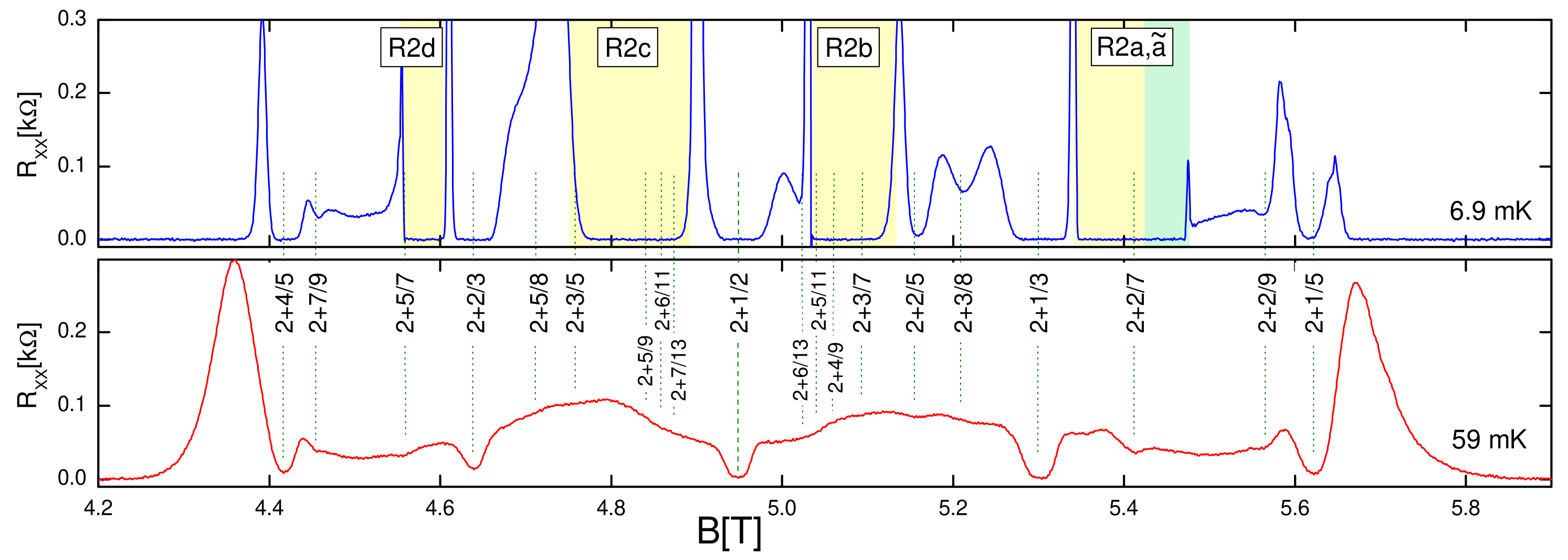
Figure 1 captures the temperature evolution of magnetoresistance traces in the second Landau level between $T=59$ and $6.9$ mK. We observe several FQHSs; the most prominent of these are the ones at $\nu=2+1/2,2+1/3,2+2/3,2+1/5$, and $2+4/5$. Traces of Fig.1 appear very different from those measured in the lowest Landau level tsui because of the presence of the reentrant integer quantum Hall states eisen02 ; deng12 . These reentrant states are believed to be exotic electronic solids called the bubble phases fogler ; lilly99 ; du99 . The bubble phases we observe are marked by shading in Fig.1. At the lowest temperatures, the bubble phases are signaled by a vanishing $R_{xx}$ and a Hall resistance quantized to either $h/2e^{2}$ or $h/3e^{2}$ (not shown) eisen02 . Furthermore, the bubble phases are delimited by two distinct peaks in $R_{xx}$, which can be seen near the edges of the shaded areas deng12 . The size of such peaks may exceed $1.8$ k$\Omega$, hence they dominate the magnetoresistive landscape. It was found that as the temperature is raised, the two peaks delimiting a bubble phase first merge into a single peak, this single peak then disappears as the temperature is increased further. Since these single peaks are the highest temperature signatures of the bubble phases, they can be thought of as the precursors of the bubble phases. In Fig.1 there are several examples marked by vertical arrows, such as the precursor peak at $B\simeq 5.37$ T in the $T=55$ mK trace. At lower temperatures, near $B=5.4$ T there are two distinct bubble phases, which will be discussed later.

A magnified view of the $T=6.9$ and $59$ mK traces is seen in Fig.2. We singled out the $T=59$ mK trace since this is the lowest temperature at which there are no discernible features of the bubble phases. On this trace we marked several filling factors of interest: the prominent FQHSs at $\nu=2+1/2,2+1/3,2+2/3,2+1/5$, and $2+4/5$. Additional features are seen at several other filling factors. Some are relatively narrow depressions in $R_{xx}$, such as the ones at $\nu=2+2/5$, $2+2/7$, $2+2/9$, $2+7/9$, $2+5/7$ and $2+3/8$. Other features are broader, such as the ones near $\nu=2+3/5$ and also in the vicinity of $\nu=2+1/2$, on each side. Of these features not all develop into a FQHS at $T=6.9$ mK. Indeed, in the $T=6.9$ mK trace we identify fully developed FQHSs at $\nu=2+1/2$, $2+1/3$, $2+2/3$, $2+2/5$ and less developed FQHSs at $\nu=2+6/13$, $2+2/9$, $2+7/9$, and $2+3/8$. In the following we will examine the temperature dependence of the additional features of $R_{xx}$ shown in the $T=59$ mK trace of Fig.2. We will search, in particular, for signs of developing FQHSs which may be present at intermediate temperatures, but which may not survive to the lowest accessible temperatures.

We first focus at filling factors related by particle-hole conjugation $\nu=2+3/5$ and $2+2/5$. Interest in these quantum numbers stems from proposals and numerical evidence that FQHSs here have a very special topological order supporting non-Abelian anyons of the Fibonacci type rr1 ; rr2 . Features in magnetotransport at these two filling factors were first found and tentatively associated with FQHSs in Ref.pan99 . However, quantized Hall resistance was not observed; the Hall resistance instead had features which were later attributed to the bubble phases. A fully developed $\nu=2+2/5$ FQHS was observed in Ref.xia04 and it is now routinely measured xia04 ; kumar10 ; ethan15 ; pan12 ; qi17 ; dean08 ; choi08 ; deng12b ; pan08 ; nodar11 ; watson15 . In contrast to observations at $\nu=2+2/5$, at $\nu=2+3/5$ a FQHS was not detected in most experiments xia04 ; kumar10 ; ethan15 ; pan12 ; qi17 ; dean08 ; deng12b ; pan08 ; nodar11 ; watson15 . The filling factor $\nu=2+3/5$ often falls very close to the bubble phase $R2c$ instead. We are aware of only one work, in which a concave feature in $R_{xx}$ was seen at $\nu=2+3/5$ choi08 at a temperature $T=36$ mK. We note that results in wide quantum wells are qualitatively different; we defer discussing these results to a later paragraph.

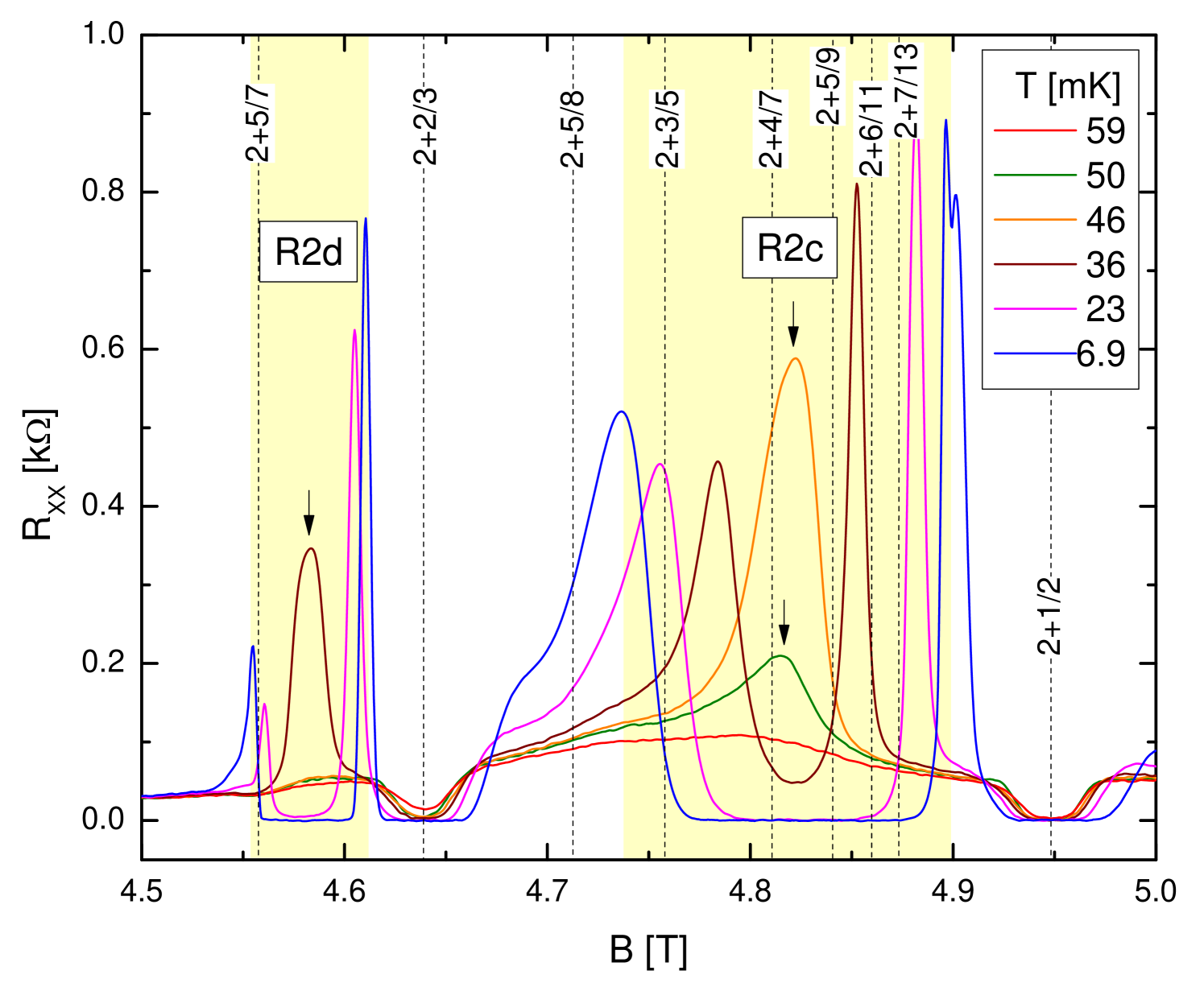
As seen in Fig.2, our $T=6.9$ mK trace in the vicinity of $\nu=2+3/5$ is similar to that seen in Refs.xia04 ; kumar10 ; ethan15 ; qi17 ; deng12b ; pan08 ; nodar11 ; watson15 , as $\nu=2+3/5$ falls near a bubble phase. The $T=59$ mK trace of Fig.2, however, is not perfectly smooth and it has a slight curvature at $\nu=2+3/5$. In order to establish whether this feature develops into a FQHS at intermediate temperatures, in Fig.3 we examine data at intermediate temperatures. We notice, that at $T=50$ mK a resistance peak appears near $B=4.82$ T. This peak was associated with the bubble phase and can be thought of as the precursor of the bubble phase labeled $R2c$. As the temperature is lowered to $T=46$ mK this peak grows, then at $T=36$ mK it splits into two peaks, giving way to a pronounced resistance minimum between them. Inspecting the data shown in Fig.3 we see that the precursor peaks of the bubble phase at $T=46$ and $50$ mK have a concave curvature on both sides, including one near $\nu=2+3/5$. These concave features, however, cannot be associated with a developing FQHS. We thus conclude that, in spite of a fully developed FQHS at $\nu=2+2/5$, in our sample we do not observe signs of fractional correlations at $\nu=2+3/5$. Recent theory work has considerably strengthened the case for a Read-Rezayi state at $\nu=2+2/5$ papic ; sheng ; peterson and has addressed the experimentally observed asymmetry between $\nu=2+2/5$ and $2+3/5$. Two causes for the suppression of fractional correlations at $\nu=2+3/5$ were identified: an enhanced Landau level mixing peterson and an extremely close energetic competition between the Read-Rezayi state and the bubble phase papic . While in experiments both effects are likely to be present, results of Ref.papic are particularly relevant for our observations.

We note that different physics may be at play at $\nu=2+2/5$ and $2+3/5$ in GaAs/AlGaAs electron gases in which two electric subbands are occupied, such as electron gases confined to wide quantum wells. It was shown that, in contrast to samples with a single subband populated, in these systems the $\nu=2+2/5$ and $2+3/5$ filling factors can be reached while the chemical potential is in the lowest Landau level shay10 ; shay11 . Under such circumstances, FQHSs have been observed both at $\nu=2+2/5$ and $2+3/5$. These FQHSs, however, inherit the Laughlin-Jain correlations of the $\nu=2/5$ and $3/5$ FQHSs commonly observed in the lowest Landau level. Furthermore, under such circumstances no bubble phases were observed, therefore a competition between FQHSs and bubble phases does not occur shay10 ; shay11 .

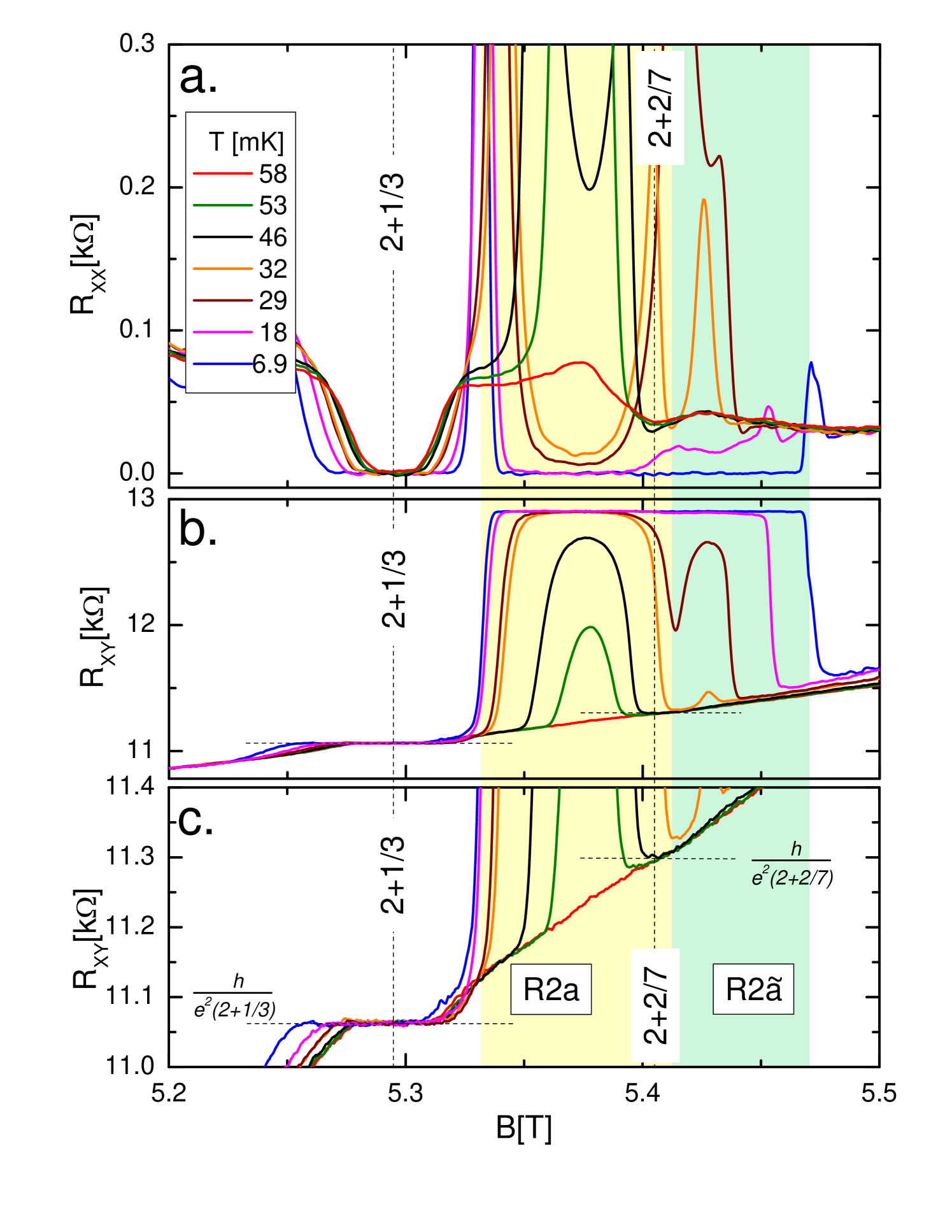
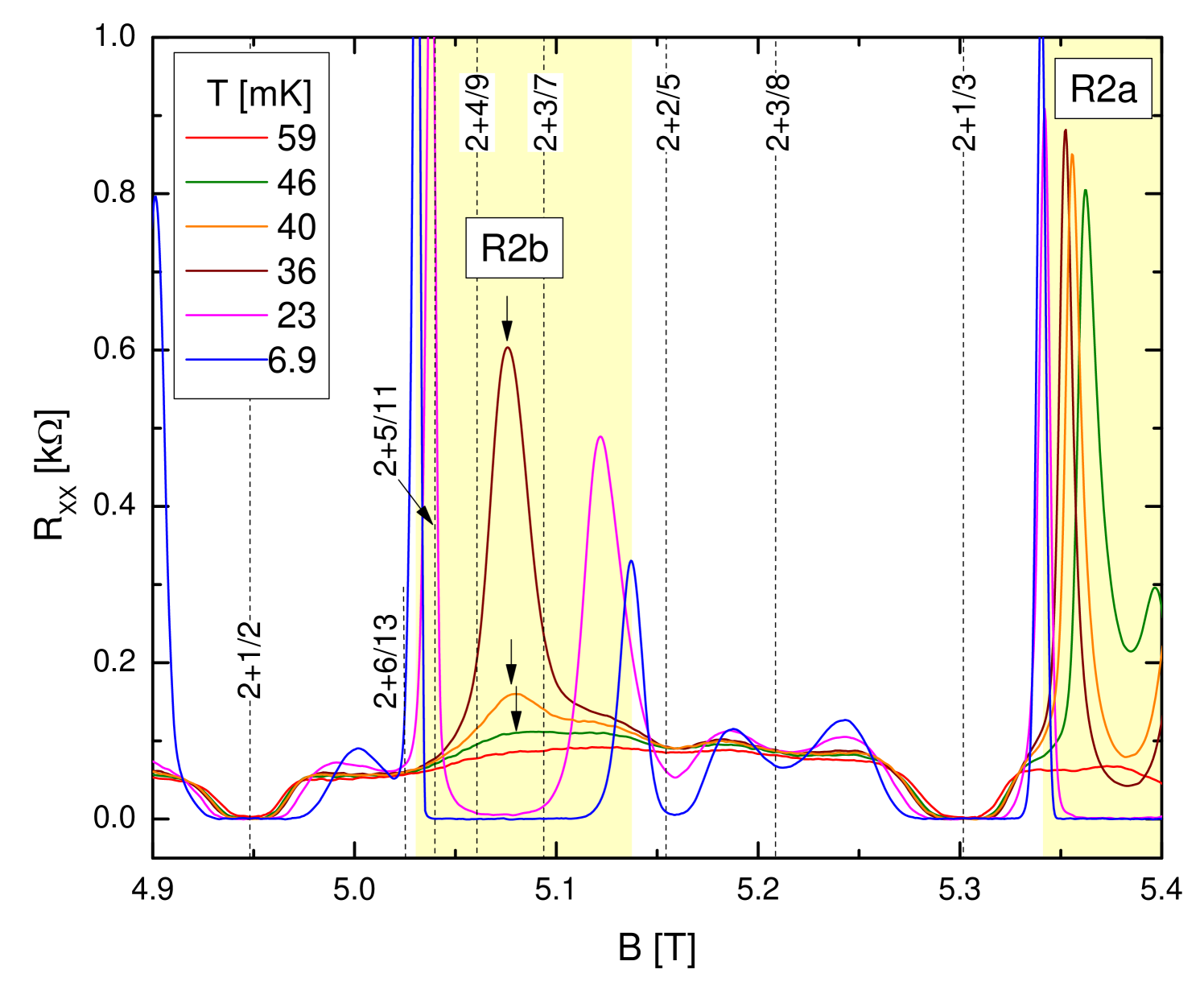
We now examine the range of filling factors from $\nu=2+1/2$ to $2+2/5$. There are several references that report either a bubble phase eisen02 ; xia04 ; pan08 ; nodar11 ; deng12 ; deng12b ; kumar10 ; chick13 or a precursor to the bubble phase in this region dean08 ; nuebler10 . The bubble phase in this range of fillings is labeled $R2b$ in Fig.4. Signatures of fractional correlations in this region were reported only in a handful of experiments. A FQHS was reported at $\nu=2+6/13$ in Ref.kumar10 ; this state has since been seen in other high mobility samples deng12b ; pan12 ; qi17 ; watson15 . In these experiments no other FQHSs were observed in the $2+2/5<\nu<2+1/2$ region kumar10 ; deng12b ; pan12 ; qi17 . In contrast, local minima were reported at $\nu=2+3/7$ and $2+4/9$, but the bubble phase $R2b$ was not observed in Ref.choi08 . In addition, in Ref.ensslin14 , a local minimum in $R_{xx}$ was also observed at $\nu=2+4/9$, although the Hall resistance at this filling factor was not quantized. In our sample we observe a developing FQHS at $\nu=2+6/13$. Furthermore, at $T=36,40,46$ mK in our data we observe precursor peaks associated with the bubble phase $R2b$. These precursor peaks exhibit a concave curvature on both of their sides, near $\nu=2+4/9$ and $2+3/7$. However, the concave features in our sample in the vicinity of these two filling factors cannot be associated with a developing FQHS. We thus conclude, that in our sample there is no evidence of FQHSs at $\nu=2+3/7,2+4/9,2+5/11$ at any of the temperatures examined. Fig.3 shows that a similar conclusion can be reached at filling factors $\nu=2+7/13$, $2+6/11$, $2+5/9$, $2+4/7$, $2+3/5$, and $2+5/8$; of these filling factors a local minimum in $R_{xx}$ was seen at $\nu=2+5/9$ in Refs.choi08 ; ensslin14 and at $\nu=2+5/8$ in Ref.pan12 . We thus found that curvatures in the magnetoresistance of our sample at the filling factors enumerated above cannot be associated with incipient fractional quantum Hall states; instead they originate from magnetoresistive fingerprints of the electronic bubble phases.

In contrast to the behavior of the magnetoresistance at the filling factors discussed above, that at $\nu=2+2/7$ is quite different. As discussed in Ref.xia04 , with the lowering of the temperature, $R_{xx}$ at this filling factor drops and $R_{xy}$ approaches full quantization. Our sample shows a similar behavior. Fig.5a shows that at $T=46$ mK and $\nu=2+2/7$, $R_{xx}$ reaches its lowest value. As shown in Fig.5b and Fig.5c, at this temperature and filling $R_{xy}$ becomes equal to $h/(2+2/7)e^{2}$ within our measurement error. In contrast to Refs.xia04 ; dean08 ; choi08 ; pan12 , transport at the lowest temperature in our sample at $\nu=2+2/7$ exhibits a fully developed reentrant insulator, i.e. $R_{xx}=0$ and $R_{xy}=h/2e^{2}$. As already reported, near $\nu=2+2/7$ there are two distinct bubble phases xia04 ; deng12 , labeled $R2a$ and $R2\tilde{a}$ in Fig.5. Shading in this figure denotes the stability range of these bubble phases at $6.9$ mK; the two different bubbles are delimited by the deep minimum in $R_{xy}$ shown in Fig.5b. It is interesting to note that this deep minimum in $R_{xy}$ is close to, but not at $\nu=2+2/7$. We find a similar behavior at the related filling factor $\nu=2+5/7$. Indeed, in Fig.2 we observe a conspicuous minimum in $R_{xx}$ at $T=59$ mK at this filling factor. Such a local minimum was also observed in Ref.ensslin14 and it may indicate developing fractional correlations. However, as shown in Fig.3, this minimum at $\nu=2+5/7$ disappears with the lowering of the temperature and the $R2d$ bubble phase prevails.

Our observations are expected to be relevant for the two-dimensional electron gas confined to bilayer graphene. Improvements in the quality of this system revealed an increasing number of FQHSs, including even denominator FQHSs gr1 ; gr2 . Details, such as the nature of the wavefunction in the $N=1$ Landau level and the presence of the valley degree of freedom in bilayer graphene, result in differences in the physics, when compared to that in the GaAs/AlGaAs system gr1 ; gr2 . Nonetheless, in addition to FQHSs, the most recent measurements in bilayer graphene also reveal reentrant integer quantum Hall effect commonly associated with bubble phases cory . Bilayer graphene is thus expected to display phase competition between FQHSs and bubble phases similar to that seen in the GaAs/AlGaAs system.

To conclude, the development of precursors of the electronic bubble phases in the second Landau level of two-dimensional electron gases confers strong concave features to the magnetoresistance. In the high quality sample we studied, these concave features cannot be associated with any developing FQHSs. In contrast, the local minima present in the magnetoresistance at intermediate temperatures developing at $\nu=2+2/7$ and $2+5/7$ are interpreted as being due to incipient fractional quantum Hall states. However, as the temperature is lowered, these incipient FQHSs collapse due to a phase competition with an electronic bubble phase.

Measurements at Purdue were supported by the NSF Grant No. DMR 1505866. Sample growth effort of L.N.P. and K.W.W. of Princeton University was supported by the Gordon and Betty Moore Foundation Grant No. GBMF 4420, and the National Science Foundation MRSEC Grant No. DMR-1420541.