First analysis of world polarized DIS data with small-$x$ helicity evolution

The partonic origin of the proton spin remains one of the most intriguing and persistent problems in hadronic physics. Spin sum rules Jaffe and Manohar (1990); Ji (1997) decompose the proton spin of $1/2$ (in units of $\hbar$) into the contributions from quark and gluon helicities ($\Delta\Sigma$, $\Delta G$) and orbital angular momenta. Extensive experimental programs at facilities around the world over the past three decades have provided important insights into the proton spin decomposition Aidala et al. (2013). However, outstanding questions remain, especially about the detailed momentum dependence of the associated quark and gluon helicity parton distribution functions (PDFs) $\Delta q$ and $\Delta g$, respectively. These PDFs are related to the total quark and gluon spin contributions to the proton spin via integrals over the partonic momentum fraction $x$,

where $\Delta q^{+}\equiv\Delta q+\Delta{\bar{q}}$, and the sum runs over the quark flavors $q=u$, $d$, $s$, with $Q^{2}$ the resolution scale.

Determining the quark and gluon contributions to the proton spin crucially depends on knowing the $x$ dependence of the PDFs $\Delta q^{+}(x,Q^{2})$ and $\Delta g(x,Q^{2})$. This is especially true at small values of $x$, where the computation of the moments (1) involves extrapolation below the experimentally accessible region, down to $x=0$. In recent years, an effort to develop small-$x$ evolution equations for helicity PDFs has been underway Kovchegov et al. (2016); Hatta et al. (2017); Kovchegov et al. (2017a, b); Chirilli (2019); Kovchegov (2019); Boussarie et al. (2019); Chirilli (2021), building in part on Refs. Kirschner and Lipatov (1983); Bartels et al. (1996a, b). Specifically, small-$x$ evolution equations (herein referred to as KPS evolution) for the so-called “polarized dipole amplitude” have been derived Kovchegov et al. (2016, 2017a, 2017b, 2017c, 2017d); Kovchegov and Sievert (2019); Cougoulic and Kovchegov (2019).

The polarized dipole amplitude is a critical object for spin-dependent phenomena at small values of $x$ (see Fig. 1): it allows one to obtain the spin-dependent $g_{1}$ structure function, along with the (collinear and transverse momentum dependent) helicity PDFs Kovchegov et al. (2016, 2017a). At leading order (LO) in the strong coupling $\alpha_{s}$, these equations resum powers of $\alpha_{s}\,\ln^{2}(1/x)$, which is known as the double-logarithmic approximation (DLA). The KPS evolution equations close in the large-$N_{c}$ limit Kovchegov et al. (2016), where $N_{c}$ is the number of colors. Numerical and analytic solutions for these have previously been constructed Kovchegov et al. (2017b, c, d). However, an analysis of the world polarized deep-inelastic scattering (DIS) data at small $x$ utilizing KPS evolution has never been performed.

In this Letter, we present such an analysis. We emphasize that KPS evolves in $x$ instead of the traditional evolution in $Q^{2}$ Gribov and Lipatov (1972); Altarelli and Parisi (1977); Dokshitzer (1977). Unpolarized small-$x$ evolution Balitsky (1996, 1999); Kovchegov (1999, 2000); Kovchegov and Weigert (2007); Balitsky (2007) was previously used to describe DIS data on the proton $F_{2}$ and $F_{L}$ structure functions Albacete et al. (2011, 2009); Beuf et al. (2020). We show for the first time that an analogous helicity-dependent small-$x$ approach can successfully describe the polarized DIS $g_{1}$ structure function for the proton and neutron extracted from data at $x<0.1$. This approach differs from earlier work Blümlein and Vogt (1996) which incorporated the small-$x$ resummation from Ref. Bartels et al. (1996b) into the polarized DGLAP splitting functions Gribov and Lipatov (1972); Altarelli and Parisi (1977); Dokshitzer (1977), thereby mixing the small-$x$ and $Q^{2}$ resummations.

In addition, we use pseudodata from the future Electron-Ion Collider (EIC) on electromagnetic and parity-violating polarization asymmetries to demonstrate an extraction of helicity PDFs at small $x$ within the KPS formalism and assess the impact on $g_{1}$. This is a first step towards ultimately using small-$x$ evolution with experimental data from various reactions to genuinely predict the amount of spin carried by small-$x$ partons, which is crucial to resolving the puzzle of the partonic origin of the proton spin.

In the DLA the quark helicity PDFs can be written in terms of the polarized dipole amplitude $G_{q}\big{(}r_{10}^{2},\beta s\big{)}$ Kovchegov et al. (2016, 2017a, 2017b) (see Fig. 1),

where $s\approx Q^{2}(1-x)/x$ is the invariant mass squared of the $\gamma^{*}N$ system and $\beta$ is the fraction of the virtual photon’s momentum carried by the less energetic parton in the $q\bar{q}$ dipole. The amplitude $G_{q}$ is also integrated over all impact parameters Kovchegov et al. (2016, 2017a, 2017b, 2017c, 2017d); Kovchegov and Sievert (2019); Cougoulic and Kovchegov (2019), $r_{10}=|\bm{r}_{1}-\bm{r}_{0}|$ is the dipole transverse size, where $\bm{r}_{i}$ is a coordinate vector in the transverse plane, and $r^{2}_{\rm max}=\min\!\left\{1/\Lambda^{2},1/(\beta Q^{2})\right\}$. We regulate the long-distance behavior of $r_{10}$ with an infrared cutoff $1/\Lambda$ and set $\Lambda=1\,{\rm GeV}$.

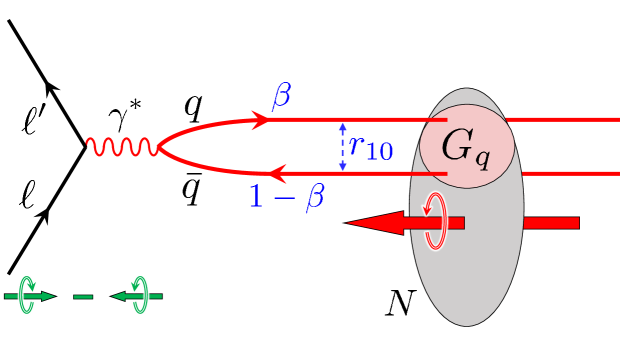
Changing variables to

we can rewrite Eq. (2) in the form Kovchegov et al. (2017b)

where the limits on the $\eta$ and $s_{10}$ integrations are given by $\eta_{\rm max}=\sqrt{\alpha_{s}N_{c}/2\pi}\,\ln(Q^{2}/x\Lambda^{2})$, and $s_{10}^{\rm min}=\max\!\left\{\eta-\sqrt{\alpha_{s}N_{c}/2\pi}\ln(1/x),0\right\}$, respectively.

In the large-$N_{c}$ limit the polarized dipole amplitude $G_{q}$ obeys the evolution equations Kovchegov et al. (2016, 2017a, 2017b),

where $s_{32}^{\rm min}\!=\!\max\!\left\{\!s_{10}\,,\,s_{21}-\eta^{\prime}+\eta^{\prime\prime}\right\}$, and $\Gamma_{q}(s_{10},s_{21},\eta^{\prime})$ is an auxiliary polarized “neighbor” dipole amplitude, defined in Ref. Kovchegov et al. (2016), whose evolution mixes with $G_{q}\!\left(s_{10},\eta\right)$. Note that only $G_{q}\!\left(s_{10},\eta\right)$ contributes to $\Delta q^{+}$ in Eq. (4). The evolution kernel in Eqs. (5) is LO in $\alpha_{s}$ and has been further simplified to contain only the DLA terms. Since running coupling corrections are higher order, we freeze the coupling in Eq. (4) at $\alpha_{s}=0.3$, a typical value in the DIS $Q^{2}$ range we study.

For given initial conditions $G_{q}^{(0)}(s_{10},\eta)$, we can solve Eqs. (5) for $G_{q}(s_{10},\eta)$ and use it in Eq. (4) to calculate $\Delta q^{+}$. Inspired by the Born-level perturbative calculation of $G_{q}(s_{10},\eta)$ Kovchegov et al. (2016, 2017a, 2017b), we employ the ansatz

for the initial conditions, with flavor-dependent coefficients $a_{q}$, $b_{q}$, and $c_{q}$ ($q=u,d,s$) as free parameters.

The evolution in Eqs. (5) starts at $\eta=s_{10}$, or $\beta s=1/r_{10}^{2}$. Since $r_{10}\sim 1/Q$ and the $\beta$ integral in Eq. (2) extends up to 1, the evolution in Eqs. (5) begins at $x=1$. This cannot be the case for small-$x$ evolution, so (5) must be modified to reflect the start of evolution only at $x=x_{0}\ll 1$. For unpolarized small-$x$ evolution, which can be written as a differential equation in $x$, this usually means that one only needs to set the initial conditions at $x=x_{0}$ Albacete et al. (2011, 2009); Beuf et al. (2020). However, the modifications in the polarized case are more involved because (5) are integral equations and cannot be cast in a differential form. Defining $y_{0}\equiv\sqrt{\alpha_{s}N_{c}/2\pi}\ln(1/x_{0})$, for $\eta-s_{10}>y_{0}$ and $\eta^{\prime}-s_{10}>y_{0}$, the modified evolution equations are

In the region below $y_{0}$, the polarized dipole amplitude is given by the initial conditions $G_{q}(s_{10},\eta-s_{10}<y_{0})=\Gamma_{q}(s_{10},s_{21},\eta^{\prime}-s_{10}<y_{0})=G_{q}^{(0)}(s_{10},\eta)$. This prescription implements our matching onto large-$x$ physics, with development of a more rigorous matching procedure left for future work. The numerical solution of Eqs. (7) is accomplished with the discretization utilized in Ref. Kovchegov et al. (2017b) and employing the algorithm presented in Ref. Kovchegov and Tawabutr (2020).

In this work we focus on polarized inclusive DIS data to demonstrate that KPS evolution can describe the existing measurements at small $x$ using the simple initial conditions (6). The main observables used in our analysis are the double-longitudinal spin asymmetries $A_{||}$ and $A_{1}$ from the scattering of polarized leptons on polarized nucleons. At large $Q^{2}$, these are given by ratios of the $g_{1}$ to $F_{1}$ structure functions, $A_{||}\propto A_{1}\propto g_{1}/F_{1}$, where in the DLA the $g_{1}$ structure function is

The denominator $F_{1}$ is taken from data in the form of the LO JAM global analysis Cocuzza et al. (2021); Sato et al. (2020). Note that to this order the Bjorken $x$ variable coincides with the partonic momentum fraction, although at higher orders these are of course different.

Analyses solely utilizing inclusive proton and neutron (deuteron or ³He) DIS data Jimenez-Delgado et al. (2014); Sato et al. (2016) need additional input to separately determine each of the flavors $\Delta u^{+}$, $\Delta d^{+}$, and $\Delta s^{+}$. This can be partially achieved by assuming SU(3) flavor symmetry in the sea and employing the octet axial charge, $a_{8}=\int_{0}^{1}\!dx\big{(}\Delta u^{+}+\Delta d^{+}-2\Delta s^{+}\big{)}$, as a constraint on these moments. However, this is insufficient to uniquely determine the $x$ dependence, so at least one more observable is needed to solve for all three distributions. One approach is to include semi-inclusive DIS (SIDIS) data, with $\pi$ and $K$ fragmentation functions (FFs) as tags of individual flavors. However, to avoid additional uncertainties due to FFs, which would need to be fitted simultaneously with the PDFs Ethier et al. (2017); Sato et al. (2020); Moffat et al. (2021), we leave this to future work.

A new opportunity presented by the future EIC, in addition to precision measurements of $A_{||}$ at smaller values of $x$, is the possibility to perform parity-violating (PV) DIS with unpolarized electrons scattering from longitudinally polarized nucleons. By utilizing the interference between the electromagnetic and weak neutral currents, the resulting asymmetry $A_{\rm PV}$ can provide independent combinations of helicity PDFs that could allow clean flavor separation at low $x$.

One contribution to the $A_{\rm PV}$ asymmetry comes from the lepton axial vector–hadron vector coupling, which is proportional to the $g_{1}^{\gamma Z}$ interference structure function, weighted by the weak axial vector electron charge $g_{A}^{e}=-\frac{1}{2}$. The other comes from the lepton vector–hadron axial vector coupling, given by the $g_{5}^{\gamma Z}$ structure function weighted by the weak vector electron charge, $g_{V}^{e}=-\frac{1}{2}(1-4\sin^{2}\theta_{W})$ Hobbs and Melnitchouk (2008); Zhao et al. (2017). The $g_{5}^{\gamma Z}$ structure function provides information on nonsinglet combinations $\Delta q^{-}\equiv\Delta q-\Delta\bar{q}$. However, since $|g_{V}^{e}|\ll 1$, and at small $x$ one has $\Delta q^{-}\ll\Delta q^{+}$ Kovchegov et al. (2017a), its contribution to $A_{\rm PV}$ is strongly suppressed. For three quark flavors, the PV asymmetry is then determined by the ratio $g_{1}^{\gamma Z}/F_{1}$, where in the DLA we have,

with $g_{V}^{q}=\pm\frac{1}{2}-2e_{q}\sin^{2}\theta_{W}$ the weak vector coupling to $u$- and $d$-type quarks, respectively. Since $\sin^{2}\theta_{W}\approx 1/4$, the $g_{1}^{\gamma Z}$ structure function is approximately given by $g_{1}^{\gamma Z}(x,Q^{2})\approx\frac{1}{9}\sum_{q}\Delta q^{+}(x,Q^{2})\equiv\frac{1}{9}\Delta\Sigma(x,Q^{2})$. With sufficient precision, the combination of $A_{\rm PV}$ and $A_{||}$ for the proton and neutron could enable an extraction of $\Delta u^{+}$, $\Delta d^{+}$, and $\Delta s^{+}$ separately.

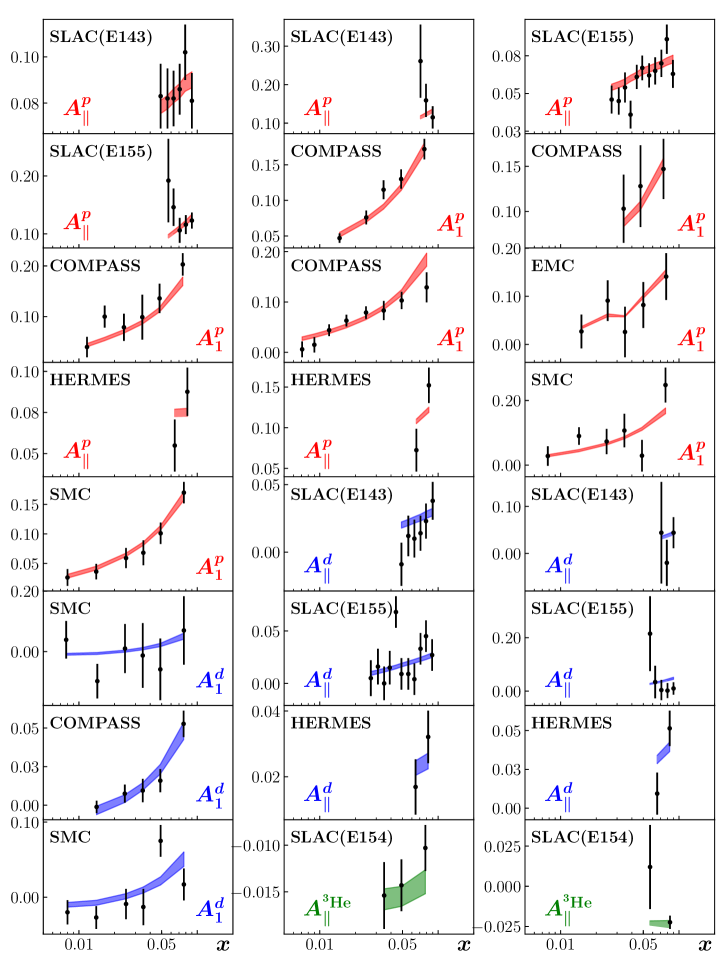
For our baseline analysis, we fit the existing world polarized DIS data on the longitudinal double-spin asymmetries for proton, deuteron, and ³He targets. We restrict the data to the kinematics relevant for this study: $x<0.1$ with $Q^{2}>m_{c}^{2}\approx 1.69$ GeV², and, to avoid the nucleon resonance region, $s>4$ GeV², where $s$ is the invariant mass squared of the final state hadrons. The data sets included are from the SLAC Anthony et al. (1996); Abe et al. (1997, 1998); Anthony et al. (1999, 2000), EMC Ashman et al. (1989), SMC Adeva et al. (1998, 1999), COMPASS Alekseev et al. (2010); Adolph et al. (2016, 2017), and HERMES Ackerstaff et al. (1997); Airapetian et al. (2007) experiments, giving a total number of points $N_{\rm pts}=122$ that survive the cuts. Note that the variable $y_{0}=\sqrt{\alpha_{s}N_{c}/2\pi}\ln(1/x_{0})$ that enters the evolution equations (7) has been fixed using $x_{0}=0.1$, consistent with the $x$ cut on the data.

As discussed above, these data alone are not sufficient to extract the individual PDFs $\Delta u^{+}$, $\Delta d^{+}$, and $\Delta s^{+}$. Instead, we can only constrain the linear combinations of $a_{q}$, $b_{q}$, and $c_{q}$ from Eq. (6) that enter into the proton $g_{1}^{p}$ and neutron $g_{1}^{n}$ structure functions (8). This gives effectively six free parameters (in addition to $x_{0}$ and $\Lambda$). That is, the initial conditions for the polarized dipole amplitudes associated with $g_{1}^{p}$ and $g_{1}^{n}$, respectively, read,

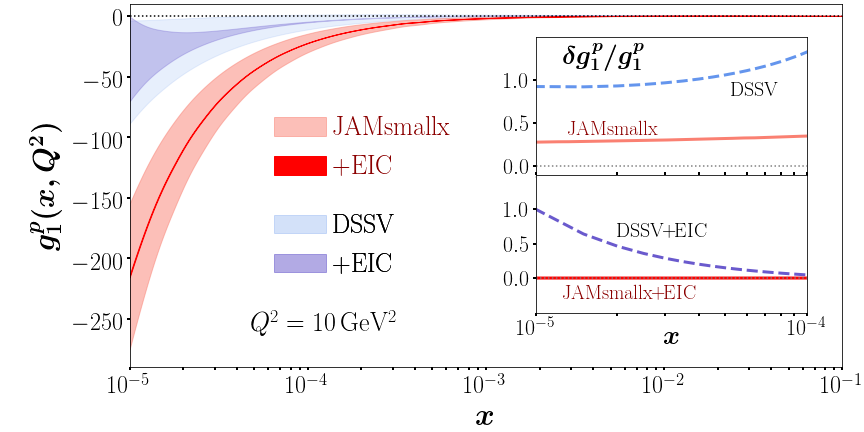
We determine these parameters using Bayesian inference within the JAM Monte Carlo framework Sato et al. (2020); Moffat et al. (2021) and find the following values: $a_{p}=-1.33\pm 0.30,b_{p}=0.49\pm 0.44,c_{p}=2.24\pm 0.16$, and $a_{n}=-2.47\pm 0.65,b_{n}=3.03\pm 1.01,c_{n}=0.30\pm 0.36$. The comparison between our fit (which we refer to as “JAMsmallx”) at 1$\sigma$ confidence level and the $x<0.1$ data on the proton, deuteron, and ³He double-spin asymmetries is shown in Fig. 2, with the associated $g_{1}^{p}$ structure function displayed in Fig. 3. We find a very good fit to the data, with $\chi^{2}/N_{\rm pts}=1.01$.

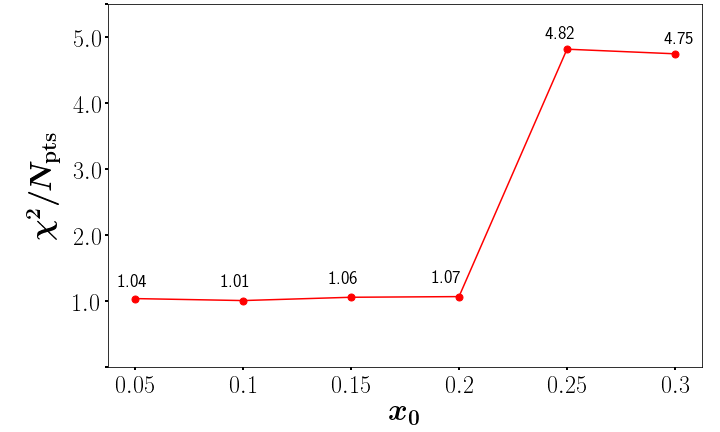
The precise value of $x_{0}$ at which KPS evolution sets in, corresponding to the cut $x<x_{0}$ applied to the data, is not known a priori. In Fig. 4, we show $\chi^{2}/N_{\rm pts}$ for $x_{0}=\{0.05,0.1,0.15,0.2,0.25,0.3\}$, where $N_{\rm pts}=\{62,122,187,229,342,508\}$, respectively. We note that for $x_{0}=0.2$, a few data points from SLAC E80/E130 Baum et al. (1983) survive the $x<x_{0}$ cut, and for $x_{0}=0.25$, also data from Jefferson Lab Prok et al. (2014); Parno et al. (2015); Guler et al. (2015); Fersch et al. (2017) survive that $x<x_{0}$ cut. However, the latter data points are not the sole reason for the increase in $\chi^{2}/N_{\rm pts}$ when $x_{0}\geq 0.25$. Certain data sets from COMPASS, HERMES, and SLAC that the fit describes well when only $x<0.2$ points are included also have their individual $\chi^{2}/N_{\rm pts}$ deteriorate once additional data with $x\geq 0.25$ enter the fit.

The fact that we find good fits up to $x_{0}=0.2$ introduces an additional systematic uncertainty into the behavior of $g_{1}^{p}$ down to $x=10^{-5}$ in Fig. 3. The error band in the plot only reflects the uncertainty from the experimental data and not this systematic uncertainty due to the choice of $x_{0}$. This ambiguity in $x_{0}$ indicates that current polarized DIS data have not been measured at small enough $x$ to identify the onset of small-$x$ helicity evolution. The data do, however, constrain the value of $x_{0}$ by imposing an upper bound. Our fit is not expected to work at larger values of $x_{0}$, where the small-$x$ formalism should become inapplicable. We find that the data can indeed discriminate this breakdown, with the fit quality $\chi^{2}/N_{\rm pts}$ degrading substantially for $x_{0}\sim 0.25$ due to the inability of the small-$x$ formalism to capture the steep $(1-x)^{n}$ ($n\approx 3$) large-$x$ falloff in the data. We note that the unpolarized evolution resummation parameter $\alpha_{s}\,\ln(1/x)$ at $x=0.01$ is approximately equal to the polarized evolution parameter $\alpha_{s}\,\ln^{2}(1/x)$ at $x=0.1$, suggesting comparable accuracy for our helicity evolution with $x_{0}=0.1$ and the unpolarized small-$x$ evolution Kuraev et al. (1977); Balitsky and Lipatov (1978); Balitsky (1996, 1999); Kovchegov (1999, 2000); Jalilian-Marian et al. (1998a, b); Weigert (2002); Iancu et al. (2001a, b); Ferreiro et al. (2002) with the commonly used value of $x_{0}=0.01$ Albacete et al. (2011, 2009); Kharzeev et al. (2003); Albacete et al. (2004); Kharzeev et al. (2004); Albacete et al. (2005).

We also comment that there exist other quantities with the leading small-$x$ contribution being double-logarithmic in $x$. An example would be the flavor non-singlet unpolarized PDFs, which, at small-$x$, are dominated by the QCD Reggeon exchange Kirschner and Lipatov (1983); Kirschner (1986, 1995a, 1995b); Griffiths and Ross (2000); Ermolaev et al. (1996); Bartels and Lublinsky (2003), whose intercept, when evaluated in the DLA for $\alpha_{s}\approx 0.3$, is very close to the phenomenological value of $\alpha_{R}\approx 0.5$ Donnachie and Landshoff (1992), as shown in Itakura et al. (2004). Moreover, the Reggeon contribution to baryon stopping in heavy ion collisions was also explored in Itakura et al. (2004) (see Fig. 9 there and the discussion around it). Surprisingly, no higher-order corrections to the DLA were needed in Itakura et al. (2004) in order to obtain a good agreement with the data. Therefore, it is possible that the KPS evolution, which is also double-logarithmic at leading order, may give an accurate prediction for the small-$x$ $g_{1}$ structure function already at DLA, as employed in this work.

A unique feature of our analysis is that KPS evolution predicts the small-$x$ behavior of helicity PDFs. This is in contrast to DGLAP evolution, where the $x$ dependence of the PDFs follows from ad hoc parametrizations at an input scale $Q_{0}$, with the behavior at small $x$ obtained by extrapolation. This distinction allows better controlled uncertainties in KPS evolution at small $x$, as Fig. 3 confirms. For the fits to existing data, the relative error $\delta g_{1}^{p}/g_{1}^{p}$ at small $x$ is $\sim 25\%$ for JAMsmallx and $\sim 100\%$ for the DSSV fit with standard $Q^{2}$ evolution de Florian et al. (2014); De Florian et al. (2019).

To estimate the impact of future EIC data on the $g_{1}$ structure function, we generate pseudodata for $A_{||}$ and $A_{\rm PV}$ for proton, deuteron, and ³He beams. The fit described in Sec. IV only constrains $g_{1}^{p}$ and $g_{1}^{n}$, whereas to generate pseudodata simultaneously for $A_{||}$ and $A_{\rm PV}$, one needs $\Delta u^{+}$, $\Delta d^{+}$, and $\Delta s^{+}$ individually. Therefore, we set $\Delta s^{+}=0$ and use isospin symmetry to invert Eq. (8) to determine the initial conditions for $\Delta u^{+}$ and $\Delta d^{+}$ from those we already extracted for $g_{1}^{p}$ and $g_{1}^{n}$, such that

with $G_{p}^{(0)}$ and $G_{n}^{(0)}$ taken from Eqs. (10) for the fit in Sec. IV. We use the initial conditions (11) to solve the evolution equations (7) for the polarized dipole amplitudes corresponding to individual flavors. Using Eq. (4), we obtain helicity PDFs which allow us to generate the central values of the EIC pseudodata for $A_{||}$ and $A_{\rm PV}$. For the proton, the pseudodata cover center-of-mass energies $\sqrt{S}=\{29,45,63,141\}$ GeV with integrated luminosity of 100 fb^-1, while for the deuteron and ³He beams the pseudodata span $\sqrt{S}=\{29,66,89\}$ GeV with 10 fb^-1 integrated luminosity. These are consistent with the EIC detector design of the Yellow Report, including $2\%$ point-to-point uncorrelated systematic uncertainties Abdul Khalek et al. (2021). After imposing the kinematic cuts discussed above, 487 data points survive for each of $A_{||}$ and $A_{\rm PV}$, along with the 122 data points from existing polarized DIS data, for a total of 1096 points used in this analysis.

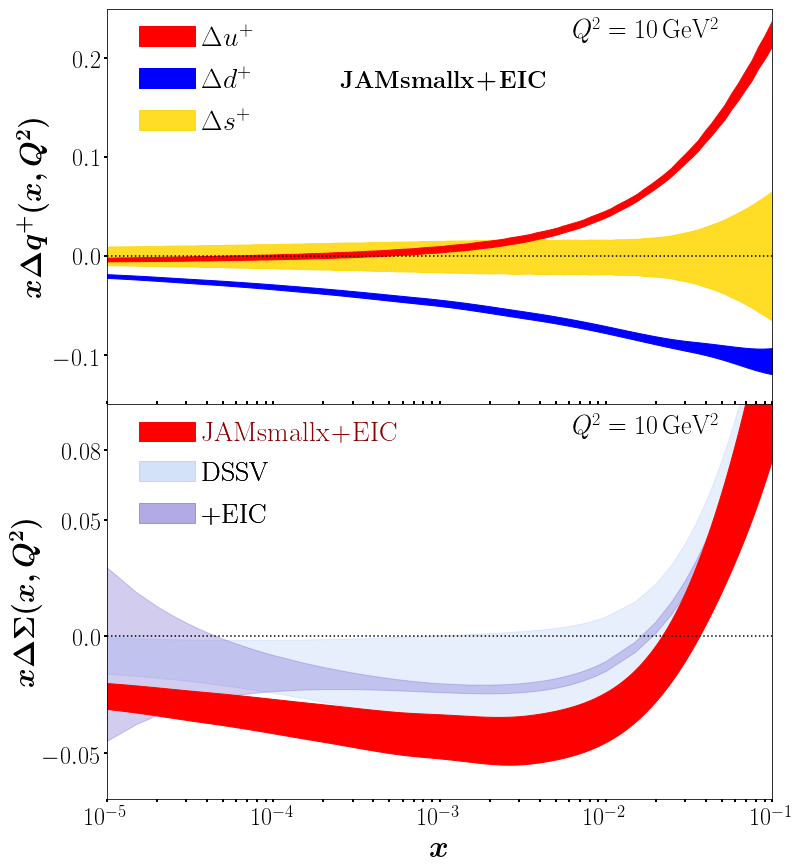
We now fit these pseudodata without making any assumptions on the helicity PDFs; in particular, we do not assume $\Delta s^{+}=0$ in the fit. The inclusion of $A_{\rm PV}$ allows us to extract the individual PDFs $\Delta u^{+}$, $\Delta d^{+}$, and $\Delta s^{+}$ using nine parameters ($a_{q}$, $b_{q}$, and $c_{q}$ (cf. Eq. (6)) for each quark flavor) in addition to our choices for $x_{0}$ and $\Lambda$.

The results for the extracted helicity PDFs, as well as for the flavor singlet sum $\Delta\Sigma(x,Q^{2})$, are shown in Fig. 5, and $g_{1}^{p}$ is given by the dark red band in Fig. 3. Clearly, the EIC pseudodata have a significant impact, reducing the relative uncertainty of $g_{1}^{p}$ to the sub-percent level. This precision will also allow for a more accurate determination of the starting point $x_{0}$ of KPS evolution. The improved control over the small-$x$ behavior with KPS evolution of the $g_{1}$ structure function and the helicity PDFs is evident in Figs. 3 and 5 when compared with the DSSV analysis de Florian et al. (2014); De Florian et al. (2019), which uses standard DGLAP evolution. Even after including EIC pseudodata, the relative error of the DSSV+EIC fit Borsa et al. (2020) for $g_{1}^{p}$ grows to $\sim 100\%$ when one enters the unmeasured region ($x\lesssim 10^{-4}$). The same trend occurs for $x\Delta\Sigma(x,Q^{2})$: the magnitude of the JAMsmallx+EIC uncertainty band stays relatively constant, while the DSSV+EIC error increases significantly at $x\lesssim 10^{-4}$. We emphasize that this is a consequence of DGLAP evolution not being able to prescribe the small-$x$ behavior of PDFs, whereas KPS evolution enables a genuine prediction at small $x$.

In this work, we have demonstrated for the first time that double-spin asymmetries in polarized DIS at $x<0.1$ can be successfully described using the KPS small-$x$ evolution equations. In the future, several extensions can be pursued, such as including $\alpha_{s}\,\ln(1/x)$ corrections to the DLA Kovchegov et al. (2021) and going beyond the large-$N_{c}$ limit employed here. The former will introduce saturation effects and may permit an extraction of $\Delta G$, while the latter may be studied either in the large-$N_{c}\,\&\,N_{f}$ limit Kovchegov et al. (2016); Kovchegov and Sievert (2019); Kovchegov and Tawabutr (2020) or by using functional methods Cougoulic and Kovchegov (2019). Our formalism can also be extended to SIDIS and $pp$ collisions in order to provide a more universal small-$x$ helicity phenomenology. The approach we have pioneered here will allow us to achieve well-controlled uncertainties as one extends into the unmeasured small-$x$ region (beyond what even the EIC can reach), a feature that ultimately will be crucial to understanding the partonic origin of the proton spin.

This work has been supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under Award Number DE-SC0004286 (DA and YK), No. DE-AC05-06OR23177 (WM and NS) under which Jefferson Science Associates, LLC, manages and operates Jefferson Lab, the National Science Foundation under Grant No. PHY-2011763 (DP), and within the framework of the TMD Topical Collaboration. The work of NS was supported by the DOE, Office of Science, Office of Nuclear Physics in the Early Career Program. DA and DP would like to thank C. Cocuzza and Y. Zhou for their tutorial on the JAM analysis code. We would also like to thank I. Borsa for providing the results of the analysis in Ref. Borsa et al. (2020).