First application of the dispersive optical model to (,) reaction analysis within the distorted-wave impulse approximation framework
Abstract
- Background
-
Both (,) and (,) reactions have been performed to study the proton single-particle character of nuclear states with its related spectroscopic factor. Recently, the dispersive optical model (DOM) was applied to the (,) analysis revealing that the traditional treatment of the single-particle overlap function, distorted waves, and nonlocality must be further improved to achieve quantitative nuclear spectroscopy.
- Purpose
-
We apply the DOM wave functions to the traditional (,) analysis and investigate the consistency of the DOM spectroscopic factor that describes the (,) cross section with the result of the (,) analysis. Additionally, we make a comparison with a phenomenological single-particle wave function and optical potential. Uncertainty arising from a choice of - interaction is also investigated.
- Method
-
We implement the DOM wave functions to the nonrelativistic distorted wave impulse approximation (DWIA) framework for (,) reactions.
- Results
-
DOM + DWIA analysis on 40Ca(,)39K data generates a proton spectroscopic factor of 0.560, which is meaningfully smaller than the DOM value of 0.71 shown to be consistent with the (,) analysis. Uncertainties arising from choices of single-particle wave function, optical potential, and - interaction do not explain this inconsistency.
- Conclusions
-
The inconsistency in the spectroscopic factor suggests there is urgent need for improving the description of - scattering in a nucleus and the resulting in-medium interaction with corresponding implications for the analysis of this reaction in inverse kinematics.
I Introduction
The independent particle picture provides an excellent first characterization of the structure of a nucleus. An important indicator of this picture is the spectroscopic factor for valence orbitals, which represents the removal probability for each nucleon orbital to a low-lying state of the system with one proton less. The nucleon knockout reaction has been one of the best tools to study this aspect of nuclei. The electron-induced proton knockout reaction, (,) [1, 2, 3, 4, 5, 6, 7, 8, 9], has been considered the cleanest spectroscopic method for decades. Despite some concerns about the uncertainties associated with proton-induced proton knockout reactions, (,) [10, 11, 12, 13, 14, 15, 16, 17], a recent review [16] established as an complementary spectroscopic tool to (,) with about 15% uncertainty for incident energy above 200 MeV.
As discussed in Ref. [16], the effect of nonlocality on the distorted waves and the bound-state wave function is considered to be a major source of the theoretical uncertainties in the description of the (,) reactions. Usually, the effect is phenomenologically taken into account by including the Perey factor [18]; the Darwin factor is used when an optical potential based on the Dirac phenomenology [19, 20, 21] is adopted. However, the validity of this phenomenological treatment of nonlocality has not been estimated quantitatively. Recently, a fully nonlocal dispersive optical model (DOM) has been developed [22, 23] extending the original work by Mahaux and Sartor [24]. The DOM describes the nucleon scattering potential and the binding potential that gives single-particle levels on the same footing, making use of a subtracted dispersion relation. The single-particle wave function (SPWF) and its spectroscopic factor as well as the distorted waves obtained by the present DOM framework were applied to the nonrelativistic distorted wave impulse approximation (DWIA) analysis of 40,48Ca(,)39,47K reactions [8, 9] without any further adjustment. It was concluded that an accurate treatment of the nonlocality as practised in the DOM is necessary to generate spectroscopic factors that automatically describe the (,) knockout cross sections after the DOM potential has been constrained by all available elastic scattering data (up to 200 MeV) and relevant ground-state information.
The finding in Refs. [8, 9] demonstrates the importance of the implementation of the DOM wave functions to the DWIA analysis of (,) processes in which three proton distorted waves are present. Therefore, the use of the DOM wave functions is expected to clarify the role of the effective interaction that is involved in the extraction of spectroscopic factors from (,) data. In this study, we report the first application of such a DWIA analysis with the DOM wave functions to 40Ca(,)39K data at 200 MeV [25].
The organization of this paper is as follows. In Sec. II, we briefly introduce the present DOM + DWIA framework. In Sec. III, a theoretical analysis of 40Ca(,)39K data and the consistency between DOM proton spectroscopic factors that automatically describe cross sections and those obtained from (,) analyses are discussed. We also compare the present framework with a conventional DWIA analysis employing a phenomenological SPWF and optical potentials. Finally, a summary is given in Sec. IV.
II Theoretical framework
II.1 Distorted wave impulse approximation
In the present study, the factorized form of the nonrelativistic DWIA with the spin degrees of freedom is employed. The transition matrix within the distorted wave impulse approximation framework is given by
| (1) |
The incident and two emitted protons are labeled as particle –, while the bound proton in the initial state is labeled as . is a distorted wave of particle having the asymptotic (local) third component () of its spin . The outgoing and incoming boundary conditions of the distorted waves are denoted by superscripts and , respectively. is the momentum (wavenumber) of the incident proton and is the mass ratio of the struck particle and the target, in this study. is the radial quantum number, and are the single-particle orbital angular momentum, total angular momentum, and third component of , respectively. is the SPWF normalized to unity. is the matrix element of the - effective interaction ,
| (2) |
where and are relative momenta of two protons in the initial and the final states, respectively. The factorization procedure of is explained using the local semiclassical approximation (LSCA) and the asymptotic momentum approximation (AMA) in the appendix. It should be noted that the factorized DWIA is often regarded as a result of the zero-range approximation but is finite-range interaction in the present study.
The triple differential cross section (TDX) with respect to the emitted proton energy and emission angles and is given as
| (3) |
with , , , being the spectroscopic factor, the Jacobian from the center-of-mass frame to the Laboratory frame, kinetic factor, and the relative velocity of the incident proton and the target, respectively. Quantities with superscript are evaluated in the laboratory frame while the others are in the center-of-mass frame. See Sec. 3.1 of Ref. [16] for details.
II.2 Dispersive optical model
The distorted waves and SPWF in Eq. (1) as well as the spectroscopic factor in Eq. (3) are calculated using the DOM. The nonlocal DOM uses both bound and scattering data to constrain the nucleon self-energy for a given nucleus. This self-energy is a complex and nonlocal potential that unites the nuclear structure and reaction domains [24, 22]. The DOM was originally developed by Mahaux and Sartor [24], employing local real and imaginary potentials connected through dispersion relations. However, only with the introduction of nonlocality can realistic self-energies be obtained [22, 23, 26, 27, 28]. The Dyson equation then determines the single-particle propagator, or Green’s function, from which bound-state and scattering observables can be deduced.
Using the DOM self-energy, a Schrödinger-like equation can be generated to calculate the SPWF in Eq. (1),
| (4) |
where and are arbitrary basis variables, correspond to the orbital and total angular momentum of the orbital, is the principle quantum number of the orbital, and is the kinetic-energy matrix element, including the centrifugal term [8]. These wave functions correspond to overlap functions
| (5) |
Such discrete solutions to Eq. (4) exist where there is no imaginary part of the self-energy, so near the Fermi energy. The normalization for these wave functions corresponds to the same spectroscopic factor of Eq. (3), which is given by [29]
| (6) |
where represents the quasihole state that solves Eq. (4). Note that because of the presence of imaginary parts of the self-energy at other energies, there is also strength located there, and thus the spectroscopic factor will be less than 1 and also less than the occupation probability. The DOM self-energies of 40Ca and 48Ca were used in Refs. [8, 30, 9] to reproduce 40CaK and 48CaK momentum distributions, respectively. The corresponding 40Ca spectroscopic factor of , which is consistent with 40CaK data, will now be used alongside the DOM SPWF and distorted waves to analyze the 40CaK knockout reaction.
III Results and discussion
In this section, we discuss extracted spectroscopic factors from the 40CaK reaction in comparison with the DOM result that is consistent with the 40CaK data. We also address uncertainties arising from the choice of the optical potential and the effective - interaction. The theoretical knockout cross section is calculated using the DWIA framework with the DOM SPWF and distorted waves. Results using phenomenological inputs are also discussed for comparison.
The spectroscopic factor of is extracted from the ratio of the theoretical cross section and the experimental data of the 40Ca(,)39K reaction at 197 MeV. The reaction kinematics is in a coplanar kinematics and the opening angles of the emitted protons are fixed at the same angle: , , and in the Madison convention [31]. The kinematics of the three particles is then uniquely determined once is given.
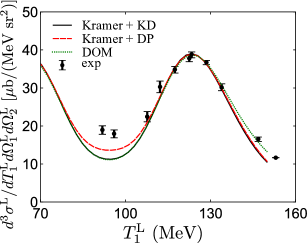
The DOM-DWIA result is compared with those of the phenomenological SPWF and the optical potential in Fig 1. For this comparison, the DOM-DWIA cross section is adjusted to the data and the DOM spectroscopic factor was not utilized. The phenomenological SPWF suggested by Kramer et al. [7], the Koning-Delaroche optical potential parameter set (KD) [32], and the Dirac phenomenology (DP) [19, 20, 21] are also considered. Calculated TDXs and the experimental data are shown in Fig. 1. Spectroscopic factors are therefore extracted from the ratio of the present calculations and the experimental data taken by the E258 experiment at RCNP [25] by minimizing
| (7) |
and are theoretical and experimental cross sections at data points, respectively, and is associated error of the experimental data. Obtained spectroscopic factors are summarized in Table 1. Following Ref. [16], only the data points around the peak, larger than b/(MeV sr2), are fitted to reduce the uncertainty.
| SPWF | Optical pot. | - int. | |
|---|---|---|---|
| Kramer | KD | FL | |
| Kramer | Dirac | FL | |
| DOM | DOM | FL | |
| DOM | DOM | Mel | |
| DOM | DOM | Mel (free) |
The spectroscopic factors obtained from the phenomenological (,) analysis are consistent with the phenomenological (,) analysis which gave [8]. On the other hand, the spectroscopic factor obtained using the DOM wave functions to reproduce the (,) cross section is in disagreement with the DOM-calculated [using Eq. (6)] value of . One of the reasons for this inconsistency may lie in a difference in the peripherality of the reaction probes, but it is not yet well understood.
The importance of having to deal with three distorted proton waves in the (,) reaction as compared to just one in the (,) case remains an issue. There is an uncertainty associated with the DOM distorted waves due to the experimental data points used in the DOM fit. Considering the strong correlation between the proton reaction cross section and the 48CaK cross section demonstrated in Ref. [9], we look to uncertainties in the experimental proton reaction cross section data points in energy regions corresponding to those of the distorted proton waves to get a rough estimate of the uncertainty associated with the DOM distorted waves. The proton reaction cross-section data points from Refs. [33, 34] suggest an uncertainty in the corresponding DOM distorted waves around 3%. Furthermore, due to the kinematics of the reaction, one of the proton energies is as low as 36 MeV. In the DOM analysis of 40CaK, the description of the experimental cross section for outgoing proton energies of 70 MeV, the lowest of the considered proton energies, is unsatisfactory [8]. This indicates that the impulse approximation may not be applicable at proton energies of 70 MeV and below. Since one of the outgoing proton energies in this 40CaK reaction is even less than 70 MeV, it is reasonable to expect some discrepancy in the 40CaK TDX. This discrepancy may be reduced when higher proton beam energies are considered but this implies that the DOM analysis has to be extended to higher energies.
As a further step to clarify this issue, we also investigated the uncertainty arising from a different choice of the - effective interactions. Three different types of the - effective interactions, the Franey-Love effective interaction (FL) [35], the Melbourne -matrix interaction at mean density (Mel) [36], and that at zero density (Mel free) were utilized. The mean density of the reaction is defined in Sec. 6.1. of Ref. [16]. The SPWF and the distorted waves from the DOM are adopted in this analysis. The choice of the - effective interaction only changes the magnitude of the TDX, keeping their shapes unchanged as shown in Fig. 2.

Extracted spectroscopic factors are summarized in Table. 1. An uncertainty of the choice of the - effective interaction results in – and does not explain the inconsistency between the DOM (,) result and the successful DOM description of the (,) cross section [8].
Validity of the finite-range treatment of and factorization approximation as well as the nonlocality correction and the relativistic correction in nonrelativistic DWIA have been discussed for decades [37, 38, 39, 40]. They make certain change in the cross section, but it is still not quantitatively conclusive. In Ref. [41], it is reported that TDX with AMA only differs 6% of that with LSCA in 120Sn(,)116Cd reaction case. Considering this situation, it is very important that we obtained good agreement in spectroscopic factors deduced from phenomenological (,) and (,) analyses before discussing DOM + DWIA analysis. It should be noted that the finite-range treatment of is more crucial in the relativistic DWIA framework, as pointed out in Ref. [42].
Ideally, the spectroscopic factor should not depend on the reactions to be adopted. As shown in Ref. [16], the spectroscopic factors for the SP levels near the Fermi energies of stable nuclei extracted from () reactions above 200 MeV are consistent with those from () with uncertainties ranging from 10% to 15%. It should be noted that the nonlocality correction to the SPWF and distorted waves are considered to be a primary source of the uncertainties of the spectroscopic factor [16]. As mentioned above, obtained with the DOM-DWIA analysis of the 40Ca() data at 200 MeV, in which the nonlocality is treated in a sophisticated manner, differs by at least 21% from the value used to reproduce data using the same SPWF and proton distorted wave calculated with the DOM. This implies the necessity of improving the treatment of - scattering inside a nucleus beyond the standard - or -matrix approach. One immediate concern is that present treatments of the effective interaction do not allow for energy transfer in the elementary process. Since in the () reaction a substantial excitation energy is involved, it implies that the mediators of the strong interaction, in particular the pion, must be allowed to propagate in the system and are certainly not static [43].
The ability of the DOM to provide both bound and scattering nucleon wave functions is opening a door to a new research opportunity for the nucleon-nucleon scattering process in many-body systems. This is of particular importance as the () reaction can be employed in inverse kinematics [44, 45]. There is therefore a clear need to pursue an improved description of the effective interaction in the medium which will also depend on the nucleon asymmetry that is studied in exotic systems.
IV Summary
The DOM SPWF and distorted waves have been applied to the DWIA analysis of (,) reaction for the first time. The proton spectroscopic factor of 40Ca was extracted from 40Ca(,)39K analysis with the present framework. The obtained spectroscopic factor is inconsistent with the DOM supplied one that reproduces 40Ca(,)39K data, . We tested several types of input for the - effective interaction: the Franey-Love interaction, the Melbourne -matrix at mean density, and that at zero density. In addition to using the DOM wave functions, Kramer’s SPWF and distorted waves obtained by the Koning-Delaroche and Dirac phenomenology optical potentials were considered. We conclude from the present analysis that the gap between the above-mentioned (,) and (,) spectroscopic factors cannot be explained by the uncertainties arising from these inputs. This result implies there is room for improving the treatment of the - binary scattering beyond the traditional - and -matrix approach combined with the impulse approximation.
ACKNOWLEDGMENTS
The authors thank T. Noro for providing them with updated experimental data before publication. This work was supported by JSPS KAKENHI Grant No. JP20K14475. This work was also supported by the U.S. National Science Foundation under Grant No. PHY-1912643. TRIUMF receives federal funding via a contribution agreement with the National Research Council of Canada.
*
Appendix A Factorization of matrix
In this appendix, the factorization procedure of the matrix is explained by means of the LSCA, following previous research [46, 47, 48, 49]. Equation (1) is originally an integral over two coordinates and :
| (8) |
, , , , and are defined as shown in Fig. 3. is a - effective interaction and is the exchange operator for the colliding two protons; thus, as usual, both the direct and exchange terms are considered. , , , , and are rewritten in terms of and as
| (9) | ||||
| (10) | ||||
| (11) |
The nucleon and the target mass number are 1 and , respectively.

The factorization of the - -matrix is done by considering three approximations as follows. First, for a short distance , the local semiclassical approximation (LSCA) [46, 47, 48, 49] can be applied to the distorted waves:
| (12) |
is the local momentum of the scattering particle at . Further approximation is made by replacing the local momentum with its asymptotic one . This is called the asymptotic momentum approximation (AMA) In Ref. [49], in which the AMA was referred to as LSCA-A, the AMA was shown to work with almost the same accuracy as of LSCA for a short propagation of the distorted waves of about 1.5 fm. It should be noted that for the factorization of the - transition matrix, the propagation range of about the half the range of needs to be approximated. According to the result of Ref. [49], both the LSCA and AMA are expected to be sufficiently accurate for this purpose. Furthermore, it is reported in Ref. [41] that the knockout cross section with AMA differs only from that with LSCA in 120Sn(,)116Cd reaction at 392 MeV.
Thus, the AMA (and the LSCA as well) can safely be applied to the distorted waves in Eq. (8), which reads
| (13) | ||||
| (14) | ||||
| (15) |
with () being the asymptotic momenta of particle . Note that in Eq. (A), we have also used the fact that is small. As for the single-particle wave function, the Fourier transformation is applied to factorize out the dependence
| (16) |
The second approximation is to assume the quasi-free - collision in the (,) reaction. Although the distorted waves are not eigenstates of momenta, the initial (final) - relative momentum () relevant to the (,) reaction are approximately given by the asymptotic momenta as
| (17) | ||||
| (18) |
It should be noted that this is a natural outcome of the use of the AMA mentioned above. Similarly, as the last approximation, the momentum conservation of the - collision is assumed:
| (19) |
Again, the appearance of the asymptotic momenta in Eq. (19) is due to the use of the AMA.
Under these approximations, once the (,) kinematics is fixed, and are uniquely determined by , and . Inserting Eqs. (A)–(16) into Eq. (8) and applying the inverse Fourier transform of , one obtains the factorized form of the matrix
| (20) |
This is equivalent to Eqs. (1) and (2), if one takes account of the spin degrees of freedom in the - matrix.
References
- Steenhoven et al. [1988] G. V. D. Steenhoven, H. Blok, E. Jans, M. D. Jong, L. Lapikás, E. Quint, and P. K. A. de Witt Huberts, Knockout of protons from 12C induced by the (,) reaction, Nuclear Physics A 480, 547 (1988).
- den Herder et al. [1988] J. den Herder, H. Blok, E. Jans, P. Keizer, L. Lapikás, E. Quint, G. van der Steenhoven, and P. K. A. de Witt Huberts, Single-particle properties of 51V and 90Zr studied with the (,) reaction, Nuclear Physics A 490, 507 (1988).
- Kramer et al. [1989] G. J. Kramer, H. P. Blok, J. F. J. Van Den Brand, H. J. Bulten, R. Ent, E. Jans, J. B. J. M. Lanen, L. Lapikás, H. Nann, E. N. M. Quint, G. Van Der Steenhoven, P. K. A. De Witt Huberts, and G. J. Wagner, Proton ground-state correlations in 40Ca studied with the reaction 40Ca(,)39K, Physics Letters B 227, 199 (1989).
- de Witt Huberts [1990] P. K. A. de Witt Huberts, Proton spectral functions and momentum distributions in nuclei from high-resolution (,) experiments, Journal of Physics G: Nuclear and Particle Physics 16, 507 (1990).
- Lapikás [1993] L. Lapikás, Quasi-elastic electron scattering off nuclei, Nuclear Physics A 553, 297 (1993).
- Pandharipande et al. [1997] V. R. Pandharipande, I. Sick, and P. K. A. de Witt Huberts, Independent particle motion and correlations in fermion systems, Rev. Mod. Phys. 69, 981 (1997).
- Kramer et al. [2001] G. Kramer, H. Blok, and L. Lapikás, A consistent analysis of (,) and (,3He) experiments, Nuclear Physics A 679, 267 (2001).
- Atkinson et al. [2018] M. C. Atkinson, H. P. Blok, L. Lapikás, R. J. Charity, and W. H. Dickhoff, Validity of the distorted-wave impulse-approximation description of data using only ingredients from a nonlocal dispersive optical model, Phys. Rev. C 98, 044627 (2018).
- Atkinson and Dickhoff [2019] M. C. Atkinson and W. H. Dickhoff, Investigating the link between proton reaction cross sections and the quenching of proton spectroscopic factors in 48Ca, Physics Letters B 798, 135027 (2019).
- Jacob and Maris [1966] G. Jacob and T. A. J. Maris, Quasi-free scattering and nuclear structure, Rev. Mod. Phys. 38, 121 (1966).
- Jacob and Maris [1973] G. Jacob and T. A. J. Maris, Quasi-free scattering and nuclear structure. ii., Rev. Mod. Phys. 45, 6 (1973).
- Chant and Roos [1977] N. S. Chant and P. G. Roos, Distorted-wave impulse-approximation calculations for quasifree cluster knockout reactions, Phys. Rev. C 15, 57 (1977).
- Chant and Roos [1983] N. S. Chant and P. G. Roos, Spin orbit effects in quasifree knockout reactions, Phys. Rev. C 27, 1060 (1983).
- Samanta et al. [1986] C. Samanta, N. S. Chant, P. G. Roos, A. Nadasen, J. Wesick, and A. A. Cowley, Tests of the factorized distorted wave impulse approximation for (,) reactions, Phys. Rev. C 34, 1610 (1986).
- Cowley et al. [1991] A. A. Cowley, J. J. Lawrie, G. C. Hillhouse, D. M. Whittal, S. V. Förtsch, J. V. Pilcher, F. D. Smit, and P. G. Roos, Quasifree knockout in 16O(,)15N at an incident energy of 151 MeV, Phys. Rev. C 44, 329 (1991).
- Wakasa et al. [2017] T. Wakasa, K. Ogata, and T. Noro, Proton-induced knockout reactions with polarized and unpolarized beams, Progress in Particle and Nuclear Physics 96, 32 (2017).
- Aumann et al. [2021] T. Aumann, C. Barbieri, D. Bazin, C. A. Bertulani, A. Bonaccorso, W. H. Dickhoff, A. Gade, M. Gómez-Ramos, B. P. Kay, A. M. Moro, T. Nakamura, A. Obertelli, K. Ogata, S. Paschalis, and T. Uesaka, Quenching of single-particle strength from direct reactions with stable and rare-isotope beams, Progress in Particle and Nuclear Physics 118, 103847 (2021).
- Perey and Buck [1962] F. Perey and B. Buck, A non-local potential model for the scattering of neutrons by nuclei, Nuclear Physics 32, 353 (1962).
- Hama et al. [1990] S. Hama, B. C. Clark, E. D. Cooper, H. S. Sherif, and R. L. Mercer, Global Dirac optical potentials for elastic proton scattering from heavy nuclei, Phys. Rev. C 41, 2737 (1990).
- Cooper et al. [1993] E. D. Cooper, S. Hama, B. C. Clark, and R. L. Mercer, Global Dirac phenomenology for proton-nucleus elastic scattering, Phys. Rev. C 47, 297 (1993).
- Cooper et al. [2009] E. D. Cooper, S. Hama, and B. C. Clark, Global dirac optical potential from helium to lead, Phys. Rev. C 80, 034605 (2009).
- Mahzoon et al. [2014] M. H. Mahzoon, R. J. Charity, W. H. Dickhoff, H. Dussan, and S. J. Waldecker, Forging the link between nuclear reactions and nuclear structure, Phys. Rev. Lett. 112, 162503 (2014).
- Dickhoff et al. [2017] W. H. Dickhoff, R. J. Charity, and M. H. Mahzoon, Novel applications of the dispersive optical model, J. of Phys. G: Nucl. and Part. Phys. 44, 033001 (2017).
- Mahaux and Sartor [1991] C. Mahaux and R. Sartor, Single-particle motion in nuclei, in Advances in Nuclear Physics, edited by J. W. Negele and E. Vogt (Springer US, Boston, MA, 1991) pp. 1–223.
- Noro [2020] T. Noro, private communication. (2020).
- Atkinson et al. [2020] M. C. Atkinson, M. H. Mahzoon, M. A. Keim, B. A. Bordelon, C. D. Pruitt, R. J. Charity, and W. H. Dickhoff, Dispersive optical model analysis of generating a neutron-skin prediction beyond the mean field, Phys. Rev. C 101, 044303 (2020).
- Pruitt et al. [2020a] C. D. Pruitt, R. J. Charity, L. G. Sobotka, M. C. Atkinson, and W. H. Dickhoff, Systematic matter and binding-energy distributions from a dispersive optical model analysis, Phys. Rev. Lett. 125, 102501 (2020a).
- Pruitt et al. [2020b] C. D. Pruitt, R. J. Charity, L. G. Sobotka, J. M. Elson, D. E. M. Hoff, K. W. Brown, M. C. Atkinson, W. H. Dickhoff, H. Y. Lee, M. Devlin, N. Fotiades, and S. Mosby, Isotopically resolved neutron total cross sections at intermediate energies, Phys. Rev. C 102, 034601 (2020b).
- Dickhoff and Van Neck [2008] W. H. Dickhoff and D. Van Neck, Many-Body Theory Exposed!, 2nd edition (World Scientific, Hackensack, NJ, 2008).
- Atkinson [2020] M. C. Atkinson, Developing Nucleon Self-Energies to Generate the Ingredients for the Description of Nuclear Reactions (Springer, 2020).
- Darden [1971] S. E. Darden, in Proceedings of the Third International Symposium on Polarization Phenomena in Nuclear Reactions, edited by H. Barschall and W. Haeberli (University of Wisconsin Press, Madison, 1971) p. 39.
- Koning and Delaroche [2003] A. Koning and J. Delaroche, Local and global nucleon optical models from 1 keV to 200 MeV, Nuclear Physics A 713, 231 (2003).
- Carlson et al. [1975] R. F. Carlson, A. J. Cox, J. R. Nimmo, N. E. Davison, S. A. Elbakr, J. L. Horton, A. Houdayer, A. M. Sourkes, W. T. H. van Oers, and D. J. Margaziotis, Proton total reaction cross sections for the doubly magic nuclei , , and in the energy range 20-50 MeV, Phys. Rev. C 12, 1167 (1975).
- Turner et al. [1964] J. Turner, B. Ridley, P. Cavanagh, G. Gard, and A. Hardacre, Optical model studies of proton scattering at 30 MeV: (ii). proton total reaction cross sections at 28.5±1.5 MeV, Nuclear Physics 58, 509 (1964).
- Franey and Love [1985] M. A. Franey and W. G. Love, Nucleon-nucleon -matrix interaction for scattering at intermediate energies, Phys. Rev. C 31, 488 (1985).
- Amos et al. [2000] K. Amos, P. J. Dortmans, H. V. von Geramb, S. Karataglidis, and J. Raynal, Nucleon-nucleus scattering: A microscopic nonrelativistic approach, Advances in Nuclear Physics 25, 276 (2000).
- Jackson [1967] D. F. Jackson, A di-proton model for the (,) reaction, Nuclear Physics A 90, 209 (1967).
- Austern [1978] N. Austern, Corrections to factorization in high-energy knockout reactions, Phys. Rev. Lett. 41, 1696 (1978).
- Jackson [1982] D. F. Jackson, Factorization corrections in the (,) reaction, Physica Scripta 25, 514 (1982).
- Kanayama et al. [1990] N. Kanayama, Y. Kudo, H. Tsunoda, and T. Wakasugi, Various Effects on the Nonrelativistic DWIA for (,) Reactions, Prog. Theor. Phys. 83, 540 (1990).
- Yoshida et al. [2016] K. Yoshida, K. Minomo, and K. Ogata, Investigating clustering on the surface of via the reaction, and the validity of the factorization approximation, Phys. Rev. C 94, 044604 (2016).
- Ikebata [1995] Y. Ikebata, (,) reaction in zero-range and finite-range relativistic distorted-wave impulse approximation, Phys. Rev. C 52, 890 (1995).
- Morris [2011] J. M. Morris, Ph.D. Thesis (Washington University in St. Louis, 2011).
- Atar et al. [2018] L. Atar, S. Paschalis, C. Barbieri, C. A. Bertulani, P. Díaz Fernández, M. Holl, M. A. Najafi, V. Panin, H. Alvarez-Pol, T. Aumann, V. Avdeichikov, S. Beceiro-Novo, D. Bemmerer, J. Benlliure, J. M. Boillos, K. Boretzky, M. J. G. Borge, M. Caamaño, C. Caesar, E. Casarejos, W. Catford, J. Cederkall, M. Chartier, L. Chulkov, D. Cortina-Gil, E. Cravo, R. Crespo, I. Dillmann, Z. Elekes, J. Enders, O. Ershova, A. Estrade, F. Farinon, L. M. Fraile, M. Freer, D. Galaviz Redondo, H. Geissel, R. Gernhäuser, P. Golubev, K. Göbel, J. Hagdahl, T. Heftrich, M. Heil, M. Heine, A. Heinz, A. Henriques, A. Hufnagel, A. Ignatov, H. T. Johansson, B. Jonson, J. Kahlbow, N. Kalantar-Nayestanaki, R. Kanungo, A. Kelic-Heil, A. Knyazev, T. Kröll, N. Kurz, M. Labiche, C. Langer, T. Le Bleis, R. Lemmon, S. Lindberg, J. Machado, J. Marganiec-Gała̧zka, A. Movsesyan, E. Nacher, E. Y. Nikolskii, T. Nilsson, C. Nociforo, A. Perea, M. Petri, S. Pietri, R. Plag, R. Reifarth, G. Ribeiro, C. Rigollet, D. M. Rossi, M. Röder, D. Savran, H. Scheit, H. Simon, O. Sorlin, I. Syndikus, J. T. Taylor, O. Tengblad, R. Thies, Y. Togano, M. Vandebrouck, P. Velho, V. Volkov, A. Wagner, F. Wamers, H. Weick, C. Wheldon, G. L. Wilson, J. S. Winfield, P. Woods, D. Yakorev, M. Zhukov, A. Zilges, and K. Zuber (B Collaboration), Quasifree (,) reactions on oxygen isotopes: Observation of isospin independence of the reduced single-particle strength, Phys. Rev. Lett. 120, 052501 (2018).
- Kawase et al. [2018] S. Kawase, T. Uesaka, T. L. Tang, D. Beaumel, M. Dozono, T. Fukunaga, T. Fujii, N. Fukuda, A. Galindo-Uribarri, S. Hwang, N. Inabe, T. Kawabata, T. Kawahara, W. Kim, K. Kisamori, M. Kobayashi, T. Kubo, Y. Kubota, K. Kusaka, C. Lee, Y. Maeda, H. Matsubara, S. Michimasa, H. Miya, T. Noro, Y. Nozawa, A. Obertelli, K. Ogata, S. Ota, E. Padilla-Rodal, S. Sakaguchi, H. Sakai, M. Sasano, S. Shimoura, S. Stepanyan, H. Suzuki, T. Suzuki, M. Takaki, H. Takeda, A. Tamii, H. Tokieda, T. Wakasa, T. Wakui, K. Yako, J. Yasuda, Y. Yanagisawa, R. Yokoyama, K. Yoshida, K. Yoshida, and J. Zenihiro, Exclusive quasi-free proton knockout from oxygen isotopes at intermediate energies, Prog. Theor. Exp. Phys. 2018, 021D01 (2018).
- Luo and Kawai [1991] Y. L. Luo and M. Kawai, Semiclassical distorted wave model of nucleon inelastic scattering to continuum, Phys. Rev. C 43, 2367 (1991).
- Watanabe et al. [1999] Y. Watanabe, R. Kuwata, S. Weili, M. Higashi, H. Shinohara, M. Kohno, K. Ogata, and M. Kawai, Semiclassical distorted wave model analysis of multistep direct (,) and (,) reactions to the continuum, Phys. Rev. C 59, 2136 (1999).
- Ogata et al. [2007] K. Ogata, G. C. Hillhouse, and B. I. S. van der Ventel, Quenching of the analyzing power for inclusive quasielastic () scattering, Phys. Rev. C 76, 021602(R) (2007).
- Minomo et al. [2010] K. Minomo, K. Ogata, M. Kohno, Y. R. Shimizu, and M. Yahiro, Brieva-Rook localization of the microscopic nucleon–nucleus potential, Journal of Physics G: Nuclear and Particle Physics 37, 085011 (2010).