First-Principles Study of Two-Dimensional Ferroelectrics Using Self-Consistent Hubbard Parameters

The DFT+$U$ Anisimov et al. (1991); Liechtenstein et al. (1995); Anisimov et al. (1997) method was formulated to correct the DFT energy by treating the electronic interactions between localized electrons in a separate way. The total energy is defined as

	$\displaystyle E_{{\rm DFT}+U}$	$\displaystyle=E_{\rm DFT}+E_{U}$		(1)
		$\displaystyle=E_{\rm DFT}+E_{\rm Hub}-E_{\rm dc}.$

$E_{\rm DFT}$ is the standard DFT energy obtained with an approximate XC functional such as LDA or PBE. $E_{\rm Hub}$ is the Hubbard correction term that considers the on-site Coulomb interactions between electrons in localized orbitals of interest. $E_{\rm dc}$ is the double-counting correction that removes the electronic correlations already included in $E_{\rm DFT}$. In the rotational-invariant formulation proposed by Dudarev et al.  Dudarev et al. (1998), the Hubbard energy $E_{\rm hub}$ as a function of occupation matrix $\textbf{n}^{I\sigma}$ of a localized basis set $\{|\phi_{m}^{I}\rangle\}$ attached to atom $I$ can be written as

$$E_{\rm hub}=\frac{U^{I}}{2}\sum_{\sigma,m,m^{\prime}}n_{mm}^{I\sigma}n_{m^{\prime}m^{\prime}}^{-I\sigma}+\frac{U^{I}-J^{I}}{2}\sum_{\sigma,m\neq m^{\prime}}n_{mm}^{I\sigma}n_{m^{\prime}m^{\prime}}^{I\sigma}$$

(2)

where $\sigma$ is the spin index, $m$ is the magnetic quantum number for a specific angular momentum $l$ ($-m\leq l\leq m$), and $U^{I}$ and $J^{I}$ are the spherically averaged on-site Coulomb repulsion and exchange interaction, respectively. For a periodic system, the occupation matrix $\textbf{n}^{I\sigma}$ is the projection of the occupied Kohn-Sham (KS) states $|\Psi_{\nu\textbf{k}}^{\sigma}\rangle$ to localized states $|\phi_{m}^{I}\rangle$:

$$n_{m_{1},m_{2}}^{I\sigma}=\sum_{\textbf{k}}^{N_{\textbf{k}}}\sum_{\nu}^{N_{\rm occ}}\langle\Psi_{\nu\textbf{k}}^{\sigma}|\phi_{m_{2}}^{I}\rangle\langle\phi_{m_{1}}^{I}|\Psi_{\nu\textbf{k}}^{\sigma}\rangle$$

(3)

where $N_{\textbf{k}}$ is the total number of k points in the first Brillouin zone and $\nu$ is the band index that runs over $N_{\rm occ}$ occupied bands. The total number of localized electrons $N^{I\sigma}$ is expressed as $N^{I\sigma}=\sum_{m}n_{mm}^{I\sigma}$. The Hubbard manifold on which the Hubbard Hamiltonian acts is defined through the projector $\hat{P}_{m_{1}m_{2}}^{I}=|\phi_{m_{2}}^{I}\rangle\langle\phi_{m_{1}}^{I}|$.

The double counting term is assumed as the Hubbard energy when the occupations of each localized orbital are either 1 or 0 ($(n_{mm}^{\sigma})^{2}=n_{mm}^{\sigma}$), leading to

$$E_{\rm dc}=\frac{U^{I}}{2}N^{I}(N^{I}-1)-\frac{J^{I}}{2}\sum_{\sigma}N^{I\sigma}(N^{I\sigma}-1)$$

(4)

with $N^{I}=\sum_{\sigma}N^{I\sigma}$. The Hubbard correction then has a simple form:

	$\displaystyle E_{U}$	$\displaystyle=E_{\rm Hub}-E_{\rm dc}$		(5)
		$\displaystyle=\sum_{I,\sigma}\frac{U^{I}_{\rm eff}}{2}\sum_{m,\sigma}\left\{n_{mm}^{I\sigma}-\sum_{m^{\prime}}n_{mm^{\prime}}^{I\sigma}n_{m^{\prime}m}^{I\sigma}\right\}$
		$\displaystyle=\sum_{I,\sigma}\frac{U^{I}_{\rm eff}}{2}\mathrm{Tr}[\textbf{n}^{I\sigma}(\textbf{1}-\textbf{n}^{I\sigma})]$

where $U_{\rm eff}^{I}\equiv U^{I}-J^{I}$ is the effective Hubbard interaction parameter. To unclutter the narrations, we will refer $U_{\rm eff}$ as $U$ and omit the spin index $\sigma$ in the following discussions unless explicitly stated otherwise.

The Hubbard correction depends strongly on the interaction parameter $U$. It is desirable to calculate $U$ in an internally consistent way. Here we outline the key steps in LR-cDFT for first-principles calculations of Hubbard $U$ Cococcioni and de Gironcoli (2005). In LR-cDFT, $U$ is interpreted as the correction needed to recover the piece-wise linear behavior of the the total energy with respect to the orbital occupation, and thus can be computed from the second-order derivative of the energy. The total energy as a function of the localized orbital occupation $q^{I}$ of Hubbard site $I$ is given by

$$E(\{q^{I}\})=\mathop{\min}_{\rho,\lambda^{I}}\left\{E_{\rm DFT}[\rho]+\sum_{I}\lambda^{I}(n^{I}-q^{I})\right\}$$

(6)

where $\rho$ is the (spin) charge density and $\lambda^{I}$ is the Lagrange multiplier employed to constrain the site occupation $n^{I}$ defined as the trace sum of the occupation matrix (Eq. 3). The physical interpretation of the Lagrange multiplier is to apply a perturbing potential of strength $\lambda^{I}$ to localized orbitals on site $I$. The Hubbard $U^{I}$ can then be computed as ${\partial^{2}E}/{\partial(q^{I})^{2}}$ via finite differences, a process requiring the evaluation of the total energy for a perturbed system with constrained $q^{I}$. In practice, it is more convenient to work with the Legendre transform of Eq. 6 which leads to a modified energy functional that depends on $\{\lambda^{I}\}$:

$$E(\{\lambda^{I}\})=\mathop{\min}_{\rho}\left\{E_{\rm DFT}[\rho]+\sum_{I}\lambda^{I}n^{I}\right\}$$

(7)

Then the total energy as a function of on-site occupations $n^{I}$ (computed using the $\rho$ that minimizes Eq. 7) is given via a Legendre transform,

$$\bar{E}(\{n^{I}\})=E(\{\lambda^{I}\})-\sum_{I}\lambda^{I}n^{I}$$

(8)

from which the first and second derivatives can be readily evaluated with

$$\frac{\partial\bar{E}}{\partial n^{I}}=-\lambda^{I}$$

(9)

$$\frac{\partial^{2}\bar{E}}{\partial(n^{I})\partial(n^{J})}=-\frac{\partial\lambda^{I}}{\partial n^{J}}.$$

(10)

Technically, the perturbed ground state $|\Psi_{\textbf{k}\nu}\rangle$ is obtained by solving following modified KS equation,

$$(\hat{H}+\lambda^{J}\hat{V}^{J}_{\rm pert})|\Psi_{\textbf{k}\nu}\rangle=\varepsilon_{\nu\textbf{k}}|\Psi_{\textbf{k}\nu}\rangle$$

(11)

where $\hat{H}$ is the unperturbed KS Hamiltonian and $\hat{V}^{J}_{\rm pert}$ is the perturbing potential operator which is the sum of projectors on localized orbitals associated with atom $J$, $\hat{V}^{J}_{\rm pert}=\sum_{m}\hat{P}_{mm}^{J}$. All the values of $n^{I}$ are then collected for the perturbed ground state; by varying $\lambda^{J}$, we can construct the response matrix $\chi_{IJ}=\partial n^{I}/\partial\lambda^{J}$, and the Hubbard $U$ is the inverse of the response matrix: $U^{I}=-\chi_{II}^{-1}$, as derived from Eq. 10. However, as pointed out by Cococcioni et al. , the complete definition of Hubbard $U$ is

$$U^{I}=(\chi_{0}^{-1}-\chi^{-1})_{II}$$

(12)

where $\chi_{0}$ is the response matrix of independent electron systems, resulting from the rehybridization of localized orbitals due to perturbations. In realistic DFT calculations, $\chi_{0}$ is evaluated with $n^{I}$ at the first iteration of the perturbed runs and $\chi$ is evaluated at self-consistency. It is noted that the off-diagonal elements $\chi_{IJ}^{-1}$ represent inter-site interactions $V$ in the extended Hubbard model Jr and Cococcioni (2010). In practical calculations of periodic systems, a large supercell is often needed to make sure the localized perturbation not interacting with its images.

Recently, Timrov et al. reformulated LR-cDFT within the framework of DFPT Timrov et al. (2018). The main steps are (1) substitute finite differences with continuous derivatives; (2) recast perturbations in supercells as a sum of monochromatic (wave-vector-specific) perturbations in a primitive cell in reciprocal space. The response matrix $\chi_{IJ}$ obtained by substituting Eq. 3 into Eq. 10 reads:

	$\displaystyle\chi_{IJ}$	$\displaystyle=\sum_{m}\frac{\partial n_{m_{1}m_{2}}^{I}}{\partial\lambda^{J}}$		(13)
		$\displaystyle=\sum_{m}\sum_{\textbf{k}}^{N_{\textbf{k}}}\sum_{\nu}^{N_{occ}}\left[\langle\Psi_{\nu\textbf{k}}|\hat{P}_{m_{2}m_{1}}|\frac{\partial\Psi_{\nu\textbf{k}}}{\partial\lambda^{J}}\rangle\right.$
		$\displaystyle\left.+\langle\frac{\partial\Psi_{\nu\textbf{k}}}{\partial\lambda^{J}}|\hat{P}_{m_{2}m_{1}}|\Psi_{\nu\textbf{k}}\rangle\right]$

where the LR KS wavefunction $|\frac{\partial\Psi_{\nu\textbf{k}}}{\partial\lambda^{J}}\rangle$ can be computed using the ordinary first-order perturbation approach (see details in ref. Timrov et al. (2018)). This real-space implementation of $\chi_{IJ}$ within DFPT is essentially the same as that in LR-cDFT, leading to no computational advantage as localized perturbations still have to be applied to each unique Hubbard atom one at a time in the supercell.

The second step is to recast perturbations in a supercell of size $L_{1}\times L_{2}\times L_{3}$ as sums over monochromatic perturbations in a primitive unit cell on a grid of q points defined by

$$\textbf{q}_{klm}=\frac{\bar{k}}{L_{1}}\textbf{b}_{1}+\frac{\bar{l}}{L_{3}}\textbf{b}_{2}+\frac{\bar{m}}{L_{3}}\textbf{b}_{3}$$

(14)

where $\{\textbf{b}_{1},\textbf{b}_{2},\textbf{b}_{3}\}$ are the reciprocal lattice vectors of the primitive unit cell, and $\bar{k}$, $\bar{l}$, $\bar{m}$ are integer numbers with $0\leq\bar{k}<L_{1},0\leq\bar{l}<L_{2},0\leq\bar{m}<L_{3}$. The atomic index $I$ in a supercell now corresponds to two indices $(s,l)$ which means the $s$th atom in the $l$th primitive unit cell. Similarly, $J$ is replaced with $(s^{\prime},l^{\prime})$. The response matrix expressed in the reciprocal space has following form:

$$\chi_{sl,s^{\prime}l^{\prime}}=\sum_{m}\frac{\partial n_{m_{1}m_{2}}^{sl}}{\partial\lambda^{s^{\prime}l^{\prime}}}=\sum_{m}\frac{1}{N_{\textbf{q}}}\sum_{\textbf{q}}^{N_{\textbf{q}}}e^{i\textbf{q}(\textbf{R}_{l}-\textbf{R}_{l^{\prime}})}\Delta_{\textbf{q}}^{s^{\prime}}\textbf{n}_{m_{1}m_{2}}^{s}$$

(15)

where $N_{\textbf{q}}$ is the number of q points, $\textbf{R}_{l}$ is the Bravais lattice vector of the $l$th primitive unit cell, and $\Delta_{\textbf{q}}^{s^{\prime}}\textbf{n}_{m_{1}m_{2}}^{s}$ is the lattice-periodic response of the localized orbital occupation to a monochromatic perturbation of wave vector q. Detailed implementations of $\Delta_{\textbf{q}}^{s^{\prime}}\textbf{n}_{m_{1}m_{2}}^{s}$ can be found in ref. Timrov et al. (2018). Compared to LR-cDFT, the DFPT approach is computationally cheaper by removing the need of supercell calculations, and has better numerical stability and convergence.

Agapito et al. introduced an efficient approach to calculate the $U$ and $J$ values self-consistently Agapito et al. (2015). In ACBN0, electron-repulsion integrals are efficiently evaluated using pseudo-atomic orbitals (PAO) expressed as a linear combination of three Gaussian-type orbitals (3G). The KS orbitals are projected onto the PAO-3G basis set using a noniterative scheme by filtering out Bloch states with high-kinetic-energy components Agapito et al. (2013). This then allows the constructions of real-space density matrices and occupation numbers needed to compute the the Hartree-Fock energy associated with the chosen Hubbard manifold $\{m\}$ given by

	$\displaystyle E_{\rm HF}^{I\{m\}}$	$\displaystyle=\frac{1}{2}\sum_{\{m\}}\sum_{\alpha,\beta}\bar{P}_{mm^{\prime}}^{I\alpha}\bar{P}_{m^{\prime\prime}m^{\prime\prime\prime}}^{I\beta}(mm^{\prime}|m^{\prime\prime}m^{\prime\prime\prime})$		(16)
		$\displaystyle-\frac{1}{2}\sum_{\{m\}}\sum_{\alpha}\bar{P}_{mm^{\prime}}^{I\alpha}\bar{P}_{m^{\prime\prime}m^{\prime\prime\prime}}^{I\alpha}(mm^{\prime\prime\prime}|m^{\prime\prime}m^{\prime})$

where $\bar{P}_{mm^{\prime}}^{I\sigma}$ ($\sigma={\alpha,\beta}$) is the renormalized density matrices

$$\bar{P}_{mm^{\prime}}^{I\sigma}=\sum_{\textbf{k}}^{N_{\textbf{k}}}\sum_{\nu}^{N_{\rm occ}}\bar{N}_{\Psi_{\nu\textbf{k}}}^{I\sigma}\langle\Psi_{\nu\textbf{k}}^{\sigma}|\phi_{m}^{I}\rangle\langle\phi_{m^{\prime}}^{I}|\Psi_{\nu\textbf{k}}^{\sigma}\rangle$$

(17)

with $\bar{N}_{\Psi_{\nu\textbf{k}}}^{I\sigma}$ being the renormalized occupations

$$\bar{N}_{\Psi_{\nu\textbf{k}}}^{I\sigma}=\sum_{\{I\}}\sum_{m}\langle\Psi_{\nu\textbf{k}}^{\sigma}|\phi_{m}^{I}\rangle\langle\phi_{m}^{I}|\Psi_{\nu\textbf{k}}^{\sigma}\rangle.$$

(18)

Following the treatment introduced by Mosey et al. Mosey and Carter (2007); Mosey et al. (2008), the two sums in Eq. 18 run over all atomic orbitals of the system that are attached to atoms of the same type as Hubbard site $I$ (referred to as $\{\bar{m}\}$ in Ref. Agapito et al. (2013)). The introduction of renormalized occupations into the density matrices accounts for the effects of screening. Note that $0\leq\bar{N}_{\Psi_{\nu\textbf{k}}}^{I\sigma}\leq 1$: in the limit of $\bar{N}_{\Psi_{\nu\textbf{k}}}^{I\sigma}=1$, Eq. 16 is the exact HF energy, whereas for $\bar{N}_{\Psi_{\nu\textbf{k}}}^{I\sigma}=0$, the DFT energy is recovered without Hubbard corrections as it should be for a fully delocalized Bloch state. The comparison of Eq. 16 and Eq. 5 leads to density functionals of $U$ and $J$ Agapito et al. (2013); Tancogne-Dejean et al. (2017):

$$U=\frac{\sum_{\{m\}}\sum_{\alpha\beta}\bar{P}_{mm^{\prime}}^{\alpha}\bar{P}_{m^{\prime\prime}m^{\prime\prime\prime}}^{\beta}(mm^{\prime}|m^{\prime\prime}m^{\prime\prime\prime})}{\sum_{m\neq m^{\prime}}\sum_{\alpha}n_{mm}^{\alpha}n_{m^{\prime}m^{\prime}}^{\alpha}+\sum_{\{m\}}\sum_{\alpha}n_{mm}^{\alpha}n_{m^{\prime}m^{\prime}}^{-\alpha}}$$

(19)

$$J=\frac{\sum_{\{m\}}\sum_{\alpha}\bar{P}_{mm^{\prime}}^{\alpha}\bar{P}_{m^{\prime\prime}m^{\prime\prime\prime}}^{\alpha}(mm^{\prime\prime\prime}|m^{\prime\prime}m^{\prime})}{\sum_{m\neq m^{\prime}}\sum_{\alpha}n_{mm}^{\alpha}n_{m^{\prime}m^{\prime}}^{\alpha}}$$

(20)

with the atomic index $I$ omitted.

In the extended Hubbard model or DFT+$U$+$V$ approach, the inter-site Hubbard parameter $V$ represents the strength of Coulomb interactions between neighboring Hubbard sites. Note that in Eq. 2, the Hartree integrals $U^{I}$ is expressed as $U=\left\langle\phi_{m}\phi_{m^{\prime}}\left|V\right|\phi_{m}\phi_{m^{\prime}}\right\rangle$. Similarly, the inter-site interaction between atom $I$ and atom $J$ can be written as $V^{IJ}=\left\langle\phi_{i}^{I}\phi_{j}^{J}\left|V\right|\phi_{i}^{I}\phi_{j}^{J}\right\rangle$, where $i$ and $j$ are corresponding state indexes. The Hubbard energy in DFT+$U$+$V$ is derived as

$$E_{\mathrm{Hub}}=\sum_{I}\frac{U^{I}}{2}\left[\left(n^{I}\right)^{2}-\sum_{\sigma}\operatorname{Tr}\left[\left(\mathbf{n}^{II\sigma}\right)^{2}\right]\right]\\ +\sum_{I,J}\frac{V^{IJ}}{2}\left[n^{I}n^{J}-\sum_{\sigma}\mathrm{Tr}\left(\mathbf{n}^{IJ\sigma}\mathbf{n}^{JI\sigma}\right)\right]$$

(21)

The double-counting term including inter-site interactions is

$$E_{\mathrm{dc}}=\sum_{I}\frac{U^{I}}{2}n^{I}\left(n^{I}-1\right)+\sum_{I,J}\frac{V^{IJ}}{2}n^{I}n^{J}$$

(22)

Finally, we obtain the DFT+$U$+$V$ correction energy by substracting Eq. 22 from Eq. 21 Campo Jr and Cococcioni (2010):

$\displaystyle E_{UV}$

$\displaystyle=E_{\mathrm{Hub}}-E_{\mathrm{dc}}$

$\displaystyle=\sum_{I,\sigma}\frac{U^{I}}{2}\mathrm{Tr}\left[\mathbf{n}^{II\sigma}\left(\mathbf{1}-\mathbf{n}^{II\sigma}\right)\right]-\sum_{I,J,\sigma}\frac{V^{IJ}}{2}\mathrm{Tr}\left[\mathbf{n}^{IJ\sigma}\mathbf{n}^{JI\sigma}\right]$

(23)

The inter-site Hubbard integral shares the same Coulomb interaction of $V$ with the on-site one but deals with its expectation value between orbitals at different positions unlike the on-site one for the same site. Thus, for the same orbitals belong to different positions, the values of $V^{IJ}$ should be proportional to $U^{I}$.

Here we mostly follow the procedure of extended ACBN0 (eACBN0) developed by Lee et al. that enables self-consistent calculations of both $U$ and $V$ Lee and Son (2019). In eACBN0, the renormalized occupation number for the pair of $I$ and $J$ is defined as

$$\bar{N}_{\Psi_{\nu\textbf{k}}}^{IJ\sigma}=\sum_{\{I,J\}}\sum_{i,j}\left[\langle\Psi_{\nu\textbf{k}}^{\sigma}|\phi_{i}^{I}\rangle\langle\phi_{i}^{I}|\Psi_{\nu\textbf{k}}^{\sigma}\rangle+\langle\Psi_{\nu\textbf{k}}^{\sigma}|\phi_{j}^{J}\rangle\langle\phi_{j}^{J}|\Psi_{\nu\textbf{k}}^{\sigma}\rangle\right].$$

(24)

In close analogy to ACBN0, the renormalized density matrix for the pair is given by

$$\bar{P}_{ij}^{IJ\sigma}=\sum_{\textbf{k}}^{N_{\textbf{k}}}\sum_{\nu}^{N_{\rm occ}}\bar{N}_{\Psi_{\nu\textbf{k}}}^{IJ\sigma}\langle\Psi_{\nu\textbf{k}}^{\sigma}|\phi_{i}^{I}\rangle\langle\phi_{j}^{J}|\Psi_{\nu\textbf{k}}^{\sigma}\rangle.$$

(25)

After expressing the inter-site HF energy with renormalized density matrices and occupations for the pair, one can obtain a density functional for $V^{IJ}$,

$$V^{IJ}=\frac{\sum_{ijkl}\sum_{\alpha\beta}\left[\bar{P}_{ik}^{II\alpha}\bar{P}_{jl}^{JJ\beta}-\delta_{\alpha\beta}\bar{P}_{il}^{IJ\alpha}\bar{P}_{jk}^{JI\beta}\right](ij|kl)}{\sum_{\alpha\beta}\sum_{ij}\left[n_{ii}^{II\alpha}n_{jj}^{JJ\beta}-\delta_{\alpha\beta}n_{ij}^{IJ\alpha}n_{ji}^{JI\beta}\right]}$$

(26)

where $n_{ij}^{IJ\sigma}$ is the generalized occupation matrix defined as

$$n_{ij}^{IJ\sigma}=\sum_{\textbf{k}}^{N_{\textbf{k}}}\sum_{\nu}^{N_{\rm occ}}\langle\Psi_{\nu\textbf{k}}^{\sigma}|\phi_{i}^{I}\rangle\langle\phi_{j}^{J}|\Psi_{\nu\textbf{k}}^{\sigma}\rangle$$

(27)

For eACBN0 computations, we use the onsite Hubbard interaction as $U_{\textrm{eff}}\equiv U-J$ where $U$ and $J$ are given by Eq. 19 and Eq. 20, respectively, and the inter-site one by Eq. 26.

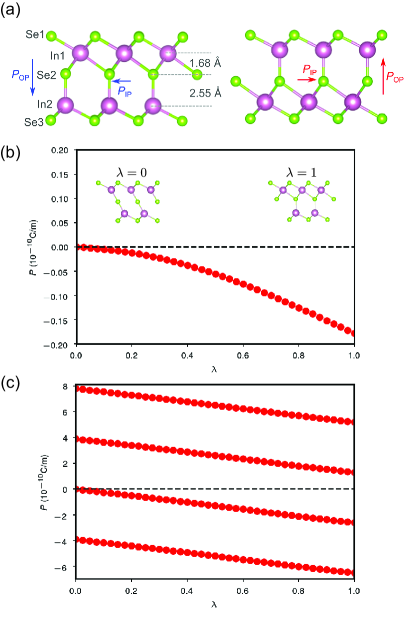
We first focus on the electronic structure of 2D $\alpha$-In₂Se₃ given that its room-temperature ferroelectricty has been confirmed experimentally. The 2D $\alpha$-In₂Se₃ is a covalently-bonded quintuple layer stacked in the sequence of Se-In-Se-In-Se with each layer containing only one type of atom arranged in a triangular lattice. Our optimized IP lattice constant with PBE is 4.10 Å, and the band gap is 0.80 eV, in agreement with previous DFT results Ding et al. (2017); Tiwari et al. (2020). The structural origin of ferroelectricity in $\alpha$-In₂Se₃ lies at the displacement of the central Se layer with respect to the top and bottom In-Se layers, which breaks the centrosymmetry along both OP and IP directions (Fig. 1). We calculate the polarization with the Berry-phase approach by tracking the change in Berry phase during a structural transformation process in which a non-polar structure is changed adiabatically to a polar structure (Fig. 1b-c). The 2D polarization is defined as $P=D/S_{\rm IP}$, where $D$ is the dipole moment and $S_{\rm IP}$ is the in-plane area of a 2D unit cell. It is noted that direction of in-plane polarization was controversial in previous studies Ding et al. (2017); Tiwari et al. (2020); Liu and Pantelides (2019). Our berry-phase calculations unambiguously determine the direction of $P_{\rm IP}$ as shown in Fig. 1a. The values of $P_{\rm IP}$ and $P_{\rm OP}$ are 0.26 nC/m and 0.018 nC/m, respectively.

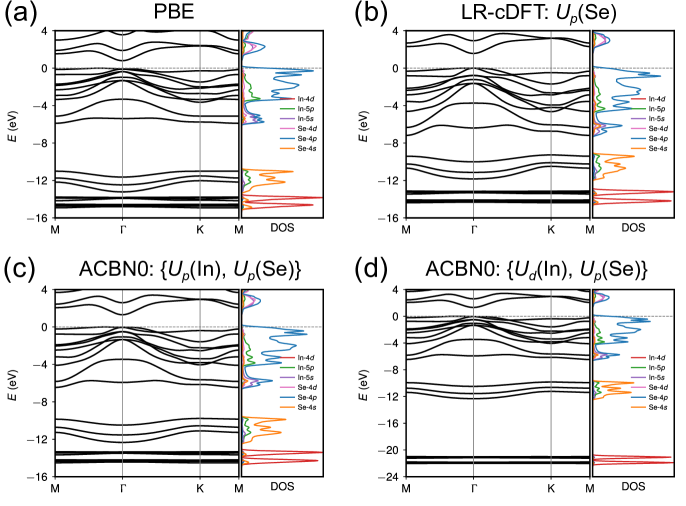
The projected density of states (PDOS) obtained with PBE (Fig. 2a) reveals that the valence states near the Fermi level ($E_{F}$) are predominantly consisted of In-$5p$ and Se-$4p$ states and the conduction states are mostly of Se-$4d$, Se-$4p$, and In-$5s$ characters. The low-dispersion deep levels between $-16$ to $-10$ eV are from Se-4$s$ and semi-core In-$4d$ states. We note here that such electronic structure is very different from those of conventional ferroelectrics such as PbTiO₃ where the states near $E_{F}$ are of Ti-3$d$ and O-2$p$ characters. It is well established that the emergence of ferroelectricity in perovskites is due to a delicate balance between the long-range Coulomb interactions (favoring the break of inversion symmetry) and the short-range repulsions (favoring the non-polar high-symmetry phase), and the $p$-$d$ hybridization between transition metal and oxygen atoms weakens the short-range repulsions thus responsible for the ferroelectric distortions Cohen (1992). It is evident that $\alpha$-In₂Se₃ with mostly $p$-$p$ hybridization does not fit into this picture, hinting at a different mechanism for ferroelectricity at reduced dimensions.

The DFT+$U$ method has the flexibility to choose the Hubbard manifold, namely the localized orbitals on which the Hubbard Hamiltonian will act. It is more common to apply $U$ corrections to open $d$ or $f$-electron shells. However, previous investigations with ACBN0 demonstrated the importance of introducing on-site repulsions to electrons on $p$-states and closed-shell $d$-states (e.g., O-2$p$ and Zn-3$d$ in ZnO Agapito et al. (2015)) as well. To serve as a complete test, we investigate following two cases: $U$ applied to Se-$4p$ and In-$4d$ states denoted as $\{U_{p}({\rm Se}),U_{d}({\rm In})\}$, and $U$ applied to Se-$4p$ and In-$5p$ states denoted as $\{U_{p}({\rm Se}),U_{p}({\rm In})\}$. The $U$ parameters are computed using LR-cRT, DFPT, ACBN0, and eACBN0, respectively. It is noted that the break of inversion symmetry along the OP direction makes all five atoms unique Hubbard sites.

Table 1 reports the $U$ parameters estimated with different first-principles schemes and the corresponding band gaps ($E_{g}$). The LR-cRT method has been widely used in the literature because of its computational simplicity, however, its application to fully occupied localized orbitals is more problematic due to the small linear response to perturbations Lee and Kim (2012). This is the case for In-$4d$ which has a shell filling of $d^{10}$: the single-shot LR-cRT calculations using a unit cell and a $2\times 2\times 1$ supercell both yield unphysically large $U$ values (thus omitted in Table 1). In comparison, DFPT and ACBN0 are capable of determining $U_{d}$(In) with comparable magnitudes. The high values of $U_{d}$(In) ($\approx 13$–$15$ eV) are unsurprising given that the magnitude of $U$ is proportional to the occupancy of the localized orbital; large $U$ values were previously reported for $d^{10}$ transition metals such as Zn²⁺ ($U_{d}=12.8$ eV) in ZnO Agapito et al. (2015). In the case of $U_{p}$(Se), the values obtained with the LR method depend on the size of supercell, i.e., $U_{p}$(Se1) changes from 7.83 eV in a unit cell to 5.32 eV in a $2\times 2\times 1$ supercell. The LR values are significantly higher than those obtained with self-consistent schemes ($U_{p}=3$–$4$ eV). In a recent study of LiFePO₄, it was also observed that the single-short LR value of $U$ for Fe-3$d$ is $\approx 7$ eV, much higher than the DFPT value of $\approx 5$ eV Cococcioni and Marzari (2019). The Hubbard $U$ parameters for In-$5p$ states estimated with different methods are comparable, and they are all small values which are expected from the $5p^{0}$ configuration of In³⁺ if In₂Se₃ is fully ionic. It is noted that different Se (In) atoms acquire different values of $U_{p}$ ($U_{d}$) despite being of the same species in the same material, which is the consequence of the OP polarization breaking inversion symmetry. This confirms Hubbard interactions are sensitive to the fine details of local atomic environments, and should not be considered as transferable/tunable parameters.

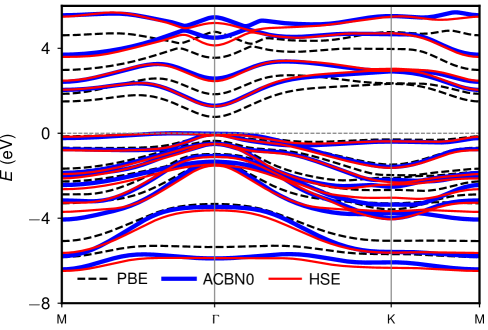
The band gaps computed using self-consistent Hubbard parameters ($E_{g}=$ 1.34 and 1.32 eV for DFPT and ACBN0, respectively) all improve upon the PBE value (0.80 eV), agreeing well with the HSE06 result (1.48 eV). We find that the band gap of $\alpha$-In₂Se₃ is insensitive to Hubbard corrections applied to In-$4d$ states but correlates positively with $U_{p}$(Se). As shown in Fig. 2d, the effect of a high value of $U_{d}$(In) is to downshift the deep-lying flat $4d$ bands that are already disentangled from the $4p$ states of Se near the Fermi level at the PBE level (Fig. 2a). Therefore, the band gap does not dependent on $U_{d}$(In). The improvement of band gap prediction with ACBN0 mainly comes from the on-site Coulomb interactions on Se. This is different from ZnO where a large $U$ correction to Zn-$3d$ is needed to reduce the $p$-$d$ repulsion between the low-lying Zn-$3d$ bands and the O-$2p$ bands that dominate the valance band edge Agapito et al. (2015). The high value of $U_{p}$(Se) from LR-cDFT leads to a larger band gap. The comparison of the band structures of PBE, ACBN0, and HSE06 is shown in Fig. 3. We find that ACBN0 has almost the same band dispersion as the hybrid functional HSE06 for states over a broad energy range from $-8$ to $4$ eV.

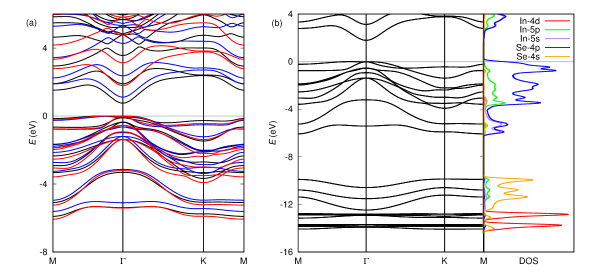
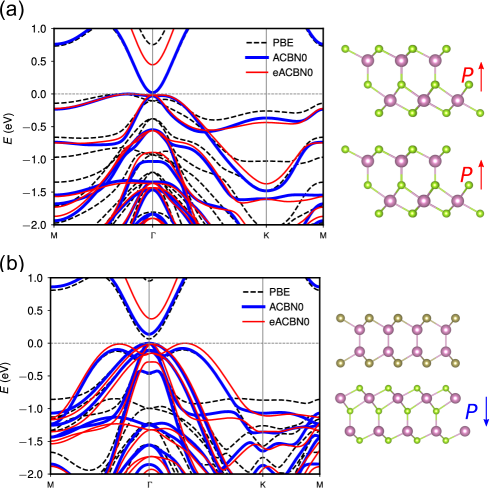
We further perform DFT+$U$+$V$ computations using the eACBN0 method to study the role of inter-site interactions $V$ in improving the band gap of $\alpha$-In₂Se₃. We obtain a band gap of 1.79 eV that is larger than those from DFT+$U$ and HSE06. This trend is consistent with a recent study on low-dimensional materials (e.g., 2D black phosphorous) Lee and Son (2019). Considering that HSE06 may not capture the rapid variation of Coulomb screening in low-dimensional materials Jain et al. (2011), the inter-site Hubbard interaction in eACBN0 approach could compute the band gap more accurately. In Table 2, the calculated Hubbard $U$ and $V$ values are summarized. Since the band gap is insensitive to the inclusion of In $4d$-orbital, we choose $p$-orbitals as a mainfold for onsite interaction and $s$- and $p$-orbitals for inter-site interactions, respectively. As shown in Table 2, the obtained on-site $U$ values are quite comparable to the values from DFPT and ACBN0 in Table 1. Moreover, the converged inter-site $V$ well reflects the variation of local screening in direction perpendicular to the plane. We also confirm that the converged $V$ decreases rapidly as the interatomic distance increases (not listed in Table 2). In Fig. 4a, we compare the band structures obtained with PBE, ACBN0 and eACBN0, respectively. Like bands from ACBN0 and HSE06 in Fig. 3, the conduction bands obtained from the eACBN0 method are almost rigidly shifted up with respect to those from PBE approximations. We also compute the PDOS from the eACBN0 method in Fig. 4b and find that the contributions from each orbitals are similar to those from ACBN0 in Fig. 2c while all conduction bands are rigidly shifted. We note that the inclusion of In-$4d$ for $U$ and $V$ interactions does not affect the band dispersions and PDOS, though giving a slightly larger band gap of 1.86 eV.

From this benchmark study, we make following arguments. The on-site Hubbard $U$ can be considered as a “fingerprint” of local atomic environment: it does not have a simple dependence on the element type or crystal structure, which highlights the necessity of using self-consistent values to be fully ab initio. The three self-consistent schemes for computing Hubbard parameters, DFPT, ACBN0, and eACBN0, give comparable values, and are numerically more stable than the single-shot LR method. The flexibility to choose the Hubbard manifold to some extent increases the variational degrees of freedom of DFT+$U$, though in practice it may be less straightforward to choose the optimal sets of localized states to apply Hubbard corrections. We argue band gaps computed using self-consistent $U$ are less sensitive to the choice of Hubbard manifold, as supported by Table 1 where two choices of Hubbard manifolds result in similar band gap values.

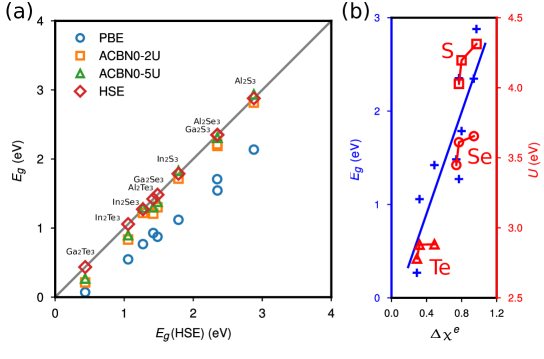
In the seminal work of Ding et al., a family of III₂-VI₃ compounds, Al₂S₃, Al₂Se₃, Al₂Te₃, Ga₂S₃, Ga₂Se₃,Ga₂Te₃, In₂S₃, and In₂Te₃, were predicted to be ferroelectric when they adopt the same structure as that of $\alpha$-In₂Se₃. This offers a platform to test the performance of DFT+$U$ using self-consistent Hubbard parameters. We calculate the band gaps for all known III₂-VI₃ 2D FEs using PBE and ACBN0, respectively. In our benchmark study of $\alpha$-In₂Se₃, each atom is treated as a unique Hubbard site due to symmetry breaking. Nevertheless, we expect in some cases it might be computationally tedious to treat all symmetry-inequivalent sites as unique Hubbard sites. At the lowest approximation, it is still reasonable to use the same $U$ for atoms of the same species, which is equivalent to averaging on-site interactions over these atoms. To gauge the subtle effect of applying averaged $U$ corrections, we compare the results obtained using two (element-specific) $U$’s and five (site-specific) $U$’s, denoted as ACBN0+2$U$ and ACBN0+5$U$, respectively. The HSE06 value is chosen as the reference because of the lack of experimental band gaps for these newly discovered 2D FEs.

Figure. 5a compares the band gaps calculated using PBE, ACBN0+2$U$, ACBN0+5$U$, and HSE06. It is clear that PBE substantially underestimates the band gaps for all III₂-VI₃ compounds. The band gaps predict with ACBN0+2$U$ and ACBN0+5$U$ are comparable to HSE06 results, with ACBN0+5$U$ being slightly better that ACBN0+2$U$. This confirms the applicability of ACBN0 to a broader range of III₂-VI₃-type 2D FEs. We also note the correlation between the band gap, the electronegative ($\chi^{e}$), and the self-consistent value of Hubbard $U$ of group-VI elements (S, Se, and Te). First, the band gap increases with the difference in the electronegative ($\Delta\chi^{e}$) of group-III and group-VI elements (Fig. 5b). Taking Ga₂Te₃ as an example, it has the smallest band gap, and $\Delta\chi^{e}=0.29$ ($\chi^{e}(\rm Ga)$ = 1.81, $\chi^{e}(\rm Te)$ = 2.1) is also the smallest among all 9 compounds. In comparison, Al₂S₃ has the largest $\Delta\chi^{e}$ as well as the largest band gap. Second, the $U$ value of an element depends on its electronegativity, as we find $U_{p}$(Te) $<U_{p}$(Se) $<U_{p}$(S) that is consistent with the trend of $\chi^{e}({\rm Te})<\chi^{e}({\rm Se})<\chi^{e}({\rm S})$. For the same group-VI element, the $U$ value also scales with $\Delta\chi^{e}$ of the material. For example, $U_{p}$(S) in In₂Se₃ is smaller than that in Al₂S₃ while the former has a smaller $\Delta\chi^{e}$. This further supports our previous argument that $U$ is not element but site/material specific. We may also take advantage of this feature to use the self-consistent $U$ to differentiate atoms of the same element in complex materials such as charge-ordering transition metal oxides.

The 2D vdW heterostructures consisted of multiple layers of 2D materials are becoming an increasingly important platform to realize novel emergent phenomena Duong et al. (2017). From a device perspective, the absence of surface dangling bonds in 2D materials and the weak vdW interactions between different layers ensure an atomically sharp interface across the heterojunction, beneficial for obtaining stable and reproducible device characteristics Chhowalla et al. (2016). The incorporation of 2D FEs into vdW heterostructures allows for convenient control of electrical properties such as band gap, band alignments, and charge transport via external electric fields. An important consequence of an OP polarization is a built-in electric field and thus an electrostatic potential across the material. It was suggested that one can take advantage of the vacuum level difference between the two surfaces of 2D FEs to realize water splitting with near-infrared light Li et al. (2014). Our investigations demonstrate that ACBN0 improves the band gap prediction for freestanding monolayer III₂-VI₃ 2D FEs. Using $\alpha$-In₂Se₃ bilayer and InTe/In₂Se₃ as examples, we further analyze the performance of PBE, ACBN0, and eACBN0 on vdW heterostructures. The in-plane lattice constants and atomic positions are optimized using PBE with the inclusion of Grimme dispersion corrections (DFT-D3) Grimme (2006). It is noted that the dipole correction has negligible impacts on the optimized geometries but slightly reduces the electronic band gaps.

For $\alpha$-In₂Se₃ bilayer with the same polarization direction for each layer, PBE predicts a nearly semimetal state ($E_{g}<5$ meV) while ACBN0 yields a small (indirect) band gap of $\approx$0.02 eV, as shown in Fig. 6a. The direct band gap at the $\Gamma$ point predicted by PBE and ACBN0 are 0.11 and 0.05 eV, respectively, both lower than the HSE06 value of 0.26 eV (obtained with $8\times 8\times 1$ $k$/$q$-point grids). This suggests both methods fail to capture the correct charge transfer between outermost layers due to the strong perpendicular electric field. In comparison, eACBN0 predicts a band gap of 0.44 eV, indicating a better description of the charge distribution along the OP direction. This is supported by the close agreement between eACBN0 (1.13 D) and HSE06 (0.95 D) values of the calculated dipole moments. Likewise, the computed band gaps for $\alpha$-In₂Se₃/InTe heterostructure highlight the important role of inter-site Hubbard interactions in 2D FE materials. The band gaps of the system from PBE and ACBN0 are found to be 0.06 and 0.14 eV, respectively, while the gap from eACBN0 is 0.37 eV (Fig. 6b), comparable to the HSE06 result of 0.29 eV. Here, we also observe eACBN0 predicts a larger band gap than HSE06, consistent with previous studies.

It is well established that ferroelectricity can affect the electronic structure of the surface and thus adsorption energies and catalytic properties, making ferroelectrics promising candidates for tunable catalysis Levchenko and Rappe (2008); Kolpak et al. (2008); Kakekhani et al. (2016); Kakekhani and Ismail-Beigi (2016). It was recently proposed that $\alpha$-In₂Se₃ may act as a reversible gas sensing substrate because NH₃, NO and NO₂ have different adsorption energies on the two oppositely charged surfaces Tang et al. (2020). The ability to accurate predicate the adsorption energy is essential for the understanding of the adsorption mechanisms on catalytic surfaces. However, local and semi-local density functionals often failed quantitatively to predict the adsorption energies of small molecules on metal surfaces (e.g.,CO on Cu) because of the incorrect predictions of the positions of the frontier orbitals of molecules Mason et al. (2004).

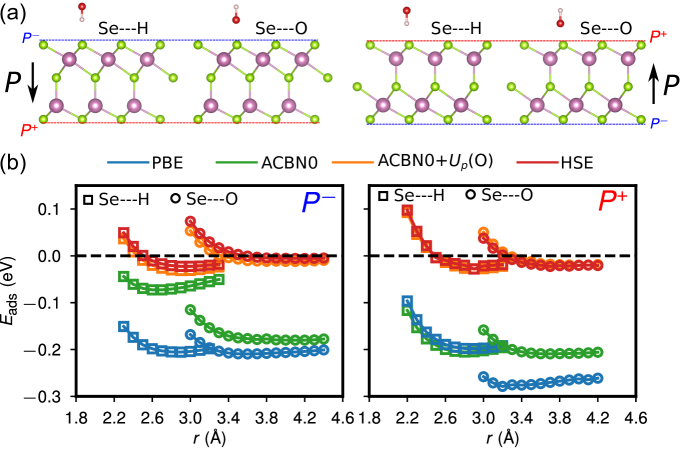
Here we first carry out a benchmark study of the adsorption of hydroxyl radical (HO) on both surfaces of $\alpha$-In₂Se₃ by constructing the energy profile as a function of adsorption distance using PBE, ACBN0, and HSE06, respectively. The adsorption energy is defined as $E_{\rm ads}=E_{\rm total}-E_{\rm molecule}-E_{\rm In_{2}Se_{3}}$, where $E_{\rm total}$, $E_{\rm molecule}$, and $E_{\rm In_{2}Se_{3}}$ are the energies of the gas molecules adsorbed on the In₂Se₃ monolayer, isolated gas molecules, and In₂Se₃ monolayer, respectively. Notably, we also investigate the effects of adding self-consistent $U$ corrections to the oxygen 2$p$ states of HO, denoted as ACBN0+$U_{p}({\rm O})$. Four adsorption cases (Fig. 7a) are explored, O-end adsorptions on $P^{+}$ and $P^{-}$ surfaces and H-end adsorptions on $P^{+}$ and $P^{-}$ surfaces. The HO remains perpendicular to the slab when varying the adsorption distance. The results are presented in Fig. 7b. We find that PBE strongly overestimates not only the binding strength compared to HSE06 but also the change in adsorption energy of HO due to polarization switching: the PBE value of $E_{\rm ads}$ for O-end adsorption changes from $-0.21$ eV on $P^{-}$ surface to $-0.28$ eV on $P^{+}$ surface, though the HSE value changes slightly from $-0.006$ eV to $-0.02$ eV. ACBN0 calculations with self-consistent $U_{p}({\rm Se})$ and $U_{d}({\rm In})$ improve the overall predictions of adsorption energies compared to PBE though the results remain qualitatively different from HSE06. It turns out the ACBN0 $U_{p}$ value of the O-2$p$ state in an isolated HO molecule is as large as 7.74 eV. After applying Hubbard $U$ corrections to the oxygen atom of the hydroxyl radical, the ACBN0+$U_{p}({\rm O})$ calculations nearly reproduce the HSE adsorption energies in all four cases (Fig. 7b). Our results suggest the importance of applying self-consistent $U$ corrections to localized states of both adsorbates and substrates.

We then calculate the adsorption energies $E_{\rm ads}$ of HO, NO, and CO on both polar surfaces of In₂Se₃ by fully optimizing the atomic positions of gas molecules using a unit cell of In₂Se₃ sheet with its in-plane lattice constants and atomic positions fixed. Specifically, ACBN0+$U_{p}$ denotes the DFT+$U$ method in which self-consistent Hubbard corrections are applied to both In₂Se₃ (In-$4d$ and Se-$4p$) and the $2p$ states of gas molecules: $U_{p}$(O)$=7.74$ eV for HO, $U_{p}$(O)$=2.47$ eV and $U_{p}$(N)$=0.95$ eV for NO, $U_{p}$(O)$=3.61$ eV and $U_{p}$(C)$=0.20$ eV for CO. Table 4 reports the adsorption energies computed with different methods. We find that for closed-shell molecule CO, the three methods, PBE, ACBN0, and ACBN0+$U_{p}$ predict similar adsorption strengths that are insensitive to the charge states of polar surfaces. Consistent with our benchmark study, the PBE and ACBN0 values of $E_{\rm ads}$ are much larger (more negative) than ACBN0+$U_{p}$ for HO adsorbed on both surfaces of In₂Se₃, with the former two methods indicating a chemical adsorption while the latter method implying a physical adsorption. Interestingly, the adsorption energies for the open-shell molecule NO computed with PBE, ACBN0, and ACBN0+$U_{p}$ are comparable. We also examine the effects of vdW interactions using the semi-empirical DFT-D3 method. The inclusion of dispersive effects generally increases the binding energies and reduce the adsorption distances.

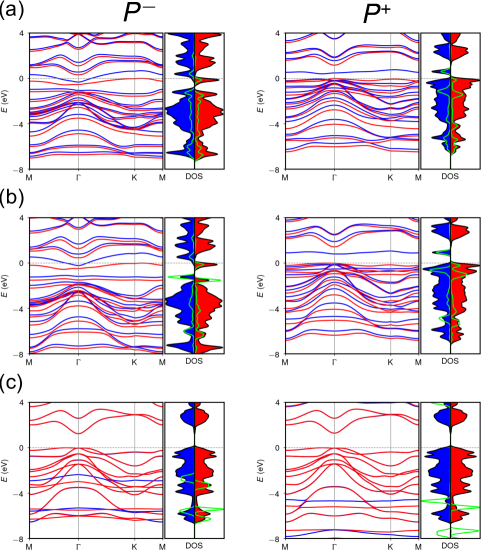
The substantially different adsorption strengths of HO predicted by PBE(ACBN0) and ACBN0+$U_{p}$ can be understood by inspecting the spin-resolved band structures and density of states. As shown in Fig. 8, the oxygen $2p$ states hybridize strongly with the states of In₂Se₃ over a broad energy window within PBE (ACBN0), indicating a strong charge transfer between In₂Se₃ and HO. Particularly, both PBE and ACBN0 predict a half-filled metallic system for HO adsorbed on the $P^{-}$ surface. In comparison, the use of $U_{p}$(O) noticeably downshifts the bands of O-$2p$ characters such that states near $E_{f}$ remain dominated by In₂Se₃, consistent with a low $E_{\rm ads}$ and a physisorption character.