The Belle Collaboration
First Simultaneous Determination of Inclusive and Exclusive
Abstract
The first simultaneous determination of the absolute value of the Cabibbo-Kobayashi-Maskawa matrix element using inclusive and exclusive decays is performed with the full Belle data set at the resonance, corresponding to an integrated luminosity of 711 fb-1. We analyze collision events in which one meson is fully reconstructed in hadronic modes. This allows for the reconstruction of the hadronic system of the semileptonic decay. We separate exclusive decays from other inclusive and backgrounds with a two-dimensional fit, that utilizes the number of charged pions in the system and the four-momentum transfer between the and system. Combining our measurement with information from lattice QCD and QCD calculations of the inclusive partial rate as well as external experimental information on the shape of the form factor, we determine and , respectively, with the uncertainties being the statistical error, systematic errors, and theory errors. The ratio of is compatible with unity.
pacs:
12.15.Hh, 13.20.-v, 14.40.NdIn this letter we report the first simultaneous determination of the absolute value of the Cabibbo-Kobayashi-Maskawa (CKM) matrix element using inclusive and exclusive decays. Exclusive determinations of focus on reconstructing explicit final states such as Amhis et al. (2023), Aaij et al. (2015), or Aaij et al. (2021), whereas inclusive determinations study meson decays undergoing transitions and are indiscriminate of the hadronization process. The world averages of either method are only marginally compatible Amhis et al. (2023),
| (1) | ||||
| (2) |
with a ratio of , which deviates 3.7 standard deviations from unity. The underlying reason for this tension is unknown. New physics explanations are challenging (see e.g. Refs. Crivellin (2010); Enomoto and Tanaka (2015); Bernlochner et al. (2014); Umeeda (2022)), leading to some to speculate the existence of until now unaccounted systematic effects Zyla et al. (2020a). This motivates the simultaneous determination in a single analysis, in which and the rates can be simultaneously extracted and systematic effects can be correlated.
The presented measurement of inclusive and exclusive decays uses the same collision events and a similar analysis strategy as Refs. Cao et al. (2021a, b). Charmless semileptonic decays are reconstructed by relying on the complete reconstruction of the second meson in the process. This approach allows for the direct reconstruction of the system of the process. Specifically, the four-momentum transfer squared, , and the number of charged pion candidates of the system, , can be reconstructed. This allows for the separation of and from other decays. The main background in the measurement stems from the much more abundant decays and a multivariate suppression strategy is used to reduce this and other background processes. Charge conjugation is implied throughout. The inclusive branching fraction is defined as the average branching fraction of and meson decays. Furthermore, we denote , and use natural units: .
We analyze meson pairs recorded at the resonance energy and of collision events recorded below the peak. Both data sets were recorded at the KEKB collider Kurokawa and Kikutani (2003) by the Belle detector. Belle is a large-solid-angle magnetic spectrometer. A detailed description of its performance and subdetectors can be found in Ref. (Abashian et al., 2002). The particle identification and selection criteria are the same as in Ref. Cao et al. (2021a).
Monte Carlo (MC) samples of meson decays and continuum processes ( with ) are simulated using the EvtGen generator (Lange, 2001). The normalization of continuum events is calibrated with the measured off-resonance data. A detailed description of all samples and decay models is given in Ref. Cao et al. (2021a). The simulated samples are used for background subtraction and to correct for detector resolution, selection, and acceptance effects. The used sample sizes correspond to approximately ten and five times, respectively, the Belle collision data for the meson production and continuum processes.
Semileptonic decays are simulated as a mixture of specific exclusive modes and nonresonant contributions using a “hybrid” approach Ramirez et al. (1990); Prim et al. (2020); Prim (2020): the triple differential rate of inclusive and exclusive predictions are combined such that the partial rates of the inclusive prediction are recovered. This is achieved by assigning weights to the inclusive contribution as a function of the generator-level , , and . Here and denote the energy of the lepton in the signal rest frame and the invariant mass of the system produced in the decay. For the inclusive contribution, we use two different calculations: the De Fazio and Neubert (DFN) model De Fazio and Neubert (1999) (with , ) and the Bosch-Lange-Neubert-Paz (BLNP) model Lange et al. (2005) (with , ). The difference between the two models is treated as a systematic uncertainty. The simulated inclusive events are hadronized with the JETSET algorithm T. Sjöstrand (1994) into final states with two or more mesons. We study two different tunes of the fragmentation parameters and assign their difference as a systematic uncertainty. The exclusive contributions are modeled as follows: decays are modeled using the Bourrely-Caprini-Lellouch (BCL) form factor parameterization (Bourrely et al., 2009); and decays are modeled using the Bharucha-Straub-Zwicky (BSZ) form factors (Bharucha et al., 2016) from the fit of Ref. (Bernlochner et al., 2021) to light-cone sum rule (LCSR) predictions (Bharucha et al., 2016) and the measurements of Refs. Sibidanov et al. (2013a); Lees et al. (2013); del Amo Sanchez et al. (2011a); and are modeled using pole form factors obtained from fits to LCSR (Duplancic and Melic, 2015). For the branching fractions the world averages from Ref. (Zyla et al., 2020b) are used.
Semileptonic decays are dominated by and decays. We simulate them with the form factors of Refs. Boyd et al. (1995); Grinstein and Kobach (2017); Bigi et al. (2017) and values determined by the measurements of Refs. Glattauer et al. (2016); Waheed et al. (2019). Other decays are simulated as a mixture of resonant and nonresonant modes, using the parameterization of Ref. Bernlochner and Ligeti (2017) for the modeling of form factors. The known difference between inclusive and the sum of measured exclusive decays is simulated with decays.
We reconstruct collision events with the multivariate tagging algorithm of Ref. Feindt et al. (2011). The algorithm uses a hierarchical approach utilizing neural networks to fully reconstruct one of the two mesons in hadronic final states (labeled as ). The reconstruction efficiency is calibrated using decays following the prescription outlined in Cao et al. (2021a). The identified final state particles forming the are masked and signal candidates are reconstructed by identifying an electron or muon candidate in the events, requiring as measured in the signal rest frame. To reject background from the much more abundant decays, eleven distinguishing features are combined into a single discriminant using boosted decision trees (BDTs) and utilizing the implementation of Ref. Chen and Guestrin (2016). The most discriminating training features are the reconstructed neutrino mass, , the vertex fit probability of the decay vertex between the hadronic system and the signal lepton , and the number of identified and in the system. Same as in Cao et al. (2021a), we select a working point that corresponds to a signal efficiency of 18.5%, which rejects 98.7% of decays, defined with respect to all events after the selection. To test the modeling of and other backgrounds in the extraction variables, and , we also utilize the events failing the BDT selection and find good agreement sup . We further separate events by the reconstructed , categorizing into five bins ranging in as a function of the multiplicity for the interval of . Events with are analyzed only in bins of as they are dominated by background. To enhance the purity in the low- and events, we apply a selection on the thrust of 0.92 and 0.85, respectively. It is defined by , when summing over the neutral and charged constituents of the reconstructed system in the center of mass frame. For events, we expect a more collimated system than for and other processes, resulting in a higher thrust value.
The bins and the distribution are analyzed using a simultaneous likelihood fit, which incorporates floating parameters for the modeling of the form factor, the binned templates, and systematic uncertainties as nuisance parameters. Specifically, the shape of template is linked to the form factors by correcting the efficiency and acceptance effects. The fit components we probe are the normalizations of decays, other signal decays, and of background events dominated by decays. The and form factors describing the decay dynamics are parameterized with expansion coefficients and using the BCL expansion,
| (3) |
at expansion order in the conformal variable (Bourrely et al., 2009; Aoki et al., 2022), and is expressed by the remaining coefficients to keep the kinematical constraint . We constrain the expansion coefficients to the lattice QCD (LQCD) values of Ref. Aoki et al. (2022), combining LQCD calculations from several groups Bailey et al. (2015); Flynn et al. (2015). Note that the measured distributions have no sensitivity for and we thus neglect its effects in the decay rate. The inclusion of the expansion coefficients, however, reduces uncertainties on the rate through the correlation to the shape. In order to utilize the full experimental knowledge of the form factors to date, we constrain its shape to the combined lattice QCD and experimental information of Refs. del Amo Sanchez et al. (2011b); Lees et al. (2012); Ha et al. (2011); Sibidanov et al. (2013b). The fit scenario with only lattice QCD constraints is studied for a standalone comparison with other experimental results.
We consider additive and multiplicative systematic uncertainties in the likelihood fit by adding bin-wise nuisance parameters for each template. The parameters are constrained to a multinormal Gaussian distribution with a covariance reflecting the sum of all considered systematic effects, and the correlation structure between templates from common sources is taken into account. This includes detector and reconstruction related uncertainties, such as the tracking efficiency for low and high momentum tracks, particle identification efficiency uncertainties, and the calibration of the reconstruction efficiency. We further consider uncertainties on the and shapes from the form factors, non-perturbative parameters, and their compositions. The fragmentation uncertainties are evaluated by changing the default Belle tune of fragmentation parameters to the values used in Ref. Aaij et al. (2014). We further vary the -production rate , spanning the range of Refs. Althoff et al. (1985); Bartel et al. (1983). The largest uncertainties on the exclusive branching fraction measurements are from the calibration of the tagging efficiency () and the modeling (). The largest uncertainties on the inclusive branching fraction measurement are from the () modeling and the fragmentation (). The uncertainties of the modeling of the background are and for the and branching fractions, respectively.
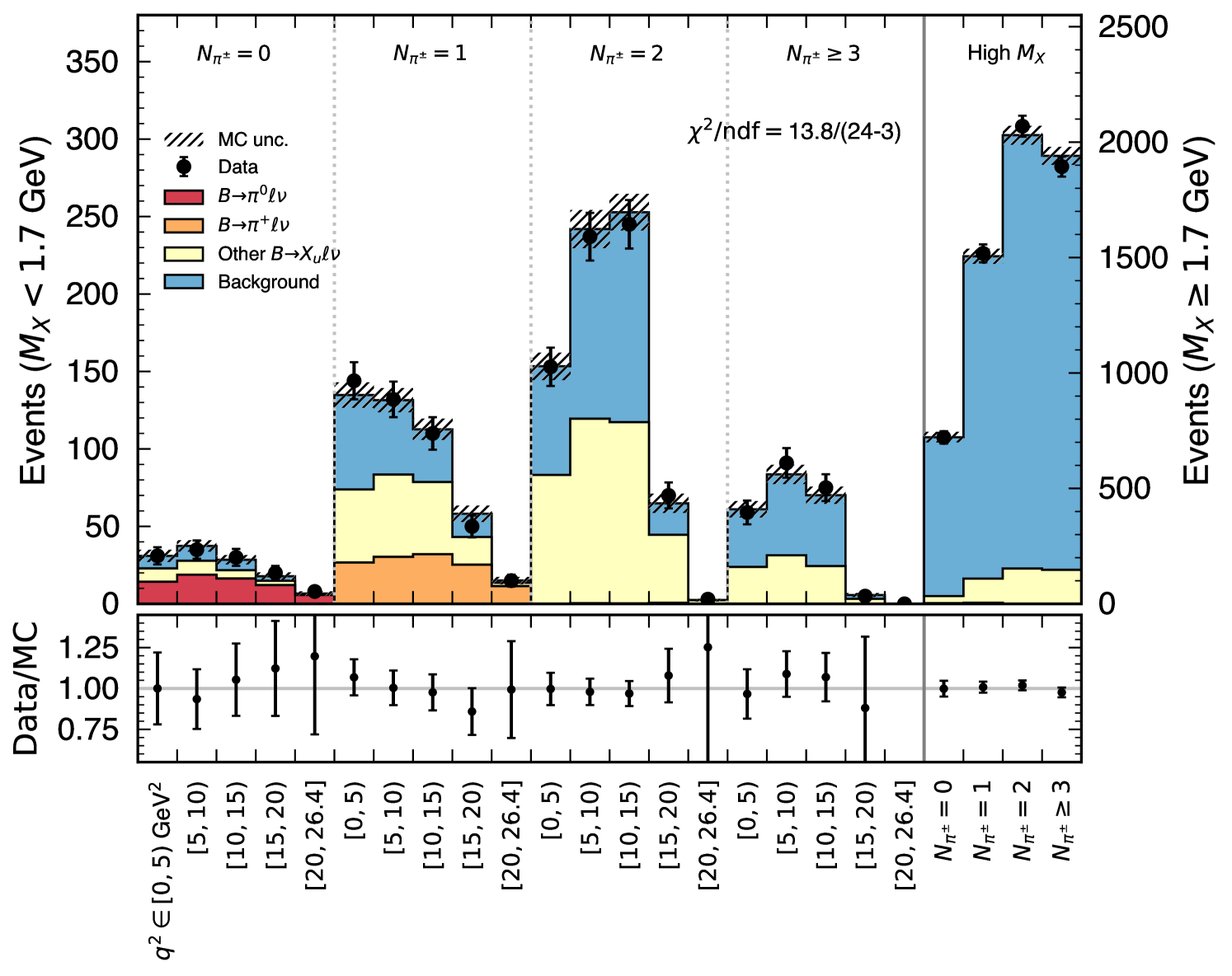
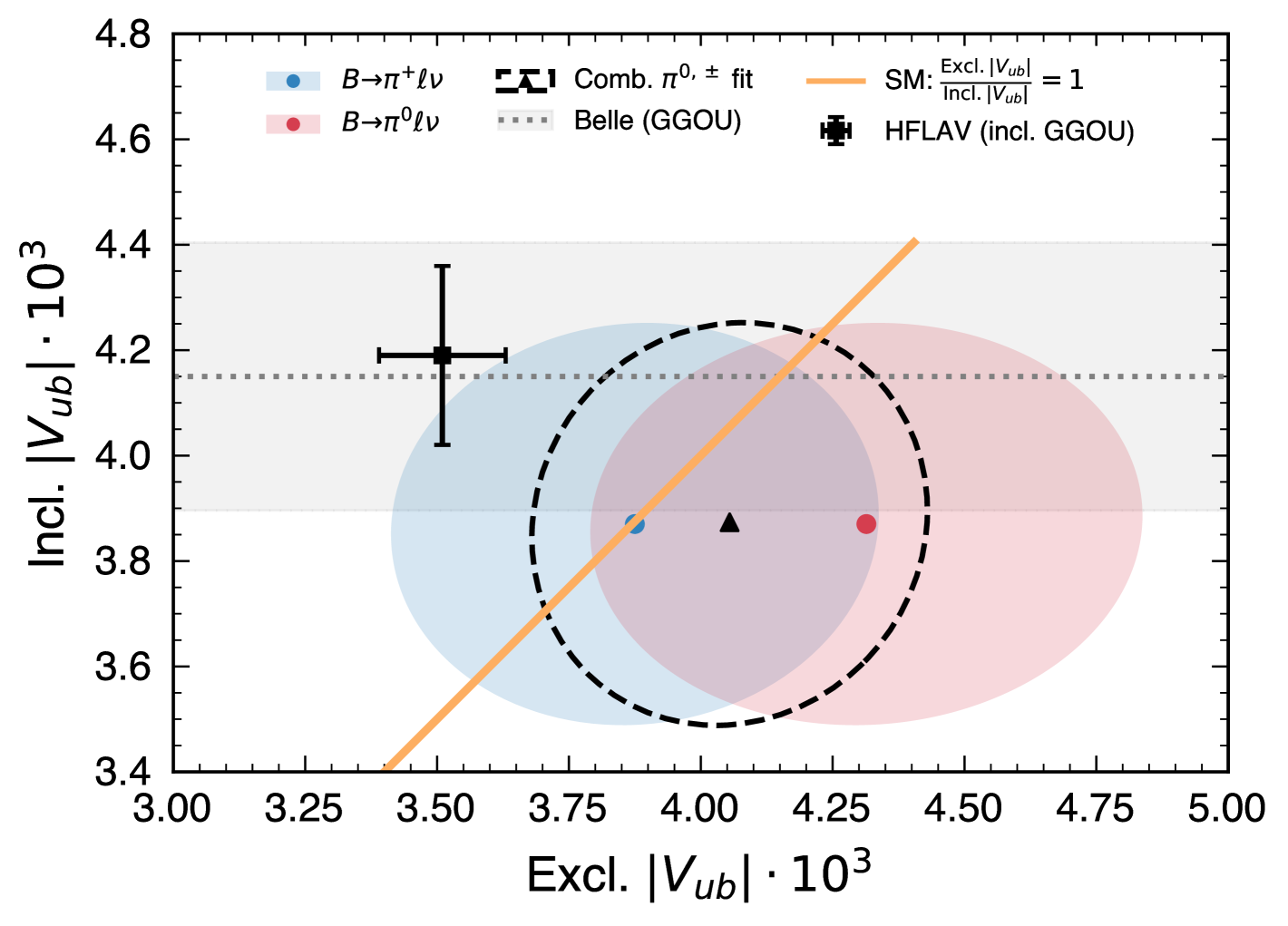
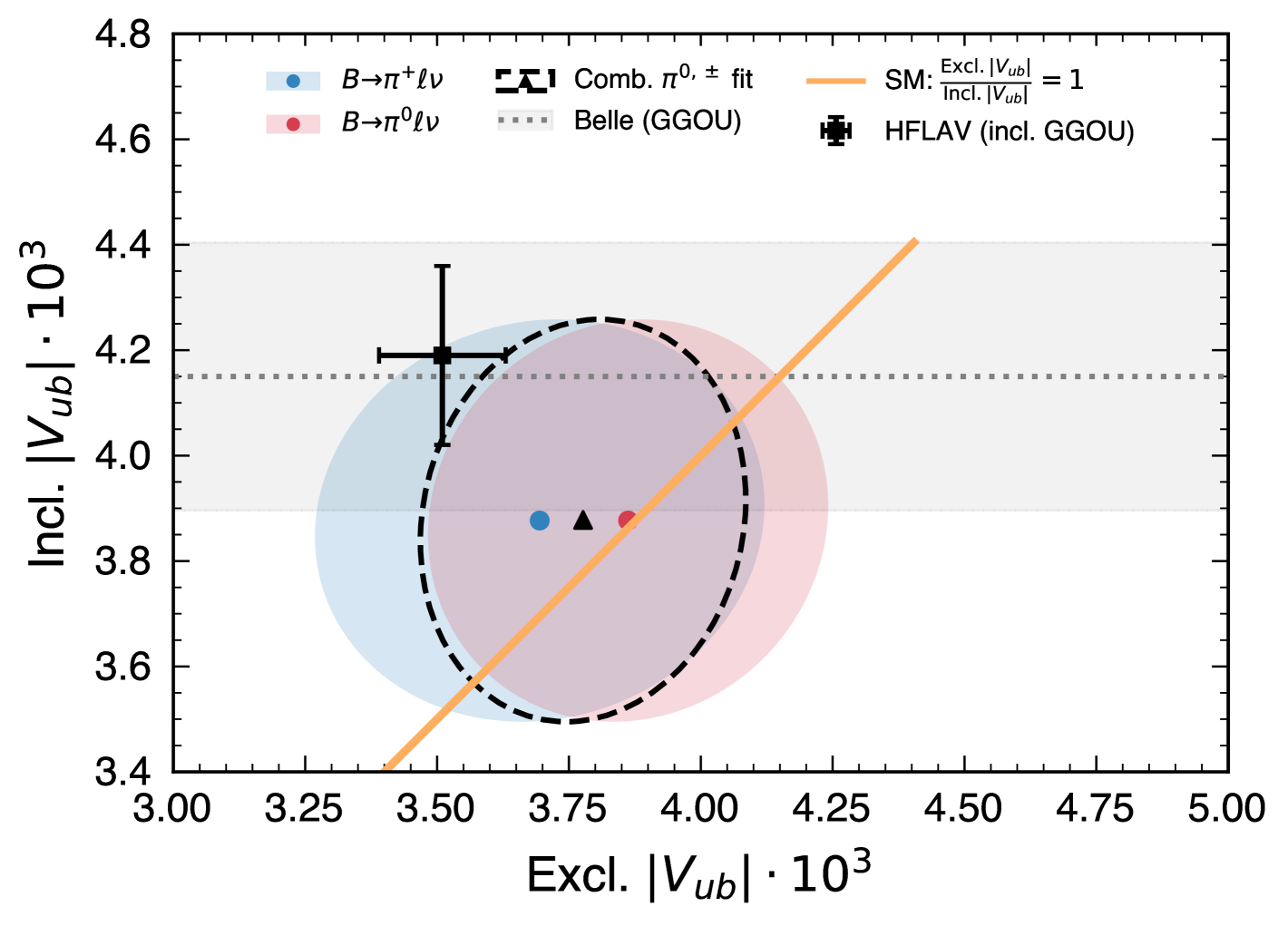
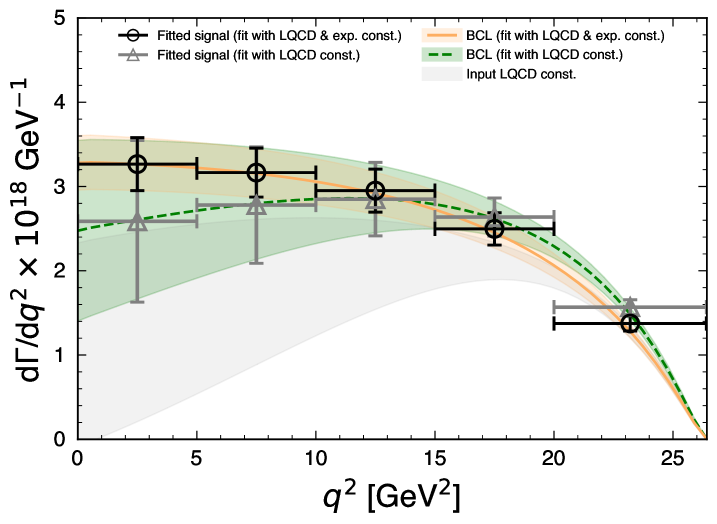
Figure 1 shows the distribution of the signal region after the fit and with only using LQCD information: and events are aggregated in the and bins, respectively, whereas contributions from other processes are in all multiplicity bins. The high bins constrain the and other background contributions. We use the isospin relation and lifetime ratio to link the yields of and . The fit has a of with degrees of freedom, corresponding to a p-value of . The measured and yields are corrected for efficiency effects to determine the corresponding branching fractions . The measured inclusive yield is calculated from the sum of , , and other events and unfolded to correspond to a partial branching fraction with , also correcting for the effect of final state radiation photons. We find
| (4) | ||||
| (5) |
with the errors denoting statistical and systematic uncertainties and we used the isospin relation between and to link both branching fractions. The recovered branching fraction for is compatible with the world average of Amhis et al. (2023). The correlation between the exclusive and inclusive branching fractions is . Using calculations for the inclusive partial rate and the fitted form factor parameters, we can determine values for . As our baseline we use the GGOU Gambino et al. (2007) calculation for the inclusive partial rate with ( ps-1), but other calculations result in similar values for inclusive . We find
| (6) | |||
| (7) |
for exclusive and inclusive with the uncertainties denoting the statistical error, systematic error, and error from theory (either from LQCD or the inclusive calculation). The correlation between the exclusive and inclusive is . The determined value for inclusive is compatible with the determination of Ref. Cao et al. (2021a). For the ratio of inclusive and exclusive values, we find
| (8) |
which is compatible with the SM expectation of unity. The value is higher and compatible with the current world average of Amhis et al. (2023) within 1.5 standard deviations. Fig. 2 (top) compares the measured individual values with the SM expectation and the current world average. We also test what happens if we relax the isospin relation between (red ellipse) and (blue) branching fractions and find compatible results for exclusive and inclusive , as well as for the exclusive values.
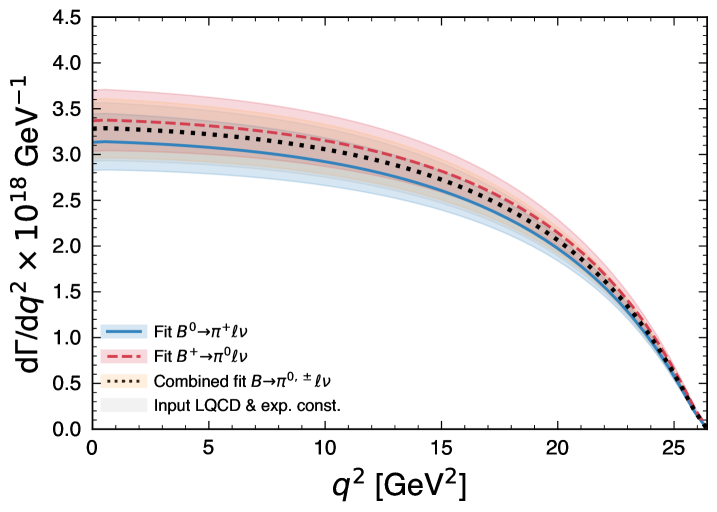
In the nominal result, we utilize the full theoretical and experimental knowledge of the form factor, combining shape information from the measured spectrum with LQCD predictions, as provided by Ref. Aoki et al. (2022). The determined (partial) branching fractions in this scenario are
| (9) | ||||
| (10) |
with a correlation of between inclusive and exclusive branching fractions and assuming isospin relation. This fit leads to a more precise value of from and we find with the same inclusive calculation
| (11) | |||
| (12) |
with a correlation and a ratio of
| (13) |
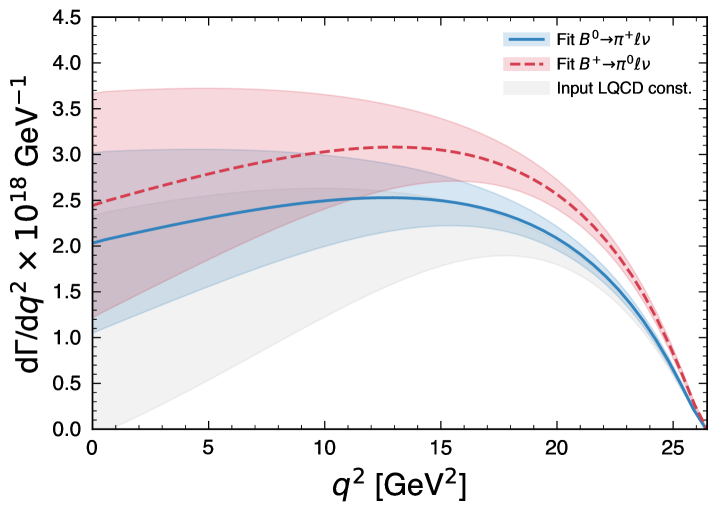
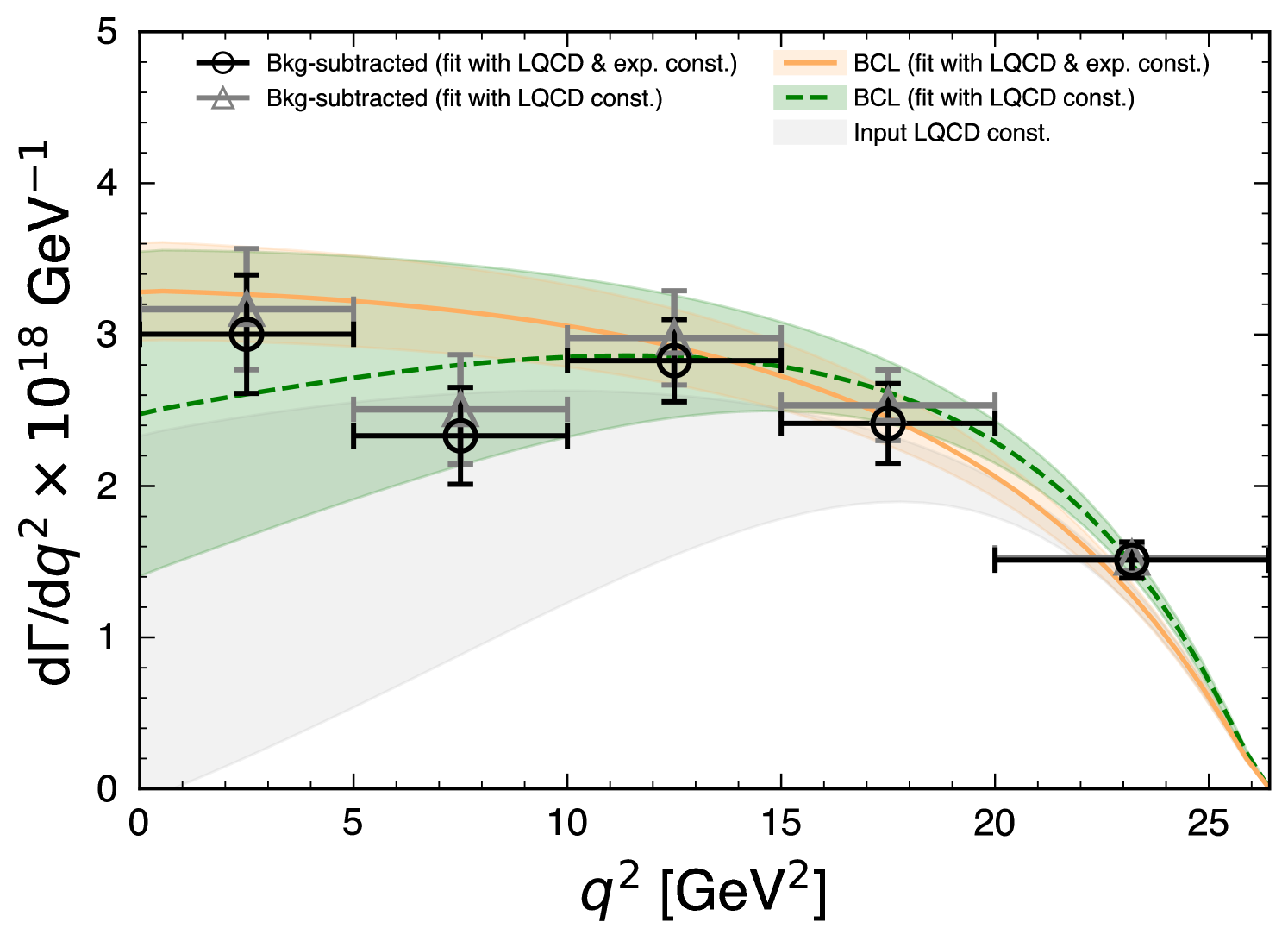
compatible with the world average within 1.2 standard deviations. Fig. 2 (bottom) compares the obtained values and we also find good agreement between the isospin conjugate exclusive values of . Figure 3 compares the fitted spectra of the differential rate of for both fit scenarios as well as for the LQCD input Aoki et al. (2022). The inclusion of the full experimental and theoretical knowledge leads to a higher rate at low .
In summary, we presented the first simultaneous determination of inclusive and exclusive within a single analysis. In the ratio of both values many systematic uncertainties such as the tagging calibration or the lepton identification uncertainties cancel and one can directly test the SM expectation of unity. We recover ratios that are compatible with this expectation, but 1.5 standard deviations higher than the ratio of the current world averages of inclusive and exclusive . This tension is reduced to 1.2 standard deviations when including the constraint based on the full theoretical and experimental knowledge of the form factor shape. We average our inclusive and exclusive values from both approaches using LQCD or LQCD and additional experimental information and find,
| (14) | ||||
| (15) |
respectively. These values can be compared with the expectation from CKM unitarity of Ref. Charles et al. (2005) of and are compatible within 1.2 and 0.8 standard deviations, respectively. The applied approach of simultaneously fitting and the number of charged pions in the system will benefit from the large anticipated data set of Belle II. Additional fit scenarios and inclusive values from other theory calculations of the partial rate are provided in the supplemental material sup .
This work, based on data collected using the Belle detector, which was operated until June 2010, was supported by the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan, the Japan Society for the Promotion of Science (JSPS), and the Tau-Lepton Physics Research Center of Nagoya University; the German Research Foundation (DFG) Emmy-Noether Grant No. BE 6075/1-1; the Helmholtz W2/W3-116 grant; the Australian Research Council including grants DP180102629, DP170102389, DP170102204, DE220100462, DP150103061, FT130100303; Austrian Federal Ministry of Education, Science and Research (FWF) and FWF Austrian Science Fund No. P 31361-N36; the National Natural Science Foundation of China under Contracts No. 11675166, No. 11705209; No. 11975076; No. 12135005; No. 12175041; No. 12161141008; Key Research Program of Frontier Sciences, Chinese Academy of Sciences (CAS), Grant No. QYZDJ-SSW-SLH011; Project ZR2022JQ02 supported by Shandong Provincial Natural Science Foundation; the Ministry of Education, Youth and Sports of the Czech Republic under Contract No. LTT17020; the Czech Science Foundation Grant No. 22-18469S; Horizon 2020 ERC Advanced Grant No. 884719 and ERC Starting Grant No. 947006 “InterLeptons” (European Union); the Carl Zeiss Foundation, the Deutsche Forschungsgemeinschaft, the Excellence Cluster Universe, and the VolkswagenStiftung; the Department of Atomic Energy (Project Identification No. RTI 4002) and the Department of Science and Technology of India; the Istituto Nazionale di Fisica Nucleare of Italy; National Research Foundation (NRF) of Korea Grant Nos. 2016R1D1A1B02012900, 2018R1A2B3003643, 2018R1A6A1A06024970, RS202200197659, 2019R1I1A3A01058933, 2021R1A6A1A03043957, 2021R1F1A1060423, 2021R1F1A1064008, 2022R1A2C1003993; Radiation Science Research Institute, Foreign Large-size Research Facility Application Supporting project, the Global Science Experimental Data Hub Center of the Korea Institute of Science and Technology Information and KREONET/GLORIAD; the Polish Ministry of Science and Higher Education and the National Science Center; the Ministry of Science and Higher Education of the Russian Federation, Agreement 14.W03.31.0026, and the HSE University Basic Research Program, Moscow; University of Tabuk research grants S-1440-0321, S-0256-1438, and S-0280-1439 (Saudi Arabia); the Slovenian Research Agency Grant Nos. J1-9124 and P1-0135; Ikerbasque, Basque Foundation for Science, Spain; the Swiss National Science Foundation; the Ministry of Education and the Ministry of Science and Technology of Taiwan; and the United States Department of Energy and the National Science Foundation. These acknowledgements are not to be interpreted as an endorsement of any statement made by any of our institutes, funding agencies, governments, or their representatives. We thank the KEKB group for the excellent operation of the accelerator; the KEK cryogenics group for the efficient operation of the solenoid; and the KEK computer group and the Pacific Northwest National Laboratory (PNNL) Environmental Molecular Sciences Laboratory (EMSL) computing group for strong computing support; and the National Institute of Informatics, and Science Information NETwork 6 (SINET6) for valuable network support. We are indebted to Alexander Ermakov for his pioneering work on the subject. We thank Frank Tackmann, Zoltan Ligeti, and Dean Robinson for discussions about the content of this manuscript.
References
- Amhis et al. (2023) Y. S. Amhis et al. (HFLAV), Phys. Rev. D 107, 052008 (2023), arXiv:2206.07501 [hep-ex] .
- Aaij et al. (2015) R. Aaij et al. (LHCb Collaboration), Nature Phys. 11, 743 (2015), arXiv:1504.01568 [hep-ex] .
- Aaij et al. (2021) R. Aaij et al. (LHCb Collaboration), Phys. Rev. Lett. 126, 081804 (2021), arXiv:2012.05143 [hep-ex] .
- Crivellin (2010) A. Crivellin, Phys. Rev. D 81, 031301 (2010), arXiv:0907.2461 [hep-ph] .
- Enomoto and Tanaka (2015) T. Enomoto and M. Tanaka, Phys. Rev. D 91, 014033 (2015), arXiv:1411.1177 [hep-ph] .
- Bernlochner et al. (2014) F. U. Bernlochner, Z. Ligeti, and S. Turczyk, Phys. Rev. D 90, 094003 (2014), arXiv:1408.2516 [hep-ph] .
- Umeeda (2022) H. Umeeda, (2022), arXiv:2208.11896 [hep-ph] .
- Zyla et al. (2020a) P. Zyla et al. (Particle Data Group, Semileptonic b-Hadron Decays, Determination of and Review), Prog. Theor. Exp. Phys. 2020 083C01 (2020a).
- Cao et al. (2021a) L. Cao et al. (Belle Collaboration), Phys. Rev. D 104, 012008 (2021a), arXiv:2102.00020 [hep-ex] .
- Cao et al. (2021b) L. Cao et al. (Belle Collaboration), Phys. Rev. Lett. 127, 261801 (2021b), arXiv:2107.13855 [hep-ex] .
- Kurokawa and Kikutani (2003) S. Kurokawa and E. Kikutani, Nucl. Instr. and. Meth. A499, 1 (2003), and other papers included in this Volume; T. Abe et al., Prog. Theor. Exp. Phys. 2013, 03A001 (2013) and references therein.
- Abashian et al. (2002) A. Abashian et al., Nucl. Instrum. Meth. A479, 117 (2002), also see detector section in J. Brodzicka et al., Prog. Theor. Exp. Phys. 2012, 04D001 (2012).
- Lange (2001) D. J. Lange, Nucl. Instr. and. Meth. A462, 152 (2001).
- Ramirez et al. (1990) C. Ramirez, J. F. Donoghue, and G. Burdman, Phys. Rev. D 41, 1496 (1990).
- Prim et al. (2020) M. Prim et al. (Belle Collaboration), Phys. Rev. D 101, 032007 (2020), arXiv:1911.03186 [hep-ex] .
- Prim (2020) M. Prim, “b2-hive/effort v0.1.0,” (2020), doi: 10.5281/zenodo.3965699.
- De Fazio and Neubert (1999) F. De Fazio and M. Neubert, JHEP 06, 017 (1999), arXiv:hep-ph/9905351 [hep-ph] .
- Lange et al. (2005) B. O. Lange, M. Neubert, and G. Paz, Phys. Rev. D 72, 073006 (2005), arXiv:hep-ph/0504071 .
- T. Sjöstrand (1994) T. Sjöstrand, Comput. Phys. Commun. 82, 74 (1994).
- Bourrely et al. (2009) C. Bourrely, I. Caprini, and L. Lellouch, Phys. Rev. D 79, 013008 (2009), [Erratum: Phys. Rev. D82, 099902 (2010)], arXiv:0807.2722 [hep-ph] .
- Bharucha et al. (2016) A. Bharucha, D. M. Straub, and R. Zwicky, JHEP 08, 098 (2016), arXiv:1503.05534 [hep-ph] .
- Bernlochner et al. (2021) F. U. Bernlochner, M. T. Prim, and D. J. Robinson, Phys. Rev. D 104, 034032 (2021), arXiv:2104.05739 [hep-ph] .
- Sibidanov et al. (2013a) A. Sibidanov et al. (Belle Collaboration), Phys. Rev. D 88, 032005 (2013a), arXiv:1306.2781 [hep-ex] .
- Lees et al. (2013) J. P. Lees et al. (BaBar Collaboration), Phys. Rev. D87, 032004 (2013), [Erratum: Phys. Rev. D87, no.9, 099904 (2013)], arXiv:1205.6245 [hep-ex] .
- del Amo Sanchez et al. (2011a) P. del Amo Sanchez et al. (BaBar Collaboration), Phys. Rev. D 83, 032007 (2011a), arXiv:1005.3288 [hep-ex] .
- Duplancic and Melic (2015) G. Duplancic and B. Melic, JHEP 11, 138 (2015), arXiv:1508.05287 [hep-ph] .
- Zyla et al. (2020b) P. Zyla et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2020 083C01 (2020b).
- Boyd et al. (1995) C. G. Boyd, B. Grinstein, and R. F. Lebed, Phys. Rev. Lett. 74, 4603 (1995), arXiv:hep-ph/9412324 [hep-ph] .
- Grinstein and Kobach (2017) B. Grinstein and A. Kobach, Phys. Lett. B 771, 359 (2017), arXiv:1703.08170 [hep-ph] .
- Bigi et al. (2017) D. Bigi, P. Gambino, and S. Schacht, Phys. Lett. B 769, 441 (2017), arXiv:1703.06124 [hep-ph] .
- Glattauer et al. (2016) R. Glattauer et al. (Belle Collaboration), Phys. Rev. D 93, 032006 (2016), arXiv:1510.03657 [hep-ex] .
- Waheed et al. (2019) E. Waheed et al. (Belle Collaboration), Phys. Rev. D 100, 052007 (2019), arXiv:1809.03290 [hep-ex] .
- Bernlochner and Ligeti (2017) F. U. Bernlochner and Z. Ligeti, Phys. Rev. D 95, 014022 (2017), arXiv:1606.09300 [hep-ph] .
- Feindt et al. (2011) M. Feindt, F. Keller, M. Kreps, T. Kuhr, S. Neubauer, D. Zander, and A. Zupanc, Nucl. Instrum. Meth. A 654, 432 (2011), arXiv:1102.3876 [hep-ex] .
- Chen and Guestrin (2016) T. Chen and C. Guestrin, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining KDD ’16, 785 (2016).
- (36) See the supplemental material at [link provided by PRL] .
- Aoki et al. (2022) Y. Aoki et al. (Flavour Lattice Averaging Group (FLAG)), Eur. Phys. J. C 82, 869 (2022), arXiv:2111.09849 [hep-lat] .
- Bailey et al. (2015) J. A. Bailey et al. (Fermilab Lattice and MILC Collaborations), Phys. Rev. D 92, 014024 (2015), arXiv:1503.07839 [hep-lat] .
- Flynn et al. (2015) J. M. Flynn, T. Izubuchi, T. Kawanai, C. Lehner, A. Soni, R. S. Van de Water, and O. Witzel, Phys. Rev. D 91, 074510 (2015), arXiv:1501.05373 [hep-lat] .
- del Amo Sanchez et al. (2011b) P. del Amo Sanchez et al. (BaBar Collaboration), Phys. Rev. D 83, 032007 (2011b), arXiv:1005.3288 [hep-ex] .
- Lees et al. (2012) J. P. Lees et al. (BaBar Collaboration), Phys. Rev. D 86, 092004 (2012), arXiv:1208.1253 [hep-ex] .
- Ha et al. (2011) H. Ha et al. (Belle Collaboration), Phys. Rev. D 83, 071101 (2011), arXiv:1012.0090 [hep-ex] .
- Sibidanov et al. (2013b) A. Sibidanov et al. (Belle Collaboration), Phys. Rev. D 88, 032005 (2013b), arXiv:1306.2781 [hep-ex] .
- Aaij et al. (2014) R. Aaij et al. (LHCb Collaboration), Eur. Phys. J. C 74, 2888 (2014), arXiv:1402.4430 [hep-ex] .
- Althoff et al. (1985) M. Althoff et al. (TASSO Collaboration), Z. Phys. C 27, 27 (1985).
- Bartel et al. (1983) W. Bartel et al. (JADE Collaboration), Z. Phys. C 20, 187 (1983).
- Gambino et al. (2007) P. Gambino, P. Giordano, G. Ossola, and N. Uraltsev, JHEP 10, 058 (2007), arXiv:0707.2493 [hep-ph] .
- Charles et al. (2005) J. Charles et al. (CKMfitter Group), Eur. Phys. J. C 41, 1 (2005), and updates of Spring 2021 on http://ckmfitter.in2p3.fr/, arXiv:0406184 [hep-ph] .
Supplemental Material
.1 Determinations with alternative inclusive calculations for the partial rate
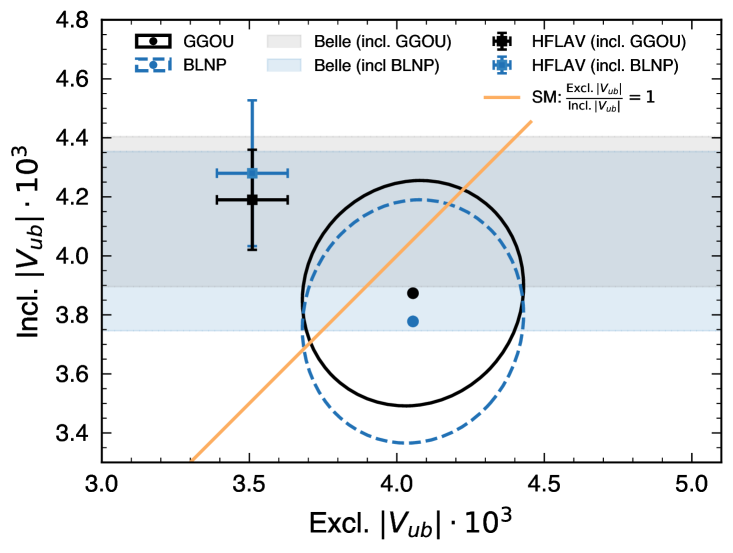
Figure 4 compares the inclusive values obtained from the GGOU calculation versus BLNP and DGE, respectively.
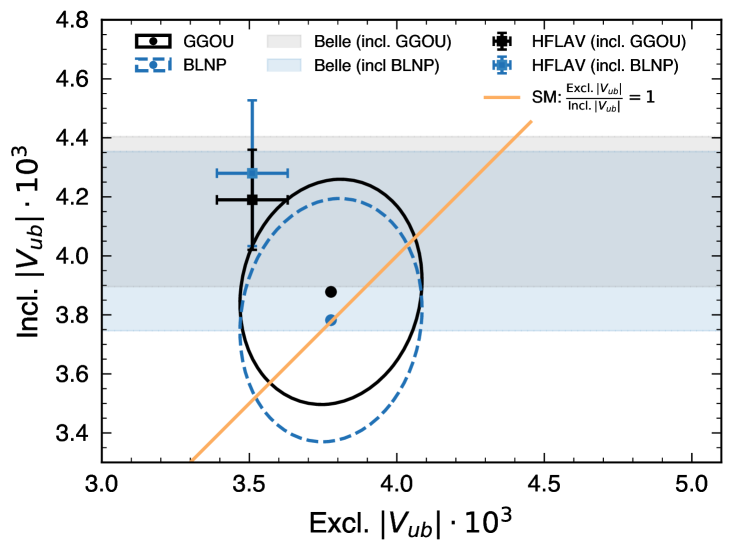
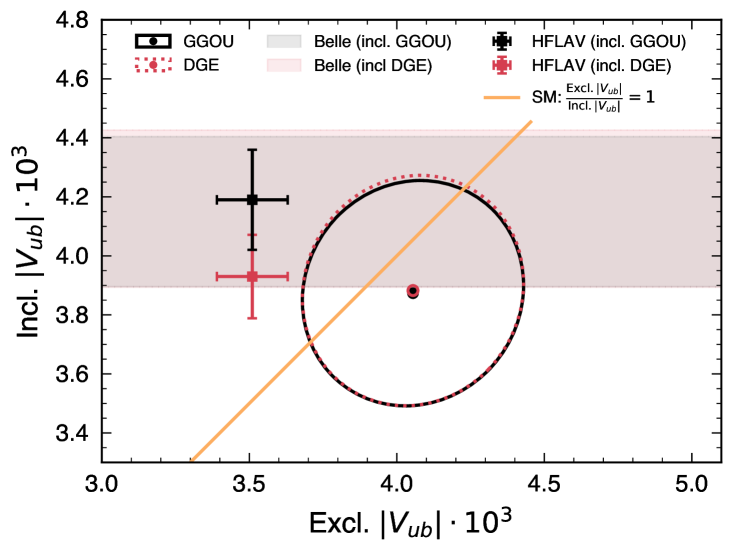
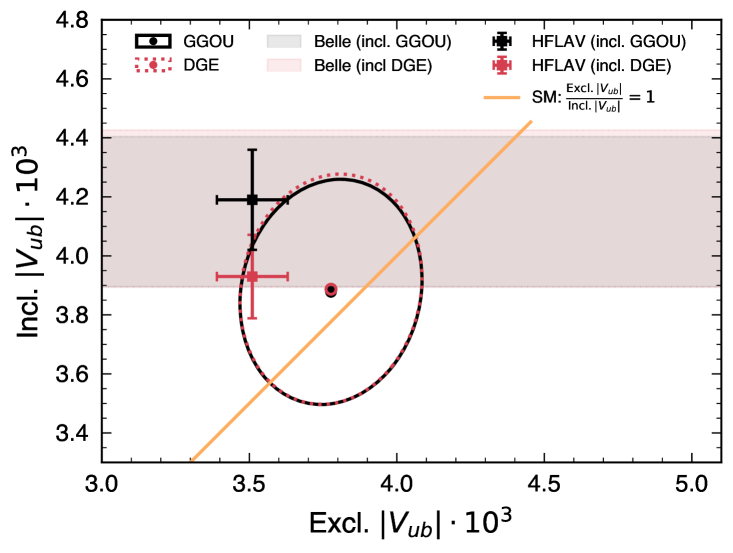
.2 Data-MC agreement in background dominated sideband
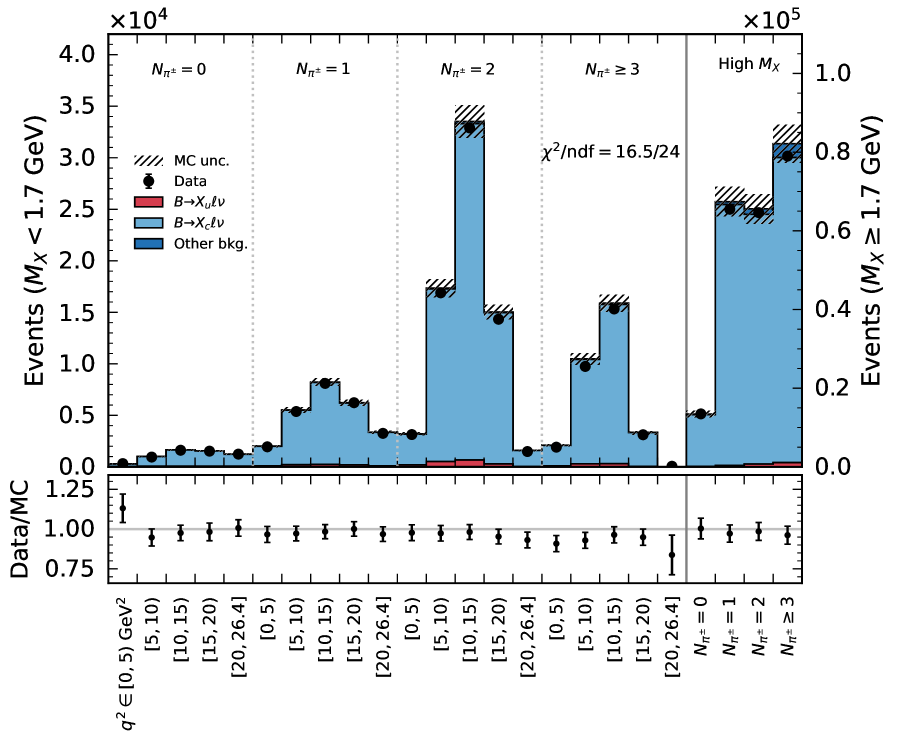
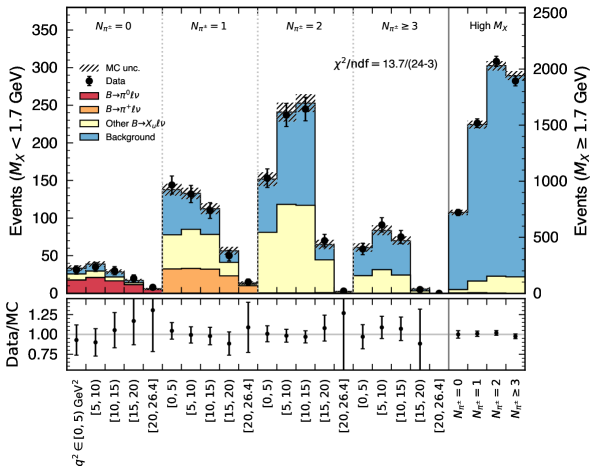
Figure 5 shows the analyzed categories in for and the four bins in the enriched BDT sideband. We observe fair agreement in the background shapes with a p-value of .
.3 Consistency cross-check
The prediction is fitted to the observed data by minimizing
| (16) | ||||
| (17) |
where the floating parameters and are the template normalization and the BCL form facotrs, respectively. The bin- and template-wise nuisance parameters are normalized to the relative bin errors , and the associated bin-to-bin correlations arising from systematics are accounted in the fit by a global correlation matrix . The BCL form factors are constrained by the covariance matrix provided by FLAG.
In this measurement, an additional fit with separate normalizations of the and decays is applied to check the consistency of the nominal results based on combining the two modes. All of the fitter setups are summarised in the following:
-
•
Setup 1-a: fit spectra with LQCD and external experimental constraint on the BCL form factor and shared normalization based on the isospin relation.
-
•
Setup 1-b: same as 1-a, but with only LQCD constraint for the form factor.
-
•
Setup 2-a: separate normalizations of the and decays and with LQCD-experimental constraint. We denote the recovered CKM matrix values as .
-
•
Setup 2-b: same as 2-a, but with only LQCD constraint.
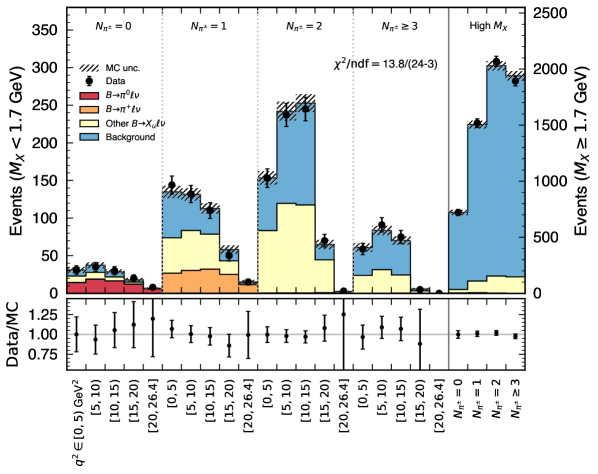
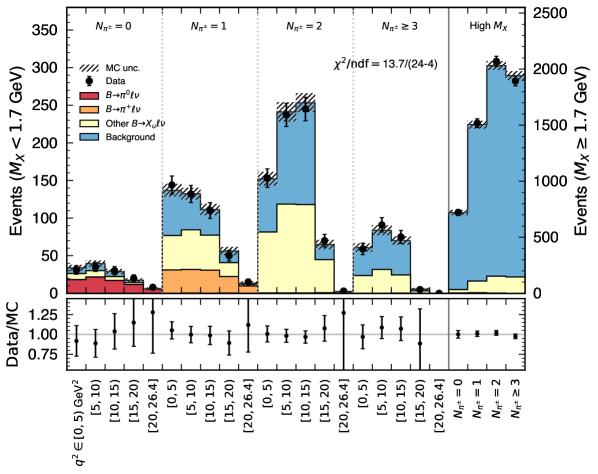
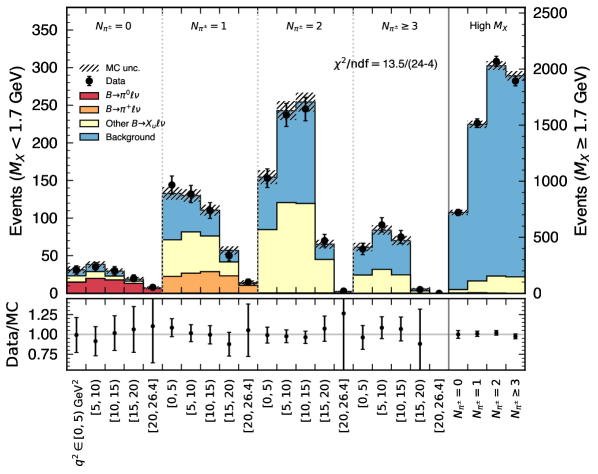
The nominal results are based on setup 1-a and 1-b. With different fit scenarios, the numerical results of the fitted yields are summarised in Table 1 as well as the signal efficiencies. After all selections, the total measured data are events. Figure 6 and Fig. 7 illustrate the post-fit spectra and the pulls of the template- and bin-wise Nuisance parameters, respectively. The featured behaviors are found to be consistent in all setups. The obtained and branching fractions are listed in Table 4 and Table 5 for the setup 2-a and 2-b, where the weighted average of two pion modes is derived based on the total covariance matrix. The final results are found to be fairly compatible with the nominal results in Table 2 and Table 3.
| Setup | Other | Bkg. | ||
|---|---|---|---|---|
| 1-a | ||||
| 1-b | ||||
| 2-a | ||||
| 2-b | ||||
| - |
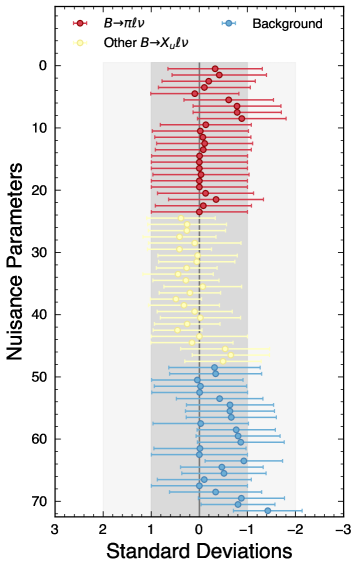
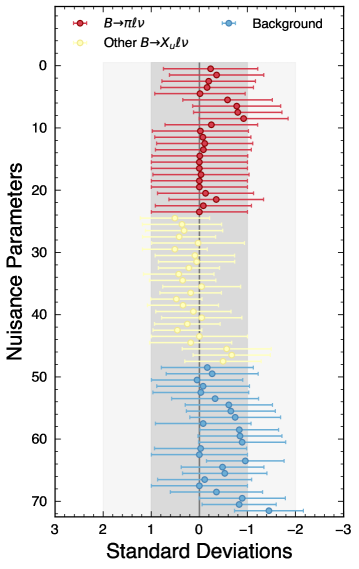
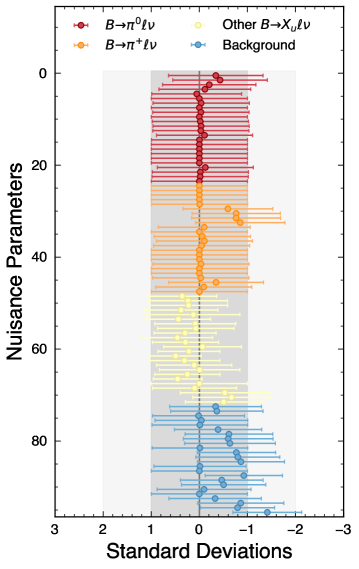
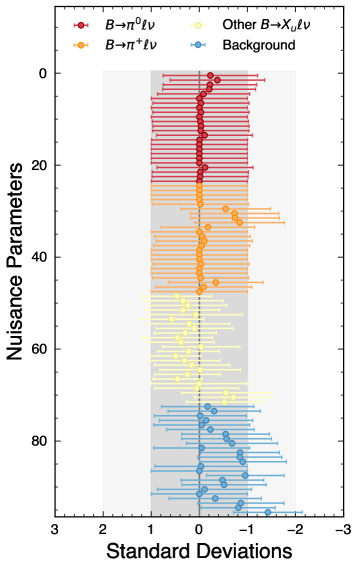
| Result | |
| Setup 1-a | |
| Setup 1-b | |
| Result | |
| Setup 1-a | |
| Setup 1-b | |
| Result | |
| Setup 2-a | |
| Avr. | |
| Setup 2-b | |
| Avr. | |
| Result | |
| Setup 2-a | |
| Setup 2-b | |
.4 BCL parameters of decay form factor
The fitted BCL parameters are summarized in Table 6 and 7 with only LQCD constraints and combined LQCD-experimental constraints, respectively. Figure 8 compares the results obtained in various fit scenarios, which are in good agreement.
| Central | 4.055 | 0.407 | -0.597 | -0.465 | 0.496 | -1.504 |
|---|---|---|---|---|---|---|
| Uncertainty | 0.375 | 0.012 | 0.080 | 0.392 | 0.020 | 0.096 |
| 1.000 | -0.416 | -0.473 | -0.308 | -0.184 | -0.462 | |
| 1.000 | 0.275 | -0.187 | 0.254 | 0.173 | ||
| 1.000 | 0.344 | 0.101 | 0.720 | |||
| 1.000 | 0.193 | 0.698 | ||||
| 1.000 | -0.039 | |||||
| 1.000 |
| Central | 3.777 | 0.414 | -0.493 | -0.297 | 0.500 | -1.426 |
|---|---|---|---|---|---|---|
| Uncertainty | 0.309 | 0.014 | 0.053 | 0.180 | 0.023 | 0.054 |
| 1.000 | -0.452 | -0.168 | 0.232 | -0.109 | -0.105 | |
| 1.000 | 0.151 | -0.451 | 0.259 | 0.142 | ||
| 1.000 | -0.798 | -0.096 | 0.214 | |||
| 1.000 | 0.012 | -0.097 | ||||
| 1.000 | -0.451 | |||||
| 1.000 |