Fitting Matérn smoothness parameters using automatic differentiation
Abstract
The Matérn covariance function is ubiquitous in the application of Gaussian processes to spatial statistics and beyond. Perhaps the most important reason for this is that the smoothness parameter gives complete control over the mean-square differentiability of the process, which has significant implications for the behavior of estimated quantities such as interpolants and forecasts. Unfortunately, derivatives of the Matérn covariance function with respect to require derivatives of the modified second-kind Bessel function with respect to . While closed form expressions of these derivatives do exist, they are prohibitively difficult and expensive to compute. For this reason, many software packages require fixing as opposed to estimating it, and all existing software packages that attempt to offer the functionality of estimating use finite difference estimates for . In this work, we introduce a new implementation of that has been designed to provide derivatives via automatic differentiation (AD), and whose resulting derivatives are significantly faster and more accurate than those computed using finite differences. We provide comprehensive testing for both speed and accuracy and show that our AD solution can be used to build accurate Hessian matrices for second-order maximum likelihood estimation in settings where Hessians built with finite difference approximations completely fail.
Keywords: Matérn covariance, Bessel functions, Gaussian processes, maximum likelihood, automatic differentiation
1 Introduction
Gaussian process modeling is a ubiquitous tool in a variety of disciplines. One attractive feature of a Gaussian process is that it is specified by its first two moments: for a Gaussian random field with (often multivariate) index , one needs only to select a mean function 111For convenience we consider only mean-zero processes, however extensions to parametric mean functions are straightforward. and a positive-definite covariance function such that to completely specify the multivariate law. A classical application of Gaussian process modeling in the mean-zero setting with data is to select a parametric family of positive-definite functions and then optimize the negative log-likelihood over the parametric family to obtain the estimator
| (1.1) |
It is common practice to then treat this MLE as a known true value and compute subsequent estimators like interpolants or forecasts using the Gaussian law specified by the MLE.
One of the most popular isotropic covariance functions, the Matérn covariance function [21], is given by
| (1.2) |
where is the gamma function, is the second-kind modified Bessel function [8], and , , and are scale, range, and smoothness parameters respectively. The Matérn class is distinguished from other standard covariance functions by the flexibility that the parameter gives, as it controls the mean-square differentiability of the process [30]. While the above functional form is complicated, the Matérn covariance is most naturally motivated by its Fourier transform pair (also called the spectral density), which for -dimensional processes has the form where and are functions of and . As it turns out, has significant effects on the behavior of derived quantities. Interpolants and forecasts, for example, are fundamentally different when , corresponding to a process that is not mean-square differentiable, and when , corresponding to a process with at least one mean-square derivative. Special concern about whether processes are (mean-square) differentiable dates back to at least Matheron [22] in the geostatistical community. For a complete discussion on the importance of this parameter and the value in estimating it, see [30].
A widely acknowledged challenge in GP modeling is that the log-likelihood surface created by is non-convex and difficult to optimize over. Figure 1 provides an example of the log-likelihood surface (profiled in , see Appendix B) for a Matérn process that illustrates the non-quadratic shape of level surfaces and the difficulty of estimating both smoothness and range parameters. A similar but arguably worse challenge occurs for estimating the range and scale even when the smoothness parameter is known [36].
An effective way to combat the log-likelihood’s lack of convexity is to optimize using derivative information. Until recently the use of derivatives to aid Gaussian process optimization was not particularly common (see [31, 23, 11, 16] for examples of separate strategies for optimization at scale using approximated derivative information). The gradient of is computable in closed form and is given by
| (1.3) |
where we use the shorthand . Setting aside the computational challenges this presents for large matrices, computing this quantity requires derivatives of the covariance function with respect to all parameters in order to assemble the matrices. This is the step in the process where attempting to estimate from data becomes problematic. Until recently, no closed form expressions for the derivative were available in the literature, and by extension accurate computation of the derivatives was not possible. While these derivatives have been studied [6], including very recent work providing completely closed-form derivatives [12], the expressions are cumbersome, for example involving higher-order generalized hypergeometric functions, and as such are difficult to implement reliably. Considering that these functions are significantly more general than , existing software implementations for them are understandably complex and in our experience come at significant speed costs on at least some parts of the domain, even if they are reliably accurate on the entire domain of .
The non-convex optimization problem posed by maximum likelihood for Matérn covariance functions may not be practically solvable using only gradient information. In an attempt to introduce higher-order information to further aide in optimization, several recent works have used the expected Fisher information matrix as a proxy for Hessians [11, 16]. True Hessians (also referred to as observed information matrices), however, while coming with an additional computational burden, are more effective than expected information matrices in our experience as well as arguably being preferable as proxies for second-order information of estimated parameters [7]. They can be computed as
where is the second derivative . The derivative in the last quadratic form can be expanded using matrix calculus but is left in this form for clarity (see the appendix of [11] for the full expression). As can be seen, the Hessian of requires second derivatives of , making the second-order optimization for the Matérn class of covariance functions more challenging still. To our knowledge, no existing literature gives explicit forms for these second derivatives. These considerations indicate that a primary bottleneck in performing maximum likelihood estimation for Matérn models is the robust evaluation of the second-kind modified Bessel function, and its first two derivatives. While we have not directly verified that the inaccuracies of finite-difference derivatives pose a substantial problem in gradient-based Bayesian methods, such as Hamiltonian Monte Carlo [25], it is possible that the improvements we discuss here could also provide meaningful gains in those methods.
is a special function defined as one of the two linearly independent solutions of a second order differential equation [8]. Alternative expressions for , such as series expansions, integrals on the real line, path integrals, as well as confluent and generalized hypergeometric functions have been used in existing special function libraries [8, 2, 32]. The primary difficulty of practical implementations is that no single strategy for accurate and efficient evaluation is valid on the entire real axis and a domain partitioning is required to obtain an optimal method to evaluate . Current libraries focus entirely on evaluations of Bessel functions, neglecting their derivatives, and even if they provide access to the source implementation, they are not easily extended to the problem of computing derivatives. Due to this difficulty in computing the derivatives of with respect to the order , it is common practice to fix prior to performing the optimization instead of treating it as a parameter to be estimated (see, for example, the popular GPyTorch software library [10], or the RobustGaSP softare [15, 14], both of which only offer a few special half-integer values of ). This often constitutes a significant sacrifice, as can have important practical implications for many tasks performed after maximum likelihood estimation, such as interpolation [30].
In an attempt to offer the functionality of estimating from data, several software libraries for fitting Matérn models provide simple finite difference approximations for the derivative approximation as , where a typical choice is . For special function libraries that provide only function evaluations this is one of the few possible choices. And for a suitable choice of , these approximations may be reasonably accurate when is not near the origin and is not overly large, although finite difference approximations are known to be prone to round-off errors. This is particularly problematic for second derivatives, as those calculations involve a divisor of . Combined with the finite precision representation of the numerator, this division can lead to severe floating point errors. To our knowledge no software library currently attempts to offer second derivative information for with respect to , or, by extension, for . Considering that the evaluation of is the dominant cost in evaluating the entire Matérn covariance function, finite differences, which require at least twice as many evaluations as direct computations, also come with a burdensome computational cost. A more efficient approach, essentially free of round-off errors for first derivatives, is the complex step method [29, 9]. This was studied for modified Bessel function order derivatives in [20], however not for edge cases such as , since they are less problematic for complex step method evaluations but are highly significant for the current work. Adaptive finite difference methods, uncommon in the statistical community, are more reliable since they select adaptively based on function values in the vicinity of differentiation points. But while they provide higher accuracy, it comes at a significant performance cost due to the many function evaluations required. And so while a sufficiently high-order adaptive finite difference method can be used to solve the problem we discuss here, the performance cost is so significant that we do not consider them further.
Arguably the most powerful differentiation approach when derivatives are not computable by hand or easily programmed manually is automatic differentiation (AD), which avoids issues such as round-off errors and allows highly efficient implementations. In this work, we develop a new implementation of that is purposefully designed to be automatically differentiable with high accuracy. The negligible accumulation of errors in the first-order derivatives using AD computations further enables highly accurate computations of second-order derivatives of with respect to . We take this approach here, making use of the Julia [5] programming language, which we consider to be an ideal tool due to its type system and powerful AD tools such as ForwardDiff.jl [27].
In the next section, we provide an overview of AD, focusing on the challenges associated with an automatically differentiable implementation of . In Section 3, we present our choices for direct evaluations and their derivatives on the entire domain of definition of . Next, in Section 4, we verify the accuracy and efficiency of the derivatives as well as the Matérn covariance. Finally, we provide a demonstration of second-order optimization in Section 5, where we compare the results of optimizing using derivatives of the log-likelihood built using our AD implementation to optimization results building the same objects with finite difference derivatives. We conclude that optimization using the software we provide here yields correct MLEs, and that the AD-generated derivatives are fast and sufficiently accurate that even very complicated derived functions such as are computed to high accuracy in settings where building the same objects using finite difference derivatives results in a complete loss of precision.
2 Derivatives via Automatic Differentiation
Automatic differentiation (AD) refers to the algorithmic transformation of function implementations into code that computes the derivative . In the forward-mode paradigm, which is the only one that will be discussed in this work, an implementation of , representing a multivariate vector function with inputs and outputs is transformed by an AD tool into an implementation of the product , where is the Jacobian vector product of the Jacobian and the vector . The tangent vectors and are the input directional derivatives and the output sensitivities, respectively. This technique can be employed recursively by applying AD to the Jacobian vector product implementation with inputs and . We refer to [13] for an extensive introduction to AD.
An AD tool applies differentiation at the programming language intrinsic
function level, having hard-coded differentiation rules covering most algebraic
operations, some special functions, and optionally higher-level constructs like
linear solvers. In Julia, the programming language of choice in the current
work, these rules are implemented by ChainRules.jl [34].
The tool then generates code that computes the function value and derivative
value at each program statement. As an example, we illustrate as pseudocode a
forward-mode AD tool which generates from the implementation
of :
function(x1, x2)
tmp = x1*x2
return exp(tmp)
end
function(x1, dx1, x2, dx2)
tmp = x1*x2
dtmp = dx1 * x2 + x1 * dx2
return exp(tmp), exp(tmp)*dtmp
end
with the prefix ’d’ denoting the generated tangents. Together
with the chain rule for more complex expressions, this purely mechanical work
can be fully automated. Using compiler code analysis, like the LLVM backend of
Julia, modern AD tools provide highly efficient implementations that rival any
hand-optimized derivative code [24]. An immediate advantage
of AD is that it enables a user to compute derivatives of a program seamlessly
without tediously differentiating by hand or contending with concerning issues
such as tuning the step size for finite differences. The reliance of AD on
basic calculus rules implemented at the lowest computational level, as opposed
to finite differences which operate at the top level once evaluations are
available, reduces the impact of round-off errors and thus limits the
propagation of errors while being very efficiently compiled, providing even more
significant advantages for higher-order derivatives. There are, however,
challenges associated with using automatic differentiation in the setting of
special functions, especially if applied to existing libraries, as will be
briefly discussed.
Differentiation of truncated series approximations
One of the most common implementations of special functions for direct evaluations is via series or asymptotic expansions. Term-wise derivatives of convergent series expansions are, for the functions considered here, also convergent series, but their convergence properties may differ from those of the original series. Thus, more terms may be needed when calculating derivatives to assure no loss of accuracy. Similar difficulties can occur with term-wise differentiation of asymptotic series, whose convergence properties hold as the argument of the function tends to some limit rather than as the number of terms increases. From an AD perspective a similar numerical challenge is encountered in the application of AD to iterative methods, e.g. [3]. In this work, this problem occurs primarily in one special setting that will be discussed at length in the implementation section and is effectively remedied by adding additional terms in the series truncation.
Limit branch problems for special functions
AD differentiated code where the control flow is dependent on the input may yield discontinuous derivatives at code branches for limiting values. We refer to this problem as the limit branch problem, and refer curious readers to [4] (which calls it the if problem) for a thorough investigation and discussion.
As an example, consider a function pertinent in this work given by
where at one of the two gamma functions will
evaluate to infinity. A code implementation that computes using a
special functions library may also throw an error at because there the
division of by will return NaN per the floating point standard.
The function is analytic at , however, and
admits finite limits, so any implementation of should return the correct
value for these inputs. Focusing for simplicity on the particular value of
, one workaround is to specify the function value using a special branch
shown here as pseudocode given by
function f_focus_on_0(x)
if x == 0
return 0.57721566... # Euler-Mascheroni constant
else
return (1/gamma(1-x) - 1/gamma(1+x))/(2*x)
end
end
Applying AD using a tool such as ForwardDiff.jl
[27] will incorrectly return a derivative of at . By
manually supplying limits, the programmer has cut the dependency graph of
with respect to at , and the program reduces to a constant function
with derivative . To solve this issue, the code expression in the if
branch has to be given in a form that preserves local derivative information in
the vicinity of . Local expansions in the if code branch allow
for the limit to be computed and differentiated numerically and ultimately
preserve derivative information. In this example, due to the smoothness of
at there exists a polynomial such that at (see Section 3.5). A (pseudo)-code implementation
given by
function f_focus_on_0(x)
if is_near(x, 0)
return poly_eval(x, p_0, p_1, p_2, ...)
else
return (1/gamma(1-x) - 1/gamma(1+x))/(2*x)
end
end
will now provide very accurate derivative information at . This approach still of course technically gives a program implementation with discontinuities in the derivative due to the inexact local approximations. But if the polynomials are only substituted in a suitably small neighborhood of the expansion points then the inexactness can be reduced to the same order as the intrinsic inexactness of finite-precision computer arithmetic and is thus not a concern for the present work.
For special function implementations this concern is far from purely academic. Many definitions of , for example when is an integer, are given as limiting forms whose implementations do not provide correct automatic derivatives. For this reason, applying AD transformations to existing special function libraries without additional scrutiny is unlikely to provide correct derivatives, which is further motivation for the current work. As indicated in [19], one alternative that would sidestep these concerns would be to use a neural network model instead of a series implementation, since automatic differentiation is an inherent feature of neural networks, and the accuracy could be controlled in the training phase.
3 A Fast and Accurate Implementation of and
To devise a robust implementation for and derivatives , with , we partition the domain of definition, (this is sufficient since ), into several intervals. This strategy of breaking up the domain and applying different strategies for different regions is ubiquitious in the implementation of all special functions, even ones as basic as trigonometric functions, and certainly has been applied in every commonly used implementation of Bessel functions (see, for example, the domain partitioning of the AMOS library [2]). A particular goal in our domain partitioning and method selection, however, is to obtain accurate and efficient automatic derivatives as well as accurate evaluations. In Figure 2, we summarize the domain partitioning based on intervals for pairs , which splits real axis into different sub-intervals, i.e. , with recommended selections for the parameters . Even in the most rigorous settings of error analysis, however, there is an element of personal judgment in the exact choices of domain partitioning parameters. While in broad strokes they are guided by when different representations that can be exactly evaluated by a computer are accurate, such as large-argument expansions being picked when the argument is “large enough”, they are also guided by practical metrics like numerical tests. This is the case in this work, and as such the boundary values we recommend here can be altered slightly without major impacts on accuracy.
Each interval is studied in its associated subsection, accompanied by discussions on implementation details for the selected method in that interval (typically a suitable series-type representation) and adjustments necessary to expedite and preserve the accuracy of automatic derivatives. Each separate expansion is truncated at different levels , and these parameters have a meaningful impact on both efficiency and accuracy. In the present work we chose the levels that provide close to computer precision. A user willing to sacrifice a few digits of accuracy to increase the efficiency may prefer to truncate the series at lower levels than the suggested values, but a comprehensive study of accuracy and efficiency impacts at such levels may be lengthy and is not considered in this work. Special values of the order , such as integers and half-integers must be be considered separately. Since for these values of is commonly expressed in a limiting form, substantial work is required to develop an implementation that avoids the limit branch problem. As the rescaled function appears in the Matérn covariance function, we also provide discussion of special optimizations for this function in Section A of the appendix.
3.1 Small arguments and small-to-moderate orders
While truncated direct series implementations may pose numerical difficulties in certain regimes, they can nonetheless be fast and accurate when applicable. Here, we identify a numerically stable series representation that extends the small argument interval up to while controlling the accumulation of round-off errors at satisfactory levels. Consider the definition of , for non-integer orders , given in terms of the modified Bessel function of the first kind, as
| (3.1) |
The function exhibits fast growth (asymptotically on the order of ); thus for large arguments Equation 3.1 leads to significant floating-point errors. Although the expression is valid for all arguments, it has practical use only for sufficiently small . The threshold for what constitutes “sufficiently small” is chosen based on accuracy and efficiency considerations, and in [32], values in the vicinity of are chosen as the cutoff.
An improved series expansion, however, can be derived using basic properties of the Gamma function . Using Euler’s reflection property (which states that ) and regrouping terms conveniently, we obtain a particularly convenient form for the series expansion of given by
| (3.2) |
One advantage that the series in Equation 3.2 has over the expression in Equation 3.1 is that it is less prone to cancellation errors by avoiding the subtraction of terms that grow rapidly with the series index or argument . The series as stated in Equation 3.2 is infinite; however a computer implementation of the infinite series in 3.2 requires a truncation level or stopping criterion. To promote accuracy we chose to stop the accumulation of terms when a tolerance of is met, which in practice corresponds to approximately or fewer terms in the sum. For consistency across all computational branches we specify in Figure 2 a truncation at , while reminding the user that in practice the stopping criterion is tolerance-based and can be adjusted. Furthermore, using the property , it is possible to evaluate this series (in fact its numerical truncation) using entirely algebraic operations after only evaluations of and . Applying AD to Equation 3.2 with the same stopping criterion as for the direct evaluation results in convergence in approximately as many terms for both first and second order derivatives. Although we do not derive a formal convergence proof, we will show in Section 4 that the performance of this expression is one of the best across the entire domain of definition.
For integer orders, the term in the denominator of Equation 3.1 leads to a singularity, and the expression is no longer valid in such cases. The function is defined at these orders, however, and by taking appropriate limits, can be written at integer orders as
| (3.3) |
While such integer-order expressions are valid in the limit and may be convenient to evaluate, they lead to limit branch problems that cause incorrect automatic derivatives, as described in Section 2. Therefore the integer case will be considered separately in Section 3.5. Additionally, we comment in the Appendix on implementation specializations to compute directly, which in some cases can improve speed and accuracy.
3.2 Intermediate arguments
Asymptotic expansions resemble series expansions in that they are also cumulative sums which require similar implementations, but they may diverge outside a prescribed range. Within the range of large orders and intermediate arguments we introduce the uniform asymptotic expansion (UAE) in for . As indicated by the word uniform, this approximation is not highly oscillatory in the argument , and as such it can be applied in argument ranges where round-off errors can be problematic. The UAE is given by
| (3.4) |
where, as in [8, Eq. 10.41.4], we have
and the polynomials are given by and
Tables of the coefficients for the polynomials exist (see [8, Sec. 10.41]), but they may be difficult to find digitally. Since they are not difficult to compute using symbolic operations, our software computes them directly (but ahead of time, to be re-used) such that the truncation order of the approximation can be arbitrarily chosen by the user.
For reasonably large truncation orders (which in our case default to or depending on the magnitude of ), this approximation is very fast to compute. As briefly noted in [8, Sec. 10.41], due to the uniqueness property of asymptotic expansions, this expansion must agree with the more commonly encountered expansion for large arguments to be introduced in Section 3.3. From this perspective, it comes as little surprise that the approximation quality of Equation 3.4 for any fixed truncation order improves as the argument or order increases, although not necessarily at the same rate (see [8, 10.41(iv)] for some discussion and a precise error bound when viewing (3.4) as a generalized asymptotic expansion in ). This strategy for evaluating is preferable in cases where small-argument methods start to lose accuracy but where the large-argument asymptotic expansion is not yet of satisfactory accuracy (for example, and ). Moreover, since this expression reduces to polynomial computations, it is highly stable under automatic differentiation and less prone to round-off errors.
3.3 Large arguments
For large arguments it is preferable to use a reduced asymptotic expansion, equipped with precise error bounds derived in [26] (see the next section for more explicit details), given as in [8, Eq. 10.40.2] by
| (3.5) |
where is generated via and
For arguments and moderate truncation orders such as (the default in our implementation), this approximation is accurate to computer precision (see [8, 10.40(iii)] for details on the error term, which without the exponential improvement introduced in the next section is challenging to work with). The automatically differentiated implementation is extremely fast since it involves differentiation of algebraic expressions, thus free of numerical artifacts, and is applied to a very low number of terms up to , which leads to a very small operation count.
3.4 Half-integer orders
An interesting property of expressed via the asymptotic expansion in Equation 3.5 is that, when , terms with drop out, and thus (3.5) is exact for all . These cases reduce to simpler forms that can be manually included in a program (for example, returning the simplified for ), but this type of program implementation would cause limit branch problems with respect to (as discussed in Section ), and as such requires additional scrutiny in our setting to ensure accurate automatic derivatives with respect to order.
As noted in Section 2, a converged direct evaluation may not yield a differentiated series that has converged to the same degree. This can be remedied using what [8, Sec. 10.40(iv)] refers to as exponentially-improved asymptotic expansions. The asymptotic expansion introduced in Equation 3.4 can be re-written as
| (3.6) |
where the remainder term , itself reasonably complicated to bound neatly (see [8, 10.40(iii)]), can then be expanded as
Here where is the upper incomplete gamma function [8, Eq. 10.17.16], and is a new and even more finely controlled remainder term that admits a much simpler controlling bound of [26, 8]. While direct evaluations of in the case where are exact, the remainder term is required to preserve derivative information, as the above additional expansion makes clear that is not zero for any . As such, additional terms from the approximation are necessary to preserve accurate derivative information.
3.5 Integer orders and small arguments with large orders
A common strategy for computer implementations of is to develop an implementation for in a neighborhood of and use a standard recursion with respect to order, valid for at any , given by
| (3.7) |
For integer orders, several options are available to compute the initial recursion terms and , for example direct polynomial or rational function approximations for and (as provided by [1]). However, this strategy will not be helpful in providing for due to the limit branch problem at and .
A suitable approach, provided in [32], is to consider series expansions of the recursion terms and , which due to (3.7) (and the property that ) need only be considered on the interval . Reproducing the notation of [32], we consider the expressions
| (3.8) | ||||
| (3.9) |
where for we have
| (3.10) | ||||
and all subsequent terms can be computed via a direct recursion using
With these expressions, the problem of obtaining an automatically differentiable program for for all is reduced to obtaining an AD-compatible implementation of for in a vicinity of the origin. As indicated in Section 2, the limit branch problem can be resolved using Taylor expansions in Equation 3.10 about :
With this strategy, we obtain an expression for which is exact at and very accurate for . By precomputing the coefficients of Taylor expansions, this entire apparatus yields function evaluations that are only approximately twice the cost of the direct series that we introduce above, and whose AD performance is quite satisfactory both with respect to speed and accuracy. For specific details on this recursion, such as accurate and efficient evaluations of and using Chebyshev expansions, we refer to [32]. As with Section 3.1, we additionally provide in the appendix a discussion of extending this method to the direct computation of for slight additional gains in accuracy and speed.
4 Speed and Accuracy Diagnostics
This section will focus on the verification and efficiency of our implementation of and its derivatives, which we will denote either or . We compare our implementation, denoted , with the one provided by the AMOS library [2], , using a reference solution , considered to be the ground truth and computed using the arbitrary-precision Arb library [18]. Derivatives of up to second order computed in two ways will be compared, namely AD-generated derivatives of our implementation, , and non-adaptive finite difference-based derivatives of the AMOS library, . These two values will be compared against a reference derivative computed using tenth-order adaptive finite difference methods of , denoted as , computed using FiniteDifferences.jl [35].
To offer access to a wider audience, we have packaged the code in the Julia language as the library BesselK.jl222https://github.com/cgeoga/BesselK.jl. The source repository additionally contains example R language bindings as well as the scripts used to generate the results and figures in this work.
4.1 Pointwise accuracy
While BesselK.jl is not designed to be a competitor of existing special functions libraries like AMOS with respect to the accuracy of direct evaluations of , we show that our implementation exhibits competitive absolute accuracy on the entire testing domain, both for direct evaluations as well as derivatives. Our chosen testing region is (a dense grid on) , which we pick for several reasons. For one, the range generously over-covers what we consider to be the range of sensible values of for fitting Matérn covariance parameters. With regard to the domain, we pick as an upper end point to verify accuracy in tail values that are small but numerically relevant. Moreover, beyond that point any software implementation for will be using an asymptotic expansion, and so naturally there will be good agreement. Secondly, we illustrate in log10-scale the relative gain of BesselK.jl over finite difference methods with AMOS for derivative computations.
Direct evaluations
Figure 3 asseses direct evaluations error for both AMOS and BesselK.jl using the absolute differences (left) and (right). The error behavior is qualitatively similar for both implementations, with the intermediate argument range accurate to computer precision, and a small ridge for very small arguments and large orders showing increasing inaccuracy. The implementation in BesselK.jl was tailored to optimize AD computations for different argument ranges and these ranges are clearly delimited in Figure 3. The loss of accuracy encountered for small to intermediate arguments, approximately error, is attributed to the difference in numerical treatment and the choice of truncation levels tuned for accuracy in derivatives. Such a small accuracy loss in trailing digits will be shown to have a negligible impact on properties of Matérn covariance matrices relevant to numerical optimization.
 |
 |
Derivatives
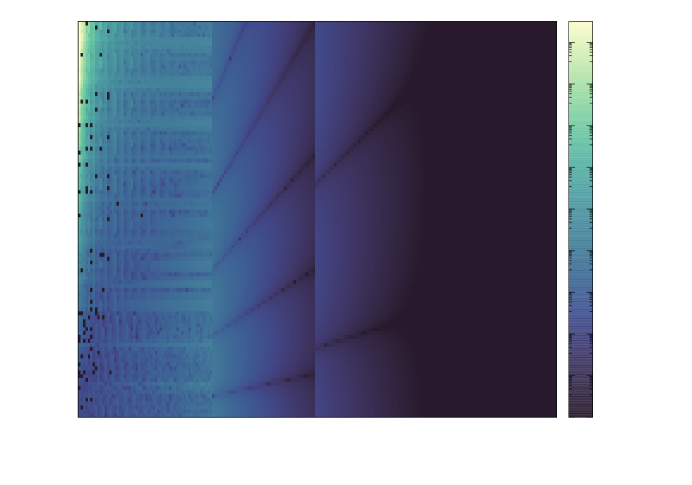
For first derivative computations, illustrated in Figure 4, we see that BesselK.jl (right) is noticeably superior to finite difference estimates with AMOS (left) in the small argument range. The latter method incurs rather large errors well within the intermediate argument range , while BesselK.jl consistently out-performs as the argument increases. As higher-order derivatives are taken, as illustrated in Figure 5 for second derivatives, this behavior becomes even more pronounced and automatic differentiation clearly overtakes finite difference computations by a significant margin.
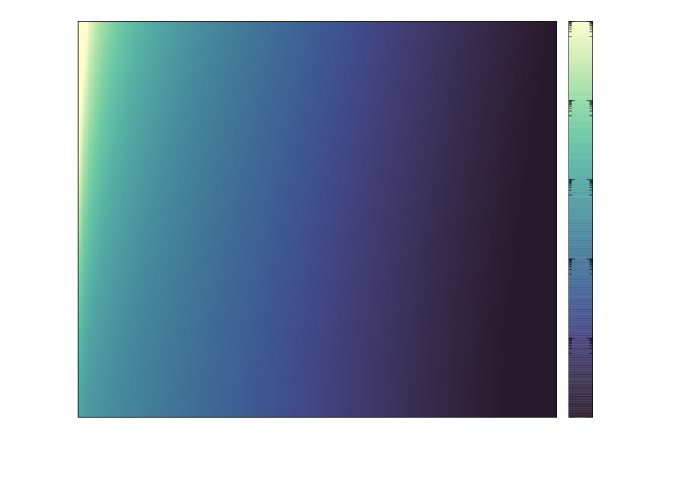 |
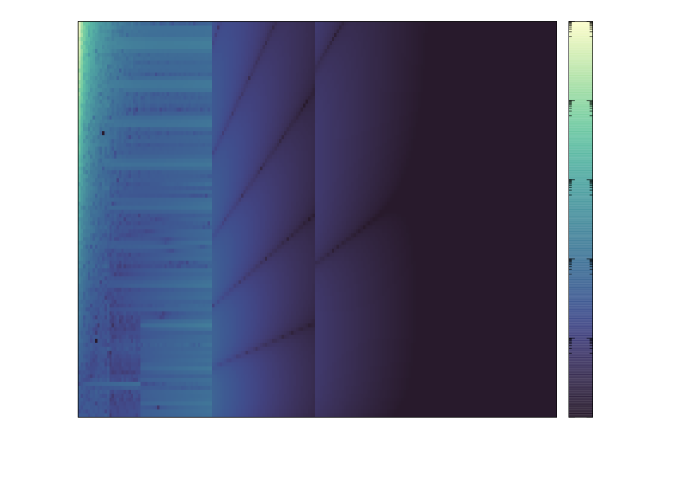 |
 |
 |
To provide a relative comparison of derivative computations using finite differences with AMOS versus BesselK.jl, we introduce the quantity
| (4.1) |
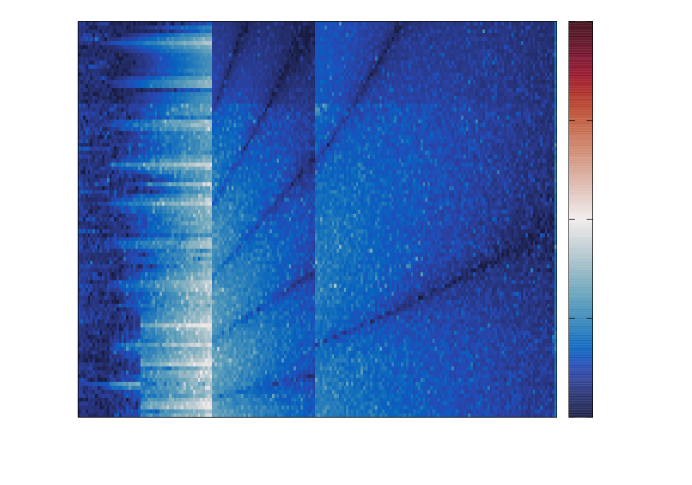
for both first derivatives () and second derivatives (). By assessing the error in log10-scale, we can identify correct digits, and by taking the difference between the errors of the two methods, we outline the regions where AD outperforms finite differences. In Figure 6 negative numbers (blue hues) indicate regions where is more accurate than (with a value of indicating one additional digit of accuracy for the AD method), and we note there are almost no positive values (red hues) over the entire domain. Upon close scrutiny we observe that the branch at may incur losses of one to two digits in a few discrete locations (visible as traces of red), which could be remedied by branching earlier than recommended at . This is a fine-tuning aspect which vanishes for second derivatives and was not explored extensively since it had no noticeable impact on our results. Finite differences, notoriously inaccurate for second-order derivatives since they involve a division by , incur increasingly higher round-off errors. In this context AD is expected to exhibit superior accuracy, and in Figure 6 its advantage over finite differences is clearly visible, consistently yielding or more extra digits of accuracy.
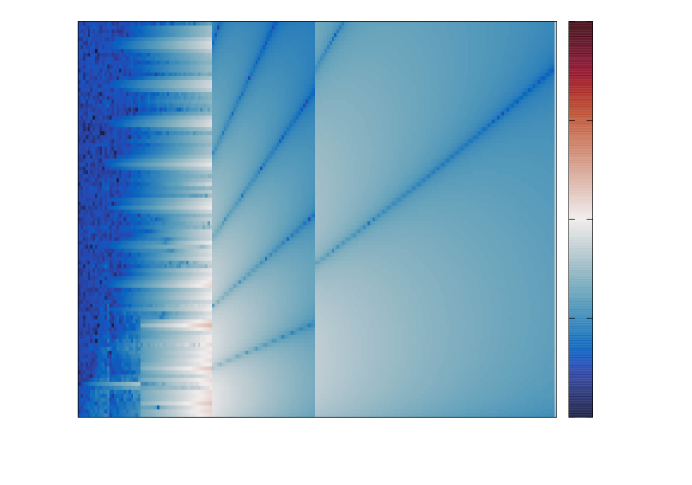 |
 |
4.2 Efficiency diagnostics
In order to compare the efficiency of with , we select pairs that cover every code branch (outlined in Figure 2) in the implementation of and provide evaluation and derivative evaluation timings performed on an Intel Core i-11600K CPU in Table 1. As can be seen, the speedup of is substantial, including in regions of the domain in which its accuracy rivals that of , as well as for all derivatives. The accuracy and efficiency considerations discussed here are summarized in Table 2 to serve as a convenient reference to the reader.
| case | |||||||
|---|---|---|---|---|---|---|---|
| (0.500, 1) | 9 | 51 | 67 | 455 | 82 | 510 | half-integer (iv) |
| (1.000, 1) | 136 | 159 | 178 | 447 | 328 | 605 | whole integer (i) |
| (3.001, 1) | 139 | 285 | 181 | 570 | 337 | 847 | near-integer order (i) |
| (3.001, 8) | 227 | 300 | 284 | 597 | 557 | 892 | near-integer order, borderline arg (i) |
| (1.850, 1) | 85 | 229 | 139 | 460 | 307 | 686 | small order (ii) |
| (1.850, 8) | 103 | 241 | 293 | 483 | 531 | 722 | small order, borderline arg (ii) |
| (1.850, 14) | 167 | 209 | 281 | 416 | 568 | 624 | intermediate arg (iii) |
| (1.850, 29) | 94 | 191 | 149 | 380 | 293 | 565 | large intermediate arg (iii) |
| (1.850, 35) | 92 | 183 | 148 | 368 | 293 | 548 | large argument (iii) |
| Comparison | Higher accuracy | Higher efficiency |
|---|---|---|
| vs. | ( 2-5 digits) | ( factor of 1-3) |
| vs. | ( 2-5 digits) | ( factor of 2-3) |
| vs. | ( digits) | ( factor of 2-5) |
4.3 Selected diagnostics for Matérn covariance matrices
The differences in accuracy and efficiency between the AMOS library and BesselK.jl are most relevant in the context of Matérn covariance matrices. To this end we compare in Table 3 several key quantities for the Matérn covariance matrices and , generated using and respectively. Points are chosen on a grid on the domain , and pairs are chosen to cover various argument ranges and branches in with respect to , with both parameters having significant effects on the condition of covariance matrices.
| (0.010, 0.40) | 4.3e-02 | 4.3e-02 | 9.52e-01 | 9.52e-01 | 1.22e-12 | -2.60e-01 | -2.60e-01 | 3.11e-13 |
| (0.010, 1.25) | 4.4e-02 | 4.3e-02 | 9.79e-01 | 9.79e-01 | 3.47e-12 | -3.45e-02 | -3.45e-02 | 9.23e-12 |
| (0.010, 3.50) | 3.5e-02 | 3.5e-02 | 9.93e-01 | 9.93e-01 | 0.00e+00 | -3.14e-03 | -3.14e-03 | 0.00e+00 |
| (1.000, 0.40) | 2.8e-02 | 4.8e-02 | 3.78e-02 | 3.78e-02 | 9.76e-15 | -1.40e+03 | -1.40e+03 | 1.84e-11 |
| (1.000, 1.25) | 2.6e-02 | 5.4e-02 | 1.03e-04 | 1.03e-04 | 6.56e-14 | -4.04e+03 | -4.04e+03 | 1.19e-09 |
| (1.000, 3.50) | 2.4e-02 | 3.5e-02 | 7.18e-11 | 7.18e-11 | 1.02e-14 | -1.02e+04 | -1.02e+04 | 2.76e-03 |
| (100.000, 0.40) | 2.7e-02 | 4.5e-02 | 9.50e-04 | 9.50e-04 | 1.15e-14 | -3.51e+03 | -3.51e+03 | 6.96e-10 |
| (100.000, 1.25) | 2.5e-02 | 4.6e-02 | 1.03e-09 | 1.03e-09 | 2.03e-15 | -1.06e+04 | -1.06e+04 | 3.87e-05 |
| (100.000, 3.50) | 1.7e-02 | 3.8e-02 | -3.43e-13 | -2.72e-13 | 7.15e-14 | NaN | NaN | NaN |
As expected from the previous benchmarks, the matrix assembly speed, for BesselK.jl, is superior to AMOS in regions where the predominant evaluation strategies for is different for each library (thus excluding, for example, cases like in which both software libraries are using asymptotic expansions) and approximately equal otherwise. As a preliminary investigation of matrix similarity, we compare the smallest eigenvalues of each matrix, and , and note that they agree to almost computer precision in all cases. We also compare log-determinants, as they are directly used in maximum likelihood estimation, and in most cases the log-determinants agree to high precision, although two situations stand out as being slightly inaccurate compared to the others. These two cases have a combination of sufficiently large and parameters, yielding especially ill-conditioned matrices that pose numerical challenges even when is computed to double precision accuracy. With this in mind, we consider the numerical agreement in these two cases to be satisfactory.
5 A Demonstration with Simulated Data
In this section, we demonstrate that in some cases even the slightest numerical inaccuracy in finite difference derivatives can accumulate so catastrophically as to yield completely incorrect Hessian matrices of the Gaussian log-likelihood, which can in turn lead to failure in second-order maximum likelihood estimation.
To demonstrate this we select random locations on the unit square and simulate ten independent realizations from a Matérn Gaussian process with parameters . Subsequently, we perform maximum likelihood estimation with the Ipopt library [33] using manually computed gradients and Hessians via the formulae provided in the introduction. In all cases, for derivatives involving only and , we use analytical derivatives of the Matérn covariance function. To study the effect of using finite difference derivatives versus our proposed AD derivatives, we consider six different optimization problems. First, we compute the first two derivatives of with respect to using finite difference approximations to compute Hessian matrices. In the second setting, we compute gradient and Hessian information using AD-generated derivatives and again optimize with true Hessians. In the next two settings, we again use finite differences and AD for derivatives that pertain to , but instead of Hessians we use expected Fisher matrices as proxies. Recalling that , the expected Fisher information, given by is, under appropriate regularity conditions, the asymptotic precision of maximum likelihood estimators. Unfortunately, these conditions are not often met for spatial processes under fixed-domain asymptotics [30]; nonetheless it is a valuable proxy for Hessian information. Moreover, it only requires first derivatives of the covariance function to compute, providing a natural way to separately investigate the effect of first and second finite difference derivatives. The final two settings are in a similar spirit and again investigate using only first derivative information, but now using the more general-purpose BFGS approximation for Hessian information.
While the parameters for the simulated data have been chosen purposefully, they are not implausible for much environmental data. The range parameter is large compared to the domain radius, which, even with 10 replicates, makes estimating the range difficult [36]. This level of dependence could occur in, for example, daily values of meteorological quantities such as temperature or pressure over a region of diameter on the order of 100 km. A smoothness of is likewise a very plausible value for a quantity like atmospheric pressure, which should be smooth but not too smooth. The primary challenge with these parameter values is that they require derivatives of very near the origin, which we have demonstrated in the previous section to be particularly problematic. With this said, computing the upper block of the Hessian with analytical derivatives in both cases limits the scope of impact of finite difference approximations as much as possible. Using finite difference derivatives directly on , which is well-behaved when its argument is near 0, rather than on directly, should also be favorable to finite differences.
| method | convergence | #iterations | terminal log-likelihood | MLE∗ |
|---|---|---|---|---|
| FD (BFGS) | No | |||
| FD (Fisher) | No | |||
| FD (Hessian) | No | |||
| AD (BFGS) | No | |||
| AD (Fisher) | Yes | |||
| AD (Hessian) | Yes |
Table 4 summarizes the results of the estimation procedures. In the case of true second-order optimization with finite difference derivatives used for Hessians, the optimization completely fails. Optimization using the expected Fisher matrix built with finite difference derivatives does successfully reach the MLE parameters to high accuracy, but due to slight inaccuracies in derivatives fails to reach the termination criteria tests used by Ipopt. Using AD derivatives to assemble the expected Fisher matrix solves this problem, and the optimization successfully terminates after iterations. Finally, optimization with the Hessians built with AD-generated derivatives is fast, accurate, and terminates successfully in just iterations. These results are consistent across various starting values and termination criterion tolerances.
To better understand why the second-order optimization with FD-based Hessians fails, we inspect these Hessians at several values. Starting at the initializer, we look at Hessian matrices computed using the two different sources of input derivatives. As a point of reference, we also provide a very high-order adaptive finite difference Hessian using the log-likelihood function itself. As above, the parameter order here is , so that the third column and row are the entries that pertain to derivatives of with respect to . Looking at the generic initializer of all parameters being equal to , we inspect the third column, using the shorthand for :
What immediately stands out in this comparison is that the component pertaining to the second derivative with finite difference-built Hessians is grossly inaccurate. For inaccuracies at this level, one has reason to be concerned that very important quantities for optimization, for example the unconstrained Newton direction , will be materially affected in a way that inhibits the progress of an optimizer.
Looking now at the third columns of these three matrices at the MLE, we see this problematic inaccuracy progressing further, using as shorthand for the MLE:
We observe once again that the AD-generated Hessians are very accurate. The FD-based Hessian is reasonably accurate save for the component pertaining to . But as before, this quantity is sufficiently inaccurate that it necessarily will change important optimization quantities. Moreover, the matrix is not even close to being positive semi-definite (with a minimum eigenvalue of compared to ’s minimum eigenvalue of ). Observing FD-generated Hessian matrices as the range parameter continues to increase, one will see a continual worsening of this specific component, which is arguably a particularly serious issue because it introduces structured inaccuracy to the optimization problem. This inaccuracy’s effect on derived quantities for optimization such as search directions is a very likely explanation for the complete failure in the optimization using Ipopt, which unlike simpler optimization software will pursue candidate directions in search of a feasible minimizer even if they do not immediately decrease the objective function value.
The conclusion from these results is clear: second-order optimization using finite difference methods for second derivatives of , and by extension , presents a significant risk. As a final observation, we reiterate that the demonstration chosen here is the best possible case for finite differences in that only the third row and column of these Hessians involve any approximation, and only one element of the Hessian matrix was incorrect to a degree of obvious concern. Even with the numerical issues of finite differences restricted to this small setting, the optimization results were a complete failure. For even slightly more complicated parametric models, such as adding a geometric anisotropy, the number of Hessian entries that involve finite difference derivatives will be greater, further increasing the risk of accumulated inaccuracies and severely incorrect point estimates.
6 Summary and Discussion
In this work, we identified a set of numerical approaches whose regions of accuracy and efficiency cover the entire domain of and that are well-suited to high-order automatic differentiation. After assessing the computational gains for first and second derivatives our approach provides, we demonstrated the practical significance of the accuracy gains through an example of maximum likelihood estimation via second-order optimization that completely fails when finite difference derivatives are employed, despite the finite difference derivatives being computed with the highly accurate AMOS library.
As modern datasets have continued to grow in size and complexity, accurately modeling dependence structure is more important than ever, and Gaussian processes have continued to serve as among the most popular tools for that purpose. We consider the full three-parameter isotropic Matérn model, in which one estimates , to be a bare minimum level of flexibility, at least for many datasets in the physical sciences. We thus hope that this work will empower practitioners to fit as easily as they do any other parameter. In order to make this as straightforward as possible, we provide the methods described in this paper in a convenient and freely available software package. While this work provides no discussion of scalable approximations to Gaussian likelihoods, they are a popular and important area of contemporary research in the field (see [17], for example, for a non-exhaustive but nonetheless expansive introduction to the topic). Particularly in the fixed-domain asymptotic regime, large datasets are especially informative about the smoothness parameter , and so there is particular synergy between the kernel derivatives we discuss here and scalable likelihood approximations that can use the information of significantly more data than would traditionally be possible with direct dense linear algebra.
Additionally, we hope that this work will reduce the complexity barrier to using Hessian matrices of the log-likelihood. Beyond the demonstration that we provide here of the value of true second-order optimization for maximum likelihood estimation, Hessian matrices of the log-likelihood are crucial to other common methods, such as Laplace approximations, including the method of integrated nested Laplace approximations (INLA) [28]. It is thus our hope that this work will be helpful to a wide variety of scientists and will make the use of the full three-parameter Matérn covariance a more standard practice.
Acknowledgements
The authors would like to thank Paul Hovland (Argonne National Laboratory) for engaging discussions on automatic differentiation as well as suggestions of relevant literature on the topic. They are also grateful to Lydia Zoells for her careful copyediting. Finally, they are very grateful to the two anonymous referees, both of whom provided exceptionally helpful comments and suggestions.
The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (“Argonne”). Argonne, a U.S. Department of Energy Office of Science laboratory, is operated under Contract No. DE-AC02-06CH11357. The U.S. Government retains for itself, and others acting on its behalf, a paid-up nonexclusive, irrevocable worldwide license in said article to reproduce, prepare derivative works, distribute copies to the public, and perform publicly and display publicly, by or on behalf of the Government. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
Appendix A Modifications for rescaling
In certain cases a scaled modified Bessel function, , may be useful in extending the interval of definition to larger arguments and avoiding numerical issues such as underflow. In the Matérn covariance function, a different prefactor comes up: . This function, while more sensitive to floating point round-off errors than its unscaled counterpart, is bounded at the origin for all orders .
This rescaled modified Bessel function is primarily useful for small arguments, and the two routines that can benefit the most from this rescaling are the direct series from Section 3.1 and the Temme recursion in Section 3.5. In Equation 3.2, one can simply bring the term inside the sum to cancel the product, completely removing the singularity at the origin as well as lowering the operation count, for both direct evaluations and AD computations.
To modify the expressions in Section 3.5 is slightly more complicated, since integer values of are computed via a recursion starting from the and terms. However, at the term contains a (logarithmically growing) singularity, problematic also for integer orders when . We have observed this can be avoided since the recursion can be re-arranged to be
where for the term starting off , i.e. , cancels entirely, simplifying the recursion for all integer orders. Introducing a branch in the code that checks for this condition results in AD-compatible differentiations of for non-zero integer values .
When and , as the terms and cannot be evaluated directly, and we have a secondary set of limit branch problems. In this case we observed that can be re-written as
By again manually performing the cancellations, we can preserve the derivative information for , and similarly for . This minor accountancy addition, which introduces special routines for for all orders , pays off in terms of accuracy, speed, and AD-simplicity.
Appendix B Profile likelihoods
For a collection of parameters , let denote the collection . Through a small amount of algebra, it can be observed that, given all parameters besides , the value of that maximizes the log-likelihood can be computed in closed-form as . Due to the observation that and some subsequent algebraic manipulations, one can thus re-write the likelihood as a function of all parameters besides to obtain
The value of this reformulation is that the dimension of the parameter estimation problem (and thus the challenging nonconvex optimization problem) has been reduced by one. For this paper, however, we only utilize the profile log-likelihood in order to visualize likelihood surfaces that would otherwise be three-dimensional.
References
- [1] M. Abramowitz and I. A Stegun. Handbook of mathematical functions with formulas, graphs, and mathematical table. In US Department of Commerce. National Bureau of Standards Applied Mathematics series 55, 1965.
- [2] D. Amos. Algorithm 644: A portable package for bessel functions of a complex argument and nonnegative order. ACM T Math Software (TOMS), 12(3):265–273, 1986.
- [3] T. Beck. Automatic differentiation of iterative processes. J Comput Appl Math, 50(1-3):109–118, 1994.
- [4] T. Beck and H. Fischer. The if-problem in automatic differentiation. J Comput Appl Math, 50(1):119–131, 1994. URL: https://www.sciencedirect.com/science/article/pii/0377042794902941.
- [5] J. Bezanson, A. Edelman, S. Karpinski, and V. B. Shah. Julia: A fresh approach to numerical computing. SIAM Review, 59(1):65–98, 2017.
- [6] Y. A. Brychkov and K. O. Geddes. On the derivatives of the Bessel and Struve functions with respect to the order. Integr Transf Spec F, 16(3):187–198, 2005.
- [7] Bradley Efron and David V Hinkley. Assessing the accuracy of the maximum likelihood estimator: Observed versus expected fisher information. Biometrika, 65(3):457–483, 1978.
- [8] F. W. J. Olver and A. B. Olde Daalhuis and D. W. Lozier and B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, B. V. Saunders, H. S. Cohl, and M. A. McClain. NIST Digital Library of Mathematical Functions, 2021. Release 1.1.2 of 2021-06-15.
- [9] J. A. Fike and J. J Alonso. Automatic differentiation through the use of hyper-dual numbers for second derivatives. In Recent Advances in Algorithmic Differentiation, pages 163–173. Springer, 2012.
- [10] Jacob Gardner, Geoff Pleiss, Kilian Q Weinberger, David Bindel, and Andrew G Wilson. Gpytorch: Blackbox matrix-matrix gaussian process inference with gpu acceleration. Advances in neural information processing systems, 31, 2018.
- [11] C. J. Geoga, M. Anitescu, and M. L. Stein. Scalable Gaussian Process Computations Using Hierarchical Matrices. J Comput Graph Stat, 29(2):227–237, 2020.
- [12] J. L. González-Santander. Closed-form expressions for derivatives of Bessel functions with respect to the order. J Math Anal Appl, 466(1):1060–1081, 2018.
- [13] A. Griewank and A. Walther. Evaluating Derivatives. Other Titles in Applied Mathematics. SIAM, 2008.
- [14] Mengyang Gu, Jesus Palomo, and James O Berger. Robustgasp: Robust gaussian stochastic process emulation in r. arXiv preprint arXiv:1801.01874, 2018.
- [15] Mengyang Gu, Xiaojing Wang, and James O Berger. Robust gaussian stochastic process emulation. The Annals of Statistics, 46(6A):3038–3066, 2018.
- [16] J. Guinness. Gaussian process learning via Fisher scoring of Vecchia’s approximation. Stat and Comput, 31(3):25, 2021.
- [17] Matthew J Heaton, Abhirup Datta, Andrew O Finley, Reinhard Furrer, Joseph Guinness, Rajarshi Guhaniyogi, Florian Gerber, Robert B Gramacy, Dorit Hammerling, Matthias Katzfuss, et al. A case study competition among methods for analyzing large spatial data. Journal of Agricultural, Biological and Environmental Statistics, 24(3):398–425, 2019.
- [18] F. Johansson. Arb: efficient arbitrary-precision midpoint-radius interval arithmetic. IEEE T Comput, 66:1281–1292, 2017.
- [19] Y. Liu and O. Marin. Special function neural network (SFNN) models. In 2021 IEEE International Conference on Cluster Computing (CLUSTER), pages 680–685, 2021.
- [20] O. Marin, C. Geoga, and M. Schanen. On automatic differentiation for the Matérn covariance. In NeurIPS, 2021. URL: https://papers.nips.cc/paper/2021.
- [21] B. Matern. Spatial Variation. Reports of the Forest Research Institute of Sweden. 1960.
- [22] G. Matheron. Estimating and choosing: an essay on probability in practice. Springer-Verlag, 1989.
- [23] V. Minden, A. Damle, Kenneth L. H., and L. Ying. Fast Spatial Gaussian Process Maximum Likelihood Estimation via Skeletonization Factorizations. Multiscale Model Sim, 15(4):1584–1611, 2017.
- [24] W. S. Moses and V. Churavy. Instead of rewriting foreign code for machine learning, automatically synthesize fast gradients. arXiv preprint arXiv:2010.01709, 2020.
- [25] Radford M Neal et al. Mcmc using hamiltonian dynamics. Handbook of markov chain monte carlo, 2(11):2, 2011.
- [26] G. Nemes. Error bounds for the large-argument asymptotic expansions of the hankel and bessel functions. Acta Appl Math, 150(1):141–177, 2017.
- [27] J. Revels, M. Lubin, and T. Papamarkou. Forward-mode automatic differentiation in Julia. arXiv:1607.07892 [cs.MS], 2016.
- [28] H. Rue, S. Martino, and N. Chopin. Approximate bayesian inference for latent gaussian models by using integrated nested laplace approximations. J R Stat Soc Ser B, 71(2):319–392, 2009.
- [29] William Squire and George Trapp. Using complex variables to estimate derivatives of real functions. SIAM review, 40(1):110–112, 1998.
- [30] M. L. Stein. Interpolation of Spatial Data: Some Theory for Kriging. Springer, 1999.
- [31] M. L. Stein, J. Chen, and M. Anitescu. Stochastic approximation of score functions for Gaussian processes. Ann Appl Stat, 7(2):1162–1191, 2013.
- [32] N. M. Temme. On the numerical evaluation of the modified bessel function of the third kind. J Comput Phys, 19:324–337, 1975.
- [33] A. Wächter and L. Biegler. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math program, 106:25–57, 2006.
- [34] L. White, M. Abbott, M. Zgubic, J. Revels, A. Arslan, S. Axen, S. Schaub, N. Robinson, Y. Ma, G. Dhingra, W. Tebbutt, N. Heim, A. D. W. Rosemberg, D. Widmann, N. Schmitz, C. Rackauckas, R. Heintzmann, F. Schae, K. Fischer, A.Robson, M. Brzezinski, A. Zhabinski, M. Besançon, P. Vertechi, S. Gowda, A. Fitzgibbon, C. Lucibello, C. Vogt, D. Gandhi, and F. Chorney. Juliadiff/chainrules.jl: v1.15.0, December 2021. doi:10.5281/zenodo.5750776.
- [35] L. White, W. Tebbutt, M. Zgubic, W. Bruinsma, R. Luo, N. Robinson, A. Arslan, S. Axen, S. Schaub, R. Finnegan, A. Robson, B. Richard, C. Vogt, E. Davies, and V. B. Shah. Juliadiff/finitedifferences.jl: v0.12.20, November 2021. doi:10.5281/zenodo.5724087.
- [36] H. Zhang. Inconsistent estimation and asymptotically equal interpolations in model-based geostatistics. J Am Stat Assoc, 99(465):250–261, 2004.