Flash-LLM: Enabling Cost-Effective and Highly-Efficient Large Generative Model Inference with Unstructured Sparsity
Abstract.
With the fast growth of parameter size, it becomes increasingly challenging to deploy large generative models as they typically require large GPU memory consumption and massive computation. Unstructured model pruning has been a common approach to reduce both GPU memory footprint and the overall computation while retaining good model accuracy. However, the existing solutions do not provide a highly-efficient support for handling unstructured sparsity on modern GPUs, especially on the highly-structured tensor core hardware. Therefore, we propose Flash-LLM for enabling low-cost and highly-efficient large generative model inference with the sophisticated support of unstructured sparsity on high performance but highly restrictive tensor cores. Based on our key observation that the main bottleneck of generative model inference is the several skinny matrix multiplications for which tensor cores would be significantly under-utilized due to low computational intensity, we propose a general Load-as-Sparse and Compute-as-Dense methodology for unstructured sparse matrix multiplication (SpMM). The basic insight is to address the significant memory bandwidth bottleneck while tolerating redundant computations that are not critical for end-to-end performance on tensor cores. Based on this, we design an effective software framework for tensor core based unstructured SpMM, leveraging on-chip resources for efficient sparse data extraction and computation/memory-access overlapping. Extensive evaluations demonstrate that (1) at SpMM kernel level, Flash-LLM significantly outperforms the state-of-the-art library, i.e., Sputnik and SparTA by an average of and , respectively.(2) At end-to-end framework level on OPT-30B/66B/175B models, for tokens per GPU-second, Flash-LLM achieves up to and improvement over DeepSpeed and FasterTransformer, respectively, with significantly lower inference cost. Flash-LLM’s source code is publicly available at https://github.com/AlibabaResearch/flash-llm.
1. Introduction
Generative models have demonstrated their effectiveness across a wide range of language and data management tasks (Radford et al., 2019; Brown et al., 2020; Trummer, 2022; Narayan et al., 2022; Tuli et al., 2022). However, with the rapid growth of the parameter size (e.g. GPT-2 (Radford et al., 2019) 1.5 billion parameters, GPT-3 (Brown et al., 2020) 175 billion, and Megatron-Turing NLG (Smith et al., 2022) 530 billion), it becomes increasingly challenging to efficiently deploy these models. On one hand, their weights could be too large to be placed on GPUs. For example, GPT-3 model requires 350GB memory to store only the parameters with FP16 data type, whereas the NVIDIA A100 GPU (NVIDIA, 2020) only has a max of 80 GB memory. On the other hand, large generative models usually cause very high inference latency even using multiple GPUs as large amounts of computation and memory access are required.
There are three basic characteristics for practical model inference: accuracy, efficiency (i.e., latency and throughput), and cost (i.e., how much hardware resource it consumes). The common approach to deploy large models by partitioning the model weights onto multiple devices (Shoeybi et al., 2019; Zheng et al., 2022a) could suffer from high cost and low efficiency. On one hand, for data-center production scenarios, using multiple GPUs for a single inference of a single model leads to a low ROI (return on investment) and can be too costly in practice. On the other hand, this conventional approach requires extra cross-device communication, further exacerbating the efficiency problem. GPU memory offloading and swapping is another approach to support large weights given limited GPU memory (Sheng et al., 2023; Aminabadi et al., 2022). However, the offloading and swapping approaches usually result in a long inference latency and thus can be impractical for online inference services.
The weight pruning methods (Hoefler et al., 2021) (sparsification) have been demonstrated to be effective in reducing memory usage and computations for model inference while retaining good accuracy through removing a portion of less salient connections in neural networks. In practice, unstructured pruning typically retains better accuracy than more restrictive structured pruning (Sun et al., 2023; Hoefler et al., 2021; Han et al., 2015a; Gomez et al., 2019; Ullrich et al., 2017; Frantar and Alistarh, 2023; Lin et al., 2022). However, it is difficult to support unstructured sparsity on modern GPU architectures efficiently, especially since the unstructured sparse MatMul (SpMM) is hard to support on the high-performance but highly-structured tensor core architecture. Thus, this design direction has been largely neglected so far since higher performance is very difficult to achieve. For example, the state-of-the-art unstructured SpMM implementations (e.g. cuSPARSE (NVIDIA, 2023b), Sputnik (Gale et al., 2020a)) can not even outperform the dense counterpart (cuBLAS (NVIDIA, 2023a)) until the model sparsity is higher than 98% and 86%, respectively. Note that tensor cores on modern GPUs usually can achieve nearly an order of magnitude higher peak performance than SIMT cores.
To address this critical issue that bottlenecks LLM inference performance and cost, we propose Flash-LLM, an efficient GPU library to support unstructured sparsity on tensor cores for large generative model inference. With unstructured sparsity, Flash-LLM addresses the memory footprint problem which leads to lower costs while retaining high model accuracy. By being able to leverage tensor cores’ high peak performance, Flash-LLM achieves lower latency for unstructured SpMM compared to the existing sparse/dense MatMul solutions. The high-level design insight of Flash-LLM is this Load-as-Sparse and Compute-as-Dense strategy. We make an important observation that the key MatMuls in generative model inference are usually very skinny. Furthermore, the performance of these skinny MatMuls is bound by global memory access (or memory bandwidth) rather than the computation capability of tensor cores. Because of this, we propose an innovative approach to support unstructured sparsity on tensor cores by leveraging sparse memory load to improve the limited memory bandwidth while effectively tolerating redundant tensor-core computation (Sec.3.2).
Given the insight above, it is still challenging to actually design and implement this high-level Load-as-Sparse and Compute-as-Dense approach. First, it requires a well-designed data format for efficient sparse data storage and extraction. The sparse data extraction is non-trivial, which requires a sophisticated design to load and extract sparse data with minimal access cost in the hierarchical GPU memory given limited on-chip memory resources. It also introduces new challenges in designing the MatMul computation pipeline beyond conventional dense MatMul strategies. In Flash-LLM, we propose a new sparse format called (Tiled-CSL) to support the tile-by-tile SpMM execution with tensor cores (Sec.4.3.1). Based on Tiled-CSL, we then design the sparse-to-dense transformation approach carefully by using the distributed registers and shared memory buffers for sparse data extraction (Sec.4.1). Then, an efficient two-level overlapping strategy of memory and computation is introduced to coordinate the sparse-to-dense transformation on weights, the dense feature map data loading, and the tensor core operations with a full software pipeline (Sec.4.2). Finally, we propose an ahead-of-time sparse data reordering approach to further reduce shared memory bank conflicts111 GPU shared memory is divided into multiple memory banks that can be accessed simultaneously. Bank conflict means multiple addresses of a memory request map to the same memory bank, causing serialized accesses. (Sec.4.3.3). In summary, this paper makes the following contributions:
-
•
We propose Flash-LLM, the first cost-effective and highly-efficient software framework for supporting large generative model inference, opening up the scope of enabling unstructured sparsity exploration on high-performance tensor cores.
-
•
We propose a general Load-as-Sparse and Compute-as-Dense approach to reduce memory footprint and increase the efficiency of the key skinny MatMuls by leveraging the insight of addressing the major memory bandwidth bottleneck in LLM inference while tolerating redundant tensor-core computations.
-
•
We propose an efficient software pipeline design to enable Flash-LLM by effectively leveraging our new sparse format, the sparse-to-dense transformation, and a two-level overlapping strategy.
-
•
Flash-LLM is implemented and integrated into FasterTransformer for ease-of-use. Extensive evaluation results have shown that (1) at the kernel level, Flash-LLM outperforms the state-of-the-art solutions Sputnik and SparTA by an average of and , respectively. (2) At end-to-end framework level on OPT-30B/66B/175B models, for tokens per GPU-second, Flash-LLM achieves up to and improvement over DeepSpeed and FasterTransformer, with significantly lower inference cost.
2. Background


2.1. Generative Model Inference
Inference Procedure of Modern Generative Models. Modern generative models’ inference is typically conducted in two phases: prompt processing and token generation. As illustrated in Fig.1a, the generative model first performs prompt processing to process user input sequences (’I love dogs’) and generates the first new token (’and’). Then the model turns into the auto-regressive token generation phase, where the single output token generated in step i-1 will be taken as input to generate the new token in step i iteratively.
In the prompt processing phase, multiple tokens within the input sequence will be processed at the same time, resulting in input tensors with shape (Fig.1a). , , and indicate the inference batch size, prompt sequence length, and the model hidden dimension, respectively. Whereas in the token generation phase, only the single token generated in the last iteration will be taken as input thus forming the input tensors in the shape of . Note that to prevent re-computations on K and V vectors 222K and V vectors of previous tokens are needed by the attention (Vaswani et al., 2017) mechanism. of the previous tokens, a pre-allocated memory buffer (a.k.a. KV-Cache shown in Fig.1b) is usually used during token generation. At each step, a new KV pair is generated (in yellow) and written to the KV-Cache.
Inference Performance Hotspot of LLMs. Fig.2 illustrates the typical decoder architecture of a single layer in modern attention-based generative models. There are in total four major matrix multiplications (or MatMuls) in the decoder layer: QKV Projection, Output Projection, MLP1, and MLP2. Unlike previous encoder-centric non-generative language models (e.g., BERT (Kenton and Toutanova, 2019)) of which the performance bottleneck is mainly at the multi-head attention computation, generative model inference’s performance is heavily bounded by these four MatMuls. According to our experiments on OPT-66B (Zhang et al., 2022a) model inference, these four MatMuls are the top contributors to the overall latency which accounts for of the end-to-end execution time and also the top contributor of the memory consumption which accounts for of the overall memory usage.

2.2. Matrix Multiply in LLM Inference
Skinny Matrix Multiply. The Matrix Multiply (MatMuls) in Fig.2 can be formalized as , where is the weight matrix of shape and is the feature map matrix of shape . In this paper, we call these MatMuls ”Skinny MatMuls”, as their dimensions are much smaller than the and dimensions. 333For these MatMuls, and are integer multiples of hidden size while equals inference batch size (typically orders of magnitude smaller than hidden size).
Differences between Tensor/SIMT cores. SIMT cores (aka. CUDA cores) are general-purpose execution units that handle a wide range of instructions for parallel execution, while tensor cores (NVIDIA, 2020, 2022b) are specialized units designed specifically to accelerate dense MatMul computations. Tensor cores provide significant acceleration for dense MatMuls, e.g. higher throughput than SIMT cores in A100 GPUs with FP32 accumulation.
Conventional techniques leveraging SIMT cores for sparse MatMuls can not be directly applied to tensor cores as SIMT and tensor cores work at very different granularity. SIMT cores work on the granularity of scalar values, e.g. the FMA instruction on scalar value. The per-element granularity makes it easy to do computation skipping at the element level for SpMM. However, tensor cores work at a much more coarse-grained granularity than SIMT cores, e.g., perform a matrix multiply between two matrices with the shapes of and in each instruction. Thus, tensor cores do not allow skipping arbitrary element-level computations.
3. Opportunities and Insights
3.1. Unstructured Sparsity on Tensor Cores
There are two typical types of pruning principals. The most flexible pruning strategy (unstructured sparsity) is to remove less salient elements without considering the distribution of the pruned elements in the weight matrix. Taking magnitude pruning for example, we can rank all the elements in the matrix based on their absolute values and then remove the weights with the smallest magnitude. Another strategy (structured sparsity) is to prune the less salient weights, but at the same time, some kind of structural criteria must be enforced. For example, the weight matrices can be split into non-overlapping vectors (Chen et al., 2021; Li et al., 2022a) or blocks (Gray et al., 2017), and then each vector/block is either kept or removed during pruning.
In short, the major difference between structured and unstructured pruning is that extra constraints must be satisfied for structured pruning. Even though structured sparsity is friendly for hardware acceleration, it suffers from more severe model accuracy degradation (Sun et al., 2023; Hoefler et al., 2021; Han et al., 2015a; Gomez et al., 2019; Ullrich et al., 2017; Frantar and Alistarh, 2023) as it limits the freedom of deciding which element to prune. As shown in (Lin et al., 2022), compared to structured sparsity which has 5% accuracy drop, unstructured sparsity only results in 1% accuracy drop. In our experiments, the OPT-like models could greatly preserve accuracy through retraining-based unstructured pruning (Liu et al., 2018; Han et al., 2015b) at 80% sparsity (e.g., the accuracy only decreases from 85.55% to 84.11% for OPT-30B).

However, the conventional techniques for supporting random unstructured sparsity in SpMM execution are not effective since they focus on leveraging SIMT cores without a sophisticated way of utilizing high-performance tensor cores. Fig.3 shows the performance comparison of different techniques for SpMM on an OPT-66B inference task with batch size 8. Note that the standard pruning for LLM inference typically requires a moderate level of sparsity (e.g., 80%) to preserve model quality while reducing memory footprint. CuSparse (NVIDIA, 2023b), the NVIDIA SpMM library, shows poor performance as it is mainly designed for scientific applications where matrices are extremely (99%+) sparse. Sputnik (Gale et al., 2020a), the state-of-the-art SIMT-core-centric optimization for unstructured SpMM on DL tasks still cannot outperform cuBLAS(dense) until a high sparsity is reached.
We observe that sparse MatMul kernels in existing sparse libraries are usually slower than their dense counterpart (cuBLAS(NVIDIA, 2023a)). The reason is that cuBLAS have leveraged the tensor cores, while sparse MatMul kernels are leveraging SIMT cores in state-of-the-art solutions. Note that A100 GPU (NVIDIA, 2020) can provide higher computational throughput using tensor cores than using SIMT cores for dense MatMuls. Although Sputnik can effectively leverage SIMT cores for unstructured sparsity processing, its performance is still limited by the peak performance of SIMT cores.
Due to the clear peak performance discrepancy between SIMT and tensor cores, there is a strong demand for high-performance unstructured SpMM support for LLM inference. However, it is non-trivial to enable high-performance unstructured SpMM onto the highly restrictive tensor cores as tensor cores do not allow skipping arbitrary scalar-level computations (described in section 2.2). Previous SpMM works are based either on highly structured sparse matrices (Chen et al., 2021; Huang et al., 2022; Gray et al., 2017) (not random unstructured sparsity), or for extremely high sparsity ratio (Wang et al., 2023) (i.e., ¿95%, inappropriate for LLMs’ inference accuracy), rather than random unstructured sparsity at a moderate sparsity ratio range for high accuracy. SparTA(Zheng et al., 2022b) leverages sparse tensor cores (Mishra et al., 2021) for major computations. However, it cannot effectively exploit high sparsity as sparse tensor cores only support 50% sparsity (i.e., 2:4 sparsity). As shown in Fig.3, the performance of SparTA is lower than Flash-LLM especially as the sparsity increases.
3.2. Design Opportunities
Given the natural mismatch between the unstructured SpMM computation and the highly structured tensor core architecture, it is essential to have a highly efficient SpMM solution on tensor cores according to the workload characteristics of modern LLMs. As discussed in Sec.2.2, MatMuls in modern LLMs inference are skinny. As a result, the bottlenecks of the skinny MatMul computations are the off-chip memory access and bandwidth limitations, rather than the arithmetic processing on tensor cores. Based on this observation, the basic idea to address this problem is through a Load-as-Sparse and Compute-as-Dense approach. Specifically, the GPU kernel loads the weight matrices from global memory in sparse format with reduced size and reconstructs the corresponding dense format in high-speed on-chip buffers for tensor core computation. The key insight is that the bottleneck for LLM inference is not at the computation side thus we can tolerate the redundant computations with tensor cores. We systematically describe how the off-chip memory transactions become the performance bottleneck in Sec.3.2.1, and why it is possible to tolerate such redundant computation for skinny SpMMs in LLMs’ inference in Sec.3.2.2.
3.2.1. Performance Bottleneck of Skinny MatMuls in LLM Inference.
We analyze the performance bottleneck of skinny MatMuls execution starting from dense MatMul workloads in LLMs. According to our profiling results for OPT-66B (Zhang et al., 2022a), the average utilization of tensor cores is around 5.0%, 10.1%, 19.9%, and 39.7% under typical batch sizes of 8,16,32 and 64 as shown in Fig.4, while the bandwidth of global memory is already fully saturated. The underlining cause for this is that the compute intensity (i.e., FLOP/Byte) of skinny MatMul is very low. For a MatMul described in sec. 2.2, the total operations conducted are floating-point operations (FLOP), and the corresponding data read is bytes with FP16 data type. Thus, the computational intensity () is:
| (1) |

According to Equation.1, it is easy to demonstrate that the overall of a MatMul can be easily restricted by either a small M or N dimension. For instance, for a skinny MatMul where is 16, will have a strict upper bound of 16 no matter how big the dimension is. Note that in generative LLM models, the dimension equals the inference batch size which is usually very small in production environments. Thus, the is strongly bounded by the dimension in real-time LLM inference. According to the roofline model (Williams et al., 2009), the performance of a kernel with low computational intensity will be easily bounded by memory bandwidth.
3.2.2. Load as Sparse, Compute as Dense
Given that the bottleneck of skinny MatMul comes from memory access/memory bandwidth rather than arithmetic computation, we propose the basic idea of Load-as-Sparse and Compute-as-Dense here which leverages the performance boost from reduced memory access while enabling the efficient use of tensor cores for unstructured sparsity (refer to Sec.4 for details). Under this basic idea, given the sparsity ratio (the weight matrix is sparse while the feature map matrix is dense), the computational intensity can be improved to:
| (2) |
Fig.5 shows the CIs and their corresponding achievable tensor core performance of a typical MatMul (: 48k, : BS, : 12k) in OPT-175B model inference with different batch sizes. According to the figure, MatMuls in generative model inference with different batch sizes all face memory wall issues. As a result, the dense MatMuls kernels can only achieve 5.1%, 10.3%, 20.5%, and 40.1% peak performance of tensor cores bounded by insufficient global memory bandwidth. These theoretical values are consistent with our actual measurements in Fig.4. In theory, with Load-as-Sparse and Compute-as-Dense approach under 40% sparsity, the tensor cores utilization can be improved to 8.5%, 17.1%, 34.2%, and 68.2%.

4. Design Methodology
Flash-LLM leverages both SIMT cores and tensor cores effectively for efficient unstructured SpMM computation. The flexible SIMT cores are exploited for Sparse-to-Dense Transformation (i.e., Load-as-Sparse) while tensor cores are used for compute-intensive tensor computations (i.e., Compute-as-Dense). We will give an overview of the high-level optimizations of Flash-LLM in Sec.4.1. Then we will describe the design of Flash-LLM’s computation pipeline in Sec.4.2. We illustrate the novel sparse format (tiled-CSL format) and the efficient memory access techniques in Sec.4.3. Finally, we described the end-to-end inference system enabled by our Flash-LLM in Sec.5.
4.1. Design Overview
We use the tiling-based approach for the SpMM computations in Flash-LLM. Fig.6a shows the tiling method of Flash-LLM, where each thread block (TB) is in charge of calculating a tile (e.g., the green tile in the shape of ) in output matrix . For each iteration, each thread block loads (shape ) in sparse and (shape ) in dense from global memory. is then transformed to dense format with Sparse-to-Dense Transformation shown in Fig.6b and stored in shared memory while is directly stored in shared memory. Finally, each thread block consumes the dense data in shared memory and generates the output tile through tensor core computations.



Fig.6b shows the overall kernel behavior of Flash-LLM from the microarchitecture aspect. Shared memory is used as the workspace to store the extracted data from sparse to dense format, where all threads within the thread block work together collaboratively to load sparse encoding (SE) 555 We refer to the data of in the sparse format as sparse encoding in this paper. of from global memory and store them in shared memory with the dense format. Note that each tile on global memory is encoded into sparse encoding with fewer bytes than the dense format, for which the corresponding global memory data movements can be reduced compared to dense MatMul. Specifically, the basic idea of Sparse-to-Dense Transformation is extracting non-zero elements from the sparse encoding on global memory to their corresponding locations in the dense format on shared memory while other locations are filled with zeros. We use the distributed registers as the intermediate buffer to store the non-zero elements before extracting them to shared memory. We do not use shared memory as this intermediate buffer to avoid the turn-around shared memory access of the sparse encoding.
4.2. Computation Pipeline Design of Flash-LLM
Given that each thread/thread-block consumes a large fraction of the overall registers/shared-memory as buffers for tiling, the GPU thread-level parallelism (TLP) is inherently low. Thus, it is important to optimize the instruction-level parallelism. We describe the software pipeline of Flash-LLM in this section where the off-chip memory loading (Sparse-to-Dense Transformation) and tensor core computations are processed in a pipeline manner efficiently.
4.2.1. Two-level Overlapping of Memory and Computation.
As described in Sec.4.1, it requires several stages to load the sparse encoding from the global memory to shared memory in dense format for each . Specifically, it requires loading sparse encoding from global memory to the distributed registers (gmem2reg stage), resetting the target shared memory buffer with zero (rst_smem stage), and writing the sparse encoding from registers to the corresponding locations on shared memory buffer (extract stage). As for , which is already in dense format, it only requires loading directly from global memory to the target shared memory buffer (ld_dense stage). Finally, the smem2tc stage loads the shared memory data of and and executes tensor core computations.
As shown in Fig.6c, Flash-LLM exploits a two-level overlapping of the above memory and computation stages for efficient execution. On one hand, it leverages the software pipeline through double buffering to overlap off-chip memory loads and Sparse-to-Dense transformation with tensor core computation, called inter-iteration overlapping. On the other hand, it overlaps the stages of off-chip memory load within Sparse-to-Dense transformation for more efficient memory activities, called intra-iteration overlapping. The horizontal axis of Fig.6c represents the execution time while the vertical axis represents the activities with the double buffer. It uses two shared memory buffers for (corresponds to A1 and A2) and (corresponds to B1 and B2), and one register buffer reused in different iterations (corresponds to SE). Specifically, SE in Iteration-1/3 (Iteration-2/4) and A1 (A2) correspond to the Sparse-to-Dense transformation process of on the first (second) set of buffer, and B1 (B2) corresponds to the data movement of on the first (second) set of buffer. As for inter-iteration overlapping, as shown in Iteration-2 in Fig.6c, while loading data from shared memory and executing tensor core computations for data on the first set of buffers, Flash-LLM loads and extracts data from global memory to shared memory for the second set of buffers. As for intra-iteration overlapping, the activities of A1 and B1 are processed in parallel, and the gmem2reg and rst_smem stages on are also processed in parallel. In this way, the sparse data loading, dense data loading, and tensor core computations can be overlapped efficiently.
A critical design for Sparse-to-Dense transformation is explicitly using registers as data buffers between global memory and shared memory. In Flash-LLM, the sparse encoding movement from global memory to shared memory is explicitly split into two stages, i.e. LDG (loading data from global memory to registers) instructions during gmem2reg and STS (storing data to shared memory from registers) instructions during extract as shown in Fig.6c. On one hand, the split two-stage design helps to increase instruction-level-parallelism (ILP) to hide high global memory access latency. Note that each pair of LDG and STS instructions have load-use dependency. If we do not split the gmem2reg and extract into two stages but launch each pair of LDG and STS instructions in the adjacent cycles (e.g. directly storing to shared memory after loading from global memory) , each GPU thread will execute instructions in the order of without ILP of global memory load (i.e., LDGs). By splitting the two instructions into two stages as in Fig.6c, the execution order will be and results in a high ILP of global memory load. On the other hand, splitting the data movement into gmem2reg and extract enables the overlapping opportunity between gmem2reg and rst_smem. Note that STS instructions within extract should not be launched before the completion of rst_smem stage, otherwise, the data written by STS instructions might be overwritten by rst_smem incorrectly. The execution of gmem2reg and rst_smem can be overlapped once the gmem2reg contains no shared memory write (all STS instructions are assigned to the extract stage), which further increases ILP.
4.2.2. Minimum Range of Synchronizations and Memory Barriers
Given the complex pipeline in Fig.6c, it requires a set of thread synchronizations and memory barriers to ensure correctness. Flash-LLM inserts the minimum range of synchronizations and memory barriers to ensure correctness while keeping the overlapping.
To avoid the data written by extract being overwritten by rst_smem incorrectly, Flash-LLM inserts the explicit thread-block level synchronization between the two stages to ensure that all the threads have finished their work resetting the A1/A2 buffer in shared memory, shown as the first yellow lines in each iteration in Fig.6c. Meanwhile, it also requires another synchronization to ensure that all data movements and tensor core operations of the current iteration are completed before starting the next iteration, shown as the second yellow lines in each iteration in Fig.6c. Take Iteration-1 as an example, we should make sure that all the threads have finished writing the A1 and B1 shared memory buffers before we start Iteration-2, as the data on the shared memory buffers will be loaded to tensor cores as inputs in Iteration-2. Besides, we have to make sure that all the threads have finished reading the data from the register buffer for extract in Iteration-1 before letting them be overwritten by the rst_smem in Iteration-2.
Beside the thread-block synchronizations, it also requires memory barriers after asynchronous copy activities of global-to-shared data movement. Flash-LLM makes use of the asynchronous copy primitives on GPU for the overlapping of data movement and other activities. Note that the asynchronous copy primitive cp.async, starting from NVIDIA Ampere GPU (NVIDIA, 2020), allows moving data from global memory to shared memory in the background asynchronously while executing other computations in the foreground. Specifically, both the rst_smem and ld_dense stages use the cp.async primitives to enable the overlapped execution on the double buffer.
To enable a fine-grained pipeline execution, Flash-LLM uses different async-copy barriers for rst_smem and ld_dense stages. As shown in Fig.6c, the extract stage waits for the completion of only rst_smem, while the final thread-block barrier of each iteration waits for the completion of all previous cp.async operations. In this way, the extract stage could be overlapped with the ld_dense stages.
4.2.3. Overall Implementation
Alg.1 shows the implementations of the pipelined computation in Flash-LLM. In line 3, the software pipeline will be initialized, preparing the data of and on shared memory for the tensor core computations of the first iteration in the main loop. The following iterations described in Fig.6c is implemented in lines 7-28. For each iteration, it issues the instructions for the asynchronous data loading for the next iteration and does the tensor core computation of the current iteration in a double buffer manner. Specifically, one for the next iteration will be loaded and extracted from global memory to shared memory (rst_smem, gmem2reg, and extract), and one dense will be loaded directly from global memory (ld_dense). The rst_smem stage is in line 17, where each thread issues cp.async operation to set buffer A to zeros. In line 19, gmem2reg is accomplished, where sparse encoding is loaded from global memory to the distributed registers. The ld_dense stage is in line 20, where the data for is loaded from global memory to shared memory buffer with cp.async operations. After launching these asynchronous memory operations, tensor core operations are launched in line 23. Note that we load dense matrices from shared memory to registers using ldmatrix.sync instruction and utilize tensor cores for the core computations by explicitly launching mma.sync instruction in the function Pipelined_Shared2Reg_TensorCoreOps().
The first async-copy barrier in Fig.6c is in line 25, guaranteeing that all asynchronous operations launched in line 17 are completed while the operations launched in line 20 can still be in progress. The extract stage is in line 26, where the data on the distributed registers are extracted to the shared memory buffer of . Finally, the async-copy and thread-block barriers are called in line 28 to make sure that all threads have completed their work in this iteration.
Different from dense MatMul where the data size to be loaded from global memory can be inferred by the tile sizes, the size of sparse encoding is determined by the number of non-zeros (nnz) within , which is unpredictable. Before loading the sparse encoding for each tile, Flash-LLM identifies its start offset and the length in global memory buffers. Such information is maintained in TileOffsets array, which is stored in global memory (more details in Sec.4.3). To avoid instruction stalls caused by long latency global memory access, this metadata should be pre-fetched. In lines 5-6, the start offset and the size of sparse encoding for the first iteration are pre-fetched. At the beginning of each iteration, the start offset and the size of the current are updated using the value in registers pre-fetched in advance. In lines 11-12, it pre-fetches the start offset and the length for the next iteration.
4.3. Sparse Encoding and Runtime Parsing
4.3.1. Tiled-CSL Format
The sparse encoding format of matrix is essential for efficient sparse data storage and Sparse-to-Dense Transformation. We propose a tile-by-tile sparse encoding format to support the optimizations in Sec.4.2 effectively. The non-zero elements are organized tile-by-tile, where each tile maintains its non-zero elements accompanied by the sparse index. As shown in Fig.7, the data of each tile within the sparse matrix are encoded into a small array, and combining all tiles will form the overall array (NonZeros Array). The TileOffsets Array maintains the starting offset of each tile in NonZeros Array. The number of non-zero elements of each Tiled-CSL tile is the difference between two corresponding elements in TileOffsets Array. For each tile in NonZeros Array, each element is stored along with its location within the tile. As shown in Fig.7, each non-zero weight is in 16-bit half-precision and each location is encoded into a 16-bit short integer.

4.3.2. Register to Shared Memory Data Extraction based on Tiled-CSL Format
As described in Alg.2, each thread extracts non-zero values from its sparse encoding buffer Reg[] to the shared memory buffer A with a loop. The v() and idx() functions are used to extract the value (high 16 bits) and its location (low 16 bits). There are some special considerations when using registers as intermediate buffers for sparse encoding. Different from shared memory and global memory, GPU registers are not addressable, which means we can not access an array of registers using a variable offset. As a result, forcing an array defined in CUDA into registers requires that, all the indices used to access the array can be determined statically at compile-time. Otherwise, the array will be stored in global memory instead. In line 1 in Alg.2, #pragma unrol is used to notify the GPU compiler to fully unroll the main loop, so that all the indices used to access the can be determined statically. Note that adding such compiling directive alone is not enough as a loop with a variable number of iterations can not be fully unrolled. Thus, we use a constant value (the upper bound of the number of iterations, typically 32/64 in our implementation) in line 2 instead of using the variable value .
4.3.3. Ahead of Time Sparse Data Reordering
There are two types of shared memory access in the computation pipeline for the sparse weight matrix . The one is shared memory load for tensor core computation in smem2tc stage. The other one is shared memory store in extract stage. It is essential to avoid bank conflict for good performance. However, the random sparsity makes it challenging to avoid bank conflict of both shared memory load and store.
As for the smem2tc stage, it makes use of ldmatrix intrinsic for efficient data loading from shared memory to registers for tensor core computation. Fig.8a shows the behavior of ldmatrix where eight threads collectively load an matrix in FP16 from shared memory. This matrix reading can be served by a single shared memory wavefront666A wavefront is the maximum unit of work that can pass through the GPU hardware pipeline per cycle. At most 1,024 bits can be loaded per wavefront for shared memory. if there is no bank conflict. The bank-conflict-free memory load of ldmatrix requires that all scalars within the matrix can be read from disjoint memory banks. Fig.8a shows an example shared memory data layout demonstrating the bank assignment (bank ID ranging from 1 to 32) to achieve bank-conflict-free ldmatrix. Thus, each scalar can be assigned a bank ID according to its location within , given a specific data layout.
However, this requirement will easily cause bank conflict of shared memory store during extract stage due to the random position of the sparse elements in matrix . In other words, we can guarantee the bank-conflict-free load according to the layout requirement of ldmatrix, but cannot avoid bank conflict store in this way during extract stage. Fig.8b gives an example, where each non-zero (NonZero) value should be stored in a target shared memory bank (SMemBank) according to their relative position within to meet the requirement of bank-conflict-free ldmatrix. As the distribution of NonZeros is random, the target SMemBank for each NonZero value is also random. As a result in Fig.8b, all CUDA WARPs (the NonZeros with the same color are processed by the same WARP) suffer from bank conflict and lead to multiple shared memory wavefront (SMem WF).



To reduce the bank conflict, we propose the ahead of time sparse data reordering approach. The basic insight is that the bank-conflict-free ldmatrix already determines the target bank of each data element, we can thus reorder the data elements in each Tiled-CSL tile so that elements correspond to different banks could be organized into the same WARP for extract execution. Specifically, it iteratively selects the sparse element that corresponds to different memory banks when generating the NonZeros sub-array for each Tiled-CSL tile. Fig.8c shows an ideal case where only one shared memory wavefront is needed to serve one WARP executing extract stage after data reordering. Note that the data reordering is within Tiled-CSL tile scope, which only changes the data distribution on global memory but does not change that on shared memory buffers. In other words, it is a way to change the data placement on global memory to achieve more efficient shared memory access.
Alg.3 shows the algorithm to generate Tiled-CSL format from the original sparse matrix according to ahead of time sparse data reordering approach. The input is the sparse matrix A with rows and columns in dense format, where some elements are already set to 0 through model pruning. The outputs are NonZeros and TileOffsets, the key components of Tiled-CSL format. NonZeros are split into groups each of which contains 32 non-zeros in line 2. Each group of non-zeros will be written to shared memory during extract stage within one shared memory request. At lines 7-24, the Tiled-CSL format of one tile () will be generated. At lines 11-14, each non-zero within matrix A will be encoded into a 32-bit word containing . Besides, non-zeros are distributed to 32 different buckets ( at line 4) according to their target shared memory bank ID ranging from 0 to 31 as calculated in line 13. In line 16, the total number of non-zeros (NNZ) is counted. At line 19-22, one group of non-zeros are formed by iteratively picking non-zeros from NZ_Bucket[id] where is the bucket with the most non-zeros not processed at that time.
5. Implementation
We provide a set of C++ APIs for high-performance Flash-LLM kernel. We integrate Flash-LLM kernel into FasterTransformer (NVIDIA, 2022a), enabling high-efficiency distributed inference with sparsified weight matrices. Specifically, we extended its corresponding class definition (i.e. DenseWeight class) to support the Tiled-CSL format. Besides, we extended its library wrapper (i.e., cuBlasMMWrapper class) to support calling either the dense MatMul library or Flash-LLM SpMM kernel according to the given data format. Flash-LLM can also be easily integrated into other deep learning frameworks through library calls with Flash-LLM API. We also provide a weight reformatting tool to generate sparse matrices in Tiled-CSL format given the pre-trained dense PyTorch model.
In our implementation, the size of in Fig. 6a is 128 or 256, is 64, and is 8/16/32/32 when the dimension of MatMul (inference batch size) is 8/16/32/64. For larger dimensions, the is 64. The thread block size is 128. These configurations work well for the workloads we evaluated in Sec.6. The configurations can be reconfigured easily for other workloads. The configuration tuning is not in the research scope of this paper.
6. Evaluation
We evaluate the performance of Flash-LLM on two levels: kernel-level benchmarking and model-level evaluation. The evaluation is conducted on the NVIDIA A100-SMX8-80GB platform (128-core Intel Xeon Platinum 8369B CPU @2.90GHz, 8 NVIDIA A100 GPU @80GB), with Ubuntu 18.04 and CUDA 11.8. We enable auto-mixed precision (AMP) for all evaluations. We mainly do experiments on NVIDIA A100 GPUs. However, the method we proposed is also a good reference for the kernel design of TPU and Intel CPUs that are equipped with customized hardware for matrix multiplication.
6.1. Kernel Performance
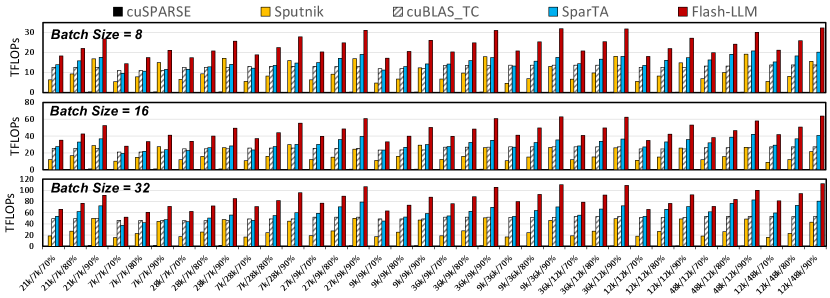
Workloads, baselines, and settings. We evaluate Flash-LLM on MatMuls under different shapes, coming from the four MatMuls described in Sec.2.1 within OPT-30B, OPT-66B, and OPT-175B (Zhang et al., 2022a) given four different batch sizes (8, 16, 32, and 64). For each MatMul shape, we evaluate the kernel latency under 70%, 80%, and 90% of random sparsity in the weight matrices. The baselines we compare include cuSPARSE (NVIDIA, 2023b), Sputnik (commit: 46e380c) (Gale et al., 2020b, a), SparTA (commit: 1f61a36) (Zheng, 2022; Zheng et al., 2022b), and cuBLAS (NVIDIA, 2023a). CuSPARSE is part of the CUDA Toolkit for handling sparse matrices. Sputnik is a library of sparse linear algebra kernels for deep learning, which achieves state-of-the-art SpMM performance based on SIMT cores. SparTA supports unstructured sparsity based on 2:4 structured sparsity on tensor core (Mishra et al., 2021). As SparTA only supports FP32 precision, we extended SparTA to support input matrices in FP16. CuBLAS targets dense MatMul rather than SpMM. We include it as a baseline here to show the practical performance gains/loss compared to the basic dense implementations of LLM inference.
Results. Fig.9 shows the kernel performance (TFLOPs) of Flash-LLM and the baselines. The throughput can be calculated by . As shown in Fig.9, Flash-LLM performs the best constantly compared to the baselines. On average, Flash-LLM outperforms Sputnik/SparTA by /, /, and / under 70%, 80%, and 90% sparsity respectively. Besides, Flash-LLM can also outperform the state-of-the-art dense kernels cuBLAS with tensor core enabled by , , and . CuSPARSE shows poor performance under such moderate-level sparsity, as it is designed for matrices with ¿95% sparsity(NVIDIA, 2023b). As for Sputnik, it is very challenging to outperform cuBLAS kernels with tensor core enabled. According to the benchmark results, Sputnik can outperform cuBLAS_TC only when the sparsity is ¿90% when the N dimension is 8, 16, or 32. As for SparTA, as described in Sec.3.1, it leverages sparse tensor core (Mishra et al., 2021) for the major part of the computations, which can not effectively exploit the sparsity available as sparse tensor cores only support 50% sparsity (2:4 sparsity). If the sparsity available is higher than 50%, SparTA has to pad zeros to the sparse matrix resulting in redundant global memory access during runtime. Besides, for the non-zeros that can not meet the 2:4 requirement, another SIMT core based kernel is launched for the corresponding computations, resulting in extra overhead. Therefore, Flash-LLM outperforms SparTA in our evaluations.
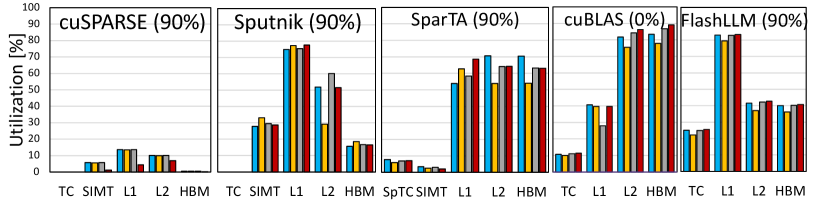

6.2. Kernel Analysis
Optimized GPU Utilization. Fig.10 777For cuBLAS(NVIDIA, 2023a), the number of tensor core instructions (HMMA) executed will not change as the N dimension varies (e.g. 8, 16, 32, 64). It means that there are redundant tensor core operations launched in cuBLAS kernels for N=8, 16, and 32. These redundant HMMA operations are excluded properly in our evaluations. shows the utilization of GPU hardware units including tensor cores (TC), combined L1 and shared memory (L1), L2 cache (L2), and GPU global memory (HBM) during Flash-LLM kernel execution. All the data is collected by the NSight Compute profiler (NVIDIA, 2023e). We present the profiling results of N = 16 and N = 32 under 90% sparsity. We also include cuBLAS here as the dense baseline (sparsity = 0%). cuSPARSE and Sputnik are SIMT-based designs where tensor cores are not used at all. Although Sputnik achieves good SIMT core utilization (29.8% at BS=16, 40.1% at BS=32), it achieves much slower performance than other tensor-core-based kernels as SIMT cores show much lower peak computational throughput than tensor cores. SparTA utilizes the tensor core but with lower utilization than cuBLAS. For cuBLAS, the bandwidth of the L2 cache and GPU DRAM is exhausted while the tensor cores only reach 10.7% and 21.0% of its peak performance on average when the N dimension is 16 and 32 respectively. In Flash-LLM, the sparse matrices are in Tiled-CSL format (Sec.3.2.2) with reduced size in bytes. The global memory bandwidth is no longer the bottleneck with the Load-as-Sparse and Compute-as-Dense method. On average, tensor core utilization is improved to 24.4% and 42.6%. As tensor core utilization is improved, it consumes higher bandwidth of shared memory. In addition to that, the extract in Fig.6c will cause extra shared memory stores. Thus, L1/shared-memory bandwidth is exhausted by Flash-LLM, which prohibits further performance improvements. Note that the ahead of time sparse data reordering (Sec.4.3.3) is designed to increase the shared memory access efficiency, which helps to mitigate the bandwidth bottleneck of shared memory. How to further reduce the pressure on shared memory could be future work.
Balanced pipeline for memory/tensor core operations. Flash-LLM kernel contains three major types of operations: global memory access (Gmem), shared memory access (Smem), and tensor core operations (TC). Ideally, these three types of operations should be overlapped and conducted in parallel for maximum GPU hardware utilization. As shown in Fig.11, We measure the latency of each type of operation separately by erasing other computations in the source code. We also re-implement the dense GeMM kernel based on the design of NVIDIA cutlass (NVIDIA, 2023d), which achieves similar performance compared to cuBLAS. Due to the Buckets effect, the overall kernel time is mainly determined by the global memory operations which require the longest execution time. With Load-as-Sparse and Compute-as-Dense method, the latency of Gmem operations is significantly reduced, leading to overall performance improvements. Although the Smem latency is increased due to the extra shared memory access required by the extract in Fig.6c, it does not prevent Flash-LLM kernel from achieving better performance than cuBLAS. It is a good trade-off between global memory and shared memory utilization. What’s more, Flash-LLM shows similar latency with dense GeMM kernel in terms of tensor core operations as we do not skip any computations here. However, it is clear that tensor core operations are not the bottleneck for the overall kernel performance.


Performance on more MatMul shapes. As discussed in Sec.3.2.1, we mainly want to mitigate the inefficiency caused by Skinny MatMuls in common LLM inference. For more comprehensive understanding evaluations, we provide kernel performance on more shapes even when the shape is not common for LLM inferences. As shown in Fig.12, Flash-LLM becomes slower than cuBLAS if the N dimension is larger than 256, noting the memory footprint of Flash-LLM is still smaller than dense counterparts. The reason behind this is twofold. First, the inefficiency of cuBLAS is no longer significant as the N dimension is large enough, which makes cuBLAS more performant. Second, Flash-LLM has more complicated kernel designs and extra shared memory access, which slows it down a little bit. We also notice that Sputnik becomes much slower than other tensor-core-based designs as the N dimension increases. Even though SIMT-core-based solutions such as Sputnik can skip computations exploiting sparsity, such computational savings still can not make up for the huge performance gap between SIMT cores and tensor cores.

6.3. End-to-End Model Evaluation
Baselines. We include NVIDIA FasterTransformer (FT) (git commit: 9770d30) (NVIDIA, 2022a) and DeepSpeed (DS) (Aminabadi et al., 2022) as baselines, the state-of-the-art inference frameworks supporting model parallelism (Shoeybi et al., 2019) to fit large models that would otherwise not fit in GPU memory.
| Batch Size | 8 | 16 | 32 | 64 | 128 |
|---|---|---|---|---|---|
| Ours-1GPU | 34.7 | 40.8 | 52.9 | 77.1 | OOM |
| FT-1GPU | 62.7 | 68.7 | OOM | OOM | OOM |
| DS-1GPU | 64.1 | 70.9 | OOM | OOM | OOM |
| FT-2GPU | 65.6 | 71.7 | 83.9 | 108.3 | OOM |
| DS-2GPU | 68.3 | 75.7 | 90.6 | 120.4 | OOM |
Workloads. We benchmark the end-to-end inference latency of the OPT models (Zhang et al., 2022a), including OPT-30B, OPT-66B, and OPT-175B. In order to accommodate only the model parameters in dense format, 60/132/350GB GPU memory is required for OPT-30B/66B/175B. Note that SOTA GPUs only have 80GB of memory each, at least 1/2/8 GPUs are required 888The number of GPUs must be a power of 2 for model parallelism(Face, 2023). for the inference of OPT-30B/66B/175B. Besides, extra GPU memory is required to store the KV-Cache (refer to Fig. 1b, with its size positively related to inference batch size) during runtime. According to Table. 1, the existing inference frameworks (FT-1GPU, DS-1GPU) can easily run out of GPU memory during the inference of OPT-30B for batch sizes larger than 16 if storing the model parameters in dense format. For all experiments, the input/prompt sequence length is 64 and the output/generated sequence length is 512.
Metric. We propose the metric tokens per GPU-second to indicate the normalized inference throughput with the consideration of both execution time and hardware cost (i.e., the number of GPUs used). It is calculated with the following equation:
| (3) |
means the number of tokens generated, whereas and mean the GPU number and the time spent on the i’th GPU for execution. We use this metric to evaluate the system’s performance. Note that for real-time inference serving, the inference throughput is the higher the better once the inference latency is less than a specific threshold.
6.3.1. Case Study: OPT-30B
Model Pruning. To show that pruned model has comparable performance with the original model, we evaluate the accuracy of the pruned model with OPT-30B (Zhang et al., 2022a) and GPT-NEOX-20B (Black et al., 2022; EleutherAI, 2022) on Recognizing Textual Entailment task in SuperGLUE (Wang et al., 2019). To achieve better accuracy, we adopt the popular pruning method Taylor Pruning (Molchanov et al., 2019) to prune these models and keep the front quarter and the last quarter feedforward input layers dense. Based on that, we achieve 80% sparsity on OPT-30B and GPT-NEOX-20B with only 1.44% and 0.72% accuracy decrease, respectively. Specifically, accuracy decreases from 85.55% to 84.11% on OPT-30B, and from 83.03% to 82.31% on GPT-NEOX-20B.
Results. As shown in Fig.13a, Flash-LLM achieves and higher performance than DeepSpeed (DS) and FasterTransformer(FT) with a single GPU. DS and FT can at most achieve 348 and 359 tokens per GPU-second with a single A100 GPU. If further increase the inference batch size, DS/FT will run out of memory as inference tasks with larger batch sizes need more GPU memory to store the cached-KV and activations. In contrast, Flash-LLM achieves up to 1187 tokens per GPU-second on batch size 64. It is because the memory used for storing model weights is reduced with the Tiled-CSL format, and thus more Cached-KV and activations can be accommodated. We also compare the performance of Flash-LLM to DS and FT with two-way model-parallelism(Shoeybi et al., 2019), with which DS and FT can support batch size 64. As shown in Fig.13b, FT and DS achieve similar performance in terms of tokens per GPU-second. Compared to DS/FT, Flash-LLM achieves /, /, /, and / higher performance at batch sizes 8, 16, 32, and 64 respectively. The detailed GPU memory usage of Flash-LLM, FT, and DS are shown in Table.1.


Breakdown. In order to figure out why Flash-LLM can achieve better performance, we conduct the time breakdown of end-to-end inference shown in Fig.14a. Note that we conduct all the end-to-end breakdowns in this paper leveraging the NSight System (NVIDIA, 2023f). Compared to FT-2GPU (FasterTransformer with 2 GPU used), Flash-LLM with 1 GPU can achieve lower normalized inference latency 999To also take inference cost into consideration and compare the inference efficiency with different system configs (e.g. different numbers of GPUs may be used), we sum the execution time on all used GPUs as the normalized latency. mainly because of 1) the more efficient MatMul and 2) the elimination of cross-GPU communication overhead.


6.3.2. Case Study: OPT-66B Model
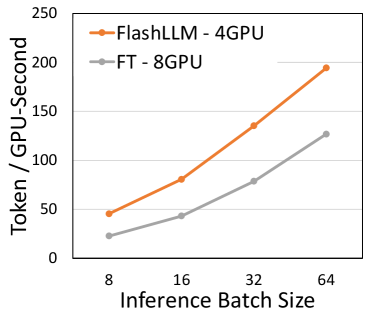
Result As shown in Fig.15a, Flash-LLM achieves and higher token generation throughput than DS and FT with two GPUs. DS and FT can at most achieve 139 and 144 tokens per GPU-second with batch size 16 as they will run out of memory if further increasing the batch size. In contrast, Flash-LLM achieves up to 522 tokens per GPU-second at batch size 64. We also compare the performance of Flash-LLM to DS-4GPU/FT-4GPU where Flash-LLM still uses two GPUs, while DS-4GPU/FT-4GPU uses four GPUs to enable bigger batch sizes for the baselines. Compared to DS-4GPU/FT-4GPU, Flash-LLM achieves /, /, /, and / higher performance of tokens per GPU-second at batch sizes 8, 16, 32, and 64 respectively.


Breakdown. We conduct the time breakdown of end-to-end inference with FT and Flash-LLM for OPT-66B as shown in Fig.14b. Compared to FT-4GPU (FasterTransformer with 4 GPU used), Flash-LLM with two GPUs can achieve lower normalized inference latency than FT-4GPU mainly because of 1) the reduction of MatMul time and 2) the reduction of cross-GPU communication overhead.
6.3.3. Case Study: OPT-175B Model
Results & Breakdown We successfully run the inference of OPT-175B models with Flash-LLM using 4 A100 GPUs. In contrast, the weight of OPT-175B can not fit into 4 A100 GPUs with traditional solutions. Thus, we do not show the performance of FT/DS using 4 GPUs here as they all run out of GPU memory. In addition, we failed to run OPT-175B with DS using 8 GPUs. Fig.16a compares the performance of Flash-LLM and FT where we only use 4 GPUs while FT uses 8 GPUs. Compared to FT-8GPU, Flash-LLM achieves , , , and higher performance at batch sizes 8, 16, 32, and 64 respectively. As shown in fig.16b, both the MatMul time and the cross-GPU communication time are significantly reduced using Flash-LLM.

7. Related Work and Discussion
The parallel and distributed ML task execution is widely used for model training (Face, 2023; Rajbhandari et al., 2020; Shoeybi et al., 2019; Jia et al., 2019; Huang et al., 2019; Fan et al., 2021; Jia et al., 2022; Yi et al., 2020; Nie et al., 2023; Miao et al., 2021; Zhang et al., 2022b; Miao et al., 2022; Koliousis et al., 2019; Li et al., 2022b, 2020). With the growth of the model size, people start to support the LLM inference through tensor parallelism (Shoeybi et al., 2019; Jia et al., 2019) to put parameters onto distributed devices (NVIDIA, 2022a; Aminabadi et al., 2022). However, the distributed execution of model inference introduces high communication costs and high economic investment. Some works support LLM inference on a single GPU through memory offloading of data onto CPU memory and even disk (Aminabadi et al., 2022; Sheng et al., 2023). The offloading approach only works for latency non-sensitive applications (e.g. offline inference with large batch size), rather than the online inference tasks demanding very low latency. In this work, we enable efficient LLM inference execution with fewer GPUs through efficient SpMM execution.
Model pruning is a common approach to reducing parameter numbers. The structured sparsity is to enforce a structured distribution of non-zero elements during pruning, which usually could be friendly to hardware acceleration. NVIDIA Ampere GPU (NVIDIA, 2020) supports 2:4 structured sparsity (Mishra et al., 2021) to execute on tensor cores. CuSPARSE(NVIDIA, 2023b) can support structured SpMM on tensor core based on the Blocked-ELL (Gray et al., 2017) format, which is a coarse-grained structured sparsity where model parameters are pruned in the granularity of a squared block (e.g. ). Some works prune the model parameters in the granularity of vectors to form the structured sparse format and make use of GPU tensor cores (Chen et al., 2021; Li et al., 2022a; Huang et al., 2022). While tensor cores can be enabled with certain structured sparsity, the major concern is that deep learning models pruned with structured sparsity usually suffer from more severe model accuracy degradation than unstructured sparsity (Sun et al., 2023; Hoefler et al., 2021; Han et al., 2015a; Gomez et al., 2019; Ullrich et al., 2017; Frantar and Alistarh, 2023).
The unstructured sparsity is to prune the elements without forming a structured distribution, which is usually hard to accelerate on modern hardware architectures. STOREL (Schleich et al., 2023) and TACO (Kjolstad et al., 2017) are CPU-based designs that can support SpMM with unstructured sparsity. Instead, Flash-LLM mainly focuses on the GPU-based SpMM with unstructured sparsity, as GPU is more widely used for large-scale deep-learning tasks since it usually has higher memory bandwidth, computational throughput, and energy efficiency. The typical approach to execute the unstructured SpMM on GPU is through SIMT cores, e.g. cuSPARSE(NVIDIA, 2023b), ASpT(Hong et al., 2019), and Sputnik(Gale et al., 2020a). Under a moderate level of sparsity (¡90%), Sputnik significantly outperforms cuSPARSE and ASpT, but it struggles to beat its dense counterpart cuBLAS (NVIDIA, 2023a) as it cannot utilize tensor cores. TC-GNN (Wang et al., 2023) supports unstructured sparsity with tensor cores, which is customized for GNN where the sparsity ratio is extremely high (e.g. ¿99%) and is not efficient for generative models requiring moderate-level sparsity. SparTA (Zheng et al., 2022b) proposes to utilize both sparse tensor cores (Mishra et al., 2021) and SIMT cores to support unstructured sparsity by splitting the original sparse matrix into a 2:4 structured sparse matrix for tensor core execution (by cuSPARSELt (NVIDIA, 2023c))) and an unstructured sparse matrix for SIMT core execution (by Sputnik(Gale et al., 2020a))). However, if the sparse ratio is high, it has to excessively pad zeros to the 2:4 sparse matrix. Besides, if there are too many non-zeros that can not meet the 2:4 requirement, the SIMT kernel would cause high latency and slow down the overall processing. Flash-LLM supports the moderate-level sparsity on tensor cores efficiently and does not require the 2:4-like distribution. SparseTIR (Ye et al., 2023) supports unstructured sparsity with tensor cores by splitting sparse matrices into column vectors and omitting the vectors containing only zeros. It can not work well under moderate sparsity (e.g., 80%) as very few vectors can be skipped. It can not outperform the dense baseline cuBLAS until the sparsity is higher than 95%, while Flash-LLM can outperform cuBLAS since 60% sparsity.
The retraining-based pruning (Liu et al., 2018; Han et al., 2015b) can achieve moderate-level sparsity with good accuracy, while the post-training pruning (Frantar and Alistarh, 2023) can only achieve quite low sparse ratios. Flash-LLM aims to optimize the SpMM with the moderate-level sparsity (e.g. 60%-90%) generated with the retraining-based pruning. The retraining-based pruning usually consumes a high fine-tuning cost, which as a result becomes one limitation of Flash-LLM.
Model quantization (Hoefler et al., 2021) is another approach to reduce the memory and computation for ML models, by transforming the data type into lower bits (e.g., 8-bits, 4-bits) (Frantar et al., 2022; Li et al., 2022a). Model pruning and quantization are two orthogonal and complementary approaches to model compression. This paper mainly focuses on supporting model pruning, which is orthogonal to model quantization.
8. Conclusion
We propose Flash-LLM, a library for efficient large generative model inference through unstructured sparsity with tensor cores. We observe that MatMuls in generative models inference are usually skinny, and are bounded by off-chip memory access. We propose the Load-as-Sparse and Compute-as-Dense approach for tensor core SpMM, reducing global memory footprint, addressing the memory access bottleneck, and tolerating redundant computations of skinny MatMuls. We propose an effective software pipeline for unstructured SpMM with tensor cores, efficiently leveraging on-chip resources for sparse data extraction and coordinating sparse data extraction, dense data loading, and tensor core computation in an overlapped manner. Flash-LLM outperforms cuBLAS/Sputnik/SparTA by //, //, // under 70%, 80% and 90% sparsity. We integrate Flash-LLM kernels into Faster-Transformer for end-to-end generative model inference. For tokens per GPU-second, Flash-LLM achieves up to and improvement over DeepSpeed and FasterTransformer on OPT-30B/66B/175B models with significantly lower inference cost.
References
- (1)
- Aminabadi et al. (2022) Reza Yazdani Aminabadi, Samyam Rajbhandari, Ammar Ahmad Awan, Cheng Li, Du Li, Elton Zheng, Olatunji Ruwase, Shaden Smith, Minjia Zhang, Jeff Rasley, et al. 2022. DeepSpeed-inference: enabling efficient inference of transformer models at unprecedented scale. In Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis. 1–15.
- Black et al. (2022) Sid Black, Stella Biderman, Eric Hallahan, Quentin Anthony, Leo Gao, Laurence Golding, Horace He, Connor Leahy, Kyle McDonell, Jason Phang, Michael Pieler, USVSN Sai Prashanth, Shivanshu Purohit, Laria Reynolds, Jonathan Tow, Ben Wang, and Samuel Weinbach. 2022. GPT-NeoX-20B: An Open-Source Autoregressive Language Model. In Proceedings of the ACL Workshop on Challenges & Perspectives in Creating Large Language Models. https://arxiv.org/abs/2204.06745
- Brown et al. (2020) Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. 2020. Language models are few-shot learners. Advances in neural information processing systems 33 (2020), 1877–1901.
- Chen et al. (2021) Zhaodong Chen, Zheng Qu, Liu Liu, Yufei Ding, and Yuan Xie. 2021. Efficient tensor core-based GPU kernels for structured sparsity under reduced precision. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. 1–14.
- EleutherAI (2022) EleutherAI. 2022. GPT-NeoX-20B. https://huggingface.co/EleutherAI/gpt-neox-20b
- Face (2023) Hugging Face. 2023. Model Parallelism. https://huggingface.co/docs/transformers/v4.15.0/parallelism
- Fan et al. (2021) Shiqing Fan, Yi Rong, Chen Meng, Zongyan Cao, Siyu Wang, Zhen Zheng, Chuan Wu, Guoping Long, Jun Yang, Lixue Xia, Lansong Diao, Xiaoyong Liu, and Wei Lin. 2021. DAPPLE: A pipelined data parallel approach for training large models. In Proceedings of the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. 431–445.
- Frantar and Alistarh (2023) Elias Frantar and Dan Alistarh. 2023. Massive Language Models Can Be Accurately Pruned in One-Shot. arXiv preprint arXiv:2301.00774 (2023).
- Frantar et al. (2022) Elias Frantar, Saleh Ashkboos, Torsten Hoefler, and Dan Alistarh. 2022. GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers. arXiv preprint arXiv:2210.17323 (2022).
- Gale et al. (2020a) Trevor Gale, Matei Zaharia, Cliff Young, and Erich Elsen. 2020a. Sparse gpu kernels for deep learning. In SC20: International Conference for High Performance Computing, Networking, Storage and Analysis. IEEE, 1–14.
- Gale et al. (2020b) Trevor Gale, Matei Zaharia, Cliff Young, and Erich Elsen. 2020b. sputnik github. https://github.com/google-research/sputnik/
- Gomez et al. (2019) Aidan N Gomez, Ivan Zhang, Siddhartha Rao Kamalakara, Divyam Madaan, Kevin Swersky, Yarin Gal, and Geoffrey E Hinton. 2019. Learning sparse networks using targeted dropout. arXiv preprint arXiv:1905.13678 (2019).
- Gray et al. (2017) Scott Gray, Alec Radford, and Diederik P Kingma. 2017. Gpu kernels for block-sparse weights. arXiv preprint arXiv:1711.09224 3 (2017), 2.
- Han et al. (2015a) Song Han, Huizi Mao, and William J Dally. 2015a. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv preprint arXiv:1510.00149 (2015).
- Han et al. (2015b) Song Han, Jeff Pool, John Tran, and William Dally. 2015b. Learning both weights and connections for efficient neural network. Advances in neural information processing systems 28 (2015).
- Hoefler et al. (2021) Torsten Hoefler, Dan Alistarh, Tal Ben-Nun, Nikoli Dryden, and Alexandra Peste. 2021. Sparsity in Deep Learning: Pruning and growth for efficient inference and training in neural networks. J. Mach. Learn. Res. 22, 241 (2021), 1–124.
- Hong et al. (2019) Changwan Hong, Aravind Sukumaran-Rajam, Israt Nisa, Kunal Singh, and P Sadayappan. 2019. Adaptive sparse tiling for sparse matrix multiplication. In Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming. 300–314.
- Huang et al. (2022) Guyue Huang, Haoran Li, Minghai Qin, Fei Sun, Yufei Ding, and Yuan Xie. 2022. Shfl-BW: Accelerating Deep Neural Network Inference with Tensor-Core Aware Weight Pruning. In Proceedings of the 59th ACM/IEEE Design Automation Conference (San Francisco, California) (DAC ’22). Association for Computing Machinery, New York, NY, USA, 1153–1158. https://doi.org/10.1145/3489517.3530588
- Huang et al. (2019) Yanping Huang, Youlong Cheng, Ankur Bapna, Orhan Firat, Dehao Chen, Mia Chen, HyoukJoong Lee, Jiquan Ngiam, Quoc V Le, Yonghui Wu, et al. 2019. Gpipe: Efficient training of giant neural networks using pipeline parallelism. Advances in neural information processing systems 32 (2019).
- Jia et al. (2022) Xianyan Jia, Le Jiang, Ang Wang, Wencong Xiao, Ziji Shi, Jie Zhang, Xinyuan Li, Langshi Chen, Yong Li, Zhen Zheng, Xiaoyong Liu, and Wei Lin. 2022. Whale: Efficient Giant Model Training over Heterogeneous GPUs. In 2022 USENIX Annual Technical Conference, USENIX ATC 2022, Carlsbad, CA, USA, July 11-13, 2022, Jiri Schindler and Noa Zilberman (Eds.). USENIX Association, 673–688.
- Jia et al. (2019) Zhihao Jia, Matei Zaharia, and Alex Aiken. 2019. Beyond Data and Model Parallelism for Deep Neural Networks. Proceedings of Machine Learning and Systems 1 (2019), 1–13.
- Kenton and Toutanova (2019) Jacob Devlin Ming-Wei Chang Kenton and Lee Kristina Toutanova. 2019. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of NAACL-HLT. 4171–4186.
- Kjolstad et al. (2017) Fredrik Kjolstad, Shoaib Kamil, Stephen Chou, David Lugato, and Saman Amarasinghe. 2017. The Tensor Algebra Compiler. Proc. ACM Program. Lang. 1, OOPSLA, Article 77 (oct 2017), 29 pages. https://doi.org/10.1145/3133901
- Koliousis et al. (2019) Alexandros Koliousis, Pijika Watcharapichat, Matthias Weidlich, Luo Mai, Paolo Costa, and Peter Pietzuch. 2019. CROSSBOW: Scaling Deep Learning with Small Batch Sizes on Multi-GPU Servers. Proceedings of the VLDB Endowment 12, 11 (2019).
- Li et al. (2022a) Shigang Li, Kazuki Osawa, and Torsten Hoefler. 2022a. Efficient quantized sparse matrix operations on tensor cores. In Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis. 1–15.
- Li et al. (2020) Shen Li, Yanli Zhao, Rohan Varma, Omkar Salpekar, Pieter Noordhuis, Teng Li, Adam Paszke, Jeff Smith, Brian Vaughan, Pritam Damania, et al. 2020. PyTorch Distributed: Experiences on Accelerating Data Parallel Training. Proceedings of the VLDB Endowment 13, 12 (2020).
- Li et al. (2022b) Youjie Li, Amar Phanishayee, Derek Murray, Jakub Tarnawski, and Nam Sung Kim. 2022b. Harmony: Overcoming the Hurdles of GPU Memory Capacity to Train Massive DNN Models on Commodity Servers. Proc. VLDB Endow. 15, 11 (jul 2022), 2747–2760.
- Lin et al. (2022) Mingbao Lin, Yuxin Zhang, Yuchao Li, Bohong Chen, Fei Chao, Mengdi Wang, Shen Li, Yonghong Tian, and Rongrong Ji. 2022. 1xn pattern for pruning convolutional neural networks. IEEE Transactions on Pattern Analysis and Machine Intelligence (2022).
- Liu et al. (2018) Zhuang Liu, Mingjie Sun, Tinghui Zhou, Gao Huang, and Trevor Darrell. 2018. Rethinking the value of network pruning. arXiv preprint arXiv:1810.05270 (2018).
- Miao et al. (2021) Xupeng Miao, Xiaonan Nie, Yingxia Shao, Zhi Yang, Jiawei Jiang, Lingxiao Ma, and Bin Cui. 2021. Heterogeneity-aware distributed machine learning training via partial reduce. In Proceedings of the 2021 International Conference on Management of Data. 2262–2270.
- Miao et al. (2022) Xupeng Miao, Yujie Wang, Youhe Jiang, Chunan Shi, Xiaonan Nie, Hailin Zhang, and Bin Cui. 2022. Galvatron: Efficient Transformer Training over Multiple GPUs Using Automatic Parallelism. Proc. VLDB Endow. 16, 3 (nov 2022), 470–479.
- Mishra et al. (2021) Asit Mishra, Jorge Albericio Latorre, Jeff Pool, Darko Stosic, Dusan Stosic, Ganesh Venkatesh, Chong Yu, and Paulius Micikevicius. 2021. Accelerating Sparse Deep Neural Networks. arXiv:2104.08378 [cs.LG]
- Molchanov et al. (2019) Pavlo Molchanov, Arun Mallya, Stephen Tyree, Iuri Frosio, and Jan Kautz. 2019. Importance estimation for neural network pruning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 11264–11272.
- Narayan et al. (2022) Avanika Narayan, Ines Chami, Laurel Orr, and Christopher Ré. 2022. Can Foundation Models Wrangle Your Data? Proc. VLDB Endow. 16, 4 (dec 2022), 738–746.
- Nie et al. (2023) Xiaonan Nie, Xupeng Miao, Zilong Wang, Zichao Yang, Jilong Xue, Lingxiao Ma, Gang Cao, and Bin Cui. 2023. FlexMoE: Scaling Large-scale Sparse Pre-trained Model Training via Dynamic Device Placement. arXiv preprint arXiv:2304.03946 (2023).
- NVIDIA (2020) NVIDIA. 2020. NVIDIA A100 Tensor Core GPU Architecture. https://images.nvidia.com/aem-dam/en-zz/Solutions/data-center/nvidia-ampere-architecture-whitepaper.pdf
- NVIDIA (2022a) NVIDIA. 2022a. NVIDIA Faster-Transformer. https://github.com/NVIDIA/FasterTransformer
- NVIDIA (2022b) NVIDIA. 2022b. NVIDIA H100 Tensor Core GPU Architecture. https://www.hpctech.co.jp/catalog/gtc22-whitepaper-hopper_v1.01.pdf
- NVIDIA (2023a) NVIDIA. 2023a. cuBLAS Docs. https://docs.nvidia.com/cuda/cublas/index.html
- NVIDIA (2023b) NVIDIA. 2023b. cuSPARSE Library. https://docs.nvidia.com/cuda/cusparse/index.html
- NVIDIA (2023c) NVIDIA. 2023c. cuSPARSELt Library. https://docs.nvidia.com/cuda/cusparselt/
- NVIDIA (2023d) NVIDIA. 2023d. CUTLASS 3.2. https://github.com/NVIDIA/cutlass
- NVIDIA (2023e) NVIDIA. 2023e. Nsight Compute Profiling Guide. https://docs.nvidia.com/nsight-compute/ProfilingGuide/#introduction
- NVIDIA (2023f) NVIDIA. 2023f. Nsight System. https://developer.nvidia.com/nsight-systems
- Radford et al. (2019) Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, Ilya Sutskever, et al. 2019. Language models are unsupervised multitask learners. OpenAI blog 1, 8 (2019), 9.
- Rajbhandari et al. (2020) Samyam Rajbhandari, Jeff Rasley, Olatunji Ruwase, and Yuxiong He. 2020. Zero: Memory optimizations toward training trillion parameter models. In SC20: International Conference for High Performance Computing, Networking, Storage and Analysis. IEEE, 1–16.
- Schleich et al. (2023) Maximilian Schleich, Amir Shaikhha, and Dan Suciu. 2023. Optimizing Tensor Programs on Flexible Storage. Proceedings of the ACM on Management of Data 1, 1 (2023), 1–27.
- Sheng et al. (2023) Ying Sheng, Lianmin Zheng, Binhang Yuan, Zhuohan Li, Max Ryabinin, Daniel Y Fu, Zhiqiang Xie, Beidi Chen, Clark Barrett, Joseph E Gonzalez, et al. 2023. High-throughput generative inference of large language models with a single gpu. arXiv preprint arXiv:2303.06865 (2023).
- Shoeybi et al. (2019) Mohammad Shoeybi, Mostofa Patwary, Raul Puri, Patrick LeGresley, Jared Casper, and Bryan Catanzaro. 2019. Megatron-lm: Training multi-billion parameter language models using model parallelism. arXiv preprint arXiv:1909.08053 (2019).
- Smith et al. (2022) Shaden Smith, Mostofa Patwary, Brandon Norick, Patrick LeGresley, Samyam Rajbhandari, Jared Casper, Zhun Liu, Shrimai Prabhumoye, George Zerveas, Vijay Korthikanti, Elton Zhang, Rewon Child, Reza Yazdani Aminabadi, Julie Bernauer, Xia Song, Mohammad Shoeybi, Yuxiong He, Michael Houston, Saurabh Tiwary, and Bryan Catanzaro. 2022. Using DeepSpeed and Megatron to Train Megatron-Turing NLG 530B, A Large-Scale Generative Language Model. arXiv:2201.11990 [cs.CL]
- Sun et al. (2023) Mingjie Sun, Zhuang Liu, Anna Bair, and J. Zico Kolter. 2023. A Simple and Effective Pruning Approach for Large Language Models. arXiv:2306.11695 [cs.CL]
- Trummer (2022) Immanuel Trummer. 2022. From BERT to GPT-3 Codex: Harnessing the Potential of Very Large Language Models for Data Management. Proc. VLDB Endow. 15, 12 (aug 2022), 3770–3773.
- Tuli et al. (2022) Shreshth Tuli, Giuliano Casale, and Nicholas R. Jennings. 2022. TranAD: Deep Transformer Networks for Anomaly Detection in Multivariate Time Series Data. Proc. VLDB Endow. 15, 6 (feb 2022), 1201–1214.
- Ullrich et al. (2017) Karen Ullrich, Edward Meeds, and Max Welling. 2017. Soft weight-sharing for neural network compression. arXiv preprint arXiv:1702.04008 (2017).
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. Advances in neural information processing systems 30 (2017).
- Wang et al. (2019) Alex Wang, Yada Pruksachatkun, Nikita Nangia, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel Bowman. 2019. Superglue: A stickier benchmark for general-purpose language understanding systems. Advances in neural information processing systems 32 (2019).
- Wang et al. (2023) Yuke Wang, Boyuan Feng, Zheng Wang, and Yufei Ding. 2023. TC-GNN: Accelerating Sparse Graph Neural Network Computation Via Dense Tensor Core on GPUs. arXiv:2112.02052 [cs.LG]
- Williams et al. (2009) Samuel Williams, Andrew Waterman, and David Patterson. 2009. Roofline: an insightful visual performance model for multicore architectures. Commun. ACM 52, 4 (2009), 65–76.
- Ye et al. (2023) Zihao Ye, Ruihang Lai, Junru Shao, Tianqi Chen, and Luis Ceze. 2023. SparseTIR: Composable abstractions for sparse compilation in deep learning. In Proceedings of the 28th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Volume 3. 660–678.
- Yi et al. (2020) Xiaodong Yi, Shiwei Zhang, Ziyue Luo, Guoping Long, Lansong Diao, Chuan Wu, Zhen Zheng, Jun Yang, and Wei Lin. 2020. Optimizing distributed training deployment in heterogeneous GPU clusters. In CoNEXT ’20: The 16th International Conference on emerging Networking EXperiments and Technologies, Barcelona, Spain, December, 2020, Dongsu Han and Anja Feldmann (Eds.). ACM, 93–107.
- Zhang et al. (2022a) Susan Zhang, Stephen Roller, Naman Goyal, Mikel Artetxe, Moya Chen, Shuohui Chen, Christopher Dewan, Mona Diab, Xian Li, Xi Victoria Lin, Todor Mihaylov, Myle Ott, Sam Shleifer, Kurt Shuster, Daniel Simig, Punit Singh Koura, Anjali Sridhar, Tianlu Wang, and Luke Zettlemoyer. 2022a. OPT: Open Pre-trained Transformer Language Models. arXiv:2205.01068 [cs.CL]
- Zhang et al. (2022b) Zhen Zhang, Shuai Zheng, Yida Wang, Justin Chiu, George Karypis, Trishul Chilimbi, Mu Li, and Xin Jin. 2022b. MiCS: near-linear scaling for training gigantic model on public cloud. Proceedings of the VLDB Endowment 16, 1 (2022), 37–50.
- Zheng et al. (2022a) Lianmin Zheng, Zhuohan Li, Hao Zhang, Yonghao Zhuang, Zhifeng Chen, Yanping Huang, Yida Wang, Yuanzhong Xu, Danyang Zhuo, Eric P. Xing, Joseph E. Gonzalez, and Ion Stoica. 2022a. Alpa: Automating Inter- and Intra-Operator Parallelism for Distributed Deep Learning. In 16th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2022, Carlsbad, CA, USA, July 11-13, 2022, Marcos K. Aguilera and Hakim Weatherspoon (Eds.). USENIX Association, 559–578.
- Zheng (2022) Ningxin Zheng. 2022. SparTA github. https://github.com/microsoft/SparTA/tree/sparta_artifact
- Zheng et al. (2022b) Ningxin Zheng, Bin Lin, Quanlu Zhang, Lingxiao Ma, Yuqing Yang, Fan Yang, Yang Wang, Mao Yang, and Lidong Zhou. 2022b. SparTA:Deep-Learning Model Sparsity via Tensor-with-Sparsity-Attribute. In 16th USENIX Symposium on Operating Systems Design and Implementation (OSDI 22). 213–232.