\typearea

Floer cohomologies of non-torus fibers
of the Gelfand-Cetlin system

Yuichi Nohara and Kazushi Ueda

Abstract

The Gelfand-Cetlin system has non-torus Lagrangian fibers on some of the boundary strata of the moment polytope. We compute Floer cohomologies of such non-torus Lagrangian fibers in the cases of the 3-dimensional full flag manifold and the Grassmannian of 2-planes in a 4-space.

1 Introduction

Let $P$ be a parabolic subgroup of $\operatorname{GL}(n,\mathbb{C})$ and $F:=\operatorname{GL}(n,\mathbb{C})/P$ be the associated flag manifold. The Gelfand-Cetlin system, introduced by Guillemin and Sternberg [GS83], is a completely integrable system

\Phi:F\longrightarrow\mathbb{R}^{(\dim_{\mathbb{R}}F)/2},

i.e., a set of functionally independent and Poisson commuting functions. The image $\Delta=\Phi(F)$ is a convex polytope called the Gelfand-Cetlin polytope, and $\Phi$ gives a Lagrangian torus fibration structure over the interior $\operatorname{Int}\Delta$ of $\Delta$ . Unlike the case of toric manifolds where the fibers over the relative interior of a $d$ -dimensional face of the moment polytope are $d$ -dimensional isotropic tori, the Gelfand-Cetlin system has non-torus Lagrangian fibers over the relative interiors of some of the faces of $\Delta$ .

Let $(X,\omega)$ be a compact toric manifold of $\dim_{\mathbb{C}}X=N$ , and $\Phi:X\to\mathbb{R}^{N}$ be the toric moment map with the moment polytope $\Delta=\Phi(X)$ . For an interior point ${\boldsymbol{u}}\in\operatorname{Int}\Delta$ , let $L({\boldsymbol{u}})$ denote the Lagrangian torus fiber $\Phi^{-1}({\boldsymbol{u}})$ . Lagrangian intersection Floer theory endows the cohomology group $H^{*}(L({\boldsymbol{u}});\Lambda_{0})$ over the Novikov ring

\Lambda_{0}:=\left\{\left.\sum_{i=1}^{\infty}a_{i}T^{\lambda_{i}}\,\right|\,a_{i}\in\mathbb{C},\ \lambda_{i}\geq 0,\ \lim_{i\to\infty}\lambda_{i}=\infty\right\}

with a structure $\{\mathfrak{m}_{k}\}_{k\geq 0}$ of a unital filtered $A_{\infty}$ -algebra [FOOO09]. Let $\Lambda$ and $\Lambda_{+}$ be the quotient field and the maximal ideal of the local ring $\Lambda_{0}$ respectively. An odd-degree element $b\in H^{\mathrm{odd}}(L({\boldsymbol{u}});\Lambda_{0})$ is said to be a bounding cochain if it satisfies the Maurer-Cartan equation

\sum_{k=0}^{\infty}\mathfrak{m}_{k}(b^{\otimes k})=0.

(1.1)

A solution $b\in H^{\mathrm{odd}}(L({\boldsymbol{u}});\Lambda_{0})$ to the weak Maurer-Cartan equation

\displaystyle\sum_{k=0}^{\infty}\mathfrak{m}_{k}(b^{\otimes k})\equiv 0\mod\Lambda_{0}\,\mathbf{e}_{0}

(1.2)

is called a weak bounding cochain, where $\mathbf{e}_{0}$ is the unit in $H^{*}(L({\boldsymbol{u}});\Lambda_{0})$ . The set of weak bounding cochains will be denoted by $\widehat{\mathcal{M}}_{\mathrm{weak}}(L({\boldsymbol{u}}))$ . The potential function is a map $\mathfrak{PO}\colon\widehat{\mathcal{M}}_{\mathrm{weak}}(L({\boldsymbol{u}}))\to\Lambda_{0}$ defined by

\displaystyle\sum_{k=0}^{\infty}\mathfrak{m}_{k}(b,\ldots,b)=\mathfrak{PO}(b)\mathbf{e}_{0}.

(1.3)

A weak bounding cochain gives a deformed filtered $A_{\infty}$ -algebra whose $A_{\infty}$ -operations are given by

\displaystyle\mathfrak{m}^{b}_{k}(x_{1},\ldots,x_{k})=\sum_{m_{0}=0}^{\infty}\cdots\sum_{m_{k}=0}^{\infty}\mathfrak{m}_{m_{0}+\cdots+m_{k}+k}(b^{\otimes m_{0}}\otimes x_{1}\otimes b^{\otimes m_{1}}\otimes\cdots\otimes x_{k}\otimes b^{\otimes m_{k}}).

(1.4)

The weak Maurer-Cartan equation implies that $\mathfrak{m}_{1}^{b}$ squares to zero, and the deformed Floer cohomology is defined by

\displaystyle\mathop{H\!F}\nolimits((L({\boldsymbol{u}}),b),(L({\boldsymbol{u}}),b);\Lambda_{0})=\left.\operatorname{Ker}(\mathfrak{m}_{1}^{b})\right/\operatorname{Im}(\mathfrak{m}_{1}^{b}).

(1.5)

More generally, one can deform the Floer differential $\mathfrak{m}_{1}$ by

\delta_{b_{0},b_{1}}(x)=\sum_{k_{0},k_{1}\geq 0}\mathfrak{m}_{k_{0}+k_{1}+1}(\underbrace{b_{0},\dots,b_{0}}_{k_{0}},x,\underbrace{b_{1},\dots,b_{1}}_{k_{1}})

(1.6)

for a pair $(b_{0},b_{1})$ of weak bounding cochains with $\mathfrak{PO}(b_{0})=\mathfrak{PO}(b_{1})$ . The Floer cohomology of the pair $((L({\boldsymbol{u}}),b_{0}),(L({\boldsymbol{u}}),b_{1}))$ is defined by

\displaystyle\mathop{H\!F}\nolimits((L({\boldsymbol{u}}),b_{0}),(L({\boldsymbol{u}}),b_{1});\Lambda_{0})=\left.\operatorname{Ker}(\delta_{b_{0},b_{1}})\right/\operatorname{Im}(\delta_{b_{0},b_{1}}).

(1.7)

If the toric manifold $X$ is Fano, then the following hold [FOOO10]:

•

$H^{1}(L({\boldsymbol{u}});\Lambda_{0})$ is contained in $\widehat{\mathcal{M}}_{\mathrm{weak}}(L({\boldsymbol{u}}))$ .

•

The potential function $\mathfrak{PO}$ on

\bigcup_{{\boldsymbol{u}}\in\operatorname{Int}\Delta}H^{1}(L({\boldsymbol{u}});\Lambda_{0}/2\pi\sqrt{-1}\mathbb{Z})\cong\operatorname{Int}\Delta\times(\Lambda_{0}/2\pi\sqrt{-1}\mathbb{Z})^{N}

(1.8)

can be considered as a Laurent polynomial, which can be identified with the superpotential of the Landau-Ginzburg mirror of $X$ .

•

Each critical point of $\mathfrak{PO}$ corresponds to a pair $({\boldsymbol{u}},b)$ such that the deformed Floer cohomology $\mathop{H\!F}\nolimits((L({\boldsymbol{u}}),b),(L({\boldsymbol{u}}),b);\Lambda)$ over the Novikov field $\Lambda$ is non-trivial.
•

If the deformed Floer cohomology group over the Novikov field is non-trivial, then it is isomorphic to the classical cohomology group;

$\displaystyle\mathop{H\!F}\nolimits((L({\boldsymbol{u}}),b),(L({\boldsymbol{u}}),b);\Lambda)\cong H^{*}(T^{N};\Lambda).$ (1.9)
•

The quantum cohomology ring $\mathop{QH}\nolimits(X;\Lambda)$ is isomorphic to the Jacobi ring $\operatorname{Jac}(\mathfrak{PO})$ of the potential function.

In particular, the number of pairs $(L({\boldsymbol{u}}),b)$ with nontrivial Floer cohomology coincides with $\operatorname{rank}\mathop{QH}\nolimits(X;\Lambda)=\operatorname{rank}H^{*}(X;\Lambda).$

Nishinou and the authors [NNU10] introduced the notion of a toric degeneration of an integrable system, and used it to compute the potential function of Lagrangian torus fibers of the Gelfand-Cetlin system. The resulting potential function can be considered as a Laurent polynomial just as in the toric Fano case, which can be identified with the superpotential of the Landau-Ginzburg mirror of the flag manifold given in [Giv97, BCFKvS00]. In contrast to the toric case, the rank of $H^{*}(F;\Lambda)$ is greater in general than the rank of the Jacobi ring $\operatorname{Jac}(\mathfrak{PO})$ , and hence than the number of Lagrangian torus fibers with non-trivial Floer cohomology. In the case of the 3-dimensional flag manifold $\operatorname{Fl}(3)$ , the potential function has six critical points, which is equal to the rank of $H^{*}(\operatorname{Fl}(3);\Lambda)$ . Similarly, the potential function for the Grassmannian $\operatorname{Gr}(2,5)$ of 2-planes in $\mathbb{C}^{5}$ has ten critical points, which is equal to the rank of $H^{*}(\operatorname{Gr}(2,5);\Lambda)$ . On the other hand, the number of critical points of the potential function for the Grassmannian $\operatorname{Gr}(2,4)$ of 2-planes in $\mathbb{C}^{4}$ is four, which is less than the rank of $H^{*}(\operatorname{Gr}(2,4);\Lambda)$ , which is six.

In this paper, we study non-torus Lagrangian fibers of the Gelfand-Cetlin system over the boundary of the Gelfand-Cetlin polytope in the cases of $\operatorname{Fl}(3)$ and $\operatorname{Gr}(2,4)$ . The main results are the following:

Theorem 1.1.

Let $\Phi\colon\operatorname{Fl}(3)\to\mathbb{R}^{3}$ be the Gelfand-Cetlin system with the Gelfand-Cetlin polytope $\Delta=\Phi(\operatorname{Fl}(3))$ .

1.

There exists a vertex ${\boldsymbol{u}}_{0}$ of $\Delta$ such that a fiber $L({\boldsymbol{u}})=\Phi^{-1}({\boldsymbol{u}})$ over a boundary point ${\boldsymbol{u}}\in\partial\Delta$ is a Lagrangian submanifold if and only if ${\boldsymbol{u}}={\boldsymbol{u}}_{0}$ .
2.

The Lagrangian fiber $L({\boldsymbol{u}}_{0})$ is diffeomorphic to $\operatorname{SU}(2)\cong S^{3}$ .
3.

The Floer cohomology of $L({\boldsymbol{u}}_{0})$ over the Novikov field $\Lambda$ is trivial;

$\mathop{H\!F}\nolimits(L({\boldsymbol{u}}_{0}),L({\boldsymbol{u}}_{0});\Lambda)=0.$ (1.10)

Theorem 1.2.

Let $\Phi\colon\operatorname{Gr}(2,4)\to\mathbb{R}^{4}$ be the Gelfand-Cetlin system with the Gelfand-Cetlin polytope $\Delta=\Phi(\operatorname{Gr}(2,4))$ .

1.

There exists an edge of $\Delta$ such that a fiber $L({\boldsymbol{u}})=\Phi^{-1}({\boldsymbol{u}})$ over ${\boldsymbol{u}}\in\partial\Delta$ is a Lagrangian submanifold if and only if ${\boldsymbol{u}}$ is in the relative interior of the edge.
2.

The Lagrangian fiber $L({\boldsymbol{u}})$ over any point ${\boldsymbol{u}}$ in the relative interior of the edge is diffeomorphic to $\operatorname{U}(2)\cong S^{1}\times S^{3}$ .
3.

$H^{1}(L({\boldsymbol{u}});\Lambda_{0})$ is contained in $\widehat{\mathcal{M}}_{\mathrm{weak}}(L({\boldsymbol{u}}))$ .
4.

The potential function is identically zero on $H^{1}(L({\boldsymbol{u}});\Lambda_{0})$ .
5.

The Floer cohomology $\mathop{H\!F}\nolimits((L({\boldsymbol{u}}),b),(L({\boldsymbol{u}}),b);\Lambda)$ of a Lagrangian $\operatorname{U}(2)$ -fiber $L({\boldsymbol{u}})$ over the Novikov field $\Lambda$ is non-trivial if and only if ${\boldsymbol{u}}$ is the barycenter ${\boldsymbol{u}}_{0}$ of the edge and $b=\pm\pi\sqrt{-1}/2\,\mathbf{e}_{1}$ , where $\mathbf{e}_{1}$ is a generator of $H^{1}(L({\boldsymbol{u}});\mathbb{Z})\cong\mathbb{Z}$ .

If the deformed Floer cohomology group over the Novikov field is non-trivial, then it is isomorphic to the classical cohomology group;

\displaystyle\mathop{H\!F}\nolimits((L({\boldsymbol{u}}_{0}),\pm\pi\sqrt{-1}/2\,\mathbf{e}_{1}),(L({\boldsymbol{u}}_{0}),\pm\pi\sqrt{-1}/2\,\mathbf{e}_{1});\Lambda)\cong H^{*}(S^{1}\times S^{3};\Lambda).

(1.11)

The Floer cohomology of the pair $((L({\boldsymbol{u}}_{0}),\pi\sqrt{-1}/2\,\mathbf{e}_{1}),(L({\boldsymbol{u}}_{0}),-\pi\sqrt{-1}/2\,\mathbf{e}_{1}))$ is trivial;

\displaystyle\mathop{H\!F}\nolimits((L({\boldsymbol{u}}_{0}),\pi\sqrt{-1}/2\,\mathbf{e}_{1}),(L({\boldsymbol{u}}_{0}),\pi\sqrt{-1}/2\,\mathbf{e}_{1});\Lambda)=0.

(1.12)

More precise statements, which describe the Floer cohomology groups over the Novikov ring $\Lambda_{0}$ , are given in Theorem 4.8, Theorem 4.16, and Theorem 4.20.

A symplectic manifold $(X,\omega)$ is monotone if the cohomology class $[\omega]$ is positively proportional to the first Chern class;

\displaystyle\exists\lambda>0\quad[\omega]=\lambda c_{1}(X).

(1.13)

The quantum cohomology ring of a monotone symplectic manifold does not have any convergence issue, and hence is defined over $\mathbb{C}$ . A Lagrangian submanifold $L$ is monotone if the symplectic area of a disk bounded by $L$ is positively proportional to the Maslov index;

\displaystyle\exists\lambda>0\quad\forall\beta\in\pi_{2}(M,L)\quad\beta\cap\omega=\lambda\mu(\beta).

(1.14)

The $A_{\infty}$ -operations on the Lagrangian intersection Floer complex of a monotone Lagrangian submanifold is defined over $\mathbb{C}$ . The minimal Maslov number of oriented monotone Lagrangian submanifold is greater than or equal to 2, so that the obstruction class $\mathfrak{m}_{0}(1)$ can be written as $\mathfrak{m}_{0}(1)=\mathfrak{m}_{0}(L)\,\mathbf{e}_{0},$ where $\mathfrak{m}_{0}(L)\in\mathbb{C}$ is the count of Maslov index 2 disks bounded by $L$ , weighted by their symplectic areas and holonomies of a flat $U(1)$ -bundle on $L$ along the boundaries of the disks. The monotone Fukaya category is defined as the direct sum

\displaystyle\mathcal{F}(X):=\bigoplus_{\lambda\in\mathbb{C}}\mathcal{F}(X;\lambda),

(1.15)

where $\mathcal{F}(X;\lambda)$ is an $A_{\infty}$ -category over $\mathbb{C}$ whose objects are monotone Lagrangian submanifolds, equipped with flat $U(1)$ -bundles, satisfying $\mathfrak{m}_{0}(L)=\lambda$ . For any monotone Lagrangian submanifold $L$ , there is a natural ring homomorphism

\displaystyle\mathop{QH}\nolimits(X)\to\mathop{H\!F}\nolimits(L,L),

(1.16)

which is known by Auroux [Aur07], Kontsevich, and Seidel to send $c_{1}(X)\in\mathop{QH}\nolimits(X)$ to $\mathfrak{m}_{0}(1)\in\mathop{H\!F}\nolimits(L,L)$ . It follows that $\mathcal{F}(X;\lambda)$ is trivial unless $\lambda$ is an eigenvalue of the quantum cup product by $c_{1}(X)$ .

Now consider the case when $X=\operatorname{Gr}(2,4)$ , which can be written as a quadric hypersurface

\displaystyle X=\left\{[z_{0}:\cdots:z_{5}]\in\mathbb{P}^{5}\mathrel{}\middle|\mathrel{}z_{0}^{2}=z_{1}^{2}+\cdots+z_{5}^{2}\right\}.

(1.17)

The real locus $X_{\mathbb{R}}$ is a monotone Lagrangian sphere, which is the vanishing cycle along a degeneration into a nodal quadric and split-generates the nilpotent summand $D^{\pi}\mathcal{F}(X;0)$ of the monotone Fukaya category [Smi12, Lemma 4.6]. The Floer cohomology $\mathop{H\!F}\nolimits(X_{\mathbb{R}},X_{\mathbb{R}})$ is semisimple, and carries a formal $A_{\infty}$ -structure [Smi12, Lemma 4.7]. It follows that $D^{\pi}\mathcal{F}(X;0)$ is equivalent to the direct sum of two copies of the derived category $D^{b}(\mathbb{C})$ of $\mathbb{C}$ -vector spaces. On the other hand, $(L({\boldsymbol{u}}_{0}),\pm\pi\sqrt{-1}/2\,\mathbf{e}_{1})$ are also objects of the nilpotent summand $D^{\pi}\mathcal{F}(X;0)$ of the monotone Fukaya category, which are non-zero by (1.11). Since $(L({\boldsymbol{u}}_{0}),\pm\sqrt{-1}/2\,\mathbf{e}_{1})$ is a pair of orthogonal non-zero objects in a triangulated category equivalent to $D^{b}(\mathbb{C})\oplus D^{b}(\mathbb{C})$ , they split-generate the whole category:

Corollary 1.3.

The pair $(L({\boldsymbol{u}}_{0}),\pm\pi\sqrt{-1}/2\,\mathbf{e}_{1})$ split-generate $D^{\pi}\mathcal{F}(\operatorname{Gr}(2,4);0)$ .

Acknowledgment: We thank Hiroshi Ohta, Kaoru Ono, and Yoshihiro Ohnita for useful conversations. Y. N. is supported by Grant-in-Aid for Young Scientists (No.23740055). K. U. is supported by Grant-in-Aid for Young Scientists (No.24740043).

2 Non-torus fibers of the Gelfand-Cetlin system

2.1 Flag manifolds

For a sequence $0=n_{0}<n_{1}<\dots<n_{r}<n_{r+1}=n$ of integers, let $F=F(n_{1},\dots,n_{r},n)$ be the flag manifold consisting of flags

0\subset V_{1}\subset\dots\subset V_{r}\subset\mathbb{C}^{n},\quad\dim V_{i}=n_{i}

of $\mathbb{C}^{n}$ . We write the full flag manifold and the Grassmannian as $\operatorname{Fl}(n)=F(1,2,\dots,n)$ and $\operatorname{Gr}(k,n)=F(k,n)$ respectively. The complex dimension of $F(n_{1},\dots,n_{r},n)$ is given by

N=N(n_{1},\dots,n_{r},n):=\dim_{\mathbb{C}}F(n_{1},\dots,n_{r},n)=\sum_{i=1}^{r}(n_{i}-n_{i-1})(n-n_{i}).

Let $P=P(n_{1},\dots,n_{r},n)\subset\operatorname{GL}(n,\mathbb{C})$ be the stabilizer subgroup of the standard flag $(V_{i}=\langle e_{1},\dots,e_{n_{i}}\rangle)_{i=1}^{r},$ where $\{e_{i}\}_{i=1}^{n}$ is the standard basis of $\mathbb{C}^{n}$ . The intersection of $P$ and $\operatorname{U}(n)$ is $\operatorname{U}(k_{1})\times\dots\times\operatorname{U}(k_{r+1})$ for $k_{i}=n_{i}-n_{i-1}$ , and $F$ is written as

F=\operatorname{GL}(n,\mathbb{C})/P=\operatorname{U}(n)/(\operatorname{U}(k_{1})\times\dots\times\operatorname{U}(k_{r+1})).

We take a $\operatorname{U}(n)$ -invariant inner product $\langle x,y\rangle=\operatorname{tr}xy^{*}$ on the Lie algebra $\mathfrak{u}(n)$ of $\operatorname{U}(n)$ , and identify the dual vector space $\mathfrak{u}(n)^{*}$ of $\mathfrak{u}(n)$ with the space $\sqrt{-1}\mathfrak{u}(n)$ of Hermitian matrices. For ${\boldsymbol{\lambda}}=\mathrm{diag}\,(\lambda_{1},\dots,\lambda_{n})\in\sqrt{-1}\mathfrak{u}(n)$ with

\underbrace{\lambda_{1}=\dots=\lambda_{n_{1}}}_{k_{1}}>\underbrace{\lambda_{n_{1}+1}=\dots=\lambda_{n_{2}}}_{k_{2}}>\dots>\underbrace{\lambda_{n_{r}+1}=\dots=\lambda_{n}}_{k_{r+1}},

(2.1)

the flag manifold $F$ is identified with the adjoint orbit $\mathcal{O}_{{\boldsymbol{\lambda}}}\subset\sqrt{-1}\mathfrak{u}(n)$ of ${\boldsymbol{\lambda}}$ . Note that $\mathcal{O}_{{\boldsymbol{\lambda}}}$ consists of Hermitian matrices with fixed eigenvalues $\lambda_{1},\dots,\lambda_{n}$ . Let

\omega(\operatorname{ad}_{\xi}(x),\operatorname{ad}_{\eta}(x))=\frac{1}{2\pi}\langle x,[\xi,\eta]\rangle,\quad\xi,\eta\in\mathfrak{u}(n)

be the (normalized) Kostant-Kirillov form on $\mathcal{O}_{{\boldsymbol{\lambda}}}$ .

For each $i=1,\dots,r$ , we set $\mathbb{P}_{i}:=\mathbb{P}\bigl{(}\bigwedge^{n_{i}}\mathbb{C}^{n}\bigr{)}\cong\mathbb{P}^{\binom{n}{n_{i}}-1}$ . Then the Plücker embedding is given by

\iota:F\hookrightarrow\prod_{i=1}^{r}\mathbb{P}_{i},\quad(0\subset V_{1}\subset\dots\subset V_{r}\subset\mathbb{C}^{n})\mapsto(\textstyle{\bigwedge^{n_{1}}}V_{1},\dots,\textstyle{\bigwedge^{n_{r}}}V_{r}).

Let $\omega_{\mathbb{P}_{i}}$ be the Fubini-Study form on $\mathbb{P}_{i}$ normalized in such a way that it represents the first Chern class $c_{1}(\mathcal{O}(1))$ of the hyperplane bundle. Then the Kostant-Kirillov form $\omega$ and the first Chern form $c_{1}(F)$ of $F$ are given by

\displaystyle\omega

\displaystyle=\sum_{i=1}^{r}(\lambda_{n_{i}}-\lambda_{n_{i+1}})\omega_{\mathbb{P}_{i}}

and

\displaystyle c_{1}(F)

\displaystyle=\sum_{i=1}^{r}(n_{i+1}-n_{i-1})\omega_{\mathbb{P}_{i}}

respectively.

Example 2.1.

The 3-dimensional full flag manifold $\operatorname{Fl}(3)$ is embedded into

\mathbb{P}_{1}\times\mathbb{P}_{2}=\mathbb{P}(\mathbb{C}^{3})\times\mathbb{P}(\textstyle{\bigwedge^{2}\mathbb{C}^{3}})\cong\mathbb{P}^{2}\times\mathbb{P}^{2}

as a hypersurface. The image of $\operatorname{Fl}(3)$ is given by the Plücker relation

Z_{1}Z_{23}+Z_{2}Z_{31}+Z_{3}Z_{12}=0,

where $[Z_{1}:Z_{2}:Z_{3}]$ and $[Z_{23}:Z_{31}:Z_{12}]$ are the Plücker coordinates on $\mathbb{P}_{1}$ and $\mathbb{P}_{2}$ respectively.

Example 2.2.

The Grassmannian $\operatorname{Gr}(2,4)$ of 2-plans in $\mathbb{C}^{4}$ is embedded into $\mathbb{P}(\bigwedge^{2}\mathbb{C}^{4})\cong\mathbb{P}^{5}$ as a hypersurface. The Plücker relation is given by

Z_{12}Z_{34}-Z_{13}Z_{24}+Z_{14}Z_{23}=0,

where $[Z_{12}:Z_{13}:Z_{14}:Z_{23}:Z_{24}:Z_{34}]$ is the Plücker coordinates.

2.2 The Gelfand-Cetlin system

For $x\in\mathcal{O}_{{\boldsymbol{\lambda}}}$ and $k=1,\dots,n-1$ , let $x^{(k)}$ denote the upper-left $k\times k$ submatrix of $x$ . Since $x^{(k)}$ is also a Hermitian matrix, it has real eigenvalues $\lambda^{(k)}_{1}(x)\geq\lambda^{(k)}_{2}(x)\geq\dots\geq\lambda^{(k)}_{k}(x)$ . By taking the eigenvalues for all $k=1,\dots,n-1$ , we obtain a set $(\lambda^{(k)}_{i})_{1\leq i\leq k\leq n-1}$ of $n(n-1)/2$ functions, which satisfy the inequalities

\begin{aligned} \hbox to16.49995pt{$\hfill\lambda_{1}\hfill$}&&&&\hbox to16.49995pt{$\hfill\lambda_{2}\hfill$}&&&&\hbox to16.49995pt{$\hfill\lambda_{3}\hfill$}&&\cdots&&\hbox to16.49995pt{$\hfill\lambda_{n-1}\hfill$}&&&&\hbox to16.49995pt{$\hfill\lambda_{n}\hfill$}\\ &\rotatebox[origin={c}]{315.0}{$\geq$}&&\rotatebox[origin={c}]{45.0}{$\geq$}&&\rotatebox[origin={c}]{315.0}{$\geq$}&&\rotatebox[origin={c}]{45.0}{$\geq$}&&&&&&\rotatebox[origin={c}]{315.0}{$\geq$}&&\rotatebox[origin={c}]{45.0}{$\geq$}&\\ &&\hbox to16.49995pt{$\lambda_{1}^{(n-1)}$}&&&&\hbox to16.49995pt{$\lambda_{2}^{(n-1)}$}&&&&&&&&\hbox to16.49995pt{$\lambda_{n-1}^{(n-1)}$}&&\\ &&&\rotatebox[origin={c}]{315.0}{$\geq$}&&\rotatebox[origin={c}]{45.0}{$\geq$}&&&&&&&&\rotatebox[origin={c}]{45.0}{$\geq$}&&&\\ &&&&\hbox to16.49995pt{$\lambda_{1}^{(n-2)}$}&&&&&&&&\hbox to16.49995pt{$\lambda_{n-2}^{(n-2)}$}&&&&\\ &&&&&\rotatebox[origin={c}]{315.0}{$\geq$}&&&&&&\rotatebox[origin={c}]{45.0}{$\geq$}&&&&&\\ &&&&&&\rotatebox[origin={c}]{315.0}{$\cdots$}&&&&\rotatebox[origin={c}]{45.0}{$\cdots$}&&&&&&\\ &&&&&&&\rotatebox[origin={c}]{315.0}{$\geq$}&&\rotatebox[origin={c}]{45.0}{$\geq$}&&&&&&&\\ &&&&&&&&\hbox to16.49995pt{$\lambda_{1}^{(1)}$}&&&&&&&&&\end{aligned}.

(2.2)

It follows that the number of non-constant $\lambda^{(k)}_{i}$ coincides with $N=\dim_{\mathbb{C}}F$ . Let $I=I(n_{1},\dots,n_{r},n)$ denotes the set of pairs $(i,k)$ such that $\lambda_{i}^{(k)}$ is non-constant. Then the Gelfand-Cetlin system is defined by

\Phi=(\lambda^{(k)}_{i})_{(i,k)\in I}:F(n_{1},\dots,n_{r},n)\longrightarrow\mathbb{R}^{N(n_{1},\dots,n_{r},n)}.

Proposition 2.3 (Guillemin and Sternberg [GS83]).

The map $\Phi$ is a completely integrable system on $(F(n_{1},\dots,n_{r},n),\omega)$ . The functions $\lambda_{i}^{(k)}$ are action variables, and the image $\Delta=\Phi(F)$ is a convex polytope defined by (2.2). The fiber $L({\boldsymbol{u}})=\Phi^{-1}({\boldsymbol{u}})$ over each interior point ${\boldsymbol{u}}\in\operatorname{Int}\Delta$ is a Lagrangian torus.

The image $\Delta\subset\mathbb{R}^{N(n_{1},\dots,n_{r},n)}$ is called the Gelfand-Cetlin polytope. The Gelfand-Cetlin system is not smooth on the locus where $\lambda_{k}^{(i)}=\lambda_{k}^{(i+1)}$ for some $(i,k)$ , or equivalently, where the Gelfand-Cetlin pattern (2.2) contains a set of equalities of the form

\begin{aligned} &&\hbox to16.49995pt{$\hfill{\lambda_{k+1}^{(i+1)}}\hfill$}&&\\ &\rotatebox[origin={c}]{45.0}{$=$}&&\rotatebox[origin={c}]{315.0}{$=$}&&\phantom{\rotatebox[origin={c}]{315.0}{$\geq$}}&\\ \hbox to16.49995pt{$\hfill{\lambda_{k}^{(i)}}\hfill$}&&&&\hbox to16.49995pt{$\hfill{\lambda_{k}^{(i+1)}}\hfill$}&&\\ &\rotatebox[origin={c}]{315.0}{$=$}&&\rotatebox[origin={c}]{45.0}{$=$}&&&\\ &&\hbox to16.49995pt{$\hfill{\lambda_{k-1}^{(i)}}\hfill$}&&&&\end{aligned}.

The image of such loci are faces of $\Delta$ of codimension greater than two where $\Delta$ does not satisfy the Delzant condition. Away from such faces, each fiber $\Phi^{-1}({\boldsymbol{u}})$ of $\Phi$ is an isotropic torus whose dimension is that of the face of $\Delta$ containing ${\boldsymbol{u}}$ in its relative interior.

2.3 The case of $\operatorname{Fl}(3)$

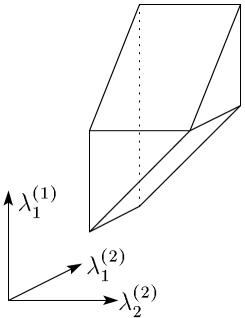
Refer to caption — Figure 2.1: The Gelfand-Cetlin polytope for $\operatorname{Fl}(3)$

After a translation by a scalar matrix, we may assume that $\operatorname{Fl}(3)$ is identified with the adjoint orbit of ${\boldsymbol{\lambda}}=\operatorname{diag}(\lambda_{1},0,-\lambda_{2})$ for $\lambda_{1},\lambda_{2}>0$ . Then the Gelfand-Cetlin polytope $\Delta$ consists of $(u_{1},u_{2},u_{3})\in\mathbb{R}^{3}$ satisfying

$\displaystyle$		$\displaystyle$		$\displaystyle$			(2.3)
	$\displaystyle\rotatebox[origin={c}]{315.0}{$\geq$}$		$\displaystyle\rotatebox[origin={c}]{45.0}{$\geq$}$		$\displaystyle\rotatebox[origin={c}]{315.0}{$\geq$}$	$\displaystyle\rotatebox[origin={c}]{45.0}{$\geq$}$
$\displaystyle$		$\displaystyle$
	$\displaystyle\rotatebox[origin={c}]{315.0}{$\geq$}$		$\displaystyle\rotatebox[origin={c}]{45.0}{$\geq$}$
$\displaystyle$

as shown in Figure 2.1. The non-smooth locus of $\Phi$ is the fiber $L_{0}=\Phi^{-1}({\boldsymbol{0}})$ over the vertex ${\boldsymbol{0}}=(0,0,0)\in\Delta$ where four edges intersect.

Definition 2.4 (Evans and Lekili [EL, Definition 1.1.1]).

Let $K$ be a compact connected Lie group. A Lagrangian submanifold $L$ in a Kähler manifold $X$ is said to be $K$ -homogeneous if $K$ acts holomorphically on $X$ in such a way that $L$ is a $K$ -orbit.

Proposition 2.5.

The fiber $L_{0}=\Phi^{-1}({\boldsymbol{0}})$ is a Lagrangian 3-sphere given by

L_{0}=\left\{\left.\begin{pmatrix}0&0&z_{1}\\ 0&0&z_{2}\\ \overline{z}_{1}&\overline{z}_{2}&\lambda_{1}-\lambda_{2}\end{pmatrix}\in\sqrt{-1}\mathfrak{u}(3)\right||z_{1}|^{2}+|z_{2}|^{2}=\lambda_{1}\lambda_{2}\right\},

which is $K$ -homogeneous for

K=\left\{\left.\begin{pmatrix}a_{1}&-\overline{a}_{2}&0\\ a_{2}&\overline{a}_{1}&0\\ 0&0&1\end{pmatrix}\right||a_{1}|^{2}+|a_{2}|^{2}=1\right\}\cong\operatorname{SU}(2).

Proof.

Suppose that $x\in L_{0}$ . Then $\lambda_{1}^{(2)}(x)=\lambda_{2}^{(2)}(x)=0$ implies that $x^{(2)}=0$ and thus $x$ has the form

x=\begin{pmatrix}0&0&z_{1}\\ 0&0&z_{2}\\ \overline{z}_{1}&\overline{z}_{2}&x_{33}\end{pmatrix}

for some $z_{1},z_{2}\in\mathbb{C}$ and $x_{33}\in\mathbb{R}$ . Since

\operatorname{det}(\lambda-x)=\lambda\left(\lambda^{2}-x_{33}\lambda-(|z_{1}|^{2}+|z_{2}|^{2})\right)=0

has solutions $\lambda=\lambda_{1},0,-\lambda_{2}$ , we have $x_{33}=\lambda_{1}-\lambda_{2}$ and $|z_{1}|^{2}+|z_{2}|^{2}=\lambda_{1}\lambda_{2}$ . Hence the fiber $L_{0}$ is the $K$ -orbit of

\begin{pmatrix}0&0&\sqrt{\lambda_{1}\lambda_{2}}\\ 0&0&0\\ \sqrt{\lambda_{1}\lambda_{2}}&0&\lambda_{1}-\lambda_{2}\end{pmatrix}=\operatorname{Ad}_{g_{0}}\begin{pmatrix}\lambda_{1}&0&0\\ 0&0&0\\ 0&0&-\lambda_{2}\end{pmatrix}\in\mathcal{O}_{{\boldsymbol{\lambda}}},

where

g_{0}=\begin{pmatrix}\sqrt{\lambda_{2}/(\lambda_{1}+\lambda_{2})}&0&-\sqrt{\lambda_{1}/(\lambda_{1}+\lambda_{2})}\\ 0&1&0\\ \sqrt{\lambda_{1}/(\lambda_{1}+\lambda_{2})}&0&\sqrt{\lambda_{2}/(\lambda_{1}+\lambda_{2})}\end{pmatrix}\in\operatorname{SU}(3).

Next we see that $L_{0}$ is Lagrangian. Since $K$ acts transitively on $L_{0}$ , the tangent space $T_{x}L_{0}$ is spanned by infinitesimal actions $\operatorname{ad}_{\xi}(x)$ of $\xi\in\mathfrak{k}$ , where

\mathfrak{k}=\biggl{\{}\xi=\begin{pmatrix}\xi^{(2)}&0\\ 0&0\end{pmatrix}\in\mathfrak{u}(3)\biggm{|}\xi^{(2)}\in\mathfrak{su}(2)\biggr{\}}\cong\mathfrak{su}(2)

is the Lie algebra of $K$ . Since $x^{(2)}=0$ for $x\in L_{0}$ , we have

\omega(\operatorname{ad}_{\xi}(x),\operatorname{ad}_{\eta}(x))=\frac{\sqrt{-1}}{2\pi}\operatorname{tr}\Bigl{(}x^{(2)}[\xi^{(2)},\eta^{(2)}]\Bigr{)}=0

for any $\xi,\eta\in\mathfrak{k}$ . ∎

Let $\iota:\operatorname{Fl}(3)\to\mathbb{P}_{1}\times\mathbb{P}_{2}=\mathbb{P}(\mathbb{C}^{3})\times\mathbb{P}(\bigwedge^{2}\mathbb{C}^{3})$ be the Plücker embedding and $([Z_{1}:Z_{2}:Z_{3}],[Z_{23}:Z_{31}:Z_{12}])$ be the Plücker coordinates. The Kostant-Kirillov form is given by

\omega=\lambda_{1}\omega_{\mathbb{P}_{1}}+\lambda_{2}\omega_{\mathbb{P}_{2}}.

Since the Lagrangian fiber $L_{0}$ as a submanifold in $\operatorname{SU}(3)/T$ consists of

\begin{pmatrix}a_{1}&-\overline{a}_{2}&0\\ a_{2}&\overline{a}_{1}&0\\ 0&0&1\end{pmatrix}g_{0}=\frac{1}{\sqrt{\lambda_{1}+\lambda_{2}}}\begin{pmatrix}\sqrt{\lambda_{2}}a_{1}&-\sqrt{\lambda_{1}+\lambda_{2}}\overline{a}_{2}&-\sqrt{\lambda_{1}}a_{1}\\ \sqrt{\lambda_{2}}a_{2}&\sqrt{\lambda_{1}+\lambda_{2}}\overline{a}_{1}&-\sqrt{\lambda_{1}}a_{2}\\ \sqrt{\lambda_{1}}&0&\sqrt{\lambda_{2}}\end{pmatrix}\mod T

with $|a_{1}|^{2}+|a_{2}|^{2}=1$ , the image $\iota(L_{0})$ is given by

\iota(L_{0})=\Biggl{\{}\Biggm{(}\left[a_{1}:a_{2}:\sqrt{\frac{\lambda_{1}}{\lambda_{2}}}\right],\left[\overline{a}_{1}:\overline{a}_{2}:-\sqrt{\frac{\lambda_{2}}{\lambda_{1}}}\right]\Biggm{)}\,\Biggm{|}\,|a_{1}|^{2}+|a_{2}|^{2}=1\Biggr{\}}.

(2.4)

Define an anti-holomorphic involution $\tau$ on $\operatorname{Fl}(3)$ by

\displaystyle\tau\left([Z_{1}:Z_{2}:Z_{3}],[Z_{23}:Z_{31}:Z_{12}]\right)

\displaystyle=\left(\left[{\overline{Z}}_{23}:{\overline{Z}}_{31}:-\frac{\lambda_{1}}{\lambda_{2}}{\overline{Z}}_{12}\right],\left[\overline{Z}_{1}:\overline{Z}_{2}:-\frac{\lambda_{2}}{\lambda_{1}}\overline{Z}_{3}\right]\right).

(2.5)

Proposition 2.6.

The Lagrangian $L_{0}$ is the fixed point set of $\tau$ .

One can easily see that $\tau$ is an anti-symplectic involution if and only if $\lambda_{1}=\lambda_{2}$ .

2.4 The case of $\operatorname{Gr}(2,4)$

For $k<n$ , let ${\widetilde{V}}(k,n)$ be the space of $n\times k$ matrices of rank $k$ , and set

V(k,n)=\{Z\in{\widetilde{V}}(k,n)\mid Z^{*}Z=I_{k}\}.

Then the Grassmannian $\operatorname{Gr}(k,n)$ is given by

\operatorname{Gr}(k,n)={\widetilde{V}}(k,n)/\operatorname{GL}(k,\mathbb{C})=V(k,n)/\operatorname{U}(k).

We first consider the Gelfand-Cetlin system on $\operatorname{Gr}(n,2n)$ for general $n$ . Fix $\lambda>0$ and identify $\operatorname{Gr}(n,2n)$ with the adjoint orbit $\mathcal{O}_{{\boldsymbol{\lambda}}}$ of

\displaystyle{\boldsymbol{\lambda}}

\displaystyle=\operatorname{diag}(\underbrace{\lambda,\dots,\lambda}_{n},\underbrace{-\lambda,\dots,-\lambda}_{n}).

The orbit $\mathcal{O}_{{\boldsymbol{\lambda}}}$ consists of matrices of the form $2\lambda ZZ^{*}-\lambda I_{2n}$ for $Z\in V(n,2n)$ . The Gelfand-Cetlin polytope $\Delta$ of $\operatorname{Gr}(n,2n)$ consists of ${\boldsymbol{u}}=(u_{i}^{(k)})_{(i,k)\in I}\in\mathbb{R}^{n^{2}}$ satisfying

\begin{aligned} &&&&&&\hbox to16.49995pt{$\hfill{u_{n}^{(2n-1)}}\hfill$}\\ &&&&&\rotatebox[origin={c}]{45.0}{$\geq$}&&\rotatebox[origin={c}]{315.0}{$\geq$}\\ \hbox to16.49995pt{$\hfill{\lambda}\hfill$}&&&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{45.0}{$\cdots$}}\hfill$}&&&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{315.0}{$\cdots$}}\hfill$}&&&&\hbox to16.49995pt{$\hfill{-\lambda}\hfill$}\\ &\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{315.0}{$\geq$}}\hfill$}&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{45.0}{$\geq$}}\hfill$}&&&&&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{315.0}{$\geq$}}\hfill$}&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{45.0}{$\geq$}}\hfill$}\\ &&\hbox to16.49995pt{$\hfill{u_{1}^{(n)}}\hfill$}&&&&\hbox to16.49995pt{$\hfill{\cdots}\hfill$}&&&&\hbox to16.49995pt{$\hfill{u_{n}^{(n)}}\hfill$}\\ &&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{315.0}{$\geq$}}\hfill$}&&&&&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{45.0}{$\geq$}}\hfill$}\\ &&&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{315.0}{$\cdots$}}\hfill$}&&&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{45.0}{$\cdots$}}\hfill$}\\ &&&&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{315.0}{$\geq$}}\hfill$}&&\hbox to16.49995pt{$\hfill{\rotatebox[origin={c}]{45.0}{$\geq$}}\hfill$}\\ &&&&&&\hbox to16.49995pt{$\hfill{u_{1}^{(1)}}\hfill$}\end{aligned}.

For $-\lambda<t<\lambda$ , let $L_{t}=\Phi^{-1}(t,\dots,t)$ be the fiber over the boundary point $u_{1}^{(1)}=\dots=u^{(2n-1)}_{n}=t$ of $\Delta$ .

Proposition 2.7.

The fiber $L_{t}$ is a Lagrangian submanifold given by

L_{t}=\biggl{\{}\begin{pmatrix}tI_{n}&\sqrt{\lambda^{2}-t^{2}}A^{*}\\ \sqrt{\lambda^{2}-t^{2}}A&-tI_{n}\end{pmatrix}\in\sqrt{-1}\mathfrak{u}(2n)\biggm{|}A\in\operatorname{U}(n)\biggr{\}}\cong\operatorname{U}(n),

which is $K$ -homogeneous for

K=\left\{\left.\begin{pmatrix}P&0\\ 0&I_{n}\end{pmatrix}\in\operatorname{U}(2n)\,\right|\,P\in\operatorname{U}(n)\right\}\cong\operatorname{U}(n).

Proof.

We write $x\in\mathcal{O}_{{\boldsymbol{\lambda}}}$ as

x=2\lambda ZZ^{*}-\lambda I_{2n}=\lambda\begin{pmatrix}2Z_{1}Z_{1}^{*}-I_{n}&2Z_{1}Z_{2}^{*}\\ 2Z_{2}Z_{1}^{*}&2Z_{2}Z_{2}^{*}-I_{n}\end{pmatrix}

for $n\times n$ matrices $Z_{1}$ , $Z_{2}$ with

Z=\begin{pmatrix}Z_{1}\\ Z_{2}\end{pmatrix}\in V(n,2n).

Suppose that $x\in L_{t}$ , or equivalently, $\lambda_{1}^{(n)}(x)=\dots=\lambda_{n}^{(n)}(x)=t$ . Then the upper-left $n\times n$ block of $x$ satisfies

x^{(n)}=2\lambda Z_{1}Z_{1}^{*}-\lambda I_{n}=tI_{n},

which means that $Z_{1}\in\sqrt{(\lambda+t)/2\lambda}\operatorname{U}(n)$ . After the right $\operatorname{U}(n)$ -action on $V(n,2n)$ , we may assume that $Z_{1}=\sqrt{(\lambda+t)/2\lambda}I_{n}$ . Then the condition $Z^{*}Z=I_{n}$ implies that

Z_{2}^{*}Z_{2}=I_{n}-\frac{\lambda+t}{2\lambda}I_{n}=\frac{\lambda-t}{2\lambda}I_{n}.

Hence $Z$ has the form

Z=\begin{pmatrix}\sqrt{(\lambda+t)/2\lambda}I_{n}\\ \sqrt{(\lambda-t)/2\lambda}A\end{pmatrix}\in V(n,2n)

(2.6)

for some $A\in\operatorname{U}(n)$ , which shows that

x=2\lambda ZZ^{*}-\lambda I_{2n}=\begin{pmatrix}tI_{n}&\sqrt{\lambda^{2}-t^{2}}A^{*}\\ \sqrt{\lambda^{2}-t^{2}}A&-tI_{n}\end{pmatrix}.

The $K$ -homogeneity is obvious from this expression. Since the tangent space $T_{x}L_{t}$ is spanned by the infinitesimal action of the Lie algebra $\mathfrak{k}$ of $K$ , and $x^{(n)}=tI_{n}$ is a scalar matrix, we have

\omega_{x}(\operatorname{ad}_{\xi}(x),\operatorname{ad}_{\eta}(x))=\frac{1}{2\pi}\operatorname{tr}x^{(n)}[\xi^{(n)},\eta^{(n)}]=0

for

\xi=\begin{pmatrix}\xi^{(n)}&\\ &0\end{pmatrix},\ \eta=\begin{pmatrix}\eta^{(n)}&\\ &0\end{pmatrix}\in\mathfrak{k},

which shows that $L_{t}$ is Lagrangian. ∎

Corollary 2.8.

For $t\neq 0$ , the fiber $L_{t}$ is displaceable, i.e., there exists a Hamiltonian diffeomorphism $\varphi$ on $\operatorname{Gr}(n,2n)$ such that $\varphi(L_{t})\cap L_{t}=\emptyset$ .

Proof.

One has $g(L_{t})=L_{-t}$ for $g=\begin{pmatrix}0&-I_{n}\\ I_{n}&0\end{pmatrix}\in\operatorname{U}(2n).$ ∎

In the rest of this subsection, we restrict ourselves to the case of $\operatorname{Gr}(2,4)$ . We write $(u_{1},u_{2},u_{3},u_{4})=(u_{2}^{(3)},u_{1}^{(2)},u_{2}^{(2)},u_{1}^{(1)})$ for simplicity. Figure 2.2 shows the projection

\Delta\longrightarrow[-\lambda,\lambda],\quad{\boldsymbol{u}}=(u_{1},u_{2},u_{3},u_{4})\longmapsto u_{1}.

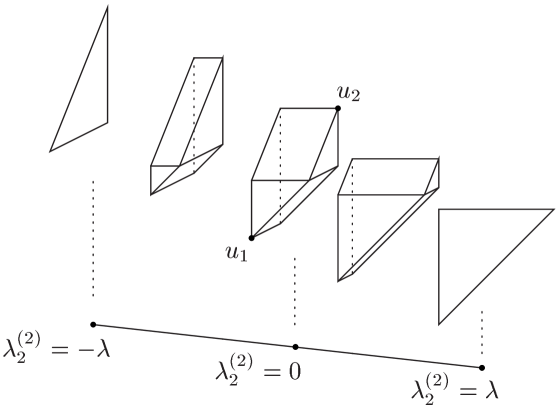
The non-smooth locus of $\Phi$ is the inverse image of the edge of $\Delta$ defined by $u_{1}=\dots=u_{4}$ . The fiber $L_{t}$ over $(t,t,t,t)\in\partial\Delta$ is a Lagrangian submanifold consists of $2\lambda ZZ^{*}-\lambda I_{2n}$ with

Z=\frac{1}{\sqrt{2\lambda}}\begin{pmatrix}\sqrt{\lambda+t}I_{2}\\ \sqrt{\lambda-t}A\end{pmatrix}\mod\operatorname{U}(2)

for $A\in\operatorname{U}(2)$ . We identify $\operatorname{U}(2)$ with $\operatorname{U}(1)\times\operatorname{SU}(2)\cong S^{1}\times S^{3}$ by

\operatorname{U}(1)\times\operatorname{SU}(2)\longrightarrow\operatorname{U}(2),\quad\left(a_{0},\begin{pmatrix}a_{1}&-\overline{a}_{2}\\ a_{2}&\overline{a}_{1}\end{pmatrix}\right)\longmapsto\begin{pmatrix}a_{0}&0\\ 0&1\end{pmatrix}\begin{pmatrix}a_{1}&-\overline{a}_{2}\\ a_{2}&\overline{a}_{1}\end{pmatrix}.

Then the image of $L_{t}$ under the Plücker embedding $\iota:\operatorname{Gr}(2,4)\to\mathbb{P}(\bigwedge^{2}\mathbb{C}^{4})\cong\mathbb{P}^{5}$ is given by

\iota(L_{t})=\Biggl{\{}\biggl{[}\sqrt{\frac{\lambda+t}{\lambda-t}}:-a_{0}\overline{a}_{2}:\overline{a}_{1}:-a_{0}a_{1}:-a_{2}:\sqrt{\frac{\lambda-t}{\lambda+t}}a_{0}\biggr{]}\Biggm{|}|a_{0}|^{2}=|a_{1}|^{2}+|a_{2}|^{2}=1\Biggr{\}}.

This expression implies the following.

Proposition 2.9.

For each $t\in(-\lambda,\lambda)$ , we define an anti-holomorphic involution $\tau_{t}$ on $\operatorname{Gr}(2,4)$ defined by

\tau_{t}([Z_{12}:Z_{13}:Z_{14}:Z_{23}:Z_{24}:Z_{34}])=\biggl{[}\frac{\lambda+t}{\lambda-t}\overline{Z}_{34}:\overline{Z}_{24}:-\overline{Z}_{23}:-\overline{Z}_{14}:\overline{Z}_{13}:\frac{\lambda-t}{\lambda+t}\overline{Z}_{12}\biggr{]}

(2.7)

Then $L_{t}$ is the fixed point set of $\tau_{t}$ .

Remark 2.10.

The map $\tau_{0}$ for $t=0$ is an anti-symplectic involution as well, and satisfies $\tau_{0}(L_{t})=L_{-t}$ for each $t\in(-\lambda,\lambda)$ .

2.5 The case of $\operatorname{Gr}(2,5)$

We fix $\lambda>0$ and identify $\operatorname{Gr}(2,5)$ with the adjoint orbit $\mathcal{O}_{{\boldsymbol{\lambda}}}$ of $\operatorname{diag}(\lambda,\lambda,0,0,0)\in\sqrt{-1}\mathfrak{u}(5)$ . The Gelfand-Cetlin polytope $\Delta$ is defined by

$\displaystyle$		$\displaystyle$					(2.8)
	$\displaystyle\rotatebox[origin={c}]{315.0}{$\geq$}$		$\displaystyle\rotatebox[origin={c}]{45.0}{$\geq$}$		$\displaystyle\rotatebox[origin={c}]{315.0}{$\geq$}$
$\displaystyle$		$\displaystyle$		$\displaystyle$
	$\displaystyle\rotatebox[origin={c}]{315.0}{$\geq$}$		$\displaystyle\rotatebox[origin={c}]{45.0}{$\geq$}$		$\displaystyle\rotatebox[origin={c}]{315.0}{$\geq$}$	$\displaystyle\rotatebox[origin={c}]{45.0}{$\geq$}$
$\displaystyle$		$\displaystyle$
	$\displaystyle\rotatebox[origin={c}]{315.0}{$\geq$}$		$\displaystyle\rotatebox[origin={c}]{45.0}{$\geq$}$
$\displaystyle$

We first consider the fiber $L_{1}(s_{1},s_{2},t)$ over a boundary point given by

\begin{aligned} \hbox to16.49995pt{$\hfill{\lambda}\hfill$}&&&&\hbox to16.49995pt{$\hfill{s_{2}}\hfill$}\\ &\rotatebox[origin={c}]{315.0}{$>$}&&\rotatebox[origin={c}]{45.0}{$>$}&&\rotatebox[origin={c}]{315.0}{$>$}\\ &&\hbox to16.49995pt{$\hfill{s_{1}}\hfill$}&&&&\hbox to16.49995pt{$\hfill{t}\hfill$}&&&&\hbox to16.49995pt{$\hfill{0}\hfill$}\\ &&&\rotatebox[origin={c}]{315.0}{$>$}&&\rotatebox[origin={c}]{45.0}{$=$}&&\rotatebox[origin={c}]{315.0}{$=$}&&\rotatebox[origin={c}]{45.0}{$>$}\\ &&&&\hbox to16.49995pt{$\hfill{t}\hfill$}&&&&\hbox to16.49995pt{$\hfill{t}\hfill$}\\ &&&&&\rotatebox[origin={c}]{315.0}{$=$}&&\rotatebox[origin={c}]{45.0}{$=$}\\ &&&&&&\hbox to16.49995pt{$\hfill{t}\hfill$}\end{aligned}.

Proposition 2.11.

The fiber $L_{1}(s_{1},s_{2},t)$ is a Lagrangian submanifold diffeomorphic to $\operatorname{U}(2)\times T^{2}\cong S^{3}\times T^{3}$ . Moreover, $L_{1}(s_{1},s_{2},t)$ is $K$ -homogeneous for

K=\left\{\left.\begin{pmatrix}P\\ &e^{\sqrt{-1}\theta_{1}}\\ &&e^{\sqrt{-1}\theta_{2}}\\ &&&1\end{pmatrix}\in\operatorname{U}(5)\right|P\in\operatorname{U}(2),\,\theta_{1},\theta_{2}\in\mathbb{R}\right\}\cong\operatorname{U}(2)\times T^{2}.

Proof.

Note that $\mathcal{O}_{{\boldsymbol{\lambda}}}$ consists of matrices of the form

\displaystyle x=\lambda ZZ^{*}=\lambda(z_{i}\overline{z}_{j}+w_{i}\overline{w}_{j})_{1\leq i,j\leq 5}

(2.9)

for

Z=\begin{pmatrix}z_{1}&w_{1}\\ z_{2}&w_{2}\\ z_{3}&w_{3}\\ z_{4}&w_{4}\\ z_{5}&w_{5}\end{pmatrix}\in V(2,5),

i.e.,

\displaystyle\sum_{i=1}^{5}|z_{i}|^{2}=\sum_{i=1}^{5}|w_{i}|^{2}=1,\quad\sum_{i=1}^{5}z_{i}\overline{w}_{i}=0.

(2.10)

Since the upper-left $2\times 2$ submatrix of $x=\lambda(z_{i}\overline{z}_{j}+w_{i}\overline{w}_{j})\in L_{1}(s_{1},s_{2},t)$ satisfies

\displaystyle x^{(2)}=\lambda\begin{pmatrix}|z_{1}|^{2}+|w_{1}|^{2}&z_{1}\overline{z}_{2}+w_{1}\overline{w}_{2}\\ z_{2}\overline{z}_{1}+w_{2}\overline{w}_{1}&|z_{2}|^{2}+|w_{2}|^{2}\end{pmatrix}=\begin{pmatrix}t&0\\ 0&t\end{pmatrix},

(2.11)

we have

\displaystyle\sqrt{\frac{\lambda}{t}}\begin{pmatrix}z_{1}&w_{1}\\ z_{2}&w_{2}\end{pmatrix}\in\operatorname{U}(2),

(2.12)

and in particular, $|z_{1}|^{2}+|z_{2}|^{2}=|w_{1}|^{2}+|w_{2}|^{2}=t/\lambda$ . Then the condition (2.10) implies

$\displaystyle\|z_{3}\|^{2}+\|z_{4}\|^{2}+\|z_{5}\|^{2}$	$\displaystyle=(\lambda-t)/\lambda,$	(2.13)
$\displaystyle\|w_{3}\|^{2}+\|w_{4}\|^{2}+\|w_{5}\|^{2}$	$\displaystyle=(\lambda-t)/\lambda,$	(2.14)
$\displaystyle z_{3}\overline{w}_{3}+z_{4}\overline{w}_{4}+z_{5}\overline{w}_{5}$	$\displaystyle=0.$	(2.15)

On the other hand, the conditions $\operatorname{tr}x^{(3)}=s_{1}+t$ , $\operatorname{tr}x^{(4)}=\lambda+s_{2}$ imply

$\displaystyle\|z_{3}\|^{2}+\|w_{3}\|^{2}$	$\displaystyle=(s_{1}-t)/\lambda,$	(2.16)
$\displaystyle\|z_{4}\|^{2}+\|w_{4}\|^{2}$	$\displaystyle=(\lambda-s_{1}+s_{2}-t)/\lambda,$	(2.17)
$\displaystyle\|z_{5}\|^{2}+\|w_{5}\|^{2}$	$\displaystyle=(\lambda-s_{2})/\lambda.$	(2.18)

After the right $\operatorname{SU}(2)$ -action on $(z,w)$ , we may assume that $(z_{5},w_{5})=\bigl{(}\sqrt{(\lambda-s_{2})/\lambda},0\bigr{)}$ . Then (2.13), (2.14), and (2.15) become

	$\displaystyle\|z_{3}\|^{2}+\|z_{4}\|^{2}$	$\displaystyle=(s_{2}-t)/\lambda,$
	$\displaystyle\|w_{3}\|^{2}+\|w_{4}\|^{2}$	$\displaystyle=(\lambda-t)/\lambda,$
	$\displaystyle z_{3}\overline{w}_{3}+z_{4}\overline{w}_{4}$	$\displaystyle=0,$

which mean that the $2\times 2$ submatrix $(z_{i},w_{i})_{i=3,4}$ has the form

\begin{pmatrix}z_{3}&w_{3}\\ z_{4}&w_{4}\end{pmatrix}=\begin{pmatrix}\sqrt{(s_{2}-t)/\lambda}\,a&-\sqrt{(\lambda-t)/\lambda}\,\overline{b}c\\ \sqrt{(s_{2}-t)/\lambda}\,b&\sqrt{(\lambda-t)/\lambda}\,\overline{a}c\end{pmatrix}

for some

\begin{pmatrix}a&-\overline{b}\\ b&\overline{a}\end{pmatrix}\in\operatorname{SU}(2),\quad c\in\operatorname{U}(1).

Combining this with (2.16) and (2.17) we have

|a|^{2}=\frac{\lambda-s_{1}}{\lambda-s_{2}},\quad|b|^{2}=\frac{s_{1}-s_{2}}{\lambda-s_{2}},

and hence

\begin{pmatrix}z_{3}&w_{3}\\ z_{4}&w_{4}\end{pmatrix}=\frac{1}{\sqrt{\lambda(\lambda-s_{2})}}\begin{pmatrix}\sqrt{(s_{2}-t)(\lambda-s_{1})}\,e^{\sqrt{-1}\theta_{1}}&-\sqrt{(\lambda-t)(s_{1}-s_{2})}\,e^{-\sqrt{-1}\theta_{2}}c\\ \sqrt{(s_{2}-t)(s_{1}-s_{2})}\,e^{\sqrt{-1}\theta_{2}}&\sqrt{(\lambda-t)(\lambda-s_{1})}\,e^{-\sqrt{-1}\theta_{1}}c\end{pmatrix}

for some $\theta_{1},\theta_{2}\in\mathbb{R}$ . After the action of

\left\{\left.\begin{pmatrix}1&0\\ 0&e^{\sqrt{-1}\varphi}\end{pmatrix}\in\operatorname{U}(2)\right|\varphi\in\mathbb{R}\right\}\cong\operatorname{U}(1)

from the right, we may assume that

\begin{pmatrix}z_{3}&w_{3}\\ z_{4}&w_{4}\end{pmatrix}=\frac{1}{\sqrt{\lambda(\lambda-s_{2})}}\begin{pmatrix}\sqrt{(s_{2}-t)(\lambda-s_{1})}\,e^{\sqrt{-1}\theta_{1}}&-\sqrt{(\lambda-t)(s_{1}-s_{2})}\,e^{\sqrt{-1}\theta_{1}}\\ \sqrt{(s_{2}-t)(s_{1}-s_{2})}\,e^{\sqrt{-1}\theta_{2}}&\sqrt{(\lambda-t)(\lambda-s_{1})}\,e^{\sqrt{-1}\theta_{2}}\end{pmatrix}.

Therefore $Z=(z_{i},w_{i})_{i}$ is normalized as

\begin{pmatrix}z_{1}&w_{1}\\ \vdots&\vdots\\ z_{5}&w_{5}\\ \end{pmatrix}=\begin{pmatrix}z_{1}&w_{1}\\ z_{2}&w_{2}\\ \sqrt{(s_{2}-t)(\lambda-s_{1})/\lambda(\lambda-s_{2})}\,e^{\sqrt{-1}\theta_{1}}&-\sqrt{(\lambda-t)(s_{1}-s_{2})/\lambda(\lambda-s_{2})}\,e^{\sqrt{-1}\theta_{1}}\\ \sqrt{(s_{2}-t)(s_{1}-s_{2})/\lambda(\lambda-s_{2})}\,e^{\sqrt{-1}\theta_{2}}&\sqrt{(\lambda-t)(\lambda-s_{1})/\lambda(\lambda-s_{2})}\,e^{\sqrt{-1}\theta_{2}}\\ \sqrt{(\lambda-s_{2})/\lambda}&0\end{pmatrix}

with (2.12), which implies that $L_{1}(s_{1},s_{2},t)$ is a $K$ -orbit and diffeomorphic to $\operatorname{U}(2)\times T^{2}$ .

The assertion that $L_{1}(s_{1},s_{2},t)$ is Lagrangian follows from the $K$ -homogeneity as in the cases of $\operatorname{Fl}(3)$ and $\operatorname{Gr}(n,2n)$ . ∎

Next we consider the fiber $L_{2}(s_{1},s_{2},t)$ over

\begin{aligned} \hbox to16.49995pt{$\hfill{\lambda}\hfill$}&&&&\hbox to16.49995pt{$\hfill{t}\hfill$}\\ &\rotatebox[origin={c}]{315.0}{$>$}&&\rotatebox[origin={c}]{45.0}{$=$}&&\rotatebox[origin={c}]{315.0}{$=$}\\ &&\hbox to16.49995pt{$\hfill{t}\hfill$}&&&&\hbox to16.49995pt{$\hfill{t}\hfill$}&&&&\hbox to16.49995pt{$\hfill{0}\hfill$}\\ &&&\rotatebox[origin={c}]{315.0}{$=$}&&\rotatebox[origin={c}]{45.0}{$=$}&&\rotatebox[origin={c}]{315.0}{$>$}&&\rotatebox[origin={c}]{45.0}{$>$}\\ &&&&\hbox to16.49995pt{$\hfill{t}\hfill$}&&&&\hbox to16.49995pt{$\hfill{s_{1}}\hfill$}\\ &&&&&\rotatebox[origin={c}]{315.0}{$>$}&&\rotatebox[origin={c}]{45.0}{$>$}\\ &&&&&&\hbox to16.49995pt{$\hfill{s_{2}}\hfill$}\end{aligned}.

Suppose that $x=\lambda(z_{i}\overline{z}_{j}+w_{i}\overline{w}_{j})_{1\leq i,j\leq 5}\in L_{2}(s_{1},s_{2},t)$ . The condition that $x^{(3)}=\lambda(z_{i}\overline{z}_{j}+w_{i}\overline{w}_{j})_{1\leq i,j\leq 3}$ has eigenvalues $t,t,0$ is equivalent to

$\displaystyle\|z_{1}\|^{2}+\|z_{2}\|^{2}+\|z_{3}\|^{2}$	$\displaystyle=t/\lambda,$	(2.19)
$\displaystyle\|w_{1}\|^{2}+\|w_{2}\|^{2}+\|w_{3}\|^{2}$	$\displaystyle=t/\lambda,$	(2.20)
$\displaystyle z_{1}\overline{w}_{1}+z_{2}\overline{w}_{2}+z_{3}\overline{w}_{3}$	$\displaystyle=0,$	(2.21)

and hence

\sqrt{\frac{\lambda}{\lambda-t}}\begin{pmatrix}z_{4}&w_{4}\\ z_{5}&w_{5}\end{pmatrix}\in U(2).

On the other hand, the conditions $x^{(1)}=s_{2}$ , $\operatorname{tr}x^{(2)}=t+s_{1}$ , and $\operatorname{tr}x^{(3)}=2t$ imply

	$\displaystyle\|z_{1}\|^{2}+\|w_{1}\|^{2}$	$\displaystyle=s_{2}/\lambda,$
	$\displaystyle\|z_{2}\|^{2}+\|w_{2}\|^{2}$	$\displaystyle=(t-s_{2}+s_{1})/\lambda,$
	$\displaystyle\|z_{3}\|^{2}+\|w_{3}\|^{2}$	$\displaystyle=(t-s_{1})/\lambda.$

Then we have the following.

Proposition 2.12.

The fiber $L_{2}(s_{1},s_{2},t)$ is a $\operatorname{U}(2)\times T^{2}$ -homogeneous Lagrangian submanifold diffeomorphic to $\operatorname{U}(2)\times T^{2}\cong S^{3}\times T^{3}$ . Moreover, the fibers $L_{1}(s_{1},s_{2},t)$ and $L_{2}(s_{1},s_{2},t)$ satisfy

g(L_{2}(s_{1},s_{2},t))=L_{1}(\lambda-s_{1},\lambda-s_{2},\lambda-t)

for

g=\begin{pmatrix}0&&1\\ &\rotatebox[origin={c}]{45.0}{$\cdots$}&\\ 1&&0\end{pmatrix}\in\operatorname{U}(5).

In particular, $L_{1}(s_{1},s_{2},t)$ and $L_{2}(s_{1},s_{2},t)$ are displaceable.

The Hamiltonian isotopy invariance of the Floer cohomology over the Novikov field [FOOO09, Theorem G] implies the following.

Corollary 2.13.

For $i=1,2$ , we have

\mathop{H\!F}\nolimits((L_{i}(s_{1},s_{2},t),b),(L_{i}(s_{1},s_{2},t),b);\Lambda)=0

for any weak bounding cochain $b$ .

Remark 2.14.

Other boundary fibers have lower dimensions. For example, the fiber over

$\displaystyle$		$\displaystyle$
	$\displaystyle\rotatebox[origin={c}]{315.0}{$>$}$		$\displaystyle\rotatebox[origin={c}]{45.0}{$=$}$		$\displaystyle\rotatebox[origin={c}]{315.0}{$=$}$
$\displaystyle$		$\displaystyle$		$\displaystyle$
	$\displaystyle\rotatebox[origin={c}]{315.0}{$=$}$		$\displaystyle\rotatebox[origin={c}]{45.0}{$=$}$		$\displaystyle\rotatebox[origin={c}]{315.0}{$=$}$	$\displaystyle\rotatebox[origin={c}]{45.0}{$>$}$
$\displaystyle$		$\displaystyle$
	$\displaystyle\rotatebox[origin={c}]{315.0}{$=$}$		$\displaystyle\rotatebox[origin={c}]{45.0}{$=$}$
$\displaystyle$

consists of

\begin{pmatrix}\sqrt{t/\lambda}&0\\ 0&\sqrt{t/\lambda}\\ 0&0\\ z_{4}&w_{4}\\ z_{5}&w_{5}\end{pmatrix}\mod\operatorname{U}(2)

with

\begin{pmatrix}z_{4}&w_{4}\\ z_{5}&w_{5}\end{pmatrix}\in\sqrt{(\lambda-t)/\lambda}\operatorname{U}(2),

which means that the fiber is diffeomorphic to $\operatorname{U}(2)$ .

3 Critical points of the potential function

Let $\Phi:F=F(n_{1},\dots,n_{r},n)\to\Delta$ be the Gelfand-Cetlin system on the flag manifold, and $\{\theta^{(k)}_{i}\}_{(i,k)\in I}$ be the angle variables dual to the action variables $\{\lambda_{i}^{(k)}\}_{(i,k)\in I}$ . For each ${\boldsymbol{u}}=(u_{k}^{(i)})_{(i,k)\in I}\in\operatorname{Int}\Delta$ , we identify $H^{1}(L({\boldsymbol{u}});\Lambda_{0})$ with $\Lambda_{0}^{N}$ by

b=\sum_{(i,k)\in I}x^{(k)}_{i}d\theta^{(k)}_{i}\in H^{1}(L({\boldsymbol{u}});\Lambda_{0})\longleftrightarrow{\boldsymbol{x}}=(x^{(k)}_{i})_{(i,k)\in I}\in\Lambda_{0}^{N},

and set

	$\displaystyle y_{i}^{(k)}$	$\displaystyle=e^{x_{i}^{(k)}}T^{u_{i}^{(k)}},\qquad(i,k)\in I,$
	$\displaystyle Q_{j}$	$\displaystyle=T^{\lambda_{n_{j}}},\qquad j=1,\dots,r+1.$

Theorem 3.1 ([NNU10, Theorem 10.1]).

For any interior point ${\boldsymbol{u}}\in\operatorname{Int}\Delta$ , we have an inclusion $H^{1}(L({\boldsymbol{u}});\Lambda_{0})\subset\widehat{\mathcal{M}}_{\mathrm{weak}}(L({\boldsymbol{u}}))$ . As a function on

\bigcup_{{\boldsymbol{u}}\in\operatorname{Int}\Delta}H^{1}(L({\boldsymbol{u}});\Lambda_{0})\cong\operatorname{Int}\Delta\times\Lambda_{0}^{N},

the potential function is given by

\mathfrak{PO}({\boldsymbol{u}},{\boldsymbol{x}})=\sum_{(i,k)\in I}\left(\frac{y_{i}^{(k+1)}}{y_{i}^{(k)}}+\frac{y_{i}^{(k)}}{y_{i+1}^{(k+1)}}\right),

where we put $y_{i}^{(k+1)}=Q_{j}$ if $\lambda_{i}^{(k+1)}=\lambda_{n_{j}}$ is a constant function.

Example 3.2.

We identify the 3-dimensional flag manifold $\operatorname{Fl}(3)$ with the adjoint orbit of ${\boldsymbol{\lambda}}=\operatorname{diag}(\lambda_{1},\lambda_{2},\lambda_{3})$ . The potential function is given by

	$\displaystyle\mathfrak{PO}$	$\displaystyle=e^{-x_{1}}T^{-u_{1}+\lambda_{1}}+e^{x_{1}}T^{u_{1}-\lambda_{2}}+e^{-x_{2}}T^{-u_{2}+\lambda_{2}}$
		$\displaystyle\qquad+e^{x_{2}}T^{u_{2}-\lambda_{3}}+e^{x_{1}-x_{3}}T^{u_{1}-u_{3}}+e^{-x_{2}+x_{3}}T^{-u_{2}+u_{3}}$
		$\displaystyle=\frac{Q_{1}}{y_{1}}+\frac{y_{1}}{Q_{2}}+\frac{Q_{2}}{y_{2}}+\frac{y_{2}}{Q_{3}}+\frac{y_{1}}{y_{3}}+\frac{y_{3}}{y_{2}}.$

The potential function $\mathfrak{PO}$ has six critical points given by

	$\displaystyle y_{1}$	$\displaystyle={y_{3}^{2}}/{y_{2}},$
	$\displaystyle y_{2}$	$\displaystyle=\pm\sqrt{Q_{3}(y_{3}+Q_{2})},$
	$\displaystyle y_{3}$	$\displaystyle=\sqrt[3]{Q_{1}Q_{2}Q_{3}},\ e^{2\pi\sqrt{-1}/3}\sqrt[3]{Q_{1}Q_{2}Q_{3}},\ e^{4\pi\sqrt{-1}/3}\sqrt[3]{Q_{1}Q_{2}Q_{3}}.$

It is easy to see that all critical points are non-degenerate and have the same valuation which lies in the interior of the Gelfand-Cetlin polytope. Hence we have as many critical points as $\dim H^{*}(\operatorname{Fl}(3))=6$ in this case. One can show, using the presentation of the quantum cohomology in [GK95, Theorem 1], that the set of eigenvalues of the quantum cup product by $c_{1}(\operatorname{Fl}(3))$ coincides with the set of critical values of the potential function.

The Floer differential $\mathfrak{m}_{1}^{b}$ is trivial for each critical point $({\boldsymbol{u}},{\boldsymbol{x}})$ of $\mathfrak{PO}$ , and the corresponding Floer cohomology is given by

\mathop{H\!F}\nolimits((L({\boldsymbol{u}}),b),(L({\boldsymbol{u}}),b);\Lambda_{0})\cong H^{*}(L({\boldsymbol{u}});\Lambda_{0})\cong H^{*}(T^{3};\Lambda_{0}).

Example 3.3.

We identify $\operatorname{Gr}(2,4)$ with the adjoint orbit of $\operatorname{diag}(2\lambda,2\lambda,0,0)$ . Setting $Q=T^{2\lambda}$ , the potential function is given by

$\displaystyle\mathfrak{PO}$	$\displaystyle=e^{-x_{2}}T^{-u_{2}+2\lambda}+e^{-x_{1}+x_{2}}T^{-u_{1}+u_{2}}+e^{x_{1}-x_{3}}T^{u_{1}-u_{3}}$
	$\displaystyle\qquad+e^{x_{3}}T^{u_{3}}+e^{x_{2}-x_{4}}T^{u_{2}-u_{4}}+e^{-x_{3}+x_{4}}T^{-u_{3}+u_{4}}$
	$\displaystyle=\frac{Q}{y_{2}}+\frac{y_{2}}{y_{1}}+\frac{y_{1}}{y_{3}}+y_{3}+\frac{y_{2}}{y_{4}}+\frac{y_{4}}{y_{3}}.$	(3.1)

This function has four critical points

(y_{1},y_{2},y_{3},y_{4})=\left((-1)^{i}\sqrt[4]{Q^{2}},\sqrt{-1}^{i}\sqrt[4]{\frac{Q^{3}}{4}},\sqrt{-1}^{i}\sqrt[4]{4Q},(-1)^{i}\sqrt[4]{Q^{2}}\right)

for $i=0,1,2,3$ , and the corresponding critical values are

\displaystyle\mathfrak{PO}=4\sqrt{2}\sqrt{-1}^{i}\sqrt[4]{Q}.

(3.2)

Since $\dim H^{*}(\operatorname{Gr}(2,4))=6$ , one has less critical point than $\dim H^{*}(\operatorname{Gr}(2,4))$ . These critical points are non-degenerate and have a common valuation

{\boldsymbol{u}}_{0}=(\lambda,3\lambda/2,\lambda/2,\lambda)\in\operatorname{Int}\Delta.

Hence there exist four weak bounding cochains $b_{0},\dots,b_{3}$ such that

\mathop{H\!F}\nolimits((L({\boldsymbol{u}}_{0}),b_{i}),(L({\boldsymbol{u}}_{0}),b_{i});\Lambda_{0})\cong H^{*}(L({\boldsymbol{u}}_{0});\Lambda_{0})\cong H^{*}(T^{4};\Lambda_{0})

for $i=0,1,2,3$ . One can show, using the presentation of the quantum cohomology in [ST97, Theorem 0.1], that the set eigenvalues of the quantum cup product by $c_{1}(\operatorname{Gr}(2,4))$ consists of the four critical values of the potential function and the zero eigenvalue with multiplicity two.

Example 3.4.

We identify $\operatorname{Gr}(2,5)$ with the adjoint orbit of $\operatorname{diag}(\lambda,\lambda,0,0,0)$ . Since the Gelfand-Cetlin polytope is defined by (2.8), the potential function is given by

\displaystyle\mathfrak{PO}=\frac{Q}{y_{2}}+\frac{y_{2}}{y_{1}}+\frac{y_{1}}{y_{3}}+\frac{y_{2}}{y_{4}}+\frac{y_{4}}{y_{3}}+\frac{y_{3}}{y_{5}}+y_{5}+\frac{y_{4}}{y_{6}}+\frac{y_{6}}{y_{5}}.

(3.3)

This function has ten critical points defined by

y_{6}^{5}=Q^{5},\quad Qy_{4}=y_{6}(y_{6}^{3}-y_{4}^{2}),

and

y_{1}=\frac{Q}{y_{6}},\quad y_{2}=\frac{Q}{y_{5}},\quad y_{3}=\frac{Q}{y_{4}},\quad y_{5}=\frac{y_{6}^{2}}{y_{4}}.

The set

\displaystyle\left\{5(\zeta_{5}^{i}+\zeta_{5}^{j})Q^{1/5}\mathrel{}\middle|\mathrel{}\zeta_{5}=\exp(2\pi\sqrt{-1}/5)\text{ and }0\leq i<j\leq 4\right\}

(3.4)

of critical values of the potential function coincides with the set of eigenvalues of the quantum cup product by $c_{1}(\operatorname{Gr}(2,5))$ .

4 Floer cohomologies of non-torus fibers

We briefly recall the construction of the $A_{\infty}$ structure $\{\mathfrak{m}_{k}\}_{k\geq 0}$ , omitting various technical details. Let $L$ be a spin, oriented, and compact Lagrangian submanifold in a symplectic manifold $(X,\omega)$ . For an almost complex structure $J$ compatible with $\omega$ , let $\mathcal{M}_{k+1}(J,\beta)$ be the moduli space of stable $J$ -holomorphic maps $v:(\Sigma,\partial\Sigma)\to(X,L)$ from a bordered Riemann surface $\Sigma$ in the class $\beta\in\pi_{2}(X,L)$ of genus zero with $(k+1)$ boundary marked points $z_{0},z_{1},\dots,z_{k}\in\partial\Sigma$ . Then $\mathfrak{m}_{k}=\sum_{\beta\in\pi_{2}(X,L)}T^{\beta\cap\omega}\mathfrak{m}_{k,\beta}\colon H^{*}(L;\Lambda_{0})^{\otimes k}\to H^{*}(L;\Lambda_{0})$ is defined by

\mathfrak{m}_{k,\beta}(x_{1},\dots,x_{k})=(\operatorname{ev}_{0})_{*}(\operatorname{ev}_{1}^{*}x_{1}\cup\dots\cup\operatorname{ev}_{k}^{*}x_{k}),

where $\operatorname{ev}_{i}\colon\mathcal{M}_{k+1}(J,\beta)\to L$ , $[v,(z_{0},\dots,z_{k})]\mapsto v(z_{i})$ is the evaluation map at the $i$ th marked point.

4.1 Holomorphic disks in $(\operatorname{Fl}(3),L_{0})$

We identify $\operatorname{Fl}(3)$ with the adjoint orbit of $\operatorname{diag}(\lambda_{1},0,-\lambda_{2})$ for $\lambda_{1},\lambda_{2}>0$ as in Subsection 2.3. Note that the symplectic form and the first Chern class are given by $\omega=\lambda_{1}\omega_{\mathbb{P}_{1}}+\lambda_{2}\omega_{\mathbb{P}_{2}}$ and $c_{1}(\operatorname{Fl}(3))=2(\omega_{\mathbb{P}_{1}}+\omega_{\mathbb{P}_{2}})$ , respectively.

Recall that the homotopy group $\pi_{2}(\operatorname{Fl}(3))\cong\mathbb{Z}^{2}$ is generated by 1-dimensional Schubert varieties $X_{1}$ and $X_{2}$ , which are rational curves of bidegree $(1,0)$ and $(0,1)$ in $\mathbb{P}_{1}\times\mathbb{P}_{2}\cong\mathbb{P}^{2}\times\mathbb{P}^{2}$ , respectively. Since $L_{0}$ is diffeomorphic to $\operatorname{SU}(2)\cong S^{3}$ , we have $\pi_{1}(L_{0})=\pi_{2}(L_{0})=0$ . The long exact sequence of homotopy groups yields

\pi_{2}(\operatorname{Fl}(3),L_{0})\cong\pi_{2}(\operatorname{Fl}(3))\cong\mathbb{Z}^{2}.

Let $\beta_{1}$ , $\beta_{2}$ be generators of $\pi_{2}(\operatorname{Fl}(3),L_{0})$ corresponding to $X_{1}$ and $X_{2}$ , respectively. The symplectic area of $\beta_{i}$ is given by

\beta_{i}\cap\omega=[X_{i}]\cap(\lambda_{1}\omega_{\mathbb{P}_{1}}+\lambda_{2}\omega_{\mathbb{P}_{2}})=\lambda_{i}.

Let $\tau$ be the anti-holomorphic involution on $\operatorname{Fl}(3)$ defined in (2.5). For a holomorphic disk $v:(D^{2},\partial D^{2})\to(\operatorname{Fl}(3),L_{0})$ , we define a new holomorphic disk $\tau_{*}v:(D^{2},\partial D^{2})\to(\operatorname{Fl}(3),L_{0})$ by

\tau_{*}v(z)=\tau(v(\overline{z})).

Since $L_{0}$ is the fixed point set of $\tau$ , one can glue $v$ and $\tau_{*}v$ along the boundary to obtain a holomorphic curve $w=v\#\tau_{*}v:\mathbb{P}^{1}\to\operatorname{Fl}(3)$ . The induced involution on $\pi_{2}(\operatorname{Fl}(3),L_{0})$ , which is also denoted by $\tau_{*}$ , is given by $\tau_{*}\beta_{1}=\beta_{2}$ . If $v$ represents $\beta_{1}$ or $\beta_{2}$ , then $[w]=\beta_{1}+\beta_{2}=[X_{1}]+[X_{2}]$ , i.e., $w$ is a rational curve of bidegree $(1,1)$ .

Let $\mu_{L_{0}}:\pi_{2}(\operatorname{Fl}(3),L_{0})\to\mathbb{Z}$ be the Maslov index. If we assume $\lambda_{1}=\lambda_{2}$ so that $\tau$ is an anti-symplectic involution, then we have

\mu_{L_{0}}(\beta_{i})=\frac{1}{2}(\mu_{L_{0}}(\beta_{i})+\mu_{L_{0}}(\tau_{*}\beta_{i}))=([X_{1}]+[X_{2}])\cap c_{1}(\operatorname{Fl}(3))=4

for $i=1,2$ . Since the symplectic form $\omega$ and the Lagrangian submanifold $L_{0}$ depend continuously on $\lambda_{1},\lambda_{2}>0$ , the Maslov index $\mu_{L_{0}}(\beta_{1})=\mu_{L_{0}}(\beta_{2})=4$ is independent of $\lambda_{1},\lambda_{2}$ .

To describe holomorphic disks with Lagrangian boundary condition, we identify the unit disk $D^{2}$ with the upper half plane $\mathbb{H}=\mathbb{H}_{+}$ .

Proposition 4.1.

Let $w\colon\mathbb{P}^{1}\to\operatorname{Fl}(3)$ be a holomorphic curve of bidegree $(1,1)$ such that $w(\mathbb{R}\cup\{\infty\})\subset L_{0}$ . After the $\operatorname{SU}(2)$ -action, we may assume

w(\infty)=([1:0:\sqrt{\lambda_{1}/\lambda_{2}}],[1:0:-\sqrt{\lambda_{2}/\lambda_{1}}]).

(4.1)

We can write

w(0)=\Bigl{(}\bigl{[}a_{1}:a_{2}:\sqrt{\lambda_{1}/\lambda_{2}}\bigr{]},\bigl{[}\overline{a}_{1}:\overline{a}_{2}:-\sqrt{\lambda_{2}/\lambda_{1}}\bigr{]}\Bigr{)}\in L_{0}

(4.2)

for some $(a_{1},a_{2})\in S^{3}\setminus\{(1,0)\}$ . Then $w$ is given by

w(z)=\Bigl{(}\bigl{[}cz+a_{1}:a_{2}:\sqrt{\lambda_{1}/\lambda_{2}}(cz+1)\bigr{]},\bigl{[}\overline{c}z+\overline{a}_{1}:\overline{a}_{2}:-\sqrt{\lambda_{2}/\lambda_{1}}(\overline{c}z+1)\bigr{]}\Bigr{)}

with $c/\overline{c}=-(a_{1}-1)/(\overline{a}_{1}-1)$ .

Remark 4.2.

After the action of

\{g\in\operatorname{PSL}(2,\mathbb{R})\,|\,g(0)=0,\,g(\infty)=\infty\}\cong\mathbb{R}_{>0}

on $\mathbb{H}$ , we may assume that $|c|=1$ .

Proof.

The assumptions (4.1) and (4.2) implies that $w$ has the form

w(z)=\Bigl{(}\bigl{[}c_{1}z+a_{1}:a_{2}:\sqrt{\lambda_{1}/\lambda_{2}}(c_{1}z+1)\bigr{]},\bigl{[}c_{2}z+\overline{a}_{1}:\overline{a}_{2}:-\sqrt{\lambda_{2}/\lambda_{1}}(c_{2}z+1)\bigr{]}\Bigr{)}

for some $c_{1},c_{2}\in\mathbb{C}^{*}$ . The Plücker relation

	$\displaystyle 0$	$\displaystyle=-(c_{1}z+a_{1})(c_{2}z+\overline{a}_{1})-\|a_{2}\|^{2}+(c_{1}z+1)(c_{2}z+1)$
		$\displaystyle=(c_{1}-a_{1}c_{1}+c_{2}-\overline{a}_{1}c_{2})z$

implies $c_{1}(\overline{a}_{1}-1)+c_{2}(a-1)=0$ . On the other hand, the Lagrangian boundary condition $w(\mathbb{R})\subset L_{0}$ implies that

\frac{c_{1}x+a_{1}}{c_{1}x+1}=\frac{\overline{c_{2}}x+a_{1}}{\overline{c_{2}}x+1},\quad\frac{a_{2}}{c_{1}x+1}=\frac{a_{2}}{\overline{c_{2}}x+1},\quad x\in\mathbb{R},

which means $c_{2}=\overline{c_{1}}$ . ∎

Note that $\arg c$ is determined by $a_{1}$ up to sign, and the sign corresponds to whether $v=w|_{\mathbb{H}}$ represents $\beta_{1}$ or $\beta_{2}$ . Namely any holomorphic disk in the class $\beta_{i}$ satisfying (4.1) and (4.2) is uniquely determined by $(a_{1},a_{2})$ for $i=1,2$ .

Example 4.3.

Suppose that $(a_{1},a_{2})=(-1,0)$ . Then $c=\pm\sqrt{-1}$ , and the corresponding holomorphic disks are given by

v_{\pm}(z)=\Bigl{(}\bigl{[}z\pm\sqrt{-1}:0:\sqrt{\frac{\lambda_{1}}{\lambda_{2}}}(z\mp\sqrt{-1})\bigr{]},\bigl{[}z\mp\sqrt{-1}:0:-\sqrt{\frac{\lambda_{2}}{\lambda_{1}}}(z\pm\sqrt{-1})\bigr{]}\Bigr{)}.

It is easy to see that the image $v_{+}(\mathbb{H})$ (resp. $v_{-}(\mathbb{H})$ ) is the inverse image of the edge of $\Delta$ given by $u^{(1)}_{1}=u^{(2)}_{1}$ and $u^{(2)}_{2}=0$ (resp. $u^{(1)}_{1}=u^{(2)}_{2}$ and $u^{(2)}_{1}=0$ ), which is the upper (resp. lower) vertical edge emanating from the vertex ${\boldsymbol{0}}=(0,0,0)$ . The generators $\beta_{1},\beta_{2}$ of $\pi_{2}(\operatorname{Fl}(3),L_{0})$ are represented by $v_{+}$ and $v_{-}$ respectively.

4.2 Floer cohomology of the $\operatorname{SU}(2)$ -fiber in $\operatorname{Fl}(3)$

Let $J$ be the standard complex structure on $\operatorname{Fl}(3)$ . Since the fiber $L_{0}$ is $\operatorname{SU}(2)$ -homogeneous, [EL, Proposition 3.2.1] implies the following.

Proposition 4.4.

Any $J$ -holomorphic disk in $(\operatorname{Fl}(3),L_{0})$ is Fredholm regular. Hence the moduli space $\mathcal{M}_{k+1}^{\mathrm{reg}}(J,\beta)$ of $J$ -holomorphic disks in the class $\beta$ with $k+1$ boundary marked points is a smooth manifold of dimension

	$\displaystyle\dim\mathcal{M}_{k+1}^{\mathrm{reg}}(J,\beta)$	$\displaystyle=\dim L_{0}+\mu_{L_{0}}(\beta)+k+1-3$
		$\displaystyle=\mu_{L_{0}}(\beta)+k+1.$

In particular, we have $\dim\mathcal{M}_{2}(J,\beta_{i})=6$ for $i=1,2$ . Proposition 4.1 implies the following:

Corollary 4.5.

Let $U=\operatorname{SU}(2)\setminus\{1\}\cong\{(a_{1},a_{2})\in S^{3}\,|\,a_{1}\neq 1\}$ . Then $\mathcal{M}_{2}(J,\beta_{i})$ has an open dense subset diffeomorphic to $\operatorname{SU}(2)\times U$ on which the evaluation map is given by

\operatorname{SU}(2)\times U\longrightarrow L_{0}\times L_{0}\cong\operatorname{SU}(2)\times\operatorname{SU}(2),\quad(g_{1},g_{2})\longmapsto(g_{1},g_{1}g_{2}).

In particular, $\operatorname{ev}:\mathcal{M}_{2}(J,\beta_{i})\to L_{0}\times L_{0}$ is generically one-to-one.

Since the minimal Maslov number is $\mu_{L_{0}}(\beta_{1})=\mu_{L_{0}}(\beta_{2})=4$ and

\deg\mathfrak{m}_{1,\beta}(x)=\deg x+1-\mu_{L_{0}}(\beta),\quad x\in H^{*}(L_{0};\Lambda_{0}),

the only nontrivial parts of the Floer differential are

\mathfrak{m}_{1,\beta_{i}}:H^{3}(L_{0})\cong H_{0}(L_{0})\longrightarrow H^{0}(L_{0})\cong H_{3}(L_{0})

for $i=1,2$ . Corollary 4.5 implies that for the class $[p]\in H_{0}(L_{0})$ of a point, we have

\mathfrak{m}_{1,\beta_{i}}([p])={\operatorname{ev}_{0}}_{*}[\mathcal{M}_{2}(J,\beta_{i}){}_{\operatorname{ev}_{1}}\!\times\{p\}]=\pm[L_{0}].

To see the sign, we use a result on the orientation of the moduli spaces of pseudo-holomorphic disks by Fukaya, Oh, Ohta, and Ono [FOOO, Theorem 1.5]. The following statement is a slightly weaker version of the result, which is sufficient for our purpose.

Theorem 4.6.

Let $(X,\omega)$ be a compact symplectic manifold, and $\tau$ an anti-symplectic involution on $X$ whose fixed point set $L=\operatorname{Fix}(\tau)$ is non-empty, compact, connected, and spin. Then $\mathfrak{m}_{k,\beta}$ and $\mathfrak{m}_{k,\tau_{*}\beta}$ satisfy

\mathfrak{m}_{k,\beta}(P_{1},\dots,P_{k})=(-1)^{\epsilon}\mathfrak{m}_{k,\tau_{*}\beta}(P_{k},\dots,P_{1}),

where

\epsilon=\frac{\mu_{L}(\beta)}{2}+k+1+\sum_{1\leq i<j\leq k}(\deg P_{i}-1)(\deg P_{j}-1).

Corollary 4.7.

We have $\mathfrak{m}_{1,\beta_{1}}=\mathfrak{m}_{1,\beta_{2}}$ for general $\lambda_{1},\lambda_{2}>0$ .

Proof.

If $\lambda_{1}=\lambda_{2}$ , then $\tau$ is anti-symplectic, and thus Theorem 4.6 implies

\mathfrak{m}_{1,\beta_{1}}=(-1)^{\mu_{L_{0}}(\beta_{1})/2+2}\mathfrak{m}_{1,\tau_{*}\beta_{1}}=\mathfrak{m}_{1,\beta_{2}}.

(4.3)

Corollary 4.5 implies that $\mathcal{M}_{2}(J,\beta_{i})$ depends continuously on $\lambda_{1},\lambda_{2}$ , and hence its orientation is independent of $\lambda_{1},\lambda_{2}$ . Thus (4.3) holds for general $\lambda_{1},\lambda_{2}$ . ∎

Then we have

\mathfrak{m}_{1}([p])=\sum_{i=1}^{2}\mathfrak{m}_{1,\beta_{i}}([p])T^{\beta_{i}\cap\omega}=\pm(T^{\lambda_{1}}+T^{\lambda_{2}})[L_{0}],

which implies the following.

Theorem 4.8.

The Floer cohomology of $L_{0}$ over the Novikov ring $\Lambda_{0}$ is

\mathop{H\!F}\nolimits(L_{0},L_{0};\Lambda_{0})\cong\Lambda_{0}/T^{\min\{\lambda_{1},\lambda_{2}\}}\Lambda_{0}.

Theorem 1.1 is an immediate consequence of Theorem 4.8.

4.3 Holomorphic disks in $(\operatorname{Gr}(2,4),L_{t})$

We identify $\operatorname{Gr}(2,4)$ with the adjoint orbit of $\operatorname{diag}(\lambda,\lambda,-\lambda,-\lambda)$ for $\lambda>0$ . Note that the Kostant-Kirillov form and the first Chern class are given by

\omega=2\lambda\omega_{\mathrm{FS}},\quad c_{1}(\operatorname{Gr}(2,4))=4\omega_{\mathrm{FS}},

respectively, where $\omega_{\mathrm{FS}}$ is the Fubini-Study form on $\mathbb{P}(\bigwedge^{2}\mathbb{C}^{4})$ .

Recall that $\pi_{2}(\operatorname{Gr}(2,4))\cong\mathbb{Z}$ is generated by a 1-dimensional Schubert variety $X_{1}$ , which is a rational curve of degree one in $\mathbb{P}(\bigwedge^{2}\mathbb{C}^{4})$ . Since $\pi_{1}(\operatorname{Gr}(2,4))=\pi_{2}(L_{t})=0$ and $\pi_{1}(L_{t})\cong\mathbb{Z}$ , the exact sequence

0\longrightarrow\pi_{2}(\operatorname{Gr}(2,4))\longrightarrow\pi_{2}(\operatorname{Gr}(2,4),L_{t})\longrightarrow\pi_{1}(L_{t})\longrightarrow 0

implies that $\pi_{2}(\operatorname{Gr}(2,4),L_{t})\cong\mathbb{Z}^{2}$ . Let $\beta_{1},\beta_{2}$ be generators of $\pi_{2}(\operatorname{Gr}(2,4),L_{t})$ such that $\beta_{1}+\beta_{2}=[X_{1}]\in\pi_{2}(\operatorname{Gr}(2,4))$ .

Example 4.9.

Consider a holomorphic curve $w:\mathbb{P}^{1}\to\operatorname{Gr}(2,4)$ of degree one defined by

w(z)=\left[\sqrt{\frac{\lambda+t}{\lambda-t}}(z-\sqrt{-1}):0:z-\sqrt{-1}:-z-\sqrt{-1}:0:\sqrt{\frac{\lambda-t}{\lambda+t}}(z+\sqrt{-1})\right].

(4.4)

Since $w$ maps $\mathbb{R}\cup\{\infty\}$ to $L_{t}$ , the restrictions

	$\displaystyle v_{+}$	$\displaystyle=w\|_{\mathbb{H}_{+}}:(\mathbb{H}_{+},\partial\mathbb{H}_{+})\longrightarrow(\operatorname{Gr}(2,4),L_{t}),$
	$\displaystyle v_{-}$	$\displaystyle=w\|_{\mathbb{H}_{-}}:(\mathbb{H}_{-},\partial\mathbb{H}_{-})\longrightarrow(\operatorname{Gr}(2,4),L_{t})$

to the upper and lower half planes give holomorphic disks representing $\beta_{1}$ and $\beta_{2}$ . We define $\beta_{1}=[v_{+}]$ and $\beta_{2}=[v_{-}]$ . It is easy to see that the symplectic areas of $v_{\pm}$ are given by

\omega(\beta_{1})=\int_{\mathbb{H}_{+}}v_{+}^{*}\omega=\lambda+t,\quad\omega(\beta_{2})=\int_{\mathbb{H}_{-}}v_{-}^{*}\omega=\lambda-t.

In the case where $t=0$ , the disk $v_{+}$ sends $\sqrt{-1}\in\mathbb{H}$ to $v_{+}(\sqrt{-1})=[0:0:0:-1:0:1]$ , which is in the fiber $\Phi^{-1}({\boldsymbol{u}}_{1})$ over the point ${\boldsymbol{u}}_{1}\in\Delta$ defined by $u_{1}^{(2)}=u_{1}^{(1)}=\lambda$ and $u_{2}^{(2)}=0$ (see Figure 2.2). On the other hand, $v_{-}(-\sqrt{-1})=[1:0:1:0:0:0]$ lies on the fiber over the point ${\boldsymbol{u}}_{2}\in\Delta$ defined by $u_{2}^{(2)}=u_{1}^{(1)}=-\lambda$ and $u_{1}^{(2)}=0$ .

Let $\tau_{t}$ be the anti-holomorphic involution on $\operatorname{Gr}(2,4)$ defined in (2.7). Note that $(\tau_{t})_{*}$ is given by $(\tau_{t})_{*}v(z)=\tau_{t}(v(-\overline{z}))$ for $v:(\mathbb{H},\partial\mathbb{H})\to(\operatorname{Gr}(2,4),L_{t})$ . Since $(\tau_{t})_{*}v_{+}=v_{-}$ , the induced involution on $\pi_{2}(\operatorname{Gr}(2,4),L_{t})$ is given by $(\tau_{t})_{*}\beta_{1}=\beta_{2}$ . Then the Maslov index of $\beta_{i}$ is given by

\mu_{L_{t}}(\beta_{i})=\frac{1}{2}\left(\mu_{L_{t}}(\beta_{i})+\mu_{L_{t}}((\tau_{t})_{*}\beta_{i})\right)=[X_{1}]\cap c_{1}(\operatorname{Gr}(2,4))=4

for $i=1,2$ .

We describe holomorphic curves $w\colon\mathbb{P}^{1}\to\operatorname{Gr}(n,2n)$ of degree one such that $w(\mathbb{R}\cup\{\infty\})$ is contained in the Lagrangian fiber $L_{t}$ . Proposition 4.10 below is taken from [Sot01, Theorem 2.1], which is well-known in control theory (cf. e.g. [Ros70]).

Proposition 4.10.

Suppose that a holomorphic curve $w\colon\mathbb{P}^{1}\to\operatorname{Gr}(k,n)={\widetilde{V}}(k,n)/\operatorname{GL}(k,\mathbb{C})$ of degree $d$ is given by

w\colon z\longmapsto\begin{pmatrix}I_{k}\\ F(z)\end{pmatrix}\mod\operatorname{GL}(k,\mathbb{C})

for a rational function $F(z)$ with values in $(n-k)\times K$ matrices. Then there exist matrix valued polynomials $P(z)$ , $Q(z)$ of size $k\times k$ and $(n-k)\times k$ respectively such that

1.

$F(z)=Q(z)P(z)^{-1}$ , i.e., the curve $w$ is given by

$w\colon z\longmapsto\begin{pmatrix}P(z)\\ Q(z)\end{pmatrix}\mod\operatorname{GL}(k,\mathbb{C}),$
2.

$P(z)$ and $Q(z)$ are coprime in the sense there exist matrix valued polynomials $X(z)$ , $Y(z)$ such that $X(z)P(z)+Y(z)Q(z)=I_{k}$ , and
3.

$\deg(\operatorname{det}P(z))=d$ .

Such $P(z)$ and $Q(z)$ are unique up to multiplication of elements in $\operatorname{GL}(k,\mathbb{C}[z])$ .

Note that (2.6) implies that the $\operatorname{U}(n)$ -fiber $L_{t}\subset\operatorname{Gr}(n,2n)={\widetilde{V}}(n,2n)/\operatorname{GL}(n,\mathbb{C})$ consists of

\begin{pmatrix}I_{n}\\ \sqrt{(\lambda-t)/(\lambda+t)}\,A\end{pmatrix}\mod\operatorname{GL}(n,\mathbb{C})

for $A\in\operatorname{U}(n)$ .

Proposition 4.11.

Let $w\colon\mathbb{P}^{1}\to\operatorname{Gr}(n,2n)$ be a holomorphic curve of degree one such that $w(\mathbb{R}\cup\{\infty\})\subset L_{t}$ , and let $F(z)$ denote the corresponding rational function with values in $n\times n$ matrices. By the $\operatorname{U}(n)$ -action, we assume that

F(\infty)=\sqrt{\frac{\lambda-t}{\lambda+t}}I_{n}\in\sqrt{\frac{\lambda-t}{\lambda+t}}\operatorname{U}(n),

(4.5)

and set

F(0)=\sqrt{\frac{\lambda-t}{\lambda+t}}A

(4.6)

for $A\in\operatorname{U}(n)$ . Then there exist

a=\begin{pmatrix}a_{1}\\ \vdots\\ a_{n}\end{pmatrix}\in S^{2n-1}/S^{1}=\mathbb{P}^{n-1}

and $c\in\mathbb{C}\setminus\mathbb{R}$ such that

A=I_{n}+\left(\frac{c^{2}}{|c|^{2}}-1\right)aa^{*},

and

F(z)=\sqrt{\frac{\lambda-t}{\lambda+t}}\frac{1}{z-\overline{c}}(zI_{n}-\overline{c}A)=\sqrt{\frac{\lambda-t}{\lambda+t}}\left(I_{n}-\frac{c-\overline{c}}{z-\overline{c}}aa^{*}\right).

(4.7)

Proof.

Let $F(z)=Q(z)P(z)^{-1}$ be the factorization given in Proposition 4.10. Then the assumptions (4.5), (4.6), and $\deg(\operatorname{det}P(z))=1$ imply that $F(z)$ has the form

F(z)=\sqrt{\frac{\lambda-t}{\lambda+t}}\frac{1}{z-\overline{c}}(zI_{n}-\overline{c}A)

for some $c\in\mathbb{C}$ . The Lagrangian boundary condition $w(\mathbb{R}\cup\{\infty\})\subset L_{t}$ implies that

\frac{1}{x-\overline{c}}(xI_{n}-\overline{c}A)\in\operatorname{U}(n)

for any $x\in\mathbb{R}$ , which means $\overline{c}A+cA^{*}=(c+\overline{c})I_{n}$ , or equivalently, $\overline{c}A-\operatorname{Re}(c)I_{n}$ is skew-hermitian. Hence $\overline{c}A-\operatorname{Re}(c)I_{n}$ has pure imaginary eigenvalues $\sqrt{-1}\alpha_{1},\dots,\sqrt{-1}\alpha_{n}$ , and can be diagonalized by some $g\in\operatorname{U}(n)$ ;

g^{*}(\overline{c}A-\operatorname{Re}(c)I_{n})g=\operatorname{diag}(\sqrt{-1}\alpha_{1},\dots,\sqrt{-1}\alpha_{n}).

Since

g^{*}Ag=\operatorname{diag}\left(\frac{\operatorname{Re}(c)+\sqrt{-1}\alpha_{1}}{\overline{c}},\dots,\frac{\operatorname{Re}(c)+\sqrt{-1}\alpha_{n}}{\overline{c}}\right)\in\operatorname{U}(n)

has eigenvalues of unit norm, we have $\alpha_{i}=\pm\operatorname{Im}(c)$ for $i=1,\dots,n$ . After the action of a permutation matrix, we may assume that $g^{*}Ag$ has the form

g^{*}Ag=\operatorname{diag}(\underbrace{c/\overline{c},\dots,c/\overline{c}}_{k},\underbrace{1,\dots,1}_{n-k})=:C

(4.8)

for some $k$ . Then $F(z)$ is given by

F(z)=\sqrt{\frac{\lambda-t}{\lambda+t}}\frac{1}{z-\overline{c}}g(zI_{n}-\overline{c}C)g^{*}=\sqrt{\frac{\lambda-t}{\lambda+t}}g\operatorname{diag}\left(\frac{z-c}{z-\overline{c}},\dots,\frac{z-c}{z-\overline{c}},1,\dots,1\right)g^{*}

In particular, we have

\operatorname{det}F(z)=\left(\frac{\lambda-t}{\lambda+t}\right)^{n/2}\left(\frac{z-c}{z-\overline{c}}\right)^{k}.

The condition $\deg(\operatorname{det}P(z))=1$ implies that $k=1$ , i.e.,

C=\operatorname{diag}(c/\overline{c},1,\dots,1)=(c/\overline{c}-1)E_{11}+I_{n},

where $E_{11}=\operatorname{diag}(1,0,\dots,0)\in\mathfrak{gl}(n,\mathbb{C})$ . Let $a\in S^{2n-1}\subset\mathbb{C}^{n}$ be the first column of $g$ . Then we have

A=g\left(\left(\frac{c^{2}}{|c|^{2}}-1\right)E_{11}+I_{n}\right)g^{*}=\left(\frac{c^{2}}{|c|^{2}}-1\right)aa^{*}+I_{n},

which proves the proposition. ∎

Remark 4.12.

1.

The equation (4.8) (with $k=1$ ) implies that $\operatorname{det}A=c/\overline{c}=c^{2}/|c|^{2}$ .
2.

After the $\mathbb{R}_{>0}$ -action on the domain, we may assume that $|c|=1$ .

We now assume that $n=2$ . The sign of $\operatorname{Im}(c)=\operatorname{Im}\sqrt{\operatorname{det}A}$ corresponds to the homotopy class of the holomorphic disk $v=w|_{\mathbb{H}}$ . The curve $w$ corresponding to $a=[1:0]$ and $c=-\sqrt{-1}$ coincides with (4.4), and hence $w|_{\mathbb{H}}=v_{+}$ represents $\beta_{1}$ . Thus $v=w|_{\mathbb{H}}$ represents $\beta_{1}$ (resp. $\beta_{2}$ ) when $\operatorname{Im}(c)=\operatorname{Im}\sqrt{\operatorname{det}A}<0$ (resp. $\operatorname{Im}(c)>0$ ).

4.4 Floer cohomologies of the $\operatorname{U}(2)$ -fibers in $\operatorname{Gr}(2,4)$

Since the minimal Maslov number of the $U(2)$ -fiber $L_{t}$ is $\mu_{L_{t}}(\beta_{i})=4$ , we have the following by degree reason.

Lemma 4.13.

The potential function $\mathfrak{PO}\colon H^{1}(L_{t};\Lambda_{0})\to\Lambda_{0}$ for $L_{t}$ is trivial:

\mathfrak{PO}\equiv 0.

The cohomology of $L_{t}\cong S^{1}\times S^{3}$ is given by

H^{*}(L_{t})\cong H^{*}(S^{1})\otimes H^{*}(S^{3}).

Let $\mathbf{e}_{1}\in H^{1}(L_{t};\mathbb{Z})\cong H^{1}(S^{1};\mathbb{Z})$ and $\mathbf{e}_{3}\in H^{3}(L_{t};\mathbb{Z})\cong H^{3}(S^{3};\mathbb{Z})$ be the generators, and write $b=x\mathbf{e}_{1}\in H^{1}(L_{t};\Lambda_{0})$ . Since $\deg\mathfrak{m}_{1,\beta}^{b}=1-\mu_{L_{t}}(\beta)$ and the minimal Maslov number is four, the only nontrivial parts of the Floer differential $\mathfrak{m}_{1}^{b}$ are

	$\displaystyle\mathfrak{m}_{1,\beta_{i}}^{b}$	$\displaystyle:H^{4}(L_{t})\cong H^{1}(S^{1})\otimes H^{3}(S^{3})\longrightarrow H^{1}(L_{t})\cong H^{1}(S^{1}),$
	$\displaystyle\mathfrak{m}_{1,\beta_{i}}^{b}$	$\displaystyle:H^{3}(L_{t})\cong H^{3}(S^{3})\longrightarrow H^{0}(L_{t})\cong\Lambda_{0}$

for $i=1,2$ .

Since $(\operatorname{Gr}(2,4),L_{t})$ is $\operatorname{U}(2)$ -homogeneous, any $J$ -holomorphic disk is Fredholm regular for the standard complex structure $J$ by [EL, Proposition 3.2.1]. Hence one has $\dim\mathcal{M}_{2}(J,\beta_{i})=7$ for $i=1,2$ . Now Proposition 4.11 implies the following:

Corollary 4.14.

Define $f\colon(0,2\pi)\times\mathbb{P}^{1}\to\operatorname{U}(2)$ by $f(\theta,a)=(e^{\sqrt{-1}\theta}-1)aa^{*}+I_{2}$ . For $i=1,2$ , the moduli space $\mathcal{M}_{2}(J,\beta_{i})$ has an open dense subset diffeomorphic to $\operatorname{U}(2)\times(0,2\pi)\times\mathbb{P}^{1}$ such that the evaluation map is given by

\operatorname{U}(2)\times(0,2\pi)\times\mathbb{P}^{1}\longrightarrow L_{t}\times L_{t}\cong\operatorname{U}(2)\times\operatorname{U}(2),\quad(g,\theta,a)\longmapsto(g,g\cdot f(\theta,a)).

Note that $e^{\sqrt{-1}\theta}=\operatorname{det}f(\theta,a)$ is related to $c\in S^{1}$ in Proposition 4.11 by $c=\exp(\sqrt{-1}(\theta/2+\pi))$ or $c=\exp(\sqrt{-1}\theta/2)$ corresponding to $i=1,2$ .

Next we consider $\mathcal{M}_{k+l+2}(J,\beta_{i})$ . For a rational curve $w\colon\mathbb{P}^{1}\to\operatorname{Gr}(2,4)$ given by (4.7), the composition $\operatorname{det}\circ w|_{\partial\mathbb{H}}\colon\partial\mathbb{H}=\mathbb{R}\to L_{t}\cong\operatorname{U}(2)\to S^{1}$ is given by

x\longmapsto\frac{x-c}{x-\overline{c}}.

Hence each boundary point $x\in\partial\mathbb{H}$ is determined by the argument of $\operatorname{det}w(x)=(x-c)/(x-\overline{c})$ . Fixing the $0$ -th and $(k+1)$ -st boundary marked points, we have the following.

Corollary 4.15.

The moduli space $\mathcal{M}_{k+l+2}(J,\beta_{i})$ has an open dense subset diffeomorphic to

\biggl{\{}(g,\theta,a,(t_{i}),(s_{j}))\in\operatorname{U}(2)\times(0,2\pi)\times\mathbb{P}^{1}\times\mathbb{R}^{k}\times\mathbb{R}^{l}\biggm{|}\begin{array}[]{c}0<t_{1}<\dots<t_{k}<\theta,\\ \theta<s_{1}<\dots<s_{l}<2\pi\end{array}\biggr{\}}

on which the evaluation maps $\operatorname{ev}\colon\mathcal{M}_{k+l+2}(J,\beta_{i})\to L_{t}\cong\operatorname{U}(2)$ satisfy

(\operatorname{ev}_{0},\operatorname{ev}_{k+1})\colon(g,\theta,a,(t_{i}),(s_{j}))\longmapsto(g,g\cdot f(\theta,a))

and

\operatorname{det}\operatorname{ev}_{i}(g,\theta,a,(t_{i}),(s_{j}))=\begin{cases}e^{\sqrt{-1}t_{i}}\operatorname{det}g,&i=1,\dots,k,\\ e^{\sqrt{-1}\theta}\operatorname{det}g,&i=k+1,\\ e^{\sqrt{-1}s_{i-k-1}}\operatorname{det}g,&i=k+2,\dots,k+l+2.\end{cases}

Theorem 4.16.

For $b=x\mathbf{e}_{1}\in H^{1}(L_{0};\Lambda_{0}/2\pi\sqrt{-1}\mathbb{Z})\cong\Lambda_{0}/2\pi\sqrt{-1}\mathbb{Z}$ , the deformed Floer differential $\mathfrak{m}_{1}^{b}$ is given by

	$\displaystyle\mathfrak{m}_{1}^{b}(\mathbf{e}_{3})$	$\displaystyle=e^{x}T^{\lambda+t}+e^{-x}T^{\lambda-t},$		(4.9)
	$\displaystyle\mathfrak{m}_{1}^{b}(\mathbf{e}_{1}\otimes\mathbf{e}_{3})$	$\displaystyle=(e^{x}T^{\lambda+t}+e^{-x}T^{\lambda-t})\mathbf{e}_{1}.$		(4.10)

Hence the Floer cohomology of $(L_{t},b)$ is

\mathop{H\!F}\nolimits((L_{t},b),(L_{t},b);\Lambda_{0})\cong\begin{cases}H^{*}(L_{0};\Lambda_{0})\quad&\text{if $t=0$ and $x=\pm\pi\sqrt{-1}/2$},\\ (\Lambda_{0}/T^{\min\{\lambda-t,\lambda+t\}}\Lambda_{0})^{2}&\text{otherwise}.\end{cases}

The Floer cohomology over the Novikov field is given by

\mathop{H\!F}\nolimits((L_{t},b),(L_{t},b);\Lambda)\cong\begin{cases}H^{*}(L_{0};\Lambda)\quad&\text{if $t=0$ and $x=\pm\pi\sqrt{-1}/2$},\\ 0&\text{otherwise}.\end{cases}

Recall that $\mathbf{e}_{1},\mathbf{e}_{3}\in H^{*}(\operatorname{U}(2))$ are given by

\mathbf{e}_{1}=\frac{1}{2\pi\sqrt{-1}}\operatorname{tr}(g^{-1}dg)=\frac{1}{2\pi\sqrt{-1}}d\log(\operatorname{det}g),\quad\mathbf{e}_{3}=\frac{1}{24\pi^{2}}\operatorname{tr}\left[(g^{-1}dg)^{3}\right],

where $g^{-1}dg$ is the left-invariant Maurer-Cartan form on $\operatorname{U}(2)$ .

Lemma 4.17.

For $f(\theta,a)=(e^{\sqrt{-1}\theta}-1)aa^{*}+I_{2}$ , we have

	$\displaystyle f^{*}\mathbf{e}_{1}$	$\displaystyle=\frac{1}{2\pi}\operatorname{tr}(f^{-1}df)=\frac{d\theta}{2\pi},$		(4.11)
	$\displaystyle f^{*}\mathbf{e}_{3}$	$\displaystyle=\frac{1}{24\pi^{2}}\operatorname{tr}(f^{-1}df)^{3}=(1-\cos\theta)\frac{d\theta}{2\pi}\wedge\omega_{\mathbb{P}^{1}},$		(4.12)

where $\omega_{\mathbb{P}^{1}}$ is the Fubini-Study form on $\mathbb{P}^{1}$ normalized in such a way that

\int_{\mathbb{P}^{1}}\omega_{\mathbb{P}^{1}}=1.

Proof.

The first assertion (4.11) follows from $\operatorname{det}f=e^{\sqrt{-1}\theta}$ . Since $f$ is $\operatorname{SU}(2)$ -equivariant with respect to the natural action on $\mathbb{P}^{1}$ and the adjoint action on $\operatorname{U}(2)$ , it suffices to show (4.12) at $a=[1:0]\in\mathbb{P}^{1}$ . A direct calculation gives

f^{-1}df=\begin{pmatrix}\sqrt{-1}d\theta&-(e^{-\sqrt{-1}\theta}-1)d\overline{a}_{2}\\ (e^{\sqrt{-1}\theta}-1)da_{2}&0\end{pmatrix},

so that

\operatorname{tr}(f^{-1}df)^{3}=3(2-e^{\sqrt{-1}\theta}-e^{-\sqrt{-1}\theta})\sqrt{-1}d\theta\wedge da_{2}\wedge d\overline{a}_{2}

at $a=[1:0]$ . On the other hand, the Fubini-Study form on $\mathbb{P}^{1}$ is given by

\omega_{\mathbb{P}^{1}}=\frac{\sqrt{-1}}{2\pi}da_{2}\wedge d\overline{a}_{2}

at $a=[1:0]$ , which proves (4.12). ∎

Proof of Theorem 4.16.

Note that for $m:\operatorname{U}(2)\times\operatorname{U}(2)\to\operatorname{U}(2)$ , $(g_{1},g_{2})\mapsto g_{1}g_{2}$ , we have $m^{*}\mathbf{e}_{i}=\pi_{1}^{*}\mathbf{e}_{i}+\pi_{2}^{*}\mathbf{e}_{i}$ for $i=1,3$ , where $\pi_{1},\pi_{2}\colon\operatorname{U}(2)\times\operatorname{U}(2)\to\operatorname{U}(2)$ are the projections to the first and the second factors. Then $\operatorname{ev}_{j}^{*}\mathbf{e}_{i}$ are given by

	$\displaystyle\operatorname{ev}_{i}^{*}\mathbf{e}_{1}$	$\displaystyle=\frac{1}{2\pi}dt_{i}+g^{*}\mathbf{e}_{1},\quad i=1,\dots,k,$
	$\displaystyle\operatorname{ev}_{k+1+i}^{*}\mathbf{e}_{1}$	$\displaystyle=\frac{1}{2\pi}dt_{i}+g^{*}\mathbf{e}_{1},\quad i=1,\dots,l,$
	$\displaystyle\operatorname{ev}_{k+1}^{*}\mathbf{e}_{3}$	$\displaystyle=f^{}\mathbf{e}_{3}+g^{}\mathbf{e}_{3}=(1-\cos\theta)\frac{d\theta}{2\pi}\wedge\omega_{\mathbb{P}^{1}}+g^{*}\mathbf{e}_{3},$

where $g^{*}\mathbf{e}_{i}$ is the pull-back of $\mathbf{e}_{i}$ by the projection

\operatorname{U}(2)\times(0,2\pi)\times\mathbb{P}^{1}\longrightarrow\operatorname{U}(2),\quad(g,\theta,a)\longmapsto g

to the first factor. For $\theta\in(0,2\pi)$ , set

	$\displaystyle D_{1}(\theta)$	$\displaystyle=\{(t_{1},\dots,t_{k})\in\mathbb{R}^{k}\mid 0<t_{1}<\dots<t_{k}<\theta\},$
	$\displaystyle D_{2}(\theta)$	$\displaystyle=\{(s_{1},\dots,s_{l})\in\mathbb{R}^{l}\mid\theta<s_{1}<\dots<s_{l}<2\pi\}.$

Taking a suitable orientation on $\mathcal{M}_{k+l+2}(\beta_{1},J)$ , we have from Corollary 4.15 that

	$\displaystyle\mathfrak{m}_{k+l+1,\beta_{1}}(\underbrace{b,\dots,b}_{k},\mathbf{e}_{3},\underbrace{b,\dots,b}_{l})$
	$\displaystyle\quad=\int_{(0,2\pi)\times\mathbb{P}^{1}}\left(\int_{D_{1}(\theta)}\left(\frac{x}{2\pi}\right)^{k}dt_{1}\wedge\dots\wedge dt_{k}\right)\left(\int_{D_{2}(\theta)}\left(\frac{x}{2\pi}\right)^{l}ds_{1}\wedge\dots\wedge ds_{l}\right)(1-\cos\theta)\frac{d\theta}{2\pi}\wedge\omega_{\mathbb{P}^{1}}$
	$\displaystyle\quad=\int_{(0,2\pi)}\frac{1}{k!}\left(\frac{\theta}{2\pi}\cdot x\right)^{k}\frac{1}{l!}\left(\left(1-\frac{\theta}{2\pi}\right)x\right)^{l}(1-\cos\theta)\frac{d\theta}{2\pi}.$		(4.13)

Hence

	$\displaystyle\mathfrak{m}_{1,\beta_{1}}^{b}(\mathbf{e}_{3})$	$\displaystyle=\int_{0}^{2\pi}\sum_{k,l\geq 0}\frac{1}{k!}\left(\frac{\theta}{2\pi}\cdot x\right)^{k}\frac{1}{l!}\left(\left(1-\frac{\theta}{2\pi}\right)x\right)^{l}(1-\cos\theta)\frac{d\theta}{2\pi}$
		$\displaystyle=\int_{0}^{2\pi}e^{(\theta/2\pi)x}e^{(1-\theta/2\pi)x}(1-\cos\theta)\frac{d\theta}{2\pi}$
		$\displaystyle=\int_{0}^{2\pi}e^{x}(1-\cos\theta)\frac{d\theta}{2\pi}$
		$\displaystyle=e^{x}.$

The same argument as the proof of Corollary 4.7 gives

	$\displaystyle\mathfrak{m}_{k+l+1,\beta_{2}}(\underbrace{b,\dots,b}_{k},\mathbf{e}_{3},\underbrace{b,\dots,b}_{l})$	$\displaystyle=(-1)^{k+l}\mathfrak{m}_{k+l+1,\beta_{1}}(\underbrace{b,\dots,b}_{l},\mathbf{e}_{3},\underbrace{b,\dots,b}_{k})$
		$\displaystyle=\mathfrak{m}_{k+l+1,\beta_{1}}(\underbrace{-b,\dots,-b}_{l},\mathbf{e}_{3},\underbrace{-b,\dots,-b}_{k}),$

so that

\mathfrak{m}_{1,\beta_{2}}^{b}(\mathbf{e}_{3})=e^{-x}.

Hence we have

\mathfrak{m}_{1}^{b}(\mathbf{e}_{3})=\sum_{i=1}^{2}\mathfrak{m}_{1,\beta_{i}}^{b}(\mathbf{e}_{3})T^{\beta_{i}\cap\omega}=e^{x}T^{\lambda+t}+e^{-x}T^{\lambda-t}.

Next we compute $\mathfrak{m}_{1}^{b}(\mathbf{e}_{1}\otimes\mathbf{e}_{3})\in H^{1}(L_{0})$ . Note that

\operatorname{ev}_{k+1}(\mathbf{e}_{1}\otimes\mathbf{e}_{3})=(g^{*}\mathbf{e}_{1}+f^{*}\mathbf{e}_{1})\otimes(g^{*}\mathbf{e}_{3}+f^{*}\mathbf{e}_{3})=g^{*}\mathbf{e}_{1}\otimes f^{*}\mathbf{e}_{3}+\dots.

Since only the term $g^{*}\mathbf{e}_{1}\otimes f^{*}\mathbf{e}_{3}$ contribute to $\mathfrak{m}_{k+l+1,\beta_{i}}(b,\dots,b,\mathbf{e}_{1}\otimes\mathbf{e}_{3},b,\dots,b)$ by degree reason, we have

\mathfrak{m}_{k+l+1,\beta_{i}}(\underbrace{b,\dots,b}_{k},\mathbf{e}_{1}\otimes\mathbf{e}_{3},\underbrace{b,\dots,b}_{l})=\mathfrak{m}_{k+l+1,\beta_{i}}(\underbrace{b,\dots,b}_{k},\mathbf{e}_{1},\underbrace{b,\dots,b}_{l})g^{*}\mathbf{e}_{1}.

Hence we obtain

	$\displaystyle\mathfrak{m}_{1}^{b}(\mathbf{e}_{1}\otimes\mathbf{e}_{3})$	$\displaystyle=\sum_{i=1}^{2}\mathfrak{m}_{1,\beta_{i}}^{b}(\mathbf{e}_{1}\otimes\mathbf{e}_{3})T^{\beta_{i}\cap\omega}$
		$\displaystyle=\sum_{i=1}^{2}\mathfrak{m}_{1,\beta_{i}}^{b}(\mathbf{e}_{1})T^{\beta_{i}\cap\omega}\mathbf{e}_{1}$
		$\displaystyle=(e^{x}T^{\lambda+t}+e^{-x}T^{\lambda-t})\mathbf{e}_{1}.$

∎

Remark 4.18.

Iriyeh, Sakai, and Tasaki [IST13] computed Floer cohomologies $\mathop{H\!F}\nolimits(L,L^{\prime};\mathbb{Z}/2\mathbb{Z})$ of real forms in a compact Hermitian symmetric space, i.e., fixed point sets $L=\operatorname{Fix}(\tau)$ , $L^{\prime}=\operatorname{Fix}(\tau^{\prime})$ of anti-holomorphic and anti-symplectic involutions $\tau$ , $\tau^{\prime}$ . In particular, the Floer cohomology of the $\operatorname{U}(2)$ -fiber $L_{0}=\operatorname{Fix}(\tau_{0})$ with coefficients in $\mathbb{Z}/2\mathbb{Z}$ is given by

\mathop{H\!F}\nolimits(L_{0},L_{0};\mathbb{Z}/2\mathbb{Z})\cong H^{*}(L_{0};\mathbb{Z}/2\mathbb{Z})\cong(\mathbb{Z}/2\mathbb{Z})^{4}.

On the other hand, (4.9) and (4.10) implies that

\mathop{H\!F}\nolimits(L_{0},L_{0};\Lambda^{\mathbb{Z}}_{0})\cong(\Lambda_{0}^{\mathbb{Z}}/2T^{\lambda}\Lambda_{0}^{\mathbb{Z}})^{2},

where

\Lambda_{0}^{\mathbb{Z}}=\left\{\left.\sum_{i=1}^{\infty}a_{i}T^{\lambda_{i}}\,\right|\,a_{i}\in\mathbb{Z},\ \lambda_{i}\geq 0,\ \lim_{i\to\infty}\lambda_{i}=\infty\right\}

is the Novikov ring over $\mathbb{Z}$ .

Remark 4.19.

Here we consider a Lagrangian $\operatorname{U}(n)$ -fiber $L_{t}$ in $\operatorname{Gr}(n,2n)$ for general $n$ . The one-parameter subgroup $g_{\theta}=\exp(\theta\xi)$ of $\operatorname{U}(2n)$ given by

\xi=\begin{pmatrix}0&-E_{11}\\ E_{11}&0\end{pmatrix}\in\mathfrak{u}(2n)

sends

x=\left(\begin{array}[]{ccc|ccc}t&&&\overline{x}^{1}_{1}&\dots&\overline{x}^{n}_{1}\\ &\ddots&&\vdots&&\vdots\\ &&t&\overline{x}^{1}_{n}&\dots&\overline{x}^{n}_{n}\\ \hline\cr x^{1}_{1}&\dots&x^{1}_{n}&-t&&\\ \vdots&&\vdots&&\ddots&\\ x^{n}_{1}&\dots&x^{n}_{n}&&&-t\end{array}\right)\in L_{t}

to $\operatorname{Ad}_{g_{\theta}}(x)\in\mathcal{O}_{{\boldsymbol{\lambda}}}$ whose upper-left $n\times n$ block is given by

(\operatorname{Ad}_{g_{\theta}}(x))^{(n)}=\begin{pmatrix}t(1-2\sin^{2}\theta)-(x^{1}_{1}+\overline{x}^{1}_{1})\sin\theta\cos\theta&-x^{1}_{2}\sin\theta&\dots&-x^{1}_{n}\sin\theta\\ -\overline{x}^{1}_{n}\sin\theta&t\\ \vdots&&\ddots\\ -\overline{x}^{1}_{n}\sin\theta&&&t\end{pmatrix}.

If $\operatorname{Ad}_{g_{\theta}}(x)$ is still in $L_{t}$ , i.e., $(g_{\theta}xg_{\theta}^{*})^{(n)}=tI_{n}$ , then we have $x^{1}_{2}=\dots=x^{1}_{n}=0$ and $\operatorname{Re}x^{1}_{1}=-t\tan\theta$ . Since $|\operatorname{Re}x^{1}_{1}|\leq\sqrt{\lambda^{2}-t^{2}}$ , one has $g_{\theta}(L_{t})\cap L_{t}=\emptyset$ if

|\theta|>\arctan\sqrt{\frac{\lambda^{2}-t^{2}}{t^{2}}}.

Note that the moment map $\mu:\mathcal{O}_{{\boldsymbol{\lambda}}}\to\mathfrak{u}(2n)$ of the $\operatorname{U}(2n)$ -action is given by $\mu(x)=(\sqrt{-1}/2\pi)x$ in our setting. Hence the Hamiltonian of $g_{\theta}$ is given by

H(x)=\frac{\sqrt{-1}}{2\pi}\langle x,\xi\rangle.

Since $\max_{\mathcal{O}_{\lambda}}H=\lambda/\pi$ and $\min_{\mathcal{O}_{\lambda}}H=-\lambda/\pi$ , the norm of $g_{\theta}$ is given by

\int_{0}^{\theta}\Bigl{(}\max_{\mathcal{O}_{\lambda}}H-\min_{\mathcal{O}_{\lambda}}H\Bigr{)}d\theta=\frac{2\lambda}{\pi}\theta.

Hence the displacement energy of $L_{t}$ is bounded from above by

h(t)=\frac{2\lambda}{\pi}\arctan\sqrt{\frac{\lambda^{2}-t^{2}}{t^{2}}}.

Note that $h(t)$ is a concave function on $[-\lambda,\lambda]$ such that $h(\pm\lambda)=0$ , $h(0)=\lambda$ , and $h(t)>\min\{\lambda-t,\lambda+t\}$ for $t\neq 0,\pm\lambda$ .

Theorem 4.20.

The Floer cohomology of the pair $(L_{0},\pi\sqrt{-1}/2\mathbf{e}_{1})$ , $(L_{0},-\pi\sqrt{-1}/2\mathbf{e}_{1})$ is given by

\mathop{H\!F}\nolimits((L_{0},\pm\pi\sqrt{-1}/2\mathbf{e}_{1}),(L_{0},\mp\pi\sqrt{-1}/2\mathbf{e}_{1});\Lambda_{0})\cong(\Lambda_{0}/T^{\lambda}\Lambda_{0})^{2}.

In particular, the Floer cohomology over the Novikov field is trivial;

\mathop{H\!F}\nolimits((L_{0},\pm\pi\sqrt{-1}/2\mathbf{e}_{1}),(L_{0},\mp\pi\sqrt{-1}/2\mathbf{e}_{1});\Lambda)=0.

Proof.

For $b=\sqrt{-1}\pi/2\mathbf{e}_{1}\in H^{1}(L_{0};\Lambda_{0})$ , we have from (4.13) that

	$\displaystyle\mathfrak{m}_{k+l+1,\beta_{i}}(\underbrace{b,\dots,b}_{k},\mathbf{e}_{3},\underbrace{-b,\dots,-b}_{l})$
	$\displaystyle\quad=\int_{(0,2\pi)}\frac{1}{k!}\left(\frac{\sqrt{-1}}{4}\theta\right)^{k}\frac{1}{l!}\left(\frac{\sqrt{-1}}{4}\theta-\frac{\pi\sqrt{-1}}{2}\right)^{l}(1-\cos\theta)\frac{d\theta}{2\pi}.$

Hence the Floer differential is given by

	$\displaystyle\delta_{b,-b}(\mathbf{e}_{3})$	$\displaystyle=\sum_{i=1,2}\sum_{k,l\geq 0}\mathfrak{m}_{k+l+1,\beta_{i}}(\underbrace{b,\dots,b}_{k},\mathbf{e}_{3},\underbrace{-b,\dots,-b}_{l})T^{\beta_{i}\cap\omega}$
		$\displaystyle=2T^{\lambda}\int_{0}^{2\pi}\sum_{k,l\geq 0}\frac{1}{k!}\left(\frac{\sqrt{-1}}{4}\theta\right)^{k}\frac{1}{l!}\left(\sqrt{-1}\left(\frac{\theta}{4}-\frac{\pi}{2}\right)\right)^{l}(1-\cos\theta)\frac{d\theta}{2\pi}$
		$\displaystyle=2T^{\lambda}\int_{0}^{2\pi}e^{\sqrt{-1}(\theta/2-\pi/2)}(1-\cos\theta)\frac{d\theta}{2\pi}$
		$\displaystyle=\frac{16}{3\pi}T^{\lambda}.$

Similarly we have

\delta_{b,-b}(\mathbf{e}_{1}\otimes\mathbf{e}_{3})=\frac{32}{3\pi}T^{\lambda}\mathbf{e}_{1},

and consequently,

\mathop{H\!F}\nolimits((L_{0},\pi\sqrt{-1}/2\mathbf{e}_{1}),(L_{0},-\pi\sqrt{-1}/2\mathbf{e}_{1});\Lambda_{0})\cong(\Lambda_{0}/T^{\lambda}\Lambda_{0})^{2}.

The computation of $\mathop{H\!F}\nolimits((L_{0},-\pi\sqrt{-1}/2\mathbf{e}_{1}),(L_{0},\pi\sqrt{-1}/2\mathbf{e}_{1});\Lambda_{0})$ is completely parallel. ∎

References

[Aur07] Denis Auroux, Mirror symmetry and $T$ -duality in the complement of an anticanonical divisor, J. Gökova Geom. Topol. GGT 1 (2007), 51–91. MR 2386535 (2009f:53141)
[BCFKvS00] Victor V. Batyrev, Ionuţ Ciocan-Fontanine, Bumsig Kim, and Duco van Straten, Mirror symmetry and toric degenerations of partial flag manifolds, Acta Math. 184 (2000), no. 1, 1–39. MR MR1756568 (2001f:14077)
[EL] Jonathan David Evans and Yanki Lekili, Floer cohomology of the Chiang Lagrangian, arXiv:1401.4073.
[FOOO] Kenji Fukaya, Yong-Geun Oh, Hiroshi Ohta, and Kaoru Ono, Anti-symplectic involution and Floer cohomology, arXiv:0912.2646.
[FOOO09] , Lagrangian intersection Floer theory: anomaly and obstruction, AMS/IP Studies in Advanced Mathematics, vol. 46, American Mathematical Society, Providence, RI, 2009. MR MR2553465
[FOOO10] , Lagrangian Floer theory on compact toric manifolds. I, Duke Math. J. 151 (2010), no. 1, 23–174. MR 2573826
[Giv97] Alexander Givental, Stationary phase integrals, quantum Toda lattices, flag manifolds and the mirror conjecture, Topics in singularity theory, Amer. Math. Soc. Transl. Ser. 2, vol. 180, Amer. Math. Soc., Providence, RI, 1997, pp. 103–115. MR MR1767115 (2001d:14063)
[GK95] Alexander Givental and Bumsig Kim, Quantum cohomology of flag manifolds and Toda lattices, Comm. Math. Phys. 168 (1995), no. 3, 609–641. MR MR1328256 (96c:58027)
[GS83] V. Guillemin and S. Sternberg, The Gel^′fand-Cetlin system and quantization of the complex flag manifolds, J. Funct. Anal. 52 (1983), no. 1, 106–128. MR MR705993 (85e:58069)
[IST13] Hiroshi Iriyeh, Takashi Sakai, and Hiroyuki Tasaki, Lagrangian Floer homology of a pair of real forms in Hermitian symmetric spaces of compact type, J. Math. Soc. Japan 65 (2013), no. 4, 1135–1151. MR 3127820
[NNU10] Takeo Nishinou, Yuichi Nohara, and Kazushi Ueda, Toric degenerations of Gelfand-Cetlin systems and potential functions, Adv. Math. 224 (2010), no. 2, 648–706. MR 2609019
[Ros70] H. H. Rosenbrock, State-space and multivariable theory, John Wiley & Sons, Inc. [Wiley Interscience Division], New York, 1970. MR 0325201 (48 #3550)
[Smi12] Ivan Smith, Floer cohomology and pencils of quadrics, Invent. Math. 189 (2012), no. 1, 149–250. MR 2929086
[Sot01] Frank Sottile, Rational curves on Grassmannians: systems theory, reality, and transversality, Advances in algebraic geometry motivated by physics (Lowell, MA, 2000), Contemp. Math., vol. 276, Amer. Math. Soc., Providence, RI, 2001, pp. 9–42. MR 1837108 (2002d:14080)
[ST97] Bernd Siebert and Gang Tian, On quantum cohomology rings of Fano manifolds and a formula of Vafa and Intriligator, Asian J. Math. 1 (1997), no. 4, 679–695. MR 1621570 (99d:14060)

Yuichi Nohara

Faculty of Education, Kagawa University, Saiwai-cho 1-1, Takamatsu, Kagawa, 760-8522, Japan.

e-mail address : nohara@ed.kagawa-u.ac.jp

Kazushi Ueda

Department of Mathematics, Graduate School of Science, Osaka University, Machikaneyama 1-1, Toyonaka, Osaka, 560-0043, Japan.

e-mail address : kazushi@math.sci.osaka-u.ac.jp

Floer cohomologies of non-torus fibers of the Gelfand-Cetlin system

Abstract

1 Introduction

Theorem 1.1.

Theorem 1.2.

Corollary 1.3.

2 Non-torus fibers of the Gelfand-Cetlin system

2.1 Flag manifolds

Example 2.1.

Example 2.2.

2.2 The Gelfand-Cetlin system

Proposition 2.3 (Guillemin and Sternberg [GS83]).

2.3 The case of Fl⁡(3)\operatorname{Fl}(3)

Definition 2.4 (Evans and Lekili [EL, Definition 1.1.1]).

Proposition 2.5.

Proof.

Proposition 2.6.

2.4 The case of Gr⁡(2,4)\operatorname{Gr}(2,4)

Proposition 2.7.

Proof.

Corollary 2.8.

Proof.

Proposition 2.9.

Remark 2.10.

2.5 The case of Gr⁡(2,5)\operatorname{Gr}(2,5)

Proposition 2.11.

Proof.

Proposition 2.12.

Corollary 2.13.

Remark 2.14.

3 Critical points of the potential function

Theorem 3.1 ([NNU10, Theorem 10.1]).

Example 3.2.

Example 3.3.

Example 3.4.

4 Floer cohomologies of non-torus fibers

4.1 Holomorphic disks in (Fl⁡(3),L0)(\operatorname{Fl}(3),L_{0})

Proposition 4.1.

Remark 4.2.

Proof.

Example 4.3.

4.2 Floer cohomology of the SU⁡(2)\operatorname{SU}(2)-fiber in Fl⁡(3)\operatorname{Fl}(3)

Proposition 4.4.

Corollary 4.5.

Theorem 4.6.

Corollary 4.7.

Proof.

Theorem 4.8.

4.3 Holomorphic disks in (Gr⁡(2,4),Lt)(\operatorname{Gr}(2,4),L_{t})

Example 4.9.

Proposition 4.10.

Proposition 4.11.

Proof.

Remark 4.12.

4.4 Floer cohomologies of the U⁡(2)\operatorname{U}(2)-fibers in Gr⁡(2,4)\operatorname{Gr}(2,4)

Lemma 4.13.

Corollary 4.14.

Corollary 4.15.

Theorem 4.16.

Lemma 4.17.

Proof.

Proof of Theorem 4.16.

Remark 4.18.

Remark 4.19.

Theorem 4.20.

Proof.

References

Floer cohomologies of non-torus fibers
of the Gelfand-Cetlin system

2.3 The case of $\operatorname{Fl}(3)$

2.4 The case of $\operatorname{Gr}(2,4)$

2.5 The case of $\operatorname{Gr}(2,5)$

4.1 Holomorphic disks in $(\operatorname{Fl}(3),L_{0})$

4.2 Floer cohomology of the $\operatorname{SU}(2)$ -fiber in $\operatorname{Fl}(3)$

4.3 Holomorphic disks in $(\operatorname{Gr}(2,4),L_{t})$

4.4 Floer cohomologies of the $\operatorname{U}(2)$ -fibers in $\operatorname{Gr}(2,4)$