Force Dependent Hopping Rates of RNA Hairpins can be Estimated from Accurate Measurement of the Folding Landscapes

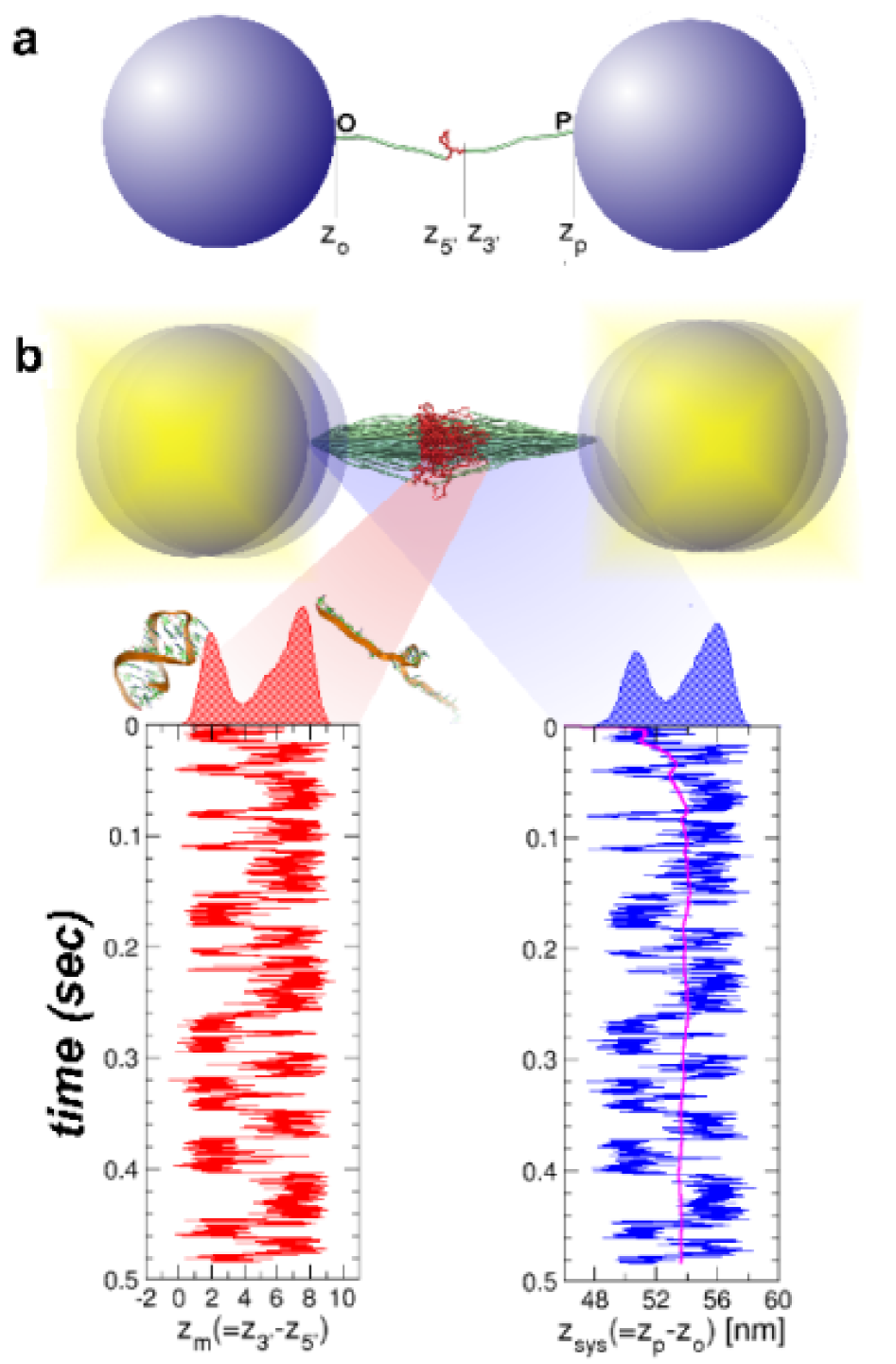
A molecular understanding of how proteins and RNA fold is needed to describe the functions of enzymes FershtBook and ribozymes DoudnaNature02 , interactions between biomolecules, and the origins of misfolding that is linked to a number of diseases Dobson99TBS . The energy landscape perspective has provided a conceptual framework for describing the mechanisms by which unfolded molecules navigate the large conformational space in search of the native state DillNSB97 ; OnuchicCOSB04 ; HyeonBC05 . Recently, single molecule techniques have been used to probe features of the energy landscape of proteins and RNA that are not easily accessible in ensemble experiments Fisher00NSB ; Bustamante01Science ; Haran03PNAS ; TinocoBJ06 ; SchulerNATURE2002 ; ZhuangCOSB03 ; EvansNature99 ; Woodside06PNAS ; Block06Science ; Li07PNAS ; DietzPNAS04 ; Mickler07PNAS . It is possible to construct the shape of the energy landscape, including the energy scales of ruggedness HyeonPNAS03 ; ReichEMBOrep05 , using dynamical trajectories that are generated by applying a constant force ($f$) to the ends of proteins and RNA Schlierf04PNAS ; Woodside06PNAS ; Fernandez06NaturePhysics ; Block06Science . If the observation time is long enough for the molecule to sample the accessible conformational space, then the time average of an observable $X$ recorded for the $\alpha^{th}$ molecule ($\langle X\rangle=\lim_{t\rightarrow\infty}\frac{1}{t}\int^{t}_{0}d\tau X_{\alpha}(\tau)$) should equal the ensemble average ($\langle X\rangle=\lim_{N\rightarrow\infty}\frac{1}{N}\sum_{i=1}^{N}X_{i}$), and the distribution $P(X)$ should converge to the equilibrium distribution function $P_{eq}(X)$. Using this strategy, laser optical tweezer (LOT) experiments have been used to obtain the sequence-dependent folding landscape of a number of RNA and DNA hairpins Bustamante01Science ; Woodside06PNAS ; Bustamante03Science ; Block06Science , using $X=R_{m}$, the end-to-end distance of the hairpin that is conjugate to $f$, as a natural reaction coordinate. In LOT experiments, the hairpin is held between two long handles (DNA Block06Science or DNA/RNA hybrids Bustamante01Science ), whose ends are attached to polystyrene beads (Fig. 1a). The equilibrium free energy profile $\beta F_{eq}(R_{m})=-\log{P_{eq}(R_{m})}$ ($\beta\equiv 1/k_{B}T$, $k_{B}$ is the Boltzmann constant, and $T$ is the absolute temperature) may be useful in describing the dynamics of the molecule, provided $R_{m}$ is an appropriate reaction coordinate.

The dynamics of the RNA extension in the presence of $f$ ($z_{m}=z_{3^{\prime}}-z_{5^{\prime}}\approx R_{m}$, provided transverse fluctuations are small) is indirectly obtained in an LOT experiment by monitoring the distance between the attached polystyrene beads ($z_{sys}=z_{p}-z_{o}$), one of which is optically trapped at the center of the laser focus (Fig 1a). The goal of these experiments is to extract the folding landscape ($\beta F_{eq}^{o}(z_{m})$) and the dynamics of the hairpin in the absence of handles, using the $f$-dependent trajectories $z_{sys}(t)$. To achieve these goals, the fluctuations in the handles should minimally perturb the dynamics of the hairpin in order to probe the true dynamics of a molecule of interest. However, depending on $L$ and $l_{p}$ ($L$ is the contour length of the handle and $l_{p}$ is its persistence length), the intrinsic fluctuations of the handles can not only disort the signal from the hairpin, but also directly affect its dynamics. The first is a problem that pertains to the measurement process, while the second is a problem of the coupling between the instruments and the dynamics of RNA.

Here, we use coarse-grained molecular simulations of RNA hairpin and theory to show that, in order to obtain accurate $\beta F_{eq}(R_{m})$, the linkers used in the LOT have to be stiff, i.e., the value of $L/l_{p}$ has to be small. To investigate the handle effects on the energy landscape and hopping kinetics, we simulated the hairpin dynamics under force-clamp conditions by explicitly modeling the linkers as polymers with varying $L$ and $l_{p}$. Surprisingly, the force-dependent folding and unfolding rates that are directly measured using the time traces, $z_{m}(t)$, are close to the ideal values (those that are obtained by directly applying $f$, without the handles, to the 3’ end with a fixed 5’ end) only when the handles are flexible. Most importantly, accurate estimates of the $f$-dependent hopping rates over a wide range of $f$-values, in the absence of handles, can be made using $\beta F_{eq}(R)$, in the presence of handles obtained at $f=f_{m}$, the transition midpoint at which the native basin of attraction (NBA) and the unfolded basin of attraction (UBA) of the RNA are equally populated. The physics of a hairpin attached to handles is captured using a generalized Rouse model (GRM), in which there is a favorable interaction between the two non-covalently linked ends. The GRM gives quantitative agreement with the simulation results. The key results announced here provide a framework for using the measured folding landscape of nucleic acid hairpins at $f\approx f_{m}$ to obtain $f$-dependent folding and unfolding times and the transition state movements as $f$ is varied KlimovPNAS99 ; HyeonPNAS05 ; RitortPRL06 ; West06BJ ; Dudko06PRL ; Hyeon07JP .

RESULTS and DISCUSSIONS

Modeling the LOT experiments: In order to extract the folding landscape from LOT experiments, the time scales associated with the dynamics of the beads, handles, and the hairpin have to be well-separated RitortBJ05 ; HyeonBJ06 ; Manosas07BJ ; WestPRE . The bead fluctuations are described by the overdamped Langevin equation $\gamma dx_{p}/dt=-kx_{p}+F(t)$ where $k$ is the spring constant associated with the restoring force, and the random white-noise force $F(t)$ satisfies $\langle F(t)\rangle=0$ and $\langle F(t)F(t^{\prime})\rangle=2\gamma k_{B}T\delta(t-t^{\prime})$. The bead relaxes to its equilibrium position on a time scale $\tau_{r}=\gamma/k$. In terms of the trap stiffness, $k_{p}$, and the stiffness $k_{m}$ associated with the Handle-RNA-Handle (H-RNA-H; see Fig. 1), $k=k_{p}+k_{m}$. With $\gamma=6\pi\eta a$, $a=1\mu$m, $\eta\approx 1$cP, $k_{p}\approx 0.01$ pN/nm Block94ARBBS , and $k_{m}\approx 0.1$ pN/nm, we find $\tau_{r}\lesssim 1$ ms. In LOT experiments RitortBJ05 ; Manosas07BJ ; WestPRE , separation in time scales is satisfied such that $\tau^{o}_{U}\approx\tau_{F}^{o}\gg\tau_{r}$ at $f\approx f_{m}$, where $\tau_{U}^{o}$ and $\tau_{F}^{o}$ are the intrinsic values of the RNA (un)folding times in the absence of handles.

Since $z_{m}$ is a natural reaction coordinate in force experiments, the dispersion of the bead position may affect the measurement of $F_{eq}(z_{m})$. At equilibrium, the fluctuations in the bead positions satisfy $\delta x^{2}_{eq}\sim k_{B}T/(k_{p}+k_{m})\sim k_{B}T/k_{m}$, and hence $k_{m}$ should be large enough to minimize the dispersion of the bead position. The force fluctuation, $\delta f^{2}_{eq}\sim k_{B}Tk_{p}^{2}/(k_{p}+k_{m})$, is negligible in the LOT because $k_{p}\ll k_{m}$, and as a result $\delta f_{eq}/f_{m}\sim 0$, since $\delta f_{eq}\approx 0.1$ pN while $f_{m}\sim 15$ pN. Thus, we model the LOT setup by assuming that the force and position fluctuations due to the bead are small, and exclusively focus on the effect of handle dynamics on the folding landscape and hopping kinetics of RNA (Figs. 1a-b).

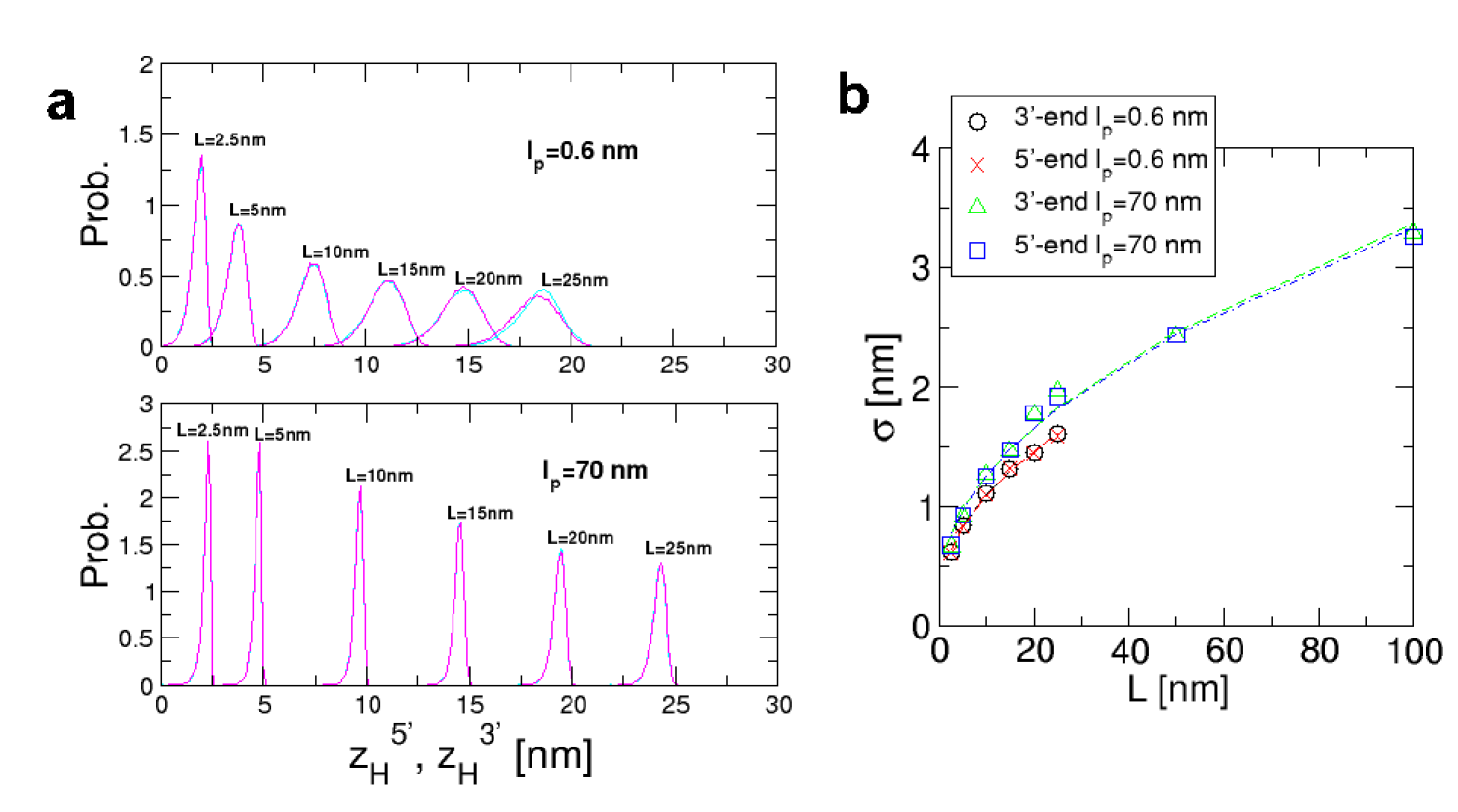
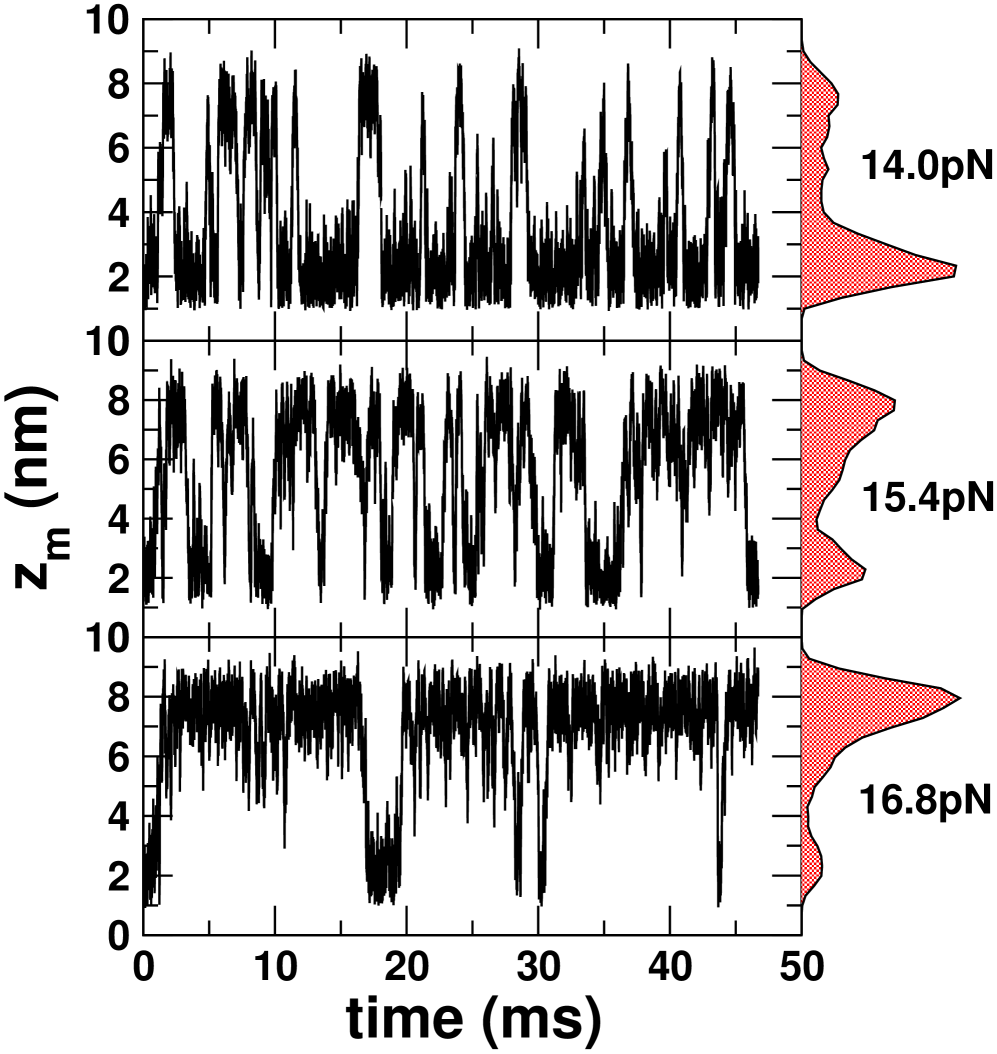
Short, stiff handles are required for accurate free energy profiles: For purposes of illustration, we used the self-organized polymer (SOP) model of the P5GA hairpin HyeonBJ07 , and applied a force $f=f_{m}\approx 15.4$ pN. The force is exerted on the end of the handle attached to the 3’ end of the RNA (P in Fig.1a), while fixing the other end (O in Fig.1a). Simulations of P5GA with handles of length $L=25$ nm and persistence length $l_{p}=70$ nm show that the extension of the entire system ($z_{sys}=z_{p}-z_{0}$) fluctuates between two limits centered around $z_{sys}\approx 50$ nm and $z_{sys}\approx 56$ nm (Fig. 1b). The time-dependent transitions in $z_{sys}$ between 50 nm and 56 nm correspond to the hopping of the RNA between the Native Basin of Attraction (NBA) and Unfolded Basin of Attraction (UBA). Decomposition of $z_{sys}$ as $z_{sys}=z_{H}^{5^{\prime}}+z_{m}+z_{H}^{3^{\prime}}$, where $z_{H}^{5^{\prime}}(=z_{5^{\prime}}-z_{o})$ and $z_{H}^{3^{\prime}}(=z_{p}-z_{3^{\prime}})$ are the extensions of the handles parallel to the force direction (Fig. 1a), shows that $z_{sys}(t)$ reflects the transitions in $z_{m}(t)$ (Fig. 1b). Because the simulation time is long enough for the harpin to ergodically explore the conformations between the NBA and UBA, the histograms collected from the time traces amount to the equilibrium distributions $P_{eq}(X)$ where $X=z_{sys}$, $z_{H}^{5^{\prime}}$, $z_{m}$, or $z_{H}^{3^{\prime}}$ (Fig 1b; for $P_{eq}(z_{H}^{5^{\prime}})$ and $P_{eq}(z_{H}^{3^{\prime}})$, see the Supporting Information SI Fig. 6a). To establish that the time traces are ergodic, we show that $\overline{z}_{T}(t)=\frac{1}{t}\int^{t}_{0}d\tau z_{sys}(\tau)$ reaches the thermodynamic average ($\approx$ $\int_{-\infty}^{\infty}z_{sys}P_{eq}(z_{sys})dz_{sys}$=53.7 nm) after $t\gtrsim 0.1$ sec (the magenta line on $z_{sys}(t)$ in Fig. 1b).

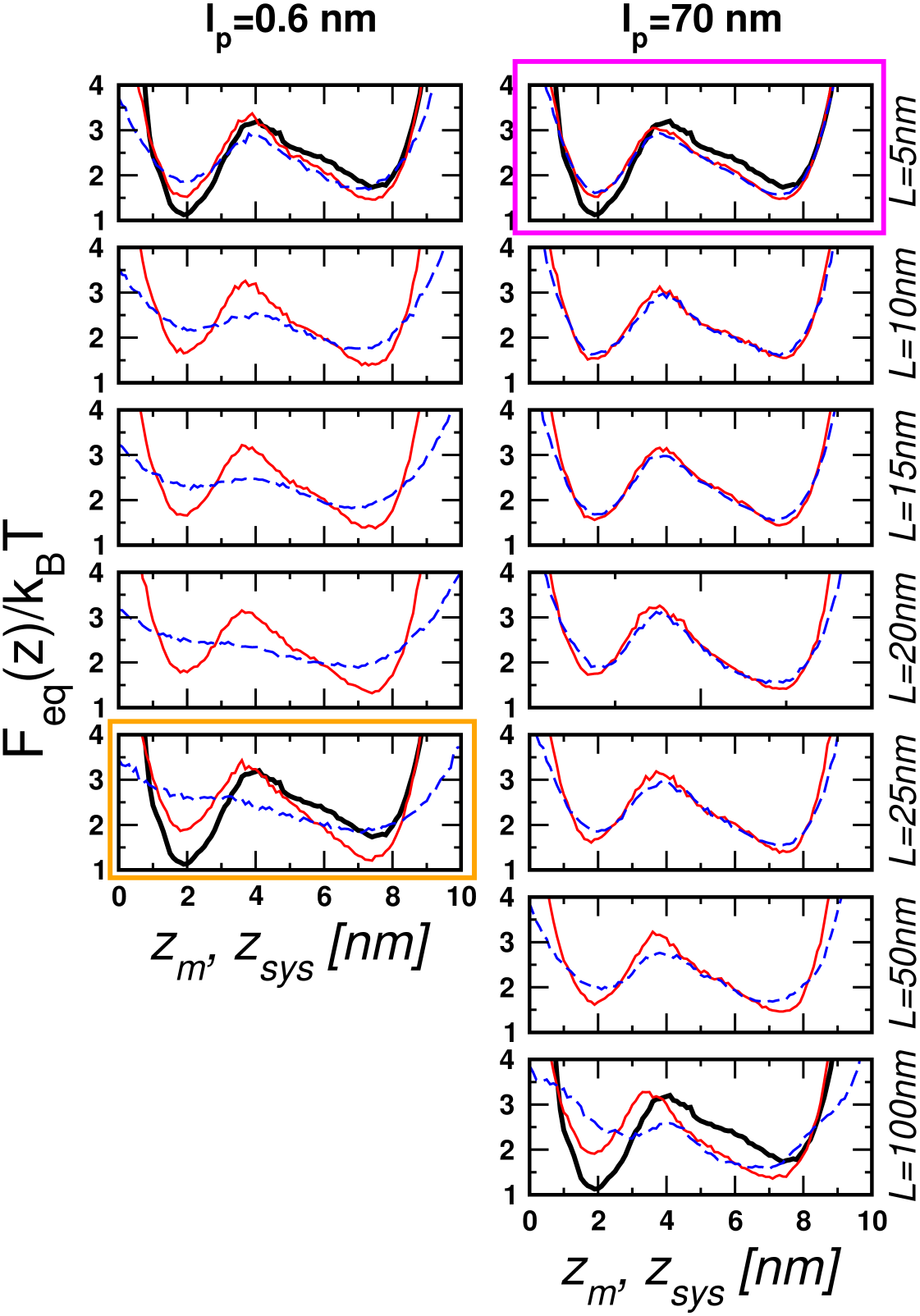
Fig. 1b shows that the positions of the handles along the $f$ direction fluctuate, even in the presence of tension, which results in slight differences between $P_{eq}(z_{sys})$ and $P_{eq}(z_{m})$. Comparison between the free energy profiles obtained from the $z_{sys}(t)$ and $z_{m}(t)$ can be used to investigate the effect of the characteristics of the handles on the free energy landscape. To this end, we repeated the force-clamp simulations by varying the contour length ($L=5-100$ nm) and persistence length ($l_{p}=0.6$ and 70 nm) of the handles. Fig. 2 shows that the discrepancy between the measured free energy $F_{eq}(z_{sys})$ (dashed lines in blue) and the molecular free energy $F_{eq}(z_{m})$ (solid lines in red) increases for the more flexible and longer handles (see the SI text and SI Fig. 6 for further discussion of the dependence of the handle fluctuations on $L$ and $l_{p}$). For small $l_{p}$ and large $L$, the basins of attraction in $F_{eq}(z_{m})$ are not well resolved. The largest deviation between $F_{eq}(z_{sys})$ and $F_{eq}(z_{m})$ is found when $l_{p}=0.6$ nm and $L=25$ nm ($L/l_{p}\approx 40$) (the graph enclosed by the orange box in Fig. 2a). In contrast, the best agreement between $F_{eq}(z_{sys})$ and $F_{eq}(z_{m})$ is found for $l_{p}=70$ nm and $L=5$ nm (the graph inside the magenta box in Fig. 2), which corresponds to $L/l_{p}\approx 0.07$. In the LOT experiments, $L/l_{p}\approx 6-7$ Bustamante01Science ; Woodside06PNAS ; Block06Science .

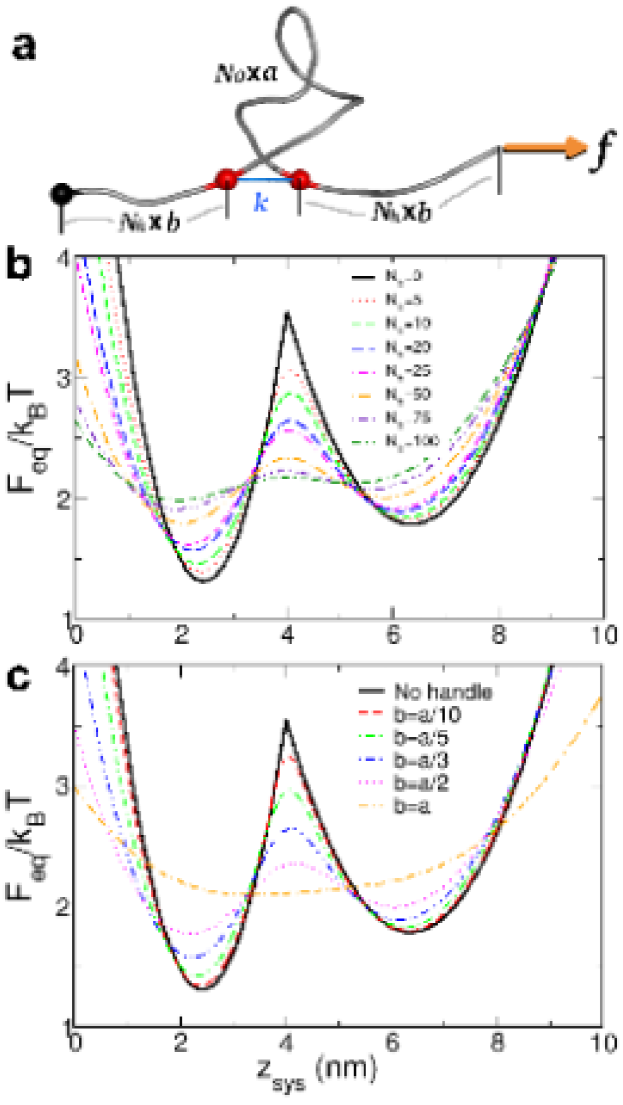
Generalized Rouse model (GRM) captures the physics of H-RNA-H under tension: In order to establish the generality of the relationship between the free energy profiles as measured by $z_{m}$ and those measured by $z_{sys}$, we introduce an exactly solvable model that minimally represents the RNA and handles (Fig. 3a). We mimic the hairpin using a Gaussian chain with $N_{0}$ monomers and Kuhn length $a$. The endpoints of the RNA mimic are harmonically trapped in a potential with stiffness $k$ as long as they are within a cutoff distance $c=4$nm. Two handles, each with $N_{h}$ monomers and Kuhn length $b$, are attached to the ends of the RNA (see Methods). We fix one endpoint of the entire chain at the origin, and apply a force $f_{m}\approx 15.4$ pN to the other end. The free energies as a function of both the RNA’s extension, $R_{m}=|\mathbf{r}_{3^{\prime}}-\mathbf{r}_{5^{\prime}}|$ ($\approx z_{m}$ at high $f$) and the system’s extension $R_{sys}=|{\mathbf{r}}_{P}-{\mathbf{r}}_{0}|$ ($\approx z_{sys}$ at high $f$) are exactly solvable in the continuum representation. We choose $k$ such that $f_{m}$ is near the midpoint of the transition, so that $\int_{0}^{c}d^{3}{\mathbf{r}}\,P_{eq}({\mathbf{r}})\approx\int_{c}^{\infty}d^{3}{\mathbf{r}}\,P_{eq}({\mathbf{r}})$. We tune $N_{0}$ so that the barrier heights for the GRM and P5GA are similar at $f=f_{m}$. These requirements give $N_{0}=20$ and $k\approx 0.54$ pN/nm.

While the stiffness in the handles of the simulated system (Fig. 1) cannot be accurately modeled using a Gaussian chain, the primary effect of attaching the handles is to alter the fluctuations of the endpoints of the RNA. By equating the longitudinal fluctuations for the WLC, $\langle\delta{\mathbf{R}}^{2}_{||}\rangle_{WLC}\sim Ll_{p}^{-1/2}(\beta f)^{-3/2}$, with the fluctuations for the Gaussian handles, $\langle\delta{\mathbf{R}}^{2}_{||}\rangle_{G}\sim Lb$, we estimate that the effective persistence length of the handles scales as $l_{p}^{eff}\sim b^{-2}f^{-3}$ (see the SI for details). Thus, smaller spacing in the Gaussian handles in the GRM will mimic stiffer handles in the H-RNA-H system. The free energies computed for the GRM, shown in Fig. 3b-c, are consistent with the results of the simulations. The free energy profiles deviate significantly from $F^{o}_{eq}(z_{m})$ as $N_{h}$ increases or ‘stiffness’ decreases. The relevant variable that determines the accuracy of $F_{eq}(z_{sys})$ is $N_{h}b^{2}\sim L/l_{p}^{eff}$, with the free energies remaining unchanged if $N_{h}b^{2}$ is kept constant. The barrier height and well depths as a function of $z_{m}$ are unchanged as a function of $L$ and $b$. However, the apparent activation energy is decreased as measured by $z_{sys}$ (seen in Fig. 2 as well). The GRM confirms that accurate measurement of the folding landscape using $z_{sys}$ requires stiff handles.

Accurate estimates of the hopping kinetics requires short and flexible handles: Because LOT experiments can also be used to measure the force-dependent rates of hopping between the NBA and the UBA, it is important to assess the influence of the dynamics of the handles on the intrinsic hopping kinetics of the RNA hairpin. In other words, how should the structural characteristics of the linkers be chosen so that the measured hopping rates using the time traces $z(t)$ and the intrinsic rates are as close as possible?

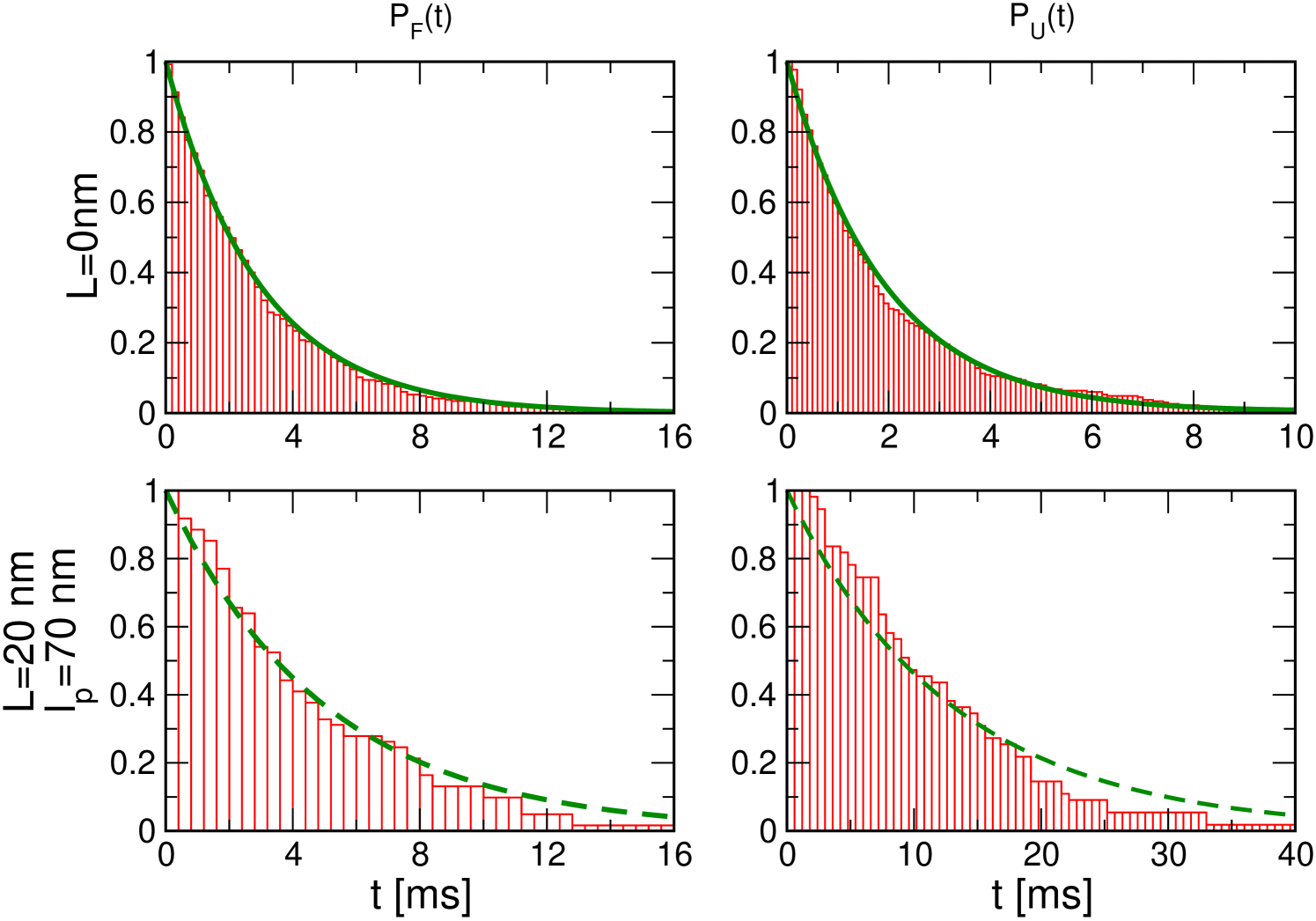
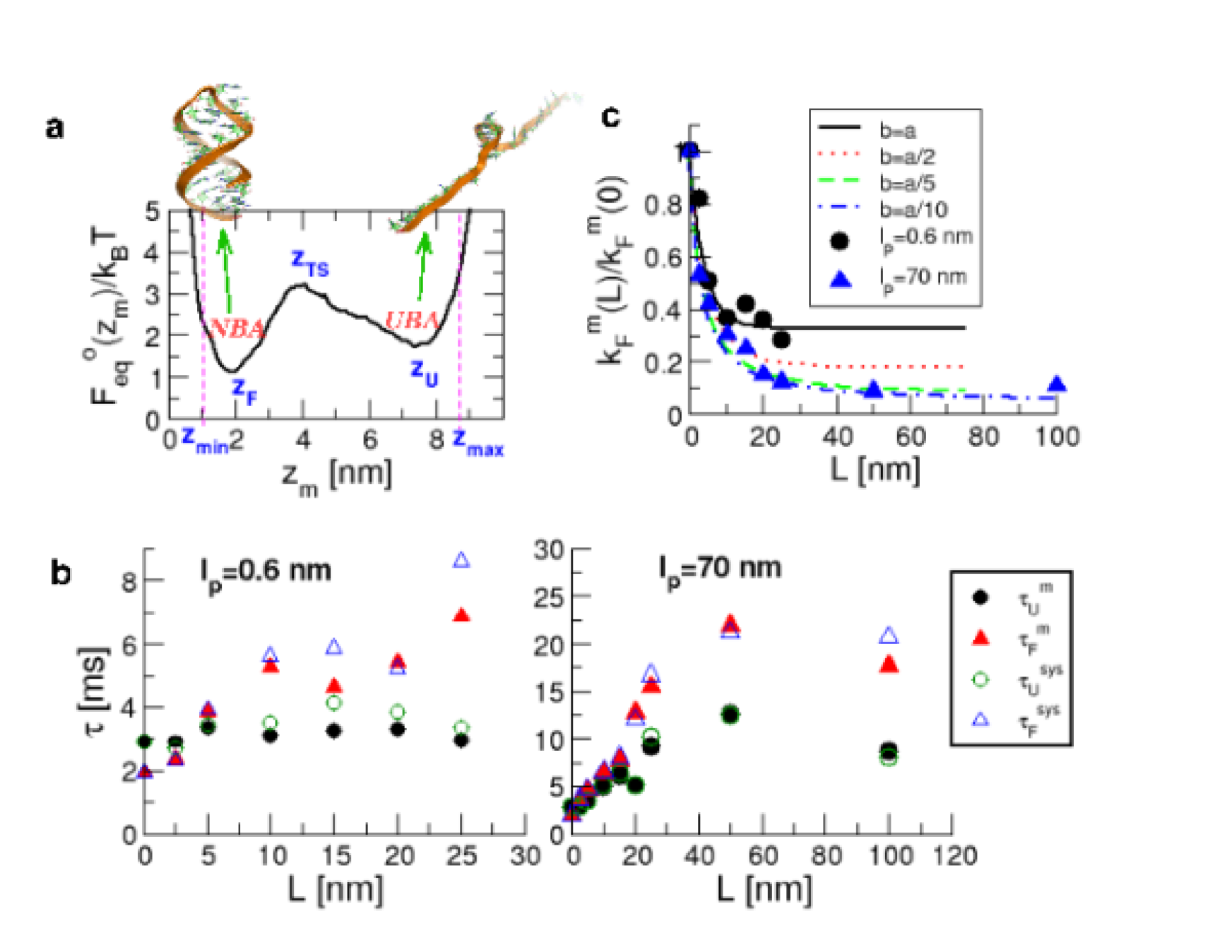
Folding and unfolding rates of P5GA and the free energy profile without handles : We first performed force clamp simulations of P5GA in the absence of handles to obtain the intrinsic (or ideal) folding ($\tau_{F}^{o}$) or unfolding ($\tau_{U}^{o}$) times, that serve as a reference for the H-RNA-H system. To obtain the boundary conditions for calculating the mean refolding and unfolding times, we collected the histograms of the time traces and determined the positions of the minima of the NBA and UBA, $z_{F}=1.9$ nm and $z_{U}=7.4$ nm (Fig. 4a). The analysis of the time traces provides the transition times in which $z_{m}$ reaches $z_{m}=z_{U}$ starting from $z_{m}=z_{F}$. The mean unfolding time $\tau_{U}$ is obtained using either $\tau_{U}=1/N\sum_{i}\tau_{U}(i)$, or from the fits to the survival probability $P_{F}(t)=e^{-t/\tau_{U}}$ (SI Fig. 8). The mean folding time is similarly calculated, and the two methods give similar results. The values of $\tau_{U}^{o}$ and $\tau_{F}^{o}$ computed from the time trace of $z_{m}(t)$ are 2.9 ms and 1.9 ms, respectively. At $f_{m}=15.4$ pN and $L=0$ nm, the equilibrium constant $K_{eq}=\tau^{o}_{F}/\tau^{o}_{U}=0.67$, which shows that the bare molecular free energy is slightly tilted towards NBA at $f=15.4$ pN.

Hopping times depend on the handle characteristics : The values of the folding ($\tau_{F}^{m}$) and unfolding($\tau_{U}^{m}$) times were also calculated for the P5GA hairpin with attached handles (Fig. 1). As the length of the handles increases both $\tau_{U}^{m}$ and $\tau_{F}^{m}$ increase gradually, and the equilibrium distribution shifts towards the UBA, i.e. $K_{eq}=\tau^{m}_{F}/\tau_{U}^{m}$ increases (Fig. 4b). Strikingly, the use of flexible handles results in minimal deviations of $\tau_{U}^{m}$ and $\tau_{F}^{m}$ from their intrinsic values (Fig.4b). Attachment of handles (stiff or flexible) to the 5’ and 3’ ends restricts their movement, which results in a decrease in the number of paths to the NBA and UBA. Thus, both $\tau_{U}^{m}$ and $\tau_{F}^{m}$ increase (Fig.4b). As the stiffness of the handle increases the extent of pinning increses. These arguments show that flexible and short handles, that have the least restriction on the fluctuations of the 5’ and 3’ ends of the hairpin, cause minimal perturbation to the intrinsic RNA dynamics, and hence the hopping rates.

Because the experimentally accessible quantity is the extension of the H-RNA-H, it is important to show that the transition times can be reliably obtained using $z_{sys}(t)$. Although $z_{sys}(t)$ differs from $z_{m}(t)$ in amplitude, the “phase” between the two quantities track each other reliably throughout the simulation, even when the handles are long and flexible (see SI Fig.7). We calculated $\tau_{U}^{sys}$ and $\tau_{F}^{sys}$ by analyzing the trajectories $z_{sys}(t)$ using the same procedure used to compute their intrinsic values. Comparison of $\tau_{U}^{sys}$ ($\tau_{F}^{sys}$) and $\tau_{U}^{m}$ ($\tau_{F}^{m}$) for both stiff and flexible handles shows excellent agreement at all $L$ values (Fig.4b). Thus, it is possible to infer the RNA dynamics $z_{m}(t)$ by measuring $z_{sys}(t)$.

Theoretical predictions using the GRM are consistent with the simulations: The simulation results can be fully understood using the GRM (Fig 3a), for which we can exactly solve the overdamped Langevin equation using the discrete representation of the Gaussian chain (see Methods). By assuming that transverse fluctuations are small (which is reasonable under the relatively high tension of $f=15.4$ pN), we use the Wilemski and Fixman (WF) theory FixmanJCP74II to determine an approximate time of contact formation ($\tau_{F}^{m}=(k_{F}^{m})^{-1}$) as a function of $b$ (i.e. increasing handle ‘stiffness’) and $N_{h}$. The refolding rate of the RNA hairpin under tension is analogous to $k_{F}^{m}$. A plot of $k^{m}_{F}(L)/k^{m}_{F}(0)$ versus $L$ (Fig. 4c) illustrates that smaller deviations from the handle-free values occur when $l_{p}$ is small. Moreover, Fig. 4c shows that the refolding rate decreases for increasing $N_{h}$ regardless of the stiffness of the chain. The saturating value of $k_{F}^{m}$ as $N_{h}\to\infty$ depends on $b$, with ‘stiffer’ handles having a much larger effect on the folding rate. While the handles used in LOT experiments are significantly longer than the handle lengths considered here, the saturation of the folding rate suggests that $L\sim 100$ nm is sufficiently long for finite-size effects to be negligible.

We also find the dependence of $k_{F}$ on $L$ agrees well with the behavior observed in the simulation of P5GA. The ratio $k_{F}^{m}(L)/k_{F}^{m}(0)$ for $b=a$ agrees well with the trends of the flexible linker ($l_{p}=0.6$ nm) for all of the simulated lengths, with both saturating at $k_{F}(L)\approx 0.35k_{F}(0)$ for large $L$. The trends for ‘stiffer’ chains (smaller $b$) in the GRM qualitatively agree with the P5GA simulation with stiff handles ($l_{p}=70$ nm), with remarkably good agreement for $0.1\leq b/a\leq 0.2$ over the entire range of $L$. The GRM, which captures the physics of both the equilibrium and kinetic properties of the more complicated H-RNA-H, provides a theoretical basis for extracting kinetic information from experimentally (or computationally) determined folding landscapes.

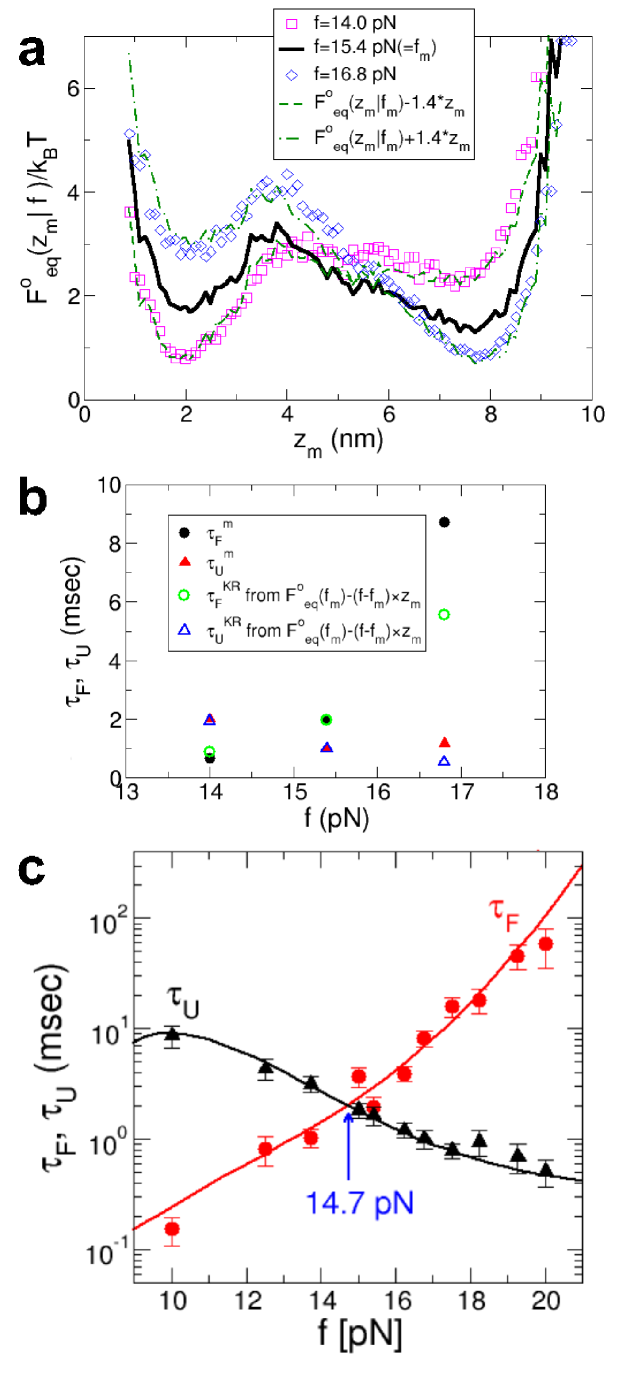
Free energy landscapes and hopping rates: Stiff handles are needed to obtain $F_{eq}(z_{sys})$ Block06Science that resembles $F_{eq}^{o}(z_{m})$, whereas the flexible handles produce hopping rates that are close to their handle-free values. These two findings appear to demand two mutually exclusive requirements in the choice of the handles in LOT experiments. However, if $z_{m}$ is a good reaction coordinate, then it should be possible to extract the hopping rates using accurately measured $F_{eq}(z_{sys})(\approx F_{eq}(z_{m})\approx F_{eq}^{o}(z_{m}))$ at $f\approx f_{m}$, using handles with small $L/l_{p}$. The (un)folding times can be calculated using the mean first passage time (Kramers’ rate expression) with appropriate boundary conditions ZwanzigBook ,

where $z_{min}$, $z_{max}$, $z_{U}$ and $z_{F}$ are defined in Fig. 4a. The effective diffusion coefficient $D_{F}(D_{U})$ is obtained by equating $\tau_{F}^{KR}$ ($\tau_{U}^{KR}$) in equation (1), with $F_{eq}(z_{m})=F_{eq}^{o}(z_{m})$, to the simulated $\tau_{F}^{o}\ (\tau_{U}^{o})$. We calculated the $f$-dependent $\tau_{U}^{m}(f)$ and $\tau_{F}^{m}(f)$ by evaluating equation (1) using $F_{eq}^{o}(z_{m}|f)=F_{eq}^{o}(z_{m}|f_{m})-(f-f_{m})\cdot z_{m}$. The calculated and simulated results for P5GA are in good agreement (Fig 5a-b). At the higher force ($f=16.8$ pN), the statistics of hopping transition within our simulation time is not sufficient to establish ergodicity. As a result, the simulation results are not as accurate at high forces (see SI Fig. 9). To further show that the use of $F_{eq}^{o}(z_{m}|f)$ in equation (1) gives accurate hopping rates, we calculated $\tau_{U}^{o}(f)$ for the GRM and compared the results with direct simulations of the handle-free GRM, which allows the study of a wider range of forces (see Methods). The results in Fig. 5c show that $F_{eq}^{o}(z_{m}|f)$ indeed gives very accurate values for the transition times from the UBA and NBA over a wide force range.

SUPPORTING INFORMATION (SI)

Fluctuations of the handle polymer under tension : Using the force clamp simulations of the RNA hairpin in the presence of handles, the dynamics of the fluctuations of the handle can be independently extracted by probing the time-dependent changes in the 5’ and 3’ ends of the RNA molecule. The distribution of the longitudinal fluctuations ($z_{H}^{5^{\prime}}\equiv z_{5^{\prime}}-z_{o}$ and $z_{H}^{3^{\prime}}\equiv z_{p}-z_{3^{\prime}}$) and the dispersion in the transverse fluctuations ($x_{5^{\prime}}$ or $y_{5^{\prime}}$ and $x_{3^{\prime}}$ or $y_{3^{\prime}}$) are shown in SI Fig. 6. Assuming that the force ${\mathbf{f}}=f_{\parallel}\hat{\mathbf{e}}_{\parallel}+f_{\perp}\hat{\mathbf{e}}_{\perp}$ is decomposed into $f=|{\mathbf{f}}|\approx f_{\parallel}+f_{\perp}^{2}/2f_{\parallel}+\mathcal{O}(f^{4}_{\perp})$ (with $f_{\parallel}\gg f_{\perp}$), and using the partition function of the worm-like chain polymer under tension, $Z=\int d\Omega e^{-(H_{WLC}/k_{B}T-\vec{f}\cdot\vec{R}/k_{B}T)}$ Marko05PRE , one can express the longitudinal fluctuation as

where the force extension relations of a worm-like chain $R_{\parallel}/L\approx fl_{p}/k_{B}T$ for $f<k_{B}T/l_{p}$ and $R_{\parallel}/L\approx 1-\sqrt{k_{B}T/4l_{p}f}$ for $f>k_{B}T/l_{p}$ are used for small and large forces, respectively Marko95Macro . These results are consistent with the fluctuations observed in the simulations. When $f<k_{B}T/l_{p}$, the transverse fluctuations are independent of the force, and are determined solely by the nature of the linker. For $f=f_{m}\approx 15.4$ pN, the tension is in the regime that satisfies $f>k_{B}T/l_{p}$ for both values of $l_{p}$ used in the simulations, and the longitudinal fluctuations $\langle\delta R_{||}^{2}\rangle$ decrease as the stiffness of the polymer increases for all $L$ (SI Fig.6a). The distribution of the extensions coincide for both the 3’ and 5’ ends of the handles for all $L$ and $l_{p}$ (SI Fig. 6a). This suggests that the constant force applied at the point $z_{p}$ propagates uniformly throughout the whole system.

The transverse fluctuations are given by

The transverse fluctuations also decrease as $f(>k_{B}T/l_{p})$ increases, with a different power. It is worth noting that the transverse fluctuations, which also increase as $L$ increases, are nearly independent of the handle stiffness if $f>k_{B}T/l_{p}$. The standard deviations of distributions are plotted with respect to the contour length at each bending rigidity (SI Fig. 6b). The fit shows that $\sigma\sim 0.28\times L^{1/2}$ nm and $\sigma\sim 0.30\times L^{1/2}$ nm for $l_{p}=0.6$ nm and $l_{p}=70$ nm, respectively, which is consistent with the analysis in equation 9.
Determination of the persistence length of the handles : In order to determine the persistence length of the handles, we numerically generated the end-to-end distribution function $P(R)$ of the free handles in the absence of tension, and fit the simulated distribution to the analytical result HaBook ; HyeonJCP06

with $\rho=R/L$ and $\alpha=3L/4l_{p}$. The normalization constant $C=$$\left[\pi^{3/2}e^{-\alpha}\alpha^{3/2}(1+3\alpha^{-1}+15\alpha^{-2}/4)\right]^{-1}$ ensures $\int_{0}^{L}dR\ P_{WLC}(R)=1$.

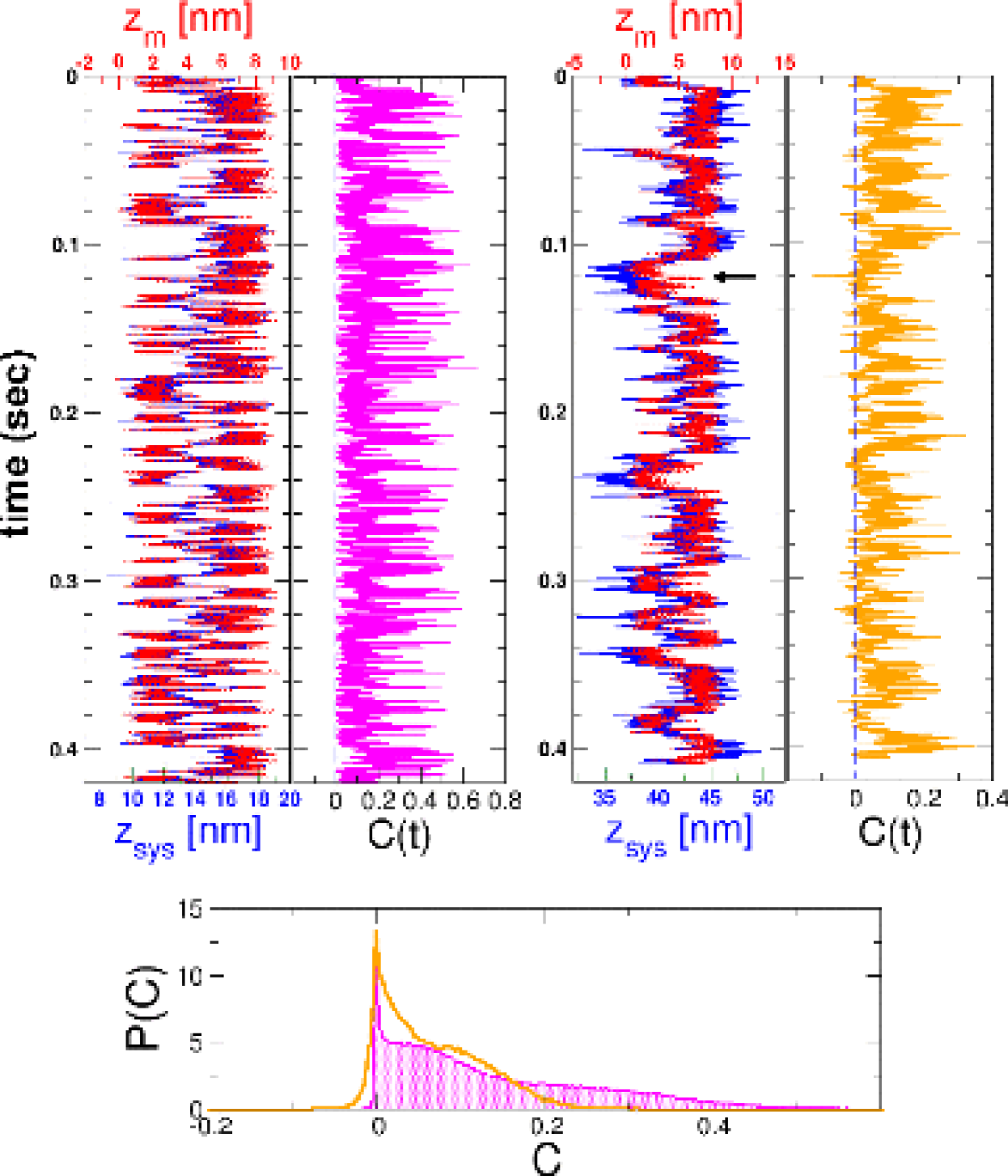
Quantifying the synchronization of $z_{sys}(t)$ and $z_{m}(t)$ : The origin of the small discrepancy between $F_{eq}(z_{sys})$ and $F_{eq}(z_{m})$ when the handles are flexible can be found by comparing $z_{sys}(t)$ with $z_{m}(t)$ for the two extreme cases in Fig. 2 of the main text. To quantitatively express the synchronization between $z_{sys}(t)$ and $z_{m}(t)$, we defined a correlation function at each time $t$ using

where $z_{sys}^{TS}$ and $z_{m}^{TS}$ are the positions of the transition states determined from $F_{eq}(z_{sys})$ and $F_{eq}(z_{m})$ respectively. If $C(t)>0$ at time $t$, both $z_{sys}(t)$ and $z_{m}(t)$ are in the same basins of attraction, i.e. the status of $z_{m}(t)$ is correctly detected by the measurement through the handles. If $C(t)<0$, then the information of $z_{m}(t)$ is lost due to fluctuations or the slow response of the handles. The near perfect synchronization between $z_{sys}(t)$ and $z_{m}(t)$ for $l_{p}=60$ nm and $L=5$ nm are reflected in $C(t)>0$ for almost all $t$. Thus, when the handles are stiff, $z_{m}(t)\approx z_{sys}(t)-2L$, which implies that $z_{sys}(t)$ faithfully reflects the dynamics ($z_{m}(t)$) of the hairpin. In contrast, with $l_{p}=0.6$ nm and $L=25$ nm, $z_{m}(t)$ can not be determined from $z_{sys}(t)$ using $z_{sys}(t)-2\times L\neq z_{m}(t)$. The amplitudes of $z_{sys}(t)$ are typically larger than that of $z_{m}(t)$, leading to $C(t)<0$ occasionally (shown by an arrow on the right plot in SI Fig. 7). The histograms of $P(C)$ for the two extreme cases show that the dynamics between $z_{sys}(t)$ and $z_{m}(t)$ are more synchronous for the rigid and short handles ($0.0<P(C)<0.5$) than for the flexible and longer handles ($-0.05<P(C)<0.2$) (see the graph at the bottom in the SI Fig.7). The finding that short and stiff ($L/l_{p}\sim O(1)$) handles minimize the differences between $F_{eq}(z_{m})$ and $F_{eq}(z_{sys})$ is related to the tension-dependent fluctuations in the linkers.