Force transduction by the microtubule-bound Dam1 ring
Abstract
The coupling between the depolymerization of microtubules (MTs) and the motion of the Dam1 ring complex is now thought to play an important role in the generation of forces during mitosis. Our current understanding of this motion is based on a number of detailed computational models. Although these models realize possible mechanisms for force transduction, they can be extended by variation of any of a large number of poorly measured parameters and there is no clear strategy for determining how they might be distinguished experimentally. Here we seek to identify and analyze two distinct mechanisms present in the computational models. In the first the splayed protofilaments at the end of the depolymerizing MT physically prevent the Dam1 ring from falling off the end, in the other an attractive binding secures the ring to the microtubule. Based on this analysis, we discuss how to distinguish between competing models that seek to explain how the Dam1 ring stays on the MT. We propose novel experimental approaches that could resolve these models for the first time, either by changing the diffusion constant of the Dam1 ring (e.g., by tethering a long polymer to it) or by using a time varying load.
Key words: Brownian ratchet; burnt bridges; DASH; protofilaments; mitosis; motors
Introduction
Mitosis is the mechanism of cell division in eukaryotic cells. In mitosis, chromosomes condense and are arranged at the center of the cell by the mitotic spindle. Microtubules (MTs) are protein fibers, composed of parallel protofilaments (PFs, typically ) forming a hollow cylinder. Each PF is built from stacked tubulin protein dimers. MTs emanate from centrosomes and attach to chromosome-bound kinetochores. Centrosomes are positioned at both poles of the cell forming a bipolar spindle. During anaphase chromosomes are segregated and transported to the cell poles by the retraction of MTs, providing both daughter cells with a single copy of the cell’s chromosomes (1). To achieve segregation, depolymerizing kinetochore-attached microtubules (KMTs) must generate forces, e.g., to overcome chromosomal drag in the cytosol (2). There is evidence that mitotic MT force generation occurs in the absence of MT minus-end directed motor proteins (3) and when minus-end depolymerization is inhibited (4). Previously, a hypothetical sleeve had been proposed to couple MT depolymerization to kinetochores (5, 6). A 10-protein complex, purified from budding yeast (7), called Dam1 (or DASH) has been observed to form rings around MTs (8, 9). Dam1 rings have been observed tracking depolymerizing MT plus ends in vitro (10) and an optical trap has been used to measure force-distance traces for Dam1-coated polystyrene beads attached to depolymerizing MTs (11, 12, 13). Intriguingly, Dam1 has been shown to be essential for chromosome segregation in budding yeast (14, 15) and important for avoiding mis-segregation problems in fission yeast (16).
Mechanisms of force transduction
Several models have been proposed to explain how the Dam1 ring can couple the kinetochore to a depolymerizing MT so as to produce a force. Over two decades ago Hill proposed the first quantitative model describing how a depolymerizing microtubule could be harnessed for the production of force (6). In this model a hypothetical sleeve surrounds the MT and provides the attachment to the kinetochore. An attraction between the sleeve and MT provides an energy barrier preventing detachment, but this sleeve may still be able to slide along the MT without paying the energy of detachment. More recent computational models are detailed, mechanistic and micromechanical. One such model has taken into account the energy predicted to be available due to the curling of PFs (17, 18, 19) and, following the discovery of the Dam1 ring, was extended to reflect current structural knowledge and incorporate the hypothesis that Dam1 forms rigid transient links to the MT (20). Another independent model postulated an electrostatic attraction maintaining the rings position at the tip of the MT (21), combined with a powerstroke. All recent models include a combination of the following features: 1) the intrinsic diffusion of the Dam1 ring; 2) an effective powerstroke due to curling PFs; 3) an attractive potential between Dam1 and the MT. However, whilst these models include many of the relevant physical features of the system and produce satisfactory simulations of a reliable force transduction system, the problem cannot be considered “solved” because many variants on these models are possible and they have not been quantitatively compared to data. Furthermore, the lack of discriminatory experimental data precludes validation. In light of this we feel that much can be gained from rigorously analyzing the contribution of the various features in order to determine their possible role.
In what follows we describe two distinct “minimal” models, both of which describe a functional Dam1-mediated force transduction system. In the protofilament model the splaying PFs at the depolymerizing end physically prevent the ring from sliding off. In binding models an attraction between the ring and MT provides an energy barrier preventing detachment. The two models are not mutually exclusive – a hybrid model, incorporating both contributions, may also apply although one of the constituent mechanisms will typically dominate. While it is straightforward to modify our analysis to include such hybrid models we neglect them here for clarity, since our purpose is to differentiate the contributions. In common with previous models we also neglect other molecular components, e.g., microtuble-associated proteins (MAPs) and kinases (22, 23), that certainly play important additional roles in vivo.
Some previous studies have incorporated a powerstroke, arising from the motion of PFs, in driving the motion of the Dam1 ring (17, 20, 21). Indeed, it has been demonstrated that PFs can push a bead attached to the side of a MT (24), with a force of about 5 pN per 1–2 PFs. However, it is also known that models in the “burnt bridges” (25) class require no powerstroke per se to generate motion (26). Rather, purely diffusive Brownian motion can be rectified if “bridges” (here segments of MT) are lost (depolymerize) after they have been crossed. No instantaneous physical force is required, although the resultant rectified Brownian motion does give rise to a force in the thermodynamic sense. Such models are, in turn, members of a larger class of models known as “Brownian ratchets” (27). These models exhibit velocities that depend on applied force, and stall for sufficiently high forces, as also seen in more complex models (21). It is not clear a priori to what extent the powerstroke plays an important role. In the present work we also seek to answer this question.
Generalized model
We seek to analyze a general model that includes both a diffusive burnt bridge mechanism and a powerstroke, in order to determine their relative contribution. Here the powerstroke involves a depolymerization event which “unzips” PFs and moves the position of the last unbroken section of MT; a new section takes on this identity when the previous one unzips (contains separated, splayed protofilaments). As a highly energetic powerstroke this is assumed to occur even when the ring is very close to the MT end, with a rate that gives rise to a depolymerization velocity . The sequence of microscopic PF unzippering events gives rise to a well defined velocity for the last fully intact MT section, irrespective of the sequence in which the neighboring PFs unzip, and the precise MT helicity. Critically, we also assume that polymerized MT can be lost with a second rate, giving a depolymerization velocity , whenever the ring has diffused a distance from the end. This can be thought of as the depolymerization velocity of a bare MT because, in this case, there is no Dam1 ring anywhere on the MT. We make no prior assumptions as to which contribution dominates, rather we determine this by fitting the parameters , and to data for the variation of the Dam1 velocity with load (12).
Our model involves a clear distinction between two mechanisms (only) and represents the simplest possible model capable of explaining this data. It can be biophysically motivated on the grounds that the Dam1 ring interacts with neighboring tubulin and so the rate of PF unzippering at the MT end should depend on how close the Dam1 ring is to the end (a concept already introduced in (21)). In the section below we discuss this mechanism in terms of a putative energy landscape for the depolymerization (unzipping) reaction. We believe that it would be unjustified to postulate the existence of any features on this energy landscape beyond the minimum required to explain the data. This amounts to a model involving two (distinct) depolymerization mechanisms. Our results suggest that both mechanisms play important roles at moderate loads. In particular powerstroke-only models are clearly inconsistent with the data showing a velocity that is dependent on force (11, 12), assuming a strong power-stroke as previously measured on the order of pN (24). This is because, with a powerstroke-only model, we would not expect the velocity of Dam1 ring to be significantly slowed under a force as low as pN; the data shows a significant slowing. We find that the length scale controlling burnt-bridge reactions, a free fit parameter, is close to the axial length of a tubulin dimer. We speculate that this may provide indication of “crack”-like splitting of the MT, as discussed below.
Model
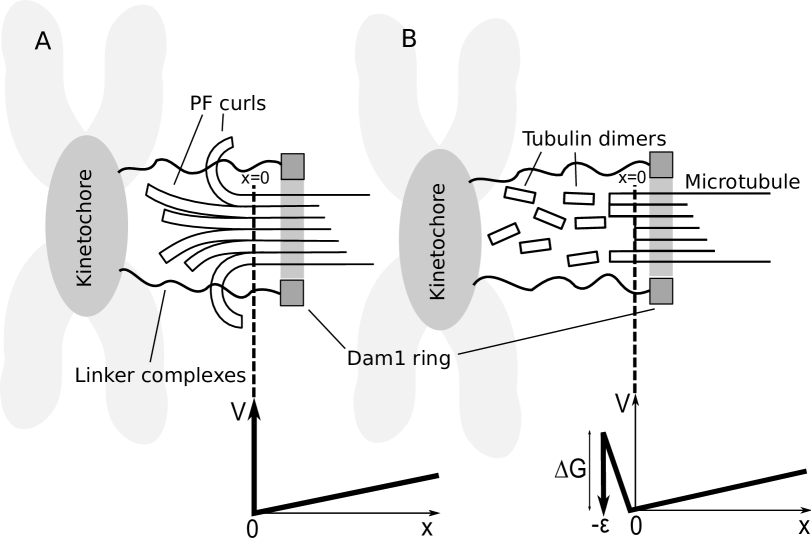
The Dam1 ring complex is reported to be capable of axial movement with respect to the MT (10). Therefore, we treat the Dam1 ring as a particle undergoing one-dimensional Brownian motion in a potential (shown for two different models in Fig. 1). The fully intact MT extends away from the depolymerizing end for and the point at which the MT lattice unravels is (see Fig. 1 A). The following Fokker-Plank equation (28) determines the probability density for the ring’s position relative to the (moving) end,
| (1) |
where is the diffusion constant of the ring. This approach is appropriate providing the depolymerization velocity of the MT is not too fast (bounds given later in this section), otherwise we must instead treat this as a full moving boundary problem. Since the microtubule depolymerization is here quasistatically slow with respect to the diffusive relaxation of the ring, we can neglect the drag force on the ring, except as discussed in Supporting Material.
In the following we assume the Dam1 ring is sufficiently stable that it can only dissociate by slipping off the tip. For simplicity we restrict our analysis to continuous depolymerization processes only and discount the possibility of rescue and polymerization. Although it would be straightforward to include such processes we believe that they would distract from the central results of this paper.
A force appears in Eq. 1. This is the magnitude of the applied force on the Dam1 ring while on the MT () since the ring must do work to move against this force. Hence, from Eq. 1 it can be shown that, for constant (or slowly varying) the probability distribution is of Boltzmann form
| (2) |
where the ring typically explores a characteristic diffusion length from the MT end and positive values of here indicate loads pulling in the negative direction (towards the MT end). We assume that the depolymerization is quasistatically slow. This is appropriate provided the time for the MT to depolymerize the distance is much larger than the relaxation time for a ring to diffuse this distance. This in turn requires . In this case the distribution of the ring position is always close to the equilibrium probability distribution that it would have on an MT that was not depolymerizing. This sets an upper bound on the depolymerization velocity, or equivalently a lower bound on the load force, beyond which our theory is at best semiquantitative; solving with Eq. 4, we estimate these values to be 500 nm/s and 0.04 pN respectively. Under these conditions the average ring velocity is equivalent to the depolymerization velocity of the MT.
Force dependent depolymerization velocity
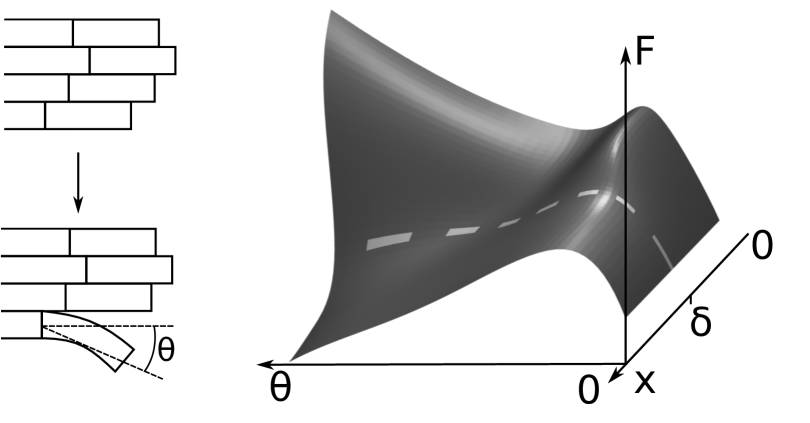
The powerstroke and burnt-bridge reactions can be thought of as arising from transitions over an energy barrier of the form shown in Fig. 2, where the free energy of PF curling is shown as varying with protofilament angle and the distance of the Dam1 ring from the MT tip . The figure shows only a putative schematic of the free energy of PF curling reaction, and should not be confused with the potential in which the Dam1 ring diffuses.
PFs may produce a power stroke that pushes the ring with force , estimated from experimental evidence to be pN (24). This is the slope down the descending valley, diagonally right to left, in Fig. 2. Provided that the load force the powerstroke will give rise to a depolymerization velocity that is the rate at which the last intact dimer on the MT crosses the highest part of the ridge-like energy barrier in Fig. 2 (). Since the estimate for is so much larger than any force considered here, it is reasonable to make the limited assumption that is constant for all experimentally measurable load forces of a few pN or less.
In addition the MT can also depolymerize when the Dam1 ring is further than a critical distance from the end of the MT. In this case the burnt-bridge reaction gives rise to a depolymerization velocity that is the rate at which the last intact dimer on the MT crosses the lower part of the ridge-like energy barrier in Fig. 2 (). That the rate of MT unzippering is retarded when the Dam1 ring is near the MT end is a result of the fact that the velocity decreases as the load force is increased and the ring is more often closer to the MT end. Although it is not necessary to interpret our model in terms of the Dam1 ring physically occluding the unzippering of the tubulin dimers, this interpretation may not be unreasonable, particularly in view of the fact that we find to be comparable with the axial length of the last intact ring of tubulin dimers.
The resultant velocity due to both mechanisms is the sum of the probability that the ring is close to the MT end , multiplied by the powerstroke velocity, and the probability that it is far , multiplied by the burnt-bridge velocity,
| (3) |
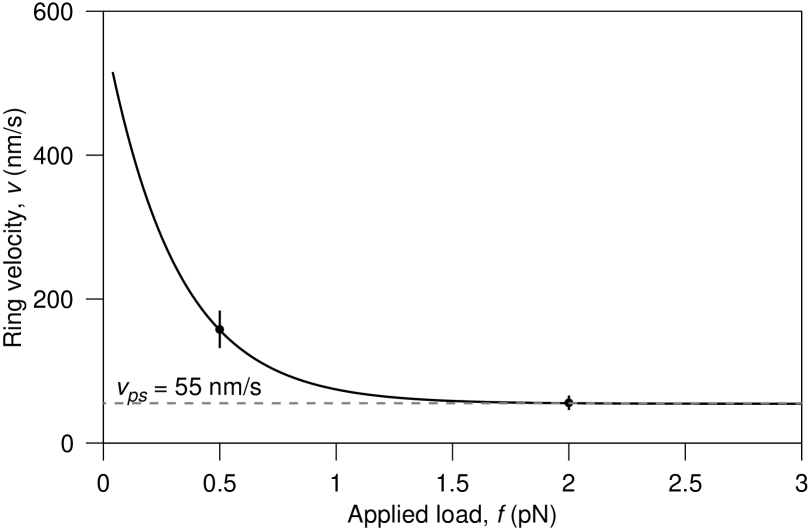
The variation of this velocity with load is shown in Fig. 3 for nm/s (29), and the values nm/s and nm that correspond to the best fit to data (12). Since a “burnt-bridges”-only model fails to fit the data sufficiently (i.e. ) it suggests that a powerstroke plays a role in forced Dam1 motion. It should be noted that, although in this model as , we do not suggest this is a physical feature of the system. Rather it is the consequence of the assumption that protofilaments are perfectly rigid and the powerstroke reaction is asymptotically strong. Our model would need modification for forces approaching . As discussed later, PFs are estimated to require tens of pN to bend.
Two models for Dam1 ring retention
We now proceed to calculate the mean time the Dam1 ring will remain on a MT and transduce force111Recently it has been discovered that the Dam1 oligomers track the tip of depolymerizing MTs without forming a ring (30, 31). It seems unlikely that a protofilament model could operate without a full ring, however, it is not known to what extent, if at all, small oligomers contribute to force production. Furthermore, it has been shown that 16-20 Dam1 complexes are present at the kinetochore during metaphase (32), enough to form the ring. We await the result of experiments where tension is applied to putative Dam1 oligomers. . This time is controlled by different physics in the protofilament and the binding models, see Figs. 1 and 4. However, in both cases, the velocity of the ring is governed by the model described above, see Eq. 4.
Runtime: Binding model
The binding model involves a ring diffusing on a MT according to Eq. 1, leading to a depolymerization velocity as given in Eq. 4. However, in order to detach from the MT end the ring must overcome a linear potential imposed by the Dam1-MT binding energy as it slides off the end of the ring. In this respect it is similar to Hill’s model (6). Previous models invoked a that also determined the roughness of the energy landscape through “linkers” (20) whose existence is supported by binding studies (33). Here we don’t make this assumption, rather could be due to less specific interactions without significant energy barriers between neighboring sites (34) but, importantly, can vary independently of the diffusion constant . This, in turn, is fixed by the smoothness of the underlying energy landscape experienced by the ring as it diffuses along the MT (distinct from the energy landscape experienced by an unzippering PF shown in Fig. 2). This model assumes that the splayed PFs play no role, either because they are transient (rapidly breaking) or otherwise interact negligibly with the ring as it slides off the end of the MT. Although clearly an extreme approximation it forms the natural opposite limit to the protofilament model discussed in the next section. Under a load force the ring is in the well of a “tick”-shaped potential with two linear domains (inset Fig. 1 B). To move to the left (towards negative ) it must partially unbind from the MT, to move to the right (positive ) it must do work against the applied force. The potential gradients experienced by the Dam1 ring determine the load force (while on the MT, ) and the resultant force (while detaching from the MT over the small distance ). The force on the ring, adopting a sign convention where a positive force acts in the direction of positive , is therefore given by
| (5) |
where is the unbinding region. If the ring is in the region then it is lost, and if lost we assume it never returns, hence we have for .
Symmetry from electron microscopy (10) and copy number (32) experiments suggest 16 complexes are required to form the Dam1 ring, however, the total bond energy may not be additive and this should therefore be regarded as an extreme upper bound on the total binding energy.
The detachment of the ring can be cast as a classical Kramers escape problem (35). To solve Eq. 1 with Eq. 5 we followed the method in (36, 37). In this way we obtain the lifetime of the metastable state directly from the Laplace transformed version of Eq. 1, with initial condition , where is the Dirac delta function, although the precise form of this initial condition is unimportant. The mean time the ring remains on the MT is the runtime
| (6) |
where is a small distance.
Runtime: Protofilament model
The protofilament model involves a ring diffusing on a MT according to Eq. 1, leading to a depolymerization velocity Eq. 4, as before. However, in order to detach from the MT end the ring has to wait until all protofilaments have broken (depolymerized), leaving a sufficiently “blunt” end to the MT for the ring to simply slide off, see Fig. 1 A. We no longer require the Dam1 ring to overcome a Dam1-MT binding energy. Electron microscopy reveals that short, separated PFs splay outwards at the depolymerizing MT end (18, 19) and it is quite plausible that these block the escape of the ring; the elastic energy required to straighten a curled PF (38) follows from measurements of their rigidity (39, 40) and is of the order of tens of per subunit, i.e. very large.
The “frayed” PFs near the end of the MT are curved and laterally separate. The unzipping (depolymerization) of the MT lattice (see Fig. 1A) is most accurately described as a process which transfers length from the polymerized MT into separated PFs. The unzipping is thought to be driven by the stored elastic energy in the -tubulin units in the lattice (41). When not constrained by lateral bonds, PFs relax into a curved state. We model unzipping as a Poisson process with rate . Each unzipping event extends every PF curl by some microscopic, or subunit, length , leading to a depolymerization velocity . This microscopic length might be the tubulin dimer repeat distance , if the MT splits between a particular pair of PFs, or otherwise smaller than this. When the ring is within a small length unzipping is inhibited. To more carefully analyze this process note that the time between unzipping events is an exponential random variable, with probability density function , and mean
| (7) |
The distribution of the ring position in this model follows Eq. 2. Detachment occurs when all PF curl lengths reach zero222Extensions of our model to the case of loosely-fitting rings is straightforward, involving attachment whenever the PF curls exceed some finite length . Our results are qualitatively insensitive to this modification, provided the ring rarely detaches at low force. Furthermore, for such rings the molecular length becomes irrelevant as the characteristic timescale is .. Since is a function of the applied force , according to Eq. 4, increases under load. From Eq. 2, we have that the characteristic distance of the ring from the tip is . The characteristic time for the ring to diffuse this length and escape is which is much less than for typical parameters whenever pN (see Supporting Material). Thus it is not unreasonable to assume that the ring might disengage from the MT extremely rapidly as soon as all curled PFs reach zero length.
We assume that tubulin subunits on the frayed PFs break independently according to a Poisson process with rate . The depolymerization of PFs then follows from the loss of all PF material beyond the break, as in previous computational models (42). A PF curl reaches zero length if the axial bond nearest to the unzipping point breaks, see Fig. 1 A. Since this occurs with a rate the waiting time for PF curl to break off completely is an exponential random variable. The wait time for all PF curls breaking is the order statistic . The distribution function for this time is and the mean wait time (see section 4.6 from (43) or (44)) is
| (8) |
where is the harmonic number, roughly for as can be seen by converting the sum to an integral, denotes the ensemble average. The Dam1 ring will therefore no longer be secured to the MT end and will detach after a time provided that no unzipping events having taken place during the time . If the MT has unzipped then the PFs extend (from their base), effectively “restarting” the waiting process.
Fundamentally we are interested in the mean runtime , this being the time taken for the curled PFs to all depolymerize completely even while the MT is simultaneously undergoing stochastic unzipping events. can be found by counting the number of unzipping events that occur before the PFs all successfully break and the Dam1 ring can disengage. is geometrically distributed with mean with the probability that the curled PFs depolymerize completely before the next unzippering event. Thus
| (9) |
The ring detaches if the PFs break before an unzipping occurs, i.e. with probability that ,
| (10) |
where is the probability density function for . Evaluating the integral with respect to
| (11) |
Binomially expanding the integrand, integrating term-by-term and substituting back into Eq. 9 we obtain
| (12) |
where .
Time varying applied forces
We now consider an oscillating applied force of the form
| (13) |
Provided the period is sufficiently long our quasi-static approximation for the ring position should give an accurate estimate for its probability density .
The depolymerization velocity will be retarded according to Eq. 4, relating to .
Protofilament model under oscillating force
The probability that the MT does not unzip in a time after the time at which the last unzipping occurred is
| (14) |
Since Eq. 14 depends explicitly on , we perform an average over , appropriately weighted, to give the complementary distribution of times between unzipping events
| (15) |
involving a normalization constant .
To calculate the runtime as in Eq. 9, we first determine the probability the unzip time exceeds the curled PF breaking time
| (16) |
The probability density of is
| (17) |
Finally the runtime is
| (18) |
where is the mean number of steps before detachment.
Binding model under oscillating force
Results and Discussion
We identified the following parameters using data reported in the experimental literature; nm/s (29), (10); for the protofilament model we assume nm and to be typical.
Table 1 in Franck et al. (12) (see Table S1 in the Supporting Material) lists velocities at pN and pN. Using the velocity data we fit to obtain nm and nm/s. As has already been mentioned the range is intriguingly close to a tubulin axial repeat length ( nm or 1.5 times this, due to helicity). A simple picture might be of a sleeve that suppresses depolymerization while it sits over the next intact tubulin dimers in the PFs that are about to split. This supports the idea that the MT depolymerizes by first splitting in a linear fashion, perhaps along its seam, with the other PF pairs splitting apart somewhat behind this leading crack-like defect. Indeed, materials do typically split along linear cracks, where the elastic stresses are concentrated (45). In particular, splitting between random PFs would yield step sizes that, due to helicity, could be a small fraction of the tubulin size. It would be hard to physically motivate a range that is more than ten times the incremental depolymerization step size. Why would such a depolymerization process, involving little or no motion of PFs more than nm from the last fully polymerized section of MT, be highly sensitive to the presence of a Dam1 ring more than nm distant? We therefore consider our estimate of the characteristic range for the burnt-bridges reaction (within which the Dam1 ring occludes unzipping) to be quite reasonable.
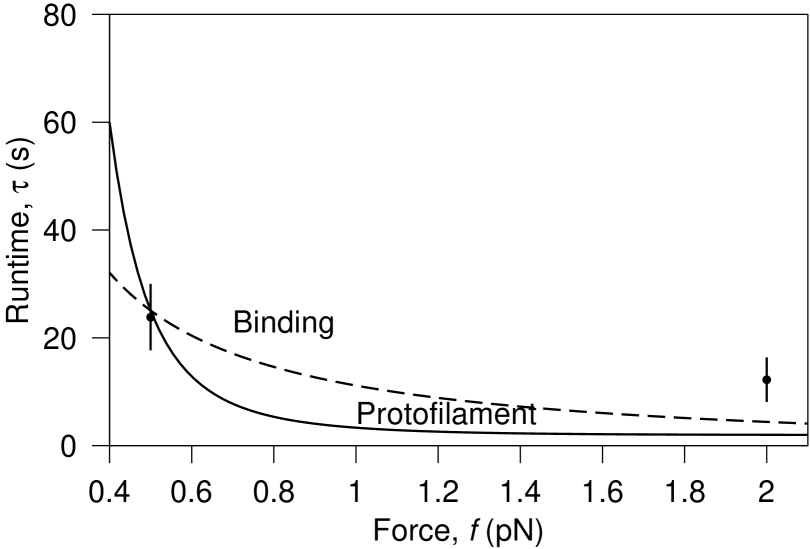
Combining the available data for velocity and detachment frequency we find, on average, s and s, for pN and pN respectively. To fit the binding model for we choose nm, as a reasonable distance over which an attraction might act, and find . Independently, we fit for the protofilament model and find . Fitting these parameters to just two data points does not provide strong evidence for these particular values. However, uncertainty in the exact parameter values should not detract from the main value of this work; to provide a model that explains the Dam1 force sensitivity and to distinguish between binding and protofilament models. Comparison of the fit with data is shown in Fig. 5.

Variation of intrinsic depolymerization velocity
The protofilament model exhibits the most sensitivity to the intrinsic (bare) MT depolymerization velocity , as is shown in Fig. 6 A. For the protofilament model, is strongly dependent on and consequently . The binding model, on the other hand, is only weakly dependent on (see Supporting Material), and on this range of we can assume that depolymerization is quasistatically slow with respect to ring diffusion. The result can be understood physically by realising that as increases, the rate of PF unzipping also increases, while remains constant making it less likely that the PFs will break off sufficiently quickly to release the ring.
An experimental test that might be able to distinguish which model operates could be achieved, e.g., by addition of a depolymerization inducing agent, such as or XMCAK1.
Changing of diffusion coefficient
The diffusion constant of the ring is determined by the ring’s dimensions and the roughness of the binding energy landscape along the MT, rather than the magnitude of the binding energy itself. A more rough landscape reduces the mobility of the ring. Fig. 6 B shows the effect of the diffusion constant on the runtime for both models. Only the binding model is sensitive to change in , having reduced runtime with faster diffusion. This is because the increased mobility of the ring increases the chance it is able to scale the potential barrier constraining it to the MT.
Although it may be possible to alter biochemically, for example by phosphorylation (30), it is difficult to do so independently of . Decreasing may be better accomplished by attaching a long inert polymer to the complex to increase viscous drag.
Effect of time-varying loading force
The runtime in the binding model is sensitive only to the instantaneous force provided , see the low frequency portion of Fig. 6 C. If pN then is on the order of 1 kHz. The runtime in the protofilament model is sensitive to the time over which changes in persist. If the force is oscillating with a long period then the rate of detachment will be greater in the high force part of the cycle than if the period is short. This is because the Dam1 ring takes some time to detach if it needs to first wait for the PF curls to break, see Fig. 6 C. Sigmoidal increase of would be a signature of a system that depends on a second time (1/), like the protofilament model; insensitivity of to frequency would imply a binding-style coupling.
Conclusion
Our results indicate a power stroke does contribute to the effective force generated during depolymerization but only becomes dominant at over 2 pN load. We show how a faster depolymerization mechanism must operate at lower loads and argue that the Dam1 ring suppresses depolymerization when it is close to the MT end.
We have shown that either of two rather different Dam1-MT coupling mechanisms might be operating under piconewton loads. Both models have comparable performance under load; their differences only become apparent under novel experimental conditions. Structural studies cannot resolve the question of which model operates in vivo. We suggest several methods for using runtime statistics to determine which class of model best describes the coupling of the Dam1 ring to depolymerizing MTs. Note that throughout this study we have assumed that depolymerization is sufficiently slow compared to ring diffusion that we can consider the distribution of the ring’s position to be quasi-equilibrated. Over the range of parameters we have considered this assumption is valid to within of the predicted velocity. The characteristic range over which Dam1 inhibits depolymerization can be estimated by comparing our model with data. It is intriguingly close to the size of the microscopic (tubulin) repeat length of the MT. We have argued that this provides evidence that the MT is splitting, possibly along its seam, at the leading edge of the depolymerization front. In this case the PFs move outwards a similar distance along the MT from the last polymerized section.
It is important to note that the present work has neglected in vivo factors such as microtubule-associated proteins (MAPs) or kinases. However, some of these factors operate to increase or reduce the depolymerization rate of the microtubule, a parameter included in the model. We therefore expect the general results to remain largely applicable. Furthermore, we have assumed Dam1 to be present as a ring. Recent work (30, 31) has raised the possibility that Dam1 may operate as short oligomers or single complexes. If we can assume these oligomers interact with PFs in a comparable fashion as a ring would, our model would be indistinguishable for rings or oligomers. If not, our model may be of use to determine whether ring or oligomer is present based on e.g., differing diffusion constant.
Acknowledgements
The authors thank George Rowlands and Jonathan Millar for useful discussions.
References
- Alberts et al. (2002) Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2002. Molecular biology of the cell. Garland Science, New York, fourth edition.
- Inoué and Salmon (1995) Inoué, S., and E. Salmon. 1995. Force generation by microtubule assembly/disassembly in mitosis and related movements. Mol. Biol. Cell 6:1619–1640.
- Coue et al. (1991) Coue, M., V. Lombillo, and J. McIntosh. 1991. Microtubule depolymerization promotes particle and chromosome movement in vitro. J. Cell Biol. 112:1165–1175.
- Ganem et al. (2005) Ganem, N. J., K. Upton, and D. A. Compton. 2005. Efficient Mitosis in Human Cells Lacking Poleward Microtubule Flux. Curr. Biol. 15:1827–1832.
- Koshland et al. (1988) Koshland, D. E., T. J. Mitchison, and M. W. Kirschner. 1988. Polewards chromosome movement driven by microtubule depolymerization in vitro. Nature 331:499–504.
- Hill (1985) Hill, T. L. 1985. Theoretical Problems Related to the Attachment of Microtubules to Kinetochores. Proc. Natl. Acad. Sci. U. S. A. 82:4404–4408.
- Cheeseman et al. (2001a) Cheeseman, I. M., C. Brew, M. Wolyniak, A. Desai, S. Anderson, N. Muster, J. R. Yates, T. C. Huffaker, D. G. Drubin, and G. Barnes. 2001. Implication of a novel multiprotein Dam1p complex in outer kinetochore function. J. Cell Biol. 155:1137–1146.
- Miranda et al. (2005) Miranda, J. L., P. D. Wulf, P. K. Sorger, and S. C. Harrison. 2005. The yeast DASH complex forms closed rings on microtubules. Nat. Struct. Mol. Biol. 12:138–143.
- Westermann et al. (2005) Westermann, S., A. Avila-Sakar, H.-W. Wang, H. Niederstrasser, J. Wong, D. G. Drubin, E. Nogales, and G. Barnes. 2005. Formation of a Dynamic Kinetochore-Microtubule Interface through Assembly of the Dam1 Ring Complex. Mol. Cell 17:277–290.
- Westermann et al. (2006) Westermann, S., H.-W. Wang, A. Avila-Sakar, D. G. Drubin, E. Nogales, and G. Barnes. 2006. The Dam1 kinetochore ring complex moves processively on depolymerizing microtubule ends. Nature 440:565–569.
- Asbury et al. (2006) Asbury, C. L., D. R. Gestaut, A. F. Powers, A. D. Franck, and T. N. Davis. 2006. The Dam1 kinetochore complex harnesses microtubule dynamics to produce force and movement. Proc. Natl. Acad. Sci. U. S. A. 103:9873–9878.
- Franck et al. (2007) Franck, A. D., A. F. Powers, D. R. Gestaut, T. Gonen, T. N. Davis, and C. L. Asbury. 2007. Tension applied through the Dam1 complex promotes microtubule elongation providing a direct mechanism for length control in mitosis. Nat. Cell Biol. 9:832–837.
- Grishchuk et al. (2008a) Grishchuk, E. L., A. K. Efremov, V. A. Volkov, I. S. Spiridonov, N. Gudimchuk, S. Westermann, D. Drubin, G. Barnes, J. R. McIntosh, and F. I. Ataullakhanov. 2008. The Dam1 ring binds microtubules strongly enough to be a processive as well as energy-efficient coupler for chromosome motion. Proc. Natl. Acad. Sci. U. S. A. 105:15423–15428.
- Jones et al. (2001) Jones, M. H., X. He, T. H. Giddings, and M. Winey. 2001. Yeast Dam1p has a role at the kinetochore in assembly of the mitotic spindle. Proc. Natl. Acad. Sci. U. S. A. 98:13675–13680.
- Cheeseman et al. (2001b) Cheeseman, I. M., M. Enquist-Newman, T. Muller-Reichert, D. G. Drubin, and G. Barnes. 2001. Mitotic Spindle Integrity and Kinetochore Function Linked by the Duo1p/Dam1p Complex. J. Cell Biol. 152:197–212.
- Franco et al. (2007) Franco, A., J. C. Meadows, and J. B. A. Millar. 2007. The Dam1/DASH complex is required for the retrieval of unclustered kinetochores in fission yeast. J. Cell Sci. 120:3345–3351.
- Molodtsov et al. (2005) Molodtsov, M. I., E. L. Grishchuk, A. K. Efremov, J. R. McIntosh, and F. I. Ataullakhanov. 2005. Force production by depolymerizing microtubules: A theoretical study. Proc. Natl. Acad. Sci. U. S. A. 102:4353–4358.
- Mandelkow et al. (1991) Mandelkow, E.-M., E. Mandelkow, and R. A. Milligan. 1991. Microtubule dynamics and microtubule caps: a time-resolved cryo-electron microscopy study. J. Cell Biol. 114:977–991.
- Chrétien et al. (1995) Chrétien, D., S. D. Fuller, and E. Karsenti. 1995. Structure of growing microtubule ends: two-dimensional sheets close into tubes at variable rates. J. Cell Biol. 129:1311–1328.
- Efremov et al. (2007) Efremov, A., E. L. Grishchuk, J. R. McIntosh, and F. I. Ataullakhanov. 2007. In search of an optimal ring to couple microtubule depolymerization to processive chromosome motions. Proc. Natl. Acad. Sci. U. S. A. 104:19017–19022.
- Liu and Onuchic (2006) Liu, J., and J. N. Onuchic. 2006. A driving and coupling ”Pac-Man” mechanism for chromosome poleward translocation in anaphase A. Proc. Natl. Acad. Sci. U. S. A. 103:18432–18437.
- Cheeseman et al. (2002) Cheeseman, I. M., S. Anderson, M. Jwa, E. M. Green, J.-s. Kang, J. R. Yates, C. S. Chan, D. G. Drubin, and G. Barnes. 2002. Phospho-Regulation of Kinetochore-Microtubule Attachments by the Aurora Kinase Ipl1p. Cell 111:163–172.
- Shimogawa et al. (2006) Shimogawa, M. M., B. Graczyk, M. K. Gardner, S. E. Francis, E. A. White, M. Ess, J. N. Molk, C. Ruse, S. Niessen, J. R. Yates, E. G. Muller, K. Bloom, D. J. Odde, and T. N. Davis. 2006. Mps1 Phosphorylation of Dam1 Couples Kinetochores to Microtubule Plus Ends at Metaphase. Curr. Biol. 16:1489–1501.
- Grishchuk et al. (2005) Grishchuk, E. L., M. L. Molodtsov, F. I. Ataullakhanov, and J. R. McIntosh. 2005. Force production by disassembling microtubules. Nature 438:384–388.
- Morozov et al. (2007) Morozov, A. Y., E. Pronina, A. B. Kolomeisky, and M. N. Artyomov. 2007. Solutions of burnt-bridge models for molecular motor transport. Phys. Rev. E 75:031910.
- Artyomov et al. (2008) Artyomov, M. N., A. Y. Morozov, and A. B. Kolomeisky. 2008. Molecular motors interacting with their own tracks. Phys. Rev. E 77:040901.
- Peskin et al. (1993) Peskin, C. S., G. M. Odell, and G. F. Oster. 1993. Cellular motions and thermal fluctuations: the Brownian ratchet. Biophys. J. 65:316–324.
- Risken (1984) Risken, H. 1984. The Fokker-Planck equation. Springer-Verlag.
- Hunt and McIntosh (1998) Hunt, A. J., and J. R. McIntosh. 1998. The Dynamic Behavior of Individual Microtubules Associated with Chromosomes In Vitro. Mol. Biol. Cell 9:2857–2871.
- Gestaut et al. (2008) Gestaut, D. R., B. Graczyk, J. Cooper, P. O. Widlund, A. Zelter, L. Wordeman, C. L. Asbury, and T. N. Davis. 2008. Phosphoregulation and depolymerization-driven movement of the Dam1 complex do not require ring formation. Nat. Cell Biol. 10:407–414.
- Grishchuk et al. (2008b) Grishchuk, E. L., I. S. Spiridonov, V. A. Volkov, A. Efremov, S. Westermann, D. Drubin, G. Barnes, F. I. Ataullakhanov, and J. R. McIntosh. 2008. Different assemblies of the DAM1 complex follow shortening microtubules by distinct mechanisms. Proc. Natl. Acad. Sci. U. S. A. 105:6918–6923.
- Joglekar et al. (2008) Joglekar, A. P., D. Bouck, K. Finley, X. Liu, Y. Wan, J. Berman, X. He, E. Salmon, and K. S. Bloom. 2008. Molecular architecture of the kinetochore-microtubule attachment site is conserved between point and regional centromeres. J. Cell Biol. 181:587–594.
- Miranda et al. (2007) Miranda, J. L., D. S. King, and S. C. Harrison. 2007. Protein Arms in the Kinetochore-Microtubule Interface of the Yeast DASH Complex. Mol. Biol. Cell 18:2503–2510.
- Wang et al. (2007) Wang, H.-W., V. H. Ramey, S. Westermann, A. E. Leschziner, J. P. I. Welburn, Y. Nakajima, D. G. Drubin, G. Barnes, and E. Nogales. 2007. Architecture of the Dam1 kinetochore ring complex and implications for microtubule-driven assembly and force-coupling mechanisms. Nat. Struct. Mol. Biol. 14:721–726.
- Kramers (1940) Kramers, H. A. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 7:284–304.
- Agudov and Malakhov (1993) Agudov, N. V., and A. N. Malakhov. 1993. Nonstationary diffusion through arbitrary piecewise-linear potential profile. Exact solution and time characteristics. Radiophys. Quantum Electron. 36:97–109.
- Malakhov and Pankratov (2002) Malakhov, A. N., and A. L. Pankratov. 2002. Evolution times of probability distributions and averages - exact solutions of the Kramers’ problem. Adv. Chem. Phys. 121:357–438.
- Landau and Lifshitz (1986) Landau, L. D., and E. M. Lifshitz. 1986. Theory of elasticity. Butterworth Heinemann, third edition.
- Kikumoto et al. (2006) Kikumoto, M., M. Kurachi, V. Tosa, and H. Tashiro. 2006. Flexural Rigidity of Individual Microtubules Measured by a Buckling Force with Optical Traps. Biophys. J. 90:1687–1696.
- Gittes et al. (1993) Gittes, F., B. Mickey, J. Nettleton, and J. Howard. 1993. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 120:923–934.
- Rice et al. (2008) Rice, L. M., E. A. Montabana, and D. A. Agard. 2008. The lattice as allosteric effector: Structural studies of alphabeta- and gamma-tubulin clarify the role of GTP in microtubule assembly. Proc. Natl. Acad. Sci. U. S. A. 105:5378–5383.
- VanBuren et al. (2002) VanBuren, V., D. J. Odde, and L. Cassimeris. 2002. Estimates of lateral and longitudinal bond energies within the microtubule lattice. Proc. Natl. Acad. Sci. U. S. A. 99:6035–6040.
- Arnold et al. (1992) Arnold, B. C., N. Balakrishnan, and H. N. Nagaraja. 1992. A First Course in Order Statistics. John Wiley and Sons, Inc.
- Rényi (1953) Rényi, A. 1953. On the theory of order statistics. Acta Math. Hungarica 4:191–231.
- Kanninen and Popelar (1985) Kanninen, M. F., and C. H. Popelar. 1985. Advanced fracture mechanics. Oxford University Press.