Four-body Semileptonic Charm Decays $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ Based on
SU(3) Flavor Analysis

Ru-Min Wang^1,†, Yi Qiao¹, Yi-Jie Zhang¹, Xiao-Dong Cheng^2,§, Yuan-Guo Xu^1,♯
¹College of Physics and Communication Electronics, Jiangxi Normal University, Nanchang, Jiangxi 330022, China
²College of Physics and Electronic Engineering, Xinyang Normal University, Xinyang, Henan 464000, China
^†ruminwang@sina.com ^§chengxd@mails.ccnu.edu.cn ^♯yuanguoxu@jxnu.edu.cn ruminwang@sina.com

Abstract

Motivated by the significant experimental progress in probing semileptonic decays $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}\leavevmode\nobreak\ (\ell=\mu,e)$ , we analyze the branching ratios of the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays with the nonresonant, the light scalar meson resonant and the vector meson resonant contributions in this work. We obtain the hadronic amplitude relations between different decay modes by the SU(3) flavor analysis, and then predict relevant branching ratios of the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays by the present experimental data with $2\sigma$ errors. Most of our predicted branching ratios are consistent with present experimental data within $2\sigma$ error bars, and others are consistent with the data within $3\sigma$ error bars. We find that the branching ratios of the nonresonant decays $D^{0}\to\pi^{-}\overline{K}^{0}\ell^{+}\nu_{\ell},\pi^{0}K^{-}\ell^{+}\nu_{\ell}$ , $D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell},\pi^{0}\overline{K}^{0}\ell^{+}\nu_{\ell},\pi^{+}\pi^{-}\ell^{+}\nu_{\ell},\pi^{0}\pi^{0}\ell^{+}\nu_{\ell}$ , and $D^{+}_{s}\to K^{+}K^{-}\ell^{+}\nu_{\ell},K^{0}\overline{K}^{0}\ell^{+}\nu_{\ell}$ are on the order of $\mathcal{O}(10^{-3}-10^{-4})$ . The vector meson resonant contributions are dominant in the $D^{0}\to\pi^{-}\overline{K}^{0}\ell^{+}\nu_{\ell},\pi^{0}K^{-}\ell^{+}\nu_{\ell},\pi^{0}\pi^{-}\ell^{+}\nu_{\ell}$ , $D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell},\pi^{0}\overline{K}^{0}\ell^{+}\nu_{\ell},\pi^{+}\pi^{-}\ell^{+}\nu_{\ell}$ , and $D^{+}_{s}\to K^{+}K^{-}\ell^{+}\nu_{\ell},K^{0}\overline{K}^{0}\ell^{+}\nu_{\ell},K^{+}\pi^{-}\ell^{+}\nu_{\ell},K^{0}\pi^{0}\ell^{+}\nu_{\ell}$ decays. The nonresonant, the vector meson resonant and the scalar resonant contributions are all important in the $D^{0}\to\eta\pi^{-}\ell^{+}\nu_{\ell}$ decays. The $D^{0}\to K^{-}K^{0}\ell^{+}\nu_{\ell},\eta^{\prime}\pi^{-}\ell^{+}\nu_{\ell}$ and $D^{+}\to\overline{K}^{0}K^{0}\ell^{+}\nu_{\ell},\pi^{0}\pi^{0}\ell^{+}\nu_{\ell},\eta\pi^{0}\ell^{+}\nu_{\ell},\eta^{\prime}\pi^{0}\ell^{+}\nu_{\ell}$ decays only receive both the nonresonant and the scalar resonant contributions, and both contributions are important in their branching ratios. According to our predictions, many decay modes could be observed in the experiments like BESIII, LHCb, and BelleII, and some decay modes might be measured in these experiments in the near future.

I INTRODUCTION

Semileptonic heavy meson decays dominated by tree-level exchange of $W$ -bosons in the SM are very important processes in testing the standard model and in searching for the new physics beyond the standard model, for example, the extraction of the Cabbibo-Kobayashi-Maskawa (CKM) matrix elements. Four-body semileptonic exclusive decays $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ are generated by the $c\to s/d\ell^{+}\nu_{\ell}$ transitions, and they can receive contributions from the nonresonant, the light scalar meson resonant and the vector meson resonant contributions, etc. Therefore, these decays are also a good laboratory for probing the internal structure of light hadrons Wang:2009azc ; Oset:2016lyh ; Achasov:2012kk . Some nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays, the light scalar meson resonant decays $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ and the vector meson resonant decays $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ have been observed by BESIII, BABAR, CLEO, and MARKIII PDG2022 ; BESIII:2018qmf ; BESIII:2018sjg ; BESIII:2021tfk ; BESIII:2021pdt ; BaBar:2010vmf ; CLEO:2009ugx ; MARK-III:1990bbt . Present experimental measurements give us an opportunity to additionally test theoretical approaches.

Experimental backgrounds of the semileptonic decays are cleaner than ones of the hadronic decays, and theoretical description of the semileptonic exclusive decays are relatively simple. Since leptons do not participate in the strong interaction, the weak and strong dynamics can be separated in these processes. All the strong dynamics in the initial and final hadrons is included in the hadronic transition form factors, which are important for testing the theoretical calculations of the involved strong interaction. The form factors can be calculated, for example, by the chiral perturbation theory Kang:2013jaa , the unitarized chiral perturbation theory Shi:2017pgh ; Shi:2020rkz , the light-cone sum rules Sekihara:2015iha ; Cheng:2017smj ; Hambrock:2015aor , and the QCD factorization Boer:2016iez . Nevertheless, due to our poor understanding of hadronic interactions, the evaluations of the form factors are difficult and often plugged with large uncertainties. One needs to find ways to minimize the uncertainties to extract useful information.

In the lack of reliable calculations, symmetries provide very important information for particle physics. SU(3) flavor symmetry is a symmetry in QCD for strong interaction. From the perspective of the SU(3) flavor symmetry, the leptonic part of the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decay is the SU(3) flavor singlet, which makes no difference between different decay modes with certain lepton ( $e$ or $\mu$ ). The different hadronic parts (the hadronic amplitudes or the hadronic form factors) of the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays could be related by the SU(3) flavor symmetry without the detailed dynamics. Nevertheless, the size of the hadronic amplitudes or the form factors cannot be determined by itself in the SU(3) flavor symmetry approach. However, if experimental data are enough, one may use the data to extract the hadronic amplitudes or the form factors, which can be viewed as predictions based on symmetry, and has a smaller dependency on estimated form factors. Although the SU(3) flavor symmetry is only an approximate symmetry because up, down and strange quarks have different masses, it still provides some very useful information about the decays. The SU(3) flavor symmetry has been widely used to study hadron decays, for instance, $b$ -hadron decays He:1998rq ; He:2000ys ; Fu:2003fy ; Hsiao:2015iiu ; He:2015fwa ; He:2015fsa ; Deshpande:1994ii ; Gronau:1994rj ; Gronau:1995hm ; Shivashankara:2015cta ; Zhou:2016jkv ; Cheng:2014rfa ; Wang:2021uzi ; Wang:2020wxn , $c$ -hadron decays Wang:2021uzi ; Wang:2020wxn ; Grossman:2012ry ; Pirtskhalava:2011va ; Savage:1989qr ; Savage:1991wu ; Altarelli:1975ye ; Lu:2016ogy ; Geng:2017esc ; Geng:2018plk ; Geng:2017mxn ; Geng:2019bfz ; Wang:2017azm ; Wang:2019dls ; Wang:2017gxe ; Muller:2015lua , and light hadron decays Wang:2019alu ; Wang:2021uzi ; Xu:2020jfr ; Chang:2014iba ; Zenczykowski:2005cs ; Zenczykowski:2006se ; Cabibbo:1963yz .

Although the SU(3) flavor symmetry works well in heavy hadron decays, the calculations of SU(3) flavor breaking effects would play a key role in the precise theoretical predictions of the observables and a precise test of the unitarity of the CKM matrix. If up and down quark masses are neglected, a nonzero strange quark mass breaks the SU(3) flavor symmetry down to the isospin symmetry. When up and down quark mass difference is kept, isospin symmetry is also broken. Applications of the SU(3) flavor breaking approach on hadron decays can be found in Refs. Dery:2020lbc ; Sasaki:2008ha ; Pham:2012db ; Geng:2018bow ; Flores-Mendieta:1998tfv ; Cheng:2012xb ; Xu:2013dta ; He:2014xha . The SU(3) flavor breaking effects due to the fact of $m_{s}\gg m_{u,d}$ will be considered in our analysis of the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays.

Four-body semileptonic decays $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ have been studied, for instance, in Refs. Shi:2021bvy ; Shi:2017pgh ; Kim:2017dfr ; Achasov:2020qfx ; Wiss:2007mr ; Wang:2016wpc ; Achasov:2021dvt . In this work, we will study the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays with the SU(3) flavor symmetry/breaking. In three cases of the nonresonant decays, the light scalar meson resonant decays and the vector meson resonant decays, we will firstly construct the hadronic amplitude relations between different decay modes, use the available data to extract the hadronic amplitudes, then predict the not-yet-measured modes for further tests in experiments, and finally analyze the contributions with the non-resonance, the light scalar meson resonances and the vector meson resonances in the branching ratios.

This paper is organized as follows. In Sec. II, the expressions of the branching ratios are given. In Sec. III, we will give our numerical results of the $D\to P_{1}P_{2}\ell^{+}\nu$ decays with the nonresonant, the light scalar meson resonant and the vector meson resonant contributions. Our conclusions are given in Sec. IV.

II Theoretical frame

II.1 Decay branching ratios

The effective Hamiltonian for $c\to q_{i}\ell^{+}\nu_{\ell}$ transition can be written as

\displaystyle\mathcal{H}_{eff}(c\rightarrow q_{i}\ell^{+}\nu_{\ell})

\displaystyle=

\displaystyle\frac{G_{F}}{\sqrt{2}}V_{cq_{i}}\bar{q}_{i}\gamma^{\mu}(1-\gamma_{5})c\leavevmode\nobreak\ \bar{\nu}_{\ell}\gamma_{\mu}(1-\gamma_{5})\ell,

(1)

where $G_{F}$ is the Fermi constant, $V_{cq_{i}}$ is the CKM matrix element, and $q_{i}=d,s$ for $i=2,3$ . The decay amplitude of the $D(p)\to P_{1}(k_{1})P_{2}(k_{2})\ell^{+}(q_{1})\nu_{\ell}(q_{2})$ decay can be divided into leptonic and hadronic parts

	$\displaystyle\mathcal{A}(D\rightarrow P_{1}P_{2}\ell^{+}\nu_{\ell})$	$\displaystyle=$	$\displaystyle\langle P_{1}(k_{1})P_{2}(k_{2})\ell^{+}(q_{1})\nu_{\ell}(q_{2})\|\mathcal{H}_{eff}(c\rightarrow q_{i}\ell^{+}\nu_{\ell})\|D(p)\rangle$		(2)
		$\displaystyle=$	$\displaystyle\frac{G_{F}}{\sqrt{2}}V_{cq_{i}}L_{\mu}H^{\mu},$		(3)

where $L_{\mu}=\bar{\nu_{\ell}}\gamma_{\mu}(1-\gamma_{5})\ell$ is the leptonic charged current, and $H^{\mu}=\langle P_{1}(k_{1})P_{2}(k_{2})|\bar{s}/\bar{d}\gamma^{\mu}(1-\gamma_{5})c|D(p)\rangle$ is the hadronic matrix element. The leptonic part $L_{\mu}$ is calculable using the perturbation theory, while the hadronic part $H^{\mu}$ is encoded into the transition form factors. Following Refs. Boer:2016iez ; Faller:2013dwa , the $D\to P_{1}P_{2}$ form factors are given as

	$\displaystyle\langle P_{1}(k_{1})P_{2}(k_{2})\|\bar{s}/\bar{d}\gamma^{\mu}c\|D(p)\rangle$	$\displaystyle=$	$\displaystyle iF_{\perp}\frac{1}{\sqrt{k^{2}}}q^{\mu}_{\perp},$		(4)
	$\displaystyle-\langle P_{1}(k_{1})P_{2}(k_{2})\|\bar{s}/\bar{d}\gamma^{\mu}\gamma_{5}c\|D(p)\rangle$	$\displaystyle=$	$\displaystyle F_{t}\frac{q^{\mu}}{\sqrt{q^{2}}}+F_{0}\frac{2\sqrt{q^{2}}}{\sqrt{\lambda}}k^{\mu}_{0}+F_{\parallel}\frac{1}{\sqrt{k^{2}}}\bar{k}^{\mu}_{\parallel},$		(5)

with

$\displaystyle k^{\mu}_{0}$	$\displaystyle=$	$\displaystyle k^{\mu}-\frac{k\cdot q}{q^{2}}q^{\mu},$	(6)
$\displaystyle\bar{k}^{\mu}_{\parallel}$	$\displaystyle=$	$\displaystyle\bar{k}^{\mu}-\frac{4(k\cdot q)(q\cdot\bar{k})}{\lambda}k^{\mu}+\frac{4k^{2}(q\cdot\bar{k})}{\lambda}q^{\mu},$	(7)
$\displaystyle q^{\mu}_{\perp}$	$\displaystyle=$	$\displaystyle 2\epsilon^{\mu\alpha\beta\gamma}\frac{q_{\alpha}k_{\beta}\bar{k}_{\gamma}}{\sqrt{\lambda}},$	(8)

where $k\equiv k_{1}+k_{2}$ , $q\equiv q_{1}+q_{2}$ , $\bar{k}\equiv k_{1}-k_{2}$ , $\bar{q}\equiv q_{2}-q_{1}$ , and $\lambda=\lambda(m_{D}^{2},q^{2},k^{2})$ with $\lambda(a,b,c)=a^{2}+b^{2}+c^{2}-2ab-2bc-2ac$ .

In terms of the form factors, the differential branching ratio of the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays can be written as Boer:2016iez

\displaystyle\frac{d\mathcal{B}(D\to P_{1}P_{2}\ell^{+}\nu)_{N}}{dq^{2}\leavevmode\nobreak\ dk^{2}}=\frac{1}{2}\tau_{D}|\mathcal{N}|^{2}\beta_{\ell}(3-\beta_{\ell})|F_{A}|^{2},

(9)

with

	$\displaystyle\|\mathcal{N}\|^{2}$	$\displaystyle=$	$\displaystyle G_{F}^{2}\|V_{cq}\|^{2}\frac{\beta_{\ell}q^{2}\sqrt{\lambda(m_{D}^{2},q^{2},k^{2})}}{3\cdot 2^{10}\pi^{5}m_{D}^{3}}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{with}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \beta_{\ell}=1-\frac{m_{\ell}^{2}}{q^{2}},$
	$\displaystyle\|F_{A}\|^{2}$	$\displaystyle=$	$\displaystyle\|F_{0}\|^{2}+\frac{2}{3}(\|F_{\parallel}\|^{2}+\|F_{\perp}\|^{2})+\frac{3m_{\ell}^{2}}{q^{2}(3-\beta_{\ell})}\|F_{t}\|^{2},$		(10)

where $\tau_{M}$ ( $m_{M}$ ) is lifetime(mass) of $M$ particle. In this work, we ignore the small contributions of the $|F_{t}|^{2}$ term, which is proportional to $m_{\ell}^{2}$ . The corresponding limits of integration are given by $(m_{P_{1}}+m_{P_{2}})^{2}\leq k^{2}\leq(m_{D_{q}}-m_{\ell})^{2}$ and $m_{\ell}^{2}\leq q^{2}\leq(m_{D_{q}}-\sqrt{k^{2}})^{2}$ . The calculations of the form factors $F_{0},\leavevmode\nobreak\ F_{\parallel},\leavevmode\nobreak\ F_{\perp}$ , and $F_{t}$ are quite complicated, and their specific expressions in the QCD factorization limit can be found in Ref. Boer:2016iez . Nevertheless, we will not use the specific expressions in this work, and we will relate the different hadronic decay amplitudes or the different form factors between different decay modes by the SU(3) flavor symmetry/breaking, which are discussed in later Sec. II.3.

Except for the nonresonant $D\rightarrow P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays, the resonant $D\to R(R\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays with the scalar( $R=S$ ) resonance and the vector( $R=V$ ) resonance are also studied in this work. In the case of the decay widths of the resonances are very narrow, the resonant decay branching ratios respect a simple factorization relation

\displaystyle\mathcal{B}(D\to R\ell^{+}\nu_{\ell},R\to P_{1}P_{2})=\mathcal{B}(D\to R\ell^{+}\nu_{\ell})\times\mathcal{B}(R\to P_{1}P_{2}),

(11)

and this result is also a good approximation for wider resonances. Above Eq. (11) will be used in our analysis for the scalar resonant $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays and the vector resonant $D\to V(V\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays in Secs. III.2 and III.3, respectively. Relevant $\mathcal{B}(D\to R\ell^{+}\nu_{\ell})$ and $\mathcal{B}(R\to P_{1}P_{2})$ are also obtained by the SU(3) flavor symmetry in our later analysis.

II.2 Meson multiplets

Before giving the hadronic amplitudes based on the SU(3) flavor analysis, we will collect the representations for the multiplets of the SU(3) flavor group first in this subsection.

Charmed mesons containing one heavy $c$ quark are flavor SU(3) antitriplets

\displaystyle D_{i}=\Big{(}D^{0}(c\bar{u}),\leavevmode\nobreak\ D^{+}(c\bar{d}),\leavevmode\nobreak\ D^{+}_{s}(c\bar{s})\Big{)}.

(12)

Light pseudoscalar meson ( $P$ ) and vector meson ( $V$ ) octets and singlets under the SU(3) flavor symmetry of light $u,d,s$ quarks are He:2018joe

	$\displaystyle P$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{ccc}\frac{\pi^{0}}{\sqrt{2}}+\frac{\eta_{8}}{\sqrt{6}}+\frac{\eta_{1}}{\sqrt{3}}&\pi^{+}&K^{+}\\ \pi^{-}&-\frac{\pi^{0}}{\sqrt{2}}+\frac{\eta_{8}}{\sqrt{6}}+\frac{\eta_{1}}{\sqrt{3}}&K^{0}\\ K^{-}&\overline{K}^{0}&-\frac{2\eta_{8}}{\sqrt{6}}+\frac{\eta_{1}}{\sqrt{3}}\end{array}\right)\,,$		(16)
	$\displaystyle V$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{ccc}\frac{\rho^{0}}{\sqrt{2}}+\frac{\omega}{\sqrt{2}}&\rho^{+}&K^{+}\\ \rho^{-}&-\frac{\rho^{0}}{\sqrt{2}}+\frac{\omega}{\sqrt{2}}&K^{0}\\ K^{-}&\overline{K}^{0}&\phi\end{array}\right)\,,$		(20)

where the $\eta$ and $\eta^{\prime}$ are mixtures of $\eta_{1}=\frac{u\bar{u}+d\bar{d}+s\bar{s}}{\sqrt{3}}$ and $\eta_{8}=\frac{u\bar{u}+d\bar{d}-2s\bar{s}}{\sqrt{6}}$ with the mixing angle $\theta_{P}$

\displaystyle\left(\begin{array}[]{c}\eta\\ \eta^{\prime}\end{array}\right)\,=\left(\begin{array}[]{cc}\mbox{cos}\theta_{P}&-\mbox{sin}\theta_{P}\\ \mbox{sin}\theta_{P}&\mbox{cos}\theta_{P}\end{array}\right)\,\left(\begin{array}[]{c}\eta_{8}\\ \eta_{1}\end{array}\right)\,.

(27)

And $\theta_{P}=[-20^{\circ},-10^{\circ}]$ from the Particle Data Group (PDG) PDG2022 will be used in our numerical analysis.

The structures of the light scalar mesons are not fully understood yet. Many suggestions are discussed, such as ordinary two-quark state, four-quark state, meson-meson bound state, molecular state, glueball state, or hybrid state; for examples, see Refs. Dai:2018fmx ; Maiani:2004uc ; tHooft:2008rus ; Pelaez:2003dy ; Sun:2010nv ; Oller:1997ti ; Baru:2003qq ; Cheng:2005nb ; Achasov:1996ei . In this work, we will consider the two-quark and the four-quark scenarios for the scalar mesons below or near 1 GeV. In the two-quark picture, the light scalar mesons can be written as Momeni:2022gqb

\displaystyle S

\displaystyle=

\displaystyle\left(\begin{array}[]{ccc}\frac{a^{0}_{0}}{\sqrt{2}}+\frac{\sigma}{\sqrt{2}}&a^{+}_{0}&K^{+}_{0}\\ a_{0}^{-}&-\frac{a_{0}^{0}}{\sqrt{2}}+\frac{\sigma}{\sqrt{2}}&K^{0}_{0}\\ K^{-}_{0}&\overline{K}^{0}_{0}&f_{0}\end{array}\right)\,.

(31)

The two isoscalars $f_{0}(980)$ and $f_{0}(500)$ are obtained by the mixing of $\sigma=\frac{u\bar{u}+d\bar{d}}{\sqrt{2}}$ and $f_{0}=s\bar{s}$ ,

\displaystyle\left(\begin{array}[]{c}f_{0}(980)\\ f_{0}(500)\end{array}\right)\,=\left(\begin{array}[]{cc}\mbox{cos}\theta_{S}&\mbox{sin}\theta_{S}\\ -\mbox{sin}\theta_{S}&\mbox{cos}\theta_{S}\end{array}\right)\,\left(\begin{array}[]{c}f_{0}\\ \sigma\end{array}\right)\,,

(38)

where the three possible ranges of the mixing angle $\theta_{S}$ Cheng:2005nb ; LHCb:2013dkk , $25^{\circ}<\theta_{S}<40^{\circ}$ , $140^{\circ}<\theta_{S}<165^{\circ}$ and $\leavevmode\nobreak\ -30^{\circ}<\theta_{S}<30^{\circ}$ will be analyzed in our numerical results. In the four-quark picture, the light scalar mesons are given as Jaffe:1976ig ; PDG2022

	$\displaystyle\sigma=u\bar{u}d\bar{d},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ f_{0}=(u\bar{u}+d\bar{d})s\bar{s}/\sqrt{2},$
	$\displaystyle a^{0}_{0}=(u\bar{u}-d\bar{d})s\bar{s}/\sqrt{2},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ a^{+}_{0}=u\bar{d}s\bar{s},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ a^{-}_{0}=d\bar{u}s\bar{s},$
	$\displaystyle K^{+}_{0}=u\bar{s}d\bar{d},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ K^{0}_{0}=d\bar{s}u\bar{u},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \overline{K}^{0}_{0}=s\bar{d}u\bar{u},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ K^{-}_{0}=s\bar{u}d\bar{d},$		(39)

and the two isoscalars are expressed as

\displaystyle\left(\begin{array}[]{c}f_{0}(980)\\ f_{0}(500)\end{array}\right)\,=\left(\begin{array}[]{cc}\mbox{cos}\phi_{S}&\mbox{sin}\phi_{S}\\ -\mbox{sin}\phi_{S}&\mbox{cos}\phi_{S}\end{array}\right)\,\left(\begin{array}[]{c}f_{0}\\ \sigma\end{array}\right)\,,

(46)

where the constrained mixing angle $\phi_{S}=(174.6^{+3.4}_{-3.2})^{\circ}$ Maiani:2004uc .

II.3 Nonresonant hadronic amplitudes

Since the hadronic amplitudes of the semileptonic $D\to V/S\ell^{+}\nu_{\ell}$ decays based on the SU(3) flavor symmetry/breaking have been discussed in Ref. Wang:D2MlvSU3 , we will focus on the hadronic amplitudes of the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays in this subsection.

In terms of the SU(3) flavor symmetry, the quark current $\bar{q}_{i}\gamma^{\mu}(1-\gamma_{5})c$ can be expressed as a SU(3) flavor anti-triplet $(\bar{3})$ , and the effective Hamiltonian in Eq. (1) is transformed as Geng:2017mxn

\displaystyle\mathcal{H}_{eff}(c\rightarrow q_{i}\ell^{+}\nu_{\ell})

\displaystyle=

\displaystyle\frac{G_{F}}{\sqrt{2}}H(\bar{3})\leavevmode\nobreak\ \bar{\nu}_{\ell}\gamma_{\mu}(1-\gamma_{5})\ell,

(47)

with $H(\bar{3})=(0,V_{cd},V_{cs})$ . The decay amplitude of the nonresonant $D\rightarrow P_{1}P_{2}\ell^{+}\nu_{\ell}$ decay can be written as

\displaystyle\mathcal{A}(D\rightarrow P_{1}P_{2}\ell^{+}\nu_{\ell})_{N}=\frac{G_{F}}{\sqrt{2}}H(D\to P_{1}P_{2})_{N}\leavevmode\nobreak\ \bar{\nu}_{\ell}\gamma_{\mu}(1-\gamma_{5})\ell,

(48)

and the hadronic amplitude $H(D\to P_{1}P_{2})_{N}$ can be parameterized as

\displaystyle H(D\to P_{1}P_{2})_{N}=c_{10}D_{i}P^{i}_{j}P^{j}_{k}H(\bar{3})^{k}+c_{20}D_{i}P^{i}_{j}H(\bar{3})^{j}P^{k}_{k}+c_{30}D_{i}H(\bar{3})^{i}P^{j}_{k}P^{k}_{j}+c_{40}D_{i}H(\bar{3})^{i}P^{k}_{k}P^{j}_{j},

(49)

where $c_{i0}(i=1,2,3,4)$ are the nonperturbative coefficients under the SU(3) flavor symmetry. Feynman diagrams for the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays are displayed in Fig. 1.

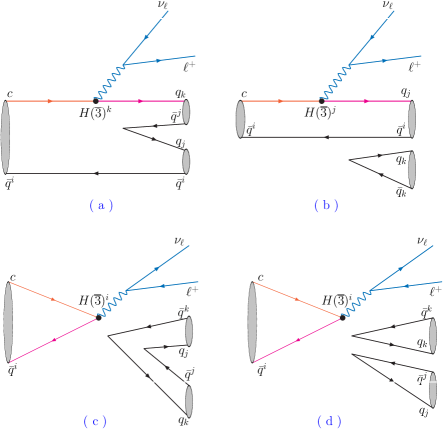
Refer to caption — Figure 1: Diagrams of the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays.

SU(3) flavor breaking effects come from different masses of $u$ , $d$ and $s$ quarks, and they will become useful once we have measurements of several $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays that are precise enough to see deviations from the SU(3) flavor symmetry. The diagonalized mass matrix can be expressed as Xu:2013dta ; He:2014xha

\displaystyle\left(\begin{array}[]{ccc}m_{u}&0&0\\ 0&m_{d}&0\\ 0&0&m_{s}\end{array}\right)=\frac{1}{3}(m_{u}+m_{d}+m_{s})I+\frac{1}{2}(m_{u}-m_{d})X+\frac{1}{6}(m_{u}+m_{d}-2m_{s})W,

(53)

with

\displaystyle X=\left(\begin{array}[]{ccc}1&0&0\\ 0&-1&0\\ 0&0&0\end{array}\right),\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ W=\left(\begin{array}[]{ccc}1&0&0\\ 0&1&0\\ 0&0&-2\end{array}\right).

(60)

Compared with $s$ quark mass, the $u$ and $d$ quark masses are much smaller which can be ignored. The SU(3) flavor breaking effects due to a nonzero $s$ quark mass dominate the SU(3) breaking effects. When $u$ and $d$ quark mass difference is ignored, the residual SU(3) flavor symmetry becomes the isospin symmetry and the term proportional to $X$ can be dropped. The identity $I$ part contributes to the $D\rightarrow P_{1}P_{2}\ell^{+}\nu_{\ell}$ decay amplitudes in a similar way as that given in Eq. (48) which can be absorbed into the coefficients $c_{i0}$ . Only the $W$ part will contribute to the SU(3) breaking effects. The SU(3) breaking contributions to the hadronic amplitudes due to the fact of $m_{s}\gg m_{u,d}$ are

$\displaystyle\Delta H(D\to P_{1}P_{2})_{N}$	$\displaystyle=$	$\displaystyle c_{11}D_{i}W^{i}_{a}P^{a}_{j}P^{j}_{k}H(\bar{3})^{k}+c_{12}D_{i}P^{i}_{j}W^{j}_{a}P^{a}_{k}H(\bar{3})^{k}+c_{13}D_{i}P^{i}_{j}P^{j}_{k}W^{k}_{a}H(\bar{3})^{a}$	(61)
	$\displaystyle+$	$\displaystyle c_{21}D_{i}W^{i}_{a}P^{a}_{j}H(\bar{3})^{j}P^{k}_{k}+c_{22}D_{i}P^{i}_{j}W^{j}_{a}H(\bar{3})^{a}P^{k}_{k}$
	$\displaystyle+$	$\displaystyle c_{31}D_{i}W^{i}_{a}H(\bar{3})^{a}P^{j}_{k}P^{k}_{j}+c_{32}D_{i}H(\bar{3})^{i}P^{j}_{k}W^{k}_{a}P^{a}_{j}$
	$\displaystyle+$	$\displaystyle c_{41}D_{i}W^{i}_{a}H(\bar{3})^{a}P^{k}_{k}P^{j}_{j},$

where $c_{ij}\leavevmode\nobreak\ (i,j=1,2,3,4)$ are the nonperturbative SU(3) flavor breaking coefficients.

Full hadronic amplitudes of the different nonresonant $D\to P_{1}P_{2}\ell^{+}\nu$ decays and their relations under the SU(3) flavor symmetry/breaking are given in Sec. III.1.

III Numerical results of the $D\to P_{1}P_{2}\ell^{+}\nu$ decays

The branching ratios with the nonresonant contributions, the light scalar meson resonant contributions and the vector meson resonant contributions will be analyzed in this section. If not specially specified, the theoretical input parameters, such as the lifetimes and the masses, and the experimental data within the $2\sigma$ error bars from PDG PDG2022 will be used in our numerical analysis.

III.1 Nonresonant $D\to P_{1}P_{2}\ell^{+}\nu$ decays

The hadronic amplitudes of the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays including both the SU(3) flavor symmetry and the SU(3) flavor breaking terms are summarized in the second column of Tab. 1, in which we can see the relations of different hadronic amplitudes. The following relations are held in both the SU(3) flavor symmetry and the SU(3) flavor breaking due to a strange quark mass:

$\displaystyle H(D^{0}\to\pi^{-}\overline{K}^{0}\ell^{+}\nu_{\ell})_{N}$	$\displaystyle=$	$\displaystyle H(D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell})_{N}=\sqrt{2}H(D^{0}\to\pi^{0}K^{-}\ell^{+}\nu_{\ell})_{N}=-\sqrt{2}H(D^{+}\to\pi^{0}\overline{K}^{0}\ell^{+}\nu_{\ell})_{N},$
$\displaystyle H(D^{0}\to\eta_{8}K^{-}\ell^{+}\nu_{\ell})_{N}$	$\displaystyle=$	$\displaystyle H(D^{+}\to\eta_{8}\overline{K}^{0}\ell^{+}\nu_{\ell})_{N},$
$\displaystyle H(D^{0}\to\eta_{1}K^{-}\ell^{+}\nu_{\ell})_{N}$	$\displaystyle=$	$\displaystyle H(D^{+}\to\eta_{1}\overline{K}^{0}\ell^{+}\nu_{\ell})_{N},$
$\displaystyle H(D^{+}_{s}\to K^{+}K^{-}\ell^{+}\nu_{\ell})_{N}$	$\displaystyle=$	$\displaystyle H(D^{+}_{s}\to K^{0}\overline{K}^{0}\ell^{+}\nu_{\ell})_{N},$
$\displaystyle H(D^{0}\to K^{-}K^{0}\ell^{+}\nu_{\ell})_{N}$	$\displaystyle=$	$\displaystyle H(D^{+}\to\overline{K}^{0}K^{0}\ell^{+}\nu_{\ell})_{N}-H(D^{+}\to K^{+}K^{-}\ell^{+}\nu_{\ell})_{N},$
$\displaystyle H(D^{+}_{s}\to K^{+}\pi^{-}\ell^{+}\nu_{\ell})_{N}$	$\displaystyle=$	$\displaystyle-\sqrt{2}H(D^{+}_{s}\to K^{0}\pi^{0}\ell^{+}\nu_{\ell})_{N}.$	(62)

Table 1: The hadronic amplitudes for the

D\to P_{1}P_{2}\ell^{+}\nu_{\ell}

decays.

C_{1}\equiv c_{10}+c_{11}+c_{12}-2c_{13}

C_{2}\equiv c_{20}+c_{21}-2c_{22}

C_{3}\equiv c_{30}-2c_{31}

C_{4}\equiv c_{40}-2c_{41}

, and

[C^{{}^{\prime},^{\prime\prime}}]_{R}

denotes the contributions come from the decays with

R

resonances.

Decay modes	Nonresonant hadronic amplitudes	Scalar resonant ones	Vector resonant ones
$c\to s\ell^{+}\nu_{\ell}$ :
$D^{0}\to\pi^{-}\overline{K}^{0}\ell^{+}\nu_{\ell}$	$C_{1}$	$\big{[}C^{\prime}_{1}\big{]}_{K^{-}_{0}}$	$\big{[}C^{\prime\prime}_{1}\big{]}_{K^{*-}}$
$D^{0}\to\pi^{0}K^{-}\ell^{+}\nu_{\ell}$	$\frac{1}{\sqrt{2}}C_{1}$	$\big{[}\frac{1}{\sqrt{2}}C^{\prime}_{1}\big{]}_{K^{-}_{0}}$	$\big{[}\frac{1}{\sqrt{2}}C^{\prime\prime}_{1}\big{]}_{K^{*-}}$
$D^{0}\to\eta_{8}K^{-}\ell^{+}\nu_{\ell}$	$-\frac{1}{\sqrt{6}}C_{1}$ $+\sqrt{6}c_{12}$	$\cdots$	$\cdots$
$D^{0}\to\eta_{1}K^{-}\ell^{+}\nu_{\ell}$	$\frac{2}{\sqrt{3}}\big{(}C_{1}+\frac{3}{2}C_{2}\big{)}$ $-\sqrt{3}c_{12}$	$\cdots$	$\cdots$
$D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell}$	$C_{1}$	$\big{[}C^{\prime}_{1}\big{]}_{\overline{K}^{0}_{0}}$	$\big{[}C^{\prime\prime}_{1}\big{]}_{K^{*0}}$
$D^{+}\to\pi^{0}\overline{K}^{0}\ell^{+}\nu_{\ell}$	$-\frac{1}{\sqrt{2}}C_{1}$	$\big{[}\frac{1}{\sqrt{2}}C^{\prime}_{1}\big{]}_{\overline{K}^{0}_{0}}$	$\big{[}\frac{1}{\sqrt{2}}C^{\prime\prime}_{1}\big{]}_{K^{*0}}$
$D^{+}\to\eta_{8}\overline{K}^{0}\ell^{+}\nu_{\ell}$	$-\frac{1}{\sqrt{6}}C_{1}$ $+\sqrt{6}c_{12}$	$\cdots$	$\cdots$
$D^{+}\to\eta_{1}\overline{K}^{0}\ell^{+}\nu_{\ell}$	$\frac{2}{\sqrt{3}}\big{(}C_{1}+\frac{3}{2}C_{2}\big{)}$ $-\sqrt{3}c_{12}$	$\cdots$	$\cdots$
$D^{+}_{s}\to K^{+}K^{-}\ell^{+}\nu_{\ell}$	$C_{1}+2C_{3}$ $-3c_{11}-c_{32}$	$\big{[}cos^{2}\theta_{S}\leavevmode\nobreak\ C^{\prime}_{1}\big{]}_{f_{0}(980)}$	$\big{[}C^{\prime\prime}_{1}\big{]}_{\phi}$
$D^{+}_{s}\to K^{0}\overline{K}^{0}\ell^{+}\nu_{\ell}$	$C_{1}+2C_{3}$ $-3c_{11}-c_{32}$	$\big{[}cos^{2}\theta_{S}\leavevmode\nobreak\ C^{\prime}_{1}\big{]}_{f_{0}(980)}$	$\big{[}C^{\prime\prime}_{1}\big{]}_{\phi}$
$D^{+}_{s}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell}$	$\sqrt{2}C_{3}$ $+\sqrt{2}c_{32}$	${}^{\big{[}sin\theta_{S}cos\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(980)}}_{\big{[}-sin\theta_{S}cos\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(500)}}$	$\cdots$
$D^{+}_{s}\to\pi^{+}\pi^{-}\ell^{+}\nu_{\ell}$	$2(C_{3}+c_{32})$	${}^{\big{[}\sqrt{2}sin\theta_{S}cos\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(980)}}_{\big{[}-\sqrt{2}sin\theta_{S}cos\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(500)}}$	$\cdots$
$D^{+}_{s}\to\eta_{8}\eta_{8}\ell^{+}\nu_{\ell}$	$\frac{2\sqrt{2}}{3}\big{(}C_{1}+\frac{3}{2}C_{3}\big{)}$ $-\sqrt{2}\big{(}2c_{11}+2c_{12}+c_{32}\big{)}$	$\cdots$	$\cdots$
$D^{+}_{s}\to\eta_{1}\eta_{1}\ell^{+}\nu_{\ell}$	$\frac{\sqrt{2}}{3}(C_{1}+3C_{2}+3C_{3}+9C_{4})$ $-\sqrt{2}(c_{11}+c_{12}+3c_{21})$	$\cdots$	$\cdots$
$D^{+}_{s}\to\eta_{8}\eta_{1}\ell^{+}\nu_{\ell}$	$-\frac{2\sqrt{2}}{3}\big{(}C_{1}+\frac{3}{2}C_{2}\big{)}$ $+2\sqrt{2}(c_{11}+c_{12}+\frac{3}{2}c_{21}+c_{32})$	$\cdots$	$\cdots$
$c\to d\ell^{+}\nu_{\ell}$ :
$D^{0}\to K^{-}K^{0}\ell^{+}\nu_{\ell}$	$C_{1}$ $-3(c_{12}-c_{13})$	$\big{[}C^{\prime}_{1}\big{]}_{a_{0}(980)}$	$\cdots$
$D^{0}\to\pi^{0}\pi^{-}\ell^{+}\nu_{\ell}$	$\cdots$	$\cdots$	$\big{[}\frac{1}{\sqrt{2}}C^{\prime\prime}_{1}\big{]}_{\rho^{-}}$
$D^{0}\to\eta_{8}\pi^{-}\ell^{+}\nu_{\ell}$	$\sqrt{\frac{2}{3}}C_{1}$ $+\sqrt{6}c_{13}$	[ $\sqrt{\frac{2}{3}}C^{\prime}_{1}\big{]}_{a_{0}(980)}$	$\big{[}\frac{1}{\sqrt{6}}C^{\prime\prime}_{1}\big{]}_{\rho^{-}}$
$D^{0}\to\eta_{1}\pi^{-}\ell^{+}\nu_{\ell}$	$\frac{2}{\sqrt{3}}\big{(}C_{1}+\frac{3}{2}C_{2}\big{)}$ $+\sqrt{3}(2c_{13}+3c_{22})$	$\big{[}\frac{2}{\sqrt{3}}C^{\prime}_{1}\big{]}_{a_{0}(980)}$	$\big{[}\frac{1}{\sqrt{3}}C^{\prime\prime}_{1}\big{]}_{\rho^{-}}$
$D^{+}\to\overline{K}^{0}K^{0}\ell^{+}\nu_{\ell}$	$C_{1}+2C_{3}$ $-3(c_{12}-c_{13}-2c_{31})-c_{32}$	${}^{\big{[}\frac{1}{2}C^{\prime}_{1}\big{]}_{a_{0}(980)}}_{\big{[}\frac{1}{\sqrt{2}}sin\theta_{S}cos\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(980)}}$	$\cdots$
$D^{+}\to K^{+}K^{-}\ell^{+}\nu_{\ell}$	$2C_{3}$ $+6c_{31}-c_{32}$	${}^{\big{[}-\frac{1}{2}C^{\prime}_{1}\big{]}_{a_{0}(980)}}_{\big{[}\frac{1}{\sqrt{2}}sin\theta_{S}cos\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(980)}}$	$\cdots$
$D^{+}\to\pi^{+}\pi^{-}\ell^{+}\nu_{\ell}$	$C_{1}+2C_{3}$ $+3c_{13}+6c_{31}+2c_{32}$	${}^{\big{[}sin^{2}\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(980)}}_{\big{[}cos^{2}\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(500)}}$	$\big{[}\frac{1}{2}C^{\prime\prime}_{1}\big{]}_{\rho^{0},\omega}$
$D^{+}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell}$	$\frac{1}{\sqrt{2}}(C_{1}+2C_{3})$ $+\frac{1}{\sqrt{2}}(3c_{13}+6c_{31}+2c_{32})$	${}^{\big{[}\frac{1}{\sqrt{2}}sin^{2}\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(980)}}_{\big{[}\frac{1}{\sqrt{2}}cos^{2}\theta_{S}C^{\prime}_{1}\big{]}_{f_{0}(500)}}$	$\cdots$
$D^{+}\to\eta_{8}\pi^{0}\ell^{+}\nu_{\ell}$	$-\frac{1}{\sqrt{3}}\big{(}C_{1}+C_{2}\big{)}$ $-\sqrt{3}\big{(}c_{13}+c_{22}\big{)}$	$\big{[}-\frac{1}{\sqrt{6}}C^{\prime}_{1}\big{]}_{a_{0}(980)}$	$\cdots$
$D^{+}\to\eta_{1}\pi^{0}\ell^{+}\nu_{\ell}$	$-\sqrt{\frac{2}{3}}\big{(}C_{1}+C_{2}\big{)}$ $-\frac{1}{\sqrt{6}}\big{(}6c_{13}+9c_{22}\big{)}$	$\big{[}-\frac{1}{\sqrt{3}}C^{\prime}_{1}\big{]}_{a_{0}(980)}$	$\cdots$
$D^{+}\to\eta_{8}\eta_{8}\ell^{+}\nu_{\ell}$	$\frac{\sqrt{2}}{6}\big{(}C_{1}+6C_{3}\big{)}$ $+\frac{1}{\sqrt{2}}(c_{13}+6c_{31}-2c_{32})$	$\cdots$	$\cdots$
$D^{+}\to\eta_{1}\eta_{1}\ell^{+}\nu_{\ell}$	$\frac{\sqrt{2}}{3}(C_{1}+3C_{2}+3C_{3}+9C_{4})+\sqrt{2}(c_{13}+3c_{22}+3c_{31}+9c_{41})$	$\cdots$	$\cdots$
$D^{+}\to\eta_{8}\eta_{1}\ell^{+}\nu_{\ell}$	$\frac{\sqrt{2}}{3}\big{(}C_{1}+\frac{3}{2}C_{2}\big{)}$ $+\sqrt{2}\big{(}c_{13}+\frac{3}{2}c_{22}+2c_{32}\big{)}$	$\cdots$	$\cdots$
$D^{+}_{s}\to K^{+}\pi^{-}\ell^{+}\nu_{\ell}$	$C_{1}$ $-3c_{11}+3c_{13}$	$\big{[}C^{\prime}_{1}\big{]}_{K^{0}_{0}}$	$\big{[}C^{\prime\prime}_{1}\big{]}_{K^{*0}}$
$D^{+}_{s}\to K^{0}\pi^{0}\ell^{+}\nu_{\ell}$	$-\frac{1}{\sqrt{2}}C_{1}$ $-\frac{1}{\sqrt{2}}(-3c_{11}+3c_{13})$	$\big{[}-\frac{1}{\sqrt{2}}C^{\prime}_{1}\big{]}_{K^{0}_{0}}$	$\big{[}\frac{1}{\sqrt{2}}C^{\prime\prime}_{1}\big{]}_{K^{*0}}$
$D^{+}_{s}\to\eta_{8}K^{0}\ell^{+}\nu_{\ell}$	$-\frac{1}{\sqrt{6}}C_{1}$ $+\frac{1}{\sqrt{6}}\big{(}3c_{11}+6c_{12}-3c_{13}\big{)}$	$\cdots$	$\cdots$
$D^{+}_{s}\to\eta_{1}K^{0}\ell^{+}\nu_{\ell}$	$\frac{2}{\sqrt{3}}\big{(}C_{1}+\frac{3}{2}C_{2}\big{)}$ $-\sqrt{3}\big{(}2c_{11}+c_{12}-2c_{13}+3c_{21}-3c_{22}\big{)}$	$\cdots$	$\cdots$

If assuming the SU(3) flavor breaking effects are small and can be ignored, more amplitude relations will be obtained. Moreover, as shown in Fig. 1, the SU(3) flavor symmetry contributions of Fig. 1 (b-d) are suppressed by the Okubo-Zweig-Iizuka (OZI) rule Okubo:1963fa ; Lipkin:1986bi ; Lipkin:1996ny . If ignoring both the OZI suppressed SU(3) flavor symmetry contributions and the SU(3) flavor breaking contributions, almost all hadronic amplitudes of the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays can be related by the coefficient $c_{10}$ .

Since the leptonic charged current $\bar{\nu}_{\ell}\gamma_{\mu}(1-\gamma_{5})\ell$ is the SU(3) flavor singlet, and it is completely generic between different decay modes with certain $\ell=e$ or $\mu$ . The same relations as the hadronic amplitudes listed in Tab. 1 are valid in the decay amplitudes of the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays and the form factors of the $D\to P_{1}P_{2}$ transitions. For the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays, only $\mathcal{B}(D^{+}\to\pi^{+}K^{-}\mu^{+}\nu_{\mu})_{N}$ has been measured, and $\mathcal{B}(D^{+}\to\pi^{+}K^{-}e^{+}\nu_{e})_{N}$ has been upper limited. Because the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays have not been measured enough to reveal the OZI suppressed SU(3) flavor symmetry contributions and the SU(3) symmetry breaking effects, we ignore both of them in our analysis, and then almost all hadronic amplitudes, form factors or decay amplitudes can be related by the SU(3) flavor symmetry coefficient $c_{10}$ . The simple relations associated by the coefficient $c_{10}$ for $F_{A}$ given in Eq. (10) will be used to obtain our numerical results. Note that, for consistency, only the SU(3) flavor symmetry contributions will be considered in the light scalar meson resonant $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays and the vector meson resonant $D\to V(V\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays in Sec. III.2 and Sec. III.3, respectively.

The experimental data of $\mathcal{B}(D^{+}\to\pi^{+}K^{-}\mu^{+}\nu_{\mu})_{N}$ within $2\sigma$ errors and the upper limit of $\mathcal{B}(D^{+}\to\pi^{+}K^{-}e^{+}\nu_{e})_{N}$ at 90% confidence level from PDG PDG2022 are listed in the second column of Tab. 2, which will be used to determine $c_{10}$ in the nonresonant $D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell}$ decays, and we obtain $|c_{01}|=12.95\pm 3.75$ after considering $2\sigma$ theoretical and experimental errors. Then many other branching ratios of the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays can be predicted by using the constrained $c_{10}$ from the data of $\mathcal{B}(D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell})_{N}$ listed in the second column of Tab. 2. Our predictions are listed in the third column of Tab. 2 for the $c\to s\ell^{+}\nu_{\ell}$ transitions and in the second column of Tab. 3 for the $c\to d\ell^{+}\nu_{\ell}$ transitions.

From Tabs. 2-3, one can see that many branching ratios of the nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays, such as $\mathcal{B}(D^{0}\to\pi^{-}\overline{K}^{0}\ell^{+}\nu_{\ell})_{N}$ , $\mathcal{B}(D^{0}\to\pi^{0}K^{-}\ell^{+}\nu_{\ell})_{N}$ , $\mathcal{B}(D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell})_{N}$ , $\mathcal{B}(D^{+}\to\pi^{0}\overline{K}^{0}\ell^{+}\nu_{\ell})_{N}$ , $\mathcal{B}(D^{+}_{s}\to K^{+}K^{-}\ell^{+}\nu_{\ell})_{N}$ , $\mathcal{B}(D^{+}_{s}\to K^{0}\overline{K}^{0}\ell^{+}\nu_{\ell})_{N}$ , $\mathcal{B}(D^{+}\to\pi^{+}\pi^{-}\ell^{+}\nu_{\ell})_{N}$ and $\mathcal{B}(D^{+}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell})_{N}$ , are on the orders of $\mathcal{O}(10^{-3}-10^{-4})$ , which could be measured by the BESIII, LHCb, and BelleII experiments. Nevertheless, for other decays, for example, the nonresonant $D\to\eta P\ell^{+}\nu_{\ell}$ decays, are strongly suppressed by the narrow phase spaces, the mixing angle $\theta_{P}$ , or the CKM matrix element $V_{cd}$ , their branching ratios are on the orders of $\mathcal{O}(10^{-5}-10^{-7})$ , and many of them might be observed by the BESIII and Belle II experiments in the near future.

Table 2: The experimental data and the SU(3) flavor symmetry predictions of the nonresonant branching ratios and the total branching ratios of the

D\to P_{1}P_{2}\ell^{+}\nu_{\ell}

decays with the

c\to s\ell^{+}\nu_{\ell}

transitions within the

2\sigma

errors. The experimental data are taken from PDG PDG2022 , ‘N’ denotes the nonresonant contributions, and ‘T’ denotes the total contributions including the non-resonance, the light scalar meson resonances as well as the vector meson resonances. The same below.

Branching ratios	Exp. data with N	Ones with N	Exp. data with T	Ones with T
$\mathcal{B}(D^{0}\to\pi^{-}\overline{K}^{0}e^{+}\nu_{e})(\times 10^{-2})$	$\cdots$	$0.076\pm 0.041$	$1.44\pm 0.08$	$1.57\pm 0.14$
$\mathcal{B}(D^{0}\to\pi^{0}K^{-}e^{+}\nu_{e})(\times 10^{-2})$	$\cdots$	$0.039\pm 0.021$	$1.6^{+2.6}_{-1.0}$	$0.80\pm 0.07$
$\mathcal{B}(D^{0}\to\eta K^{-}e^{+}\nu_{e})(\times 10^{-6})$	$\cdots$	$3.51\pm 3.51$	$\cdots$	$3.51\pm 3.51$
$\mathcal{B}(D^{0}\to\eta^{\prime}K^{-}e^{+}\nu_{e})(\times 10^{-6})$	$\cdots$	$4.03\pm 2.17$	$\cdots$	$4.03\pm 2.17$
$\mathcal{B}(D^{+}\to\pi^{+}K^{-}e^{+}\nu_{e})(\times 10^{-2})$	$<0.7$	$0.20\pm 0.10$	$4.02\pm 0.36$	$4.06\pm 0.30$
$\mathcal{B}(D^{+}\to\pi^{0}\overline{K}^{0}e^{+}\nu_{e})(\times 10^{-2})$	$\cdots$	$0.100\pm 0.052$	$\cdots$	$2.01\pm 0.15$
$\mathcal{B}(D^{+}\to\eta\overline{K}^{0}e^{+}\nu_{e})(\times 10^{-5})$	$\cdots$	$0.89\pm 0.89$	$\cdots$	$0.89\pm 0.89$
$\mathcal{B}(D^{+}\to\eta^{\prime}\overline{K}^{0}e^{+}\nu_{e})(\times 10^{-5})$	$\cdots$	$1.03\pm 0.55$	$\cdots$	$1.03\pm 0.55$
$\mathcal{B}(D^{+}_{s}\to K^{+}K^{-}e^{+}\nu_{e})(\times 10^{-2})$	$\cdots$	$0.034\pm 0.018$	$\cdots$	$1.27\pm 0.13$
$\mathcal{B}(D^{+}_{s}\to K^{0}\overline{K}^{0}e^{+}\nu_{e})(\times 10^{-3})$	$\cdots$	$0.33\pm 0.18$	$\cdots$	$8.58\pm 0.95$
$\mathcal{B}(D^{+}_{s}\to\pi^{+}\pi^{-}e^{+}\nu_{e})(\times 10^{-3})$	$\cdots$	$\cdots$	$\cdots$	$1.47\pm 0.79$
$\mathcal{B}(D^{+}_{s}\to\pi^{0}\pi^{0}e^{+}\nu_{e})(\times 10^{-4})$	$\cdots$	$\cdots$	$\cdots$	$8.58\pm 3.50$
$\mathcal{B}(D^{+}_{s}\to\eta\eta e^{+}\nu_{e})(\times 10^{-4})$	$\cdots$	$0.56\pm 0.49$	$\cdots$	$0.56\pm 0.49$
$\mathcal{B}(D^{+}_{s}\to\eta\eta^{\prime}e^{+}\nu_{e})(\times 10^{-6})$	$\cdots$	$5.38\pm 3.19$	$\cdots$	$5.38\pm 3.19$
$\mathcal{B}(D^{0}\to\pi^{-}\overline{K}^{0}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$\cdots$	$0.073\pm 0.039$	$\cdots$	$1.47\pm 0.13$
$\mathcal{B}(D^{0}\to\pi^{0}K^{-}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$\cdots$	$0.038\pm 0.020$	$\cdots$	$0.75\pm 0.07$
$\mathcal{B}(D^{0}\to\eta K^{-}\mu^{+}\nu_{\mu})(\times 10^{-6})$	$\cdots$	$3.18\pm 3.18$	$\cdots$	$3.18\pm 3.18$
$\mathcal{B}(D^{0}\to\eta^{\prime}K^{-}\mu^{+}\nu_{\mu})(\times 10^{-6})$	$\cdots$	$2.76\pm 1.49$	$\cdots$	$2.76\pm 1.49$
$\mathcal{B}(D^{+}\to\pi^{+}K^{-}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$0.19\pm 0.10$	$0.19\pm 0.10$	$3.65\pm 0.68$	$3.80\pm 0.27$
$\mathcal{B}(D^{+}\to\pi^{0}\overline{K}^{0}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$\cdots$	$0.095\pm 0.050$	$\cdots$	$1.89\pm 0.13$
$\mathcal{B}(D^{+}\to\eta\overline{K}^{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$\cdots$	$0.81\pm 0.81$	$\cdots$	$0.81\pm 0.81$
$\mathcal{B}(D^{+}\to\eta^{\prime}\overline{K}^{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$\cdots$	$0.71\pm 0.38$	$\cdots$	$0.71\pm 0.38$
$\mathcal{B}(D^{+}_{s}\to K^{+}K^{-}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$\cdots$	$0.032\pm 0.017$	$\cdots$	$1.19\pm 0.12$
$\mathcal{B}(D^{+}_{s}\to K^{0}\overline{K}^{0}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$\cdots$	$0.30\pm 0.16$	$\cdots$	$8.02\pm 0.88$
$\mathcal{B}(D^{+}_{s}\to\pi^{+}\pi^{-}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$\cdots$	$\cdots$	$\cdots$	$1.25\pm 0.69$
$\mathcal{B}(D^{+}_{s}\to\pi^{0}\pi^{0}\mu^{+}\nu_{\mu})(\times 10^{-4})$	$\cdots$	$\cdots$	$\cdots$	$7.34\pm 3.09$
$\mathcal{B}(D^{+}_{s}\to\eta\eta\mu^{+}\nu_{\mu})(\times 10^{-4})$	$\cdots$	$0.51\pm 0.45$	$\cdots$	$0.51\pm 0.45$
$\mathcal{B}(D^{+}_{s}\to\eta\eta^{\prime}\mu^{+}\nu_{\mu})(\times 10^{-6})$	$\cdots$	$3.98\pm 2.36$	$\cdots$	$3.98\pm 2.36$

Table 3: The experimental data and the SU(3) flavor symmetry predictions of the nonresonant branching ratios and the total branching ratios of the

D\to P_{1}P_{2}\ell^{+}\nu_{\ell}

decays with the

c\to d\ell^{+}\nu_{\ell}

transitions within the

2\sigma

errors.

Branching ratios	Ones with N	Exp. data with T	Ones with T
$\mathcal{B}(D^{0}\to K^{-}K^{0}e^{+}\nu_{e})(\times 10^{-5})$	$0.83\pm 0.45$	$\cdots$	$1.25\pm 0.64$
$\mathcal{B}(D^{0}\to\pi^{0}\pi^{-}e^{+}\nu_{e})(\times 10^{-3})$	$0$	$1.45\pm 0.14$	$1.85\pm 0.11$
$\mathcal{B}(D^{0}\to\eta\pi^{-}e^{+}\nu_{e})(\times 10^{-5})$	$4.34\pm 2.68$	$\cdots$	$16.38\pm 5.10$
$\mathcal{B}(D^{0}\to\eta^{\prime}\pi^{-}e^{+}\nu_{e})(\times 10^{-5})$	$0.39\pm 0.26$	$\cdots$	$0.57\pm 0.35$
$\mathcal{B}(D^{+}\to\overline{K}^{0}K^{0}e^{+}\nu_{e})(\times 10^{-5})$	$2.11\pm 1.13$	$\cdots$	$3.31\pm 1.69$
$\mathcal{B}(D^{+}\to K^{+}K^{-}e^{+}\nu_{e})(\times 10^{-5})$	$\cdots$	$\cdots$	$1.31\pm 0.63$
$\mathcal{B}(D^{+}\to\pi^{+}\pi^{-}e^{+}\nu_{e})(\times 10^{-3})$	$0.26\pm 0.14$	$2.45\pm 0.20$	$3.08\pm 0.51$
$\mathcal{B}(D^{+}\to\pi^{0}\pi^{0}e^{+}\nu_{e})(\times 10^{-4})$	$1.33\pm 0.71$	$\cdots$	$2.88\pm 1.75$
$\mathcal{B}(D^{+}\to\eta\pi^{0}e^{+}\nu_{e})(\times 10^{-5})$	$5.68\pm 3.50$	$\cdots$	$9.68\pm 4.49$
$\mathcal{B}(D^{+}\to\eta^{\prime}\pi^{0}e^{+}\nu_{e})(\times 10^{-6})$	$5.21\pm 3.46$	$\cdots$	$8.28\pm 5.00$
$\mathcal{B}(D^{+}\to\eta\eta e^{+}\nu_{e})(\times 10^{-6})$	$3.16\pm 2.26$	$\cdots$	$3.16\pm 2.26$
$\mathcal{B}(D^{+}\to\eta\eta^{\prime}e^{+}\nu_{e})(\times 10^{-8})$	$3.96\pm 2.37$	$\cdots$	$3.96\pm 2.37$
$\mathcal{B}(D^{+}_{s}\to K^{+}\pi^{-}e^{+}\nu_{e})(\times 10^{-3})$	$0.075\pm 0.041$	$\cdots$	$1.66\pm 0.17$
$\mathcal{B}(D^{+}_{s}\to K^{0}\pi^{0}e^{+}\nu_{e})(\times 10^{-4})$	$0.38\pm 0.21$	$\cdots$	$8.24\pm 0.85$
$\mathcal{B}(D^{+}_{s}\to\eta K^{0}e^{+}\nu_{e})(\times 10^{-5})$	$1.70\pm 1.06$	$\cdots$	$1.70\pm 1.06$
$\mathcal{B}(D^{+}_{s}\to\eta^{\prime}K^{0}e^{+}\nu_{e})(\times 10^{-7})$	$5.21\pm 3.47$	$\cdots$	$5.21\pm 3.47$
$\mathcal{B}(D^{0}\to K^{-}K^{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$0.76\pm 0.43$	$\cdots$	$1.11\pm 0.57$
$\mathcal{B}(D^{0}\to\pi^{0}\pi^{-}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$0$	$\cdots$	$1.76\pm 0.10$
$\mathcal{B}(D^{0}\to\eta\pi^{-}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$4.13\pm 2.55$	$\cdots$	$15.04\pm 4.76$
$\mathcal{B}(D^{0}\to\eta^{\prime}\pi^{-}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$0.34\pm 0.23$	$\cdots$	$0.50\pm 0.31$
$\mathcal{B}(D^{+}\to\overline{K}^{0}K^{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$1.93\pm 1.04$	$\cdots$	$2.94\pm 1.50$
$\mathcal{B}(D^{+}\to K^{+}K^{-}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$\cdots$	$\cdots$	$1.09\pm 0.53$
$\mathcal{B}(D^{+}\to\pi^{+}\pi^{-}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$0.25\pm 0.14$	$\cdots$	$2.92\pm 0.48$
$\mathcal{B}(D^{+}\to\pi^{0}\pi^{0}\mu^{+}\nu_{\mu})(\times 10^{-4})$	$1.29\pm 0.69$	$\cdots$	$2.68\pm 1.65$
$\mathcal{B}(D^{+}\to\eta\pi^{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$5.40\pm 3.33$	$\cdots$	$8.71\pm 4.16$
$\mathcal{B}(D^{+}\to\eta^{\prime}\pi^{0}\mu^{+}\nu_{\mu})(\times 10^{-6})$	$4.67\pm 3.10$	$\cdots$	$7.23\pm 4.37$
$\mathcal{B}(D^{+}\to\eta\eta\mu^{+}\nu_{\mu})(\times 10^{-6})$	$2.83\pm 2.02$	$\cdots$	$2.83\pm 2.02$
$\mathcal{B}(D^{+}\to\eta\eta^{\prime}\mu^{+}\nu_{\mu})(\times 10^{-8})$	$2.43\pm 1.46$	$\cdots$	$2.43\pm 1.46$
$\mathcal{B}(D^{+}_{s}\to K^{+}\pi^{-}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$0.072\pm 0.039$	$\cdots$	$1.58\pm 0.16$
$\mathcal{B}(D^{+}_{s}\to K^{0}\pi^{0}\mu^{+}\nu_{\mu})(\times 10^{-4})$	$0.36\pm 0.20$	$\cdots$	$7.81\pm 0.80$
$\mathcal{B}(D^{+}_{s}\to\eta K^{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$1.57\pm 0.98$	$\cdots$	$1.57\pm 0.98$
$\mathcal{B}(D^{+}_{s}\to\eta^{\prime}K^{0}\mu^{+}\nu_{\mu})(\times 10^{-7})$	$4.08\pm 2.72$	$\cdots$	$4.08\pm 2.72$

III.2 $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays

We will analyze the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays with the light scalar resonances in this subsection. As given in Eq. (11), their branching ratios can be obtained by using $\mathcal{B}(D\to S\ell^{+}\nu_{\ell})$ and $\mathcal{B}(S\to P_{1}P_{2})$ . The detailed analysis of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell})$ by the SU(3) flavor symmetry can be found in Ref. Wang:D2MlvSU3 .

III.2.1 Branching ratios of the $S\to P_{1}P_{2}$ decays

As for the $S\to P_{1}P_{2}$ decays, the partial decay widths can be written as Cheng:2020ipp

\displaystyle\Gamma(S\to P_{1}P_{2})=\frac{p_{c}}{8\pi m^{2}_{S}}g^{2}_{S\to P_{1}P_{2}},

(63)

where the center-of-mass momentum $p_{c}\equiv\frac{\sqrt{\lambda(m_{S}^{2},m_{P_{1}}^{2},m_{P_{2}}^{2})}}{2m_{S}}$ , and $g_{S\to P_{1}P_{2}}$ is the strong coupling constant. With the SU(3) flavor symmetry, the strong coupling constant can be parametrized as

\displaystyle g^{2q}_{S\to P_{1}P_{2}}=g_{2}S^{i}_{j}P^{k}_{i}P^{j}_{k}

(64)

for the two-quark scalar states, and

\displaystyle g^{4q}_{S\to P_{1}P_{2}}=g_{4}S^{im}_{jn}P^{j}_{i}P^{n}_{m}+g^{\prime}_{4}S^{im}_{jm}P^{n}_{i}P^{j}_{n}

(65)

for the four-quark scalar states, where $g_{2}$ , $g_{4}$ and $g^{\prime}_{4}$ are the nonperturbative parameters. The strong coupling constants of these decays are listed in the second and third columns of Tab. 4 for the two-quark scalar states and the four-quark scalar states, respectively.

Table 4: The strong coupling constants of the

S\to P_{1}P_{2}

decays by the SU(3) flavor symmetry.

Strong couplings	Ones for two-quark state	Ones for four-quark state
$g_{K_{0}^{-}\to\pi^{0}K^{-}}$	$\frac{1}{\sqrt{2}}\leavevmode\nobreak\ g_{2}$	$-\frac{1}{\sqrt{2}}g_{4}$
$g_{K_{0}^{-}\to\pi^{-}\overline{K}^{0}}$	$g_{2}$	$g_{4}$
$g_{\overline{K}_{0}^{0}\to\pi^{+}K^{-}}$	$g_{2}$	$g_{4}$
$g_{\overline{K}_{0}^{0}\to\pi^{0}\overline{K}^{0}}$	$-\frac{1}{\sqrt{2}}\leavevmode\nobreak\ g_{2}$	$\frac{1}{\sqrt{2}}g_{4}$
$g_{a_{0}(980)^{-}\to\eta\pi^{-}}$	$2\leavevmode\nobreak\ g_{2}\leavevmode\nobreak\ \big{(}\frac{1}{\sqrt{6}}cos\theta_{P}-\frac{1}{\sqrt{3}}sin\theta_{P}\big{)}$	$2\leavevmode\nobreak\ g^{\prime}_{4}\leavevmode\nobreak\ \big{(}\frac{1}{\sqrt{6}}cos\theta_{P}-\frac{1}{\sqrt{3}}sin\theta_{P}\big{)}$
$g_{a_{0}(980)^{-}\to\eta^{\prime}\pi^{-}}$	$2\leavevmode\nobreak\ g_{2}\leavevmode\nobreak\ \big{(}\frac{1}{\sqrt{6}}sin\theta_{P}+\frac{1}{\sqrt{3}}cos\theta_{P}\big{)}$	$2\leavevmode\nobreak\ g^{\prime}_{4}\leavevmode\nobreak\ \big{(}\frac{1}{\sqrt{6}}sin\theta_{P}+\frac{1}{\sqrt{3}}cos\theta_{P}\big{)}$
$g_{a_{0}(980)^{-}\to K^{0}K^{-}}$	$g_{2}$	$g_{4}$
$g_{a_{0}(980)^{0}\to\eta\pi^{0}}$	$g_{2}\leavevmode\nobreak\ \big{(}\frac{1}{\sqrt{3}}cos\theta_{P}-\sqrt{\frac{2}{3}}sin\theta_{P}\big{)}$	$g^{\prime}_{4}\leavevmode\nobreak\ \big{(}\frac{1}{\sqrt{6}}cos\theta_{P}-\frac{1}{\sqrt{3}}sin\theta_{P}\big{)}$
$g_{a_{0}(980)^{0}\to\eta^{\prime}\pi^{0}}$	$g_{2}\leavevmode\nobreak\ \big{(}\frac{1}{\sqrt{3}}sin\theta_{P}+\sqrt{\frac{2}{3}}cos\theta_{P}\big{)}$	$g^{\prime}_{4}\leavevmode\nobreak\ \big{(}\frac{1}{\sqrt{6}}sin\theta_{P}+\frac{1}{\sqrt{3}}cos\theta_{P}\big{)}$
$g_{a_{0}(980)^{0}\to K^{+}K^{-}}$	$\frac{1}{\sqrt{2}}\leavevmode\nobreak\ g_{2}$	$\frac{1}{\sqrt{2}}\leavevmode\nobreak\ g_{4}$
$g_{a_{0}(980)^{0}\to K^{0}\overline{K}^{0}}$	$-\frac{1}{\sqrt{2}}\leavevmode\nobreak\ g_{2}$	$-\frac{1}{\sqrt{2}}\leavevmode\nobreak\ g_{4}$
$g_{f_{0}(980)\to\pi^{+}\pi^{-}}$	$\sqrt{2}\leavevmode\nobreak\ g_{2}\leavevmode\nobreak\ sin\theta_{S}$	$\sqrt{2}\leavevmode\nobreak\ g^{\prime}_{4}\leavevmode\nobreak\ cos\phi_{S}+g_{4}sin\phi_{S}$
$g_{f_{0}(980)\to\pi^{0}\pi^{0}}$	$g_{2}\leavevmode\nobreak\ sin\theta_{S}$	$g^{\prime}_{4}\leavevmode\nobreak\ cos\phi_{S}-\frac{1}{\sqrt{2}}g_{4}sin\phi_{S}$
$g_{f_{0}(980)\to K^{+}K^{-}}$	$g_{2}\leavevmode\nobreak\ cos\theta_{S}$	$\frac{1}{\sqrt{2}}g_{4}cos\phi_{S}$
$g_{f_{0}(980)\to K^{0}\overline{K}^{0}}$	$g_{2}\leavevmode\nobreak\ cos\theta_{S}$	$\frac{1}{\sqrt{2}}g_{4}cos\phi_{S}$
$g_{f_{0}(500)\to\pi^{+}\pi^{-}}$	$\sqrt{2}\leavevmode\nobreak\ g_{2}\leavevmode\nobreak\ cos\theta_{S}$	$-\sqrt{2}\leavevmode\nobreak\ g^{\prime}_{4}\leavevmode\nobreak\ sin\phi_{S}+g_{4}cos\phi_{S}$
$g_{f_{0}(500)\to\pi^{0}\pi^{0}}$	$g_{2}\leavevmode\nobreak\ cos\theta_{S}$	$-g^{\prime}_{4}\leavevmode\nobreak\ sin\phi_{S}-\frac{1}{\sqrt{2}}g_{4}cos\phi_{S}$

Since the width determination is very model dependent, there are not accurate values about the decay widths of $a_{0}(980)$ , $f_{0}(980)$ and $f_{0}(500)$ mesons in Ref. PDG2022 . Therefore, it is difficult to obtain accurate $\mathcal{B}(S\to P_{1}P_{2})$ in terms of $\Gamma(S\to P_{1}P_{2})/\Gamma_{S}$ , where $\Gamma_{S}$ is the decay width of scalar meson. We assume the light scalar mesons decay dominantly into pairs of pseudoscalar mesons and all other decay channels are negligible, and then one can obtain $\mathcal{B}(S\to P_{1}P_{2})$ without the decay width values of the light scalar mesons, for example, $\mathcal{B}(f_{0}(500)\to\pi^{+}\pi^{-})\approx\frac{\Gamma(f_{0}(500)\to\pi^{+}\pi^{-})}{\Gamma(f_{0}(500)\to\pi^{+}\pi^{-})+\Gamma(f_{0}(500)\to\pi^{0}\pi^{0})}$ .

In the two-quark picture, the parameter $g_{2}$ is cancelled in the branching ratios. Therefore, $\mathcal{B}(K_{0}\to\pi K,a_{0}(980)\to KK,f_{0}(500)\to\pi\pi)$ only depend on the masses of relevant mesons, $\mathcal{B}(a_{0}(980)\to\eta^{\prime}\pi,\eta^{\prime}\pi)$ depend on the meson masses and the mixing angle $\theta_{P}$ , and $\mathcal{B}(f_{0}(980)\to\pi\pi,KK)$ depend on the meson masses and the mixing angle $\theta_{S}$ . The numerical results of $\mathcal{B}(S\to P_{1}P_{2})$ in the two-quark picture are listed in the second column of Tab. 5. One can see that the branching ratios of the $K_{0},a_{0}(980),f_{0}(500)$ decays are accurately predicted; nevertheless, $\mathcal{B}(f_{0}(980)\to\pi\pi,KK)$ are predicted with large error due to the indeterminate mixing angle $\theta_{S}$ . The three possible ranges for the mixing angle $\theta_{S}$ , $25^{\circ}<\theta_{S}<40^{\circ}$ , $140^{\circ}<\theta_{S}<165^{\circ}$ and $\leavevmode\nobreak\ -30^{\circ}<\theta_{S}<30^{\circ}$ Cheng:2005nb ; LHCb:2013dkk , have been considered, and the predictions of $\mathcal{B}(f_{0}(980)\to\pi\pi,KK)$ are quite dependent on the mixing angle $\theta_{S}$ .

In the third column of Tab. 5, we also give the predictions with two-quark picture of $\mathcal{B}(S\to P_{1}P_{2})$ further constrained from the relevant experimental data of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ listed in later Tabs. 6-7. The predictions of $\mathcal{B}(f_{0}(980)\to P_{1}P_{2})$ are quite accurate when $\theta_{S}$ is further constrained from $[25^{\circ},40^{\circ}]$ to $[25^{\circ},36^{\circ}]$ , from $[140^{\circ},165^{\circ}]$ to $[144^{\circ},151^{\circ}]$ and from $|\phi_{S}|\leq 30^{\circ}$ to $22^{\circ}\leq|\phi_{S}|\leq 30^{\circ}$ by the relevant experimental data of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ with $2\sigma$ errors. Since $\theta_{S}$ in the two-quark picture has been further constrained by $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ , the predictions of $\mathcal{B}(f(980)\to\pi\pi,KK)$ are more accurate as listed in the third column of Tab. 5. Other $\mathcal{B}(S\to P_{1}P_{2})$ are not further constrained from the data of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ , so we do not list them in the third column of Tab. 5.

In the four-quark picture, the two nonperturbative parameters $g_{4}$ and $g^{\prime}_{4}$ in the $a_{0}(980),f_{0}(980),f_{0}(500)$ decays, and $|g^{\prime}_{4}/g_{4}|=0.61\pm 0.13$ are obtained by the data $\Gamma(a_{0}(980)\to K\bar{K})/\Gamma(a_{0}(980)\to\eta\pi)=0.177\pm 0.048$ from PDG PDG2022 . In this work, we treat $g_{4}$ and $g^{\prime}_{4}$ as real number, then two possible cases ( $g^{\prime}_{4}/g_{4}>0$ and $g^{\prime}_{4}/g_{4}<0$ ) are analyzed. The numerical results with the four-quark picture are listed in the last column of Tab. 5. As for $\mathcal{B}(f_{0}(980)\to\pi\pi)$ and $\mathcal{B}(f_{0}(500)\to\pi\pi)$ , very large errors come from the mixing angles $\phi_{S}$ , and they are obviously different in the $g^{\prime}_{4}/g_{4}>0$ and $g^{\prime}_{4}/g_{4}<0$ cases. In general, there is a relative strong phase between $g^{\prime}_{4}$ and $g_{4}$ ; therefore, the common relevant branching ratios are between those in the $g^{\prime}_{4}/g_{4}>0$ case and those in the $g^{\prime}_{4}/g_{4}<0$ case. In addition, $\mathcal{B}(K_{0}\to P_{1}P_{2})$ are the same in both the two-quark and four-quark pictures.

III.2.2 Branching ratios of the $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays

Then $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ can be obtained in terms of $\mathcal{B}(S\to P_{1}P_{2})$ listed in Tab. 5 and the expressions of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell})$ given in Ref. Wang:D2MlvSU3 . Using the experimental data of $\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e})=(2.3\pm 0.8)\times 10^{-3}$ PDG2022 as well as $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ listed in the second columns of Tabs. 6 and 7. The numerical results of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ with $2\sigma$ errors for the two-quark and four-quark pictures are given in Tab. 6 and 7 for the $c\to s\ell^{+}\nu_{\ell}$ and $c\to d\ell^{+}\nu_{\ell}$ transitions, respectively. Our comments on the results are as follows.

•

The experimental lower limits of $\mathcal{B}(D^{0}\to a_{0}(980)^{-}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{-}\to\eta\pi^{-})$ and $\mathcal{B}(D^{+}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{+}\pi^{-})$ have not been used to constrain the predictions of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ , since the two lower limits of the SU(3) flavor symmetry predictions are slightly lower than their experimental data in both the two-quark and four-quark pictures. For $\mathcal{B}(D^{0}\to a_{0}(980)^{-}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{-}\to\eta\pi^{-})$ , one can see that the prediction in the two-quark picture agrees with experimental data within $2\sigma$ error bars; nevertheless, the prediction in the four-quark picture is smaller, which only agrees with experimental data within $3\sigma$ error bars. As for $\mathcal{B}(D^{+}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{+}\pi^{-})$ , the prediction in the two-quark picture is much smaller than its experimental lower limit with $2\sigma$ error, nevertheless, the prediction with $\frac{g^{\prime}_{4}}{g_{4}}>0$ ( $\frac{g^{\prime}_{4}}{g_{4}}<0$ ) in the four-quark picture agrees with its data within $2\sigma$ ( $3\sigma$ ) error bars. Therefore, in the later analysis of total contributions to $\mathcal{B}(D\to P_{1}P_{2}\ell^{+}\nu_{\ell})$ , the predictions of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ with $\frac{g^{\prime}_{4}}{g_{4}}>0$ in the four-quark picture will be used.
•

In the two-quark picture, though the mixing angle $\theta_{S}$ only appears in the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays with $f_{0}(980)$ and $f_{0}(500)$ resonances, all other predictions of the branching ratios are slightly affected by the experimental constraints. So we list all predictions in the three possible ranges of the mixing angle $\theta_{S}$ in the third through fifth columns of Tabs. 6 and 7. One can see that all of the predictions that included the decays with $f_{0}(980)$ and $f_{0}(500)$ resonances are similar in the three possible ranges of the mixing angle $\theta_{S}$ . As mentioned before, $\theta_{S}$ is constrained from $[25^{\circ},40^{\circ}]$ to $[25^{\circ},36^{\circ}]$ , from $[140^{\circ},165^{\circ}]$ to $[144^{\circ},151^{\circ}]$ and from $|\phi_{S}|\leq 30^{\circ}$ to $22^{\circ}\leq|\phi_{S}|\leq 30^{\circ}$ by the relevant experimental data with $2\sigma$ errors.
•

A lot of the branching ratio predictions are quite different between the two-quark picture and the four-quark picture. Present datum of $\mathcal{B}(D^{+}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{+}\pi^{-})$ favors the four-quark picture of scalar mesons. $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ with the $c\to s\ell^{+}\nu_{\ell}$ transitions are predicted on the order of $\mathcal{O}(10^{-3}-10^{-4})$ . Due to the CKM matrix element $V_{cd}$ suppressed, $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ with the $c\to d\ell^{+}\nu_{\ell}$ transitions are predicted on the order of $\mathcal{O}(10^{-4}-10^{-6})$ .
•

Some branching ratios of the $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays have been obtained in Refs. Shi:2017pgh ; Shi:2021bvy . $\mathcal{B}(D^{+}\to Se^{+}\nu_{e},S\to\pi^{+}\pi^{-})=(6.99\pm 2.46)\times 10^{-4}$ Shi:2017pgh , $\mathcal{B}(D^{+}\to S\mu^{+}\nu_{\mu},S\to\pi^{+}\pi^{-})=(7.20\pm 2.52)\times 10^{-4}$ Shi:2017pgh , and $\mathcal{B}(D^{0}\to a_{0}(980)^{-}\ell^{+}\nu_{\ell},a_{0}(980)^{-}\to\eta\pi^{-})=(1.36\pm 0.21)\times 10^{-4}$ Shi:2021bvy . Our predictions in the four-quark picture of $\mathcal{B}(D^{+}\to S\ell^{+}\nu_{\ell},S\to\pi^{+}\pi^{-})$ are consistent with ones in Ref. Shi:2017pgh ; our predictions in the two-quark picture of $\mathcal{B}(D^{0}\to a_{0}(980)^{-}\ell^{+}\nu_{\ell},a_{0}(980)^{-}\to\eta\pi^{-})$ are consistent with ones in Ref. Shi:2021bvy ; nevertheless, our predictions in the four-quark picture are smaller than ones in Ref. Shi:2021bvy .

Table 5: Branching ratios of the

S\to P_{1}P_{2}

decays within

2\sigma

errors. The results are obtained by the SU(3) flavor symmetry relations and

\Gamma(a_{0}(980)\to K\bar{K})/\Gamma(a_{0}(980)\to\eta\pi)=0.177\pm 0.048

PDG2022 . ^†denotes the results with

\frac{g^{\prime}_{4}}{g_{4}}>0

, and ^♯denotes ones with

\frac{g^{\prime}_{4}}{g_{4}}<0

Branching ratios	ones with $2q$ state in $S_{1}$ case	ones with $2q$ state in $S_{2}$ case	ones with $4q$ state
$\mathcal{B}(K_{0}^{-}\to\pi^{0}K^{-})$	$0.34\pm 0.00$		$0.34\pm 0.00$
$\mathcal{B}(K_{0}^{-}\to\pi^{-}\overline{K}^{0})$	$0.66\pm 0.00$		$0.66\pm 0.00$
$\mathcal{B}(\overline{K}_{0}^{0}\to\pi^{+}K^{-})$	$0.67\pm 0.00$		$0.67\pm 0.00$
$\mathcal{B}(\overline{K}_{0}^{0}\to\pi^{0}\overline{K}^{0})$	$0.33\pm 0.00$		$0.33\pm 0.00$
$\mathcal{B}(a_{0}(980)^{-}\to\eta\pi^{-})$	$0.64\pm 0.04$		$0.86\pm 0.03$
$\mathcal{B}(a_{0}(980)^{-}\to\eta^{\prime}\pi^{-})$	$0.03\pm 0.01$		$0.04\pm 0.01$
$\mathcal{B}(a_{0}(980)^{-}\to K^{0}K^{-})$	$0.33\pm 0.03$		$0.10\pm 0.02$
$\mathcal{B}(a_{0}(980)^{0}\to\eta\pi^{0})$	$0.60\pm 0.04$		$0.67\pm 0.06$
$\mathcal{B}(a_{0}(980)^{0}\to\eta^{\prime}\pi^{0})$	$0.04\pm 0.01$		$0.05\pm 0.02$
$\mathcal{B}(a_{0}(980)^{0}\to K^{+}K^{-})$	$0.19\pm 0.02$		$0.15\pm 0.03$
$\mathcal{B}(a_{0}(980)^{0}\to K^{0}\bar{K}^{0})$	$0.17\pm 0.01$		$0.13\pm 0.03$
	$0.45\pm 0.09_{\theta_{S}=[25^{\circ},40^{\circ}]}$	$0.43\pm 0.07_{\theta_{S}=[25^{\circ},35^{\circ}]}$	$0.42\pm 0.16^{\dagger}$
$\mathcal{B}(f_{0}(980)\to\pi^{+}\pi^{-})$	$0.36\pm 0.17_{\theta_{S}=[140^{\circ},165^{\circ}]}$	$0.41\pm 0.09_{\theta_{S}=[144^{\circ},158^{\circ}]}$	$0.59\pm 0.13^{\sharp}$
	$0.22\pm 0.22_{\theta_{S}=[-30^{\circ},30^{\circ}]}$	$0.38\pm 0.06_{[22^{\circ}\leq\|\theta_{S}\|\leq 30^{\circ}]}$
	$0.22\pm 0.04_{\theta_{S}=[25^{\circ},40^{\circ}]}$	$0.21\pm 0.03_{\theta_{S}=[25^{\circ},35^{\circ}]}$	$0.34\pm 0.11^{\dagger}$
$\mathcal{B}(f_{0}(980)\to\pi^{0}\pi^{0})$	$0.18\pm 0.09_{\theta_{S}=[140^{\circ},165^{\circ}]}$	$0.21\pm 0.04_{\theta_{S}=[144^{\circ},158^{\circ}]}$	$0.20\pm 0.10^{\sharp}$
	$0.11\pm 0.11_{\theta_{S}=[-30^{\circ},30^{\circ}]}$	$0.19\pm 0.03_{[22^{\circ}\leq\|\theta_{S}\|\leq 30^{\circ}]}$
	$0.17\pm 0.07_{\theta_{S}=[25^{\circ},40^{\circ}]}$	$0.19\pm 0.05_{\theta_{S}=[25^{\circ},35^{\circ}]}$
$\mathcal{B}(f_{0}(980)\to K^{+}K^{-})$	$0.24\pm 0.14_{\theta_{S}=[140^{\circ},165^{\circ}]}$	$0.20\pm 0.07_{\theta_{S}=[144^{\circ},158^{\circ}]}$	$0.12\pm 0.04$
	$0.35\pm 0.17_{\theta_{S}=[-30^{\circ},30^{\circ}]}$	$0.22\pm 0.04_{[22^{\circ}\leq\|\theta_{S}\|\leq 30^{\circ}]}$
	$0.16\pm 0.06_{\theta_{S}=[25^{\circ},40^{\circ}]}$	$0.17\pm 0.05_{\theta_{S}=[25^{\circ},35^{\circ}]}$
$\mathcal{B}(f_{0}(980)\to K^{0}\bar{K}^{0})$	$0.22\pm 0.12_{\theta_{S}=[140^{\circ},165^{\circ}]}$	$0.18\pm 0.06_{\theta_{S}=[144^{\circ},158^{\circ}]}$	$0.11\pm 0.04$
	$0.32\pm 0.16_{\theta_{S}=[-30^{\circ},30^{\circ}]}$	$0.20\pm 0.04_{[22^{\circ}\leq\|\theta_{S}\|\leq 30^{\circ}]}$
$\mathcal{B}(f_{0}(500)\to\pi^{+}\pi^{-})$	$0.66\pm 0.00$		$0.73\pm 0.09^{\dagger}$
			$0.57\pm 0.12^{\sharp}$
$\mathcal{B}(f_{0}(500)\to\pi^{0}\pi^{0})$	$0.34\pm 0.00$		$0.27\pm 0.09^{\dagger}$
			$0.43\pm 0.12^{\sharp}$

Table 6: The experimental data and the SU(3) flavor symmetry predictions of the

D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}

decays with the

c\to s\ell^{+}\nu_{\ell}

transitions within

2\sigma

errors. ^†denotes the results with

\frac{g^{\prime}_{4}}{g_{4}}>0

, and ^♯ denotes ones with

\frac{g^{\prime}_{4}}{g_{4}}<0

Branching ratios	Exp. Data	Ones in the 2-quark picture with			Ones in the 4-quark picture
		$\theta_{S}=[25^{\circ},35^{\circ}]$	$\theta_{S}=[144^{\circ},158^{\circ}]$	$22^{\circ}\leq\|\theta_{S}\|\leq 30^{\circ}$
$\mathcal{B}(D^{0}\to K^{-}_{0}e^{+}\nu_{e},\leavevmode\nobreak\ K^{-}_{0}\to\pi^{-}\overline{K}^{0})(\times 10^{-4})$	$\cdots$	$19.99\pm 7.34$	$19.86\pm 7.26$	$19.74\pm 6.97$	$8.37\pm 3.01$
$\mathcal{B}(D^{0}\to K^{-}_{0}e^{+}\nu_{e},\leavevmode\nobreak\ K^{-}_{0}\to\pi^{0}K^{-})(\times 10^{-4})$	$\cdots$	$10.18\pm 3.77$	$10.12\pm 3.73$	$10.05\pm 3.57$	$4.19\pm 1.50$
$\mathcal{B}(D^{+}\to\overline{K}^{0}_{0}e^{+}\nu_{e},\leavevmode\nobreak\ \overline{K}^{0}_{0}\to\pi^{+}K^{-})(\times 10^{-3})$	$\cdots$	$5.17\pm 1.92$	$5.19\pm 1.85$	$5.12\pm 1.86$	$2.24\pm 0.83$
$\mathcal{B}(D^{+}\to\overline{K}^{0}_{0}e^{+}\nu_{e},\leavevmode\nobreak\ \overline{K}^{0}_{0}\to\pi^{0}\overline{K}^{0})(\times 10^{-3})$	$\cdots$	$2.57\pm 0.96$	$2.59\pm 0.92$	$2.55\pm 0.92$	$1.12\pm 0.42$
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to\pi^{+}\pi^{-})(\times 10^{-3})$	$1.30\pm 0.63$ Hietala:2015jqa	$1.19\pm 0.18$	$1.17\pm 0.17$	$1.18\pm 0.17$	$1.22\pm 0.55^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 1.44\pm 0.49^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to\pi^{0}\pi^{0})(\times 10^{-4})$	$7.9\pm 2.9$ BESIII:2021pdt	$5.95\pm 0.92$	$5.89\pm 0.85$	$5.90\pm 0.86$	$7.91\pm 2.85^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 7.13\pm 2.10^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to K^{+}K^{-})(\times 10^{-4})$	$\cdots$	$5.11\pm 2.34$	$5.53\pm 2.78$	$6.28\pm 2.07$	$3.33\pm 1.53^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 3.07\pm 1.34^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to K^{0}\overline{K}^{0})(\times 10^{-4})$	$\cdots$	$4.62\pm 2.12$	$5.01\pm 2.52$	$5.68\pm 1.87$	$3.01\pm 1.39^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 2.78\pm 1.22^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{+}\pi^{-})(\times 10^{-4})$	$\cdots$	$9.91\pm 2.83$	$9.67\pm 3.07$	$9.44\pm 3.30$	$2.49\pm 2.49^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 0.90\pm 0.90^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{0}\pi^{0})(\times 10^{-5})$	$<64$ BESIII:2021pdt	$49.77\pm 14.23$	$48.57\pm 15.43$	$47.44\pm 16.56$	$6.66\pm 6.66^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 0.78\pm 0.78^{\sharp}$
$\mathcal{B}(D^{0}\to K^{-}_{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ K^{-}_{0}\to\pi^{-}K^{0})(\times 10^{-4})$	$\cdots$	$17.27\pm 6.48$	$17.16\pm 6.41$	$17.04\pm 6.14$	$7.19\pm 2.63$
$\mathcal{B}(D^{0}\to K^{-}_{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ K^{-}_{0}\to\pi^{0}K^{-})(\times 10^{-4})$	$\cdots$	$8.63\pm 3.24$	$8.58\pm 3.20$	$8.52\pm 3.07$	$3.59\pm 1.32$
$\mathcal{B}(D^{+}\to\overline{K}^{0}_{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \overline{K}^{0}_{0}\to\pi^{+}K^{-})(\times 10^{-3})$	$\cdots$	$4.43\pm 1.68$	$4.46\pm 1.62$	$4.40\pm 1.62$	$1.92\pm 0.73$
$\mathcal{B}(D^{+}\to\overline{K}^{0}_{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \overline{K}^{0}_{0}\to\pi^{0}K^{0})(\times 10^{-3})$	$\cdots$	$2.22\pm 0.84$	$2.23\pm 0.81$	$2.20\pm 0.81$	$0.96\pm 0.36$
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to\pi^{+}\pi^{-})(\times 10^{-3})$	$\cdots$	$1.01\pm 0.16$	$1.00\pm 0.15$	$1.00\pm 0.16$	$1.02\pm 0.46^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 1.23\pm 0.42^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to\pi^{0}\pi^{0})(\times 10^{-4})$	$\cdots$	$5.05\pm 0.83$	$4.99\pm 0.77$	$5.00\pm 0.78$	$6.72\pm 2.48^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 6.04\pm 1.82^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to K^{+}K^{-})(\times 10^{-4})$	$\cdots$	$4.31\pm 1.94$	$4.70\pm 2.34$	$5.34\pm 1.75$	$2.79\pm 1.28^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 2.59\pm 1.14^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to K^{0}\overline{K}^{0})(\times 10^{-4})$	$\cdots$	$3.90\pm 1.76$	$4.25\pm 2.12$	$4.83\pm 1.58$	$2.52\pm 1.16^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 2.34\pm 1.03^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(500)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(500)\to\pi^{+}\pi^{-})(\times 10^{-4})$	$\cdots$	$8.88\pm 2.62$	$8.70\pm 2.86$	$8.49\pm 3.05$	$2.30\pm 2.30^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 0.83\pm 0.83^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(500)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(500)\to\pi^{0}\pi^{0})(\times 10^{-5})$	$\cdots$	$44.67\pm 13.23$	$43.85\pm 14.53$	$42.77\pm 15.49$	$6.16\pm 6.16^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 7.23\pm 7.23^{\sharp}$

Table 7: The experimental data and the SU(3) flavor symmetry predictions of the

D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}

decays with the

c\to d\ell^{+}\nu_{\ell}

transitions within

2\sigma

errors. ^† denotes the results with

\frac{g^{\prime}_{4}}{g_{4}}>0

, ^♯ denotes ones with

\frac{g^{\prime}_{4}}{g_{4}}<0

, and ^a denotes the experimental lower limits not used to constrain the predictions.

Branching ratios	Exp. Data	Ones in the 2-quark picture with			Ones in the 4-quark picture
		$\theta_{S}=[25^{\circ},35^{\circ}]$	$\theta_{S}=[144^{\circ},158^{\circ}]$	$22^{\circ}\leq\|\theta_{S}\|\leq 30^{\circ}$
$\mathcal{B}(D^{0}\to a_{0}(980)^{-}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{-}\to\eta\pi^{-})(\times 10^{-5})$	$13.3^{+6.8}_{-6.0^{a}}$	$5.99\pm 2.69$	$5.86\pm 2.48$	$6.05\pm 2.57$	$3.81\pm 0.98$
$\mathcal{B}(D^{0}\to a_{0}(980)^{-}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{-}\to\eta^{\prime}\pi^{-})(\times 10^{-6})$	$\cdots$	$2.88\pm 1.71$	$2.97\pm 1.77$	$2.97\pm 1.73$	$1.88\pm 0.98$
$\mathcal{B}(D^{0}\to a_{0}(980)^{-}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{-}\to K^{0}K^{-})(\times 10^{-6})$	$\cdots$	$29.99\pm 13.81$	$30.73\pm 13.81$	$30.57\pm 13.70$	$4.22\pm 1.93$
$\mathcal{B}(D^{+}\to a_{0}(980)^{0}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{0}\to\eta\pi^{0})(\times 10^{-5})$	$17^{+16}_{-14}$	$7.35\pm 3.28$	$7.25\pm 3.13$	$7.32\pm 3.17$	$4.00\pm 1.00$
$\mathcal{B}(D^{+}\to a_{0}(980)^{0}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{0}\to\eta^{\prime}\pi^{0})(\times 10^{-6})$	$\cdots$	$5.53\pm 3.26$	$5.69\pm 3.32$	$5.65\pm 3.20$	$3.08\pm 1.56$
$\mathcal{B}(D^{+}\to a_{0}(980)^{0}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{0}\to K^{+}K^{-})(\times 10^{-5})$	$\cdots$	$2.28\pm 1.06$	$2.30\pm 1.00$	$2.29\pm 0.99$	$0.88\pm 0.36$
$\mathcal{B}(D^{+}\to a_{0}(980)^{0}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{0}\to K^{0}\overline{K}^{0})(\times 10^{-5})$	$\cdots$	$1.99\pm 0.92$	$2.01\pm 0.88$	$2.00\pm 0.86$	$0.77\pm 0.31$
$\mathcal{B}(D^{+}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to\pi^{+}\pi^{-})(\times 10^{-5})$	$<2.8\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{BESIII:2018qmf}{\@@citephrase{(}}{\@@citephrase{)}}}}$	$1.15\pm 0.50$	$1.10\pm 0.58$	$0.96\pm 0.43$	$1.65\pm 1.15^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 2.14\pm 0.65^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to\pi^{0}\pi^{0})(\times 10^{-6})$	$\cdots$	$5.75\pm 2.53$	$5.51\pm 2.92$	$4.80\pm 2.18$	$10.53\pm 3.67^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 10.10\pm 5.37^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to K^{+}K^{-})(\times 10^{-6})$	$\cdots$	$5.07\pm 0.88$	$5.06\pm 0.85$	$5.01\pm 0.80$	$4.35\pm 2.78^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 4.60\pm 2.76^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to K^{0}\overline{K}^{0})(\times 10^{-6})$	$\cdots$	$5.07\pm 0.88$	$5.06\pm 0.85$	$5.01\pm 0.80$	$4.35\pm 2.78^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 4.60\pm 2.76^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{+}\pi^{-})(\times 10^{-4})$	$6.3\pm 1.0^{a}$	$1.44\pm 0.64$	$1.72\pm 0.92$	$1.79\pm 0.85$	$3.64\pm 2.57^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 2.95\pm 1.87^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{0}\pi^{0})(\times 10^{-4})$	$\cdots$	$0.72\pm 0.32$	$0.87\pm 0.46$	$0.91\pm 0.43$	$1.45\pm 1.02^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 2.08\pm 1.57^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to K^{0}_{0}e^{+}\nu_{e},\leavevmode\nobreak\ K^{0}_{0}\to\pi^{-}K^{+})(\times 10^{-5})$	$\cdots$	$22.34\pm 8.09$	$22.13\pm 7.97$	$22.34\pm 7.64$	$9.54\pm 3.38$
$\mathcal{B}(D^{+}_{s}\to K^{0}_{0}e^{+}\nu_{e},\leavevmode\nobreak\ K^{0}_{0}\to\pi^{0}K^{0})(\times 10^{-5})$	$\cdots$	$11.17\pm 4.04$	$11.07\pm 3.99$	$11.17\pm 3.82$	$4.77\pm 1.69$
$\mathcal{B}(D^{0}\to a_{0}(980)^{-}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ a_{0}(980)^{-}\to\eta\pi^{-})(\times 10^{-5})$	$\cdots$	$4.95\pm 2.27$	$4.84\pm 2.10$	$5.00\pm 2.18$	$3.14\pm 0.84$
$\mathcal{B}(D^{0}\to a_{0}(980)^{-}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ a_{0}(980)^{-}\to\eta^{\prime}\pi^{-})(\times 10^{-6})$	$\cdots$	$2.39\pm 1.44$	$2.46\pm 1.48$	$2.45\pm 1.45$	$1.56\pm 0.82$
$\mathcal{B}(D^{0}\to a_{0}(980)^{-}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ a_{0}(980)^{-}\to K^{0}K^{-})(\times 10^{-6})$	$\cdots$	$24.78\pm 11.68$	$25.37\pm 11.62$	$25.20\pm 11.53$	$3.51\pm 1.62$
$\mathcal{B}(D^{+}\to a_{0}(980)^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ a_{0}(980)^{0}\to\eta\pi^{0})(\times 10^{-5})$	$\cdots$	$6.09\pm 2.78$	$6.00\pm 2.65$	$6.06\pm 2.69$	$3.30\pm 0.86$
$\mathcal{B}(D^{+}\to a_{0}(980)^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ a_{0}(980)^{0}\to\eta^{\prime}\pi^{0})(\times 10^{-6})$	$\cdots$	$4.58\pm 2.74$	$4.72\pm 2.79$	$4.67\pm 2.69$	$2.55\pm 1.31$
$\mathcal{B}(D^{+}\to a_{0}(980)^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ a_{0}(980)^{0}\to K^{+}K^{-})(\times 10^{-5})$	$\cdots$	$1.89\pm 0.89$	$1.91\pm 0.85$	$1.89\pm 0.83$	$0.73\pm 0.30$
$\mathcal{B}(D^{+}\to a_{0}(980)^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ a_{0}(980)^{0}\to K^{0}\overline{K}^{0})(\times 10^{-5})$	$\cdots$	$1.65\pm 0.78$	$1.66\pm 0.74$	$1.65\pm 0.73$	$0.64\pm 0.27$
$\mathcal{B}(D^{+}\to f_{0}(980)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to\pi^{+}\pi^{-})(\times 10^{-5})$	$\cdots$	$0.94\pm 0.43$	$0.91\pm 0.48$	$0.79\pm 0.36$	$1.37\pm 0.96^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 1.76\pm 0.55^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(980)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to\pi^{0}\pi^{0})(\times 10^{-6})$	$\cdots$	$4.74\pm 2.14$	$4.58\pm 2.43$	$3.97\pm 1.82$	$8.67\pm 3.13^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 8.32\pm 4.47^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(980)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to K^{+}K^{-})(\times 10^{-6})$	$\cdots$	$4.21\pm 0.73$	$4.19\pm 0.71$	$4.15\pm 0.67$	$3.55\pm 2.29^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 3.76\pm 2.26^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(980)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to K^{0}\overline{K}^{0})(\times 10^{-6})$	$\cdots$	$4.21\pm 0.73$	$4.19\pm 0.71$	$4.15\pm 0.67$	$3.55\pm 2.29^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 3.76\pm 2.26^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(500)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to\pi^{+}\pi^{-})(\times 10^{-4})$	$\cdots$	$1.28\pm 0.59$	$1.54\pm 0.84$	$1.61\pm 0.79$	$3.30\pm 2.39^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 2.68\pm 1.74^{\sharp}$
$\mathcal{B}(D^{+}\to f_{0}(500)\mu^{+}\nu_{\mu},\leavevmode\nobreak\ f_{0}(980)\to\pi^{0}\pi^{0})(\times 10^{-4})$	$\cdots$	$0.64\pm 0.30$	$0.78\pm 0.43$	$0.81\pm 0.40$	$1.32\pm 0.95^{\dagger},\leavevmode\nobreak\ \leavevmode\nobreak\ 1.89\pm 1.46^{\sharp}$
$\mathcal{B}(D^{+}_{s}\to K^{0}_{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ K^{0}_{0}\to\pi^{-}K^{+})(\times 10^{-5})$	$\cdots$	$19.61\pm 7.20$	$19.43\pm 7.10$	$19.60\pm 6.80$	$8.38\pm 3.01$
$\mathcal{B}(D^{+}_{s}\to K^{0}_{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ K^{0}_{0}\to\pi^{0}K^{0})(\times 10^{-5})$	$\cdots$	$9.80\pm 3.60$	$9.71\pm 3.55$	$9.80\pm 3.40$	$4.19\pm 1.50$

III.3 $D\to V(V\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays

We will analyze the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays with the vector resonances in this subsection. Since the light vector mesons are understood well, the calculations of $\mathcal{B}(D\to V\ell^{+}\nu_{\ell},V\to P_{1}P_{2})$ are much easier than the ones of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ . From Eq. (11), their branching ratios of $D\to V(V\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ can be obtained by using $\mathcal{B}(D\to V\ell^{+}\nu_{\ell})$ and $\mathcal{B}(V\to P_{1}P_{2})$ . The $D\to V\ell^{+}\nu_{\ell}$ decays have been studied by the SU(3) flavor symmetry in Ref. Wang:D2MlvSU3 . Many $\mathcal{B}(D\to V\ell^{+}\nu_{\ell})$ have been accurately measured and have been listed in the second column of Tab. V in Ref. Wang:D2MlvSU3 . The expressions of $\mathcal{B}(D\to V\ell^{+}\nu_{\ell})$ within the $C_{3}$ case in Ref. Wang:D2MlvSU3 will be taken for our analysis.

Following Ref. Cheng:2020ipp , $\mathcal{B}(V\to P_{1}P_{2})$ can be written as

\displaystyle\mathcal{B}(V\to P_{1}P_{2})=\frac{\tau_{V}p^{\prime 3}_{c}}{6\pi m^{2}_{V}}g^{2}_{V\to P_{1}P_{2}},

(66)

where $p^{\prime}_{c}\equiv\frac{\sqrt{\lambda(m_{V}^{2},m_{P_{1}}^{2},m_{P_{2}}^{2})}}{2m_{V}}$ and $g_{V\to P_{1}P_{2}}$ are the strong coupling constants. Similar to $g_{S\to P_{1}P_{2}}^{2q}$ in Eq. (64), $g_{V\to P_{1}P_{2}}$ can be parametrized by the SU(3) flavor symmetry

\displaystyle g_{V\to P_{1}P_{2}}=g_{V}V^{i}_{j}P^{k}_{i}P^{j}_{k},

(67)

where $g_{V}$ is the corresponding nonperturbative parameter.

At present, many involved $\mathcal{B}(V\to P_{1}P_{2})$ have been well measured PDG2022

$\displaystyle\mathcal{B}(K^{*+}\to\pi K)=(99.902\pm 0.018)\%,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\mathcal{B}(K^{*0}\to\pi K)=(99.754\pm 0.042)\%,$	(68)
$\displaystyle\mathcal{B}(\rho^{+}\to\pi^{0}\pi^{+})=100\%,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\mathcal{B}(\rho^{0}\to\pi^{+}\pi^{-})=100\%,$
$\displaystyle\mathcal{B}(\phi\to K^{+}K^{-})=(49.1\pm 1.0)\%,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\mathcal{B}(\omega\to\pi^{+}\pi^{-})=(1.53^{+0.22}_{-0.26})\%.$

From Eq. (67), the relations of the strong coupling constants can be obtained

	$\displaystyle\sqrt{2}g_{K^{-}\to\pi^{0}K^{-}}=g_{K^{-}\to\pi^{-}K^{0}},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \sqrt{2}g_{K^{0}\to\pi^{0}K^{0}}=g_{K^{0}\to\pi^{-}K^{+}},$
	$\displaystyle g_{\rho^{-}\to\pi^{0}\pi^{-}}=\sqrt{3}g_{\rho^{-}\to\eta_{8}\pi^{-}}=\sqrt{3/2}g_{\rho^{-}\to\eta_{1}\pi^{-}},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ g_{\phi\to K^{+}K^{-}}=g_{\phi\to K^{0}\overline{K}^{0}},$		(69)

In terms of Eq. (68) and Eq. (69), the strong coupling constants are

$\displaystyle\|g_{K^{*-}\to\pi^{-}K^{0}}\|=4.62\pm 0.08,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\|g_{K^{*0}\to\pi^{-}K^{+}}\|=4.40\pm 0.10,$	(70)
$\displaystyle\|g_{\rho^{-}\to\pi^{0}\pi^{-}}\|=6.00\pm 0.03,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\|g_{\rho^{0}\to\pi^{+}\pi^{-}}\|=5.95\pm 0.04,$
$\displaystyle\|g_{\phi\to K^{+}K^{-}}\|=4.47\pm 0.08,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\|g_{\omega\to\pi^{+}\pi^{-}}\|=0.18\pm 0.02.$

Then the following $\mathcal{B}(V\to P_{1}P_{2})$ can be written as

$\displaystyle\mathcal{B}(K^{*0}\to\pi^{0}K^{0})=(33.02\pm 0.02)\%,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\mathcal{B}(K^{*0}\to\pi^{-}K^{+})=(66.74\pm 0.04)\%,$	(71)
$\displaystyle\mathcal{B}(K^{*+}\to\pi^{0}K^{+})=(33.62\pm 0.01)\%,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\mathcal{B}(K^{*+}\to\pi^{+}K^{0})=(66.28\pm 0.01)\%,$
$\displaystyle\mathcal{B}(\rho^{+}\to\eta\pi^{+})=(4.38\pm 0.66)\%,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\mathcal{B}(\phi\to K^{0}K^{0})=(32.42\pm 1.04)\%.$

Table 8: The experimental data and the SU(3) flavor symmetry predictions of

D\to V(V\to P_{1}P_{2})\ell^{+}\nu_{\ell}

decays within

2\sigma

errors.

Branching ratios	Exp. Data	Our predictions	Previous ones
$c\to se^{+}\nu_{e}$ :
$\mathcal{B}(D^{0}\to K^{-}e^{+}\nu_{e},\leavevmode\nobreak\ K^{-}\to\pi^{-}\overline{K}^{0})(\times 10^{-2})$	$\dots$	$1.42\pm 0.07$	$\dots$
$\mathcal{B}(D^{0}\to K^{-}e^{+}\nu_{e},\leavevmode\nobreak\ K^{-}\to\pi^{0}K^{-})(\times 10^{-3})$	$\dots$	$7.18\pm 0.37$	$7.17$ Kim:2017dfr
$\mathcal{B}(D^{+}\to\overline{K}^{0}e^{+}\nu_{e},\leavevmode\nobreak\ \overline{K}^{0}\to\pi^{+}K^{-})(\times 10^{-2})$	$3.77\pm 0.34$	$3.64\pm 0.11$	$3.51$ Kim:2017dfr
$\mathcal{B}(D^{+}\to\overline{K}^{0}e^{+}\nu_{e},\leavevmode\nobreak\ \overline{K}^{0}\to\pi^{0}\overline{K}^{0})(\times 10^{-2})$	$\dots$	$1.80\pm 0.06$	$\dots$
$\mathcal{B}(D^{+}_{s}\to\phi e^{+}\nu_{e},\leavevmode\nobreak\ \phi\to K^{+}K^{-})(\times 10^{-2})$	$\dots$	$1.20\pm 0.10$	$\dots$
$\mathcal{B}(D^{+}_{s}\to\phi e^{+}\nu_{e},\leavevmode\nobreak\ \phi\to K^{0}\overline{K}^{0})(\times 10^{-3})$	$\dots$	$7.94\pm 0.65$	$\dots$
$c\to s\mu^{+}\nu_{\mu}$ :
$\mathcal{B}(D^{0}\to K^{-}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ K^{-}\to\pi^{-}\overline{K}^{0})(\times 10^{-2})$	$\dots$	$1.33\pm 0.07$	$\dots$
$\mathcal{B}(D^{0}\to K^{-}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ K^{-}\to\pi^{0}K^{-})(\times 10^{-3})$	$\dots$	$6.76\pm 0.35$	$7.17$ Kim:2017dfr
$\mathcal{B}(D^{+}\to\overline{K}^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \overline{K}^{0}\to\pi^{+}K^{-})(\times 10^{-2})$	$3.52\pm 0.20$	$3.43\pm 0.11$	$3.51$ Kim:2017dfr
$\mathcal{B}(D^{+}\to\overline{K}^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \overline{K}^{0}\to\pi^{0}\overline{K}^{0})(\times 10^{-2})$	$\dots$	$1.70\pm 0.05$	$\dots$
$\mathcal{B}(D^{+}_{s}\to\phi\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \phi\to K^{+}K^{-})(\times 10^{-2})$	$\dots$	$1.13\pm 0.09$	$\dots$
$\mathcal{B}(D^{+}_{s}\to\phi\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \phi\to K^{0}\overline{K}^{0})(\times 10^{-3})$	$\dots$	$7.46\pm 0.62$	$\dots$
$c\to de^{+}\nu_{e}$ :
$\mathcal{B}(D^{0}\to\rho^{-}e^{+}\nu_{e},\leavevmode\nobreak\ \rho^{-}\to\pi^{0}\pi^{-})(\times 10^{-3})$	$\dots$	$1.85\pm 0.11$	$1.63$ Kim:2017dfr
$\mathcal{B}(D^{0}\to\rho^{-}e^{+}\nu_{e},\leavevmode\nobreak\ \rho^{-}\to\eta\pi^{-})(\times 10^{-5})$	$\dots$	$8.23\pm 1.59$	$\dots$
$\mathcal{B}(D^{+}\to\rho^{0}e^{+}\nu_{e},\leavevmode\nobreak\ \rho^{0}\to\pi^{+}\pi^{-})(\times 10^{-3})$	$\dots$	$2.40\pm 0.12$	$1.57\pm 0.07\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Shi:2017pgh}{\@@citephrase{(}}{\@@citephrase{)}}}},\leavevmode\nobreak\ \leavevmode\nobreak\ 2.10\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Kim:2017dfr}{\@@citephrase{(}}{\@@citephrase{)}}}}$
$\mathcal{B}(D^{+}\to\omega e^{+}\nu_{e},\leavevmode\nobreak\ \omega\to\pi^{+}\pi^{-})(\times 10^{-5})$	$\dots$	$3.55\pm 0.82$	$\dots$
$\mathcal{B}(D^{+}_{s}\to K^{0}e^{+}\nu_{e},\leavevmode\nobreak\ K^{0}\to\pi^{-}K^{+})(\times 10^{-3})$	$\dots$	$1.49\pm 0.10$	$\dots$
$\mathcal{B}(D^{+}_{s}\to K^{0}e^{+}\nu_{e},\leavevmode\nobreak\ K^{0}\to\pi^{0}K^{0})(\times 10^{-4})$	$\dots$	$7.39\pm 0.51$	$\dots$
$c\to d\mu^{+}\nu_{\mu}$ :
$\mathcal{B}(D^{0}\to\rho^{-}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \rho^{-}\to\pi^{0}\pi^{-})(\times 10^{-3})$	$\dots$	$1.76\pm 0.10$	$\dots$
$\mathcal{B}(D^{0}\to\rho^{-}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \rho^{-}\to\eta\pi^{-})(\times 10^{-5})$	$\dots$	$7.83\pm 1.51$	$\dots$
$\mathcal{B}(D^{+}\to\rho^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \rho^{0}\to\pi^{+}\pi^{-})(\times 10^{-3})$	$\dots$	$2.29\pm 0.11$	$1.57\pm 0.07$ Shi:2017pgh
$\mathcal{B}(D^{+}\to\omega\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \omega\to\pi^{+}\pi^{-})(\times 10^{-5})$	$\dots$	$3.38\pm 0.78$	$\dots$
$\mathcal{B}(D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ K^{0}\to\pi^{-}K^{+})(\times 10^{-3})$	$\dots$	$1.42\pm 0.10$	$\dots$
$\mathcal{B}(D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ K^{0}\to\pi^{0}K^{0})(\times 10^{-4})$	$\dots$	$7.03\pm 0.48$	$\dots$

For $D\to V(V\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays, the branching ratios of $D^{+}\to\overline{K}^{*0}(\overline{K}^{*0}\to\pi^{+}K^{-})e^{+}\nu_{e}$ and $D^{+}\to\overline{K}^{*0}(\overline{K}^{*0}\to\pi^{+}K^{-})\mu^{+}\nu_{\mu}$ have been measured, and the experimental data with $2\sigma$ errors are listed in the second column of Tab. 8. Using the experimental data of $\mathcal{B}(D^{+}\to\overline{K}^{*0}\ell^{+}\nu_{\ell},\overline{K}^{*0}\to\pi^{+}K^{-})$ , $\mathcal{B}(V\to P_{1}P_{2})$ and $\mathcal{B}(D\to V\ell^{+}\nu_{\ell})$ , we obtain the predictions of $\mathcal{B}(D\to V\ell^{+}\nu_{\ell},V\to P_{1}P_{2})$ by the SU(3) flavor symmetry, which are given in the third column of Tab. 8. We can see that $\mathcal{B}(D\to V\ell^{+}\nu_{\ell},V\to P_{1}P_{2})$ with the $c\to s\ell^{+}\nu_{\ell}$ transitions are predicted on the order of $\mathcal{O}(10^{-2}-10^{-3})$ , and $\mathcal{B}(D\to V\ell^{+}\nu_{\ell},V\to P_{1}P_{2})$ with the $c\to d\ell^{+}\nu_{\ell}$ transitions are predicted on the order of $\mathcal{O}(10^{-3}-10^{-5})$ . The predictions of $\mathcal{B}(D\to V\ell^{+}\nu_{\ell},V\to P_{1}P_{2})$ are about one order larger than those of the corresponding $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ .

Previous predictions are also listed in the last column of Tab. 8. Our predictions of $\mathcal{B}(D^{0}\to K^{*-}\ell^{+}\nu_{\ell},\leavevmode\nobreak\ K^{*-}\to\pi^{0}K^{-})$ and $\mathcal{B}(D^{+}\to\overline{K}^{*0}\ell^{+}\nu_{\ell},\leavevmode\nobreak\ \overline{K}^{*0}\to\pi^{+}K^{-})$ are in good agreement with those in Ref. Kim:2017dfr . And our predictions of $\mathcal{B}(D^{+}\to\rho^{0}\ell^{+}\nu_{\ell},\leavevmode\nobreak\ \rho^{0}\to\pi^{+}\pi^{-})$ are slight larger than those obtained by the light-front quark model and the light-cone sum rules in Ref. Shi:2017pgh .

III.4 Total branching ratios

As analyzed above, some four-body semileptonic decays of $D$ mesons receive the contributions of the nonresonant states, the scalar resonant states, and the vector resonant states; nevertheless, some decay modes only receive one or two kinds of them. For clearly showing the resonant contributions, we also list the scalar and vector resonant amplitudes in the third and last columns of Tab. 1, respectively. The resonant amplitudes are obtained by multiplying the hadronic helicity amplitudes $H(D\to R\ell^{+}\nu_{\ell})$ given in Ref. Wang:D2MlvSU3 and the strong coupling constants $g_{R\to P_{1}P_{2}}$ obtained in this work. Note that the resonant amplitudes listed in the last two columns of Tab. 1 are given only to see clearly the kinds of the resonant contributions, and we do not use them to obtain the numerical total branching ratios $\mathcal{B}(D\to P_{1}P_{2}\ell^{+}\nu_{\ell})_{T}$ .

We have some comments for the contributions in Tab. 1. For $D_{(s)}\to\eta K\ell^{+}\nu_{\ell},\leavevmode\nobreak\ \eta^{\prime}K\ell^{+}\nu_{\ell},\leavevmode\nobreak\ \eta\eta\ell^{+}\nu_{\ell},\leavevmode\nobreak\ \eta\eta^{\prime}\ell^{+}\nu_{\ell}$ decays, since both final state mesons are quite heavy, they only receive the nonresonant contributions. The decays $D_{s}^{+}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell},$ $D_{s}^{+}\to\pi^{+}\pi^{-}\ell^{+}\nu_{\ell},$ $D^{0}\to K^{-}K^{0}\ell^{+}\nu_{\ell},$ $D^{+}\to\overline{K}^{0}K^{0}\ell^{+}\nu_{\ell},$ $D^{+}\to K^{+}K^{-}\ell^{+}\nu_{\ell},$ $D^{+}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell}$ , and $D^{+}\to\eta^{(^{\prime})}\pi^{0}\ell^{+}\nu_{\ell}$ receive both the nonresonant contributions and the scalar resonant contributions; moreover, the nonresonant contributions in the $D_{s}^{+}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell},$ $D_{s}^{+}\to\pi^{+}\pi^{-}\ell^{+}\nu_{\ell}$ and $D^{+}\to K^{+}K^{-}\ell^{+}\nu_{\ell}$ decays are suppressed by the OZI rule, and the main contributions of these decay branching ratios come from the scalar resonant states. All other decay modes except the $D^{0}\to\pi^{0}\pi^{-}\ell^{+}\nu_{\ell}$ decays receive all three kinds of the contributions, and their branching ratios are dominant by the vector resonant states. Due to the quantum number constraint, the $D^{0}\to\pi^{0}\pi^{-}\ell^{+}\nu_{\ell}$ decays only receive the contributions of the vector resonant states.

In the last columns of Tabs. 2 and 3, total branching ratio predictions of the $D\to P_{1}P_{2}\ell^{+}\nu$ decays including the possible nonresonant, scalar resonant and vector resonant contributions are listed. The present six experimental data with $2\sigma$ errors are also listed in the forth column of Tab. 2 and in third column of Tab. 3 for convenient comparison. One can see that for $\mathcal{B}(D^{0}\to\pi^{-}\overline{K}^{-}e^{+}\nu_{e})$ , $\mathcal{B}(D^{0}\to\pi^{0}K^{-}e^{+}\nu_{e})$ , $\mathcal{B}(D^{+}\to\pi^{+}K^{-}e^{+}\nu_{e})$ , $\mathcal{B}(D^{+}\to\pi^{+}K^{-}\mu^{+}\nu_{\mu})$ , and $\mathcal{B}(D^{+}\to\pi^{+}\pi^{-}e^{+}\nu_{e})$ , our SU(3) flavor symmetry predictions are consistent with present data within $2\sigma$ error bars. Our prediction of $\mathcal{B}(D^{0}\to\pi^{0}\pi^{-}e^{+}\nu_{e})$ is slightly larger than its experimental datum; nevertheless, the prediction will be very close to the datum within $3\sigma$ error bars.

For some Cabibbo suppressed decays due to $c\to d\ell^{+}\nu_{\ell}$ transitions, such as the $D^{0}\to K^{-}K^{0}\ell^{+}\nu_{\ell},$ $D^{0}\to\eta^{\prime}\pi^{-}\ell^{+}\nu_{\ell},$ $D^{+}\to\overline{K}^{0}K^{0}\ell^{+}\nu_{\ell},$ $D^{+}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell}$ , $D^{+}\to\eta\pi^{0}\ell^{+}\nu_{\ell}$ and $D^{+}\to\eta^{\prime}\pi^{0}\ell^{+}\nu_{\ell}$ decays, they only receive both the nonresonant contributions and the scalar resonant contributions, and we can see that both the nonresonant and the scalar resonant contributions are important. The nonresonant contributions in the $D^{+}\to K^{+}K^{-}\ell^{+}\nu_{\ell}$ decays are suppressed by the OZI rule, and the scalar resonant contributions in the $D^{+}\to K^{+}K^{-}\ell^{+}\nu_{\ell}$ decays are dominant.

Please note that the interference terms between nonresonant, scalar, and vector resonant contributions exist. As discussed in Refs. Kang:2013jaa ; Faller:2013dwa , the interference terms between different partial waves vanish upon angular integration in the branching ratios, but they may effect a number of angular observables of these decays, which have not been discussed in this work. Nevertheless, there still are the interference effects between nonresonant and resonant contributions as well as the ones between different scalar resonances in the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays, for example, between $D^{+}\to(a_{0}(980)\to\overline{K}^{0}K^{0})\ell^{+}\nu_{\ell}$ and $D^{+}\to(f_{0}(980)\to\overline{K}^{0}K^{0})\ell^{+}\nu_{\ell}$ . So the interference effects might also be important for the $D^{0}\to\pi^{0}K^{-}\ell^{+}\nu_{\ell},$ $D^{+}_{s}\to\pi^{+}\pi^{-}\ell^{+}\nu_{\ell},$ $D^{+}_{s}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell},$ $D^{0}\to K^{-}K^{0}\ell^{+}\nu_{\ell},$ $D^{0}\to\eta\pi^{-}\ell^{+}\nu_{\ell},$ $D^{0}\to\eta^{\prime}\pi^{-}\ell^{+}\nu_{\ell},$ $D^{+}\to\overline{K}^{0}K^{0}\ell^{+}\nu_{\ell},$ $D^{+}\to\pi^{+}\pi^{-}\ell^{+}\nu_{\ell}$ , $D^{+}\to\pi^{0}\pi^{0}\ell^{+}\nu_{\ell}$ , $D^{+}\to\eta\pi^{0}\ell^{+}\nu_{\ell}$ and $D^{+}\to\eta^{\prime}\pi^{0}\ell^{+}\nu_{\ell}$ decays, in which the two or three kinds of contributions are important. Currently, we cannot determine the size of interference effects by the SU(3) flavor symmetry.

IV Summary

Semileptonic decays of heavy mesons are quite interesting not only because of relatively simple theoretical description but also the clean experimental signals. Some semileptonic decays $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ have been measured by BESIII, CLEO, and $BABAR$ , etc. Using the present data of $\mathcal{B}(D\to P_{1}P_{2}\ell^{+}\nu_{\ell})$ and the SU(3) flavor symmetry, we have presented a theoretical analysis of the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays with the nonresonant, the light scalar meson resonant, and the vector meson resonant contributions.

•

Nonresonant $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays: The amplitude relations including the SU(3) flavor breaking effects have been obtained. Almost all amplitudes can be related after ignoring the OZI suppressed and the SU(3) flavor breaking contributions. Via the experimental data of the nonresonant branching ratios $\mathcal{B}(D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell})_{N}$ , we have predicted other nonresonant branching ratios. We have found that the branching ratios of the nonresonant decays $D^{0}\to\pi^{-}\overline{K}^{0}\ell^{+}\nu_{\ell},\pi^{0}K^{-}\ell^{+}\nu_{\ell}$ , $D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell},\pi^{0}\overline{K}^{0}\ell^{+}\nu_{\ell},\pi^{+}\pi^{-}\ell^{+}\nu_{\ell},\pi^{0}\pi^{0}\ell^{+}\nu_{\ell}$ , and $D^{+}_{s}\to K^{+}K^{-}\ell^{+}\nu_{\ell},K^{0}\overline{K}^{0}\ell^{+}\nu_{\ell}$ are on the order of $\mathcal{O}(10^{-3}-10^{-4})$ , which might be measured by the BESIII, LHCb, and Belle II experiments, and some other decays might be measured at these experiments in the near future.
•

Decays with the light scalar meson resonances: Using the SU(3) flavor symmetry and the present experimental data of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell})$ , $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ as well as $\mathcal{B}(S\to P_{1}P_{2})$ , the not-measured $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ have been obtained by the SU(3) flavor symmetry. We have found that $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ with the $c\to s\ell^{+}\nu_{\ell}$ transitions are predicted on the order of $\mathcal{O}(10^{-3}-10^{-4})$ , and $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},S\to P_{1}P_{2})$ with the $c\to d\ell^{+}\nu_{\ell}$ transitions are predicted on the order of $\mathcal{O}(10^{-4}-10^{-6})$ . The two-quark picture and the four-quark picture for the scalar mesons have been analyzed in the $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays. Present experimental data might favor the four-quark picture for the scalar mesons.
•

Decays with the vector meson resonances: Using the experimental data of $\mathcal{B}(D^{+}\to\overline{K}^{*0}e^{+}\nu_{e},\leavevmode\nobreak\ \overline{K}^{*0}\to\pi^{+}K^{-})$ , $\mathcal{B}(D^{+}\to\overline{K}^{*0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ \overline{K}^{*0}\to\pi^{+}K^{-})$ , many $\mathcal{B}(D\to V\ell^{+}\nu_{\ell})$ and many $\mathcal{B}(V\to P_{1}P_{2})$ , the not-measured $B(D\to V\ell^{+}\nu_{\ell},V\to P_{1}P_{2})$ have been predicted by the SU(3) flavor symmetry. We have found that $\mathcal{B}(D\to V\ell^{+}\nu_{\ell},V\to P_{1}P_{2})$ with the $c\to s\ell^{+}\nu_{\ell}$ transitions are predicted on the order of $\mathcal{O}(10^{-2}-10^{-3})$ , and $\mathcal{B}(D\to V\ell^{+}\nu_{\ell},V\to P_{1}P_{2})$ with the $c\to d\ell^{+}\nu_{\ell}$ transitions are predicted on the order of $\mathcal{O}(10^{-3}-10^{-5})$ .
•

Total branching ratios: Total branching ratio predictions including the possible nonresonant, light scalar meson resonant and vector meson resonant contributions have been obtained. The six total branching ratios have been measured, and we did not use them to further constrain the predictions. Our five predictions are consistent with present data within $2\sigma$ errors, and the prediction of $\mathcal{B}(D^{0}\to\pi^{0}\pi^{-}e^{+}\nu_{e})$ will be very close to the datum within $3\sigma$ error bars. We have found that the vector meson resonant contributions are dominant in the $D^{0}\to\pi^{-}\overline{K}^{0}\ell^{+}\nu_{\ell},\pi^{0}K^{-}\ell^{+}\nu_{\ell},\pi^{0}\pi^{-}\ell^{+}\nu_{\ell}$ , $D^{+}\to\pi^{+}K^{-}\ell^{+}\nu_{\ell},\pi^{0}\overline{K}^{0}\ell^{+}\nu_{\ell},\pi^{+}\pi^{-}\ell^{+}\nu_{\ell}$ , and $D^{+}_{s}\to K^{+}K^{-}\ell^{+}\nu_{\ell},K^{0}\overline{K}^{0}\ell^{+}\nu_{\ell},K^{+}\pi^{-}\ell^{+}\nu_{\ell},K^{0}\pi^{0}\ell^{+}\nu_{\ell}$ decays. All three kinds of contributions are important in $D^{0}\to\eta\pi^{-}\ell^{+}\nu_{\ell}$ decays. Both the nonresonant and the scalar resonant contributions are important in $D^{0}\to K^{-}K^{0}\ell^{+}\nu_{\ell},\eta^{\prime}\pi^{-}\ell^{+}\nu_{\ell}$ and $D^{+}\to\overline{K}^{0}K^{0}\ell^{+}\nu_{\ell},\pi^{0}\pi^{0}\ell^{+}\nu_{\ell},\eta\pi^{0}\ell^{+}\nu_{\ell},\eta^{\prime}\pi^{0}\ell^{+}\nu_{\ell}$ decays.

Although SU(3) flavor symmetry is approximate, it can still provide very useful information about these decays. According to our rough predictions, many decay modes could be observed at BESIII, LHCb, and Belle II, and some decay modes might be measured in near future experiments. Therefore, the SU(3) flavor symmetry will be further tested by these semileptonic decays in future experiments.

ACKNOWLEDGEMENTS

The work was supported by the National Natural Science Foundation of China, No. 12175088.

References

(1) W. Wang and C. D. Lü, Phys. Rev. D 82 (2010), 034016 [arXiv:0910.0613 [hep-ph]].
(2) N. N. Achasov and A. V. Kiselev, Phys. Rev. D 86 (2012), 114010 [arXiv:1206.5500 [hep-ph]].
(3) E. Oset et al. Int. J. Mod. Phys. E 25 (2016), 1630001 [arXiv:1601.03972 [hep-ph]].
(4) M. Ablikim et al. [BESIII], [arXiv:2110.13994 [hep-ex]].
(5) M. Ablikim et al. [BESIII], Phys. Rev. Lett. 122 (2019) no.6, 062001 [arXiv:1809.06496 [hep-ex]].
(6) M. Ablikim et al. [BESIII], Phys. Rev. Lett. 121 (2018) no.8, 081802 [arXiv:1803.02166 [hep-ex]].
(7) M. Ablikim et al. [BESIII], Phys. Rev. D 103 (2021) no.9, 092004 [arXiv:2103.11855 [hep-ex]].
(8) K. M. Ecklund et al. [CLEO], Phys. Rev. D 80 (2009), 052009 [arXiv:0907.3201 [hep-ex]].
(9) P. del Amo Sanchez et al. [BaBar], Phys. Rev. D 83 (2011), 072001 [arXiv:1012.1810 [hep-ex]].
(10) Z. Bai et al. [MARK-III], Phys. Rev. Lett. 66 (1991), 1011-1014.
(11) R. L. Workman et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2022, 083C01 (2022).
(12) X. W. Kang, B. Kubis, C. Hanhart and U. G. Meißner, Phys. Rev. D 89 (2014), 053015 [arXiv:1312.1193 [hep-ph]].
(13) Y. J. Shi, W. Wang and S. Zhao, Eur. Phys. J. C 77 (2017) no.7, 452 [arXiv:1701.07571 [hep-ph]].
(14) Y. J. Shi, C. Y. Seng, F. K. Guo, B. Kubis, U. G. Meißner and W. Wang, JHEP 04 (2021), 086 [arXiv:2011.00921 [hep-ph]].
(15) S. Cheng, A. Khodjamirian and J. Virto, JHEP 05 (2017), 157 [arXiv:1701.01633 [hep-ph]].
(16) T. Sekihara and E. Oset, Phys. Rev. D 92 (2015) no.5, 054038 [arXiv:1507.02026 [hep-ph]].
(17) C. Hambrock and A. Khodjamirian, Nucl. Phys. B 905 (2016), 373-390 [arXiv:1511.02509 [hep-ph]].
(18) P. Böer, T. Feldmann and D. van Dyk, JHEP 02 (2017), 133 [arXiv:1608.07127 [hep-ph]].
(19) X. G. He, Eur. Phys. J. C 9, 443 (1999) [hep-ph/9810397].
(20) X. G. He, Y. K. Hsiao, J. Q. Shi, Y. L. Wu and Y. F. Zhou, Phys. Rev. D 64, 034002 (2001) [hep-ph/0011337].
(21) H. K. Fu, X. G. He and Y. K. Hsiao, Phys. Rev. D 69, 074002 (2004) [hep-ph/0304242].
(22) Y. K. Hsiao, C. F. Chang and X. G. He, Phys. Rev. D 93, no. 11, 114002 (2016) [arXiv:1512.09223 [hep-ph]].
(23) X. G. He and G. N. Li, Phys. Lett. B 750, 82 (2015) [arXiv:1501.00646 [hep-ph]].
(24) M. Gronau, O. F. Hernandez, D. London and J. L. Rosner, Phys. Rev. D 50, 4529 (1994) [hep-ph/9404283].
(25) M. Gronau, O. F. Hernandez, D. London and J. L. Rosner, Phys. Rev. D 52, 6356 (1995) [hep-ph/9504326].
(26) S. H. Zhou, Q. A. Zhang, W. R. Lyu and C. D. Lü, Eur. Phys. J. C 77, no. 2, 125 (2017) [arXiv:1608.02819 [hep-ph]].
(27) H. Y. Cheng, C. W. Chiang and A. L. Kuo, Phys. Rev. D 91, no. 1, 014011 (2015) [arXiv:1409.5026 [hep-ph]].
(28) M. He, X. G. He and G. N. Li, Phys. Rev. D 92, no. 3, 036010 (2015) [arXiv:1507.07990 [hep-ph]].
(29) N. G. Deshpande and X. G. He, Phys. Rev. Lett. 75, 1703 (1995) [hep-ph/9412393].
(30) S. Shivashankara, W. Wu and A. Datta, Phys. Rev. D 91, 115003 (2015) [arXiv:1502.07230 [hep-ph]].
(31) R. M. Wang, Y. G. Xu, C. Hua and X. D. Cheng, Phys. Rev. D 103 (2021) no.1, 013007 [arXiv:2101.02421 [hep-ph]].
(32) R. M. Wang, X. D. Cheng, Y. Y. Fan, J. L. Zhang and Y. G. Xu, J. Phys. G 48 (2021), 085001 [arXiv:2008.06624 [hep-ph]].
(33) Y. Grossman and D. J. Robinson, JHEP 1304, 067 (2013) [arXiv:1211.3361 [hep-ph]].
(34) D. Pirtskhalava and P. Uttayarat, Phys. Lett. B 712, 81 (2012) [arXiv:1112.5451 [hep-ph]].
(35) M. J. Savage and R. P. Springer, Phys. Rev. D 42, 1527 (1990).
(36) M. J. Savage, Phys. Lett. B 257, 414 (1991).
(37) G. Altarelli, N. Cabibbo and L. Maiani, Phys. Lett. 57B, 277 (1975).
(38) C. D. Lü, W. Wang and F. S. Yu, Phys. Rev. D 93, no. 5, 056008 (2016) [arXiv:1601.04241 [hep-ph]].
(39) C. Q. Geng, Y. K. Hsiao, Y. H. Lin and L. L. Liu, Phys. Lett. B 776, 265 (2018) [arXiv:1708.02460 [hep-ph]].
(40) C. Q. Geng, Y. K. Hsiao, C. W. Liu and T. H. Tsai, Phys. Rev. D 97, no. 7, 073006 (2018) [arXiv:1801.03276 [hep-ph]].
(41) C. Q. Geng, Y. K. Hsiao, C. W. Liu and T. H. Tsai, JHEP 1711, 147 (2017) [arXiv:1709.00808 [hep-ph]].
(42) C. Q. Geng, C. W. Liu, T. H. Tsai and S. W. Yeh, arXiv:1901.05610 [hep-ph].
(43) W. Wang, Z. P. Xing and J. Xu, Eur. Phys. J. C 77, no. 11, 800 (2017) [arXiv:1707.06570 [hep-ph]].
(44) D. Wang, arXiv:1901.01776 [hep-ph].
(45) D. Wang, P. F. Guo, W. H. Long and F. S. Yu, JHEP 1803, 066 (2018) [arXiv:1709.09873 [hep-ph]].
(46) S. Müller, U. Nierste and S. Schacht, Phys. Rev. D 92, no. 1, 014004 (2015) [arXiv:1503.06759 [hep-ph]].
(47) R. M. Wang, M. Z. Yang, H. B. Li and X. D. Cheng, Phys. Rev. D 100 (2019) no.7, 076008 [arXiv:1906.08413 [hep-ph]].
(48) Y. G. Xu, X. D. Cheng, J. L. Zhang and R. M. Wang, J. Phys. G 47 (2020) no.8, 085005 [arXiv:2001.06907 [hep-ph]].
(49) H. M. Chang, M. González-Alonso and J. Martin Camalich, Phys. Rev. Lett. 114 (2015), 161802 [arXiv:1412.8484 [hep-ph]].
(50) P. Zenczykowski, Phys. Rev. D 73 (2006), 076005 [arXiv:hep-ph/0512122 [hep-ph]].
(51) P. Zenczykowski, Nucl. Phys. B Proc. Suppl. 167 (2007), 54-57 [arXiv:hep-ph/0610191 [hep-ph]].
(52) N. Cabibbo, Phys. Rev. Lett. 10 (1963), 531-533.
(53) H. Y. Cheng and C. W. Chiang, Phys. Rev. D 86, 014014 (2012) [arXiv:1205.0580 [hep-ph]].
(54) A. Dery, M. Ghosh, Y. Grossman and S. Schacht, JHEP 03 (2020), 165 [arXiv:2001.05397 [hep-ph]].
(55) S. Sasaki and T. Yamazaki, Phys. Rev. D 79 (2009), 074508 [arXiv:0811.1406 [hep-ph]].
(56) T. N. Pham, Phys. Rev. D 87 (2013) no.1, 016002 [arXiv:1210.3981 [hep-ph]].
(57) C. Q. Geng, Y. K. Hsiao, C. W. Liu and T. H. Tsai, Eur. Phys. J. C 78 (2018) no.7, 593 [arXiv:1804.01666 [hep-ph]].
(58) R. Flores-Mendieta, E. E. Jenkins and A. V. Manohar, Phys. Rev. D 58 (1998), 094028 [arXiv:hep-ph/9805416 [hep-ph]].
(59) D. Xu, G. N. Li and X. G. He, Int. J. Mod. Phys. A 29 (2014), 1450011 [arXiv:1307.7186 [hep-ph]].
(60) X. G. He, G. N. Li and D. Xu, Phys. Rev. D 91 (2015) no.1, 014029 [arXiv:1410.0476 [hep-ph]].
(61) Y. J. Shi and U. G. Meißner, Eur. Phys. J. C 81 (2021) no.5, 412 [arXiv:2103.12977 [hep-ph]].
(62) C. S. Kim, G. L. Castro and S. L. Tostado, Phys. Rev. D 95 (2017) no.7, 073003 [arXiv:1702.01704 [hep-ph]].
(63) N. N. Achasov, A. V. Kiselev and G. N. Shestakov, Phys. Rev. D 104 (2021) no.1, 016034 [arXiv:2106.10670 [hep-ph]].
(64) J. Wiss, eConf C070805 (2007), 34 [arXiv:0709.3247 [hep-ex]].
(65) W. Wang, Phys. Lett. B 759 (2016), 501-506 [arXiv:1602.05288 [hep-ph]].
(66) N. N. Achasov, A. V. Kiselev and G. N. Shestakov, Phys. Rev. D 102 (2020) no.1, 016022 [arXiv:2005.06455 [hep-ph]].
(67) S. Faller, T. Feldmann, A. Khodjamirian, T. Mannel and D. van Dyk, Phys. Rev. D 89 (2014) no.1, 014015 [arXiv:1310.6660 [hep-ph]].
(68) X. G. He, Y. J. Shi and W. Wang, Eur. Phys. J. C 80, no.5, 359 (2020) [arXiv:1811.03480 [hep-ph]].
(69) H. Y. Cheng, C. K. Chua and K. C. Yang, Phys. Rev. D 73 (2006), 014017 [arXiv:hep-ph/0508104 [hep-ph]].
(70) L. Maiani, F. Piccinini, A. D. Polosa and V. Riquer, Phys. Rev. Lett. 93 (2004), 212002 [arXiv:hep-ph/0407017 [hep-ph]].
(71) L. Y. Dai, X. W. Kang and U. G. Meißner, Phys. Rev. D 98 (2018) no.7, 074033 [arXiv:1808.05057 [hep-ph]].
(72) G. ’t Hooft, G. Isidori, L. Maiani, A. D. Polosa and V. Riquer, Phys. Lett. B 662 (2008), 424-430 [arXiv:0801.2288 [hep-ph]].
(73) J. R. Pelaez, Phys. Rev. Lett. 92 (2004), 102001 [arXiv:hep-ph/0309292 [hep-ph]].
(74) Y. J. Sun, Z. H. Li and T. Huang, Phys. Rev. D 83 (2011), 025024 [arXiv:1011.3901 [hep-ph]].
(75) J. A. Oller and E. Oset, Nucl. Phys. A 620 (1997), 438-456 [erratum: Nucl. Phys. A 652 (1999), 407-409] [arXiv:hep-ph/9702314 [hep-ph]].
(76) V. Baru, J. Haidenbauer, C. Hanhart, Y. Kalashnikova and A. E. Kudryavtsev, Phys. Lett. B 586 (2004), 53-61 [arXiv:hep-ph/0308129 [hep-ph]].
(77) N. N. Achasov, V. V. Gubin and V. I. Shevchenko, Phys. Rev. D 56 (1997), 203-211 doi:10.1103/PhysRevD.56.203 [arXiv:hep-ph/9605245 [hep-ph]].
(78) S. Momeni and M. Saghebfar, Eur. Phys. J. C 82 (2022) no.5, 473.
(79) R. Aaij et al. [LHCb], Phys. Rev. D 87 (2013) no.5, 052001 [arXiv:1301.5347 [hep-ex]].
(80) R. L. Jaffe, Phys. Rev. D 15 (1977), 267.
(81) Ru-Min Wang, Yue-Xin Liu, Chong Hua, Jin-Huan Sheng, Yuan-Guo Xu, arXiv:2301.00079[hep-ph].
(82) S. Okubo, Phys. Lett. 5 (1963), 165-168.
(83) H. J. Lipkin, Nucl. Phys. B 291 (1987), 720-730.
(84) H. J. Lipkin and B. s. Zou, Phys. Rev. D 53 (1996), 6693-6696.
(85) H. Y. Cheng and C. K. Chua, Phys. Rev. D 102 (2020) no.5, 053006 [arXiv:2007.02558 [hep-ph]].
(86) J. Hietala, D. Cronin-Hennessy, T. Pedlar and I. Shipsey, Phys. Rev. D 92 (2015) no.1, 012009 [arXiv:1505.04205 [hep-ex]].

	$\displaystyle\|\mathcal{N}\|^{2}$	$\displaystyle=$	$\displaystyle G_{F}^{2}\|V_{cq}\|^{2}\frac{\beta_{\ell}q^{2}\sqrt{\lambda(m_{D}^{2},q^{2},k^{2})}}{3\cdot 2^{10}\pi^{5}m_{D}^{3}}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{with}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \beta_{\ell}=1-\frac{m_{\ell}^{2}}{q^{2}},$
	$\displaystyle\|F_{A}\|^{2}$	$\displaystyle=$	$\displaystyle\|F_{0}\|^{2}+\frac{2}{3}(\|F_{\parallel}\|^{2}+\|F_{\perp}\|^{2})+\frac{3m_{\ell}^{2}}{q^{2}(3-\beta_{\ell})}\|F_{t}\|^{2},$		(10)

$\displaystyle\|g_{K^{*-}\to\pi^{-}K^{0}}\|=4.62\pm 0.08,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\|g_{K^{*0}\to\pi^{-}K^{+}}\|=4.40\pm 0.10,$	(70)
$\displaystyle\|g_{\rho^{-}\to\pi^{0}\pi^{-}}\|=6.00\pm 0.03,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\|g_{\rho^{0}\to\pi^{+}\pi^{-}}\|=5.95\pm 0.04,$
$\displaystyle\|g_{\phi\to K^{+}K^{-}}\|=4.47\pm 0.08,\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\$	$\displaystyle\|g_{\omega\to\pi^{+}\pi^{-}}\|=0.18\pm 0.02.$

Four-body Semileptonic Charm Decays D→P1​P2​ℓ+​νℓD\to P_{1}P_{2}\ell^{+}\nu_{\ell} Based on SU(3) Flavor Analysis

Abstract

I INTRODUCTION

II Theoretical frame

II.1 Decay branching ratios

II.2 Meson multiplets

II.3 Nonresonant hadronic amplitudes

III Numerical results of the D→P1​P2​ℓ+​νD\to P_{1}P_{2}\ell^{+}\nu decays

III.1 Nonresonant D→P1​P2​ℓ+​νD\to P_{1}P_{2}\ell^{+}\nu decays

III.2 D→S​(S→P1​P2)​ℓ+​νℓD\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell} decays

III.2.1 Branching ratios of the S→P1​P2S\to P_{1}P_{2} decays

III.2.2 Branching ratios of the D→S​(S→P1​P2)​ℓ+​νℓD\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell} decays

III.3 D→V​(V→P1​P2)​ℓ+​νℓD\to V(V\to P_{1}P_{2})\ell^{+}\nu_{\ell} decays

III.4 Total branching ratios

IV Summary

ACKNOWLEDGEMENTS

References

References

Four-body Semileptonic Charm Decays $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ Based on
SU(3) Flavor Analysis

III Numerical results of the $D\to P_{1}P_{2}\ell^{+}\nu$ decays

III.1 Nonresonant $D\to P_{1}P_{2}\ell^{+}\nu$ decays

III.2 $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays

III.2.1 Branching ratios of the $S\to P_{1}P_{2}$ decays

III.2.2 Branching ratios of the $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays

III.3 $D\to V(V\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays