Fractal features in accretion discs
Abstract
Fractal concepts have been introduced in the accretion disc as a new feature. Due to the fractal nature of the flow, its continuity condition undergoes modifications. The conserved stationary fractal flow admits only saddle points and centre-type points in its phase portrait. Completely analytical solutions of the equilibrium point conditions indicate that the fractal properties enable the flow to behave like an effective continuum of lesser density, and facilitates the generation of transonicity. However, strongly fractal flows inhibit multitransonicity from developing. The mass accretion rate exhibits a fractal scaling behaviour, and the entire fractal accretion disc is stable under linearised dynamic perturbations.
keywords:
accretion, accretion discs – black hole physics – hydrodynamics1 Introduction
Accretion processes are understood to be the non-self-gravitating flow of a compressible astrophysical fluid, driven by the external gravitational field of a massive astrophysical object, like an ordinary star or a compact object or, what is perhaps of greatest interest in the context of accretion studies, a black hole. The matter falling into the potential well of an accretor is commonly modelled in terms of a fluid continuum, and standard fluid dynamical equations, customized in the Newtonian framework of space and time, suffice well to provide a satisfactory description of the entire accretion process (Frank et al., 2002). While this be so, in recent times fractal modelling of astrophysical accretion is generating some interest (Roy, 2007; Roy & Ray, 2007). One astrophysical material that ought readily to lend itself to a fractal approach — as opposed to a continuum approach — is the interstellar medium (ISM). It is recognised that the ISM is not entirely to be seen as a fluid continuum, and for many purposes the ISM is believed to possess a self-similar hierarchical structure over several orders of magnitude in scale (Larson, 1981; Falgarone et al., 1992; Heithausen et al., 1998). Direct H i absorption observations and interstellar scintillation measurements suggest that the structure extends down to a scale of (Crovisier et al., 1985; Langer et al., 1995; Faison et al., 1998) and possibly even to sub- scales (Hill et al., 2005). Numerous theories have attempted to explain the origin, evolution and mass distribution of these clouds and it has been established, from both observations (Elmegreen & Falgarone, 1996) and numerical simulations (Burkert et al., 1997; Klessen et al., 1998; Semelin & Combes, 2000), that the interstellar medium has a clumpy hierarchical self-similar structure with a fractal dimension in three-dimensional space. The main reason for this is still not properly understood, but it can be the consequence of an underlying fractal geometry that may arise due to turbulent processes in the medium.
A comprehensive mathematical description of an accreting system — either a fluid continuum or a fractal structure — will necessarily have to fall within the broad domain of nonlinear dynamics. This is the principal basis of the analytical methods adopted for this study. In the context of spherically symmetric accretion, a previous work furnished a self-consistent description of the hydrodynamics in a fractal medium (Roy, 2007). A similar description has been provided in this work for the case of a conserved rotational flow, which, from a general fluid dynamical perspective, has become quite thoroughly understood (Chandrasekhar, 1981). In the context of accretion studies particularly, on many occasions such flows are devised to be an inviscid sub-Keplerian compressible flow, and as such, this model has become well-established in accretion-related literature by now (Abramowicz & Zurek, 1981; Fukue, 1987; Chakrabarti, 1989; Nakayama & Fukue, 1989; Chakrabarti, 1990; Kafatos & Yang, 1994; Yang & Kafatos, 1995; Pariev, 1996; Molteni et al., 1996; Chakrabarti, 1996; Lu et al., 1997; Das, 2002; Das et al., 2003; Ray, 2003; Barai et al., 2004; Das, 2004; Abraham et al., 2006; Das et al., 2007; Chaudhury et al., 2006; Goswami et al., 2007). As a first step, the physical processes in a fractal medium have been analysed by fractional integration and differentiation (Zaslavsky, 2002, and references therein). To do so, the fractal medium has had to be replaced by a continuous medium and the integrals on the network of the fractal medium has had to be approximated by fractional integrals (Ren et al., 2003). The interpretation of fractional integration is connected with fractional mass dimension (Mandelbrot, 1983). Fractional integrals can be considered as integrals over fractional dimension space within a numerical factor (Tarasov, 2004). This numerical factor has been chosen suitably to get the right dimension of any physical parameter and to derive the standard expression in the continuum limit. The isotropic and homogeneous nature of dimensionality, in the context of an axisymmetric flow, has also been incorporated properly.
Having established the hydrodynamic equivalence, a standard mathematical path has been followed to set up the steady fractal flow like a simple first-order autonomous dynamical system (Strogatz, 1994; Jordan & Smith, 1999) and investigate the resulting critical properties, especially the transonic character of the flow. A general prediction that can be made about the conserved steady fractal disc flow is that the equilibrium conditions will only permit the existence of saddle points and centre-type points in the phase portrait of the flow. Fully analytical methods have been employed to identify the exact critical point coordinates, under a pseudo-Newtonian prescription to study the infall process. Two very significant effects of fractal properties can be discerned in consequence of this. The first is that fractal accretion flows assume the properties of an equivalent continuum, albeit one with a more diluted effective local flow density, a result that is also known to be true for the case of spherically symmetric flows (Roy & Ray, 2007)111In the context of fractals, it would be interesting to note a similar equivalence between the discrete model of diffusion-limited aggregation and the continuum dendritic growth model (Witten & Sander, 1981).. The second effect is that fractal properties have an inhibitory influence on the multitransonic character that is commonly associated with these flows (Chakrabarti, 1989, 1990, 1996; Das, 2002, 2004). Taken together, the overall effect of strongly fractal features in a disc flow is to lend it the appearance of the spherically symmetric monotransonic flow — the paradigmatic Bondi (1952) solution.
In the Newtonian limit the mass accretion rate in a fractal flow exhibits a scaling behaviour that is governed by the fractal dimension of the flow. This scaling behaviour may have many interesting astrophysical implications. One particular case, that of accretion processes onto a pre-main-sequence (PMS) star, should have a close connection with this fractal scaling relation. It has also been shown that the stability of fractal flows under linearised time-dependent perturbations, is governed by the same equation pertaining to a standard perturbation scheme that has been used earlier for studying continuum sub-Keplerian disc flows (Ray, 2003; Chaudhury et al., 2006; Ray & Bhattacharjee, 2007). Given that the boundary conditions do not vary between the continuum case and the fractal case, all steady global solutions (transonic or otherwise) are, therefore, stable. Since fractal disc flows tend to acquire the character of spherically symmetric flows, it has become possible to invoke the analogy of the non-perturbative and dynamic evolution of the spherically symmetric flow towards its transonic state (Ray & Bhattacharjee, 2002; Roy & Ray, 2007), and suggest that in a fractal disc, the drive towards transonicity would also occur under identical guiding principles.
It would be important to note that the entire analytical treatment has been carried out in the pseudo-Newtonian formalism, with the mathematical results expressed in terms of a general potential, whose resulting force field would drive the accretion process. So most of the conclusions reached here will remain independent of the choice of a potential. However, the specific numerical plots which have been presented here, have all been derived by using the Paczyński & Wiita (1980) potential for a polytropic gas flow. In spite of this, the general claims made on the basis of these particular numerical results will suffer no qualitative alteration, under the choice of any other pseudo-Newtonian potential (Nowak & Wagoner, 1991; Artemova et al., 1996), or for an isothermal gas flow (Das et al., 2003).
2 The hydrodynamic equations for axisymmetric fractal accretion
Considering a thin accretion disc that has density fluctuations over a range of length scales, it should be possible to propose that these density fluctuations or “clumpiness” can be approximated as a fractal structure along the radial direction in the disc. This will be especially true in the thin-disc regime, where there is not much scope for significant variations to occur in the vertical direction (Frank et al., 2002). The integrals on this network of fractals can consequently be approximated by fractional integrals (Ren et al., 2003), and the interpretation of this fractional integration can be connected to the fractional mass dimension. This approximation has already been used to describe the fractal structure of spherically symmetrical accretion by Roy (2007). Likewise, a similar transformation of the infinitesimal length of the “clumpy” accretion disc is being employed here to describe it in terms of an equivalent “fractional continuous” disc. The fractional infinitesimal length for such a structure will be given by
| (1) |
with being the inner length scale of the structure, representing the physical scale of length at which the density is correlated. The fractal dimension of the accretion disc is given as . Hence, the mass enclosed in a thin disc of density, , radius, , and thickness, , will be
| (2) |
which, quite obviously, will give the standard expression in the limit .
Since there is no flow in the direction (perpendicular to the plane of the disc), the condition of hydrostatic equilibrium (Frank et al., 2002), by balancing the pressure gradient and the gravitational force acting on a fluid element in the –– space, will give
| (3) |
in which is the gas pressure, and is the gravitational potential of the central accretor that drives the flow (with the prime denoting the spatial derivative of the potential). In the case of stellar accretion, the flow is driven by the Newtonian potential, . On the other hand, frequently in studies of black hole accretion, it becomes convenient to use an effective pseudo-Newtonian potential that imitates general relativistic effects in the Newtonian construct of space and time (Paczyński & Wiita, 1980; Nowak & Wagoner, 1991; Artemova et al., 1996).
Along with the definition of a polytropic equation of state (Chandrasekhar, 1939), (with the polytropic exponent, , having the range ), equation (3) can be simplified to give the condition for the thin-disc approximation (Frank et al., 2002) as
| (4) |
in which the local speed of sound, , has been defined by . This definition, as well as the form of in equation (4), will be instrumental in determining the mass density balance (the continuity condition) in a conserved fractal accretion disc. For an infinitesimal volume of the fractal medium, , this balance will be given by
| (5) |
Making note of the connection that for the axisymmetric thin disc flow, a more informative form of equation (5) can be derived as
| (6) |
in which is the surface density, defined by (Frank et al., 2002). Using the thin-disc approximation, as given by equation (4), one can recast equation (6) further as
| (7) |
where . The foregoing expression gives the mass density balance equation (the continuity equation) for the axisymmetric fractal flow.
Similarly, in the infinitesimal volume, , the balance of momentum density will imply
| (8) |
with being the velocity vector, and being, respectively, the gravitational and centrifugal forces acting on the mass contained in the infinitesimal volume, , and being the total surface force due to the pressure acting on the full surface bounding the volume, . The first two forces have radial components only, and their magnitudes are given by
| (9) |
and
| (10) |
respectively, with in the latter being the constant specific angular momentum of the conserved disc flow (Chakrabarti, 1989, 1990, 1996). On the other hand, has , and components. However, only the radial component is relevant for the axisymmetric thin-disc flow. Any volume element, , experiences a force, , due to the pressure exerted on it by the surrounding medium (Landau & Lifshitz, 1987). Translating this effect onto an infinitesimal volume element of the fractal medium, the magnitude of the radial component of the force, , can be set down as
| (11) |
Now going back to the left-hand side of equation (8), the total change of radial momentum is extracted as
| (12) |
a result that could be derived by invoking the continuity condition, as it is given by equation (5). And so, making use of equations (9), (10), (11) and (12) in equation (8), it becomes possible to obtain the final momentum balance condition for the conserved fractal disc flow as
| (13) |
which actually gives a local conservation law and, as expected, has exactly the same form as that of the continuous medium. The fractal flow can now be described completely by equations (7) and (13), both of which describe the dynamics of the fields and , with the pressure, , having been defined as a function of .
3 The stationary fractal flow and its fixed points
It is a standard practice to consider a steady flow while studying accreting systems (Frank et al., 2002). The two corresponding stationary equations which determine the drift in the radial direction, can be obtained from equations (7) and (13) as
| (14) |
and
| (15) |
respectively. The pressure, , is prescribed by an equation of state for the flow (Chandrasekhar, 1939). As a general polytropic it is, as usual, given as , while for an isothermal flow the pressure is given by , in all of which, is a measure of the entropy in the flow, is the polytropic exponent, is Boltzmann’s constant, is the constant temperature, is the mass of a hydrogen atom and is the reduced mass, respectively. Since the local speed of sound is defined as , the way in which has been prescribed (Frank et al., 2002) will affect the transonic features of the flow, because transonicity, and all its related critical aspects, are measured by scaling the bulk flow velocity with respect to the local speed of sound. So the exact form of has distinctive consequences, and in what follows, the flow properties will be taken up separately for the two cases, i.e. polytropic and isothermal.
3.1 Polytropic flows
With the polytropic relation specified for , it is a straightforward exercise to set down in terms of the speed of sound, , a first integral of equation (15) as,
| (16) |
in which and the integration constant is the Bernoulli constant. The first integral of equation (14) could similarly be obtained as
| (17) |
where (Chakrabarti, 1990, 1996) with , an integration constant itself, being physically the matter flow rate.
To obtain the critical points of the flow, it should be necessary first to differentiate both equations (16) and (17), and then, on combining the two resulting expressions, to arrive at
| (18) |
with . The critical points of the flow will be given by the condition that the entire right-hand side of equation (18) will vanish along with the coefficient of . Explicitly written down, following some rearrangement of terms, this will give the two critical point conditions as
| (19) |
with the subscript “” labelling critical point values.
To fix the critical point coordinates, and , in terms of the system constants, one would have to make use of the conditions given by equations (19), along with equation (16), to obtain
| (20) |
from which it is easy to see that solutions of may be obtained in terms of , , (or ) and only, i.e. . Alternatively, could be fixed in terms of , , and . By making use of the critical point conditions in equation (17), one could write
| (21) |
whose obvious implication is that the dependence of will be given as .
The slope of the continuous solutions which could possibly pass through the critical points are to be obtained by applying the L’Hospital rule on equation (18), at the critical points. This will give a quadratic equation for the slope of the stationary solutions at the critical points themselves in the — phase portrait. The resulting expression will read as
| (22) |
in which the constant coefficients, and , are given by
and
respectively.
3.2 Isothermal flows
For isothermal flows, a linear dependence between and is applied in equation (15), as the appropriate equation of state. On doing so, the first integral of equation (15) is given as
| (23) |
with being a constant of integration. For flow solutions which specifically decay out to zero at very large distances, the constant can be determined in terms of the “ambient conditions” as . The thickness of the disc, , is determined simply by setting in equation (4), and in a likewise manner the first integral of equation (14) will imply the continuity condition as
| (24) |
As has been done for polytropic flows, both equations (23) and (24) are to be differentiated and the results combined to give
| (25) |
from which the critical point conditions are easily identified as
| (26) |
In this isothermal system, the speed of sound, , is a global constant, and so having arrived at the critical point conditions, it should be easy to see that and have already been fixed in terms of a global constant of the system. The speed of sound can further be written in terms of the temperature of the system as , where , and, therefore, it should be entirely possible to give a functional dependence for , as . The slope of the stationary solutions passing through the critical points in the — phase portrait is obtained simply by setting in equation (22).
4 The fractal accretion disc as a dynamical system
The equations governing the flow in an accreting system are all fluid dynamical equations, and, in the kind of inviscid regime chosen for this study, fall under the general category of first-order nonlinear differential equations (Jordan & Smith, 1999). However, there is no standard prescription for deriving rigorously analytical solutions of these equations. In this situation, while a numerical integration of the flow equations is most often the only recourse, an alternative approach could also be adopted by setting up the governing equations to form a standard first-order dynamical system (Strogatz, 1994; Jordan & Smith, 1999). This is a very usual practice in general fluid dynamical studies (Bohr et al., 1993), and avoiding involved numerical processes, this approach allows one to derive significant physical insight about the behaviour of the flows. To take a first step towards this end, for the stationary polytropic flow, as it has been given by equation (18), it should be necessary to parametrise this equation and set up a coupled autonomous first-order dynamical system as (Strogatz, 1994; Jordan & Smith, 1999)
| (27) |
with being an arbitrary mathematical parameter. Apropos of accretion studies, this kind of parametrisation has been reported before (Ray & Bhattacharjee, 2002; Afshordi & Paczyński, 2003; Chaudhury et al., 2006; Ray & Bhattacharjee, 2007; Mandal et al., 2007; Goswami et al., 2007). Some earlier works in accretion had also made use of the general mathematical aspects of this approach (Matsumoto et al., 1984; Muchotrzeb-Czerny, 1986; Abramowicz & Kato, 1989)
The critical points have themselves been fixed in terms of the flow constants. About these fixed point values, on applying a perturbation prescription of the kind , and , one could derive a set of two autonomous first-order linear differential equations in the — plane, with itself having to be first expressed in terms of and , with the help of equation (17) as
| (28) |
The resulting coupled set of linear equations in and will be given as
| (29) |
in which
Trying solutions of the kind and in equations (4), will lead to an expression for the eigenvalues, , of the stability matrix, as
| (30) |
where .
For isothermal flows, starting from equation (25), a similar expression for the related eigenvalues may also be derived, and it can be shown that this will correspond simply to the special case of in equation (30). Once a critical point coordinate, (), has been ascertained, it becomes an easy task to find the nature of that critical point by using in equation (30). Since it has been discussed in Section 3 that is a function of , , and for isothermal flows, and a function of , , and (or ) for polytropic flows, it effectively implies that can be expressed as a function of the flow parameters for either kind of flow. A generic conclusion that can be drawn about the critical points from the form of in equation (30), is that for a conserved pseudo-Schwarzschild fractal disc flow, the only admissible critical points will be saddle points and centre-type points. For a saddle point, , while for a centre-type point, . Once the behaviour of all the physically relevant critical points has been understood in this way, a complete qualitative picture of the flow solutions passing through these points (if they are saddle points), or in the neighbourhood of these points (if they are centre-type points), can be constructed, along with an impression of the direction that these solutions can have in the phase portrait of the flow (Strogatz, 1994; Jordan & Smith, 1999). An earlier study has shown how the critical point behaviour (and multitransonicity) varies with flow parameters like and (Chaudhury et al., 2006). Similar aspects of the accretion disc will be considered now with respect to the fractal properties in the flow.
5 Multitransonicity in relation to fractal features
Multitransonicity in the flow is possible when there are more than one critical point through which a continuous solution will pass, connecting the event horizon of the accretor to the outer boundary of the flow. Saddle points are most likely to fulfil this requirement, and so multitransonicity would imply the existence of more than one saddle point in the phase portrait of the flow. Disc flows, conserved or otherwise, have been known to be multitransonic (Liang & Thomson, 1980; Chakrabarti, 1990, 1996) with a variety of implications, most notably in regard to shock formation (Chakrabarti, 1990, 1996; Das, 2002). So a clear knowledge of the number of critical points in the flow, and their nature, is essential to understanding multitransonicity.
For a general polytropic flow, the position of the critical points can be determined by extracting the roots from either equation (20) or (21), after prescribing an explicit functional form for the pseudo-Newtonian potential, . Various prescriptions are used for , depending upon specific necessities (Paczyński & Wiita, 1980; Nowak & Wagoner, 1991; Artemova et al., 1996), but all of these potentials have the common purpose of describing general relativistic effects in a semi-Newtonian framework, by avoiding the difficulties of a purely general relativistic treatment. One such potential that is very regularly invoked in accretion-related literature, is due to Paczyński & Wiita (1980). It is given as
| (31) |
in which the radial distance, , has been scaled by the Schwarzschild radius, , which follows the standard definition of , with being the mass of the black hole, the universal gravitational constant, and the velocity of light in vacuum. All relevant velocities will be scaled with respect to , and for convenience one may set . All derived quantities like energy and angular momentum will be scaled accordingly (Das, 2002).
Using the functional form of , given by equation (31), in equation (20), will lead to a quartic polynomial in the standard form
| (32) |
in which
It is not difficult to see that equation (32) will yield four roots. These roots can be found completely analytically by using Ferrari’s method for solving quartic equations. In order to do so, a term going like is to be added to both sides of equation (32), and then the resulting left hand side is required to be a perfect square in the form , so that the full equation will be rendered as . This will give three conditions going as
| (33) |
Eliminating and , will deliver an auxiliary cubic equation in , going as
| (34) |
which, under the transformation, , can be reduced to the canonical form of the cubic equation,
| (35) |
with
Completely analytical solutions for the roots of equation (35) can be obtained by the application of the Cardano-Tartaglia-del Ferro method for solving cubic equations. This will lead to the solution
| (36) |
with the discriminant, , having been defined by
| (37) |
The sign of is crucial here. If , then there will be only one real root of given directly by equation (36). On the other hand, if , then there will be three real roots of , all of which, under a new definition,
| (38) |
can be expressed in a slightly modified form as
| (39) |
with the label taking the values , respectively, for the three distinct roots.
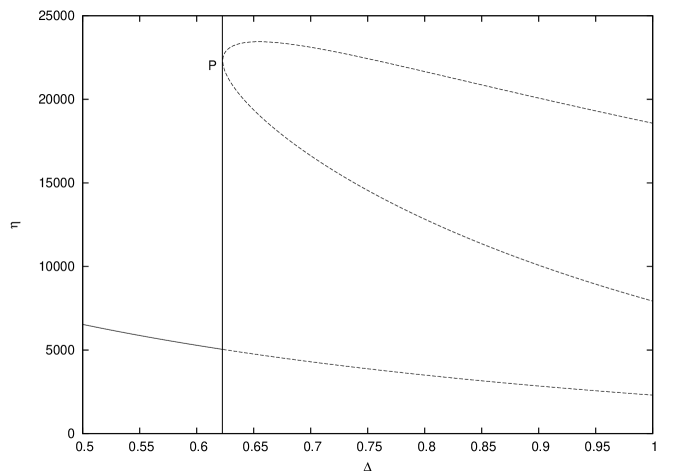
Quite evidently, the sign of and, in consequence, the number of real roots of will be determined by the value of the flow parameters like , , and (on which depends). For fixed representative values of three of these parameters — , and — the continuously varying dependence of on has been shown in Fig. 1. The two distinct regions in the plot, corresponding to and , show the existence of a single and triple real roots, respectively. The one root that runs continuously across both the regions is the one that will be relevant for all subsequent analysis.
Once is known, it is a simple task thereafter to know the value of , and . With this having been accomplished, all the four roots of from equation (32) can be identified by solving the two distinct quadratic equations,
| (40) |
corresponding to the two signs on the right hand side. Each of these roots will determine the spatial position of a critical point in the flow space. Of these four roots, one is always real, and it is always located within the event horizon of the central black hole. Hence, it will be irrelevant for this study. Of the other three roots, one remains always real, while the other two, depending on the flow parameters, can only be either both real or both complex (complex roots always occur in pairs). In the former case there will, therefore, be three real roots on physically relevant length scales outside the event horizon, and this situation will correspond to multitransonicity.
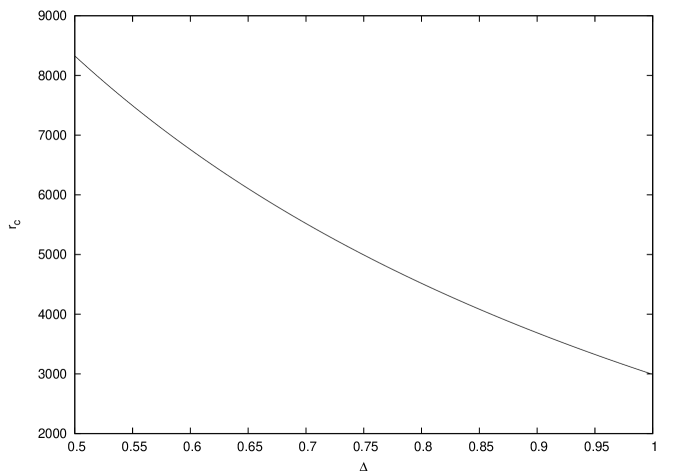
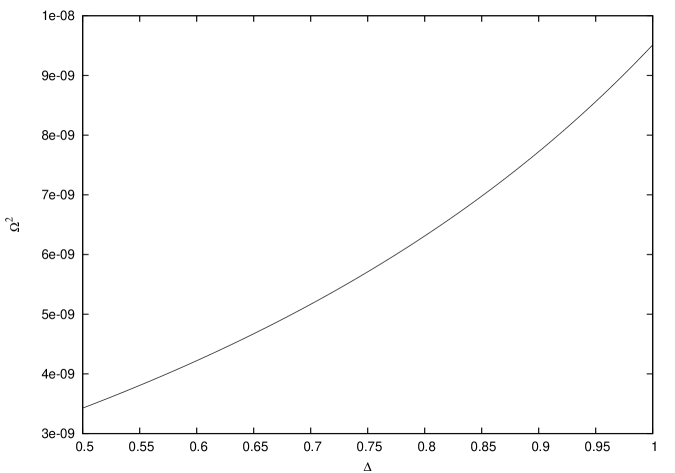
Taking up the case of the root that always remains real at a given physical distance in the flow region, it can be seen from Fig. 2 that as decreases (i.e. as the fractal properties become more pronounced), the position of this critical point, , is monotonically shifted outwards. The nature of this critical point can be determined from the plot in Fig. 3, which shows that for the entire relevant range of . This can only mean that the critical point implied by this particular root of , will always be a saddle point, and any solution passing through it, will necessarily be transonic. Practically speaking, all of this is just how it should be. To make accretion a feasible process, there has to be at least one solution that will link the outer boundary to the event horizon of the black hole. This can be achieved only if the first critical point that a fluid element encounters while travelling towards the accretor, after having started from an outer boundary region, is a saddle point. So the steadfast existence of this particular saddle point (which is the outermost critical point in the flow region), preserves the conditions necessary for transonicity to develop. But why does the position of this saddle point get shifted outwards, as the fractal properties become progressively more conspicuous? An earlier study on fractal flows in spherically symmetric geometry has addressed this very question by arguing that a fractal medium behaves like an effectively more dilute continuous medium (Roy & Ray, 2007), and in being so, allows gravity to win over gas pressure resistance. The same feature has appeared in this axisymmetric case. Here transonicity occurs when gravity wins over both the centrifugal effects and the pressure effects in an axisymmetric flow. The conditions for transonicity are, therefore, more conducive when either of the two effects is weak. A relatively more dilute gas will offer a feeble pressure build-up against gravity, and so the gravitational pull can triumph even at greater distances. It is for this reason that when the flow is more fractal, that the transonic length scale is shifted outwards. The analogy with the spherically symmetric case is quite apt here.
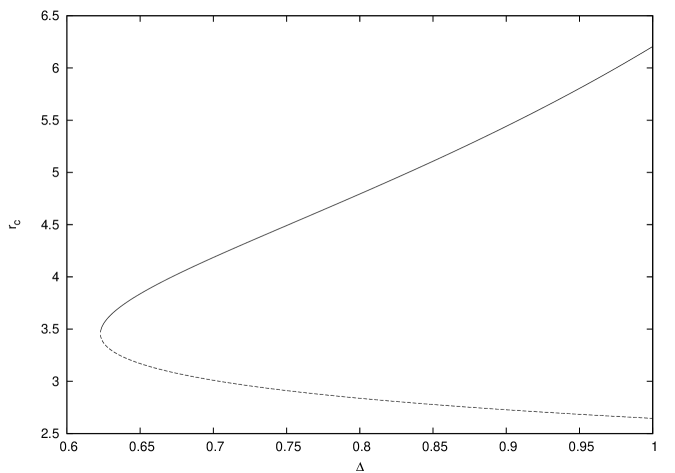
While this be the case for the outermost critical point, which is always a saddle point, to have an appreciation of how multitransonic properties get affected by the fractal nature of the flow, it shall be necessary to turn to the other two critical points — the innermost critical point and the middle critical point — both situated very close to the accretor. These two critical points cannot exist without each other, and their collective behaviour bears this out, something that is shown in Fig. 4. The positions of the innermost critical point and the middle critical point approach each other as is decreased, till they coalesce. Beyond this point, multitransonicity is not possible, and the accreting system will only have one saddle point left in its phase portrait (i.e. it will be monotransonic). The nature of both these critical points can be discerned from Fig. 5. The innermost critical point is always a saddle point, and the middle critical point is always a centre-type point. The two critical points merge under the condition, , and this merging might be viewed as the mutual annihilation of a stable centre-type point (with ) and an unstable saddle point (with ) in the phase space. Significantly enough, the two critical points meet when the lower cut-off value of . This is the same value of , for which , as defined from equation (37), vanishes, and the number of real roots of changes from one to three. In physical terms all of this will mean that if is reduced further, i.e. if the flow becomes more fractal, it will rule out the possibility of multitransonicity completely. Strongly fractal disc systems, therefore, would be devoid of the multitransonic character usually associated with conserved continuum disc accreting systems.
So the general conclusion that one might draw regarding the influence of the fractal features in the flow, is that the flow is made to behave like a more dilute continuum. While this helps in generating the transonic solution, in a somewhat paradoxical sense, the same fractal features turn out to be inimical to multitransonicity in the flow. These inferences have been made by studying a general polytropic flow, but arguably they will not be violated when the flow is to be considered as isothermal. In this limit also it is possible, from equation (26), to derive a quartic polynomial just as in equation (32), with the coefficients , , and being set down, respectively, as
The rest of the mathematical analysis will remain the same, as it has been for the polytropic flow.
6 Fractal scaling for the mass accretion rate
With the knowledge that the critical conditions in the flow can be represented entirely in terms of flow parameters like (or ) and , it now becomes possible to find a direct connection between the steady accretion rate and the mass of the accretor whose gravitational force field drives the fractal accretion flow. This should be particularly revealing for the case of the Newtonian potential, . In this limit it is can be shown from equation (20) that is scaled as and is scaled as (Ray & Bhattacharjee, 2007). Using these scaling conditions in equation (21), one can find a scaling behaviour for the accretion flow rate, , going as
| (41) |
This result is particularly interesting since it indirectly provides some insight about the nature of density clumpiness or the fractal structure of the accretion disc in a specific astrophysical situation.
In the case of accreting pre-main-sequence (PMS) stars, it has been argued (Padoan et al., 2005) that even if accretion takes place through the formation of accretion discs on relatively small length scales, on larger scales it can well be approximated as spherically symmetric Bondi (1952) or Bondi & Hoyle (1944) accretion. This scheme is in good agreement with both numerical simulations and observational results (Padoan et al., 2005). Now pre-main-sequence stars are embedded in the interstellar medium (ISM), and numerous observational and numerical studies (Crovisier et al., 1985; Falgarone et al., 1992; Langer et al., 1995; Elmegreen & Falgarone, 1996; Burkert et al., 1997; Faison et al., 1998; Heithausen et al., 1998; Klessen et al., 1998; Hill et al., 2005), using a variety of techniques, have directly or indirectly suggested that the interstellar medium has a fractal structure over a wide range of scale lengths. So, it is more realistic to consider the case of accretion onto PMS stars as fractal accretion. In this very context it has been shown by Roy (2007) that the numerical simulations and the currently available observational results pertaining to PMS star accretion rate, are consistent with the model of spherically symmetric fractal accretion. It has also been argued by Roy (2007) that the accretion rate is scaled as , where is the mass dimension of the surrounding ISM. So, if the proposed global model for accretion onto PMS stars — spherically symmetric accretion at large distances from the star and disc accretion close to it — is correct, then in the steady state, going by equation (41), one will have . This will imply that the disc will also have a fractal structure, if the surrounding medium, from which the large scale accretion takes place, is fractal in nature.
7 Dynamic aspects of the axisymmetric fractal flow
The fractal nature of the accreting matter acts against multitransonicity. Nevertheless, this does not preclude transonicity itself. If anything, the static flow shows that prominent fractal features will certainly bring about the existence of one saddle-type critical point in the phase portrait of the flow. The overall appearance of a conspicuously sub-Keplerian fractal flow will, therefore, be like that of a monotransonic spherically symmetric Bondi (1952) flow. This is fortunate in many respects, because the Bondi (1952) solution has by now become quite a well-understood and a regularly-invoked paradigm in accretion studies, and any close convergence between it and the fractal disc flow, will pave the way for making insightful comparisons.
The most significant of these is that there will at least be one continuous solution which will connect the outer boundary of the flow to the event horizon of the black hole accretor, in a process that will make black hole accretion realisable in its expected fashion. The steady state conditions will imply that this solution will pass through a saddle point, which is known to be unstable (Jordan & Smith, 1999). Any solution passing through this point will suffer from the problem of fine tuning the outer boundary condition with infinite precision (Ray & Bhattacharjee, 2002). These difficulties can be avoided through the dynamics, and indeed in the case of fractal spherically symmetric accretion, it has been shown (Roy & Ray, 2007) that the stronger is the fractal nature of the flow, the more successful is the time-evolutionary drive towards the Bondi (1952) solution. This happens simply because a fractal medium translates equivalently as a continuum with an effective lesser density, i.e. a fractal flow can be construed as a more dilute continuum. Since a sizeable resistance against gravity-driven transonicity happens due to the pressure build-up in the flow (which, through the polytropic relation, is connected to the local flow density), any dilution in the flowing medium will detract from the opposition against transonicity. Hence, this entire effect will enable an accreting solution to cross the sonic horizon smoothly, premised on the condition that this solution will also correspond to a minimum possible energy configuration, and, concomitantly, to the maximum possible inflow rate (Bondi, 1952; Garlick, 1979; Ray & Bhattacharjee, 2002; Roy & Ray, 2007).
This line of reasoning can be carried over fully to the case of inviscid axisymmetric accretion. As a matter of fact, in the context of inviscid thin-disc flows, Ray & Bhattacharjee (2007) have already argued that transonicity is determined and governed by the same dynamic and non-perturbative criteria, as they are for the Bondi (1952) flow. The analogy with the Bondi (1952) solution will be more so true for sub-Keplerian solutions with low angular momentum (having feeble centrifugal effects pitted against gravity). Fractal features in this kind of disc configuration will only serve to facilitate transonicity even further.
As opposed to a completely non-perturbative approach to the question of time-dependence in the fractal disc flow (all of which will require the mathematics of partial differential equations), it would also be worthwhile to study the properties of the background stationary flow under the influence of a linearised time-dependent perturbative effect. This will yield much information on the global stability of the flow solutions. In order to achieve that, it will first be necessary to define a new physical variable, , closely following a perturbative procedure prescribed by Petterson et al. (1980) and Theuns & David (1992) for spherically symmetric flows, and applied successfully later to thin disc flows (Ray, 2003; Chaudhury et al., 2006; Ray & Bhattacharjee, 2007). It is quite obvious from the form of equations (7) and (14), that the stationary value of will be a global constant, , which can be closely identified with the matter flux rate, within a constant geometrical factor. A perturbation prescription of the form and , will give, on linearising in the primed quantities,
| (42) |
with being a linearised time-dependent perturbation about the constant matter inflow rate, . It is significant that the foregoing expression for is free of the explicit presence of . Linearising in and about and , respectively, in both equations (7) and (13), and expressing and separately in terms of only, will ultimately lead to a linearised equation for the perturbation as
| (43) |
which is an expression that is exactly the same as what can derived upon perturbing the stationary solutions of conserved axisymmetric inflows (Ray, 2003; Chaudhury et al., 2006). Another aspect of equation (43) is that its form has no explicit dependence on the potential that is driving the flow. This is entirely to be expected, because the potential, being independent of time, will appear only in the stationary background flow. Arguments regarding stability will, therefore, be more dependent on the boundary conditions of the steady flow. As the form of the equation of motion for the linearised perturbation remains unchanged even for a flow in a fractal medium, and as the physical boundary conditions are also not altered in this case, the general conclusions reached earlier regarding non-fractal axisymmetric flows (Ray, 2003), can be extended here, and it can be safely claimed that under all reasonable boundary conditions, both the transonic and subsonic solutions will be stable. The only difference that will arise will be due to a fractal scaling of the amplitude of the perturbation. Restricting the perturbation to be like a high-frequency travelling wave, and carrying out a Wentzel–Kramers–Brillouin analysis on equation (43), will show that the time-averaged energy flux in the perturbation, , goes as (Ray, 2003; Chaudhury et al., 2006). Since , going by equation (41), one can argue that , something that gives the expected fractal scaling for the amplitude of the perturbation.
8 Concluding remarks
Two salient facts have emerged out of the entire theoretical exercise carried out here: fractal flows can be equivalently modelled as an effective continuum flow with a diminished local density, and that fractal properties of the flow have an adverse bearing on the question of multitransonicity. It is conceivable that there should be some observational imprints of these two aspects of fractal flows. The mass accretion rate in an accretion flow is intimately related to the local density field. It has already been argued here that the mass accretion rate undergoes fractal scaling, and there are observational indications of such scaling for the particular case of accretion processes onto a PMS star.
In the context of multitransonicity, shocks are a very closely related feature. Many earlier works have discussed the transition of the flow from one transonic solution to the other via a shock (Chakrabarti, 1990, 1996). Now fractal flows have been shown to be detrimental to multitransonicity. So, if shocks do or do not arise in a fractal flow, then that should cast some light on the actual mechanism behind shock formation in an accretion process. Again some observational signature of this should exist.
The exact manner in which matter infall takes place along the radius of an accretion disc, has been a subject of much study (Lynden-Bell, 1969; Pringle, 1981; Narayan & Yi, 1994; Frank et al., 2002). The standard view is that viscosity (in some form) aids the outward transport of angular momentum (Shakura & Sunyaev, 1973; Balbus & Hawley, 1998), and effects the formation of a Keplerian distribution of the accreting matter (Pringle, 1981; Frank et al., 2002). What has been shown here is that for a conserved low angular momentum sub-Keplerian disc, a fractal structure in the accreting medium would drive the flow closer to the simple Bondi (1952) accretion limit, and would therefore assist in the infall process onto a black hole. So a combination of fractal behaviour and viscosity in the flow could possibly explain the observed infall rates.
Acknowledgements
This research has made use of NASA’s Astrophysics Data System. The authors express their gratitude to Jayanta K. Bhattacharjee, Jayaram N. Chengalur, Tapas K. Das and an anonymous referee for some helpful comments.
References
- Abraham et al. (2006) Abraham H., Bilić N., Das T. K., 2006, Classical and Quantum Gravity, 23, 2371
- Abramowicz & Kato (1989) Abramowicz M. A., Kato S., 1989, ApJ, 336, 304
- Abramowicz & Zurek (1981) Abramowicz M. A., Zurek W. H. 1981, ApJ, 246, 314
- Afshordi & Paczyński (2003) Afshordi N., Paczyński B., 2003, ApJ, 592, 354
- Artemova et al. (1996) Artemova I. V., Björnsson G., Novikov I. D., 1996, ApJ, 461, 565
- Balbus & Hawley (1998) Balbus S. A., Hawley J. F., 1998, Reviews of Modern Physics, 70, 1
- Barai et al. (2004) Barai P., Das T. K., Wiita P. J., 2004, ApJ, 613, L49
- Bohr et al. (1993) Bohr T., Dimon P., Putkaradze V., 1993, Journal of Fluid Mechanics, 254, 635
- Bondi (1952) Bondi H., 1952, MNRAS, 112, 195
- Bondi & Hoyle (1944) Bondi H., Hoyle F., 1944, MNRAS, 104, 273
- Burkert et al. (1997) Burkert A., Bate M. R., Bodenheimer P., 1997, MNRAS, 289, 497
- Chakrabarti (1989) Chakrabarti S. K., 1989, ApJ, 347, 365
- Chakrabarti (1990) Chakrabarti S. K., 1990, Theory of Transonic Astrophysical Flows, World Scientific, Singapore
- Chakrabarti (1996) Chakrabarti S. K., 1996, Physics Reports, 266, 229
- Chandrasekhar (1939) Chandrasekhar S., 1939, An Introduction to the Study of Stellar Structure, The University of Chicago Press, Chicago
- Chandrasekhar (1981) Chandrasekhar, S., 1981, Hydrodynamic and Hydromagnetic Stability, Dover Publications, New York
- Chaudhury et al. (2006) Chaudhury S., Ray A. K., Das T. K., 2006, MNRAS, 373, 146
- Crovisier et al. (1985) Crovisier J., Dickey J. M., Kazès I., 1985, A&A, 146, 223
- Das (2002) Das T. K., 2002, ApJ, 577, 880
- Das (2004) Das T. K., 2004, MNRAS, 349, 375
- Das et al. (2007) Das T. K., Bilić N., Dasgupta S., 2007, JCAP, 06, 009
- Das et al. (2003) Das T. K., Pendharkar J. K., Mitra S., 2003, ApJ, 592, 1078
- Elmegreen & Falgarone (1996) Elmegreen B. G., Falgarone E., 1996, ApJ, 471, 816
- Faison et al. (1998) Faison M. D., Goss W. M., Diamond P. J., Taylor G. B., 1998, AJ, 116, 2916
- Falgarone et al. (1992) Falgarone E., Puget J.-L., Perault M., 1992, A&A, 257, 715
- Frank et al. (2002) Frank J., King A., Raine D., 2002, Accretion Power in Astrophysics, Cambridge University Press, Cambridge
- Fukue (1987) Fukue J., 1987, PASJ, 39, 309
- Garlick (1979) Garlick A. R., 1979, A&A, 73, 171
- Goswami et al. (2007) Goswami S., Khan S. N., Ray A. K., Das T. K., 2007, MNRAS, 378, 1407
- Heithausen et al. (1998) Heithausen A., Bensch F., Stutzki J., Falgarone E., Panis, J. F., 1998, A&A, 331, L65
- Hill et al. (2005) Hill A. S., Stinebring D. R., Asplund C. T., Berkwick D. E., Everett W. B., Hinkel N. R., 2005, ApJ, 619, L171
- Jordan & Smith (1999) Jordan D. W., Smith P., 1999, Nonlinear Ordinary Differential Equations, Oxford University Press, Oxford
- Kafatos & Yang (1994) Kafatos M., Yang R. X., 1994, MNRAS, 268, 925
- Klessen et al. (1998) Klessen R. S., Burkert A., Bate M. R., 1998, ApJ, 501, L205
- Landau & Lifshitz (1987) Landau L. D., Lifshitz E. M., 1987, Fluid Mechanics, Butterworth-Heinemann, Oxford
- Langer et al. (1995) Langer W. D., Velusamy T., Kuiper T. B. H., Levin S., Olsen E., Migenes V., 1995, ApJ, 453, 293
- Larson (1981) Larson R. B., 1981, MNRAS, 194, 809
- Liang & Thomson (1980) Liang E. P. T., Thomson K. A., 1980, ApJ, 240, 271
- Lu et al. (1997) Lu J. F., Yu K. N., Yuan F., Young E. C. M., 1997, A&A, 321, 665
- Lynden-Bell (1969) Lynden-Bell D., 1969, Nature, 223, 690
- Mandal et al. (2007) Mandal I., Ray A. K., Das T. K., 2007, 378, 1400
- Mandelbrot (1983) Mandelbrot B., 1983, The Fractal Geometry of Nature, W. H. Freeman, New York
- Matsumoto et al. (1984) Matsumoto R., Kato S., Fukue J., Okazaki A. T., 1984, PASJ, 36, 71
- Molteni et al. (1996) Molteni D., Sponholz H., Chakrabarti S. K., 1996, ApJ, 457, 805
- Muchotrzeb-Czerny (1986) Muchotrzeb-Czerny B., 1986, Acta Astronomica, 36, 1
- Nakayama & Fukue (1989) Nakayama K., Fukue J., 1989, PASJ, 41, 271
- Narayan & Yi (1994) Narayan R., Yi I., 1994, ApJ, 428, L13
- Nowak & Wagoner (1991) Nowak A. M., Wagoner R. V., 1991, ApJ, 378, 656
- Paczyński & Wiita (1980) Paczyński B., Wiita P. J., 1980, A&A, 88, 23
- Padoan et al. (2005) Padoan P., Kritsuk A., Norman M. L., Nordlund Å., 2005, ApJ, 622, L61
- Pariev (1996) Pariev V. I., 1996, MNRAS, 283, 1264
- Petterson et al. (1980) Petterson J. A., Silk J., Ostriker J. P., 1980, MNRAS, 191, 571
- Pringle (1981) Pringle, J. E., 1981, ARA&A, 19, 137
- Ray (2003) Ray A. K., 2003, MNRAS, 344, 83
- Ray & Bhattacharjee (2002) Ray A. K., Bhattacharjee J. K., 2002, Phys. Rev. E, 66, 066303
- Ray & Bhattacharjee (2007) Ray A. K., Bhattacharjee J. K., 2007, Classical and Quantum Gravity, 24, 1479
- Ren et al. (2003) Ren F-Y., Liang J-R., Wang X-T., Qiu W-Y., 2003, Chaos, Solitons and Fractals, 16, 107
- Roy (2007) Roy N., 2007, MNRAS, 378, L34
- Roy & Ray (2007) Roy N., Ray A. K., 2007, MNRAS, 380, 733
- Semelin & Combes (2000) Semelin B., Combes F., 2000, A&A, 360, 1096
- Shakura & Sunyaev (1973) Shakura N. I., Sunyaev R. A., 1973, A&A, 24, 337
- Strogatz (1994) Strogatz S. H., 1994, Nonlinear Dynamics and Chaos, Addison-Wesley Publishing Company, Reading, MA
- Tarasov (2004) Tarasov V. E., 2004, Chaos, 14, 123
- Theuns & David (1992) Theuns T., David M., 1992, ApJ, 384, 587
- Witten & Sander (1981) Witten T. A., Sander L. M., 1981, Phys. Rev. Lett., 47, 1400
- Yang & Kafatos (1995) Yang R. X., Kafatos M., 1995, A&A, 295, 238
- Zaslavsky (2002) Zaslavsky G. M., 2002, Physics Reports, 371, 461