Fractional Chern Insulator in Twisted Bilayer MoTe2
Abstract
A recent experiment has reported the first observation of a zero-field fractional Chern insulator (FCI) phase in twisted bilayer MoTe2 moiré superlattices [1]. The experimental observation is at an unexpected large twist angle 3.7∘ and calls for a better understanding of the FCI in real materials. In this work, we perform large-scale density functional theory calculation for the twisted bilayer MoTe2, and find that lattice reconstruction is crucial for the appearance of an isolated flat Chern band. The existence of the FCI state at is confirmed by exact diagonalization. We establish phase diagrams with respect to the twist angle and electron interaction, which reveal an optimal twist angle of for the observation of FCI. We further demonstrate that an external electric field can destroy the FCI state by changing band geometry and show evidence of the FCI state in this system. Our research highlights the importance of accurate single particle band structure in the quest for strong correlated electronic states and provides insights into engineering fractional Chern insulator in moiré superlattices.
Introduction.—Fractional Chern insulators (FCI), the analog of the fractional Quantum Hall effect [2, 3] in lattice systems, feature fractional excitations with anyonic statistics [4, 5, 6, 7]. Due to its exotic nature and potential applications in topological quantum computing [8, 9], the FCI has long been sought after in condensed matter experiments. To find FCI, the widely-accepted approach is to find a Chern band with significantly quenched kinetic energy [10, 11, 12, 13, 14]. This can be realized in two-dimensional (2D) moiré superlattices, which have been shown to be a fruitful and tunable platform to explore electronic correlation [15, 16]. Indeed, theoretical proposals of FCI have been put forward in twisted bilayer graphene [17, 18, 19, 20, 21, 22] and twisted bilayer transition metal dichalcogenide (TMD) [23, 24, 25]. Experimental evidences for FCI have also been found in graphene-based superlattices [26, 27], albeit at a finite magnetic field. Recently, the first observation of the FCI in the absence of magnetic field (i.e., the fractional quantum anomalous Hall effect) has been reported in twisted bilayer MoTe2 at hole fillings and [1]. The observation is at an unexpected large twist angle (), for which the Chern bands had been commonly believed to be too dispersive to stabilize the FCI. The experimental observation calls for a better understanding of single-particle band structure of twisted TMD bilayer as well as the emergence of the FCI in real materials.
In this work, we perform large-scale density functional theory (DFT) calculation for the twisted bilayer MoTe2. In contrast to previous theoretical studies, we find that the band structure features an isolated flat Chern band that favors FCI. By exact diagonalization (ED) calculations, we confirm the existence of FCI at . We also find that the ferromagnetism at is much weaker than that at , explaining the absence of the FCI in the experiment. We further investigate the fate of FCI under an external electric field and find that FCI become unstable at mV/Å, which is consistent with experimental observation. The suppression of FCI by external electric field is attributed to the deterioration of the flatness of band geometry. We establish phase diagrams with respect to the twist angle and electronic interaction, revealing an optimal twist angle of for the observation of FCI. Finally, we show evidences of the FCI state in this system. Our research highlights the importance of accurate single particle band structure in the quest for strong correlated electronic states and provides insights into engineering FCI in moiré superlattices.
Single-particle electronic structure.— Moiré superlattices formed by twisting a bilayer introduce a long wavelength periodic structure characterized by the moiré lattice constant , where is the lattice constant of the original 2D layer and is the twist angle. This large length scale makes it possible to model the low-energy electronic structure with a continuum model. The valence band edge of monolayer MoTe2 is located at the corners of its Brillouin zone, i.e., and points. The two points are separated by a large momentum such that and valleys can be considered independently. Following the experiment [1], we consider stacking twisted bilayer and the continuum model Hamiltonian for valley reads [28, 29]
| (1) |
Here, is the bottom () and top () layer Hamiltonian subjected to a moiré potential where the bottom (top) layer corresponds to the positive (negative) sign. is the point for the bottom and top layer and is the moiré reciprocal lattice vectors defined by . The interlayer tunneling is dictated by three-fold rotational symmetry as . is the effective mass ( is the bare electron mass) and are the free parameters in the continuum model. The continuum Hamiltonian for the valley can be obtained by applying time reversal symmetry to . Inside each valley, the electrons are fully spin polarized due to the large spin-valley coupling, and opposite valleys have opposite spin due to time-reversal symmetry [30, 31].
| (meV) | (∘) | (meV) | |
|---|---|---|---|
| Local-stacking approx. [28] | 8.0 | -89.6 | -8.5 |
| Large-scale DFT | 20.8 | +107.7 | -23.8 |
The parameters can be fixed by various approaches, among which the simplest one is to fit from DFT calculations for bilayer MoTe2 at various stackings. This approach is adopted by Ref. 28 and the parameters are reproduced in Table 1. The valence band structure with this set of parameters is shown in Fig. 1(b) at twist angle . The topmost valence band is dispersive with band width larger than 20 meV. In addition, the two topmost bands overlap each other in energy. Both features are unfavorable for the emergence of FCI.
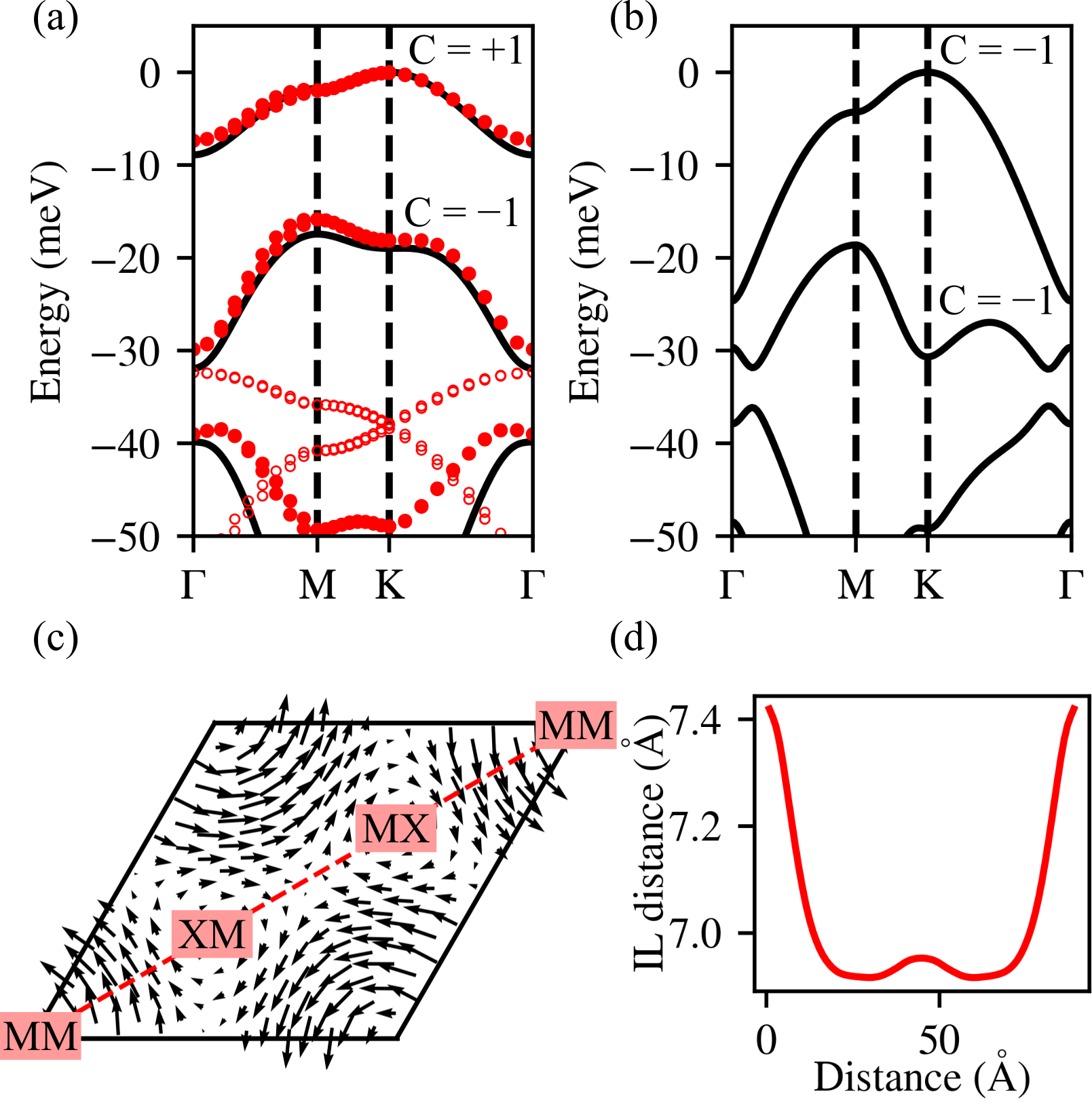
In this work, we seek to establish a better understanding of the single particle band structure by performing large-scale DFT calculations to take into account atomic relaxation, layer corrugation and interlayer electric polarization (details in the Supplemental Material [32]). We choose the closest commensurate twist angle (3.89∘) to the experimental value and construct the moiré superlattice of MoTe2 using its monolayer unit cell with the optimized lattice constant Å. The band structure of the moiré superlattice is presented in Fig. 1(a) as red dots. The DFT result shows significant lattice reconstruction in both in-plane and out-of-plane direction [Fig. 1(c-d)]. We then fit the continuum model parameters to the DFT band structure, and the result is presented in Table 1. Compared to the parameters from Ref. 28, our parameters features a much larger moiré potential and interlayer tunneling, which is likely caused by the significant lattice reconstruction [33, 34, 35], resulting in an isolated Chern band with band width of roughly 9 meV [cf. Fig. 1(a)].
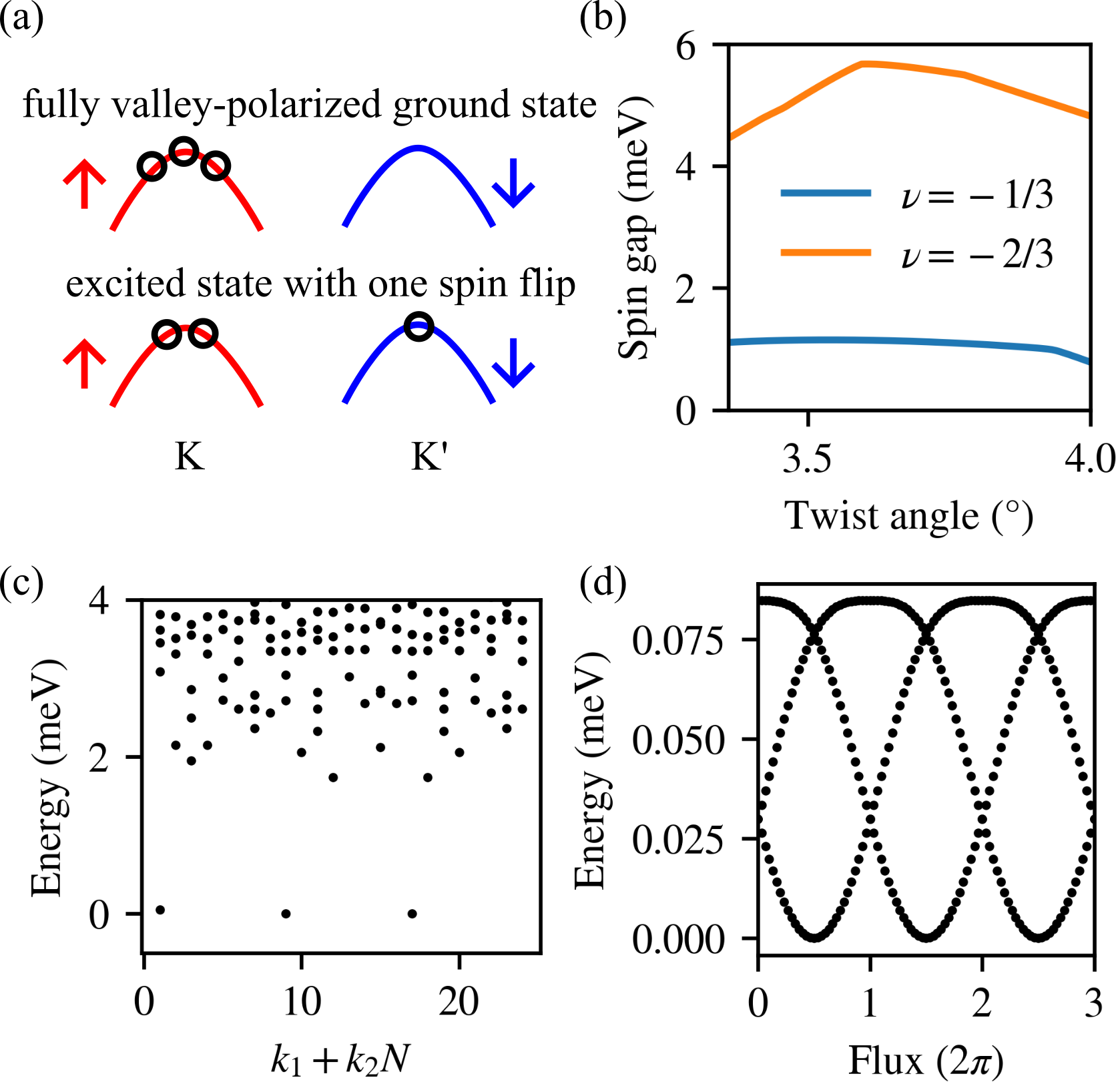
Fractional Chern insulator at .—Having established the existence of an isolated, relatively flat Chern band, we investigate whether FCI can be stabilized. We adopt the following form of the Coulomb interaction:
| (2) |
where is the Coulomb interaction with dual-gate screening, is the area of the system (proportional to the number of points in the calculations), is the distance between the twisted bilayer MoTe2 and two symmetric metal gates, is the vacuum permittivity and is the relative dielectric constant. Here, creates a plane wave with momentum at valley and layer . Due to spin-valley locking, can also be understood as the spin label. We project the interaction onto the topmost moiré band and carry out ED calculations. We choose to make the characteristic interaction strength smaller than the averaged energy gap. For smaller , we present the phase diagram in the Supplemental Material [32]. While we left a more accurate treatment to include the band mixing for future studies, there are evidences that FCI can still be stablized even when the interaction exceeds the band gap [36, 37].
The precursor to the FCI is spontaneous time-reversal symmetry breaking. We first perform ED calculations taking both valleys into account with a system size of unit cells. We find that over a broad range of twist angles, the ground state for both and is fully valley-polarized, with holes occupying only one valley [cf. Fig. 2(a)]. Since the spin and valley indices are coupled, full valley polarization implies full spin polarization. The spin gap, defined as the energy difference between the lowest-energy state that does not exhibit full valley-polarization and the fully valley-polarized ground state, is shown in Fig. 2(b) for both and . The spin gap for is much smaller than that of , indicating much weaker ferromagnetism of the former. The difference in the spin gap is consistent with the experimental observation that ferromagnetism appears at 4.5 K at , whereas no ferromagnetism is observed at down to base temperature of 1.6 K [38].
Given the large spin gap and strong ferromagnetism at , we further carry out ED calculations for a single valley, which allows us to consider a larger system with unit cells.
The most important signature of the FCI is the ground state degeneracy when the system is put on a torus [39, 40]. Indeed, the ED energy spectrum shows three nearly degenerate states, separated by an energy gap from other states, as shown in Fig. 2(c). Under flux insertion, the three ground states evolve into each other, exhibiting a periodicity [Fig. 2(d)]. We also calculate many-body Chern number [39] at this filling to be , which is consistent with the experimental observation [1]. The single particle occupation number, defined as is presented in the Supplemental Material [32]. The uniformity of is a strong indicator favoring FCI over charge density wave (CDW) states, one of FCI’s competing phases. The above evidences provide strong evidence to the existence of FCI in twisted MoTe2 at .
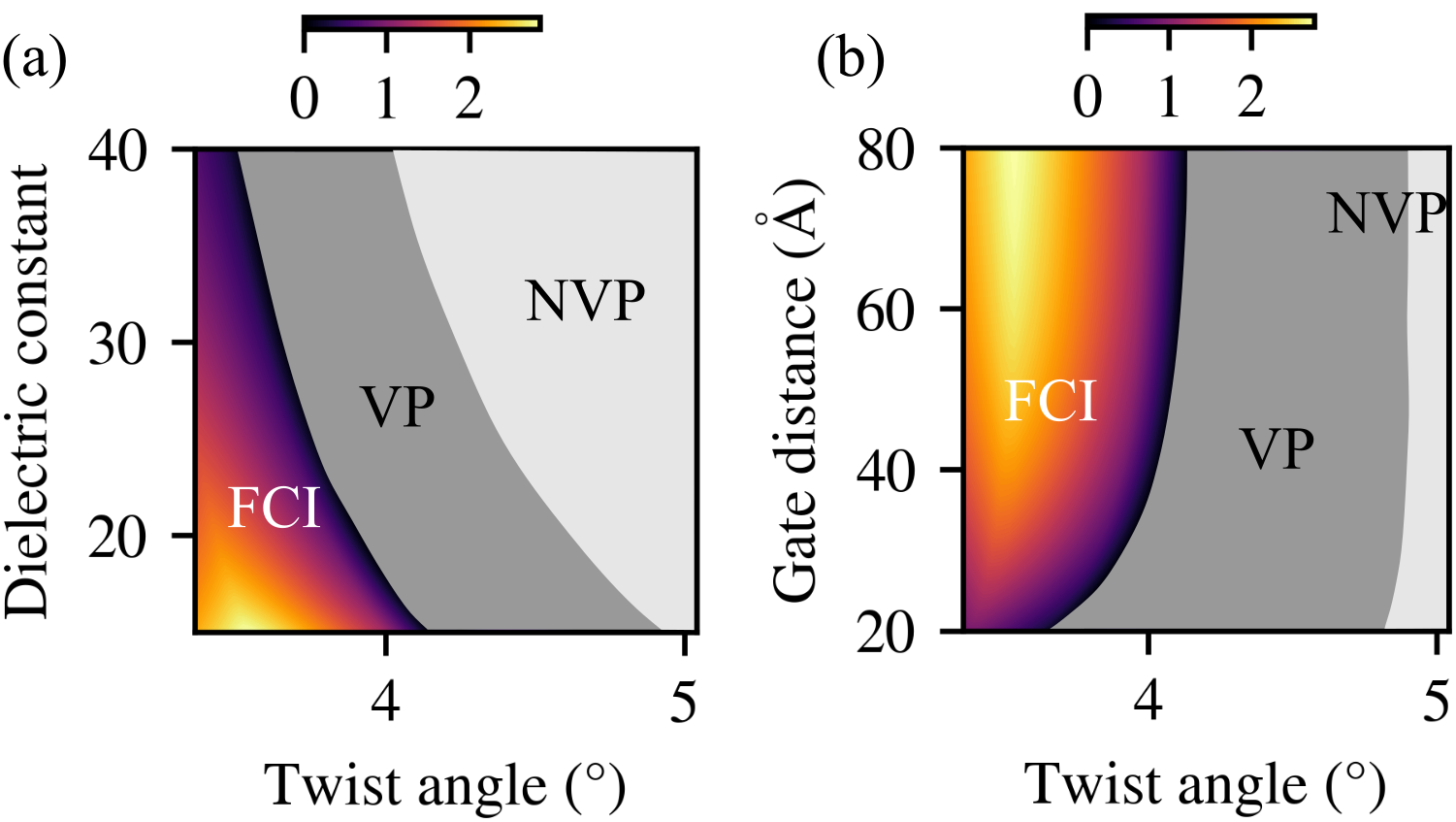
Phase diagram.—The emergence of the FCI state depends on the dominance of electron-electron interaction energy over single particle kinetic energy. This ratio between the two energy scales can be adjusted by two factors: the single-particle band width, and the environmental dielectric screening of electron-electron interactions. The most experimentally accessible knob to tune the band width is changing the twist angle. For example, in twisted bilayer graphene, flat band emerges at a series of magic angles [41]. For twisted bilayer TMD systems, the band width is less sensitive to twist angles and we find relative isolated flat bands for twist angle . The screening of the electron-electron interactions can be tuned by changing , as well as the distance between the sample and the metal gate : larger leads to weaker screening of the electron-electron interactions.
The phase diagram, as a function of and either or , is presented in Fig. 3. Within the range of the twist angle presented in Fig. 3, the band width of the topmost valence band increases monotonically with . There are three distinct phases: the FCI phase, the valley-polarized (VP) phase, and the non-valley-polarized (NVP) phase. The NVP phase emerges in the weak electron-electron interaction regime, characterized by large and large [see Fig.3(a)], or small [see Fig.3(b)]. For stronger interactions, all holes occupy the same valley, which is shown as the VP phase in Fig.3. Our numerical evidence suggests that the VP states are most likely metal states with fully polarized spin, meaning they represent a half-metal state [24]. The nature of these VP phases is left for further studies. FCI emerges from the VP phases at even stronger interactions. The many-body gap for FCI phase has a peak at , indicating an optimal twist angle for the observation of FCI. This optimal angle is close to the twist angle () of the device in which FCI is observed [1].
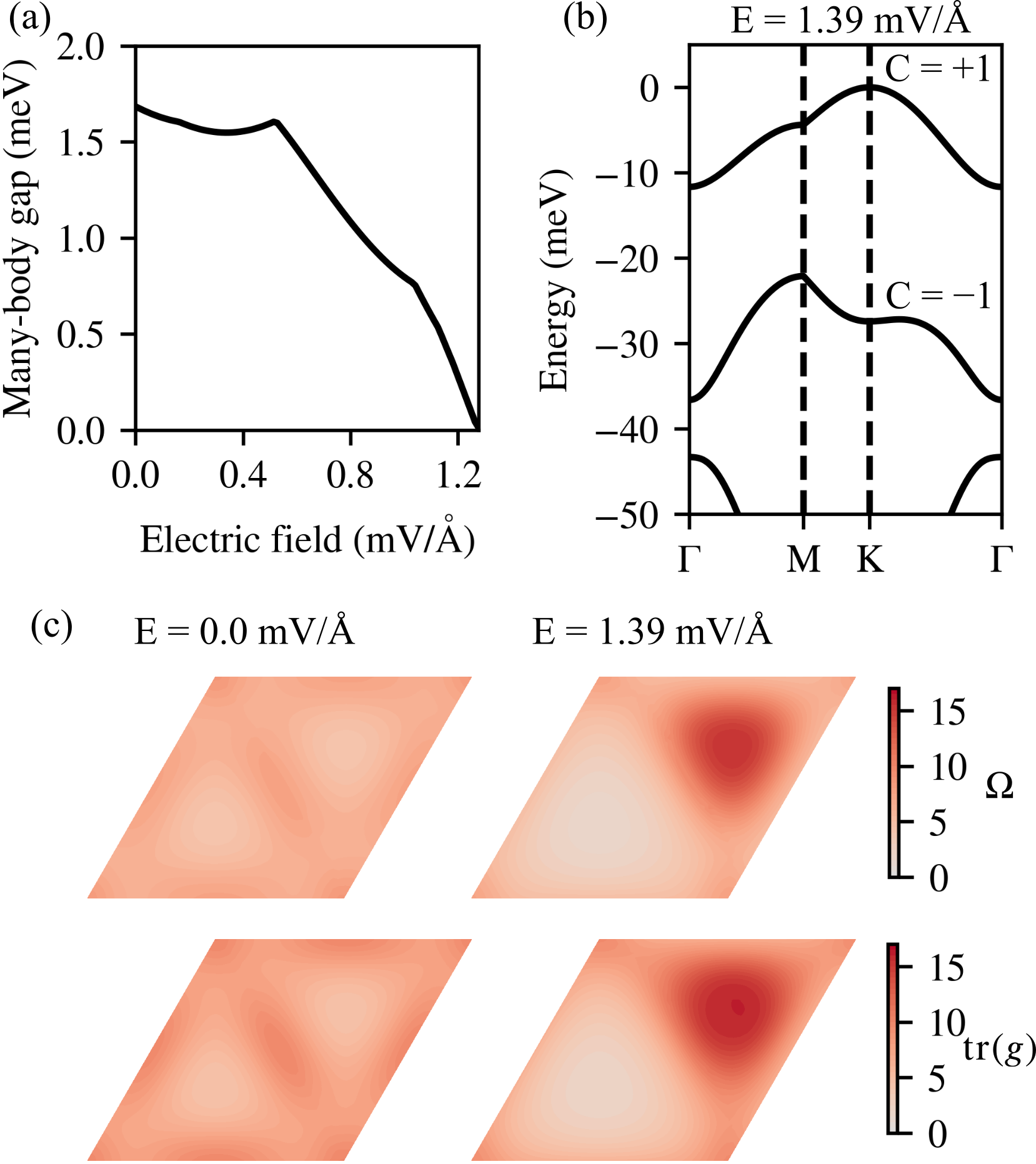
The effect of electric field.—An out-of-plane electric field generates potential differences between the top and bottom layers. Experimentally, it is observed that the FCI at can be suppressed by this out-of-plane electric field. This observation is not necessarily surprising, since layer potential differences will induce a topological phase transition at the single-particle level, making the topmost valence band topologically trivial. However, our calculations show that FCI is suppressed well before the single-particle topological phase transition. In Fig. 4(a), we show that the many-body gap closes at electric field meV/Å. In Fig. 4(b), we present the single particle band structure for meV/Å, where an isolated flat Chern band can still be observed. The band width of the Chern band at meV/Å is comparable to that at meV/Å, but the FCI is already destroyed. In experiment, the ferromagnetism disappears at meV/Å [1], implying FCI is destroyed at a smaller electric field. Our critical electric field meV/Å is consistent with this observation.
It is well-known that completely quenched kinetic energy (i.e. vanishing band width) does not ensure the existence of FCI, and a number of proposals [42, 43, 44, 45, 46] are put forward to identify the conditions for FCI to emerge. Many of these proposals aim to design wave functions in a flat Chern band such that they closely resemble the wave functions of a Landau level. For example, since the Berry curvature and quantum metric tensor is constant for Landau levels, the flatness of these two quantities [42, 43, 44] in the reciprocal space is heuristically viewed as a promising indicator for the emergence of FCI. In Fig. 4(c), we present the distributions of and for meV/Å and meV/Å. A serious deterioration of the flatness of the Berry curvature and quantum metric tensor can be observed when the FCI is destroyed. Both and at meV/Å are concentrated at the moire valley [Fig. 4(c)], which explains the suppression of the FCI state.
Fractional Chern insulator at .—In addition to the state, the experimental observation also includes the state [1]. However, in our calculations, we do not observe a clear many-body gap at for the dielectric constant of . Nonetheless, when the dielectric constant is increased to , which is closer to the experimental value, we find evidence for the FCI [32]. The characteristic interaction at is larger than the energy gap between the two topmost bands, but the result can still be viewed as supporting evidences of the existence of FCI at . We also performed ED calculations for , and and find no clear evidence of FCI for and . For , we find evidence of a FCI phase with the many-body energy gap roughly half of that at .
In summary, we have presented a comprehensive theoretical study of the recent experimental observation of fractional Chern insulator at zero magnetic field in a twisted MoTe2 bilayer. Density functional theory calculations reveal the existence of an isolated flat Chern band, which allows us to confirm the existence of a fractional Chern insulator state using exact diagonalization. Phase diagrams are presented to guide future experimental study of fractional Chern insulator in this system, and the suppression of fraction Chern insulator by external electric field is studied. Our findings offer valuable insights into the nature and properties of fractional Chern insulators in moiré superlattices.
Acknowledgements.
We thank Jie Wang, Jiaqi Cai and Heqiu Li for stimulating discussions. The exact diagonalization study is supported by DOE Award No. DE-SC0012509. The density-functional theory calculation is supported by the Center on Programmable Quantum Materials, an Energy Frontier Research Center funded by DOE BES under award DE-SC0019443. YH acknowledges support from the European Research Council (ERC) under the European Union Horizon 2020 Research and Innovation Programme (Grant Agreement Nos. 804213-TMCS). This work was facilitated through the use of advanced computational, storage, and networking infrastructure provided by the Hyak supercomputer system and funded by the University of Washington Molecular Engineering Materials Center at the University of Washington (DMR-1719797).Note added.—We recently became aware of an independent work on similar topics [47].
References
- Cai et al. [2023] J. Cai, E. Anderson, C. Wang, X. Zhang, X. Liu, W. Holtzmann, Y. Zhang, F. Fan, T. Taniguchi, K. Watanabe, Y. Ran, T. Cao, L. Fu, D. Xiao, W. Yao, and X. Xu, Signatures of fractional quantum anomalous Hall states in twisted MoTe2, Nature 622, 63 (2023).
- Tsui et al. [1982] D. C. Tsui, H. L. Stormer, and A. C. Gossard, Two-dimensional magnetotransport in the extreme quantum limit, Phys. Rev. Lett. 48, 1559 (1982).
- Laughlin [1983] R. B. Laughlin, Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations, Phys. Rev. Lett. 50, 1395 (1983).
- Parameswaran et al. [2013] S. A. Parameswaran, R. Roy, and S. L. Sondhi, Fractional quantum Hall physics in topological flat bands, C. R. Phys. 14, 816 (2013).
- Bergholtz and Liu [2013] E. J. Bergholtz and Z. Liu, Topological flat band models and fractional Chern insulators, Int. J. Mod. Phys. B 27, 1330017 (2013).
- Neupert et al. [2015] T. Neupert, C. Chamon, T. Iadecola, L. H. Santos, and C. Mudry, Fractional (Chern and topological) insulators, Phys. Scr. 2015, 014005 (2015).
- Liu and Bergholtz [2023] Z. Liu and E. J. Bergholtz, Recent developments in fractional Chern insulators, in Reference Module in Materials Science and Materials Engineering (Elsevier, 2023) p. B9780323908009001360.
- Das Sarma et al. [2005] S. Das Sarma, M. Freedman, and C. Nayak, Topologically Protected Qubits from a Possible Non-Abelian Fractional Quantum Hall State, Phys. Rev. Lett. 94, 166802 (2005).
- Nayak et al. [2008] C. Nayak, S. H. Simon, A. Stern, M. Freedman, and S. Das Sarma, Non-abelian anyons and topological quantum computation, Rev. Mod. Phys. 80, 1083 (2008).
- Neupert et al. [2011] T. Neupert, L. Santos, C. Chamon, and C. Mudry, Fractional Quantum Hall States at Zero Magnetic Field, Phys. Rev. Lett. 106, 236804 (2011).
- Tang et al. [2011] E. Tang, J.-W. Mei, and X.-G. Wen, High-Temperature Fractional Quantum Hall States, Phys. Rev. Lett. 106, 236802 (2011).
- Sheng et al. [2011] D. Sheng, Z.-C. Gu, K. Sun, and L. Sheng, Fractional quantum Hall effect in the absence of Landau levels, Nat. Commun. 2, 389 (2011).
- Regnault and Bernevig [2011] N. Regnault and B. A. Bernevig, Fractional Chern Insulator, Phys. Rev. X 1, 021014 (2011).
- Xiao et al. [2011] D. Xiao, W. Zhu, Y. Ran, N. Nagaosa, and S. Okamoto, Interface engineering of quantum Hall effects in digital transition metal oxide heterostructures, Nat. Commun. 2, 596 (2011).
- Andrei et al. [2021] E. Y. Andrei, D. K. Efetov, P. Jarillo-Herrero, A. H. MacDonald, K. F. Mak, T. Senthil, E. Tutuc, A. Yazdani, and A. F. Young, The marvels of moiré materials, Nat. Rev. Mater. 6, 201 (2021).
- Kennes et al. [2021] D. M. Kennes, M. Claassen, L. Xian, A. Georges, A. J. Millis, J. Hone, C. R. Dean, D. Basov, A. N. Pasupathy, and A. Rubio, Moiré heterostructures as a condensed-matter quantum simulator, Nat. Phys. 17, 155 (2021).
- Ledwith et al. [2020] P. J. Ledwith, G. Tarnopolsky, E. Khalaf, and A. Vishwanath, Fractional Chern insulator states in twisted bilayer graphene: An analytical approach, Phys. Rev. Res. 2, 023237 (2020).
- Repellin and Senthil [2020] C. Repellin and T. Senthil, Chern bands of twisted bilayer graphene: Fractional Chern insulators and spin phase transition, Phys. Rev. Res. 2, 023238 (2020).
- Abouelkomsan et al. [2020] A. Abouelkomsan, Z. Liu, and E. J. Bergholtz, Particle-hole duality, emergent fermi liquids, and fractional Chern insulators in moiré flatbands, Phys. Rev. Lett. 124, 106803 (2020).
- Wilhelm et al. [2021] P. Wilhelm, T. C. Lang, and A. M. Läuchli, Interplay of fractional Chern insulator and charge density wave phases in twisted bilayer graphene, Phys. Rev. B 103, 125406 (2021).
- Liu et al. [2021] Z. Liu, A. Abouelkomsan, and E. J. Bergholtz, Gate-tunable fractional Chern insulators in twisted double bilayer graphene, Phys. Rev. Lett. 126, 026801 (2021).
- Sheffer and Stern [2021] Y. Sheffer and A. Stern, Chiral magic-angle twisted bilayer graphene in a magnetic field: Landau level correspondence, exact wave functions, and fractional Chern insulators, Phys. Rev. B 104, L121405 (2021).
- Li et al. [2021a] H. Li, U. Kumar, K. Sun, and S.-Z. Lin, Spontaneous fractional Chern insulators in transition metal dichalcogenide moiré superlattices, Phys. Rev. Res. 3, L032070 (2021a).
- Crépel and Fu [2022] V. Crépel and L. Fu, Anomalous Hall metal and fractional Chern insulator in twisted transition metal dichalcogenides, arXiv:2207.08895 (2022).
- Morales-Durán et al. [2023] N. Morales-Durán, J. Wang, G. R. Schleder, M. Angeli, Z. Zhu, E. Kaxiras, C. Repellin, and J. Cano, Pressure–enhanced fractional Chern insulators in moiré transition metal dichalcogenides along a magic line, arXiv:2304.06669 (2023).
- Xie et al. [2021] Y. Xie, A. T. Pierce, J. M. Park, D. E. Parker, E. Khalaf, P. Ledwith, Y. Cao, S. H. Lee, S. Chen, P. R. Forrester, et al., Fractional Chern insulators in magic-angle twisted bilayer graphene, Nature 600, 439 (2021).
- Spanton et al. [2018] E. M. Spanton, A. A. Zibrov, H. Zhou, T. Taniguchi, K. Watanabe, M. P. Zaletel, and A. F. Young, Observation of fractional Chern insulators in a van der Waals heterostructure, Science 360, 62 (2018).
- Wu et al. [2019] F. Wu, T. Lovorn, E. Tutuc, I. Martin, and A. MacDonald, Topological Insulators in Twisted Transition Metal Dichalcogenide Homobilayers, Phys. Rev. Lett. 122, 086402 (2019).
- Yu et al. [2020] H. Yu, M. Chen, and W. Yao, Giant magnetic field from moiré induced berry phase in homobilayer semiconductors, Natl. Sci. Rev. 7, 12 (2020).
- Xiao et al. [2012] D. Xiao, G.-B. Liu, W. Feng, X. Xu, and W. Yao, Coupled spin and valley physics in monolayers of and other group-VI dichalcogenides, Phys. Rev. Lett. 108, 196802 (2012).
- Cao et al. [2012] T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu, et al., Valley-selective circular dichroism of monolayer molybdenum disulphide, Nat. Commun. 3, 887 (2012).
- [32] Supplemental Material containing DFT details and additional calculations. The Supplemental Material cites Refs. 49, 50, 51, 52, 1.
- Naik and Jain [2018] M. H. Naik and M. Jain, Ultraflatbands and shear solitons in moiré patterns of twisted bilayer transition metal dichalcogenides, Phys. Rev. Lett. 121, 266401 (2018).
- Li et al. [2021b] E. Li, J.-X. Hu, X. Feng, Z. Zhou, L. An, K. T. Law, N. Wang, and N. Lin, Lattice reconstruction induced multiple ultra-flat bands in twisted bilayer wse2, Nat. Commun. 12, 5601 (2021b).
- Li et al. [2021c] H. Li, S. Li, M. H. Naik, J. Xie, X. Li, J. Wang, E. Regan, D. Wang, W. Zhao, S. Zhao, et al., Imaging moiré flat bands in three-dimensional reconstructed WSe2/WS2 superlattices, Nat. Mater. 20, 945 (2021c).
- Kourtis et al. [2014] S. Kourtis, T. Neupert, C. Chamon, and C. Mudry, Fractional chern insulators with strong interactions that far exceed band gaps, Phys. Rev. Lett. 112, 126806 (2014).
- Grushin et al. [2015] A. G. Grushin, J. Motruk, M. P. Zaletel, and F. Pollmann, Characterization and stability of a fermionic fractional chern insulator, Phys. Rev. B 91, 035136 (2015).
- [38] Private communications with Jiaqi Cai and Xiaodong Xu.
- Niu et al. [1985] Q. Niu, D. J. Thouless, and Y.-S. Wu, Quantized Hall conductance as a topological invariant, Phys. Rev. B 31, 3372 (1985).
- Wen and Niu [1990] X. G. Wen and Q. Niu, Ground-state degeneracy of the fractional quantum Hall states in the presence of a random potential and on high-genus Riemann surfaces, Phys. Rev. B 41, 9377 (1990).
- Bistritzer and MacDonald [2011] R. Bistritzer and A. H. MacDonald, Moiré bands in twisted double-layer graphene, Proc. Natl. Acad. Sci. U.S.A. 108, 12233 (2011).
- Simon and Rudner [2020] S. H. Simon and M. S. Rudner, Contrasting lattice geometry dependent versus independent quantities: Ramifications for berry curvature, energy gaps, and dynamics, Phys. Rev. B 102, 165148 (2020).
- Parameswaran et al. [2012] S. A. Parameswaran, R. Roy, and S. L. Sondhi, Fractional Chern insulators and the algebra, Phys. Rev. B 85, 241308 (2012).
- Roy [2014] R. Roy, Band geometry of fractional topological insulators, Phys. Rev. B 90, 165139 (2014).
- Wang et al. [2021] J. Wang, J. Cano, A. J. Millis, Z. Liu, and B. Yang, Exact landau level description of geometry and interaction in a flatband, Phys. Rev. Lett. 127, 246403 (2021).
- Ledwith et al. [2022] P. J. Ledwith, A. Vishwanath, and D. E. Parker, Vortexability: A unifying criterion for ideal fractional chern insulators, arXiv:2209.15023 (2022).
- [47] A. Reddy, F. Alsallom, Y. Zhang, T. Devakul, and L. Fu, to appear .
- Yu et al. [2023] J. Yu, J. Herzog-Arbeitman, M. Wang, O. Vafek, B. A. Bernevig, and N. Regnault, Fractional Chern Insulators vs. Non-Magnetic States in Twisted Bilayer MoTe2, arXiv:2309.14429 (2023).
- Soler et al. [2002] J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón, and D. Sánchez-Portal, The SIESTA method for ab initio order-N materials simulation, J. Condens. Matter Phys. 14, 2745 (2002).
- Hamann [2013] D. Hamann, Optimized norm-conserving Vanderbilt pseudopotentials, Phys. Rev. B 88, 085117 (2013).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
- Grimme [2006] S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem. 27, 1787 (2006).