Fractional Power Control for
Decentralized Wireless Networks
Abstract
We consider a new approach to power control in decentralized wireless networks, termed fractional power control (FPC). Transmission power is chosen as the current channel quality raised to an exponent , where is a constant between 0 and 1. The choices and correspond to the familiar cases of channel inversion and constant power transmission, respectively. Choosing allows all intermediate policies between these two extremes to be evaluated, and we see that usually neither extreme is ideal. We derive closed-form approximations for the outage probability relative to a target SINR in a decentralized (ad hoc or unlicensed) network as well as for the resulting transmission capacity, which is the number of users/m2 that can achieve this SINR on average. Using these approximations, which are quite accurate over typical system parameter values, we prove that using an exponent of minimizes the outage probability, meaning that the inverse square root of the channel strength is a sensible transmit power scaling for networks with a relatively low density of interferers. We also show numerically that this choice of is robust to a wide range of variations in the network parameters. Intuitively, balances between helping disadvantaged users while making sure they do not flood the network with interference.
I Introduction
Power control is a fundamental adaptation mechanism in wireless networks, and is used to at least some extent in virtually all terrestrial wireless systems. For a single user fading channel in which the objective is to maximize expected rate, it is optimal to increase transmission power (and rate) as a function of the instantaneous channel quality according to the well-known waterfilling policy [2]. On the other hand, if the objective is to consistently achieve a target rate (or SNR), then the power should be adjusted so that this target level is exactly met. Such an objective is philosophically the opposite of waterfilling, since power is inversely related to the instantaneous channel quality: we call this channel inversion. Although suboptimal from an information theory point of view, some channel inversion is used in many modern wireless systems to adapt to the extreme dynamic range (often dB due to path loss differences as well as multipath fading) that those systems experience, to provide a baseline user experience over a long-term time-scale.
I-A Background and Motivation for Fractional Power Control
In a multi-user network in which users mutually interfere, power control can be used to adjust transmit power levels so that all users simultaneously can achieve their target SINR levels. The Foschini-Miljanic algorithm is an iterative, distributed power control method that performs this task assuming that each receiver tracks its instantaneous SINR and feeds back power adjustments to its transmitter [3]. Considerable work has deeply explored the properties of these algorithms, including developing a framework that describes all power control problems of this type [4], as well as studying the feasibility and implementation of such algorithms [5, 6], including with varying channels [7]; see the recent monographs [8][9] for excellent surveys of the vast body of literature. This body of work, while in many respects quite general, has been primarily focused on the cellular wireless communications architecture, particularly in which all users have a common receiver (i.e., the uplink). More recently, there has been considerable interest in power control for decentralized wireless networks, such as unlicensed spectrum access and ad hoc networks [10, 11, 12, 13, 14, 15]. A key distinguishing trait of a decentralized network is that users transmit to distinct receivers in the same geographic area, which causes the power control properties to change considerably.
In this paper, we explore the optimal power control policy for a multi-user decentralized wireless network with mutually interfering users and a common target SINR. We do not consider iterative algorithms and their convergence. Rather, motivated by the poor performance of channel inversion in decentralized networks [16], we develop a new transmit power policy called fractional power control, which is neither channel inversion nor fixed transmit power, but rather a trade-off between them. Motivated by a recent Motorola proposal [17] for fairness in cellular networks, we consider a policy where if is the channel power between the transmitter and receiver, a transmission power of is used, where is chosen in . Clearly, implies constant transmit power, whereas is channel inversion. The natural question then is: what is an appropriate choice of ? We presume that is decided offline and that all users in the network utilize the same .
I-B Technical Approach
We consider a spatially distributed (decentralized) network, representing either a wireless ad hoc network or unlicensed spectrum usage by many nodes (e.g., Wi-Fi or spectrum sharing systems). We consider a network that has the following key characteristics.
-
•
Each transmitter communicates with a single receiver that is a distance meters away.
-
•
Channel attenuation is determined by path loss (with exponent ) and a (flat) fading value .
-
•
Each transmitter knows the channel power to its intended receiver, but has no knowledge about other transmissions.
-
•
All multi-user interference is treated as noise.
-
•
Transmitters do not schedule their transmissions based on their channel conditions or the activities of other nodes.
-
•
Transmitter node locations are modeled by a homogeneous spatial (2-D) Poisson process.
These modeling assumptions are made to simplify the analysis, but in general reasonably model a decentralized wireless network with random transmitter locations, and limited feedback mechanisms. In particular, the above assumptions refer to the situation where a connection has been established between a transmitter and receiver, in which case the channel power can be learned quickly either through reciprocity or a few bits of feedback. It is not however as easy to learn the interference level since it may change suddenly as interferers turn on and off or physically move (and reciprocity does not help). The fixed transmit distance assumption is admittedly somewhat artificial, but is significantly easier to handle analytically, and has been shown to preserve the integrity of conclusions even with random transmit distances. For example, [16, 18] prove that picking the source-destination distance from an arbitrary random distribution reduces the transmission capacity by a constant factor of . Therefore, although fixed distance can be considered best-case as far as the numerical value of transmission capacity, this constant factor will not change fractional power control’s relative effect on the transmission capacity, which is the subject of this paper.
I-C Contributions and Organization
The contributions of the paper are the suggestion of fractional power control for wireless networks and the derivation of the optimum power control exponent . The exponent is shown to be optimal for an approximation to the outage probability/transmission that is valid for relatively low density networks that are primarily interference-limited (i.e., the effect of thermal noise is not overly large); if the relative density or the effect of noise is large, then our numerical results show that no power control () is generally preferred. In the relatively large parameter space where our primary approximation is valid, fractional power control with the choice is shown to greatly increase the transmission capacity of a 1-hop ad hoc network for small path loss exponents (as ), with more modest gains for higher attenuation channels. The results open a number of possible avenues for future work in the area of power control, and considering the prevalence of power control in practice, carry several design implications.
The remainder of the paper is organized as follows. Section II provides background material on the system model, and key prior results on transmission capacity that are utilized in this paper. Section III holds the main results, namely Theorem 3 which gives the outage probability and transmission capacity achieved by fractional power control, and Theorem 4 which determines the optimum power control exponent for the outage probability approximation. Section IV provides numerical plots that explore the numerically computed optimal , which provides insight on how to choose in a real wireless network. Section V suggests possible extensions and applications of fractional power control, while Section VI concludes the paper.
II Preliminaries
II-A System Model
We consider a set of transmitting nodes at an arbitrary snapshot in time with locations specified by a homogeneous Poisson point process (PPP), , of intensity on the infinite two-dimensional plane, . We consider a reference transmitter-receiver pair, where the reference receiver, assigned index , is located without loss of generality, at the origin. Let denote the distance of the -th transmitting node to the reference receiver. Each transmitter has an associated receiver that is assumed to be located a fixed distance meters away. Let denote the (random) distance–independent fading coefficient for the channel separating transmitter and the reference receiver at the origin; let denote the (random) distance–independent fading coefficient for the channel separating transmitter from its intended receiver. We assume that all the are i.i.d. (including ), which implies that no source-destination (S-D) pair has both a transmitter and receiver that are very close (less than a wavelength) to one another, which is reasonable. Received power is modelled by the product of transmission power, pathloss (with exponent ), and a fading coefficient. Therefore, the (random) SINR at the reference receiver is:
| (1) |
where is the noise power. Recall our assumption that transmitters have knowledge of the channel condition, , connecting it with its intended receiver. By exploiting this knowledge, the transmission power, , may depend upon the channel, . If Gaussian signaling is used, the corresponding achievable rate (per unit bandwidth) is . The Poisson model requires that nodes decide to transmit independently, which corresponds in the above model to slotted ALOHA [19]. A good scheduling algorithm by definition introduces correlation into the set of transmitting nodes, which is therefore not well modeled by a homogeneous PPP. We discuss the implications of scheduling later in the paper.
II-B Transmission Capacity
In the outage-based transmission capacity framework, an outage occurs whenever the SINR falls below a prescribed threshold , or equivalently whenever the instantaneous mutual information falls below . Therefore, the system-wide outage probability is
| (2) |
Because (2) is computed over the distribution of transmitter positions as well as the iid fading coefficients (and consequently transmission powers), it corresponds to fading that occurs on a time-scale that is comparable or slower than the packet duration (if (2) is to correspond roughly to the packet error rate). The outage probability is clearly a continuous increasing function of the intensity .
Define as the maximum intensity of attempted transmissions such that the outage probability is no larger than , i.e., is the unique solution of . The transmission capacity is then defined as , which is the maximum density of successful transmissions times the spectral efficiency of each transmission. In other words, transmission capacity is area spectral efficiency subject to an outage constraint.
For the sake of clarity, we define the constants and . Now consider a path-loss only environment ( for all ) with constant transmission power ( for all ). The main result of [18] is given in the following theorem.
Theorem 1 ([18])
Pure pathloss. Consider a network where the SINR at the reference receiver is given by (2) with and for all . Then the following expressions give bounds on the outage probability and transmission attempt intensity for small:
| (3) | |||||
| (4) |
Here pl denotes pathloss. The transmission attempt intensity upper bound, , is obtained by solving for . These bounds are shown to be approximations for small respectively, which is the usual regime of interest. Note also that , which implies that transmission density is approximately linear with the desired outage level, , for small outages. The following corollary illustrates the simplification of the above results when the noise may be ignored.
Corollary 1
When the expressions in Theorem 1 simplify to:
| (5) | |||||
| (6) |
III Fractional Power Control
The goal of the paper is to determine the effect that fractional power control has on the outage probability lower bound in (3) and hence the transmission capacity upper bound in (4). We first review the key prior result that we will use, then derive the maximum transmission densities for different power control policies. We conclude the section by finding the optimal power control exponent .
III-A Transmission capacity under constant power and channel inversion
In this subsection we restrict our attention to two well-known power control strategies: constant transmit power (or no power control) and channel inversion. Under constant power, for all for some common power level . Under channel inversion, for all . This means that the received signal power is , which is constant for all . That is, channel inversion compensates for the random channel fluctuations between each transmitter and its intended receiver. Moreover, the expected transmission power is , so that the constant power and channel inversion schemes use the same expected power. We would like to emphasize the distribution of is arbitrary and can be adapted in principle to any relevant fading or compound shadowing-fading model. For some possible distributions (such as Rayleigh fading, i.e. ), the value may be undefined, strictly speaking. In practice, the transmit power is finite and so is finite. The value is simply a normalizing factor and can be interpreted mathematically to mean that for an arbitrarily small . Such a definition would not affect the results in the paper.
A main result of [16] extended to include thermal noise is given in the following theorem, with a general proof that will apply to all three cases of interest: constant power, channel inversion and fractional power control. Note that cp and are used to denote constant power and channel inversion, respectively.
Theorem 2
Constant power. Consider a network where the SINR at the reference receiver is given by (2) with for all . Then the following expressions give good approximations of the outage probability and transmission attempt intensity for small.
| (7) |
Channel inversion. Consider the same network with for all . Then the following expressions give tight bounds on the outage probability and transmission attempt intensity for small:
| (8) | |||||
| (9) |
Proof:
The SINR at the reference receiver for a generic power vector is
| (10) |
and the corresponding outage probability is
| (11) |
Rearranging yields:
| (12) |
Note that outage is certain when . Conditioning on and using to denote the density of yields:
| (13) |
Recall the generic lower bound from [16]: if is a homogeneous marked Poisson point process with points of intensity and iid marks independent of the , then
| (14) |
Applying here with and :
| (15) | |||||
The Jensen approximation for this quantity is:
| (16) |
Note that channel inversion only makes sense when , the effective interference-free SNR after taking into account the power cost of inversion, is larger than the SINR threshold . The validity of the outage lower bound/density upper bound as well as of the Jensen’s approximation are evaluated in the numerical and simulation results in Section IV.
When the thermal noise can be ignored, these results simplify to the expressions given in the following corollary:
Corollary 2
When the expressions in Theorem 2 simplify to:
| (17) |
Note that these expressions match Theorem 3 and Corollary 3 of the SIR-analysis performed in [16].
In the absence of noise the constant power outage probability approximation equals the channel inversion outage probability lower bound: . As a result, the constant power transmission attempt intensity approximation equals the channel inversion transmission attempt intensity upper bound: . Comparing in (2) with in (6) it is evident that the impact of fading on the transmission capacity is measured by the loss factor, , defined as
| (18) |
The inequality is obtained by applying Jensen’s inequality to the convex function and the random variable . If constant power is used, the term is due to fading of the desired signal while the term is due to fading of the interfering links. Fading of the interfering signal has a positive effect while fading of the desired signal has a negative effect. If channel inversion is performed the term is due to each interfering transmitter using power proportional to . When the path loss exponent, , is close to 2 then is close to one, so the term is nearly equal to the expectation of the inverse of the fading, which can be extremely large for severe fading distributions such as Rayleigh. As a less severe example, , the loss factor for Rayleigh fading is .
III-B Transmission capacity under fractional power control
In this section we generalize the results of Theorem 2 by introducing fractional power control (FPC) with parameter . Under FPC the transmission power is set to for each . The received power at receiver is then , which depends upon aside from . The expected transmission power is , ensuring a fair comparison with the results in Theorems 1 and 2. Note that constant power corresponds to and channel inversion corresponds to . The following theorem gives good approximations on the outage probability and maximum allowable transmission intensity under FPC.
Theorem 3
Fractional power control. Consider a network where the SINR at the reference receiver is given by (2) with for all , for some . Then the following expressions give good approximations of the outage probability and maximum transmission attempt intensity for small
where .
Proof:
Under FPC, the transmit power for each user is constructed as . Substituting this value into the proof for Theorem 2 immediately gives the expression for . Again, the transmission attempt intensity approximation is obtained by solving for . ∎
As with Theorem 2, the approximation is accurate when the exponential term in is approximately linear in its argument and thus Jensen’s is tight. In other words, this approximation utilizes the fact that is nearly linear for small . Looking at the expression for we see that this reasonable when the relative density is small. If this is not true then the approximation is not sufficiently accurate, as will be further seen in the numerical results presented in Section IV. The FPC transmission attempt intensity approximation, , is obtained by solving for . The following corollary illustrates the simplification of the above results when the noise may be ignored.
Corollary 3
When the expressions in Theorem 3 simplify to:
| (19) |
The loss factor for FPC, , is the reduction in the transmission capacity approximation relative to the pure pathloss case:
| (20) |
Clearly, the loss factor for FPC depends on the design choice of the exponent .
III-C Optimal Fractional Power Control Exponent
Fractional power control represents a balance between the extremes of no power control and channel inversion. The mathematical effect of fractional power control is to replace the term with . This is because the signal fading is softened by the power control exponent so that it results in a leading term of (rather than ) in the numerator of the SINR expression, and ultimately to the term. The interference power is also softened by the fractional power control and leads to the term.
The key question of course lies in determining the optimal power control exponent. Although it does not seem possible to derive an analytical expression for the exponent that minimizes the general expression for given in Theorem 3, we can find the exponent that minimizes the outage probability approximation in the case of no noise.
Theorem 4
In the absence of noise (), the fractional power control outage probability approximation, , is minimized for . Hence, the fractional power control transmission attempt intensity approximation, is also maximized for .
Proof:
Because the outage probability/transmission density approximations depend on the exponent only through the quantity , it is sufficient to show that is minimized at . To do this, we use the following general result, which we prove in the Appendix. For any non-negative random variable , the function
| (21) |
is convex in for with a unique minimum at . Applying this result to random variable gives the desired result. ∎
The theorem shows that transmission density is maximized, or equivalently, outage probability is minimized, by balancing the positive and negative effects of power control, which are reduction of signal fading and increasing interference, respectively. Using an exponent greater than over-compensates for signal fading and leads to interference levels that are too high, while using an exponent smaller than leads to small interference levels but an under-compensation for signal fading. Note that because the key expression is convex, the loss relative to using increases monotonically both as and .
One can certainly envision “fractional” power control schemes that go even further. For example, corresponds to “super” channel inversion, in which bad channels take resources from good channels even more so than in normal channel inversion. Not surprisingly, this is not a wise policy. Less obviously, corresponds to what is sometimes called “greedy” optimization, in which good channels are given more resources at the further expense of poor channels. Waterfilling is an example of a greedy optimization procedure. But, since monotonically increases as decreases, it is clear that greedy power allocations of any type are worse than even constant transmit power under the SINR-target set up.
The numerical results in the next section show that FPC is very beneficial relative to constant transmit power or channel inversion. However, fading has a deleterious effect relative to no fading even if the optimal exponent is used. To see this, note that is a convex function and therefore Jensen’s yields for any non-negative random variable . Applying this to we get , which implies
Therefore, fractional PC cannot fully overcome fading, but it is definitely a better power control policy than constant power transmission or traditional power control (channel inversion).
IV Numerical Results and Discussion
In this section, the implications of fractional power control are illustrated through numerical plots and analytical discussion. The tightness of the bounds will be considered as a function of the system parameters, and the choice of a robust FPC exponent will be proposed. As default parameters, the simulations assume
| (22) |
Furthermore, Rayleigh fading is assumed for the numerical results.
IV-A Effect of Fading
The benefit of fractional power control can be quickly illustrated in Rayleigh fading, in which case the channel power is exponentially distributed and the moment generating function is therefore
| (23) |
where is the standard gamma function. If fractional power control is used, the transmission capacity loss due to fading is
| (24) |
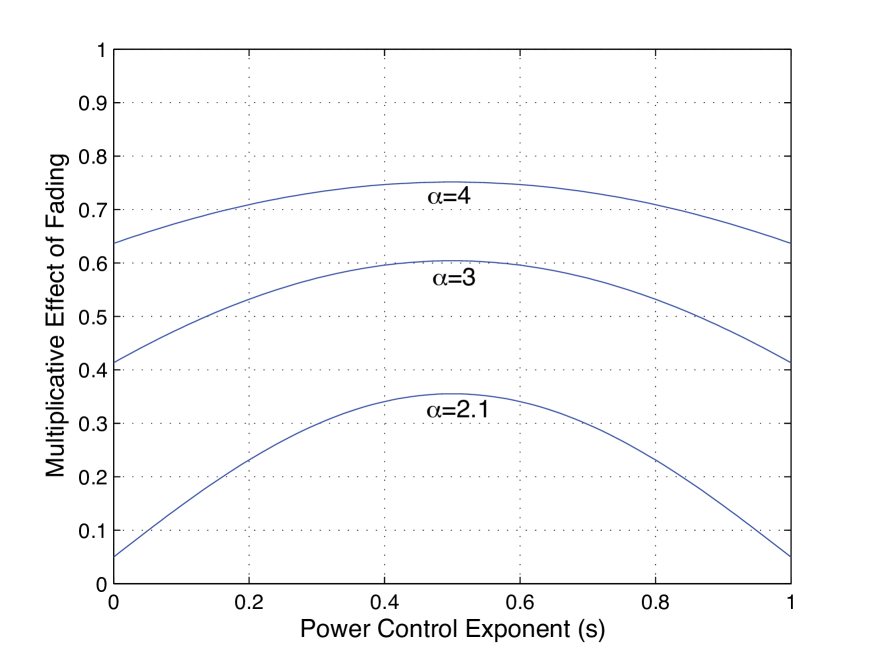
In Fig. 1 this loss factor () is plotted as a function of for path loss exponents . Notice that for each value of the maximum takes place at , and that the cost of not using fractional power control is highest for small path loss exponents because goes to infinity quite steeply as . This plot implies that in severe fading channels, the gain from FPC can be quite significant.
It should be noted that the expression in (24) is for the case of no thermal noise (). In this case the power cost of FPC completely vanishes, because the same power normalization (by ) is performed by each transmitting node and therefore this normalization cancels in the SIR expression. On the other hand, this power cost does not vanish if the noise is strictly positive and can potentially be quite significant, particularly if is not large. A simple application of Jensen’s shows that the power normalization factor is an increasing function of the exponent for any distribution on . For the particular case of Rayleigh fading this normalization factor is which makes it prohibitively expensive to choose very close to one; indeed, the choice requires infinite power and thus is not feasible. On the other hand, note that is approximately dB and thus the cost of a moderate exponent is not so large. When the interference-free is reasonably large, this normalization factor is relatively negligible and the effect of FPC is well approximated by (24).
IV-B Tightness of Bounds
There are two principle approximations made in attaining the expressions for outage probability and transmission capacity in Theorem 3. First, the inequality is due to considering only dominant interferers; that is, an interferer whose channel to the desired receiver is strong enough to cause outage even without any other interferers present. This is a lower bound on outage since it ignores non-dominant interferers, but nevertheless has been seen to be quite accurate in our prior work [18, 20, 16]. Second, Jensen’s inequality is used to bound in the opposite direction, so this results in an approximation to the outage probability rather than a lower bound; numerical results confirm that this approximation is in fact not a lower bound in general. Therefore, we consider the three relevant quantities: (1) the actual outage probability , which is determined via Monte-Carlo simulation and does not depend on any bounds or approximations, (2) a numerical computation of the outage probability lower bound , and (3) the approximation to the outage probability reached by applying Jensen’s inequality to . Note that because of the two opposing bounds (one lower and one upper), we cannot say a priori that method (2) will produce more accurate expressions than method (3).
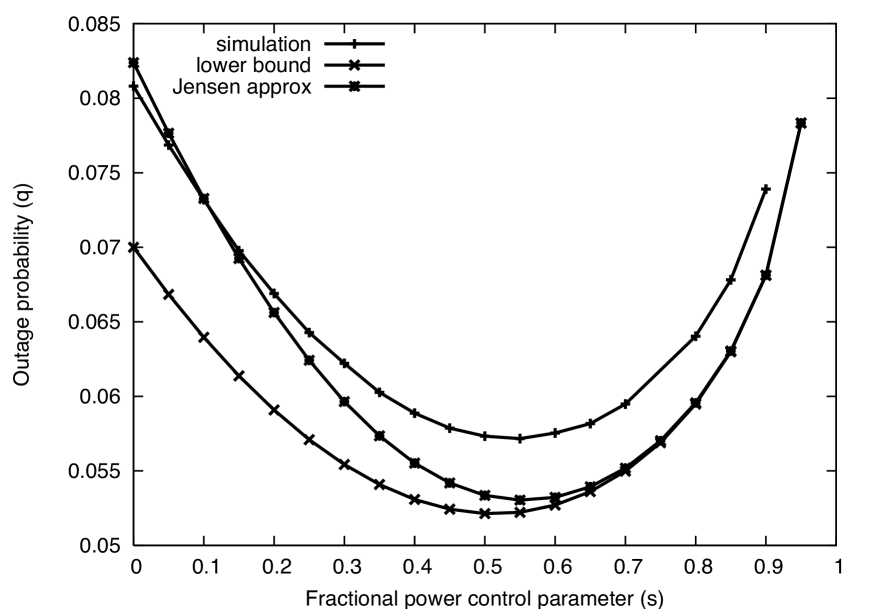
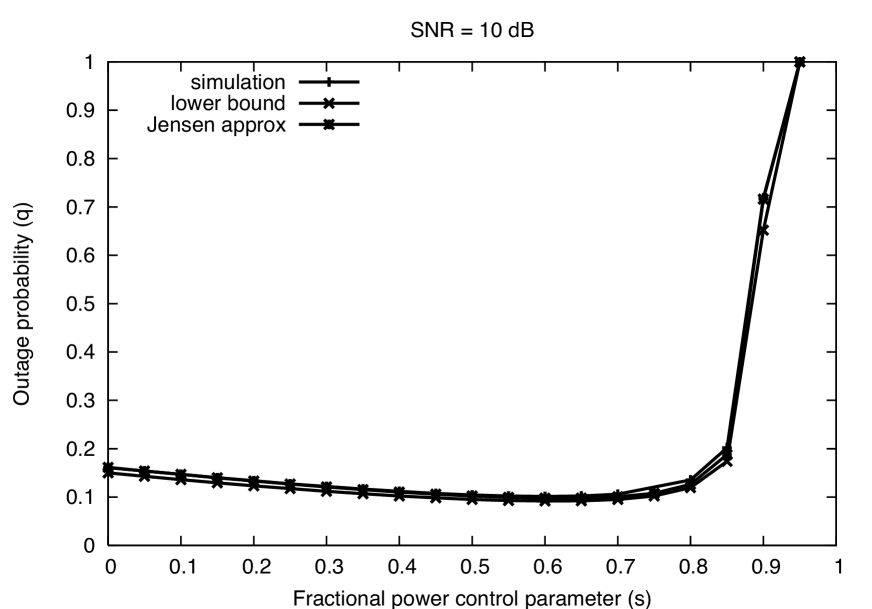
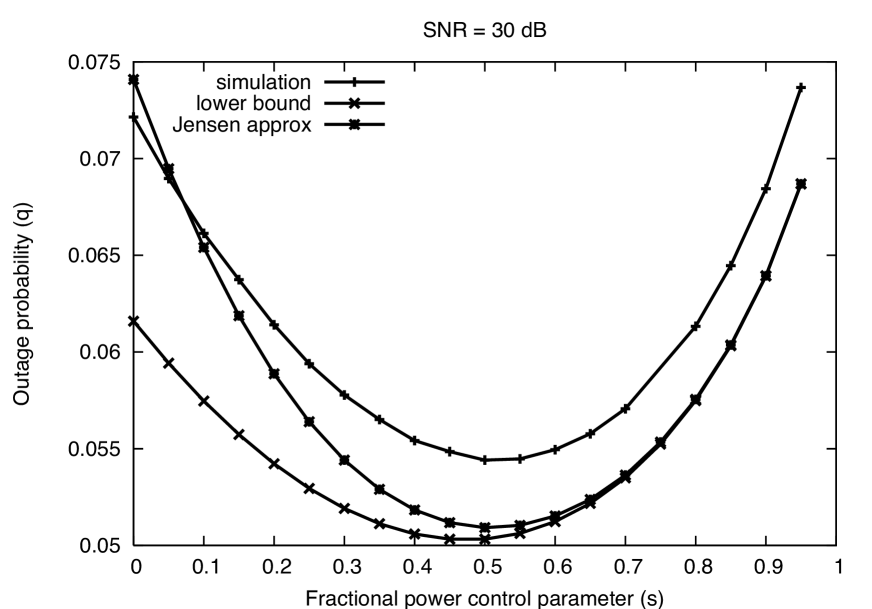
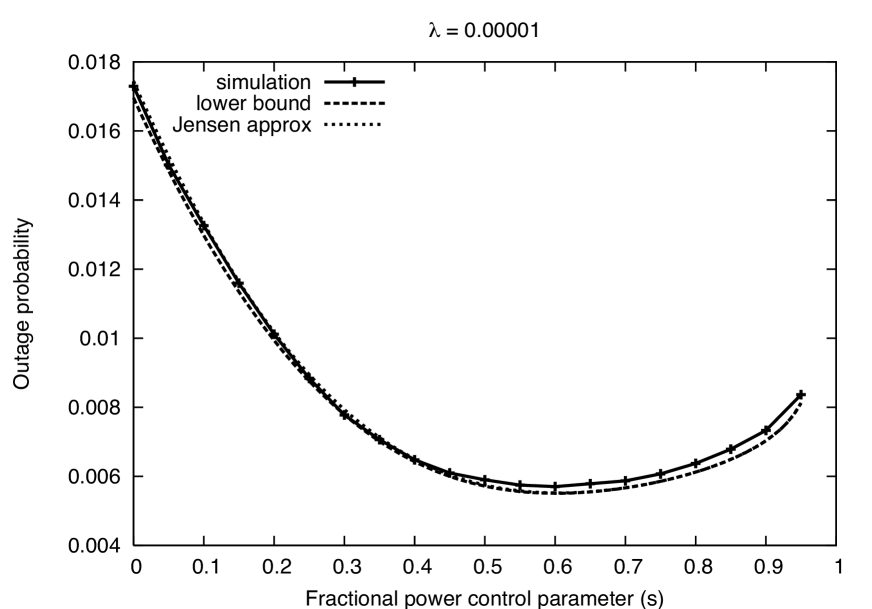
The tightness of the bounds is explored in Figs. 2 - 5. Consider first Fig. 2 for the default parameters given above. We can see that the lower bound and the Jensen approximation both reasonably approximate the simulation results, and the approximation winds up serving as a lower bound as well. The Jensen’s approximation is very accurate for large values of (i.e., closer to channel inversion), and while looser for smaller values of , this “error” actually moves the Jensen’s approximation closer to the actual (simulated) outage probability. The Jensen’s approximation approaches the lower bound as because the random variable approaches a constant, where Jensen’s inequality trivially holds with equality (see, e.g., (3)). Changing the path loss exponent , the SNR, the target SINR , or the density can have a significant effect on the bounds, as we will see. With the important exception of high density networks, the approximations are seen to be reasonably accurate for reasonable parameter values.
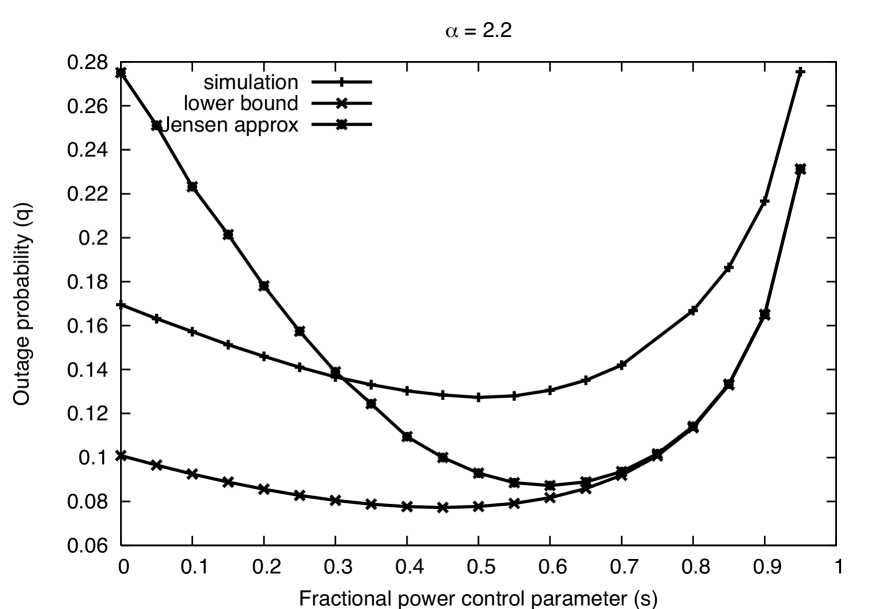
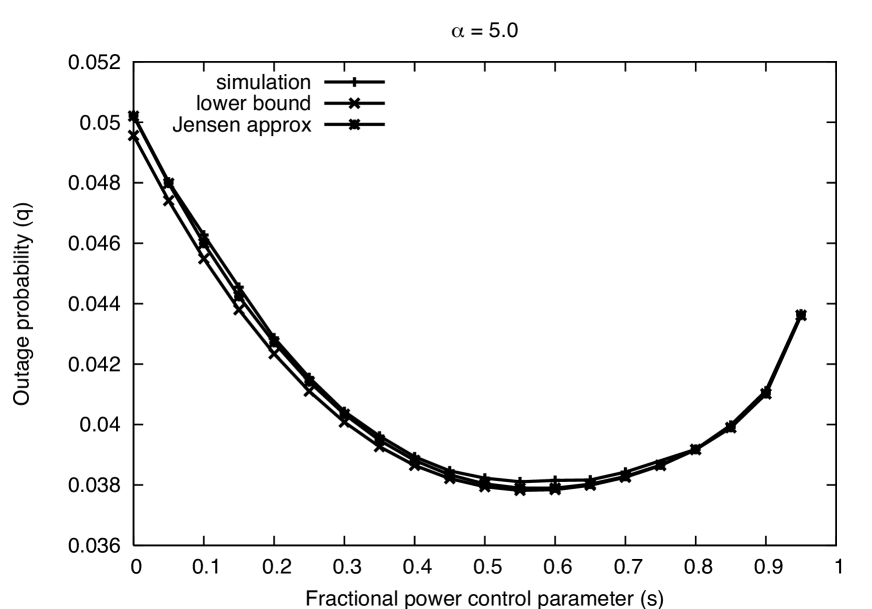
Path loss. In Fig. 3, the bounds are given for and , which correspond to much weaker and much stronger attenuation than the (more likely) default case of . For weaker attenuation, we can see that the lower bound holds the right shape but is less accurate, while the Jensen’s approximation becomes very loose when the FPC exponent is small. For path loss exponents near , the dominant interferer approximation is weakened because the attenuation of non-dominant interferers is less drastic. On the other hand, both the lower bound and Jensen’s approximation are very accurate in strong attenuation environments as seen in the plot. This is because the dominant interferer approximation is very reasonable in such cases.
SNR. The behavior of the bounds also varies as the background noise level changes, as shown in Fig. 4. When the SNR is 10 dB, the bounds are quite tight. However, the behavior of outage probability as a function of is quite different from the default case in Fig. 2: outage probability decreases slowly as is increased, and a rather sharp jump is seen as approaches one. When the interference-free SNR is only moderately larger than the target SINR (in this case there is a 10 dB difference between and ), a significant portion of outages occur because the signal power is so small that the interference-free received SNR falls below the target ; this probability is captured by the terms in Theorem 3. On the other hand, if is much larger than the target , outages are almost always due to a combination of signal fading and large interference power rather than to signal fading alone (i.e., is insignificant compared to the total outage probability). When outages caused purely by signal fading are significant, the dependence on the exponent is significantly reduced. Furthermore, the power cost of FPC becomes much more significant when the gap between and is reduced; this explains the sharp increase in outage as approaches one. When dB, the behavior is quite similar to the 20 dB case because at this point the gap between and is so large that thermal noise can effectively be neglected.
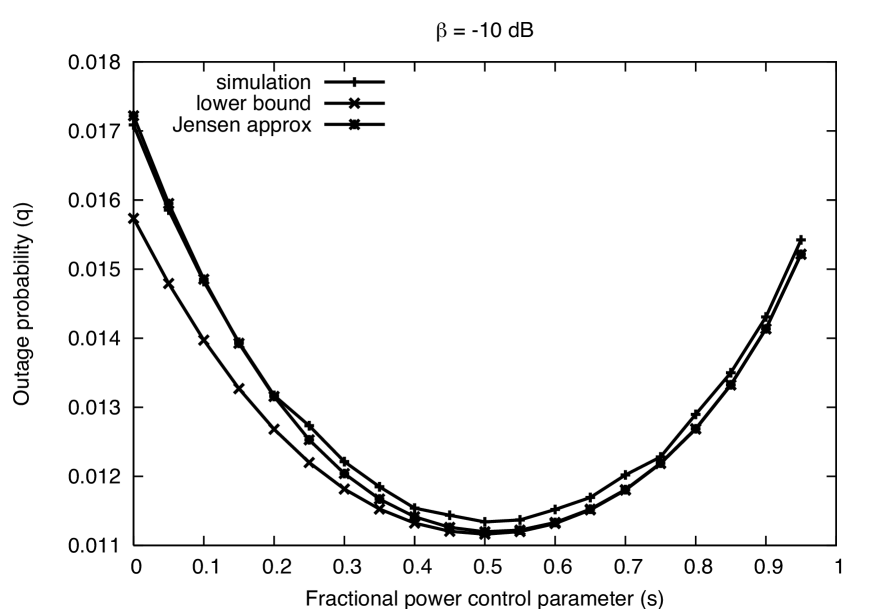
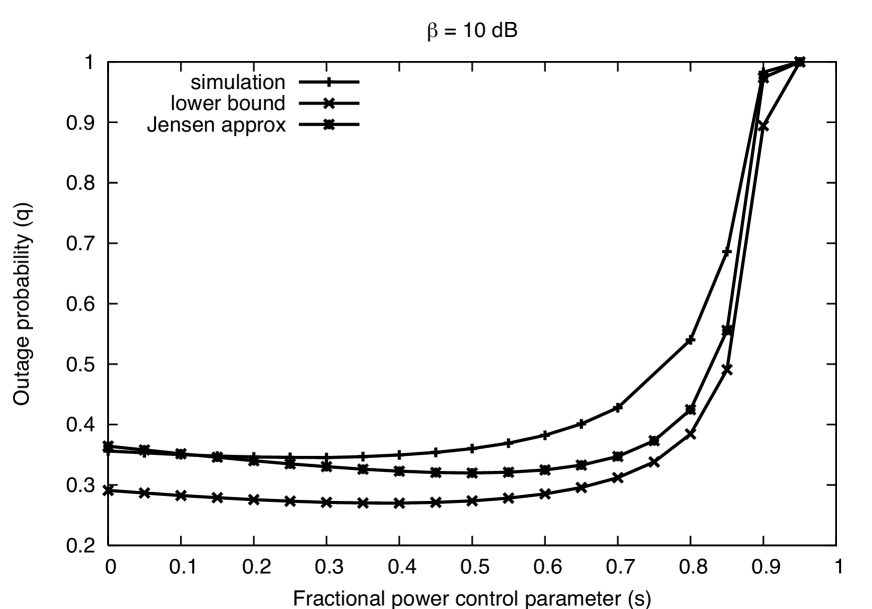
Target SINR. A default SINR of was chosen, which corresponds roughly to a spectral efficiency of 1 bps/Hz with strong coding, and lies between the low and high SINR regimes. Exploring an order of magnitude above and below the default in Fig. 5, we see that for the bounds are highly accurate, and show that is a good choice. For this choice of parameters there is a 30 dB gap between and and thus thermal noise is essentially negligible. On the other hand, if the bounds are still reasonable, but the outage behavior is very similar to the earlier case where dB and dB because there is again only a 10 dB gap between and . Despite the qualitative and quantitative differences for low SNR and high target SINR from the default values, it is interesting to note that in both cases is still a robust choice for the FPC exponent.
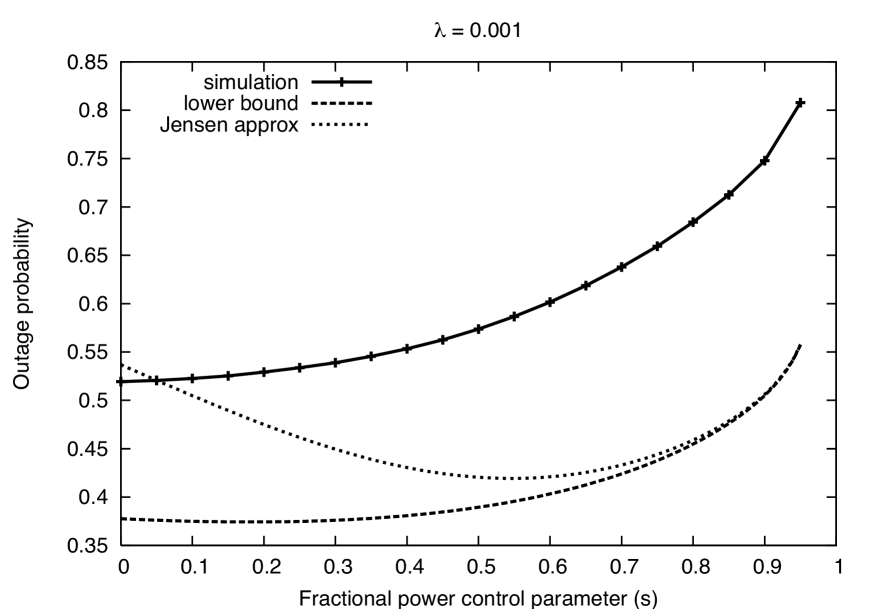
Density. The default value of corresponds to a somewhat low density network because the expected distance to the nearest interferer is approximately m, while the TX-RX distance is m. In Fig. 6 we explore a density an order of magnitude lower and higher than the default value. When the network is even sparser, the bounds are extremely accurate and we see that is a near-optimal choice. However, the behavior with is very different in a dense network where and the nearest interferer is approximately m away. In such a network we see that the nearest neighbor bound is quite loose because a substantial fraction of outages are caused by the summation of non-dominant interferers, as intuitively expected for a dense network. Although the bound is loose, it does capture the fact that outage increases with the exponent . On the other hand, the Jensen approximation is loose and does not correctly capture the relationship between and outage. The approximation is based on the fact that the function is approximately linear for small . The quantity is proportional to , which is large when the network is dense relative to TX-RX distance , and thus this approximation is not valid for relatively dense networks.
IV-C Choosing the FPC exponent
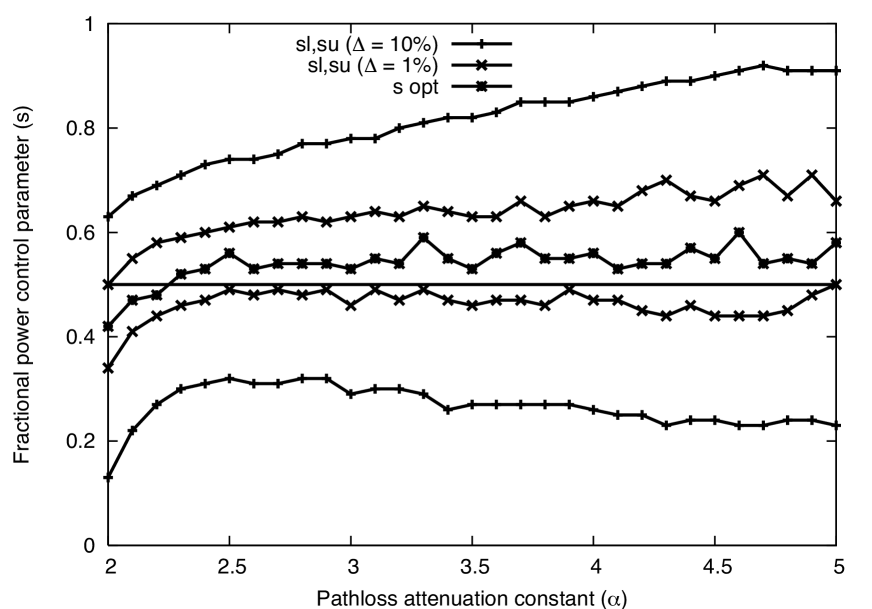
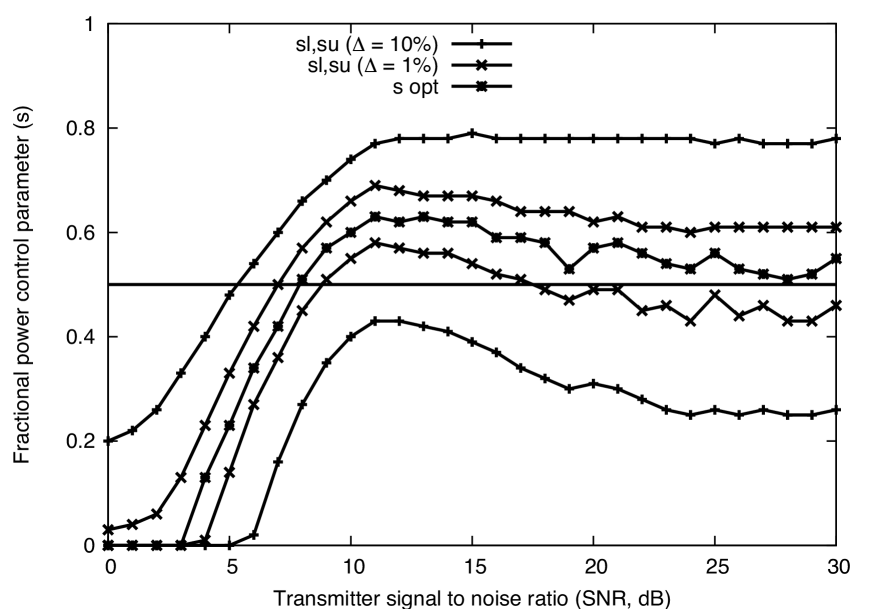
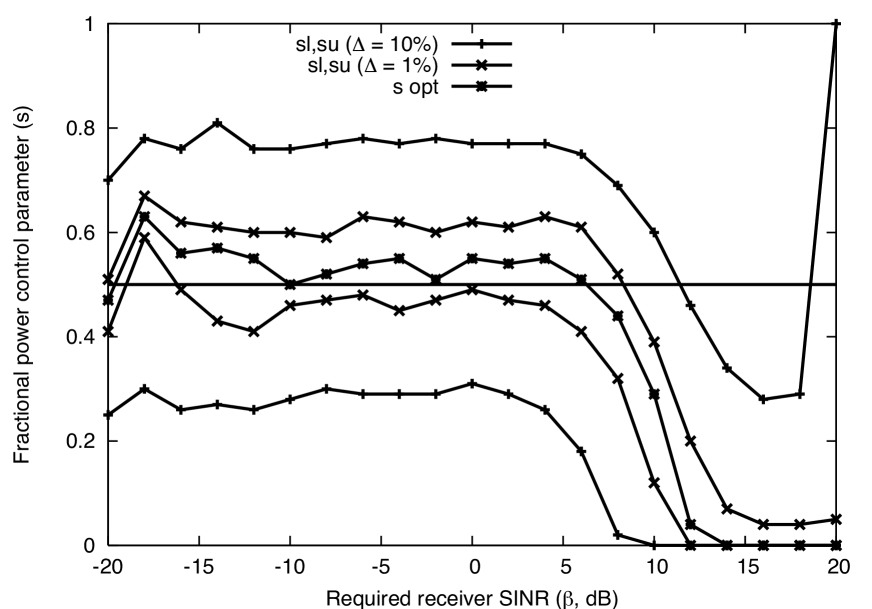
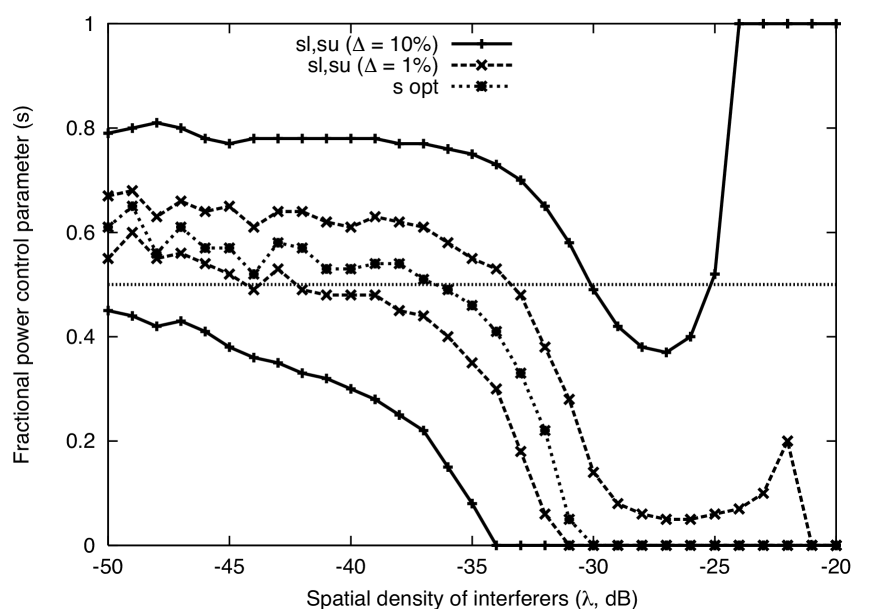
Determining the optimum choice of FPC exponent is a key interest of this paper. As seen in Sect. III-C, is optimal for the Jensen’s approximation and with no noise, both of which are questionable assumptions in many regimes of interest. In Figs. 7 – 10, we plot the truly optimal choice of for the default parameters, while varying , SNR, , and , respectively. That is, the value of that minimizes the true outage probability is determined for each set of parameters. The FPC exponents and are also plotted, which provide % error below and above the optimum outage probability. For the plots, we let and .
The key findings are: (1) In the pathloss () plot, is a very robust choice for all attenuation regimes; (2) For SNR, is only robust at high SNR, and at low SNR constant transmit power is preferable; (3) For target SINR , is robust at low and moderate SINR targets (i.e. low to moderate data rates), but for high SINR targets constant transmit power is preferred; (4) For density , is robust at low densities, but constant transmit power is preferred at high densities.
The explanation for findings (2) and (3) is due to the dependence of outage behavior on the difference between and . As seen earlier, thermal noise is essentially negligible when this gap is larger than approximately 20 dB. As a result, it is reasonable that the exponent shown to be optimal for noise-free networks () would be near-optimal for networks with very low levels of thermal noise. On the other hand, outage probability behaves quite differently when is only slightly larger than . In this case, power is very valuable and it is not worth incurring the normalization cost of FPC and thus very small FPC exponents are optimal. Intuitively, achieving high data rates in moderate SNR or moderate data rates in low SNR are difficult objectives in a decentralized network. The low SNR case is somewhat anomalous, since the SNR is close to the target SINR, so almost no interference can be tolerated. Similarly, to meet a high SINR constraint in a random network of reasonable density, the outage probability must be quite high, so this too may not be particularly meaningful.
To explain (4), recall that the Jensen-based approximation to outage probability is not accurate for dense networks and the plot shows that constant power () is preferred at high densities.111Based on the figure it may appear that choosing , which means users with good channels transmit with additional power, outperforms constant power transmission. However, numerical results (not shown here) indicate that this provides a benefit only at extremely high densities for which outage probability is unreasonably large. Intuitively, a user with a poor channel in a dense network is extremely unlikely to be able to successfully communicate and global performance is improved by having such a user not even attempt to transmit, as done in the threshold-based policy studied in [16]. Fractional power control softens signal fading at the expense of more harmful interference power, and this turns out to be a good tradeoff in relatively sparse networks. In dense networks, however, there generally are a large number of nearby interferers and as a result the benefit of reducing the effect of signal fading (by increasing exponent ) is overwhelmed by the cost of more harmful interference power. Note that this is consistent with results on channel inversion () in [16], where and are seen to be essentially equivalent at low densities (as expected by the Jensen approximation) but inversion is inferior at high densities.
V Possible Areas for Future Study
Given the historically very high level of interest in the subject of power control for wireless systems, this new approach for power control opens many new questions. It appears that FPC has potential for many applications due to its inherent simplicity, requirement for only simple pairwise feedback, and possible a priori design of the FPC parameter . Some areas that we recommend for future study include the following.
How does FPC perform in cellular systems?. Cellular systems in this case are harder to analyze than ad hoc networks, because the base stations (receivers) are located on a regular grid and thus the tractability of the spatial Poisson model cannot be exploited. On the other hand, FPC may be even more helpful in centralized systems. Note that some numerical results for cellular systems are given in reference [17], but no analysis is provided.
Can FPC be optimized for spectral efficiency?. In this paper we have focused on outage relative to an SINR constraint as being the metric. Other metrics can be considered, for example maximizing the average spectral efficiency, i.e. , which could potentially result in optimal exponents , which is conceptually similar to waterfilling.
What is the effect of scheduling on FPC? If scheduling is used, then how should power levels between a transmitter and receiver be set? Will still be optimal? Will the gain be increased or reduced? We conjecture that the gain from FPC will be smaller but non-zero for most any sensible scheduling policy, as the effect of interference inversion is softened.
Can FPC be used to improve iterative power control? At each step of the Foschini-Miljanic algorithm (as well as most of its variants), transmitters adjust their power in a manner similar to channel-inversion, i.e., each transmitter fully compensates for the current SINR. While this works well when the target SINR’s are feasible, it does not necessarily work well when it is not possible to satisfy all users’ SINR requirements. In such a setting, it may be preferable to perform partial compensation for the current SINR level during each iteration. For example, if a link with a 10 dB target is currently experiencing an SINR of 0 dB, rather than increasing its transmit power by 10 dB to fully compensate for this gap (as in the Foschini-Miljanic algorithm), an FPC-motivated iterative policy might only boost power by 5 dB (e.g., adjust power in linear units according to the square root of the gap).
VI Conclusions
This paper has applied fractional power control as a general approach to pairwise power control in decentralized (e.g. ad hoc or spectrum sharing) networks. Using two approximations, we have shown that a fractional power control exponent of is optimal in terms of outage probability and transmission capacity, in contrast to constant transmit power () or channel inversion () in networks with a relatively low density of transmitters and low noise levels. This implies that there is an optimal balance between compensating for fades in the desired signal and amplifying interference. We saw that a gain on the order of or larger (relative to no power control or channel inversion) might be typical for fractional power control in a typical wireless channel.
We prove that for any non-negative random variable , the function
| (25) |
is convex in for with a unique minimum at . In order to show is convex, we show is log-convex and use the fact that a log-convex function is convex. We define
| (26) |
and recall Hölder’s inequality:
| (27) |
The function is convex if for all and all . Using Hölder’s with and we have:
| (28) | |||||
This implies is convex, which further implies convexity of . The derivative of is
| (29) |
and it can easily be seen that is the unique minimizer satisfying .
References
- [1] N. Jindal, S. Weber, and J. G. Andrews, “Fractional power control for decentralized wireless networks,” in Proc., Allerton Conf. on Comm., Control, and Computing, Monticello, IL, Sept. 2007, available at http://www.ece.umn.edu/users/nihar/Publications.html.
- [2] A. Goldsmith and P. Varaiya, “Capacity of fading channels with channel side information,” IEEE Trans. on Info. Theory, pp. 1986–92, Nov. 1997.
- [3] G. J. Foschini and Z. Miljanic, “A simple distributed autonomous power control algorithm and its convergence,” IEEE Trans. on Veh. Technology, vol. 42, no. 8, pp. 641–646, Nov. 1993.
- [4] R. D. Yates, “A framework for uplink power control in cellular radio systems,” IEEE Journal on Sel. Areas in Communications, vol. 13, no. 7, pp. 1341–47, Sept. 1995.
- [5] N. Bambos, S. Chen, and G. J. Pottie, “Radio link admission algorithms for wireless networks with power control and active link quality protection,” in Proc., IEEE INFOCOM, Boston, MA, Apr. 1995, pp. 97–104.
- [6] J. Herdtner and E. Chong, “Analysis of a class of distributed asynchronous power control algorithms for cellular wireless systems,” IEEE Journal on Sel. Areas in Communications, vol. 18, no. 3, Mar. 2000.
- [7] J. F. Chamberland and V. V. Veeravalli, “Decentralized dynamic power control for cellular CDMA systems,” IEEE Trans. on Wireless Communications, vol. 2, no. 3, pp. 549–59, May 2003.
- [8] M. Schubert and H. Boche, QoS-Based Resource Allocation and Transceiver Optimization. NOW: Foundations and Trends in Communications and Information Theory, 2005.
- [9] M. Chiang, P. Hande, T. Lan, and C. W. Tan, Power Control in Cellular Networks. NOW: Foundations and Trends in Networking, To appear 2008.
- [10] T. ElBatt and A. Ephremides, “Joint scheduling and power control for wireless ad hoc networks,” in Proc., IEEE INFOCOM, June 2002, pp. 976–84.
- [11] R. Cruz and A. V. Santhanam, “Optimal routing, link scheduling and power control in multihop wireless networks,” in Proc., IEEE INFOCOM, Apr. 2003, pp. 702– 711.
- [12] M. Haenggi, “The impact of power amplifier characteristics on routing in random wireless networks,” in Proc., IEEE Globecom, San Francisco, CA, Dec. 2003, pp. 513–17.
- [13] S. Agarwal, S. V. Krishnamurthy, R. H. Katz, and S. K. Dao, “Distributed power control in ad-hoc wireless networks,” in Proc., IEEE PIMRC, Oct. 2001, pp. 59–66.
- [14] V. Kawadia and P. R. Kumar, “Power control and clustering in ad hoc networks,” in Proc., IEEE INFOCOM, 2003.
- [15] M. Chiang, “Balancing transport and physical layers in wireless multihop networks: Jointly optimal congestion control and power control,” IEEE Journal on Sel. Areas in Communications, vol. 23, no. 1, pp. 104–16, Jan. 2005.
- [16] S. Weber, J. G. Andrews, and N. Jindal, “The effect of fading, channel inversion, and threshold scheduling on ad hoc networks,” IEEE Trans. on Info. Theory, vol. 53, no. 11, pp. 4127 – 4149, Nov. 2007.
- [17] W. Xiao, R. Ratasuk, A. Ghosh, R. Love, Y. Sun, and R. Nory, “Uplink power control, interference coordination and resource allocation for 3GPP E-UTRA,” in Proc., IEEE Veh. Technology Conf., Sept. 2006, pp. 1–5.
- [18] S. Weber, X. Yang, J. G. Andrews, and G. de Veciana, “Transmission capacity of wireless ad hoc networks with outage constraints,” IEEE Trans. on Info. Theory, vol. 51, no. 12, pp. 4091–4102, Dec. 2005.
- [19] F. Baccelli, B. Blaszczyszyn, and P. Muhlethaler, “An Aloha protocol for multihop mobile wireless networks,” IEEE Trans. on Info. Theory, pp. 421–36, Feb. 2006.
- [20] S. Weber, J. G. Andrews, X. Yang, and G. de Veciana, “Transmission capacity of wireless ad hoc networks with successive interference cancellation,” IEEE Trans. on Info. Theory, vol. 53, no. 8, pp. 2799–2814, Aug. 2007.