FreCaS: Efficient Higher-Resolution Image
Generation via Frequency-aware
Cascaded Sampling
Abstract
While image generation with diffusion models has achieved a great success, generating images of higher resolution than the training size remains a challenging task due to the high computational cost. Current methods typically perform the entire sampling process at full resolution and process all frequency components simultaneously, contradicting with the inherent coarse-to-fine nature of latent diffusion models and wasting computations on processing premature high-frequency details at early diffusion stages. To address this issue, we introduce an efficient Frequency-aware Cascaded Sampling framework, FreCaS in short, for higher-resolution image generation. FreCaS decomposes the sampling process into cascaded stages with gradually increased resolutions, progressively expanding frequency bands and refining the corresponding details. We propose an innovative frequency-aware classifier-free guidance (FA-CFG) strategy to assign different guidance strengths for different frequency components, directing the diffusion model to add new details in the expanded frequency domain of each stage. Additionally, we fuse the cross-attention maps of previous and current stages to avoid synthesizing unfaithful layouts. Experiments demonstrate that FreCaS significantly outperforms state-of-the-art methods in image quality and generation speed. In particular, FreCaS is about 2.86 and 6.07 faster than ScaleCrafter and DemoFusion in generating a 20482048 image using a pre-trained SDXL model and achieves an improvement of 11.6 and 3.7, respectively. FreCaS can be easily extended to more complex models such as SD3. The source code of FreCaS can be found at https://github.com/xtudbxk/FreCaS.
1 Introducation
In recent years, diffusion models, such as Imagen (Saharia et al., 2022), SDXL (Podell et al., 2023), PixelArt- (Chen et al., 2023) and SD3 Esser et al. (2024), have achieved a remarkable success in generating high-quality natural images. However, these models face challenges in generating very high resolution images due to the increased complexity in high-dimensional space. Though efficient diffusion models, including ADM (Dhariwal & Nichol, 2021), CascadedDM (Ho et al., 2022) and LDM (Rombach et al., 2022), have been developed, the computational burden of training diffusion models from scratch for high-resolution image generation remains substantial. As a result, popular diffusion models, such as SDXL (Podell et al., 2023) and SD3 (Esser et al., 2024), primarily focus on generating resolution images. It is thus increasingly attractive to explore training-free strategies for generating images at higher resolutions, such as and , using pre-trained diffusion models.
MultiDiffusion (Bar-Tal et al., 2023) is among the first works to synthesize higher-resolution images using pre-trained diffusion models. However, it suffers from issues such as object duplication, which largely reduces the image quality. To address these issues, Jin et al. (2024) proposed to manually adjust the scale of entropy in the attention operations. He et al. (2023) and Huang et al. (2024) attempted to enlarge the receptive field by replacing the original convolutional layers with strided ones, while Zhang et al. (2023) explicitly resizes the intermediate feature maps to match the training size. Du et al. (2024) and Lin et al. (2024) took a different strategy by generating a reference image at the base resolution and then using it to guide the whole sampling process at higher resolutions. Despite the great advancements, these methods still suffer from significant inference latency, hindering their broader applications in real world.
In this paper, we propose an efficient Frequency-aware Cascaded Sampling framework, namely FreCaS, for training-free higher-resolution image generation. Our proposed FreCaS framework is based on the observation that latent diffusion models exhibit a coarse-to-fine generation manner in the frequency domain. In other words, they first generate low-frequency contents in early diffusion stages and gradually generate higher-frequency details in later stages. Leveraging this insight, we generate higher-resolution images through multiple stages of increased resolutions, progressively synthesizing details of increased frequencies. FreCaS avoids unnecessary computations during the early diffusion stages as high-frequency details are not yet required.
In the latent space, the image representation expands its frequency range as the resolution increases. To encourage detail generation within the expanded frequency band, we introduce a novel frequency-aware classifier-free guidance (FA-CFG) strategy, which prioritizes newly introduced frequency components by assigning them higher guidance strengths in the sampling process. Specifically, we decompose both unconditional and conditional denoising scores into two parts: low-frequency component, which captures content from earlier stages, and high-frequency component, which corresponds to the newly increased frequency band. FA-CFG applies the classifier-free guidance to different frequency components with different strengths, and outputs the final denoising score by combining the adjusted components. The FA-CFG strategy can synthesize much clear details while maintaining computational efficiency. Additionally, to alleviate the issue of unfaithful layouts, such as duplicated objects mentioned in Jin et al. (2024), we reuse the cross-attention maps (CA-maps) from the previous stage, which helps maintaining consistency in image structure across different stages and ensuring more faithful object representations.
In summary, our main contributions are as follows:
-
•
We propose FreCaS, an efficient frequency-aware cascaded sampling framework for training-free higher-resolution image generation. FreCaS leverages the coarse-to-fine nature of the latent diffusion process, thereby reducing unnecessary computations associated with processing premature high-frequency details.
-
•
We design a novel FA-CFG strategy, which assigns different guidance strengths to components of different frequencies. This strategy enables FreCaS to focus on generating contents of newly introduced frequencies in each stage, and hence synthesize clearer details. In addition, we fuse the CA-maps of previous stage and current stage to maintain a consistent image layouts across stages.
-
•
We demonstrate the efficiency and effectiveness of FreCaS through extensive experiments conducted on various pretrained diffusion models, including SD2.1, SDXL and SD3, validating its broad applicability and versatility.
2 Related Works
2.1 Diffusion Models
Diffusion models have gained significant attentions due to their abilities to generate high-quality natural images. Ho et al. (2020) pioneered the use of a variance-preserving diffusion process to bridge the gap from natural images to pure noises. Dhariwal & Nichol (2021) exploited various network architectures and achieved superior image quality than contemporaneous GAN models. Ho & Salimans (2022) introduced a novel classifier-free guidance strategy that attains both generated image quality and diversity. However, the substantial model complexity makes high-resolution image synthesis challenging. Ho et al. (2022) proposed a novel cascaded framework that progressively increases image resolutions. Rombach et al. (2022) performed the diffusion process in the latent space of a pre-trained autoencoder, enabling high-resolution image synthesis with reduced computational cost. (Esser et al., 2024) presented SD3, which employs the rectified flow matching (Lipman et al., 2022; Liu et al., 2022) at the latent space and demonstrates superior performance. Despite the great progress, it still requires substantial efforts to train a high-resolution diffusion model from scratch. Therefore, training-free higher-resolution image synthesis attracts increasing attentions.
2.2 Training-free higher-resolution Image Synthesis
A few methods have been developed to leverage pre-trained diffusion models to generate images of higher resolutions than the training size. MultiDiffusion (Bar-Tal et al., 2023) is among the first methods to bind multiple diffusion processes into one unified framework and generates seamless higher-resolution images. However, the results exhibit unreasonable image structures such as duplicated objects. AttnEntropy (Jin et al., 2024) alleviates this problem by re-normalizing the entropy of attention blocks during sampling. On the other hand, ScaleCrafter (He et al., 2023) and FouriScale (Huang et al., 2024) expand the receptive fields of pre-trained networks to match higher inference resolutions, thereby demonstrating improved image quality. HiDiffusion (Zhang et al., 2023) dynamically adjusts the feature sizes to match the training dimensions. DemoDiffusion (Du et al., 2024) and AccDiffusion (Lin et al., 2024) first generate a reference image at standard resolutions and then use this image to guide the generation of images at higher resolutions. Despite their success, the above mentioned approaches neglect the coarse-to-fine nature of image generation and generate image contents of all frequencies simultaneously, resulting in long inference latency and limiting their broader applications.
To address this issue, we propose an efficient FreCaS framework for training-free higher-resolution image synthesis. FreCaS divides the entire sampling process into stages of increasing resolutions, gradually synthesizing components of different frequency bands, thereby reducing the unnecessary computation of handling premature high-frequency details in early sampling stages. It is worth noting that DemoFusion (Du et al., 2024) and ResMaster (Shi et al., 2024) also employ a cascaded sampling scheme. However, there exist fundamental differences between FreCaS and them: DemoFusion and ResMaster perform a complete diffusion process at each resolution, whereas FreCaS transitions the diffusion from low to high resolutions in just one process. This distinction makes our method significantly more efficient than them while achieving better image quality.
3 Method
This section presents the details of the proposed FreCaS framework, which leverages the coarse-to-fine nature of latent diffusion models and constructs a frequency-aware cascaded sampling strategy to progressively refine high-frequency details. We first introduce the notations and concepts that form the basis of our approach (see Section 3.1). Then, we delve into the key components of our method: FreCaS framework (see Section 3.2), FA-CFG strategy (see Section 3.3), and CA-maps re-utilization (see Section 3.4).
3.1 Preliminaries
Diffusion models. Diffusion models (Ho et al., 2020; Dhariwal & Nichol, 2021) transform complex image distributions into the Gaussian distribution, and vice versa. They gradually inject Gaussian noises into the image samples, and then use a reverse process to remove noises from them, achieving image generation. Most recent diffusion models operate in the latent space and utilize a discrete timestep sampling process to synthesize images. Specifically, for a -step sampling process, a latent noise is drawn from a standard Gaussian distribution, and then iteratively refined through a few denoising steps until converged to the clean signal latent . Finally, the natural image is decoded from using a decoder . The whole process can be written as follows:
| (1) |
For each denoising step, current works typically adopt the classifier-free guidance (CFG) (Ho & Salimans, 2022) to improve image quality. It predicts an unconditional denoising score and a conditional denoising score . The final denoising score is obtained via a simple extra-interpolation process as , where denotes the guidance strength.
Resolution and frequency range. The resolution of a latent determines its sampling frequency (Rissanen et al., 2023), thereby influencing its frequency domain characteristics. Specifically, if a latent of unit length has a resolution of , its sampling frequency can be defined as the number of samples per unit length, which is . The Nyquist frequency is then obtained as . Therefore, the frequency of the latent ranges from [0, ]. Reducing its resolution to narrows the frequency range to [0, ]. As a result, higher resolutions capture a broader frequency domain, while lower resolutions lead to a narrower frequency spectrum.
3.2 Frequency-aware cascaded sampling
Pixel space diffusion models exhibit a coarse-to-fine behavior in the image synthesis process (Rissanen et al., 2023; Teng et al., 2024). In this section, we show that such a behavior is also exhibited for latent diffusion models during the sampling process, which inspires us to develop a frequency-aware cascaded sampling framework for generating higher-resolution images.
PSD curves in latent space. The power spectral density (PSD) is a powerful tool for analyzing the energy distribution of signals along the frequency spectrum. Rissanen et al. (2023) and Teng et al. (2024) have utilized PSD to study the behaviour of intermediate states in the pixel diffusion process. Here, we compute the PSD of the latent signals over a collection of 100 natural images using the pre-trained SDXL model (Podell et al., 2023). Figure 1 shows the PSD curves of , , and . The solid line denotes the PSD curve of intermediate noise corrupted latent, while the dashed line represents the PSD of Gaussian noise corrupted into the latent. The inner area between the two curves (marked with red slashes) indicates the energy of clean signal latent being synthesized. One can see that the clean image signals emerge from the low-frequency band (see and ) and gradually expand to the high-frequency band (see and ) during the sampling process. These observations confirm the coarse-to-fine nature of image synthesis in the latent diffusion process, where low-frequency content is generated first, followed by high-frequency details.
Framework of FreCaS. Based on the above observation, we developed an efficient FreCaS framework to progressively generate image contents of higher frequency bands, reducing unnecessary computations in processing premature high-frequency details in early diffusion stages. As shown in Figure 2(a), our FreCaS divides the entire -step sampling process into stages of increasing resolutions. The initial stage performs the sampling process at the default training size with a frequency range of [0, ]. Each of the subsequent stages increases the sampling size to its predecessor, gradually expanding the frequency domain. At the final stage, the latent reaches the target resolution , achieving a full frequency range from 0 to .
Specifically, we begin with a pure noise latent at stage , and iteratively perform reverse sampling until obtaining the last latent in this stage, denoted by . Next, we transition to the first latent, denoted by , in next stage, as illustrated by the blue dashed arrow in Figure 2(a). This procedure is repeated until the latent feature reaches the target size, resulting in . The final image is obtained by applying the decoder to so that . With such a sampling pipeline, FreCaS ensures a gradual refinement of details across coarse-to-fine scales, ultimately producing a high-quality and high-resolution image with minimum computations.
For the transition between two adjacent stages, we perform five steps to convert the last latent of previous stage to the first latent of next stage :
| (2) |
where “denoise” and “diffuse” are standard diffusion operations, “decode” and “encode” are performed using the decoder and encoder, respectively, and “interpolation” adjusts the resolutions using the bilinear interpolation. To determine the timestep of , we follow previous works (Hoogeboom et al., 2023; Chen, 2023; Gu et al., 2023; Teng et al., 2024) to keep the signal-to-noise ratio (SNR) equivalence between and . Please refer to Appendix A for more details.
3.3 FA-CFG strategy
Our FreCaS framework progressively transitions the latents to stages with higher resolutions and extended high-frequency bands. To ensure that the diffusion models focus more on generating contents of newly introduced frequencies, we propose a novel FA-CFG strategy, which assigns higher guidance strength to the new frequency components. In FreCaS, upon transitioning to stage , the latent increases its resolution from to the higher resolution , thereby expanding the frequency band from [0, ] to [0, ]. This inspires us to divide the latents into two components: a low-frequency component ranging from [0, ] and a high-frequency component covering the frequency interval (, ]. The former preserves the generated contents from previous stages, whereas the latter is reserved for the contents to be generated in this stage. Our goal is to encourage the diffusion models to generate natural details and textures in the newly expanded frequency band.
To achieve the above mentioned goal, we propose to perform CFG on the two frequency-aware parts with different guidance strengths. The entire process is illustrated in Figure 2(b). First, we obtain the unconditional denoising score and conditional denoising score using the pre-trained diffusion network. Then, we split the scores into a low-frequency part and a high-frequency part. The former is extracted by downsampling the scores and then resizing them back, while the latter is the residual by subtracting the low-frequency part from the original denoising scores. Subsequently, we apply the CFG strategy to the two parts with different weights. Specifically, for the low-frequency part, we assign the normal guidance strength , while for the high-frequency part, we use a much higher weight to prioritize content generation in this frequency band. The final denoising score is obtained by summing up the two parts. This process can be expressed as:
| (3) |
where and are the low-frequency and high-frequency parts of , respectively. Similarly, , , and follow the same notation.
3.4 CA-maps reutilization
When applied to higher resolutions, pre-trained diffusion models often present unreasonable image structures, such as duplicated objects. To address this issue, we propose to reuse the CA-maps from the previous stage to maintain layout consistency across stages. The CA-maps represent attention weights from cross-attention interactions between spatial features and textual embeddings, effectively capturing the semantic layout of the generated images. Specifically, we average the CA-maps of all cross-attention blocks when predicting at stage . After transitioning to stage , we replace the current CA-maps of each cross-attention block using its linear interpolation with the averaged CA-maps as follows:
| (4) |
where is the CA-maps at step of stage . In this way, FreCaS can effectively maintain content consistency and prevent unexpected objects or textures during higher-resolution image generation.
4 Experiments
| Methods | DO | FID | IS | CLIP SCORE | Latency(s) | SpeedUP | |||||
| SD2.1 | 4 | DirectInference | ✗ | 31.07 | 34.54 | 23.84 | 15.00 | 17.26 | 32.01 | 5.50 | 1x |
| MultiDiffusion | ✗ | 21.05 | 22.44 | 14.68 | 17.46 | 18.29 | 32.49 | 120.21 | 0.046 | ||
| \cdashline3-12 | AttnEntropy | ✓ | 28.33 | 30.63 | 21.34 | 15.67 | 17.71 | 32.28 | 5.56 | 0.99 | |
| ScaleCrafter | ✓ | 16.65 | 13.18 | 22.44 | 17.42 | 16.29 | 32.88 | 6.36 | 0.86 | ||
| FouriScale | ✓ | 19.01 | 15.33 | 23.26 | 17.11 | 15.57 | 32.92 | 11.06 | 0.50 | ||
| HiDiffusion | ✓ | 19.95 | 16.21 | 25.26 | 17.13 | 16.12 | 32.37 | 3.57 | 1.54 | ||
| Ours | ✓ | 16.38 | 13.14 | 21.23 | 17.55 | 16.04 | 32.33 | 2.56 | 2.16 | ||
| 16 | DirectInference | ✗ | 124.5 | 128.3 | 50.23 | 8.84 | 15.30 | 27.67 | 49.27 | 1 | |
| MultiDiffusion | ✗ | 67.44 | 74.15 | 15.28 | 8.75 | 18.82 | 31.14 | 926.33 | 0.05 | ||
| \cdashline3-12 | AttnEntropy | ✓ | 122.6 | 127.6 | 46.52 | 9.31 | 16.25 | 28.33 | 49.33 | 1.00 | |
| ScaleCrafter | ✓ | 34.47 | 34.55 | 57.47 | 13.02 | 12.12 | 31.44 | 92.86 | 0.53 | ||
| FouriScale | ✓ | 34.17 | 34.13 | 58.01 | 12.79 | 13.15 | 31.68 | 90.13 | 0.55 | ||
| HiDiffusion | ✓ | 33.15 | 34.17 | 70.58 | 13.49 | 11.87 | 31.09 | 18.22 | 2.70 | ||
| Ours | ✓ | 19.95 | 20.11 | 43.71 | 15.22 | 13.74 | 31.92 | 13.35 | 3.69 | ||
| SDXL | 4 | DirectInference | ✗ | 39.15 | 43.83 | 29.71 | 11.52 | 14.60 | 32.51 | 34.10 | 1 |
| \cdashline3-12 | AttnEntropy | ✓ | 36.54 | 41.30 | 27.67 | 11.69 | 15.04 | 32.71 | 34.36 | 0.99 | |
| ScaleCrafter | ✓ | 22.76 | 24.23 | 23.17 | 14.10 | 14.97 | 32.70 | 39.64 | 0.86 | ||
| FouriScale | ✓ | 26.44 | 26.88 | 27.24 | 13.97 | 14.44 | 32.90 | 66.18 | 0.52 | ||
| HiDiffusion | ✓ | 21.67 | 20.69 | 21.80 | 15.56 | 15.93 | 32.62 | 18.38 | 1.86 | ||
| AccDiffusion | ✓ | 19.87 | 17.62 | 21.11 | 17.07 | 16.15 | 32.66 | 102.46 | 0.33 | ||
| DemoFusion | ✓ | 18.77 | 16.33 | 18.77 | 17.10 | 17.21 | 33.16 | 83.95 | 0.41 | ||
| Ours | ✓ | 16.48 | 12.63 | 17.91 | 17.18 | 17.31 | 33.28 | 13.84 | 2.46 | ||
| 16 | DirectInference | ✗ | 145.4 | 151.3 | 62.39 | 6.41 | 11.66 | 28.24 | 312.36 | 1 | |
| \cdashline3-12 | AttnEntropy | ✓ | 142.1 | 148.9 | 60.54 | 6.46 | 12.44 | 28.46 | 312.46 | 1.00 | |
| ScaleCrafter | ✓ | 71.49 | 75.11 | 73.21 | 8.68 | 9.81 | 30.76 | 560.91 | 0.56 | ||
| FouriScale | ✓ | 98.01 | 77.63 | 84.05 | 8.00 | 9.41 | 30.78 | 534.08 | 0.58 | ||
| HiDiffusion | ✓ | 81.48 | 83.41 | 120.1 | 9.79 | 9.56 | 29.18 | 101.59 | 3.07 | ||
| AccDiffusion | ✓ | 50.47 | 48.15 | 46.07 | 12.11 | 11.75 | 32.26 | 763.23 | 0.41 | ||
| DemoFusion | ✓ | 47.80 | 44.54 | 35.52 | 12.38 | 13.82 | 33.03 | 649.25 | 0.48 | ||
| Ours | ✓ | 42.75 | 40.63 | 39.82 | 12.68 | 14.16 | 33.03 | 85.87 | 3.64 |
4.1 Experimental settings
Implementation details. We evaluate FreCaS on three widely-used pre-trained diffusion models: SD2.1 (Rombach et al., 2022), SDXL (Podell et al., 2023) and SD3 (Esser et al., 2024). The sizes of generated images are and the original training size. Specifically, we generate images of 10241024 and 20482048 for SD2.1, while and for SDXL. For SD3, we only generate images of due to the GPU memory limitation. We randomly select 10K, 5K, and 1K prompts from the LAION5B aesthetic subset for generating images of 10241024, 20482048, and 40964096, respectively. We follow the default settings and perform a 50-step sampling process with DDIM sampler for SD2.1 and SDXL, and perform a 28-step sampling process with a flow matching based Euler solver for SD3. For experiments, we employ two sampling stages at the training size and target size, respectively. For experiments, we employ three sampling stages at the training size, training size and training size, respectively. More details can be found in Appendix B.
Evaluation metrics. We employ the Fréchet Inception Distance (FID) (Heusel et al., 2017) and Inception Score (IS) (Salimans et al., 2016) to measure the quality of generated images. Following He et al. (2023), we also employ as the metric, which is computed on the samples of training size and target size. As suggested by Du et al. (2024), we report and , which compute the metrics at patch level, to better evaluate the image details. The CLIP score (Radford et al., 2021) is utilized to measure the text prompt alignment of generated images. As in previous works (Zhang et al., 2023), we measure the model latency on a single NVIDIA A100 GPU with a batch size of 1. We generate five images and report the averaged latency of the last three images for all methods. Moreover, we conduct a user study and employ the non-reference image quality assessment metrics to further evaluate our FreCaS. Please refer to Appendix C for the details.
4.2 Experiments on SD2.1 and SDXL
For experiments on SD2.1, we compare FreCaS with DirectInference, MultiDiffusion (Bar-Tal et al., 2023), AttnEntropy (Jin et al., 2024), ScaleCrafter (He et al., 2023), FouriScale (Huang et al., 2024) and HiDiffusion (Zhang et al., 2023). For experiments on SDXL, we compare with DirectInference, AttnEntropy, ScaleCrafter, FouriScale, HiDiffusion, AccDiffusion (Lin et al., 2024) and DemoFusion (Du et al., 2024). We further compare our FreCaS with training-based methods (Pixart-Sigma (Chen et al., 2024) and UltraPixel (Ren et al., 2024)) and super-resoution methods (ESRGAN (Wang et al., 2021) and SUPIR (Yu et al., 2024)) in Appendix D.
Quantitative results. Table 1 presents quantitative comparisons for and generation between FreCaS and its competitors. We can see that FreCaS not only outperforms other methods on synthesized image quality but also exhibits significantly faster inference speed. In specific, FreCaS achieves the best FID scores in all experiments of SD2.1 and SDXL, achieving clear advantages over the other methods. In terms of the IS metric, FreCaS performs the best in most cases, only slightly lagging behind DemoFusion on the experiments of SDXL. (Note that DirectInference and MultiDiffusion occasionally achieve higher and scores because they disregard the issue of duplicated objects.) For CLIP score, FreCaS obtains the best results on 3 out of the 4 cases, except for the less challenging generation with SD2.1.
While having superior image quality metrics, FreCaS demonstrates impressive efficiency. It shows more than speedup over DirectInference on generation experiments, and shows more than speedup on the generation experiments. DemoFusion, which is overall the second best method in terms of image quality, is significantly slower than FreCaS. Its latency is about and longer than FreCas on and experiments, respectively. On the other hand, HiDiffusion, which is the second faster method, sacrifices image quality for speed. For example, on the experiment with SD2.1, HiDiffusion achieves a latency of 18.22s but its score is 34.17. In contrast, FreCaS is faster (13.35s) and has a much better score (20.11).
Qualitative results. Figure 3 illustrates visual comparisons between FreCaS and competitive approaches. From top to bottom are four groups of examples, presenting the results of generation of SD2.1, generation of SD2.1, generation of SDXL, and generation of SDXL, respectively. In each group, the top row shows the generated images, while the bottom row shows the zoomed region for better observation. From Figure 3, we can see that FreCaS effectively synthesizes the described contents while maintaining a coherent scene structure. DirectInference, MultiDiffusion and AttnEntropy often produce duplicated objects, such as the many astronauts and warriors. ScaleCrafter and HiDiffusion achieve reasonable image contents in experiments of SD2.1 but generate unnatural layouts in the experiments of SDXL, such as the excessive flowers on the ceiling in experiment. Our FreCaS consistently maintains coherent image contents and layout in experiments of both SD2.1 and SDXL. AccDiffusion and DemoFusion also achieve natural image contents, but FreCaS generates clearer details such as the flowers and trains. Please refer to Appendix E for more visual results, including images with other aspect ratios.
4.3 Experiments on SD3
4.4 Ablation Studies
In this section, we conduct ablation studies on experiments of SDXL to investigate the effectiveness and settings of our cascaded framework, FA-CFG and CA-maps strategies.
Effectiveness of each component. We conduct a series of ablation studies to better demonstrate the effectiveness of each component of FreCaS, including the cascaded sampling framework, FA-CFG and CA-maps reutilization strategies. Please refer to Appendix G for more details.
FA-CFG strategy. The FA-CFG strategy aims to guide the model to generate content within the expanded frequency band. To achieve this, FA-CFG introduces two parameters, and , to adjust the guidance strength on the low and high frequency components, respectively. When , the FA-CFG strategy degenerates to the conventional CFG approach. We conduct a series of experiments to explore the optimal settings of the two parameters. First, we fix at 7.5 and vary . The results are shown in Figure 4(a). We observe that as increases from 1.0 to 45, the and metrics initially decrease, indicating improved image quality. However, as becomes too high, the metrics begin to deteriorate. The sweet spot lies between 25 and 35, achieving a low of nearly 12.65 and a low of 17.91. We then fix at 35 and vary . The results are presented in Figure 4(b). Reducing below 7.5 leads to a slight increase in from 17.91 to 18.06, whereas increasing over 7.5 deteriorates from 12.81 to 13.00. Compared to , adjusting brings much smaller effects on those two metrics. Thus, we set to 7.5 for experiments on SD2.1 and SDXL, and set it to 7.0 for SD3.
Figure 5 provides visual examples of adjusting . Increasing enhances the sharpness of details, such as clearer hair strands and more vivid flower petals. However, an excessively high value of (e.g., 45) will introduce artifacts, as highlighted by the red boxes in the figure. This underscores the importance of selecting an appropriate value to strike a balance between detail enhancement and artifact suppression. Based on these findings, we set to 7.5 and to 35 yields favorable outcomes in most of the cases.
CA-maps re-utilization. To evaluate the effect of weight in the re-utilization of CA-maps, we conduct an ablation study by varying from 0 to 1. The results are shown in Figure 4(c). Increasing continuously decreases but increases , indicating an improvement on the image layout but a drop on image details. To balance between the two metrics, we set . A visual example is shown in Figure 6. We see that this setting leads to a clearer textures on strawberry compared to and prevents the unreasonable surface of the blueberry in .
Inference schedule. FreCaS uses two factors to adjust the inference schedule. The first one is the count of additional stages . The second factor is the timestep of last latent in each stage. We conduct experiments on the selection of these two factors. The details can be found in Appendix G. Based on results, we set to , and set to 2 for experiments and 3 for experiments.
5 Conclusion
We developed a highly efficient Frequency-aware Cascaded Sampling framework, namely FreCaS, for training-free higher-resolution image generation. FreCaS leveraged the coarse-to-fine nature of latent diffusion process, reducing unnecessary computations in processing premature high-frequency details. Specifically, we divided the entire sampling process into several stages having increasing resolutions and expanding frequency bands, progressively generating image contents of higher frequency details. We presented a Frequency-Aware Classifier-Free Guidance (FA-CFG) strategy to enable diffusion models effectively adding details of the expanded frequencies, leading to clearer textures. In addition, we fused the cross-attention maps of previous stages and current one to maintain consistent image layouts across stages. FreCaS demonstrated advantages over previous methods in both image quality and efficiency. In particular, with SDXL, it can generate a high quality resolution image in 86 seconds on an A100 GPU.
References
- Bar-Tal et al. (2023) Omer Bar-Tal, Lior Yariv, Yaron Lipman, and Tali Dekel. Multidiffusion: Fusing diffusion paths for controlled image generation. 2023.
- Chen et al. (2023) Junsong Chen, Jincheng Yu, Chongjian Ge, Lewei Yao, Enze Xie, Yue Wu, Zhongdao Wang, James Kwok, Ping Luo, Huchuan Lu, et al. Pixart-alpha: Fast training of diffusion transformer for photorealistic text-to-image synthesis. arXiv preprint arXiv:2310.00426, 2023.
- Chen et al. (2024) Junsong Chen, Chongjian Ge, Enze Xie, Yue Wu, Lewei Yao, Xiaozhe Ren, Zhongdao Wang, Ping Luo, Huchuan Lu, and Zhenguo Li. Pixart-sigma: Weak-to-strong training of diffusion transformer for 4k text-to-image generation. arXiv preprint arXiv:2403.04692, 2024.
- Chen (2023) Ting Chen. On the importance of noise scheduling for diffusion models. arXiv preprint arXiv:2301.10972, 2023.
- Dhariwal & Nichol (2021) Prafulla Dhariwal and Alexander Nichol. Diffusion models beat gans on image synthesis. Advances in neural information processing systems, 34:8780–8794, 2021.
- Du et al. (2024) Ruoyi Du, Dongliang Chang, Timothy Hospedales, Yi-Zhe Song, and Zhanyu Ma. Demofusion: Democratising high-resolution image generation with no $$$. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 6159–6168, 2024.
- Esser et al. (2024) Patrick Esser, Sumith Kulal, Andreas Blattmann, Rahim Entezari, Jonas Müller, Harry Saini, Yam Levi, Dominik Lorenz, Axel Sauer, Frederic Boesel, et al. Scaling rectified flow transformers for high-resolution image synthesis. In Forty-first International Conference on Machine Learning, 2024.
- Gu et al. (2023) Jiatao Gu, Shuangfei Zhai, Yizhe Zhang, Miguel Ángel Bautista, and Joshua M Susskind. f-dm: A multi-stage diffusion model via progressive signal transformation. In The Eleventh International Conference on Learning Representations, 2023.
- He et al. (2023) Yingqing He, Shaoshu Yang, Haoxin Chen, Xiaodong Cun, Menghan Xia, Yong Zhang, Xintao Wang, Ran He, Qifeng Chen, and Ying Shan. Scalecrafter: Tuning-free higher-resolution visual generation with diffusion models. In The Twelfth International Conference on Learning Representations, 2023.
- Heusel et al. (2017) Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Advances in neural information processing systems, 30, 2017.
- Ho & Salimans (2022) Jonathan Ho and Tim Salimans. Classifier-free diffusion guidance. arXiv preprint arXiv:2207.12598, 2022.
- Ho et al. (2020) Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. Advances in neural information processing systems, 33:6840–6851, 2020.
- Ho et al. (2022) Jonathan Ho, Chitwan Saharia, William Chan, David J Fleet, Mohammad Norouzi, and Tim Salimans. Cascaded diffusion models for high fidelity image generation. Journal of Machine Learning Research, 23(47):1–33, 2022.
- Hoogeboom et al. (2023) Emiel Hoogeboom, Jonathan Heek, and Tim Salimans. simple diffusion: End-to-end diffusion for high resolution images. In International Conference on Machine Learning, pp. 13213–13232. PMLR, 2023.
- Huang et al. (2024) Linjiang Huang, Rongyao Fang, Guanglu Song Aiping Zhang, Si Liu, Yu Liu, and Hongsheng Li. Fouriscale: A frequency perspective on training-free high-resolution image synthesis. arxiv, 2024.
- Jin et al. (2024) Zhiyu Jin, Xuli Shen, Bin Li, and Xiangyang Xue. Training-free diffusion model adaptation for variable-sized text-to-image synthesis. Advances in Neural Information Processing Systems, 36, 2024.
- Ke et al. (2021) Junjie Ke, Qifei Wang, Yilin Wang, Peyman Milanfar, and Feng Yang. Musiq: Multi-scale image quality transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 5148–5157, 2021.
- Kingma et al. (2021) Diederik Kingma, Tim Salimans, Ben Poole, and Jonathan Ho. Variational diffusion models. Advances in neural information processing systems, 34:21696–21707, 2021.
- Lin et al. (2024) Zhihang Lin, Mingbao Lin, Meng Zhao, and Rongrong Ji. Accdiffusion: An accurate method for higher-resolution image generation. arXiv preprint arXiv:2407.10738, 2024.
- Lipman et al. (2022) Yaron Lipman, Ricky TQ Chen, Heli Ben-Hamu, Maximilian Nickel, and Matt Le. Flow matching for generative modeling. arXiv preprint arXiv:2210.02747, 2022.
- Liu et al. (2022) Xingchao Liu, Chengyue Gong, and Qiang Liu. Flow straight and fast: Learning to generate and transfer data with rectified flow. arXiv preprint arXiv:2209.03003, 2022.
- Mittal et al. (2012) Anish Mittal, Rajiv Soundararajan, and Alan C Bovik. Making a “completely blind” image quality analyzer. IEEE Signal processing letters, 20(3):209–212, 2012.
- Podell et al. (2023) Dustin Podell, Zion English, Kyle Lacey, Andreas Blattmann, Tim Dockhorn, Jonas Müller, Joe Penna, and Robin Rombach. Sdxl: Improving latent diffusion models for high-resolution image synthesis. arXiv preprint arXiv:2307.01952, 2023.
- Radford et al. (2021) Alec Radford, Jong Wook Kim, Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, et al. Learning transferable visual models from natural language supervision. In International conference on machine learning, pp. 8748–8763. PMLR, 2021.
- Ren et al. (2024) Jingjing Ren, Wenbo Li, Haoyu Chen, Renjing Pei, Bin Shao, Yong Guo, Long Peng, Fenglong Song, and Lei Zhu. Ultrapixel: Advancing ultra-high-resolution image synthesis to new peaks. arXiv preprint arXiv:2407.02158, 2024.
- Rissanen et al. (2023) Severi Rissanen, Markus Heinonen, and Arno Solin. Generative modelling with inverse heat dissipation. In The Eleventh International Conference on Learning Representations, 2023.
- Rombach et al. (2022) Robin Rombach, Andreas Blattmann, Dominik Lorenz, Patrick Esser, and Björn Ommer. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp. 10684–10695, 2022.
- Saharia et al. (2022) Chitwan Saharia, William Chan, Saurabh Saxena, Lala Li, Jay Whang, Emily L Denton, Kamyar Ghasemipour, Raphael Gontijo Lopes, Burcu Karagol Ayan, Tim Salimans, et al. Photorealistic text-to-image diffusion models with deep language understanding. Advances in neural information processing systems, 35:36479–36494, 2022.
- Salimans et al. (2016) Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and Xi Chen. Improved techniques for training gans. Advances in neural information processing systems, 29, 2016.
- Shi et al. (2024) Shuwei Shi, Wenbo Li, Yuechen Zhang, Jingwen He, Biao Gong, and Yinqiang Zheng. Resmaster: Mastering high-resolution image generation via structural and fine-grained guidance. arXiv preprint arXiv:2406.16476, 2024.
- Teng et al. (2024) Jiayan Teng, Wendi Zheng, Ming Ding, Wenyi Hong, Jianqiao Wangni, Zhuoyi Yang, and Jie Tang. Relay diffusion: Unifying diffusion process across resolutions for image synthesis. 2024.
- Wang et al. (2023) Jianyi Wang, Kelvin CK Chan, and Chen Change Loy. Exploring clip for assessing the look and feel of images. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 37, pp. 2555–2563, 2023.
- Wang et al. (2021) Xintao Wang, Liangbin Xie, Chao Dong, and Ying Shan. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In Proceedings of the IEEE/CVF international conference on computer vision, pp. 1905–1914, 2021.
- Yu et al. (2024) Fanghua Yu, Jinjin Gu, Zheyuan Li, Jinfan Hu, Xiangtao Kong, Xintao Wang, Jingwen He, Yu Qiao, and Chao Dong. Scaling up to excellence: Practicing model scaling for photo-realistic image restoration in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 25669–25680, 2024.
- Zhang et al. (2023) Shen Zhang, Zhaowei Chen, Zhenyu Zhao, Zhenyuan Chen, Yao Tang, Yuhao Chen, Wengang Cao, and Jiajun Liang. Hidiffusion: Unlocking high-resolution creativity and efficiency in low-resolution trained diffusion models. arXiv preprint arXiv:2311.17528, 2023.
Appendix to “FreCaS: Efficient Higher-Resolution Image Generation via Frequency-aware Cascaded Sampling”
In this appendix, we provide the following materials:
-
A
Details of timestep shifting in the transition process (referring to Sec. 3.2 in the main paper);
-
B
The detailed settings of FreCaS on and generation for SD2.1, SDXL and SD3 (referring to Sec. 4.1 in the main paper);
-
C
Results of user studies and non-reference image quality assessment (NR-IQA) (referring to Sec. 4.1 in the main paper);
-
D
Comparison with training-based methods and super-resolution methods (referring to Sec. 4.2 in the main paper);
-
E
More visual results and visual comparisons (referring to Sec. 4.2 in the main paper);
-
F
Experimental results of generation of SD3 (referring to Sec. 4.3 in the main paper);
-
G
Ablation studies on individual components of FreCaS and inference schedule (referring to Sec. 4.4 in the main paper).
Appendix A Shifting Timestep in the Transition Process
As mentioned in Sec. 3.2 of the main paper, FreCaS employs a five-step transition process to transform the last latent in the current stage to the first latent in the next stage . In addition to changing the resolution, we adjust the timestep from to to ensure that the signal-to-noise ratio (SNR) (Kingma et al., 2021) could be a constant in the transition process. Given a state = at timestep , the SNR is defined as , where represent the noise schedule, and is Gaussian noise. It has been found (Hoogeboom et al., 2023; Chen, 2023) that the SNR maintains a consistent ratio across resolutions for diffusion models using the same noise schedule:
where and denote different resolutions. The value of is typically set to 2.
Teng et al. (2024) and Gu et al. (2023) proposed to redesign the noise schedule to keep SNR consistent when changing the resolutions of intermediate states. Since the pre-trained diffusion models have fixed noise schedules, in this paper we adjust the timestep, instead of the noise schedule, to ensure consistent SNR between and :
| (5) |
where is the inverse function of . Proper adjustment of can yield additional improvements.
Besides, SD3 (Esser et al., 2024) employs a similar formula to shift the timestep when varying resolutions:
| (6) |
Appendix B Experimental Setting Details
The experimental setting details of our FreCaS are listed in Table 2.
| Steps | ||||||||
| SD2.1 | 4 | 2 | 40,10 | 100 | 3.0 | 7.5 | 45.0 | 0.6 |
| 16 | 3 | 30,10,10 | 200,200 | 3.0 | 7.5 | 35.0 | 0.4 | |
| SDXL | 4 | 2 | 40,10 | 200 | 1.5 | 7.5 | 35.0 | 0.6 |
| 16 | 3 | 30,5,15 | 400,200 | 2.0 | 7.5 | 35.0 | 0.6 | |
| SD3 | 4 | 2 | 20,8 | 50 | - | 7.0 | 35.0 | 0.5 |
Appendix C Results of User studies and NR-IQA Metrics
We have (a) conducted user studies and (b) employed non-reference image quality assessment (NR-IQA) metrics to further assess the performance of FreCaS and its competing methods.
C.1 User Studies
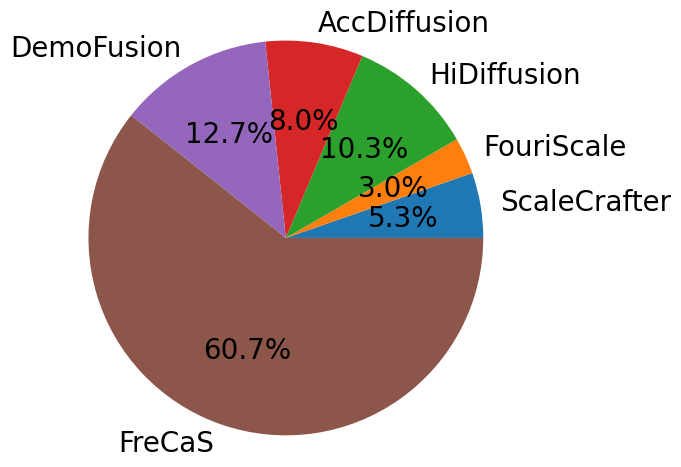
For the user studies, we compare FreCaS with ScaleCrafter, FouriScale, HiDiffusion, DemoFusion, and AccDiffusion on 20482048 image generation using SDXL. We randomly selected 30 prompts and generated one image per method for each prompt, creating 30 sets of images. Ten volunteers participated in the test, and they were asked to select the image with the best details and reasonable semantic layout from each set. The results are shown in Figure 7. We can see that FreCaS significantly outperforms other methods, with 60% votes as the best method. DemoFusion, AccDiffusion, and HiDiffusion perform similarly, with each having about 10% of the votes. In contrast, FouriScale and ScaleCrafter have the fewest votes, about 5% each.
| Methods | 4 | 16 | ||||
| clipiqa | niqe | musiq | clipiqa | niqe | musiq | |
| DirectInference | 0.522 | 4.167 | 53.98 | 0.469 | 4.370 | 29.00 |
| AttnEntropy | 0.547 | 4.210 | 54.87 | 0.528 | 4.614 | 27.98 |
| ScaleCrafter | 0.664 | 3.577 | 61.12 | 0.618 | 3.783 | 36.00 |
| FouriScale | 0.662 | 3.580 | 60.77 | 0.612 | 3.791 | 35.52 |
| HiDiffusion | 0.690 | 4.049 | 61.69 | 0.574 | 7.348 | 36.71 |
| AccDiffusion | 0.627 | 3.641 | 57.02 | 0.626 | 3.587 | 31.83 |
| DemoFusion | 0.651 | 3.410 | 58.98 | 0.637 | 3.376 | 33.46 |
| Ours | 0.668 | 3.391 | 63.10 | 0.646 | 3.367 | 37.33 |
C.2 NR-IQA Metrics
For the NR-IQA metrics, we employ CLIPIQA (Wang et al., 2023), NIQE (Mittal et al., 2012), and MUSIQ (Ke et al., 2021) on and image generations with SDXL. The results are presented in Table 3. Our FreCaS consistently outperforms all the other methods. For example, on generation, FreCaS achieves a CLIPIQA score of 0.668, a NIQE score of 3.391, and a MUSIQ score of 63.10, compared to 0.651, 3.410, and 58.98 for DemoFusion. On generation, FreCaS achieved a CLIPIQA score of 0.646, a NIQE score of 3.367, and a MUSIQ score of 37.33, compared to 0.626, 3.587, and 31.83 for AccuDiffusion. Notably, FreCaS only lags behind HiDiffusion on the CLIPIQA metric in image generation.
Appendix D Comparison with training-based methods and super-resolution methods
D.1 quantitative and visual comparison
We conducted additional experiments comparing FreCaS with training-based methods (Pixart-Sigma (Chen et al., 2024) and UltraPixel (Ren et al., 2024)) and super-resolution methods (ESRGAN (Wang et al., 2021) and SUPIR (Yu et al., 2024)). To ensure fair comparisons, we set the model precision to fp16 (bf16 for UltraPixel, as recommended by the authors) and use the DDIM sampler for diffusion-based methods. For Pixart-Sigma, we can only report its results for 20482048 image generation since its 4K model is not available. The quantitative results are summarized in Table 4.
From Table 4, we can see that FreCaS outperforms Pixart-Sigma and UltraPixel in most metrics. For example, FreCaS achieves an FID score of 16.48 and an IS score of 17.18, compared to 26.1 and 14.44 of Pixart-Sigma, and 25.56 and 17.11 of UltraPixel on the image generation task. This is because Pixart-Sigma, as acknowledged by the authors, heavily relies on the advanced samplers (see https://github.com/PixArt-alpha/PixArt-sigma/issues/65) so that the results are not very stable. UltraPixel, while achieving comparable performance to DemoFusion, still lags behind FreCaS in most metrics. Besides, the two methods are much slower than our FreCaS.
For SR-based methods, FreCaS may have lower FID, IS, and CLIP scores than SDXL+ESRGAN. This is because SR methods are designed to strictly adhere to low-resolution inputs, while these metrics (FID, IS, and CLIP) evaluate images by downsampling them to low resolution, which cannot well reflect the quality of generated high-resolution images. However, FreCaS significantly outperforms SDXL+ESRGAN in and . Specifically, FreCaS achieves an score of 39.82 and an score of 14.16, compared to 43.10 and 13.48 of SDXL+ESRGAN on image generation. This indicates its superior ability to generate high-resolution local details. This observation is consistent with the findings in the DemoFusion paper. Additionally, SDXL+SUPIR outperforms FreCaS in and , but at the cost of much longer inference latency (85.87 seconds for FreCaS vs. 512.4 seconds for SDXL+SUPIR on image generations).
We have provided some visual comparisons in Figure 8. One can see that FreCaS demonstrates better visual quality than either training-based or SR-based methods in high-resolution image generation, such as the more vivid and clearer flowers, hairs and the more natural color of lips.
| Methods | FID | IS | CLIP SCORE | Latency(s) | |||
| 4 | Pixart-Sigma | 26.11 | 38.58 | 14.44 | 14.45 | 28.10 | 71.45 |
| UltraPixel | 25.56 | 19.95 | 17.11 | 17.10 | 33.17 | 41.70 | |
| SDXL+ESRGAN | 13.03 | 18.10 | 17.30 | 16.58 | 34.13 | 6.36 | |
| SDXL+SUPIR | 12.08 | 17.31 | 17.57 | 17.12 | 34.16 | 105.5 | |
| Ours | 16.48 | 17.91 | 17.18 | 17.31 | 33.28 | 13.84 | |
| 16 | UltraPixel | 51.43 | 45.88 | 12.48 | 13.73 | 33.07 | 162.4 |
| SDXL+ESRGAN | 45.86 | 43.10 | 12.94 | 13.48 | 33.44 | 7.25 | |
| SDXL+SUPIR | 43.94 | 39.35 | 13.22 | 14.37 | 33.49 | 512.4 | |
| Ours | 42.75 | 39.82 | 12.68 | 14.16 | 33.03 | 85.87 |
D.2 Stability Metrics
| Methods | clipiqa | niqe | musiq | ||||||
| Mean | AoS | SoM | Mean | AoS | SoM | Mean | AoS | SoM | |
| Pixart-Sigma | 0.558 | 0.05 | 0.11 | 5.256 | 0.35 | 0.95 | 51.546 | 4.49 | 8.24 |
| UltraPixel | 0.540 | 0.04 | 0.11 | 4.625 | 0.42 | 1.55 | 56.215 | 2.94 | 7.95 |
| FreCaS | 0.633 | 0.11 | 0.04 | 3.886 | 0.87 | 0.27 | 59.756 | 9.64 | 2.95 |
To quantitatively analyze the stability of training-based and training-free methods, we generated 200 images for 20 randomly selected prompts (10 images for each prompt) using Pixart-Sigma (with default sampler unless otherwise stated), UltraPixel, and our FreCaS. Considering that FID and IS are not suitable for evaluating individual examples, we adopt the NR-IQA metrics (CLIPIQA, NIQE, and MUSIQ) to measure the performance of each method. In specific, we define the following three measures to evaluate the generation quality, stability and consistency of each method.
-
•
Average Score (Mean): The average score across the 200 generated images for each of the three metrics (CLIPIQA, NIQE, and MUSIQ). This metric can reflect the generation quality of each method.
-
•
Average of Standard Deviations (AoS): We first compute the standard deviation of the metrics for each prompt across 10 runs, and then report the average of these standard deviations across all 20 prompts. This metric can reflect the stability of each method.
-
•
Standard Deviation of Averages (SoM): We first compute the mean of the metrics for each prompt across 10 runs, and then report the standard deviation of these mean values across all 20 prompts. This metric can reflect the consistency of a method’s performance across different prompts.
The results are listed in Table 5. From this table, we can see that our FreCaS achieves the highest “Mean” scores across the three metrics, demonstrating the best performance in term of generation quality. Pixart-Sigma and UltraPixel have smaller AoS scores than FreCaS, indicating better stability for the same input prompt. However, FreCaS demonstrates significantly better SoM scores than Pixart-Sigma and UltraPixel, indicating that it can consistently achieve better results across various prompts.
D.3 User studies on visual quality and success rate
| Methods | Image Quality | Success Rate | ||
| Counts | Percentage | Counts | Percentage | |
| Pixart-Sigma | 5 | 5% | 52 | 20.8% |
| UltraPixel | 37 | 37% | 96 | 38.4% |
| Ours | 58 | 58% | 68 | 27.2% |
We conducted user studies to explore the generated image quality and success rate of Pixart-Sigma, UltraPixel, and our FreCaS. The results are listed in Table 6.
For the study on generation quality, we randomly select 20 prompts from Laion5B and generate one image per method for each prompt, creating 20 sets of images (3 images per set). Five volunteers (3 males and 2 females) were invited to participate in the test. All the volunteers are not working in the area of image generation to avoid potential bias. Each time, the set of 3 images for the same prompt are presented to the volunteers in random order. The volunteers can view the images multiple times, and they are asked to select the image with the best quality from each set. There are 100 votes in total.
For the study on success rate, we randomly select 10 prompts and generate five images per prompt for each method, resulting in 50 images per method. We invited the same five volunteers as in the study of generation quality to judge whether the generated image is a success or failure. When making the decision, the volunteers are instructed to consider two factors. First, whether the image content is faithful to the description of the prompt. Second, whether the image quality is satisfactory. Only when both the two requirements are met, the generation is considered as a success. There are 250 judges for each method.
As we can see from Table 6, our FreCaS outperforms significantly Pixart-Sigma and UltraPixel in terms of image generation quality, with 58% of the images being voted as the best. In terms of success rate, UltraPixel works the best, with 96 out of 250 images being marked as successful. Our FreCaS lags behind, with 68 successful cases. However, our FreCaS still generates more successful results than Pixart-Sigma (52 images), indicating that a well designed training-free method can surpass some training-based methods. Furthermore, we can also observe that none of the methods, including training-based and training-free ones, achieves a success rate higher than 40%. This implies that there are much space to improve.
Appendix E More Visual Results
E.1 More Visual Results
Figure 9 illustrates more visual results of FreCaS, including those with varying aspect ratios. From top to bottom, and left to right, the prompts used in examples are: 1. “Beautiful winter wallpapers.” 2. “A regal queen adorned with jewels.” 3. “A majestic phoenix, wings ablaze, rising from ashes, the flames casting a warm glow.” 4. “Lady in Red oil portrait painting won the John Singer Sargent People’s award.” 5. “Star of the day – Actress Evelyn Laye - 1917.” 6. “Photograph - Clouds Over Daicey Pond by Rick Berk.” 7. “little-boy-with-large-bulldog-in-a-garden-france.” 8. “03-Brussels-Maja-Wronska-Travels-Architecture-Paintings.”, 9. “Red Fox Pup Print by William H. Mullins.” 10. “Lovely Illustrations Of Cityscapes Inspired By Southeast Asia Malaysian digital illustrator Chong Fei Giap’s illustrations of cityscapes are lovely and inspiring. Fantasy Landscape, Landscape Art, Illustrator, Japon Tokyo, Animation Background, Art Background, Matte Painting, Anime Scenery, Jolie Photo.” 11. “A plate with creamy chicken and vegetables, a side of onion rings, a cup of coffee and a slice of cheesecake.” 12. “Hyper-Realistic Portrait of Redhead Girl Drawn with Bic Pens.”
To further validate the performance of FreCaS in real-world application scenarios, we have provided additional visual results in three categories:
-
•
Simple scenes. These images typically contain a single object in a realistic style. We display images of people, animals, landscapes, buildings, and other common objects. The visual results for this group are presented in Figure 10.
-
•
Various styles. This group showcases images in different artistic styles, including oil painting, pencil sketch, ink wash, watercolor, and poster art. The results are shown in the first two rows of Figure 11.
-
•
Complex scenes. These images contain multiple objects or have intricate textures. The results are displayed in the bottom two rows of are presented in Figure 11.
From these visual results, it is evident that FreCaS consistently generates high-quality images across various styles and contents, demonstrating the capability of FreCaS in real-world applications.


E.2 More Visual Comparisons
We show more visual comparisons in Figure 12. From top to bottom, the prompts used in the four groups of examples are: 1. “A small den with a couch near the window.” 2. “A painting of a candlestick holder with a candle, several pieces of fruit and a vase, with a gold frame around the painting.” 3. “A noble knight, riding a white horse, the castle gates opening.” 4. “Mystical Landscape Digital Art - Lonely Tree Idyllic Winterlandscape by Melanie Viola.”
We have provided more 4K visual comparisons under realistic scenes in Figure 13. As can be seen, our FreCaS consistently delivers better results in both image layout and semantic details.


Appendix F Experiments on SD3
| Methods | IS | CLIP SCORE | Latency (s) | SpeedUP | |||
| DirectInference | 35.68 | 45.35 | 12.52 | 12.60 | 31.45 | 38.53 | 1 |
| Demodiffusion | 15.19 | 44.34 | 17.84 | 14.99 | 31.09 | 63.33 | 0.61 |
| Ours | 9.76 | 26.62 | 17.83 | 16.72 | 31.17 | 15.94 | 2.42 |
In this section, we present the results of the generation experiments on SD3. SD3 employs a transformer-based denoising network. It eliminates all convolutional layers, thereby preventing the application of many existing methods, such as ScaleCrafter and FouriScale. Besides, SD3 exhibits fine details in the central region but shows corrupted textures in the surrounding regions (see Figure 14). This issue with the image layout also significantly impacts the performance of other methods, such as DemoFusion. Therefore, we only compare our FreCaS with DirectInference and DemoFusion. Table 7 and Figure 14 present the quantitative and qualitative results, respectively.
From Table 7, it is evident that FreCaS achieves superior performance in terms of image quality and inference speed. Specifically, FreCaS achieves the best results on , , IS, and , and only slightly lags behind DirectInference in terms of CLIP score. Moreover, FreCaS generates a image in about 16 seconds, achieving a speed-up of and compared to DirectInference and DemoFusion, respectively. Figure 14 illustrates the generated images. Directly employing the pre-trained SD3 model to generate higher-resolution images, DirectInference leads to unreasonable image layout with the surrounding parts being corrupted, such as the road and trees. The results of DemoFusion exhibits strange artifacts, such as the car faces and eyes. In contrast, our FreCaS successfully maintains the natural image structure while obtaining fine details.
Appendix G Ablation Studies on individual components and Inference Schedule
We further conduct ablation studies to verify the effectiveness of each components and the settings of inference schedule of our FreCaS.
| Model | cascaded framework | FA-CFG | CA-reuse | FID | IS | CLIP SCORE | Latency (s) | ||
| #1 | 39.14 | 29.71 | 11.52 | 14.60 | 32.51 | 34.10 | |||
| #2 | ✓ | 17.62 | 20.49 | 17.01 | 16.54 | 33.24 | 13.71 | ||
| #3 | ✓ | ✓ | 16.62 | 17.91 | 17.16 | 16.82 | 33.34 | 13.74 | |
| #4 | ✓ | ✓ | ✓ | 16.48 | 17.91 | 17.18 | 17.31 | 33.28 | 13.84 |
G.1 Effectiveness of each component
To better verify the effectiveness of each component of FreCaS, we conducted more ablation studies on our proposed cascaded framework, FA-CFG, and CA-reuse strategies. The results are shown in Table 8. One can see that our cascaded framework significantly outperforms the baseline, with a decrease of 22.52 in the FID score and a reduction of 20.39 seconds in latency. This demonstrates the high efficiency of our proposed cascaded framework. Our FA-CFG strategy improves both FID and IS scores and shows substantial improvement in , demonstrating its effectiveness in generating realistic image details. The CA-reuse strategy further enhances , indicating its effectiveness in improving semantic appearance. Moreover, these strategies introduce minimal additional latency.
G.2 Experiments on Inference Schedule
| resolutions | |||
| 0 | 2048 | 43.83 | 29.71 |
| 1 | 1024 2048 | 12.63 | 17.91 |
| 2 | 1024 1536 2048 | 41.36 | 28.68 |
| 0 | 12.57 | 18.20 |
| 100 | 12.69 | 18.10 |
| 200 | 12.63 | 17.91 |
| 300 | 13.30 | 18.57 |
| 400 | 13.34 | 18.62 |
In this section, we conduct experiments on the selection of (number of additional stages) and (the timestep of last latent in each stage). The two factors are employed to adjust the inference schedule of our FreCaS. We reports the scores of and by varying the two factors in Table 9 and Table 10, respectively.
Choice of . From Table 9, we see that achieves an score of 12.63 and an score of 17.91, significantly better than and in the generation task for SDXL. This could be attributed to the fact that a larger value of introduces more transition steps, which can lead to much information loss. Conversely, a smaller value of reduces the effectiveness of FreCaS, degenerating it to the DirectInference method.
Choice of . From Table 10, we can see that a smaller improves score but deteriorates . This is because the details generated at lower resolutions conflict with those at higher resolutions. Thus, we set to 200 to avoid generating excessive unwanted details in the early stages.