Frequency splitting of chiral phonons from broken time reversal symmetry in CrI3
Abstract
Conventional approaches for lattice dynamics based on static interatomic forces do not fully account for the effects of time-reversal-symmetry breaking in magnetic systems. Recent approaches to rectify this involve incorporating the first-order change in forces with atomic velocities under the assumption of adiabatic separation of electronic and nuclear degrees of freedom. In this work, we develop a first-principles method to calculate this velocity-force coupling in extended solids, and show via the example of ferromagnetic CrI3 that, due to the slow dynamics of the spins in the system, the assumption of adiabatic separation can result in large errors for splittings of zone-center chiral modes. We demonstrate that an accurate description of the lattice dynamics requires treating magnons and phonons on the same footing.
The atomic vibrations that are present in molecules and solids at zero and finite temperature play a crucial role in their thermodynamic and transport properties. First-principles calculations based on density-functional theory (DFT) have been established as a powerful tool for understanding and predicting lattice-dynamical properties, including phonon dispersion [1, 2] and electron-phonon coupling [3, 4]. The key quantity underlying the calculation of lattice dynamics is the interatomic force constant (IFC) matrix, which is constructed by finding derivatives of the nuclear forces with respect to nuclear positions, either directly via finite displacements or though density functional perturbation theory [1, 2].
In presence of magnetic ordering, the change in the electronic ground state compared to the nonmagnetic case propagates to the IFCs [5, 6, 7, 8, 9]. However, since it is defined and calculated as a static response function, the IFC matrix is invariant under time reversal by construction. Thus, a description of the nuclear dynamics based solely on the IFCs will not correctly reflect the vibration mode degeneracies in a magnetic system; instead, the phonon frequency spectrum will be determined by the nonmagnetic symmetry group.
There has been significant recent work on the explicit inclusion of time-reversal symmetry (TRS) breaking in the nuclear equations of motion via the velocity dependence of the interatomic forces, applied to models [10, 11, 12, 13] and magnetic molecules [14]. This “velocity-force” coupling can be obtained from the nuclear Berry curvature, which describes the evolution of the phase of the electronic wavefunction with changes in nuclear coordinates [10, 11, 14]. A key result of including this coupling is that degenerate vibrational modes may split into nondegenerate chiral modes [15] with a well-defined finite angular momentum [16, 14], even at the Brillouin-zone center. Thus, the correct treatment of magnetic symmetry is crucial for elucidating the role of atomic vibrations in thermal Hall [17, 11, 18, 19, 20] and other effects involving TRS-broken lattice dynamics [21, 22, 23, 24, 25, 26, 27, 28].
A key assumption underlying the velocity-force approach in previous works [10, 11, 12, 13, 14] is that the time scale for electronic dynamics is fast compared to nuclear dynamics. However, this may completely break down in some systems, e.g., when the nuclear Berry curvature results from nuclei coupling to spins, whose dynamics are not necessarily faster than the atomic vibrations. The breakdown of the adiabatic picture could have a profound effect on the predicted splitting of chiral phonon modes.
In this work, we illustrate such a situation using the bulk-layered magnetic insulator CrI3 as an example system. We first develop a DFT methodology amenable to both molecules and solids for computing phonons in the presence of velocity-force coupling. We apply this method to calculate the zone-center phonons in CrI3, demonstrating the splitting of otherwise degenerate phonons into chiral modes. Next, we show that the velocity-force response is dominated by the canting of the spins on the Cr sites caused by atomic displacements. The dynamics of such spin canting are characterized by the zone-center magnon frequencies. The fact that magnon frequencies in CrI3 are on the same order or smaller than the optical phonon frequencies [29, 30, 31, 32, 33, 34, 35, 36] means that we must treat spins and atomic displacements on the same footing. We develop a minimal model of this kind, and show that the adiabatic velocity-force approach can greatly overestimate the frequency splitting of the chiral modes.
We begin by reviewing the formalism of the velocity-force coupling from previous works [10, 11, 12, 13, 14], which we will refer to as the “Mead-Truhlar” (MT) approach. In order to simplify the discussion, we assume a finite system, generalizing to an infinite crystal below. The starting point of the derivation is the Born-Oppenheimer approximation, where the system wavefunction is factored into nuclear and electronic parts such that the ground-state electronic wavefunction depends parametrically on the nuclear coordinates [37]. Once the electronic degrees of freedom are integrated out, the effective Hamiltonian for the nuclear wavefunction becomes [13]
| (1) |
where Roman indices (here ) run over nuclei, Greek indices (here ) run over Cartesian directions, is the momentum operator for nucleus along direction , and is the mass of nucleus . Using the notation , is a nuclear Berry potential, and is an effective scalar potential, where is the ground-state energy for a given fixed nuclear configuration. As first pointed out by Mead and Truhlar [13], the nuclear Berry potential cannot always be made to vanish by changing the gauge of via the choice of an -dependent phase factor.
The resulting vibrational modes are then found by solving the equations of motion which, to harmonic order in nuclear displacements, are given by [10, 13, 11, 12]
| (2) |
Here is a diagonal nuclear mass matrix , is the frequency of mode , and is the component of the eigendisplacement of nucleus along direction normalized so that . is the “velocity-force matrix,” whose elements relate the force on nucleus along direction to the velocity of nucleus along direction , and is expressed as
| (3) |
which is just times the nuclear Berry curvature. The matrix is the IFC matrix, which we define to be . Note that following Eq. (1) one could alternatively define in terms of the Hessian of , which includes additional terms compared to the conventional IFC. However, the additional terms are higher order in the inverse nuclear mass and do not involve breaking of time-reversal symmetry, so that we neglect them in this work.
This formalism can be extended to the calculation of phonons in infinite crystals within DFT. We restrict ourselves to phonons at , the Brillouin zone center, and work from a discrete set of DFT calculations on primitive-cell structures in which each sublattice displacement in turn is considered. The C matrix is constructed in the usual way from finite differences of the forces, while G is built from Berry phases computed over triangular configuration paths involving a given pair of sublattice-displaced structures and the undistorted structure. Berry phases are computed on a per-unit-cell basis for the Bloch manifold at each wave vector and then averaged over the Brillouin zone to get the desired G matrix elements. The details are given in Sec. S1 of the supplemental material (SM) [38].
We perform calculations on CrI3 in the ferromagnetic ground state using the vasp code [39, 40, 41], the local density approximation exchange-correlation functional [42], and projector-augmented wave potentials [43]. Semicore (, ) and (, ) states are included in the valence for Cr and I respectively. A Monkhorst-Pack grid [44] is used to sample the Brillouin zone, and the energy cutoff for the plane-wave basis set is 520 eV. Spin-orbit coupling, which is essential to the physics described here, is included in all calculations.
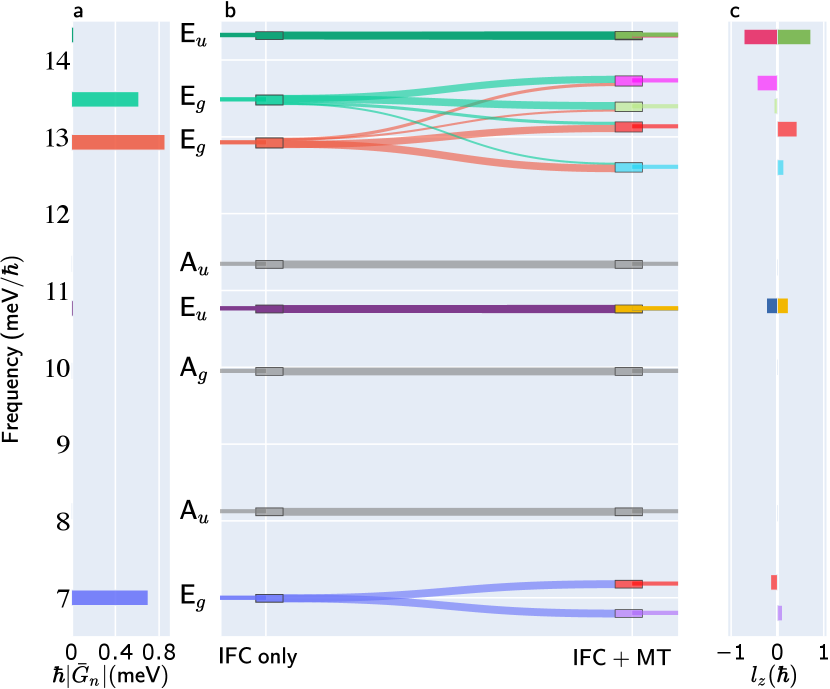
As mentioned above, the conventional calculation of phonons neglects G in Eq. (2), resulting in an equation of motion with TRS (). The resulting zone-center phonon modes with frequencies can be represented with real eigendisplacements . In CrI3 the representation of these modes at the zone center can be decomposed into the real irreducible representations (irreps) of as . The frequencies range up to 32 meV (see the SM [38] Table SIII). We can consider the velocity-force coupling between phonon modes obtained from the IFC alone by defining ; is block diagonal, with each block corresponding to a real irrep. Once G is included in Eq. (2), TRS is broken and the twofold-degenerate and modes split, as the corresponding irreps further break up into complex one-dimensional representations.
In Fig. 1(b), we show a selection of zone-center phonon frequencies of bulk ferromagnetic CrI3 (see the SM [38] Table SIII for a complete list of frequencies). On the left side we plot , i.e., the frequencies neglecting the velocity-force contribution, and on the right the frequencies including the velocity-force contribution via the MT approach (i.e., ). In Fig. 1(a) we plot the sum of the magnitudes of the velocity-force coupling terms relevant to each phonon eigenvector, as a measure of the strength of the coupling. We see that the modes have the strongest coupling. We shall see why shortly.
The splitting of each of the two-fold degeneracies shown in Fig. 1(b) results in chiral phonons with well-defined angular momentum in the direction (due to the symmetry of CrI3). For mode , the angular momentum is found via [21, 45], where runs over the atomic sublattices and is the mass of nucleus . If we neglect G in Eq. (2), then the angular momentum of modes in a degenerate subspace spanned by () depend on the basis we choose. Clearly, vanishes in the real basis introduced above, while a complex “circularly polarized” combination of degenerate modes of the form will have equal and opposite (since we are at the point [16]), with the magnitude determined by the mode displacement patterns. Neglecting terms in the matrix that mix different degenerate subspaces, the chiral modes after splitting will have exactly the eigendisplacements . Fig 1 (c) shows the angular momentum () for each mode after the inclusion of the G matrix. The fact that some of the split modes do not have equal and opposite indicates mixing between the degenerate subspaces in . See Sec. S4 of the SM for a full analysis of the angular momentum of the chiral modes[38].
We now analyze the mechanisms responsible for the velocity-force coupling in CrI3. In this material, the magnetic moments reside on the Cr atoms and are initially oriented out of plane along . We note that the modes with large matrix elements in Fig. 1 are mostly those involving displacements of the I sublattices, which carry strong spin-orbit coupling. Under such displacements, it is natural that the Cr moments may cant, reflecting a local change in magnetic easy axis. This canting will result in a spin Berry curvature, and thus a contribution to G.
In fact, we find that for CrI3, the spin Berry curvature is the dominant mechanism of velocity-force coupling. We demonstrate this by calculating the matrix elements of G under the assumption that only the spin-Berry-curvature mechanism is present. More specifically, we first approximate Eq. (3) as , where is the Berry curvature of the wavefunctions in the parameter space spanned by the Cr spins; is a “spin canting matrix” describing the static change in the equilibrium spin unit vector on magnetic Cr site in direction resulting from phonon perturbation ; and is the amplitude of mode such that the set of atomic displacements are given by 111Here runs only over directions corresponding to the two possible tilt angles. We have assumed the total magnitude of the spin is unchanged and that tilt angles are small so that . Under the assumption that the spin Berry curvature dominates, we can further approximate , where spin for Cr and is the antisymmetric tensor; then
| (4) |
A comparison between this spin-Berry approximation and the full Berry-phase calculation of the matrix is presented in Table SII of the SM [38]. For some modes, the spin-Berry approximation accounts for only % of the full velocity-force contribution; this means that other contributions, e.g., “phonon-only Berry curvature” (the Berry curvature from atomic displacements at fixed spin) are significant. However, these modes exhibit relatively small splittings from the full velocity-force contribution, so the errors are not significant in absolute terms. For the two modes that exhibit the largest splitting in the MT calculation [green, orange, and blue curves in Fig. 1(b)], the errors arising from this approximation are less than one percent.
This is a remarkable result, and is one of the main findings of the present work. By adopting the spin-Berry approximation, one can bypass the cumbersome computation of Berry phases for paths connecting distorted structures. Instead, all we need to take from the DFT calculations is the information about the spin canting in response to phonon distortions. In particular, it is now clear why the tensor elements are so much smaller for the Eu modes; these are the ones that couple to the optical magnons, whose much larger stiffness strongly suppresses the spin canting.
A critical implication of the fact that the velocity-force coupling in CrI3 results from spin canting is that the assumption underlying the MT approach of Eqs. (1-3), namely, that all electronic dynamics are fast compared to that of the phonons, is clearly unfounded. This is because the relevant time scale for spin dynamics is that of the magnon frequencies in the system. The experimentally measured zone-center magnons of CrI3 have frequencies of 0.3 meV (i.e., the magnetocrystalline anisotropy) for the acoustic branch, and 17 meV for the optical branch [36], while the relevant phonons with the largest velocity-force coupling have frequencies in the range of 6-14 meV [see Fig. 1(b)].
Thus, an appropriate description of the low-energy dynamics must treat spins and phonons in this system on the same footing. To illustrate how this can be done, we focus on a single pair of or modes, which couple respectively either to an effective acoustic spin unit vector or its optical counterpart . Denoting the phonon mode amplitudes and momenta as and , the coupled spin-phonon Hamiltonian takes the form
| (5) |
Here is the bare phonon frequency, is the spin anisotropy energy, and is the coupling between the spin and the pair of phonons (which have been chosen such that the and terms vanish). Note that the unperturbed magnon frequency is related to the anisotropy by , where is the Cr spin, and that the matrix introduced above reduces in this minimal model to . Going over to circularly polarized coordinates via and , the equations of motion become
| (6) |
which are easily solved numerically.
| splitting (meV) | |||
| irrep | (meV) | MT | SP |
| Eg | 6.9999 | 0.3820 | 0.0007 |
| 12.9287 | 0.5270 | 0.0003 | |
| 13.4876 | 0.3368 | 0.0001 | |
| 29.8521 | 0.0244 | ||
| Eu | 10.7667 | 0.0043 | 0.0046 |
| 14.3259 | 0.0090 | 0.0311 | |
| 27.8168 | 0.0349 | 0.0118 | |
In Table 1, we compare the frequency splittings of doubly-degenerate modes determined by the adiabatic Mead-Truhlar (MT) approach and spin-phonon (SP) model. The last column in Table 1 presents the results for the spin-phonon model; the modes couple to the acoustic magnon branch and the modes to the optical branch (we use experimental [36] magnon frequencies of 0.3 and 17 meV, respectively) 222A more general description of spin-phonon coupling, treating all relevant nuclear and spin degrees of freedom simultaneously, will be presented in a forthcoming communication.. A more detailed comparison of Mead-Truhlar approach and spin-phonon model is presented in Sec. S2 of the SM[38].
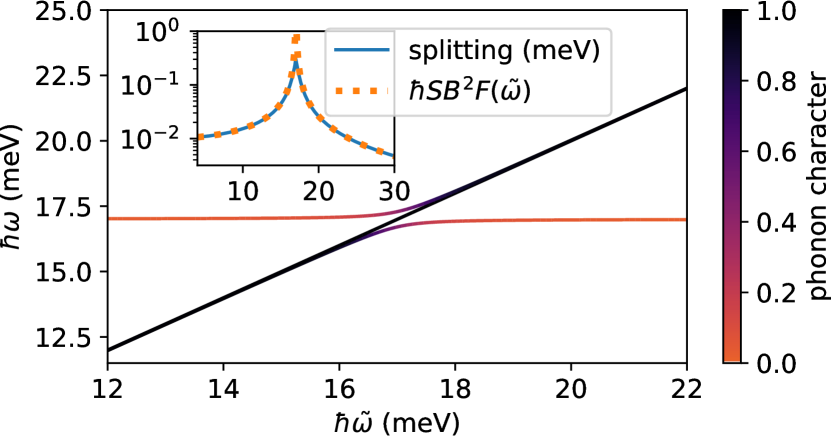
In order to understand the general features of the spin-phonon mixing embodied in Eq. (6), we plot in Fig. 2 the solutions of Eq. (6) as a function of phonon frequency , with the magnon frequency set to meV (i.e., the optical branch [36]), and fixed at 2 meV3/2/, a typical value for the modes in CrI3 (since those are the phonons that couple to the optical magnon). The solid blue curve in the inset shows the splitting of the modes with dominant phonon character also as a function of . Outside of the small “resonant” regime , where significant magnon-phonon hybridization occurs, the mode splitting is well described by (see orange dashed curve in inset of Fig. 2), where is the relevant force-velocity term in the adiabatic spin-Berry approximation [i.e., Eq. (4)] and . At small , the magnon can be treated as a high-energy degree of freedom which renormalizes the phonons, and the splitting from the MT approach is recovered. Increasing toward enhances the splitting of modes over the value at the adiabatic (MT) limit, peaking at the point where the magnon and phonon frequencies coincide and the modes have maximum hybridization. Above , the splitting decreases from its peak value, but is still enhanced over that determined by the MT approach for a range of . At the splitting is suppressed, and vanishes as .
This behavior is reflected in the splittings given in Table 1. Two of the three modes which couple to the optical magnon have frequencies below meV, but still in ranges where the splitting is enhanced above the adiabatic MT limit. The physical interpretation here is that the phonons are becoming hybridized with the magnon instead of just having their frequencies renormalized by it. However, since the splittings in the adiabatic limit (and thus the corresponding G matrix elements) are proportional to , the splittings remain quite small. The largest frequency mode has , so that the splitting is reduced compared to values obtained from the velocity-force approach.
The modes couple to the acoustic magnon ( meV), so for all modes , which is precisely the opposite of the limit in which the adiabatic velocity-force theory is applicable. This results in the drastic reduction () in the splitting of the modes in Table 1 compared to the MT description in Eq. (2). The physical interpretation of this regime is that the Cr spins cannot keep up with the phonons, and thus the area swept out from the spin canting is greatly reduced compared to the assumption that they follow the nuclear motion adiabatically.
Clearly, these results have significant implications for experimental measurements of chiral phonons in CrI3. Optical techniques, possibly utilizing circular polarization, constitute a powerful tool for studying such properties [48, 22, 49, 50, 25]. The strongly suppressed frequency splitting (SP column of Table 1) of the Raman-active modes is likely to be difficult to detect. This is consistent with recent work on CrBr3, a related system, which found signatures of the chiral phonons but did not report a splitting of these modes [25]. The larger, though still quite modest, splitting of the modes could in principle be measured by peak shifts in infrared absorption [51], while direct detection of chirality would require circularly polarized infrared spectroscopy as in Refs. [48, 49].
More generally, our results also have several implications for finding other systems with a large splitting of chiral phonon modes at . In materials like CrI3, where the spin-Berry mechanism is responsible for the majority of the velocity-force coupling, it is most promising to look for (or engineer via, e.g., strain or magnetic field) cases where the relevant phonon and magnon frequencies coincide. This avoids the suppression of the splitting in the regime, and the small spin canting likely when . Systems with lower-frequency optical magnons that maintain similar or larger spin-phonon coupling are also strong candidates for observing larger effects. In any case, we can see from Table 1 that correctly accounting for the relative dynamics of spins versus phonons is necessary to avoid significantly overestimating the splitting of certain chiral modes.
In conclusion, we have developed and implemented a first-principles methodology for capturing time-reversal-symmetry-broken lattice dynamics in magnetic solids, and applied it to the case of bulk ferromagnetic CrI3. We show that in this system, the previously-made assumption of fast electron dynamics compared to the lattice breaks down, since the relevant coupling is between Cr spins and atomic displacements. With a minimal model, we demonstrate that spins and phonons must be treated on the same footing to avoid large qualitative errors in the splitting of chiral modes.
Acknowledgements.
CED, DV, and SC acknowledge support from the National Science Foundation under Grants DMR-1918455, DMR-1954856, and DMR-1848074 respectively. The Flatiron Institute is a division of the Simons Foundation. M.S. acknowledges the support of Ministerio de Ciencia y Innovación (MICINN-Spain) through Grants No. PID2019-108573GB-C22 and CEX2019-000917-S; of Generalitat de Catalunya (Grant No. 2017 SGR1506); and of the European Research Council (ERC) through Grant No. 724529.References
- Gonze and Lee [1997] X. Gonze and C. Lee, Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory, Phys. Rev. B 55, 10355 (1997).
- Baroni et al. [2001] S. Baroni, S. de Gironcoli, A. Dal Corso, and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Reviews of Modern Physics 73, 515–562 (2001).
- Giustino [2017] F. Giustino, Electron-phonon interactions from first principles, Rev. Mod. Phys. 89, 015003 (2017).
- Monserrat [2018] B. Monserrat, Electron-phonon coupling from finite differences, Journal of Physics: Condensed Matter 30, 083001 (2018).
- Posternak et al. [2002] M. Posternak, A. Baldereschi, S. Massidda, and N. Marzari, Maximally localized Wannier functions in antiferromagnetic MnO within the FLAPW formalism, Physical Review B 65, 184422 (2002).
- Lee and Rabe [2011] J. H. Lee and K. M. Rabe, Large spin-phonon coupling and magnetically induced phonon anisotropy in SrO3 perovskites (,Cr,Mn,Fe,Co), Phys. Rev. B 84, 104440 (2011).
- Hong et al. [2012] J. Hong, A. Stroppa, J. Íñiguez, S. Picozzi, and D. Vanderbilt, Spin-phonon coupling effects in transition-metal perovskites: A DFT + and hybrid-functional study, Phys. Rev. B 85, 054417 (2012).
- Wang et al. [2021] K. Wang, W. Zhou, Y. Cheng, M. Zhang, H. Wang, and G. Zhang, Magnetic order-dependent phonon properties in 2D magnet CrI3, Nanoscale 13, 10882 (2021).
- Wu et al. [2022] J. Wu, Y. Yao, M.-L. Lin, M. Rösner, Z. Du, K. Watanabe, T. Taniguchi, P.-H. Tan, S. Haas, and H. Wang, Spin–phonon coupling in ferromagnetic monolayer chromium tribromide, Advanced Materials 34, 2108506 (2022).
- Qin et al. [2012] T. Qin, J. Zhou, and J. Shi, Berry curvature and the phonon Hall effect, Physical Review B 86, 104305 (2012).
- Saito et al. [2019] T. Saito, K. Misaki, H. Ishizuka, and N. Nagaosa, Berry phase of phonons and thermal Hall effect in nonmagnetic insulators, Phys. Rev. Lett. 123, 255901 (2019).
- Saparov et al. [2022] D. Saparov, B. Xiong, Y. Ren, and Q. Niu, Lattice dynamics with molecular Berry curvature: Chiral optical phonons, Phys. Rev. B 105, 064303 (2022).
- Mead and Truhlar [1979] C. A. Mead and D. G. Truhlar, On the determination of Born-Oppenheimer nuclear motion wave functions including complications due to conical intersections and identical nuclei, The Journal of Chemical Physics 70, 2284 (1979).
- Bistoni et al. [2021] O. Bistoni, F. Mauri, and M. Calandra, Intrinsic vibrational angular momentum from nonadiabatic effects in noncollinear magnetic molecules, Phys. Rev. Lett. 126, 225703 (2021).
- Zhang and Niu [2015] L. Zhang and Q. Niu, Chiral phonons at high-symmetry points in monolayer hexagonal lattices, Phys. Rev. Lett. 115, 115502 (2015).
- Coh [2019] S. Coh, Classification of materials with phonon angular momentum and microscopic origin of angular momentum (2019), arXiv:1911.05064 [cond-mat.mtrl-sci] .
- Grissonnanche et al. [2019] G. Grissonnanche, A. Legros, S. Badoux, E. Lefrançois, V. Zatko, M. Lizaire, F. Laliberté, A. Gourgout, J. S. Zhou, S. Pyon, T. Takayama, H. Takagi, S. Ono, N. Doiron-Leyraud, and L. Taillefer, Giant thermal Hall conductivity in the pseudogap phase of cuprate superconductors, Nature 571, 376 (2019).
- Chen et al. [2020] J.-Y. Chen, S. A. Kivelson, and X.-Q. Sun, Enhanced thermal Hall effect in nearly ferroelectric insulators, Phys. Rev. Lett. 124, 167601 (2020).
- Li et al. [2020] X. Li, B. Fauqué, Z. Zhu, and K. Behnia, Phonon thermal Hall effect in strontium titanate, Phys. Rev. Lett. 124, 105901 (2020).
- Zhang et al. [2021] H. Zhang, C. Xu, C. Carnahan, M. Sretenovic, N. Suri, D. Xiao, and X. Ke, Anomalous thermal Hall effect in an insulating van der Waals magnet, Phys. Rev. Lett. 127, 247202 (2021).
- Zhang and Niu [2014] L. Zhang and Q. Niu, Angular momentum of phonons and the Einstein–de Haas effect, Phys. Rev. Lett. 112, 085503 (2014).
- Zhu et al. [2018] H. Zhu, J. Yi, M.-Y. Li, J. Xiao, L. Zhang, C.-W. Yang, R. A. Kaindl, L.-J. Li, Y. Wang, and X. Zhang, Observation of chiral phonons, Science 359, 579 (2018).
- Chen et al. [2018] H. Chen, W. Zhang, Q. Niu, and L. Zhang, Chiral phonons in two-dimensional materials, 2D Materials 6, 012002 (2018).
- Mentink et al. [2019] J. H. Mentink, M. I. Katsnelson, and M. Lemeshko, Quantum many-body dynamics of the Einstein–de Haas effect, Phys. Rev. B 99, 064428 (2019).
- Yin et al. [2021] T. Yin, K. A. Ulman, S. Liu, A. Granados del Águila, Y. Huang, L. Zhang, M. Serra, D. Sedmidubsky, Z. Sofer, S. Y. Quek, and Q. Xiong, Chiral phonons and giant magneto-optical effect in CrBr3 2D magnet, Advanced Materials 33, 2101618 (2021).
- Chen et al. [2022] H. Chen, W. Wu, J. Zhu, Z. Yang, W. Gong, W. Gao, S. A. Yang, and L. Zhang, Chiral phonon diode effect in chiral crystals, Nano Letters 22, 1688 (2022), pMID: 35148114.
- Baydin et al. [2022] A. Baydin, F. G. G. Hernandez, M. Rodriguez-Vega, A. K. Okazaki, F. Tay, G. T. Noe, I. Katayama, J. Takeda, H. Nojiri, P. H. O. Rappl, E. Abramof, G. A. Fiete, and J. Kono, Magnetic control of soft chiral phonons in PbTe, Phys. Rev. Lett. 128, 075901 (2022).
- Juraschek et al. [2022] D. M. Juraschek, T. Neuman, and P. Narang, Giant effective magnetic fields from optically driven chiral phonons in paramagnets, Phys. Rev. Research 4, 013129 (2022).
- Zhang et al. [2015] W.-B. Zhang, Q. Qu, P. Zhu, and C.-H. Lam, Robust intrinsic ferromagnetism and half semiconductivity in stable two-dimensional single-layer chromium trihalides, J. Mater. Chem. C 3, 12457 (2015).
- Lado and Fernández-Rossier [2017] J. L. Lado and J. Fernández-Rossier, On the origin of magnetic anisotropy in two dimensional CrI3, 2D Materials 4, 035002 (2017).
- Webster and Yan [2018] L. Webster and J.-A. Yan, Strain-tunable magnetic anisotropy in monolayer , , and , Phys. Rev. B 98, 144411 (2018).
- Richter et al. [2018] N. Richter, D. Weber, F. Martin, N. Singh, U. Schwingenschlögl, B. V. Lotsch, and M. Kläui, Temperature-dependent magnetic anisotropy in the layered magnetic semiconductors and , Phys. Rev. Materials 2, 024004 (2018).
- Lee et al. [2020] I. Lee, F. G. Utermohlen, D. Weber, K. Hwang, C. Zhang, J. van Tol, J. E. Goldberger, N. Trivedi, and P. C. Hammel, Fundamental spin interactions underlying the magnetic anisotropy in the Kitaev ferromagnet , Phys. Rev. Lett. 124, 017201 (2020).
- Bacaksiz et al. [2021] C. Bacaksiz, D. Šabani, R. M. Menezes, and M. V. Milošević, Distinctive magnetic properties of and monolayers caused by spin-orbit coupling, Phys. Rev. B 103, 125418 (2021).
- Ke and Katsnelson [2021] L. Ke and M. I. Katsnelson, Electron correlation effects on exchange interactions and spin excitations in 2D van der Waals materials, npj Computational Materials 7, 4 (2021), arXiv:2007.14518 .
- Cenker et al. [2021] J. Cenker, B. Huang, N. Suri, P. Thijssen, A. Miller, T. Song, T. Taniguchi, K. Watanabe, M. A. McGuire, D. Xiao, and X. Xu, Direct observation of two-dimensional magnons in atomically thin CrI3, Nature Physics 17, 20 (2021).
- Born and Huang [1954] M. Born and K. Huang, Dynamical Theory of Crystal Lattices, International Series of Monographs on Physics (Oxford University Press, Walton Street, Oxford OX2 6DP, UK, 1954).
- [38] See supplemental material [URL to be inserted by publisher] for… .
- Kresse and Hafner [1993] G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B 47, 558 (1993).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
- Kresse and Joubert [1999] G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B 59, 1758 (1999).
- Perdew and Zunger [1981] J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B 23, 5048 (1981).
- Blöchl [1994] P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B 50, 17953 (1994).
- Monkhorst and Pack [1976] H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B 13, 5188 (1976).
- McLellan [1988] A. G. McLellan, Angular momentum states for phonons and a rotationally invariant development of lattice dynamics, Journal of Physics C: Solid State Physics 21, 1177 (1988).
- Note [1] Here runs only over directions corresponding to the two possible tilt angles. We have assumed the total magnitude of the spin is unchanged and that tilt angles are small so that .
- Note [2] A more general description of spin-phonon coupling, treating all relevant nuclear and spin degrees of freedom simultaneously, will be presented in a forthcoming communication.
- Nafie et al. [1976] L. A. Nafie, T. A. Keiderling, and P. J. Stephens, Vibrational circular dichroism, Journal of the American Chemical Society 98, 2715 (1976).
- Laiho [1975] R. Laiho, On the optical absorption and the magnetic circular dichroism of the transparent ferromagnet K2CuF4, physica status solidi (b) 69, 579 (1975).
- Du et al. [2019] L. Du, J. Tang, Y. Zhao, X. Li, R. Yang, X. Hu, X. Bai, X. Wang, K. Watanabe, T. Taniguchi, D. Shi, G. Yu, X. Bai, T. Hasan, G. Zhang, and Z. Sun, Lattice dynamics, phonon chirality, and spin–phonon coupling in 2d itinerant ferromagnet Fe3GeTe2, Advanced Functional Materials 29, 1904734 (2019).
- Tomarchio et al. [2021] L. Tomarchio, S. Macis, L. Mosesso, L. T. Nguyen, A. Grilli, M. C. Guidi, R. J. Cava, and S. Lupi, Low energy electrodynamics of CrI3 layered ferromagnet, Scientific Reports 11, 23405 (2021).