Frustrated magnetic interactions in a cyclacene crystal
Abstract
We study the emergence of magnetism and its interplay with structural properties in a two dimensional molecular crystal of cyclacenes, using density functional theory (DFT). Isolated cyclacenes with an even number of fused benzenes host two unpaired electrons in two topological protected zero modes, at the top and bottom carbon rings that form the molecule. We show that, in the gas phase, electron repulsion promotes an open-shell singlet with strong intramolecular antiferromagnetic exchange. We consider a closed packing triangular lattice crystal phase and we find a strong dependence of the band structure and magnetic interactions on the rotation angle of the cyclacenes with respect to the crystal lattice vectors. The orientational ground state maximizes the intermolecular hybridization, yet local moments survive. Intermolecular exchange is computed to be antiferromagnetic, and DFT predicts a broken symmetry 120∘ spin phase reflecting the frustration of the intermolecular spin coupling. Thus, the cyclacene crystal realizes a bilayer of two antiferromagnetically coupled triangular lattices. Our results provide a bottom-up route towards carbon based strongly correlated platforms in two dimensions.
I Introduction
Magnetism and strongly correlated phases have been traditionally alien to the realm of graphitic crystals and polycyclic aromatic hydrocarbons (PAH). Thus, graphite, graphene and carbon nanotubes feature wide bands with extended states (small or vanishing density of states at the Fermi energy) so that the effect of Coulomb interactions in these systems are mostly negligible. In spite of this, strong correlations and magnetism were predicted in graphene zigzag edgesnakada1996 ; fujita1996 ; JFR07 and radical PAHmorita11 , but in both cases their strong reactivity is expected to compromise their chemical stability.
However, recent experimental breakthroughs have significantly changed this scenario. First, the discovery of strongly correlated electronic phases in twisted bilayer graphenecao2018correlated ; cao2018unconventional has shown that narrow bands are indeed possible in suitably designed carbon based 2D materials. Second, the on-surface assisted synthesis of multiradical PAHs, that remain stable in ultrahigh vacuum, and the study of their electronic excitations using scanning tunneling microcope spectrocopy (STS) have significantly paved the way towards the fine control of their synthesis. This includes triangulenespavlivcek2017synthesis ; mishra2019synthesis ; mishra2020 ; mishra2021 and the Clar’s Gobletmishra19b , among others mishra19b ; mishra2020 . Therefore, using STSortiz2020probing to probe the fluctuating local moments, from PAH with open-shell singletsmishra19b ; mishra2020 ; mishra2021 , is a firmly stablished tool for this kind of systems.
An ingredient common to both twisted bilayer and radical PAHs is the presence of localized electronic states close to the Fermi energy that host the strongly correlated electrons. This leads us to propose here a bottom-up route to engineer strongly correlated carbon based 2D crystals. Our approach is to use as building blocks radical molecules that can assemble in such a way that intermolecular interactions lead to a weak hybridization of those molecular states hosting the unpaired electrons. In-plane assembly of radical PAH leads, with some exceptionsmishra2020 , to strong covalent bonding of the molecular states, compromising the ultimate goal of preserving the localized molecular levels.
Here we consider cyclacenes with diradical character as building blocks for a molecular crystal (see Figure 1) with a weak intermolecular interaction, so that the diradical character can be preserved in the crystal phase. These aromatic hydrocarbon nanobeltsguo2021 are very appealing molecules subject of strong interest, both from theory and experiments alike. In the gas phase, the local moments are hosted by molecular orbitals formed by atomic orbitals, that are topological symmetry protected zero modeskoshino2014topological . A natural configuration for their self-assembly is a closed packing crystal, where the separation between molecules is in the range of the interlayer distance in graphite. We find this preserves the local moments of the isolated molecules in the crystal phase. Importantly, the resulting organization in this idealized cyclacene crystal yields a network of states that does not live in a bipartite lattice. This opens the door, as we will show next, to frustrated antiferromagnetic interactions that are known to promote quantum spin liquid statesANDERSON1973153 ; Balents2010spin , and thus different from the widely studied broken symmetry molecular magnetismgatteschi2006 and from the Lieb theorem paradigm Lieb89 ; JFR07 ; ortiz19 ; mishra2021 .
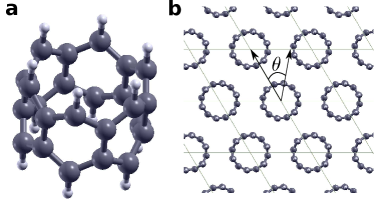
Cyclacenes, hereafter []CC’s, with denoting the number of fused benzene rings, can be thought of as the shortest possible carbon nanotubes with zigzag edges. The electronic properties of []CC’s depend on the parity of , showing an odd-even patternchoi1999structures ; chen2007open ; wu2016electronic . This is confirmed at several levels of theory, where a simple one-orbital per atom tight-binding model yields two zero energy states for [even]CC’s and four states split in two pairs for [odd]CC’sperez2019cyclic . This provides a simple picture to understand the di/tetraradical character obtained by more sophisticated calculationsperez2018role . On the experimental side, besides the multiple efforts to synthesize carbon nanobeltspovie2017synthesis ; povie2018synthesis ; chisynthesis ; cyclaceneDiego ; jacsZhang2020 ; shudo2020synthesis ; jacsShi2020 , the obtention of pristine cyclacenes is still missing.
In figure 1a we show the structure of [6]CC. We can think of this molecule as two carbon rings with a strong covalent coupling through the non-hydrogenated carbons (NHC). Their tight-binding energy spectra presents two zero energy states localized on the hydrogenated carbon (HC) sites. In this work, we consider a two dimensional crystal of these [6]CC molecules, as if they had gone through a process of self-assembly over a surfacexu1998situ ; bain1988molecular ; fukui2017control (hereafter [n]crystacene, see figure 1b). We assume that the molecules assemble in a triangular lattice, with the axis of the tubes perpendicular to the plane of the crystal. This idealized (monolayer) self-assembly agrees with that recently found for closely related systems, as cycloparaphenylene nanoringsperez2019structure . In order to characterize the orientational order of the crystal, we define the relative angle formed between the line joining the geometric center of the molecule and the projection of the hydrogenated carbon atoms on the plane containing the center. This angle is determined by minimization of the ground state energy obtained using DFT for different magnetic phases.
In the following we address the study of the electronic structure of the [6]crystacene, focusing on the emergence of molecular local moments, the nature of intermolecular exchange, and their interplay with the rotational angle .
II Methods
We describe the electronic structure of cyclacenes with three different levels of theory. Individual molecules are described with a Hubbard model with a single orbital per carbon site. The model is treated both in the mean-field approximationJFR07 and using multi-configurational methods in a complete active space (CAS) with 6 single particle states and 6 electronsortiz19 ; ortiz2020probing . The molecular crystal is treated using density functional theory(DFT) calculations, carried out with Quantum Espresso (QE) codegiannozzi2009quantum ; giannozzi2017advanced . We use a Perdew-Burke-Ernzerhof (PBE)perdew1996generalized ultrasoft non-relativistic density functional for both carbon and hydrogen atoms. The van der Waals interactions, when considered, were implemented with the ’vdw-DF’ flagthonhauser2015spin ; thonhauser2007prb ; berland2015van . The kinetic energy cut-off considered for wavefunctions was 30Ry, for the charge density and potential it was 700Ry and we employed a k-grid of 10x10x1.
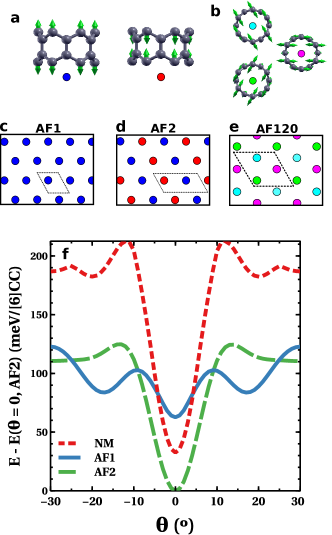
We consider 5 magnetic states for the crystal: a spin-unpolarized non-magnetic state (NM), ferromagnetic (FM), and three states with intramolecular antiferromagnetic correlations that differ by the intermolecular spin order: AF1, with ferromagnetic intermolecular correlations; AF2, a stripe phase with two antiferromagnetically coupled molecules per unit cell; and AF120, with non-collinear magnetic order where first neighbour spins are misaligned by , and 3 molecules per unit cell (see figure 3a,b,c,d,e).
In the case of NM, AF1 and AF2, we have explored the depedence of the ground state energy, using the atomic coordinates obtained upon relaxation of the unit cell at for these three magnetic configurations; this geometry was further employed for any angle and for the band structures. We have also computed the FM phase for two different angles and using the same relaxed coordinates as those employed for the AF120 phase, as we will explain in the following. The results for this ferromagnetic phases are in table 1.
In the case of the AF120 phase, the unit cell has 3 molecules. This makes the computational cost of the structural relaxation prohibitively large. We use instead atomic configurations obtained with smaller unit cells and we only consider . We have tried two different structures and, in both cases, the magnetic ground state with 3 molecules in the unit cell converges to the 120 phase. Below we show results obtained using the atomic coordinates obtained from the relaxation of the AF1 phase with , with the lattice constants Å (which corresponds to a center-to-center intermolecular distance of 8.25Å ) : the approximate position of the energy minimum in the E vs curve for the frustrated AF2 phase, see suppl. mat.). No vdW interactions were considered for the AF120 phase. For the NM and AF2 phases we employed a Marzari-Vanderbilt smearing with a gaussian spreading of Ry, whilst no smearing at all was used for the AF1 or AF120 phases. 222We have verified that AF1 phase’s energies do not depend on the smearing, that was introduced to improve the convergence of the calculations in the neighbourhood of .
In order to characterize the magnetic state of the crystals, we use two indicators:
| (1) |
and
| (2) |
where is the length of the atomic magnetic moments, as obtained from the output of our DFT calculations. The use of these two indicators is motivated by the fact that, in a given ring, there is a small residual magnetization in the non-hydrogenated carbon atoms, typical of the broken symmetry solutions in bipartite systemsJFR07 . As a reference, the absolute magnetic moment per ring in the single molecule mean-field calculation is for the FM solution, to be compared with .
The calculation of the atomic magnetic moments, carried out by Quantum Espresso by integrating the magnetic density over a sphere centered around the atom, turns out to be non-reliable in this system. For instance, let us consider the FM phase in a strongly insulating case where the total moment per CC can be determined by counting the number of occupied bands per spin channel, and is unambiguously determined to be 2. We can now obtain a lower limit for the magnetic moment per hydrogenated carbon atom using the following argument. The calculation of the magnetic density, shown in figure 4d, shows that non hydrogenated carbon atoms have a residual magnetization opposite to the dominant contribution of the hydrogenated carbon. We thus have , the magnetization per ring. However, the values given by QE for this system is which gives a good account of the unreliability of the integration method. We attribute the source of this discrepancy to the poor matching between a sphere and the shape electronic cloud that host the local moments (see figure 4).
For the phases with vanishing total spin per unit cell, we cannot rely on the use of the total moment to assess the error of the integration method. For this reason, in table 1 we choose to normalize the values of the atomic moments obtained by QE for all phases to the ones obtained for the FM phase with . This local moments can be considered as an upper limit for the magnetization per ring. We thus define:
| (3) |
and analogously for the absolute magnetization.
III Results and discussion
III.1 Single CC
Our starting point is the single-particle spectrum of the [6]CC molecule described with the tight-binding model with one orbital per atom. It features two zero modes whose molecular orbitals are localized at the hydrogenated carbons of the top and bottom rings. These zero modes arise due to the combination of the chiral symmetry associated to the bipartite character of the [6]CC graph and the additional presence of the symmetry, when is even, in spite of the fact that the number of sites in both sublattices is the same.
The argument is similar to the one presented by Koshino et alkoshino2014topological . We use the symmetry to represent the Hamiltonian of the molecule. This symmetry permits to build the molecule as the repetition of blocks of 4 atoms. We label the eigenvalues of the symmetry as , where . We thus have to impose , where , so that . The Hamiltonian is thus block diagonal (), with
| (4) |
where is the first neighbour hopping and the order of the basis goes from top to bottom in the unit cell. Now, for even , we can have for . This leads to , so that specific block has 2 zero modes, localized at top and bottom rings. Effectively, the Hamiltonian is equivalent to the molecule with two disconnected zero modes, very much like the Clar’s gobletortiz19 . Note that the argument can be trivially generalized to longer tubes.
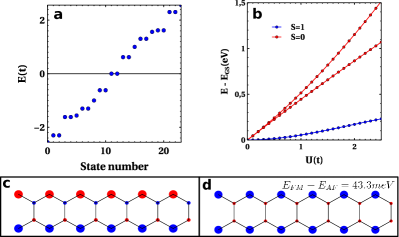
Our next step is to study the effect of electron-electron interaction, within the Hubbard approximation. First we carry out a mean-field calculation for two configurations with (AF) and (FM) . The expectation values of the local spin density for the ground states of the AF and FM solutions are shown in figure 2b and 2c for . The hydrogenated carbon atoms host a magnetic moment close to , the value expected for two unpaired electrons localized at the zero modes. The AF solution has an energy of 43.3 meV smaller than the FM solution for and .
The mean-field results are validated by the CAS(6,6) calculations. We systematically find that the ground state has , complying with Lieb’s theoremLieb89 . The first excited state has , and the energy difference grows with . For the energy difference is 53.8 meV, close to the mean-field value. The nature of the intramolecular antiferromagnetic interaction is Coulomb driven exchange, very much like in bowtie diradicalsortiz19 ; mishra19b . The emerging picture is therefore that the ground state is an open-shell singlet, very much like the bowtie molecule, with two unpaired electrons hosted at the zero modes.
III.2 Atomic structure of the crystal phases
The combination of magnetic states, intermolecular distance and angular orientation define a huge configurational space that can be explored only in part. For we find that the relaxed lattice constants for the NM phase were Å, for the AF1 phase Å, and for the AF2 phase Å and Å. The center to center distance can be related to the [6]CC radius by , where Å for the AF2 phase, similar to the interlayer distance in graphitebacon1951interlayer .
We find that, for the NM, AF1 and AF2 magnetic states, and reasonable intermolecular distances, the orientational ground state energy is minimized for (see figure 3f). Figure 3f shows for in a window, on account of the symmetry of the system. It is apparent that intermolecular exchange depends strongly on . This figure shows that for , AF2 has lower energy than NM and AF1 phases and for these three magnetic states is the ground state.
Importantly, we find that AF2 has lower energy than NM for all values of , showing that local moments survive in the crystal phase. In addition, we find that the lowest energy state for is the AF120 phase (table1), but we could not carry out a dependence in this case. This type of non-collinear magnetic state is expected to arise as a broken spin symmetry solution in triangular lattices with antiferromagnetic exchangeakagi2010spin . We therefore find that magnetic moments persist in the crystal phase and intermolecular exchange is antiferromagnetic. These are the central results of this work.
III.3 Magnetization in the crystal phases
Our next step is to address the key question of whether the open-shell nature of the molecules is preserved in the molecular crystal. This is assessed by computing the magnitude of the local moments per carbon ring that sheds light on whether the system remains in the open-shell strong coupling limit of the single molecule, with local moments in line with those obtained in the gas phase. On the contrary, magnetic moments are quenched to some degree in the crystal phase.
As discussed in the methods part, it is convenient to refer our results to the case of the FM insulating crystal, for which the total magnetization is and the magnetic moment per carbon ring is . From our calculations, summarized in table 1, we conclude that magnetic moments survive, to a large extend, in the crystal phase for the AF2, AF120 phases at and for the AF phase at , with small reductions, but they are severely quenched in the and phases for . This reflects the strong interplay between orientational order and the survival of the magnetic moments.
Inspection of figure 4 clearly shows that local moments are hosted by orbitals. Comparison of diffferent panels shows how the magnitude of the atomic magnetic moments is very different in different crystal phases, in line with the results of table 1. It is apparent that moments are predominantly located on the hydrogenated carbon atoms, as anticipated in our single-molecule calculations with the Hubbard model. The non-hydrogenated carbons host moments opposite to the majority magnetization, as seen in planar nanographenes JFR07 .
| Configuration | |||
|---|---|---|---|
| AF120 | 0.0 | 0.89 | 0.68 |
| AF2 | 6.9 | 0.92 | 0.68 |
| NM | 44.6 | 0.0 | 0.0 |
| AF1() | 47.4 | 0.14 | 0.09 |
| AF1() | 105.8 | 1.08 | 0.82 |
| FM () | 44.3 | 0.05 | 0.04 |
| FM () | 409.2 | 1.0 | 1.0 |
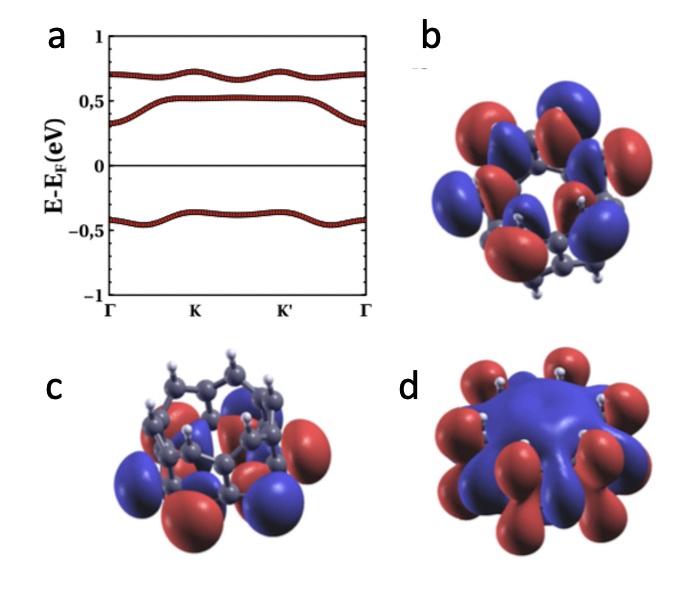
III.4 Energy bands
We now look for microscopic understanding of both the angular dependence of the ground state energy, as well as the the differences between magnetic states. For that matter it is instructive to study the energy bands, as obtained from our DFT calculations. Naively, we expect that the bands closer to the Fermi energy are formed by the two zero modes of the diradical molecule. These states are linear combination of orbitals localized along the radial direction of the molecules, which anticipate a strong dependence of the intermolecular hybridization on .
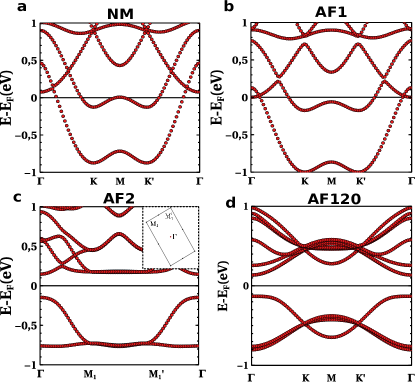
Our energy band calculations for the AF1 phase for (figure 5a) show that, in addition to the two relatively narrow bands arising from the in-gap zero modes of the molecule, there is a third band slightly above, that overlaps with the states above the Fermi energy. The angle corresponds for the second minima that appears in the curve of figure 3f, which corresponds to a crystal geometry where carbon and hydrogen atoms avoid the alignment with those of their neighbours in order to minimize sterical interactions. In this calculation we use the relaxed unit cell with , and rotate rigidly the molecules to have . A -grid of 4x4x1 was used instead since the convergence of this parameter is achieved earlier for insulators, and no smearing was used here either. These bands feature a twofold spin degeneracy that arises in centrosymmetric antiferromagnets.
In order to confirm the origin of these bands, we compute the Wannier wave functions using Wannier90mostofi2014updated ; marzari1997maximally ; souza2001maximally . We find three Wannier orbitals associated to the 3 narrow bands of figure 5a. The ones corresponding to the first valence and conduction bands are localized in the top and bottom rings of the molecule, at the orbitals of the hydrogenated carbon atoms, as expected from our previous work for the molecular phaseperez2019cyclic . The one corresponding to the higher energy band has a character and a smaller bandwidth thereby, on account of the smaller intermolecular hopping.
The width of the energy bands depends strongly on , as can be seen comparing 5a with figure 6b, showing the bands of the AF1 phase for two different values of . We see that the bandwidth of the valence band goes from less than 200 meV for to more than 1.1 eV for . This dependence is a consequence of the highly directional nature of the orbitals that form these bands.
In turn, the modulation of the bandwidth has consequences on the local moment formation. The two energy scales that govern the emergence of local moments are the bandwidth of the bands at the Fermi energy and the effective Coulomb repulsion for double occupation of the molecular orbitals, that in the Hubbard aproximation is given by , where is the amplitude of the molecular orbital at atom and is the atomic Hubbard parameter, that is in the range of 9 eVwehling2011 . Since is equally distributed in six atoms, we estimate . This is to be compared with the bandwidth.
In figure 6a,b we see how both the NM and the AF1 phases are conducting and have a Fermi surface with two pockets. In contrast, the AF2 and AF120 phases (figure 6c,d), that are more stable in energy, are insulating, also for . This shows the interplay between the intermolecular spin correlations and conduction.
Our results suggest that [6]crystacene provides a physical realization of two triangular monolayers that host local moments, with strong intralayer antiferromagnetic interactions, and antiferromagnetic interlayer exchange. In the AF120 phase the quenching of the local moments, relative to the gas phase, is small compared to the molecular case, so the system provides a physical realization of the triangular lattice bilayer Heisenberg model singh1998 . . The nature of the ground state of the S=1/2 triangular monolayer has been studied for 5 decades now ANDERSON1973153 ; bernu1994 ; capriotti99 ; Balents2010spin . Using both quantum Monte Carlo and exact diagonalizations it was established that the ground state of the Heisenberg model with first neighbour AF coupling features long range order with gapless Goldstone mode excitations and depleted magnetic moments, on account of enhanced quantum fluctuationscapriotti99 . For the triangular bilayersingh1998 it was found that, depending on the ratio between intralayer and interlayer exchange, the spectrum is gapped for small , and gapless for , signalling the critical value for the transition between a quantum disordered state and a ground state with broken symmetry and long range order. Interestingly, intramolecular exchange could be modified if we consider a crystal of longer cyclacenes. Therefore, this platform could permit to study the quantum phase transition that may occur when the ratio of intramolecular and intermolecular exchange is modified.
As for the electronic properties of the broken symmetry AF120 phase predicted by our DFT results, we expect a vanishing Chern number takatsu2010unconventional as well as a vanishing Berry curvature, and thereby null Anomalous Hall effect. In contrast, at three-quarters filling the ground state of a triangular lattice is the so-called Q-phase predicted by Martin and Batistamartin2008itinerant ; chern2012spontaneous , where the spins point to the corners of a tetrahedron, and there is a quantized anomalous Hall conductivity martin2008itinerant . The study of this phase is out of the scope of the present paper.
IV Conclusions
We have studied different magnetic configurations from a molecular crystal consisting in a two-dimensional triangular array of cyclacenes. In the gas phase, we have explored the diradical nature of the molecules using both multiconfigurational and mean-field calculations for the Hubbard model. We have shown that the diradical nature of the molecules has a topological origin, that leads to an open-shell singlet formed by two antiferomagnetically coupled electrons localized at the top and bottom ring of the molecule. We have studied the fate of these local moments in the crystal phase, using density functional theory. We have explored both the relative orientation of the molecules with respect to the crystal lattice vectors, characterized by the angle , and we have considered four different magnetic states: NM and four types of magnetic order, FM, AF1, AF2, AF120. We find a strong dependence of the electronic structure with . For all angles, the AF2 magnetic solution has lower energy than the NM case, showing that the antiferromagnetically correlated local moments of the gas phase survive in the crystal. We find that the ground state occurs for the AF120 phase, for , which indicates antiferromagnetic intermolecular interactions. Our results portray the crystacene crystal as a versatile platform to promote strongly correlated phases, akin to the twisted bilayer graphene.
We acknowledge J. L. Lado and A. Perez Guardiola for fruitful discussions. We ackowledge for funding support to Ministry of Science and Innovation of Spain (grant numbers PID2019-106114GB-I00 and PID2019-109539GB), Generalitat Valenciana and Fondo Social Europeo (grant number ACIF/2018/175) and FEDER/Junta de Andalucía Consejería de Transformación Económica, Industria, Conocimiento y Universidades, grant PY18-4834.
References
- (1) Nakada, K., Fujita, M., Dresselhaus, G. & Dresselhaus, M. S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Physical Review B 54, 17954 (1996).
- (2) Fujita, M., Wakabayashi, K., Nakada, K. & Kusakabe, K. Peculiar localized state at zigzag graphite edge. Journal of the Physical Society of Japan 65, 1920–1923 (1996).
- (3) Fernández-Rossier, J. & Palacios, J. J. Magnetism in graphene nanoislands. Physical Review Letters 99, 177204 (2007).
- (4) Morita, Y., Suzuki, S., Sato, K. & Takui, T. Synthetic organic spin chemistry for structurally well-defined open-shell graphene fragments. Nature Chemistry 3, 197 (2011).
- (5) Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
- (6) Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
- (7) Pavliček, N. et al. Synthesis and characterization of triangulene. Nature Nanotechnology 12, 308–311 (2017).
- (8) Mishra, S. et al. Synthesis and characterization of -extended triangulene. Journal of the American Chemical Society 141, 10621–10625 (2019).
- (9) Mishra, S. et al. Collective all-carbon magnetism in triangulene dimers. Angewandte Chemie International Edition (2020).
- (10) Mishra, S. et al. Observation of fractional edge excitations in nanographene spin chains. arXiv preprint arXiv:2105.09102 (2021).
- (11) Mishra, S. et al. Topological frustration induces unconventional magnetism in a nanographene. Nature Nanotechnology 1–7 (2019).
- (12) Ortiz, R. & Fernández-Rossier, J. Probing local moments in nanographenes with electron tunneling spectroscopy. Progress in Surface Science 100595 (2020).
- (13) Guo, Q.-H., Qiu, Y., Wang, M.-X. & Stoddart, J. F. Aromatic hydrocarbon belts. Nature Chemistry 13, 402–419 (2021).
- (14) Koshino, M., Morimoto, T. & Sato, M. Topological zero modes and dirac points protected by spatial symmetry and chiral symmetry. Physical Review B 90, 115207 (2014).
- (15) Anderson, P. Resonating valence bonds: A new kind of insulator? Materials Research Bulletin 8, 153 – 160 (1973).
- (16) Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
- (17) Gatteschi, D., Sessoli, R. & Villain, J. Molecular nanomagnets, vol. 5 (Oxford University Press on Demand, 2006).
- (18) Lieb, E. H. Two theorems on the hubbard model. Physical Review Letters 62, 1201–1204 (1989).
- (19) Ortiz, R. et al. Exchange rules for diradical -conjugated hydrocarbons. Nano Letters 19, 5991–5997 (2019).
- (20) Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Computational Materials Science 28, 155–168 (2003).
- (21) Choi, H. S. & Kim, K. S. Structures, magnetic properties, and aromaticity of cyclacenes. Angewandte Chemie International Edition 38, 2256–2258 (1999).
- (22) Chen, Z. et al. Open-shell singlet character of cyclacenes and short zigzag nanotubes. Organic Letters 9, 5449–5452 (2007).
- (23) Wu, C.-S., Lee, P.-Y. & Chai, J.-D. Electronic properties of cyclacenes from tao-dft. Scientific Reports 6, 1–9 (2016).
- (24) Pérez-Guardiola, A. et al. From cyclic nanorings to single-walled carbon nanotubes: disclosing the evolution of their electronic structure with the help of theoretical methods. Physical Chemistry Chemical Physics 21, 2547–2557 (2019).
- (25) Pérez-Guardiola, A. et al. The role of topology in organic molecules: origin and comparison of the radical character in linear and cyclic oligoacenes and related oligomers. Physical Chemistry Chemical Physics 20, 7112–7124 (2018).
- (26) Povie, G., Segawa, Y., Nishihara, T., Miyauchi, Y. & Itami, K. Synthesis of a carbon nanobelt. Science 356, 172–175 (2017).
- (27) Povie, G., Segawa, Y., Nishihara, T., Miyauchi, Y. & Itami, K. Synthesis and size-dependent properties of [12],[16], and [24] carbon nanobelts. Journal of the American Chemical Society 140, 10054–10059 (2018).
- (28) Han, Y., Dong, S., Shao, J., Fan, W. & Chi, C. Synthesis of a sidewall fragment of a (12,0) carbon nanotube. Angewandte Chemie International Edition 60, 2658–2662 (2021).
- (29) Schulz, F. et al. Exploring a route to cyclic acenes by on-surface synthesis. Angewandte Chemie International Edition 58, 9038–9042 (2019).
- (30) Zhang, Q., Zhang, Y.-E., Tong, S. & Wang, M.-X. Hydrocarbon belts with truncated cone structures. Journal of the American Chemical Society 142, 1196–1199 (2020).
- (31) Shudo, H., Kuwayama, M., Segawa, Y. & Itami, K. Synthesis of cycloiptycenes from carbon nanobelt. Chemical Science (2020).
- (32) Shi, T.-H., Guo, Q.-H., Tong, S. & Wang, M.-X. Toward the synthesis of a highly strained hydrocarbon belt. Journal of the American Chemical Society 142, 4576–4580 (2020).
- (33) Xu, S. et al. In situ studies of thiol self-assembly on gold from solution using atomic force microscopy. The Journal of Chemical Physics 108, 5002–5012 (1998).
- (34) Bain, C. D. & Whitesides, G. M. Molecular-level control over surface order in self-assembled monolayer films of thiols on gold. Science 240, 62–63 (1988).
- (35) Fukui, T. et al. Control over differentiation of a metastable supramolecular assembly in one and two dimensions. Nature Chemistry 9, 493 (2017).
- (36) Pérez-Guardiola, A., Pérez-Jiménez, Á. J., Muccioli, L. & Sancho-García, J. C. Structure and charge transport properties of cycloparaphenylene monolayers on graphite. Advanced Materials Interfaces 6, 1801948 (2019).
- (37) Giannozzi, P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. Journal of Physics: Condensed Matter 21, 395502 (2009).
- (38) Giannozzi, P. et al. Advanced capabilities for materials modelling with quantum espresso. Journal of Physics: Condensed Matter 29, 465901 (2017).
- (39) Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Physical Review Letters 77, 3865 (1996).
- (40) Thonhauser, T. et al. Spin signature of nonlocal correlation binding in metal-organic frameworks. Physical Review Letters 115, 136402 (2015).
- (41) Thonhauser, T. et al. Van der waals density functional: Self-consistent potential and the nature of the van der waals bond. Physical Review B 76, 125112 (2007).
- (42) Berland, K. et al. van der waals forces in density functional theory: a review of the vdw-df method. Reports on Progress in Physics 78, 066501 (2015).
- (43) Bacon, G. The interlayer spacing of graphite. Acta crystallographica 4, 558–561 (1951).
- (44) Akagi, Y. & Motome, Y. Spin chirality ordering and anomalous hall effect in the ferromagnetic kondo lattice model on a triangular lattice. Journal of the Physical Society of Japan 79, 083711 (2010).
- (45) Mostofi, A. A. et al. An updated version of wannier90: A tool for obtaining maximally-localised wannier functions. Computer Physics Communications 185, 2309–2310 (2014).
- (46) Marzari, N. & Vanderbilt, D. Maximally localized generalized wannier functions for composite energy bands. Physical Review B 56, 12847 (1997).
- (47) Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized wannier functions for entangled energy bands. Physical Review B 65, 035109 (2001).
- (48) Wehling, T. et al. Strength of effective coulomb interactions in graphene and graphite. Physical Review Letters 106, 236805 (2011).
- (49) Singh, R. R. & Elstner, N. Quantum phase transitions in the triangular-lattice bilayer heisenberg model. Physical Review Letters 81, 4732 (1998).
- (50) Bernu, B., Lecheminant, P., Lhuillier, C. & Pierre, L. Exact spectra, spin susceptibilities, and order parameter of the quantum heisenberg antiferromagnet on the triangular lattice. Physical Review B 50, 10048 (1994).
- (51) Capriotti, L., Trumper, A. E. & Sorella, S. Long-range néel order in the triangular heisenberg model. Physical Review Letters 82, 3899–3902 (1999).
- (52) Takatsu, H., Yonezawa, S., Fujimoto, S. & Maeno, Y. Unconventional anomalous hall effect in the metallic triangular-lattice magnet pdcro2. Physical Review Letters 105, 137201 (2010).
- (53) Martin, I. & Batista, C. Itinerant electron-driven chiral magnetic ordering and spontaneous quantum hall effect in triangular lattice models. Physical Review Letters 101, 156402 (2008).
- (54) Chern, G.-W. & Batista, C. Spontaneous quantum hall effect via a thermally induced quadratic fermi point. Physical Review Letters 109, 156801 (2012).