Full characterization of measurement-induced transitions of a superconducting qubit

Measurement is a central operation in quantum computation, forming the basis of quantum error correction protocols [kitaev_fault-tolerant_2003, kitaev_anyons_2006, ofek_extending_2016, google_quantum_ai_suppressing_2023, sivak_real-time_2023, google_quantum_ai_quantum_2024]. In these protocols, a high-fidelity measurement must be applied to the same qubit repeatedly, for many subsequent cycles of error correction. Therefore, in addition to being precise, the measurement should also leave the observed state intact, i.e., present a quantum non-demolition (QND) character. In circuit quantum electrodynamics, an approximation to QND measurement is achieved by dispersive readout [clerk_introduction_2010, blais_cavity_2004, wallraff_strong_2004, mallet_single-shot_2009, reed_high-fidelity_2010, jeffrey_fast_2014, walter_rapid_2017, dassonneville_fast_2020, swiadek_enhancing_2024, spring_fast_2024], see Figure 1(a,b). In this readout scheme, the qubit state is inferred from the non-resonant microwave tone elastically scattered off the qubit through the readout resonator.

Dispersive readout has to be performed much faster than the qubit relaxation time [gambetta_protocols_2007]. Shortening the duration of the measurement necessitates increasing the power of the probe tone to maintain the same signal-to-noise ratio. However, increasing the power of the tone has been found to induce unwanted transitions between the qubit states that diminish the QND character of the measurement. These drive-induced transitions can occur from one computational state to another [zhang_engineering_2019, petrescu_lifetime_2020, hanai_intrinsic_2021, thorbeck_readout-induced_2024, bista_readout-induced_2025] or from a computational state to a non-computational state [reed_high-fidelity_2010, sank_measurement-induced_2016, walter_rapid_2017, lescanne_escape_2019, khezri_measurement-induced_2023, hazra_benchmarking_2024, bista_readout-induced_2025]. The latter type of transitions – “leakage” from the computational subspace – is especially problematic. Leakage can lead to the loss of control over the qubit state and thus decapitate quantum error correction protocols [aliferis_fault-tolerant_2007, fowler_coping_2013, ghosh_understanding_2013, suchara_leakage_2015, magnard_fast_2018, bultink_protecting_2020, varbanov_leakage_2020, mcewen_et_al_removing_2021, miao_overcoming_2023]. For transmon qubits, one of the dominant mechanisms of leakage is the activation of accidental multi-excitation resonances in the transmon spectrum involving non-computational states [sank_measurement-induced_2016, shillito_dynamics_2022, xiao_diagrammatic_2023, cohen_reminiscence_2023, dumas_measurement-induced_2024, nesterov_measurement-induced_2024].

Raising the frequency of the readout tone to well beyond the frequency of the transmon allows one to avoid activating multi-excitation resonances. The advantages of such an off-resonant readout were demonstrated in our previous work [kurilovich_high-frequency_2025]. We achieved a QND fidelity above 99.9$\%$ by using a readout resonator with a frequency 12 times higher than that of the transmon. However, the performance of such a high-frequency readout could not be further improved by increasing the power. This raises the question of the mechanisms that limit the QND fidelity of the readout.

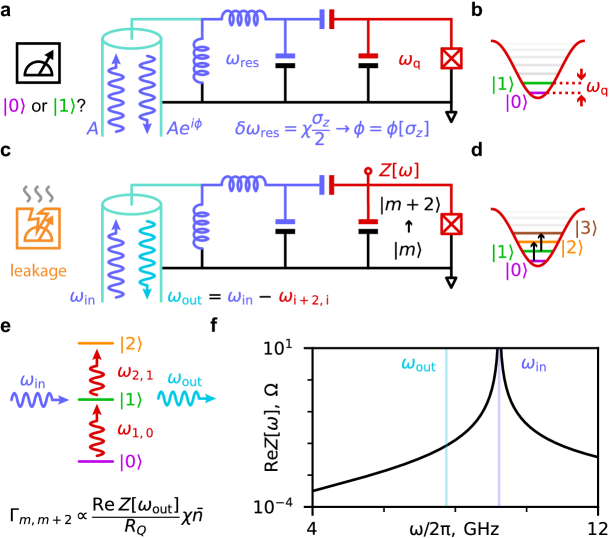
In this work, we experimentally identify the mechanisms that violate the QND nature of the high-frequency readout, where $\omega_{\mathrm{res}}\gg\omega_{\mathrm{q}}$ ($\omega_{\mathrm{res}}$ and $\omega_{\mathrm{q}}$ are frequencies of the readout resonator and the qubit, respectively). The leading leakage mechanism is similar to the well-known Raman scattering of light: a readout photon incoming from the transmission line is “split” between a qubit excitation and an outgoing photon at a lower frequency, see Figure 1(c,d). We identify this inelastic scattering process by measuring the rates of unwanted transmon state transitions, and comparing these rates to the parameter-free theory which we develop.

According to the theory, when the drive photon scatters inelastically off the transmon, the latter excites to a non-computational state, see Figure 1(e,f). We show that the strongest processes of this type are $|0\rangle\rightarrow|2\rangle$ and $|1\rangle\rightarrow|3\rangle$, where $|m\rangle$ denotes the $m$-th eigenstate of the transmon. We independently measure the rates of such transitions and show that they are in agreement with the theory. As expected, the rate of unwanted transitions is proportional to the power of the readout tone. The proportionality coefficient is sensitive to the electromagnetic environment of the transmon at the frequency of outgoing photons $\omega_{\mathrm{\rm out}}$. This frequency is different from both the qubit frequency $\omega_{\mathrm{q}}$ and the readout frequency $\omega_{\mathrm{res}}$. Undesired transitions can thus be suppressed by engineering the readout channel to reduce dissipation at frequency $\omega_{\mathrm{\rm out}}$.

The described above inelastic scattering process, tied to the readout channel itself, is only one of the possible mechanisms that violate the QND character of the measurement. By changing the qubit frequency, we resolve additional demolishing processes. They correspond to accidental resonances with spurious modes either in the electromagnetic environment or the materials of the device [thorbeck_readout-induced_2024]. Due to these resonances, the rate of undesired state transitions becomes elevated at a discrete set of qubit frequencies. At the highest achievable qubit frequencies, we also witness the onset of transitions caused by the multi-excitation resonances between the computational and non-computational states.

Our experimental and theoretical results paint a complete picture of measurement-induced state transitions caused by the dispersive readout of a superconducting qubit. The mechanisms of state transitions that we uncover are also relevant for other contexts where a strong off-resonant drive is applied to the transmon. These include parametric gates [gao_programmable_2018, chapman_high--off-ratio_2023, lu_high-fidelity_2023] and quantum control of linear oscillators [eickbusch_fast_2022, sivak_real-time_2023].

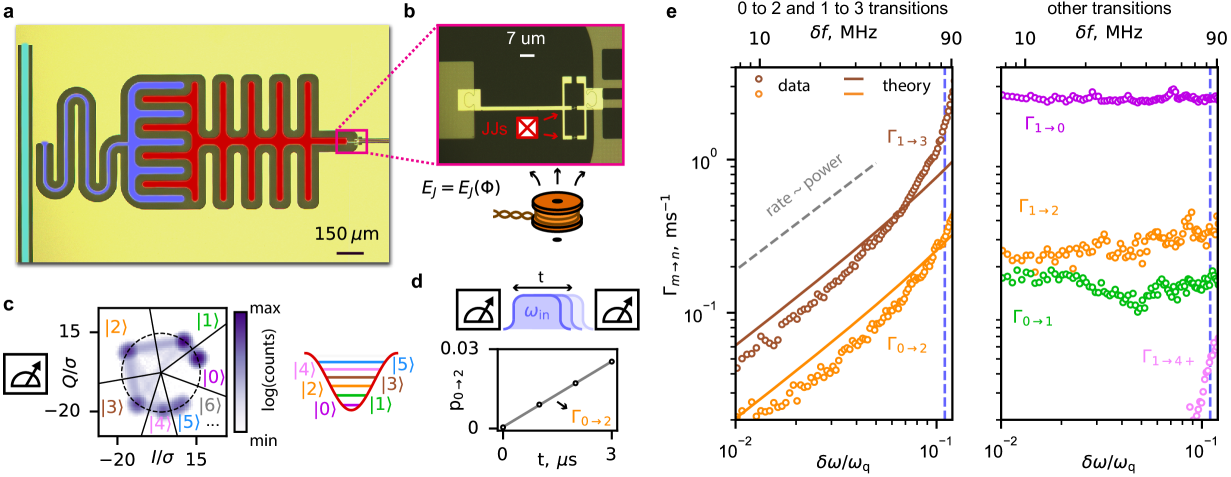
We begin by describing the details of our experimental system. It consists of a transmon qubit and a readout resonator implemented in a 2D architecture, see Figure 2(a,b). The transmon has charging energy $E_{C}/h=36\>\mathrm{MHz}$; its frequency can be tuned between $\omega_{\mathrm{q}}/2\pi=0.520\>\mathrm{GHz}$ and $\omega_{\mathrm{q}}/2\pi=1.53\>\mathrm{GHz}$ with magnetic flux through a SQUID loop. Our recent readout result [kurilovich_high-frequency_2025] was obtained with this device tuned to a frequency $\omega_{\mathrm{q}}/2\pi=0.758\>\mathrm{GHz}$ (corresponding to magnetic flux $\Phi\approx 0.42\Phi_{0}$, where $\Phi_{0}$ is the flux quantum). A quarter-wave readout resonator has frequency between $\omega_{\mathrm{res}}/2\pi=9.223\>\mathrm{GHz}$ and $\omega_{\mathrm{res}}/2\pi=9.240\>\mathrm{GHz}$ depending on the transmon flux bias. The resonator linewidth is $\kappa/2\pi=1.80\>\mathrm{MHz}$. The linewidth is determined by the inductive coupling of the resonator to the readout transmission line. At the bias point of Ref. [kurilovich_high-frequency_2025], the strength of capacitive coupling between the qubit and the resonator is $g/2\pi=515\>\mathrm{MHz}$. The presence of the transmon results in the state-dependent pull of the cavity frequency. For example, at $\omega_{\mathrm{q}}/2\pi=0.758\>\mathrm{GHz}$, the difference between the frequency shifts with transmon being in its ground or excited state is $\chi/2\pi=0.90\>\mathrm{MHz}$, allowing us to readout the transmon state.

To probe the the unwanted transitions caused by the drive, we initialize the transmon in either its ground state $|0\rangle$ or in its excited state $|1\rangle$. We then apply a pulsed tone at a frequency $\omega_{\mathrm{\rm in}}$ close to that of the readout resonator. We detune the drive by many resonator linewidths to suppresses the measurement-induced broadening of qubit transitions (by 40 to 55 MHz depending on the flux bias). This simplifies the analysis of drive-induced transitions without changing the physical picture. After the pulse, we measure the resulting transmon state $|m\rangle$; the measurement can resolve states from $|0\rangle$ to $|4\rangle$, see Figure 2(c,d). Repeating this experiment many times, we find the transition probability between initial state $|m\rangle$ and final state $|n\rangle$. Changing the duration of the pulse yields the transition rates $\Gamma_{m\rightarrow n}$. We then repeat this experiment at different powers of the drive tone. The resulting power-dependence of $\Gamma_{m\rightarrow n}$ is shown in Figure 2(e). The power is quantified by the the absolute value of the independently-calibrated AC Stark shift experienced by the transmon, $\delta\omega=\chi\bar{n}$. See supplementary materials for the details of the Stark shift calibration.

At zero drive power, the transitions of the transmon are caused by its coupling to the equilibrium environment. The only non-zero transition rates are $\Gamma_{0\rightarrow 1}$, $\Gamma_{1\rightarrow 0}$, and $\Gamma_{1\rightarrow 2}$. Relaxation rate $\Gamma_{1\rightarrow 0}$ exceeds the excitation rate $\Gamma_{0\rightarrow 1}$ roughly by a factor of 10. This is consistent with the detailed balance relation, $\Gamma_{1\rightarrow 0}=e^{\hbar\omega_{\mathrm{q}}/k_{B}T}\Gamma_{0\rightarrow 1}$, where $T=16\>\mathrm{mK}$ is close to the base temperature of our dilution refrigerator. Rates $\Gamma_{0\rightarrow 1}$, $\Gamma_{1\rightarrow 0}$, and $\Gamma_{1\rightarrow 2}$ remain roughly unchanged upon application of a high-power pulse.

Finite drive power excites the transmon to non-computational states. The dominant drive-activated processes that we observe are $|0\rangle\rightarrow|2\rangle$ and $|1\rangle\rightarrow|3\rangle$. The rates of these processes, $\Gamma_{0\rightarrow 2}$ and $\Gamma_{1\rightarrow 3}$, grow linearly with the power of the drive, as long as the power is sufficiently low. The growth becomes faster than linear at higher powers. This drive-induced excitation was the dominant leakage process limiting QND character of our high-frequency readout introduced in Ref. [kurilovich_high-frequency_2025]. Direct excitation to states $|4\rangle$ and higher starts to emerge at high drive powers. However, the rate of such excitation remains small compared to $\Gamma_{0\rightarrow 2}$ and $\Gamma_{1\rightarrow 3}$ in the range of powers relevant for readout.

Previously, readout-induced leakage transitions were attributed to the drive activating accidental multi-excitation resonances in the transmon spectrum [sank_measurement-induced_2016, xiao_diagrammatic_2023, khezri_measurement-induced_2023, dumas_measurement-induced_2024]. In this process, several readout photons are simultaneously absorbed, promoting the transmon to a non-computational state. This explanation, however, is inadequate for our data. The transitions that we observe do not have a resonant character. Moreover, since $\omega_{\mathrm{res}}\gg\omega_{\mathrm{q}}$, non-linear resonances would excite transmon to much higher non-computational states than $|2\rangle$ or $|3\rangle$. As is shown in Fig. 2(e), excitation to levels $|4\rangle$ and higher does not happen in the range of powers relevant for readout. Thus, an explanation different from transmon multi-excitation resonances is needed for the observed undesired transitions.

We attribute the undesired transitions caused by the readout tone to inelastic scattering of readout photons. As mentioned in the introduction, in the process of inelastic scattering, a readout photon with frequency $\omega_{\mathrm{\rm in}}$ splits between qubit excitation $|m\rangle\rightarrow|m+2\rangle$ and a photon reflected at a smaller frequency $\omega_{\mathrm{\rm out}}=\omega_{\mathrm{\rm in}}-\omega_{m+2,m}$ [where $\omega_{m+2,m}=(\epsilon_{m+2}-\epsilon_{m})/\hbar$, with $\epsilon_{m}$ being the energy of state $|m\rangle$ in the computational basis]. We evaluate the rate of inelastic scattering via Fermi’s Golden rule in which we treat the non-linearity as a perturbation. We set out by outlining the outcome of the calculation. We then provide the details of how the calculation is carried out.

According to our calculation, the rate of qubit excitation $|m\rangle\rightarrow|m+2\rangle$ due to the inelastic scattering of readout photons is

Here, $\delta\omega$ is the previously-introduced AC Stark shift of the qubit; the transition rate scales linearly with this parameter. Quantity $\mathrm{Re}Z[\omega]$ is the dissipative part of the impedance measured between the transmon island and the ground, see Fig. 1(c,f). It is evaluated at the frequency $\omega_{\mathrm{\rm out}}=\omega_{\mathrm{\rm in}}-\omega_{m+2,m}$ of the inelastically scattered photons. The dissipation is enhanced near the frequency of the readout resonator due to the Purcell effect. Detuning $\omega_{\mathrm{\rm out}}$ from this frequency suppresses the rate of undesired transitions. Constant $R_{Q}=h/e^{2}\approx 25.8\>\mathrm{k}\Omega$ is the resistance quantum.

Next, we compare the calculated rate with our measurement. To this end, we evaluate the impedance $Z[\omega]$ within a lumped model of our circuit depicted in Fig. 1(c) (see supplement [noauthor_see_nodate] for details) and substitute independently measured $\delta\omega$, and $\omega_{\mathrm{q}}$ in Eq. (1). The result of this calculation is shown with solid lines in Fig. 2(e). Our parameter-free theory is in a good agreement with the measurement. We attribute the discrepancy of about $25\%$ between the theory and the experiment to our imperfect knowledge of $Z[\omega]$ away from the resonator frequency, see Section IV for further discussion. At the highest powers, the theory starts to underestimate the measured rate. We believe that this happens due to the activation of the higher-order nonlinear processes. These processes stem from high-frequency modes in the qubit environment. The effects of these modes are explored in Section V.

To derive Eq. (1), we use the Hamiltonian $H=H_{t}+H_{b}+V$, modeling the transmon coupled to a transmission line through a readout resonator. The term $H_{t}=4E_{C}(N-n_{g})^{2}-E_{J}\cos\varphi$ describes the transmon; $N$ is the Cooper pair number on the island and $\varphi$ is the superconducting phase. Term $H_{b}=\sum_{k}\hbar\omega_{k}(b^{\dagger}_{k}b_{k}+1/2)$ describes the transmission line modes labeled by index $k$; $\omega_{k}$ and $b_{k}$ are the corresponding frequencies and annihilation operators, respectively. The term $V$ describes the coupling between the transmon and the transmission line mediated by the readout resonator, $V=\sum_{k}N(\lambda_{k}b^{\dagger}_{k}+\lambda_{k}^{\star}b_{k})$. In what follows, we link the coupling constants $\lambda_{k}$ to the impedance $Z[\omega]$ introduced above.

The core idea of our calculation is to treat transmon non-linearity as a perturbation. First, we diagonalize the Hamiltonian $H$ neglecting the non-linearity [nigg_black-box_2012]. This defines a set of normal modes; the phase operator can be expressed through the normal modes as $\varphi=\varphi_{\rm zpf}(ia-ia^{\dagger})+\sum_{k}(i\mu_{k}^{\star}a_{k}-i\mu_{k}a_{k}^{\dagger})$. Here, operator $a$ corresponds to the transmon mode dressed by its coupling to the environment; zero-point fluctuations of the transmon phase are given by $\varphi_{\rm zpf}=(\hbar\omega_{\mathrm{q}}/2E_{J})^{1/2}$. In turn, operators $a_{k}$ correspond to the dressed environment modes. Their participation on the transmon island is described by coefficients $\mu_{k}=2\hbar^{-1}\omega_{k}\lambda_{k}/(\omega_{k}^{2}-\omega_{\mathrm{q}}^{2})$. The nonlinearity couples the normal modes to each other. When $E_{J}/E_{C}\gg 1$, the coupling can be captured with a term $-E_{J}\varphi^{4}/4!$ obtained by Taylor-expanding the Josephson potential to the fourth order. Applying Fermi’s Golden rule with respect to this term, we compute the desired transition rates.

Specifically, we assume that the system is initialized in a state $|\Psi_{i}\rangle\propto(a_{\rm in}^{\dagger})^{n_{\rm in}}|\Omega\rangle|m\rangle$, where $|\Omega\rangle$ is the vacuum state of the transmission line and $|m\rangle$ is the state of the transmon; the photon occupation number $n_{\rm in}$ and the mode with frequency $\omega_{\rm in}$ characterize the applied drive (index $k=\mathrm{in}$ is used to denote this mode). The final state, where one of the drive photons is inelastically scattered, is $|\Psi_{f}\rangle\propto(a_{\rm in}^{\dagger})^{n_{\rm in}-1}a_{\rm out}^{\dagger}|\Omega\rangle|m+2\rangle$ (index $k=\mathrm{out}$ denotes the mode to which the drive photon is scattered). The transition rate can be written as

Here, $\nu_{\rm out}$ is the photon density of states in the transmission line at the frequency $\omega_{\rm out}$.

We compute $\mathcal{M}_{fi}$ by substituting the normal-mode decomposition of the phase operator $\varphi$ into Eq. (2). We then find

To express the result in terms of measurable quantities, we note that $\mu_{\rm in}$ can be related to the Stark shift as $\delta\omega=\frac{1}{2}\omega_{\mathrm{q}}|\mu_{\rm in}|^{2}n_{\rm in}$ [noauthor_see_nodate]. The constant $\mu_{\rm out}$ can be linked the impedance of the transmon island, $\mathrm{Re}Z[\omega_{\rm out}]/R_{Q}=\hbar\omega_{\rm out}\nu_{\rm out}|\mu_{\rm out}|^{2}/8$. Employing these substitutions in Eqs. (2) and (3) we arrive at Eq. (1).

In our derivation, we assumed that the qubit nonlinearity is weak. In the supplementary materials [noauthor_see_nodate], we show that weak non-linearity assumption can be lifted if the coupling between the transmon and the environment is small. We also develop the theory for other possible inelastic scattering processes. For example, we consider a process where two drive photons and a qubit excitation are converted into an excitation of an environment mode.

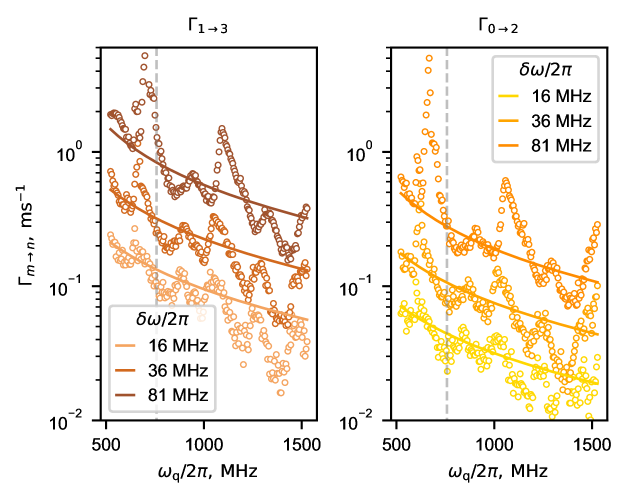
Next, to further validate the theory, we measure the rates $\Gamma_{0\rightarrow 2}$ and $\Gamma_{1\rightarrow 3}$ at different qubit frequencies. To this end, we repeat the measurement described above at different values of the magnetic flux threaded through the SQUID loop of our device. At each value of the flux we independently calibrate the qubit frequency, the resonator frequency, the relation between the Stark shift and drive power, and the readout thresholds used for state assignment, see supplementary materials [noauthor_see_nodate].

The results of this measurement for several different drive powers are shown in Fig. 3. At small powers, the theoretical prediction for the rates is close to the data at all qubit frequencies. We attribute the deviations to the impedance mismatches in the transmission line that create an uncertainty in our estimate of $\mathrm{Re}Z$ in Eq. (2). Notably, for a fixed value of the AC Stark shift $\delta\omega$, the rate of unwanted transitions is enhanced at smaller qubit frequencies. The origin of this enhancement is the Purcell effect. Indeed, due to the Purcell effect, $\mathrm{Re}Z[\omega]\propto 1/(\omega-\omega_{\mathrm{res}})^{2}$. Therefore, $\mathrm{Re}\>Z[\omega_{\mathrm{\rm out}}]\propto 1/\omega_{\mathrm{q}}^{2}$ since $\omega_{\mathrm{\rm out}}\approx\omega_{\mathrm{\rm in}}-2\omega_{\mathrm{q}}$ and $\omega_{\mathrm{\rm in}}$ is close to $\omega_{\mathrm{res}}$. Combined with the prefactor $\propto\omega_{\mathrm{q}}$ in Eq. (2), this results in $\Gamma_{m\rightarrow m+2}\propto\delta\omega/\omega_{\mathrm{q}}$.

At higher drive power additional peaks appear in the measured rates. These stem from the activation of higher-order nonlinear processes involving the spurious device modes. We explore these processes in the next section.

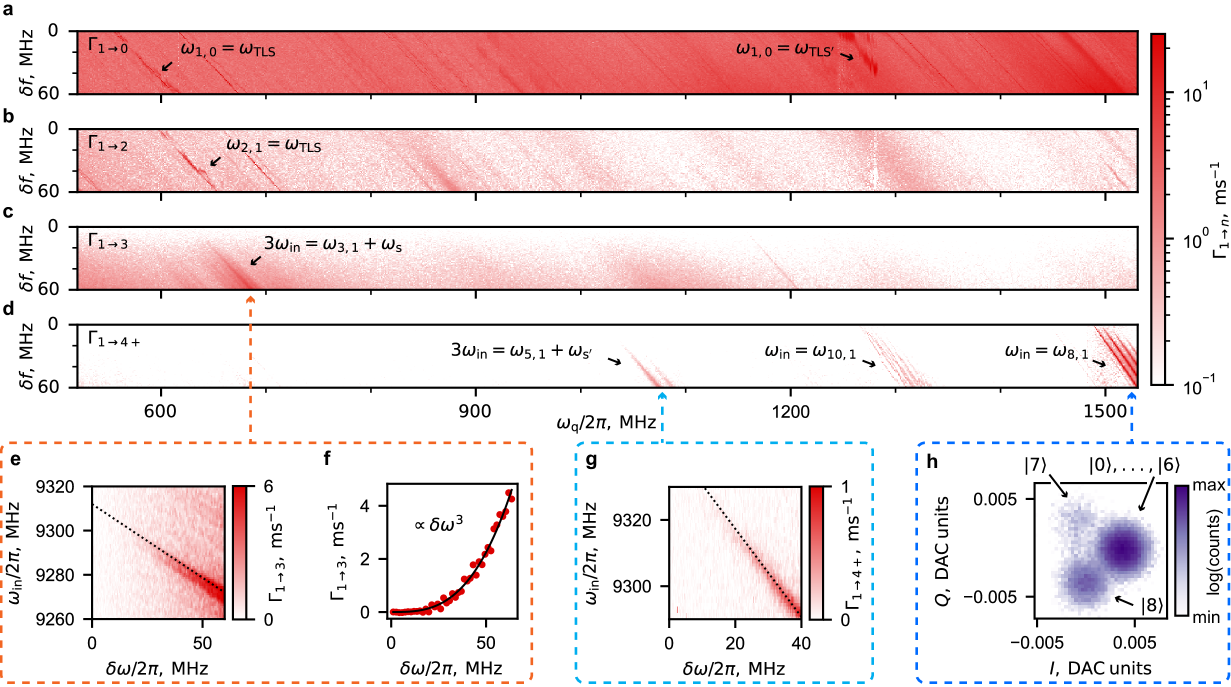
The inelastic scattering process that we describe above is only one of the possible mechanisms by which the readout drive can cause unwanted transmon state transitions. In this section, we describe the measurement that reveals the other transition mechanisms. Specifically, we sweep a range of qubit frequencies and drive powers. At each point in this sweep, we measure the transition rates $\Gamma_{m\rightarrow n}$ from the computational states $|m\rangle$ with $m=0,1$ to the states $|n\rangle$ with $n=0,1,2,3,4+$. Here, $4+$ label any excited non-computational state higher than 3, i.e., states $|4\rangle$, $|5\rangle$, $|6\rangle$ and higher.

The results of this measurement for $m=1$ are shown in Fig. 4 (similar data for $m=0$ is presented in the supplementary materials). The plots demonstrate two distinct behaviors for the transition rates. First, rates $\Gamma_{1\rightarrow 0}$, $\Gamma_{1\rightarrow 2}$, and $\Gamma_{1\rightarrow 3}$ have a smooth background present at all qubit frequencies. The background in $\Gamma_{1\rightarrow 0}$ and $\Gamma_{1\rightarrow 2}$ is roughly independent of the drive power. Second, there is a set of resonant features in the measured transition rates. These resonances manifest as peaks in the transition rates at certain combinations of qubit frequency and drive power.

For the rate $\Gamma_{1\rightarrow 0}$, the smooth background corresponds to the direct emission of the qubit excitation into the environment. This process is responsible for the relaxation of the undriven qubit. The rate of qubit decay increases with qubit frequency [noauthor_see_nodate]. The smooth background in $\Gamma_{1\rightarrow 2}$ corresponds to thermal excitation by the same environment that is responsible for $\Gamma_{1\rightarrow 0}$. Finally, the smooth background in $\Gamma_{1\rightarrow 3}$ stems from the inelastic scattering process described in Section III and IV. The rate of this process is zero in the absence of the drive.

Resonant features in the rates $\Gamma_{1\rightarrow 0}$ (or $\Gamma_{1\rightarrow 2}$) correspond to resonances in the qubit environment at some frequencies $\omega_{\mathrm{TLS}}$. Most likely, these resonances originate from excitation (or relaxation) of material defects in the device that are strongly coupled to the qubit degree of freedom [thorbeck_readout-induced_2024]. The peaks in $\Gamma_{1\rightarrow 0}$ occur when a frequency matching condition is fullfilled, $\omega_{1,0}[\delta\omega]=\omega_{\mathrm{TLS}}$. Due to the AC-Stark shift the transition frequency $\omega_{1,0}$ depends on the drive power, $\omega_{1,0}[\delta\omega]=\omega_{1,0}[0]-\delta\omega$. This explains the slope of the resonant features in Fig. 4(a). The peaks in $\Gamma_{1\rightarrow 2}$ happen when $\omega_{2,1}[\delta\omega]=\omega_{\mathrm{TLS}}$. Frequency $\omega_{2,1}$ differs from $\omega_{1,0}$ due to the qubit anharmonicity. Therefore, the resonant features are shifted by $\sim 40\>\mathrm{MHz}$ between Fig. 4(a) and Fig. 4(b).

The resonant feature in $\Gamma_{1\rightarrow 3}$ around $670\>\mathrm{MHz}$ stems from a six-wave process mixing three readout photons with two qubit excitation quanta and a spurious device mode [singh_impact_2025]. To determine the number of the involved drive photons, we vary the frequency of the drive and measure the power dependence of the transition rate (the magnetic flux is kept fixed such that in the absence of the drive the qubit frequency is $670\>\mathrm{MHz}$). The result of this measurement is shown in Fig. 4(e). For a fixed amount of AC Stark shift, the position of the resonance depends on the frequency of the drive. The dependence is well described by a resonant condition $3\omega_{\mathrm{\rm in}}=\omega_{3,1}[\delta\omega]+\omega_{s}$ that corresponds to the six-wave mixing process: absorption of three drive photons with frequency $\omega_{\mathrm{\rm in}}$ results in the qubit transition $|1\rangle\rightarrow|3\rangle$ and excitation of a spurious mode with frequency $\omega_{s}/2\pi=26.72\>\mathrm{GHz}$ (likely $3\lambda/4$ mode of the readout resonator). The transition frequency $\omega_{3,1}$ experiences AC Stark shift, $\omega_{3,1}[\delta\omega]=\omega_{3,1}[0]-2\delta\omega$; this explains the slope in Fig. 4(e). Theoretically, the rate of the described six wave-mixing process is proportional to the cube of the drive power. As is shown in Fig. 4(f), this is indeed the case in our data.

As the qubit frequency is increased, resonant features appear in the rate of excitation to higher excited states of the transmon, $\Gamma_{1\rightarrow 4+}$. The most prominent feature occurs around $\omega_{\mathrm{q}}/2\pi=1500\>\mathrm{MHz}$. This “bear claw” feature stems from the activation of a multi-excitation resonance in the transmon spectrum. The drive becomes resonant with the transition between states $|1\rangle$ and $|8\rangle$, i.e., condition $\omega_{\mathrm{\rm in}}=\omega_{8,1}$ is fulfilled. As demonstrated in Fig. 4(h), the drive does indeed excite the transmon to state $|8\rangle$. Notably, the spectroscopic line in Fig. 4(d) is followed by several parallel “replicas”. These replicas stem from the detuning of about 40 MHz between the drive frequency and the frequency of the readout resonator. The replicas correspond to a process in which $n$ drive quanta are converted into a qubit excitation from $|1\rangle$ to $|8\rangle$ and $n-1$ resonator quanta. They occur when the condition $n\omega_{\mathrm{\rm in}}=\omega_{8,1}[\delta\omega]+(n-1)\omega_{\mathrm{r}}$ is fulfilled for some integer $n$.

Some of the other resonant features in Fig. 4 are labeled according to their character. They stem from one of the following mechanisms: (i) direct interaction with isolated lossy modes, (ii) nonlinear processes involving spurious degrees of freedom, (iii) activation of multi-excitation resonances in the transmon spectrum.

Applications of superconducting circuits to quantum information tasks require coupling them to microwave tones. In particular, projective measurement of a superconducting qubit is achieved by off-resonantly driving the qubit through a readout resonator. The speed and thus the performance of the measurement can be improved by increasing the drive power. However, the increase of the drive power also leads to the appearance of unwanted state transitions. These drive-activated transitions limit the measurement fidelity. The origin of these transitions is a subject of the present investigation.

In our work, we fully characterize the mechanisms of state transitions in an off-resonantly driven transmon qubit. We focus on the case of a dispersive qubit readout achieved with a readout resonator with a high-frequency, $\omega_{\mathrm{res}}/\omega_{\mathrm{q}}\gg 1$ [kurilovich_high-frequency_2025]. By changing the qubit frequency using magnetic flux, we resolve two types of the unwanted drive-activated transitions. Transitions of the first type are ubiquitously present at all qubit frequencies. In their course, the qubit is excited to a non-computational state with a rate proportional to the drive power. These transitions occur due to the inelastic scattering of drive photons back into the readout channel, a process allowed by the transmon non-linearity. Specifically, a drive photon with frequency $\omega_{\mathrm{\rm in}}$ splits into a qubit excitation $|0\rangle\rightarrow|2\rangle$ [or $|1\rangle\rightarrow|3\rangle$] and an outgoing photon at a smaller frequency $\omega_{\mathrm{\rm out}}$, see Fig. 1. The measured rate of inelastic scattering is in a good agreement with our parameter-free theory, Eq. (1), see Fig. 3. The inelastic scattering process is the dominant source of leakage error in our recent readout result [kurilovich_high-frequency_2025].

Transitions of the second type have a resonant character, i.e., they appear at a discrete set of qubit frequencies. The causes of these resonances are excitation of degrees of freedom associated with material defects or spurious electromagnetic modes in the qubit environment. With the increase of transmon frequency, transmon multi-excitation resonances also start to interfere with the readout process. In these resonances, the drive frequency matches that of a transition between a computational and a non-computational state. This leads to leakage from the computational basis.

The understanding developed in our work gives a comprehensive roadmap to mitigating the unwanted drive-induced state transitions in superconducting circuits. Multi-excitation resonances can be suppressed by increasing the drive frequency compared to that of a transmon [kurilovich_high-frequency_2025]. Material defects contributing to the spectrum of excitations in the microwave frequency range can potentially be suppressed by improved fabrication techniques. The transitions caused by inelastic scattering of drive photons can be mitigated by means of microwave engineering. For example, the Raman-like process described above can be alleviated by filtering the transmission line at the frequency of inelastically scattered photons $\omega_{\mathrm{\rm out}}$.

While detuning of the readout tone from the qubit frequency allows one to increase the readout speed, this route eventually faces limitations due to higher-order inelastic scattering processes. For example, as described in Section V, we observe a strong process where three drive photons convert into two qubit excitations, $|1\rangle\rightarrow|3\rangle$, and an excitation of an electromagnetic mode at $\omega_{m}/2\pi\approx 27\>\mathrm{GHz}$. This shows the importance of microwave hygiene even at frequencies far exceeding that of the qubit or of the readout drive.

Finally, we note that inelastic processes involving Bogoliubov quasiparticles can also degrade the performance of superconducting qubit operations carried out with microwave tones. This type of inelastic processes was recently analyzed in Refs. [kishmar_quasiparticle-induced_2025, chowdhury_theory_2025].

Note: Recently, two relevant papers appeared [fechant_offset_2025, wang_probing_2025] that focus on drive-induced transitions caused by multi-excitation resonances.

We thank Christian K. Andersen, Arno Bargerbos, Marta Pita-Vidal, Lukas Splitthoff, Jaap Wesdorp, and Daniel Sank for discussions. We thank Alessandro Miano and Elifnaz Önder for help with the measurement setup. Finally, we thank Y. Sun, K. Woods, L. McCabe, and M. Rooks for their assistance and guidance in the device fabrication processes.

This research was sponsored by the Army Research Office (ARO) under grants no. W911NF-22-1-0053 and W911NF-23-1-0051, by DARPA under grant no. HR0011-24-2-0346, by the U.S. Department of Energy (DoE), Office of Science, National Quantum Information Science Research Centers, Co-design Center for Quantum Advantage (C2QA) under contract number DE-SC0012704, and by the Air Force Office of Scientific Research (AFOSR) under award number FA9550-21-1-0209. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the ARO, DARPA, DoE, AFOSR or the US Government. The US Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. Fabrication facilities use was supported by the Yale Institute for Nanoscience and Quantum Engineering (YINQE) and the Yale Univeristy Cleanroom. L.F. is a founder and shareholder of Quantum Circuits Inc. (QCI).