Full orbital decomposition of Yu-Shiba-Rusinov states based on first principles
Abstract
We have implemented the Bogoliubov-de Gennes (BdG) equation in a screened Korringa-Kohn-Rostoker (KKR) method for solving, self-consistently, the superconducting state for 3d crystals including substitutional impurities. In this report we extend this theoretical framework to allow for collinear magnetism and apply it to fcc Pb with 3d magnetic impurities. In the presence of magnetic impurities, there is a pair-breaking effect that results in sup-gap Yu-Shiba-Rusinov (YSR) states which we decompose into contributions from the individual orbital character. We determine the spatial extent of these impurity states, showing how the different orbital character affects the details of the YSR states within the superconducting gap. Our work highlights the importance of the first principles based description which captures the quantitative details making direct comparisons possible with experimental findings.
pacs:
Valid PACS appear hereI Introduction
Magnetism and conventional superconductivity are phenomena related to competing types of order. Theoretically, it was first shown by Abrikosov and Gor’kov Abrikosov and Gor’ Kov (1959) that at a paramagnetic impurity concentration of in a superconductor the spectral energy gap would no longer correspond to the ordering parameter . For higher concentrations of impurities the spectral gap can even vanish totally, leading to gapless superconductivity characterised by a finite TC and but with no spectral gap.Phillips (1963) Local, real space models were subsequently constructed by Yu Yu (1965), Shiba Shiba (1968) and Rusinov Rusinov (1969) using local, one band models around a classical impurity spin. They predicted the existence of a pair of localised, in-gap (YSR) states either side of the Fermi energy associated with the exchange splitting of the spin.
Subsequently, experiments investigating YSR states have predicted multiple pairs of in-gap states Ji et al. (2008); Hatter et al. (2015); Ruby et al. (2016); Choi et al. (2017); Liebhaber et al. (2020), where it was argued that the origin of multiple resonances may arise from magnetic anisotropy Hatter et al. (2015), the orbital character Ruby et al. (2016); Choi et al. (2017) or modulations in the charge density Senkpiel et al. (2019); Liebhaber et al. (2020). Ruby et al Ruby et al. (2016) investigated the (001) surface of Pb with a Mn impurity adsorbed onto the surface. They argue that the multiple YSR resonances originate from the crystal field splitting of the Mn d-orbitals. Using energy considerations and real space maps they were able to assign the relevant orbitals to the YSR resonances.
When investigating more complex superconductors like NbSe2 Senkpiel et al. (2019); Liebhaber et al. (2020) or Bi2Pd Choi et al. (2018) it becomes immediately obvious that disentangling hybridised YSR peaks, or YSR peaks entangled with coherence peaks will become increasing challenging. Symmetry arguments and energy consideration will not be sufficient to uniquely assign the large number of in-gap resonances. In this report we build upon previous work Saunderson et al. (2020a, b) to address this problem from first principles, considering all electrons and their magnetic orderings fully while capturing superconductivity within a one-parameter model of local BCS type pairing.
We use this formalism to investigate the 3d series of elements as impurities in fcc Pb. After a brief introduction of the methodological implementations we show our results for all magnetic 3d impurities discussing the distinct YSR resonance pairs arising from the anticipated t2g and eg orbitals. However, beyond that we will highlight the existence of (s-electron) YSR resonances enforcing the necessity of an all-electron description. Finally, we will analyse the spatial decay of the magnetism as well as the in-gap states within the superconducting Pb, presenting the orbital-resolved local densities.
II Method
The implementation of the Bogoliubov-de Gennes (BdG) equation in the Korringa-Kohn-Rostoker Greens function method Saunderson et al. (2020a) has been described earlier as well as the extension to real space impurity systems Saunderson et al. (2020b). Here, we present a further step namely the incorporation of collinear magnetism and in the following we will restrict the technical discussion to the equations relevant for this development.
In order to incorporate magnetism and superconductivity Oliveira et al. (1988) into density functional theory Dreizler and Gross (1990), three effective potentials are required, the electron potential , the magnetic field and the effective pairing potential ,
| (1) | ||||
| (2) | ||||
| (3) |
Here, is the exchange correlation functional for the normal state, , are the usual charge and spin densities and is the anomalous density. Finally, is the interaction parameter Saunderson et al. (2020a), which is the one free parameter in our description typically fixed to recover experimentally observed gap sizes. This framework, using a simplified phenomenological parameter, was introduced in Ref. Suvasani et al. (1993) and subsequently implementation were presented in Refs. Csire et al. (2015, 2018a). It was already been shown to effectively describe gap anisotropy Saunderson et al. (2020a) and impurity scattering Saunderson et al. (2020b), along with complex superconducting order parameters in LaNiC2 Csire et al. (2018b) and LaNiGa2 Ghosh et al. (2020) Within the non-relativistic theory the densities are given by
| (4) | ||||
| (5) | ||||
| (6) |
Hence, the resulting spin BdG Hamiltonian is defined as,
| (7) |
where
| (8) | ||||
| (9) | ||||
| (10) | ||||
| (11) | ||||
| (12) |
Equation (7) can be brought into a block-diagonal form such that
| (13) |
where and represents the opposing spin to . The corresponding Green’s function is defined as
| (14) |
where , and can be simplified into a block diagonal form accordingly
| (15) |
The relevant densities are expressed by the Green’s function
| (16) | ||||
| (17) |
Implementing this extension in the corresponding bulk Saunderson et al. (2020a) and real-space impurity code Saunderson et al. (2020b) will enable us to address the coupling between the superconducting state and magnetism. Here, we will focus on the effect of magnetic impurities with the corresponding in-gap YSR states. As test scenario we consider superconducting bulk fcc Pb Saunderson et al. (2020a) with the interaction parameter tuned such to the experimental gap size from Ruby et al. Ruby et al. (2015). For the real-space impurity cluster embedded in the infinite periodic crystals we used 87 atoms as shown in panel Fig. 1 (a).
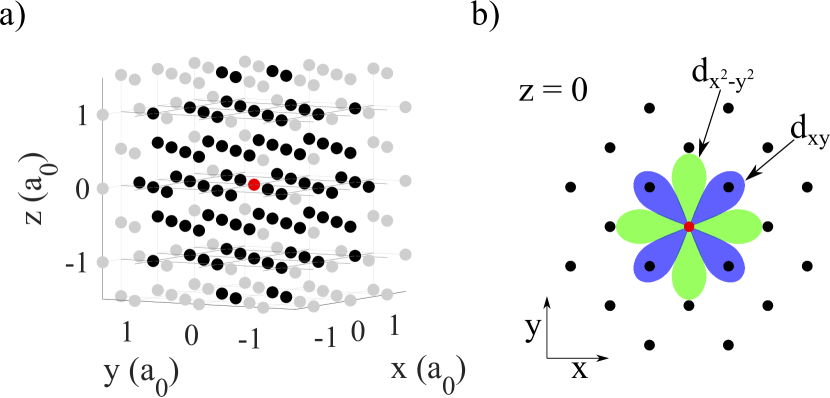
III Normal State Analysis
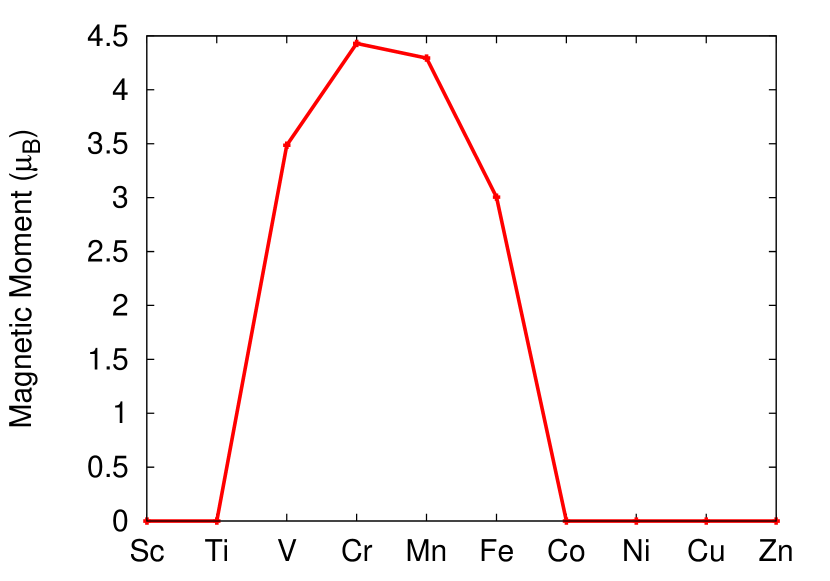
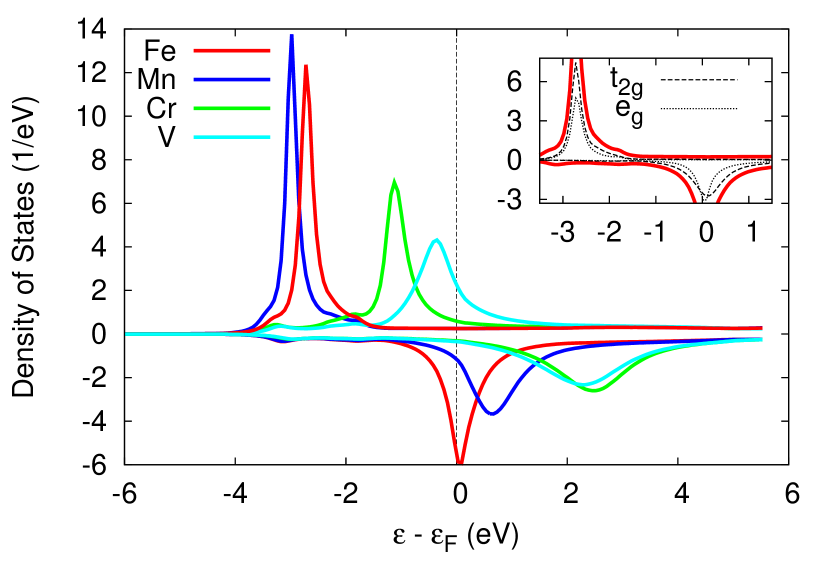
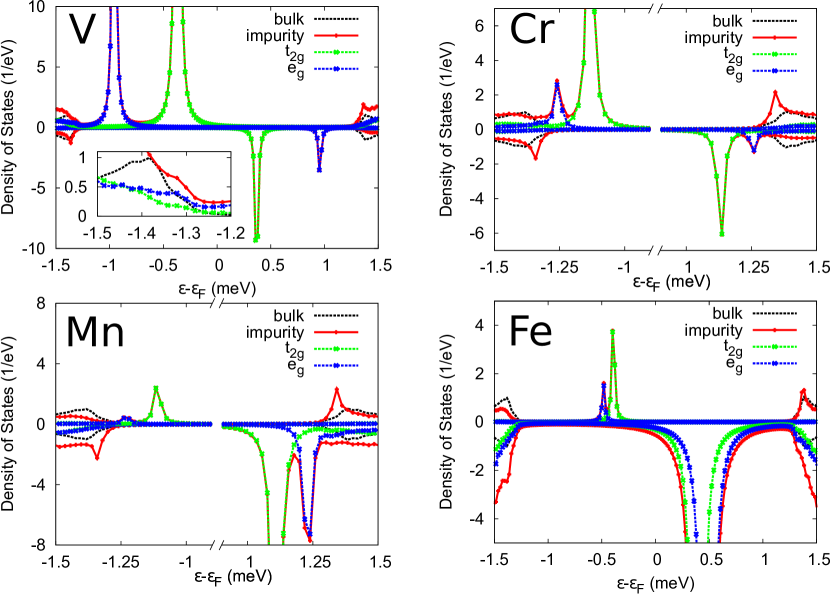
Starting with self-consistent scalar relativistic (SRA) solutions for the normal state, the resulting magnetic moments of the localised 3d impurity atoms are summarized in Fig. 2. For the Pb host we identify only V, Cr, Mn and Fe to be magnetic. For all other 3d elements only the non-magnetic solutions were established self-consistently. The resulting local density of states (LDOS) for all magnetic impurities is shown in Fig. 3. Notably, while for V it is the majority spin channel which is close to the Fermi energy, this impurity level shifts further away from the Fermi energy as we go through the 3d series. For the Fe impurity it is the minority spin channel which is situated right at the Fermi energy. For the elements in between we see a gradual transition between the two cases.
In the cubic fcc lattice the crystal field lifts the degeneracy of the d-orbitals and the impurity levels are split into the eg and t2g orbitals. Dresselhaus et al. (2007) As an example this is shown for the Fe minority level as inset in Fig. 3.
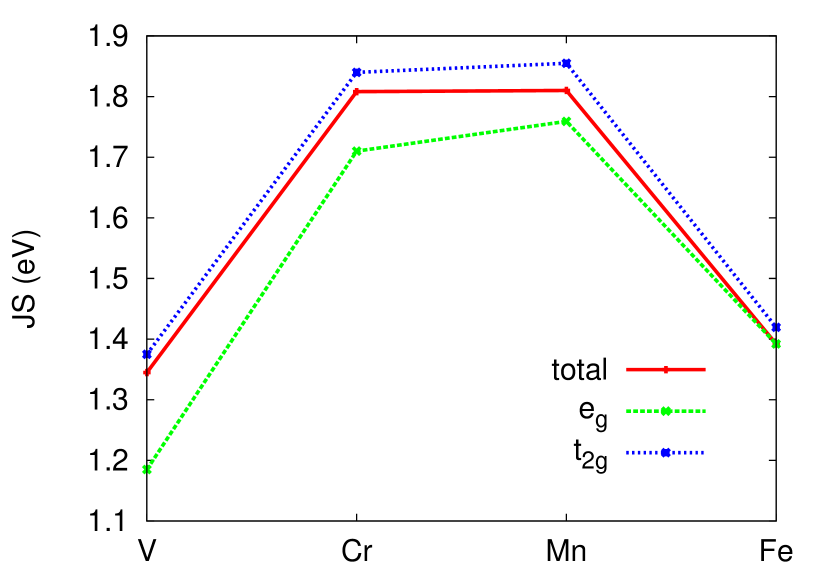
Within simplified models Yu (1965); Shiba (1968); Rusinov (1969); Balatsky et al. (2006) it has been shown that it is the energy splitting between the minority and majority levels which will determine the energy positioning of the in-gap states. For these models the impurity spin is considered as classical magnetic moment coupled to the electrons of the crystal via the exchange interaction . The resulting energies are than expressed in terms of a T-matrix scattering approach. As the eg and t2g experience slightly different splitting this will result in a clear lifting of the degeneracy between those orbitals for the in-gap states. We have summarized the corresponding exchange energies
| (18) |
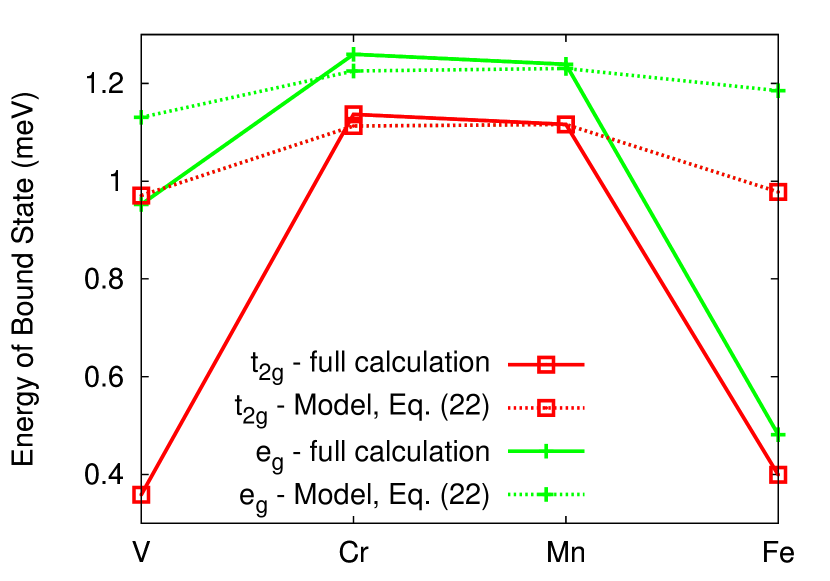
in Fig. 4. In the above definition and are the spin-up and spin-down peak positions, respectively. As expected, the trend follows the total magnetic moment being largest for Cr and Mn. Importantly, for V we find the strongest difference between the splitting in the eg and t2g states which would suggest that the corresponding in-gap states will be well separated in energy. In contrast, this is weakest for Fe as indicated by the smallest separation of the in gap states.
IV Superconducting State Analysis
Extending the analysis including superconductivity gives access to the YSR in-gap states. For each step we perform the corresponding normal state calculations first and extend it to the superconducting case in the following. In all cases we perform fully self-consistent SRA calculations based on the BdG Hamiltonian Eq. 7 to finally generate the electronic and magnetic structure for the magnetic atoms embedded in superconducting Pb. In all cases we set the interaction parameter at the impurity site to zero and keep it at the bulk value for all other sites. Saunderson et al. (2020a, b) The results are summarized in Fig. 5 for all magnetic impurities. In all four cases we find pronounced in gap states, well separated into eg and t2g states. As expected from the previous analysis the splitting between the eg and t2g is largest for V and hard to resolve for Fe. Table 1 summarizes the associated energies of the bound states. A clear correlation between Table 1 and the normal state exchange energies, summarized in Fig. 4, is evident.
Furthermore, the superconducting symmetry implies that for each in-gap state there is a minority and a majority state symmetrically placed relative to the Fermi energy, which we indicated via the in Table 1. While the energetic positions are forced to be symmetric the height of the corresponding states is determined by the normal state LDOS at the Fermi energy. As the minority state of the Fe impurity is perfectly placed at the Fermi energy (see Fig. 3) this leads to the largest in-gap peak for the minority in-gap state (see Fig. 6). Similarly for V the majority level is closest to the Fermi energy leading to the corresponding in-gap state to be significantly larger than the minority peak. In contrast, for Cr both levels have similar distance to the Fermi energy in the normal state resulting in a very similar height for the Cr in-gap states.
| Impurity atom | V | Cr | Mn | Fe |
|---|---|---|---|---|
| t2g state (meV) | ||||
| eg state (meV) |
In order to make the connection between the normal state impurity levels and the superconducting in-gap states more quantitative we follow previous models established for the YSR states Yu (1965); Shiba (1968); Rusinov (1969); Balatsky et al. (2006). For isotropic (l=0) scattering the energy can be approximated to
| (19) |
where
| (20) | |||
| (21) |
Here, is the bulk quasiparticle gap, is the density of states of Pb at the Fermi level in the normal state, and V is the non-magnetic scattering potential. Ignoring the correction from the scalar potential, , but generalizing to the case where is different for eg and t2g states, the equation reduces to
| (22) |
where stands for either eg and t2g states and is the index for the impurity V, Cr, Mn, Fe. Correspondingly, generalises to
| (23) |
As the energies depend crucially on we decided to determine this parameter by fitting Eq. 22 to the full ab initio calculations in the case of Mn. Here, we fixed to the results shown in Fig. 4. The resulting values are and . In the following we kept the same for all impurities as it should capture the properties of the nonmagnetic host Pb and calculated the in-gap states using for all the other impurities. The results in comparison to the directly extracted energies are shown in Fig. 6. While the agreement is far from perfect the trends are correctly reproduced. However, especially for V and Fe, the elements with the largest and smallest splitting between the t2g and eg states, respectively, the model fails to reproduce the quantitative results of the full calculations. This highlights the importance of the full ab initio description as the model fails to capture the quantitative details making direct comparisons to experimental findings difficult.
A further conventionally made approximation is the restriction to -orbitals only. Ruby et al. (2016); Schrieffer (1967) Given that the magnetism is dominated by the electrons and it is the magnetism which induces the in-gap states it appears natural to follow this approximation. However, in any real material all orbitals will hybridize and magnetism arising in the orbitals will ultimately induce spin-polarization in all other orbitals as well. Within our calculations this is particularly visible for Cr and Mn for which additional YSR peaks are visible near the Pb coherence peak (see Fig. 5) at energies just above . In this particular case it turns out they are orbital contributions. This finding highlights the fact that while in a first approximation it appears natural to reduce the discussion to the d orbitals, in details especially near the edge of the superconducting gap other orbitals might play a dominant role. Furthermore, determining which impurity has a large response from other orbitals will not be easy to predict without all-electron calculations.
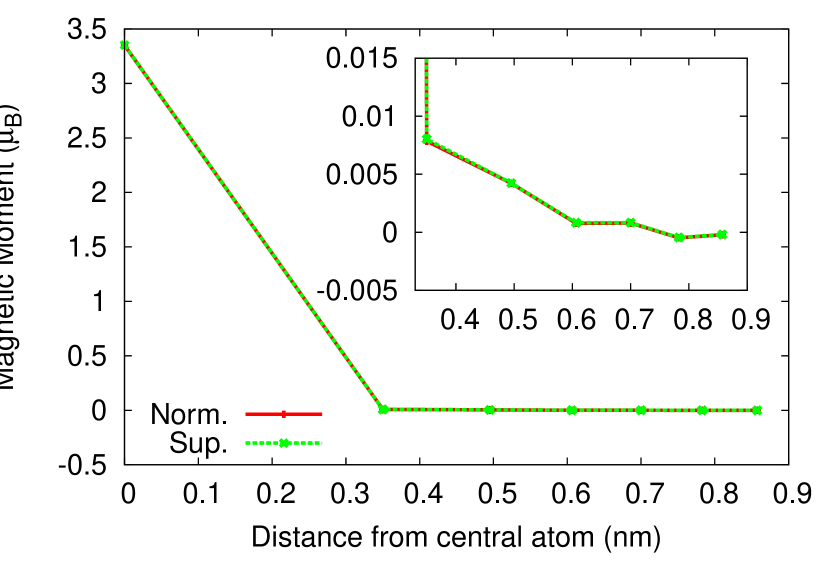
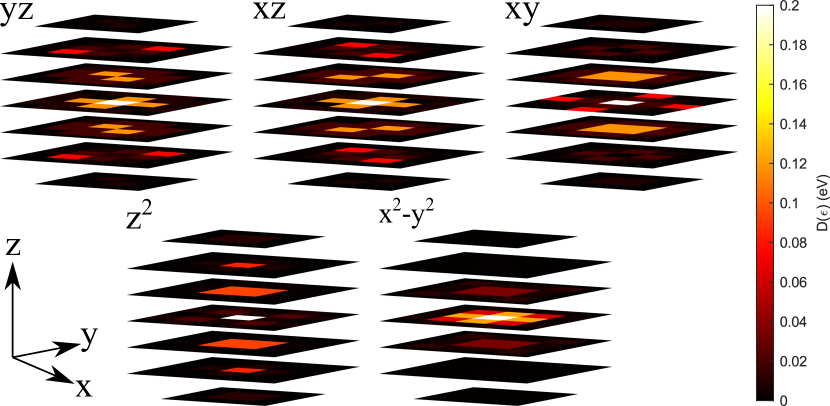
Finally, we would like to analyse the spatial dependence of the in gap states. In Fig. 7 the radial decay of the magnetic moment is shown for the case of a V impurity. It drops quickly to almost zero in the first shell already and oscillates weakly up to the 6th shell. For the total magnetic moment, there is no visible difference between the normal and the superconducting state in the spatial decay. In order to visualize the behaviour of the in-gap states we present the atom-resolved charge densities at the energy associated with the in-gap state in Fig. 8. In the case of the V impurities these energies are for the eg states meV and for the t2g states meV. As discussed earlier, the cubic lattice leads to a splitting into eg and t2g states but does not lift the degeneracy of the and orbitals within the eg-level nor for the , and orbitals within the t2g level. For this reason any visualisation for the two levels would preserve the cubic symmetry. Resolving all orbitals separately (see Fig. 8) highlights the power of full ab initio calculations. While the spatial resolution is limited to atomic sites the orbital characters are nevertheless clearly visible. The and reduce to a two-fold rotational symmetry around the z-axis rotated by degrees relative to each other. The other three orbitals show the corresponding four-fold rotational symmetry around the z-axis. Furthermore, the larger spatial extension of the orbital in the direction is clearly visible. Finally, as the the and orbitals are rotated by degrees relative to each other this results in the pointing along the nearest neighbour bonds in the plane of the impurity atom. In contrast, the orbitals show the largest contribution out of plane as there the nearest neighbours are in direction of the orbital lobes. At a surface the degeneracy of these orbitals would be lifted and the orbital induced angular dependence of the density can be resolved with STM experiments. Ruby et al. (2016); Choi et al. (2017); Ruby et al. (2018); Küster et al. (2021)
V Summary
We have extended previous work Saunderson et al. (2020a, b) of implementing the BdG equations into the KKR method with substitutional impurities and collinear magnetism. As a model system we consider 3d impurities in a Pb three dimensional crystal inspired by experiments performed by Ruby et al Ruby et al. (2016) investigating magnetism induced in-gap states at a superconducting surface. As predicted by simple models, the position and height of the induced in-gap states is strongly related to the normal state exchange splitting as observed for the magnetic impurities. However, while the over all correlation is clearly visible in the details the simplified model fails to make quantitatively correct predictions for the varying 3d impurity atoms. The most significant limitations of the model are the restriction to isotropic scattering and ignoring any hybridization of the d-electrons to other orbitals. Naturally, these models can be extended to more complex scenarios however rendering them more intractable as the parameter space increases. Within our real space superconducting DFT descriptions we are able to capture all orbital induced variations in their full complexity.
Beyond the consideration of the d-orbitals we established clear signatures of in-gap states induced via s-d hybridization. While these states are in close vicinity to the superconducting coherence peaks and as such difficult to observe in experiment, their existence highlights the complexity of any quantitative interpretation of experimental observation. Within our calculations these in-gap states were particular pronounced for Cr and Mn but hardly visible for V and Fe. This again points to the importance of a correct all-electron description of the underlying band structure. This is especially relevant as similar YSR resonances have already been investigated Senkpiel et al. (2019).
Finally, we investigate the radial decay of the magnetism and in-gap states inside the superconducting crystal. Interestingly, the decay of the magnetic moment is largely unaffected by the superconducting state. This is related to the fact that even in the normal state the magnetic moment decays quickly for the nearest neighbour atoms already. Nevertheless, by investigating the decay of the in-gap states for each orbital separately it was clearly possible to resolve the distinct orbital symmetries. This final step will enable us to make direct contact to STM experiments Ruby et al. (2016) where the breaking of further spatial symmetries at the surface of the material will lift the degeneracies among the eg and t2g states.
In summary, we have performed fully self consistent calculations for magnetic impurities within the superconducting state using the BdG equations implemented within the KKR formalism. We have discussed qualitatively and quantitatively the formation of YSR resonances associated with the magnetic moment from the eg and t2g orbitals according to the cubic symmetry. Furthermore, we have established the existence of YSR resonances, highlighting the need for an all-electron description for even a qualitatively correct description of real materials. This is further strengthened by the fact that the position of the in-gap states is at best described qualitatively with simple models even for the dominant eg and t2g resonances. With the introduction of more impurities we could investigate the hybridisation of the YSR resonances resulting in the formation of YSR bands. Zhang et al. (2020); Ruby et al. (2017) Similarly, the use of the KKR framework will enable us to extend the method to concentrated alloys exploiting the coherent potential approximation (CPA) as outlined previously. Martin et al. (1999); Moradian et al. (2000a, b) Finally, the incorporation of the fully relativistic BdG equations Csire et al. (2018a) including spin-orbit coupling will, in a next step, enable us to investigate the existence of Majorana zero modes Nadj-Perge et al. (2013); Röntynen and Ojanen (2015); Kim et al. (2018); Schneider et al. (2020) at the surface of conventional superconductors.
VI Acknowledgements
This work was carried out using the computational facilities of the Advanced Computing Research Centre, University of Bristol - http://www.bris.ac.uk/acrc/. The above work was supported by the Centre for Doctoral Training in Condensed Matter Physics, funded by EPSRC Grant No. EP/L015544/1. G.C. gratefully acknowledges support from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie Grant Agreement No. 754510. This work was supported by Spanish MINECO (the Severo Ochoa Centers of Excellence Program under Grant No. SEV- 2017-0706), Spanish MICIU, AEI and EU FEDER (Grant No. PGC2018-096955-B-C43), and Generalitat de Catalunya (Grant No. 2017SGR1506 and the CERCA Program). The work was also supported by the European Union MaX Center of Excellence (EU-H2020 Grant No. 824143). M.G. thanks the visiting professorship program of the Centre for Dynamics and Topology ad Johannes Gutenberg-University Mainz. The authors would like to thank M.-H. Wu and R. Gupta for many helpful discussions.
References
- Abrikosov and Gor’ Kov (1959) A. A. Abrikosov and L. P. Gor’ Kov, Sov. Phys. JETP 8, 220 (1959).
- Phillips (1963) J. C. Phillips, Phys. Rev. Lett. 10, 96 (1963).
- Yu (1965) L. Yu, Acta Phys. Sin. 21, 75 (1965).
- Shiba (1968) H. Shiba, Prog. Theor. Phys. 40, 435 (1968).
- Rusinov (1969) A. I. Rusinov, JETP Lett. 9, 85 (1969).
- Ji et al. (2008) S. H. Ji, T. Zhang, Y. S. Fu, X. Chen, X. C. Ma, J. Li, W. H. Duan, J. F. Jia, and Q. K. Xue, Phys. Rev. Lett. 100, 226801 (2008).
- Hatter et al. (2015) N. Hatter, B. W. Heinrich, M. Ruby, J. I. Pascual, and K. J. Franke, Nat. Commun. 6, 1 (2015).
- Ruby et al. (2016) M. Ruby, Y. Peng, F. Von Oppen, B. W. Heinrich, and K. J. Franke, Phys. Rev. Lett. 117, 186801 (2016).
- Choi et al. (2017) D. J. Choi, C. Rubio-Verdú, J. De Bruijckere, M. M. Ugeda, N. Lorente, and J. I. Pascual, Nat. Commun. 8, 15175 (2017).
- Liebhaber et al. (2020) E. Liebhaber, S. Acero González, R. Baba, G. Reecht, B. W. Heinrich, S. Rohlf, K. Rossnagel, F. Von Oppen, and K. J. Franke, Nano Lett. 20, 339 (2020), arXiv:1903.09663 .
- Senkpiel et al. (2019) J. Senkpiel, C. Rubio-Verdú, M. Etzkorn, R. Drost, L. M. Schoop, S. Dambach, C. Padurariu, B. Kubala, J. Ankerhold, C. R. Ast, and K. Kern, Phys. Rev. B 100, 014502 (2019), arXiv:1803.08726 .
- Choi et al. (2018) D. J. Choi, C. G. Fernández, E. Herrera, C. Rubio-Verdú, M. M. Ugeda, I. Guillamón, H. Suderow, J. I. Pascual, and N. Lorente, Phys. Rev. Lett. 120, 167001 (2018).
- Saunderson et al. (2020a) T. G. Saunderson, J. F. Annett, B. Újfalussy, G. Csire, and M. Gradhand, Phys. Rev. B 101, 064510 (2020a).
- Saunderson et al. (2020b) T. G. Saunderson, Z. Györgypál, J. F. Annett, G. Csire, B. Újfalussy, and M. Gradhand, Phys. Rev. B 102, 245106 (2020b).
- Oliveira et al. (1988) L. N. Oliveira, E. K. U. Gross, and W. Kohn, Phys. Rev. Lett. 60, 2430 (1988).
- Dreizler and Gross (1990) R. M. Dreizler and E. K. U. Gross, Density Functional Theory (Springer, Berlin, 1990).
- Suvasani et al. (1993) M. B. Suvasani, W. M. Temmerman, and B. Györffy, Phys. Rev. B 48, 1202 (1993).
- Csire et al. (2015) G. Csire, B. Újfalussy, J. Cserti, and B. Györffy, Phys. Rev. B 91, 165142 (2015).
- Csire et al. (2018a) G. Csire, A. Deák, B. Nyári, H. Ebert, J. F. Annett, and B. Újfalussy, Phys. Rev. B 97, 024514 (2018a).
- Csire et al. (2018b) G. Csire, B. Újfalussy, and J. F. Annett, Eur. Phys. J. B 91, 217 (2018b).
- Ghosh et al. (2020) S. K. Ghosh, G. Csire, P. Whittlesea, J. F. Annett, M. Gradhand, B. Újfalussy, and J. Quintanilla, Phys. Rev. B 101, 100506 (2020).
- Ruby et al. (2015) M. Ruby, B. W. Heinrich, J. I. Pascual, and K. J. Franke, Phys. Rev. Lett. 114, 157001 (2015).
- Dresselhaus et al. (2007) M. S. Dresselhaus, G. Dresselhaus, and A. Jorio, Group Theory: Application to the Physics of Condensed Matter (Springer, 2007).
- Balatsky et al. (2006) A. V. Balatsky, I. Vekhter, and J. X. Zhu, Rev. Mod. Phys. 78, 373 (2006).
- Schrieffer (1967) J. R. Schrieffer, J. Appl. Phys. 38, 1143 (1967).
- Ruby et al. (2018) M. Ruby, B. W. Heinrich, Y. Peng, F. Von Oppen, and K. J. Franke, Phys. Rev. Lett. 120, 156803 (2018).
- Küster et al. (2021) F. Küster, A. M. Montero, S. Guimarāes, Filipe S. M.and Brinker, S. Lounis, S. S. P. Parkin, and P. Sessi, Nature Communications 12, 1108 (2021).
- Zhang et al. (2020) G. Zhang, T. Samuely, N. Iwahara, , J. Kačmarčík, C. Wang, P. W. May, J. K. Jochum, O. Onufriienko, P. Szabó, S. Zhou, P. Samuely, V. V. Moshchalkov, L. F. Chibotaru, and H.-G. Rubahn, Science Advances 6, eaaz2536 (2020).
- Ruby et al. (2017) M. Ruby, B. W. Heinrich, Y. Peng, F. von Oppen, and K. J. Franke, Nano Letters 17, 4473 (2017), pMID: 28640633, https://doi.org/10.1021/acs.nanolett.7b01728 .
- Martin et al. (1999) A. M. Martin, G. Litak, B. L. Györffy, J. F. Annett, and K. I. Wysokiński, Phys. Rev. B 60, 7523 (1999).
- Moradian et al. (2000a) R. Moradian, J. F. Annett, and B. L. Györffy, Phys. Rev. B 62, 3508 (2000a).
- Moradian et al. (2000b) R. Moradian, J. F. Annett, B. L. Györffy, and G. Litak, Phys. Rev. B 63, 024501 (2000b).
- Nadj-Perge et al. (2013) S. Nadj-Perge, I. K. Drozdov, B. A. Bernevig, and A. Yazdani, Phys. Rev. B 88, 020407 (2013).
- Röntynen and Ojanen (2015) J. Röntynen and T. Ojanen, Phys. Rev. Lett. 114, 236803 (2015).
- Kim et al. (2018) H. Kim, A. Palacio-Morales, T. Posske, L. Rózsa, K. Palotás, L. Szunyogh, M. Thorwart, and R. Wiesendanger, Sci. Adv. 4, 1 (2018).
- Schneider et al. (2020) L. Schneider, S. Brinker, M. Steinbrecher, J. Hermenau, T. Posske, M. d. S. Dias, S. Lounis, R. Wiesendanger, and J. Wiebe, Nature Communications 11, 4707 (2020).