Functional Uniform Priors for Nonlinear Modelling
Abstract
This paper considers the topic of finding prior distributions when a major component of the statistical model depends on a nonlinear function. Using results on how to construct uniform distributions in general metric spaces, we propose a prior distribution that is uniform in the space of functional shapes of the underlying nonlinear function and then back-transform to obtain a prior distribution for the original model parameters. The primary application considered in this article is nonlinear regression, but the idea might be of interest beyond this case. For nonlinear regression the so constructed priors have the advantage that they are parametrization invariant and do not violate the likelihood principle, as opposed to uniform distributions on the parameters or the Jeffrey’s prior, respectively. The utility of the proposed priors is demonstrated in the context of nonlinear regression modelling in clinical dose-finding trials, through a real data example and simulation. In addition the proposed priors are used for calculation of an optimal Bayesian design.
1 Introduction
Mathematical models of the real world are typically nonlinear, examples in medical or biological applications can be found for instance in Lindsey (2001) or Jones et al. (2010). Setting up prior distributions in a statistical analysis of nonlinear models, however often remains a challenge. If external, numerical or non-numerical information exists, one can try to quantify it into a probability distribution, see for example the works of O’Hagan et al. (2006), Bornkamp and Ickstadt (2009), and Neuenschwander et al. (2010). The classical approach in the absence of substantive information is Jeffreys prior distribution (or variants), given by , where is the parameter, and the Fisher information matrix of the underlying statistical model. See Kass and Wasserman (1996), Ghosh et al. (2006, ch. 5) or Berger et al. (2009) for this approach and generalizations. A serious drawback is the fact that this prior can depend on observed covariates. In the case of nonlinear regression analysis, the prior depends on the design points and relative allocations to these points and thus violates the likelihood principle. Apart from the foundational issues this raises (see, e.g., O’Hagan and Forster (2004, ch. 3)) it also has undesirable practical consequences. For Bayesian optimal design calculations in nonlinear regression models, for example, Jeffreys prior cannot be used, because it depends on the design points, which is what we want to calculate in the optimal design problem. In the context of adaptive dose-finding clinical trials, patients are allocated dynamically to the doses available (see the works of Müller et al. (2006) or Dragalin et al. (2010)) so that the sequential analysis of the data will differ from the analysis combining all data, when using Jeffreys rule. In summary the main issue with the Jeffreys prior distribution is that one cannot state it before data collection, which is crucial in some applications. Surprisingly few proposals have been made to overcome this situation. In current practice often uniform distributions for on a reasonable compact subset of the parameter space are used. This approach is however extremely sensitive to the chosen parametrization (which might be more or less arbitrary) and can be much more informative than one would expect intuitively.
To illustrate the point, we will use a simple example. Suppose one would like to analyse data using the exponential model , here with , which could be the mean function in a regression analysis. Assume that no historical data or practical experiences related to the problem are available.
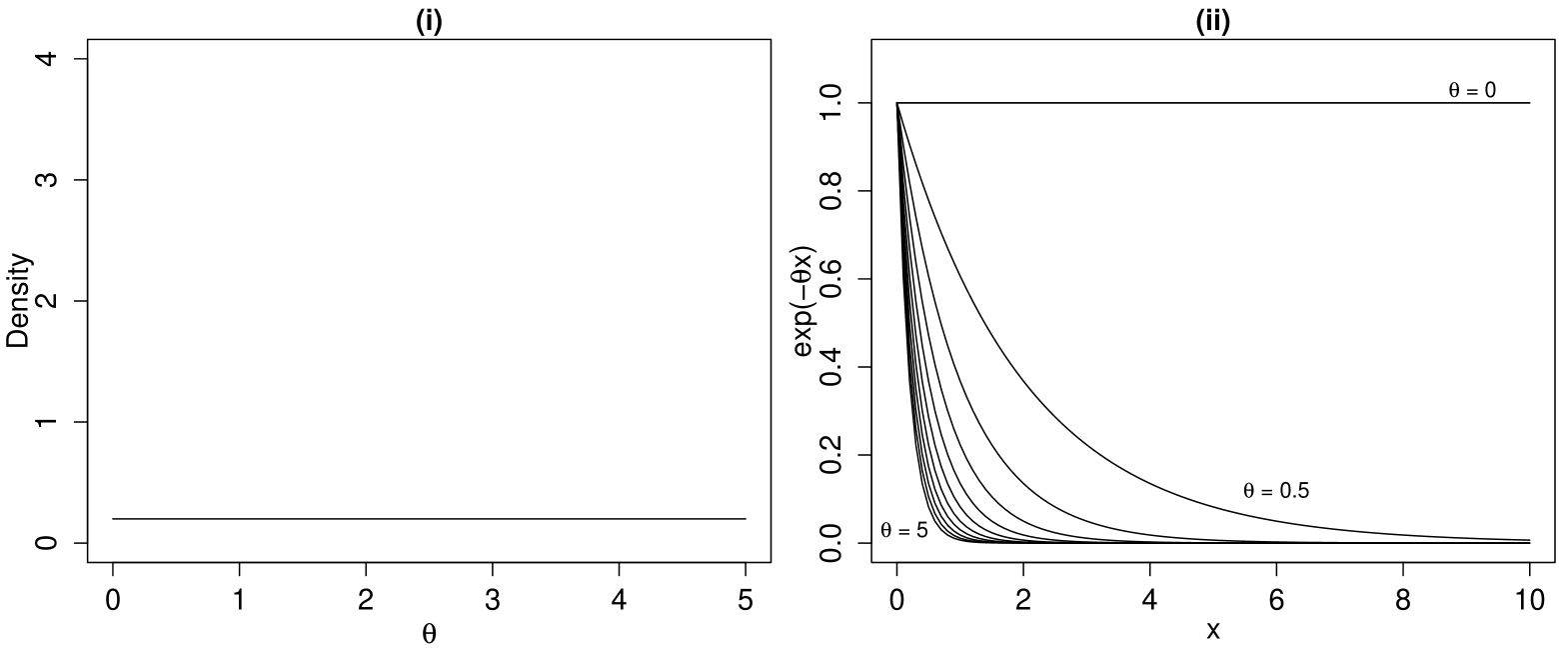
A first pragmatic approach in this situation is to use a uniform distribution on values leading to a reasonable shape coverage of the underlying regression function , for example the interval covers the underlying shapes almost entirely. The consequences of assuming a uniform prior on can be observed in Figure 1 (ii). While the prior is uniform in space, it places most of its prior probability mass on the functional shapes that decrease quickly towards zero, and we end up with a very informative prior distribution in the space of functional shapes. This is highly undesirable when limited prior information regarding the shape is available. In addition it depends crucially on the upper bound selected for , and a uniform distribution in an alternative parameterization would lead to entirely different prior in the space of shapes. One way to overcome these problems is to use a distribution that is uniform in the space of functional shapes of the underlying nonlinear function. This will be uninformative from the functional viewpoint and will not depend on the selected parameterization.
In finite dimensional situations it is a standard approach to use distributions that are uniform in an interpretable parameter transformation, when it is difficult to use the classical default prior distributions. In the context of Dirichlet process mixture modelling, one can use a uniform distribution on the probability that two observations cluster into one group and then transfer this into a prior distribution for the precision parameter of the Dirichlet process. In the challenging problem of assigning a prior distribution for variance parameters in hierarchical models, Daniels (1999) assumes a uniform distribution on the shrinkage coefficient and then transfers this to a prior distribution for the variance parameter. In these cases the standard change of variables theorem can be used to derive the necessary uniform distributions. When we want to impose a uniform distribution in the space of functional shapes of an underlying regression function, however, it is not entirely obvious how to construct a uniform distribution. In the next section we will review a methodology that allows to construct uniform distributions on general metric spaces. In Section 2.2 we will adapt this to the nonlinear models that we consider in this article. Finally in Section 3 we test the priors for nonlinear regression on a data set from a dose-finding trial, a simulation study and an optimal design problem.
2 Methodology
2.1 General Approach
Suppose one would like to find a prior distribution for a parameter in a compact subspace . The approach proposed in this paper is to map the parameter from into another compact metric space , with metric , using a differentiable bijective function , so that . The metric should ideally define a reasonable measure of closeness and distance between the parameters, and its choice will of course be model and application dependent. In the exponential regression example, for instance, it seems adequate to measure the distance between two parameter values and by a distance between the resulting functions and , rather than the Euclidean distance between the plain parameter values. In this metric space , one then imposes a uniform distribution, reflecting the appropriate notion of distance of the metric space , and transforms this distribution back to the parameter scale.
The construction of a uniform distribution in general metric spaces has been described by Dembski (1990), using the notion of packing numbers. Ghosal et al. (1997) apply this result for two particular Bayesian applications (derivation of Jeffreys prior for parametric problems and nonparametric density estimation). In the following we review and adapt this theory to our situation. Some basic mathematical notions are needed to present the ideas: Define an -net as a set , so that for all holds , and the addition of any point to destroys this property. An -lattice is the -net with maximum possible cardinality. Dembski defines the uniform distribution on as the limit of a discrete uniform distribution on an -lattice on , when .
Definition 1
The uniform distribution on defined as
for and is the discrete uniform distribution supported on the points in , i.e. , with the cardinality of .
Loosely speaking the uniform distribution is hence defined as the limit of a discrete uniform distribution on an equally spaced grid, where the notion of “equally spaced” is determined by the distance metric underlying . Even though this definition is intuitive it is not constructive. Apart from special cases, generating an -lattice is computationally difficult in a general metric space; calculating the limit of -lattices even more so. In addition it is unclear, whether there is just one limit distribution all -lattices would converge to. To overcome these problems Dembski (1990) uses the closely related notion of packing numbers. The packing number of a subset in the metric is defined as the cardinality of an -lattice on , and packing numbers are known for a number of metric spaces. An -pseudo-probability can then be defined as . It is straightforward to see that and that , but packing numbers are sub-additive and hence is not a probability measure. However for disjoint sets and with minimum distance additivity holds, i.e. . Dembski (1990) then shows that whenever exists for any , then the limit distribution is the unique uniform distribution on (see Dembski (1990) or Ghosal et al. (1997) for details). As packing numbers are known for a number of metric spaces, this result provides a constructive way for building uniform distributions, without the need for explicitly constructing -lattices.
Subsequently we consider the practically important case of a finite number of parameters and assume that the metric of , in terms of can be approximated by a local quadratic approximation of the form
| (1) |
where are constants and . Equation (1) implies that can locally be approximated by a Euclidean metric. This is not a very strong condition, for a sufficiently often differentiable metric one can make use of a Taylor expansion of second order of and apply the square root to obtain (1). The following theorem calculates the distribution induced on by imposing a uniform distribution in , when assumption (1) holds. The proof is only a slight adaption of earlier results by Ghosal et al. (1997), see Appendix A.
Theorem 1
For a metric space and a bijective function , fulfilling (1), where is a symmetric matrix with finite strictly positive eigenvalues and continuous as a function of , for converges to
The density of the uniform probability distribution is hence given by:
We note that the last result can be obtained as well by using considerations based on Riemannian manifolds, in which case (1) would be the Riemannian metric: For example Pennec (2006) explicitly considers uniform distributions on Riemannian manifolds and obtains the same result. We concentrated on Dembski’s derivation as it seems both more general and intuitive.
It is important to note that the so defined distribution is independent of the parametrization. This is intuitively clear, as the space , where the uniform distribution is imposed, is fixed, no matter, which parametrization is used. We illustrate this invariance property for the special case of a Taylor approximation in the Theorem below; for a proof see Appendix B.
Theorem 2
Assume with , where evaluated at , which leads to a prior .
When calculating the uniform distribution associated to the
transformed parameter , with a bijective twice
differentiable transformation, one obtains , where
is the inverse of and is the Jacobian
matrix associated with , which is the same result as applying the
change of variables theorem to .
A technical restriction of the theory described in this section is the concentration on compact metric spaces . However, it is possible to extend this based on taking limits of a sequence of growing compact spaces, see the works of Dembski (1990) and Ghosal et al. (1997) for details. Note that the resulting limiting density does not need to be integrable.
2.1.1 Examples
Non-functional uniform priors
While the approach outlined in Section 2.1 is developed for general metric spaces, it coincides with standard results about change of variables, when the metric space is a compact subset of as well. Suppose one would like to use a uniform distribution for with a bijective, continuously differentiable function and then back-transform to scale. Using the standard change of variables theorem one obtains: , where is the Jacobian matrix of the transformation . Framed in the approach of the last section, the metric space is a compact subset of with the Euclidean metric in the transformed space . A local linear approximation to is with remainder . Hence, one obtains . Applying Theorem 1 one ends up with the desired distribution .
Jeffreys Prior
Another special case of this general approach is Jeffreys prior itself. Jeffreys (1961) described his rule by noting that (1) approximates the empirical Hellinger distance (as well as the empirical Kullback-Leibler divergence) between the residual distributions in a statistical model, when is the Fisher information matrix. In this situation the parameters of a statistical model are mapped into the space of residual densities and this space is used to define the notion of distance between the ’s. Applying the machinery from the last section then leads to a uniform distribution on the space of residual densities. This interpretation of Jeffreys rule is rare, but has been noted among others for example by Kass and Wasserman (1996, ch. 3.6). Ghosal et al. (1997) and Balasubramanian (1997) explicitly derive Jeffreys rule from these principles. From this viewpoint Jeffreys prior is hence useful as a universal “default” prior, because it gives equal weights to all possible residual densities underlying a statistical model. However, the used metric can depend, for example, on values of covariates, which is undesirable in the nonlinear regression application, as discussed in the introduction.
Triangular Distribution
In this example Definition 1 is directly used to numerically approximate a uniform distribution on a metric space. This is can be done in the case , where the construction of lattices is easily possible numerically.
The triangular distribution, with density
| (2) |
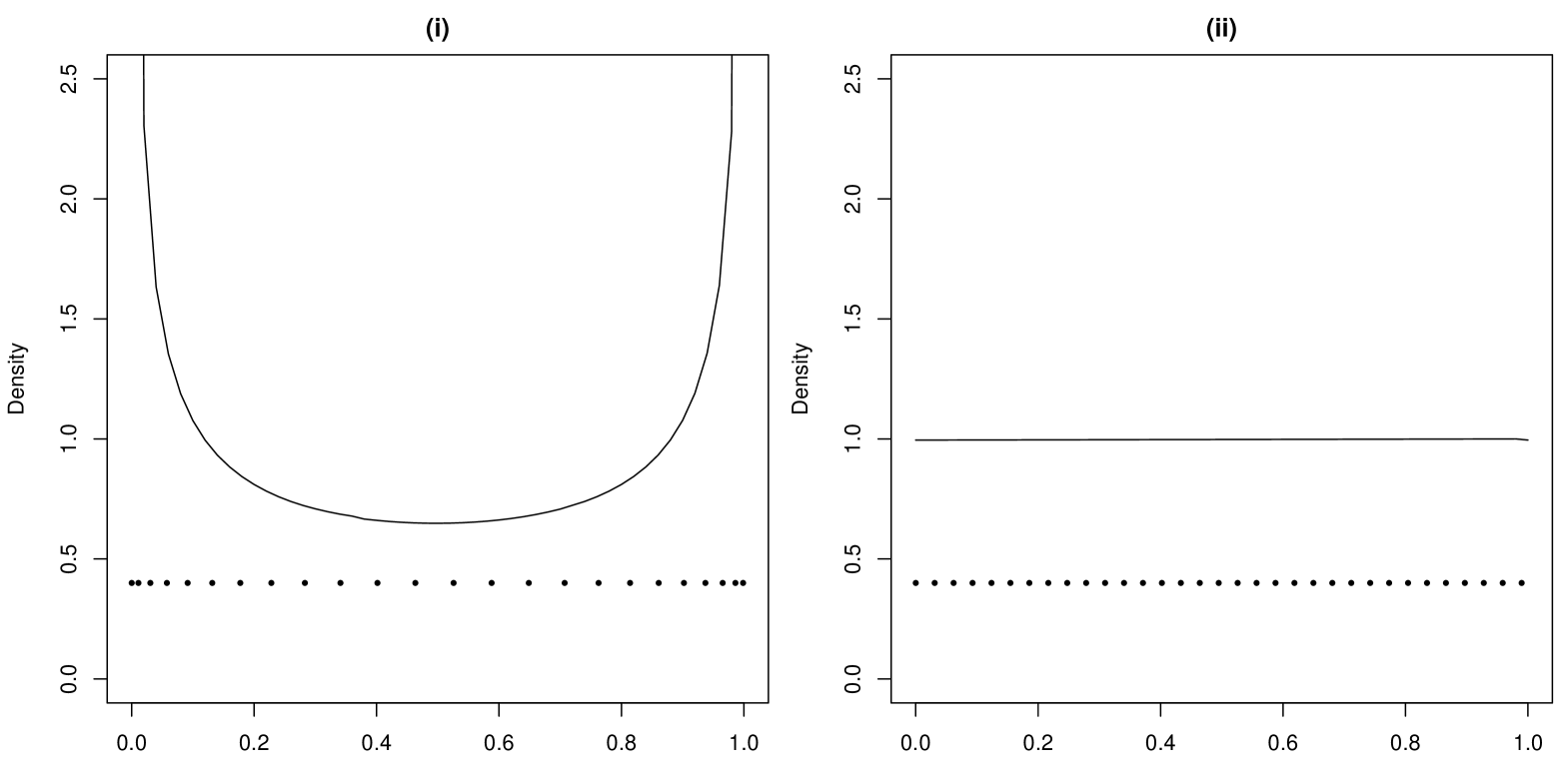
for is a simple, yet versatile distribution, for which the Jeffreys prior does not exist (Berger et al., 2009). One possible metric space where to impose the uniform distribution is the space of triangular densities or triangular distribution functions parametrized by . Several metrics might be used, we will consider the Hellinger metric and the Kolmogorov metric . Numerically calculating the corresponding lattices one obtains the distributions displayed in Figure 2. Interestingly one can observe that the calculated uniform distribution in the Hellinger metric space is equal to a distribution (as the reference prior in Berger et al. (2009)), while the calculated functional uniform distribution in the Kolmogorov metric results in a uniform distribution on .
2.2 Nonlinear Regression
The implicit assumption when employing a nonlinear regression function , is that for one the shape of the function will adequately describe reality. It is usually unclear, however, which of these shapes is the right one. A uniform distribution on the functional shapes hence seems to be a reasonable prior. A suited metric space is consequently the space of functions , with , with compact and metric for example given by the distance . By a first order Taylor expansion one obtains , where is the row vector of first partial derivatives. This results in an approximation of form . Integrating this with respect to and taking the square root, leads to an approximation of of form where . Consequently, from Theorem 1 the functional uniform distribution for equals In the special case of a linear model , the functional uniform distribution collapses to a constant prior distribution, which is the uniform distribution on for compact and improper, when extending to non-compact .
We now revisit the exponential regression example from the introduction. In this case one obtains , calculating and applying the square root, one obtains , normalizing this leads to the prior displayed in Figure 3 (i). On the scale the shape based functional uniform density hence leads to a rather non-uniform distribution. In Figure 3 (ii) one can observe that the probability mass is distributed uniformly over the different shapes, as desired.
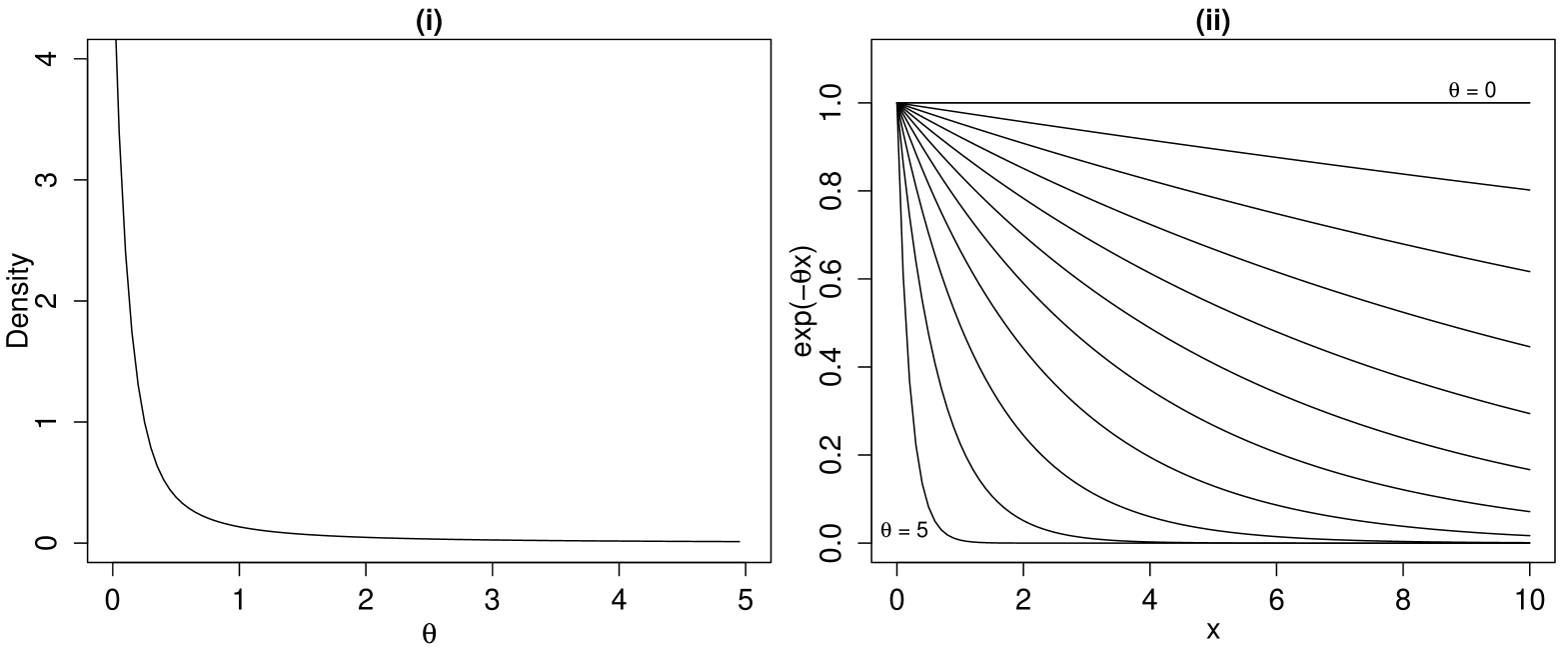
An advantage of the functional uniform prior over the uniform prior is that it is independent of the choice of parameterization and not particularly sensitive to the potential choice of the bounds, provided all major shapes of the underlying function are covered. In Figure 3 (i) one can see that the density is already rather small at as most of the underlying functional shapes are already covered. In fact in this example one can extend the functional uniform distribution from the compact interval to a proper distribution on .
Although the choice of the metric for seems reasonable in a variety of situations, other choices are possible. One could for example use a weighted version of the distance, when interest is in particular regions of the design space . In fact Jeffreys prior can be identified as a special case, when the assumed residual model is given by a homoscedastic normal distribution. In this situation the empirical measure on the design points is used as a weighting measure. The Jeffreys prior has also been mentioned by Bates and Watts (1988, p. 217), as a prior that is uniform on the response surfaces, but the possibility of an alternative weighting measures has not been considered.
One potential obstacle in the use of the proposed functional uniform prior is the fact that it can be computationally challenging to calculate. In some of the situations it might be possible to calculate analytically in others one might need to use numerical integration to approximate the underlying integrals. However, it needs to be noted that the prior only needs to be calculated once, as the prior is independent of the observed data (it only depends on the design region and on potential parameter bounds), and can then be approximated for example in terms of more commonly used distributions. This approximation can then be reused in different modelling situations.
3 Applications
In this section, we will evaluate the proposed functional uniform priors for nonlinear regression. One application of nonlinear regression is in the context of pharmaceutical dose-finding trials. A challenge in these trials is that the variability in the response is usually large and the number of used doses fairly small, so that the underlying inference problem is challenging, despite an often seemingly large sample size. The priors will first be tested in a real example, then the frequentist operating characteristics of the proposed functional uniform priors are assessed more formally in a simulation study for a binary endpoint. In the last example we will use the functional uniform distribution for calculation of a Bayesian optimal design in the exponential regression example.
3.1 Irritable Bowel Syndrome Dose-Response Study
Here the IBScovars data set taken from the DoseFinding package will be used Bornkamp et al. (2010). The data were part of a dose ranging trial on a compound for the treatment of the irritable bowel syndrome with four active doses 1, 2, 3, 4 equally distributed in the dose range and placebo. The primary endpoint was a baseline adjusted abdominal pain score with larger values corresponding to a better treatment effect. In total 369 patients completed the study, with nearly balanced allocation across the doses. Assume a normal distribution is used to model the residual error and that the hyperbolic Emax model was chosen to describe the dose-response relationship. The parameters and determine the placebo mean and the asymptotic maximum effect, while the parameter determines the dose that gives 50 percent of the asymptotic maximum effect, so that it determines the steepness of the curve. In clinical practice vague prior information typically exists for and , but for illustration here we use improper constant priors for these two parameters and a prior proportional to for . For the nonlinear parameter we will use a uniform prior and the functional uniform prior distribution. When using a uniform distribution for it is necessary to assume bounds, as otherwise an improper posterior distribution may arise. We will use the bounds here, the selection of the boundaries is based on the fact that practically all of the shapes of the underlying model are covered taking into account that the dose range is . For comparability for the functional uniform prior the same bounds were used, although one can extend it to an integrable density on . The functional uniform prior will be used based on the function space defined by . Performing the calculations described in Section 2.2 one obtains , calculating the integral and applying the square root leads to . Similar to the exponential regression example in the introduction, a uniform distribution on space induces an informative distribution in the space of functional shapes. Shapes corresponding to larger values of (say ) correspond to almost linear shapes, while only very small values of lead to more pronounced concave shapes. A uniform prior on hence induces a prior that favors linear shapes over steeply increasing model shapes.
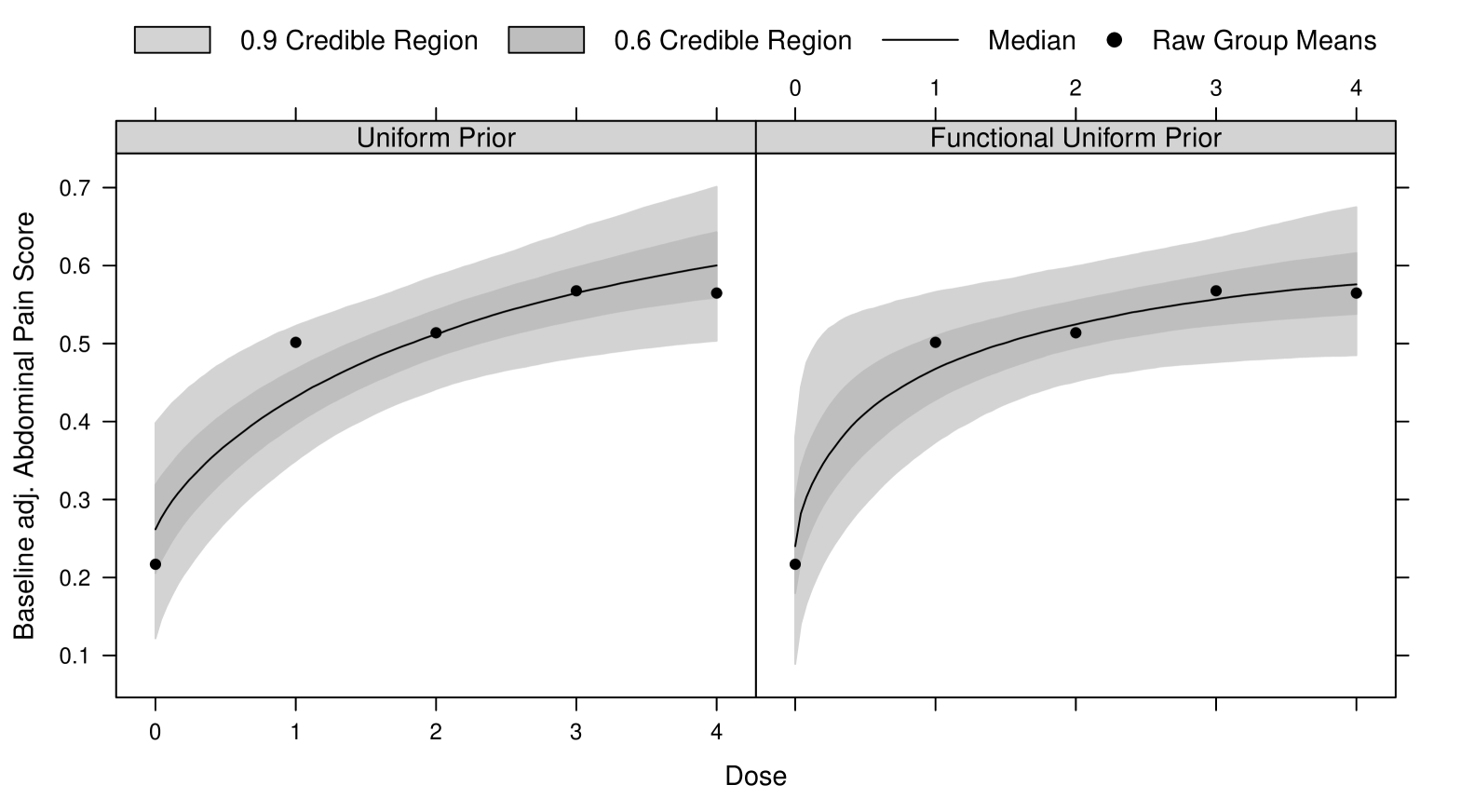
We used importance sampling resampling based on a proposal distribution generated by the iterated Laplace approximation to implement the model (see, Bornkamp (2011)). In Figure 4 one can observe the posterior uncertainty intervals under the two prior distributions. As is visible, the bias towards linear shapes, when using a uniform distribution for pertains in the posterior distribution. This happens despite the rather large sample size, and despite the fact that the response at the doses 0, 4 and particularly at dose 1 are not very well fitted by a linear shape. So the posterior seems to be rather sensitive to the prior uniform distribution. The posterior based on the shape based functional uniform prior, in contrast, fits the data better at all doses, and seems to provide a more realistic measure of uncertainty for the dose-response curve, particularly for .
3.2 Simulations
One might expect that the functional uniform prior distribution works acceptable no matter which functional shape is the true one. To investigate this in more detail and to compare this prior to other prior distributions in terms of their frequentist performance, simulation studies have been conducted. Here we report results from simulations in the context of binary nonlinear regression.
For simulation the power model will be used to model the response probability depending on . The parameters and are hence subject to and , as a probability is modelled. Note that only enters the model function non-linearly
The doses are to be used with equal allocations of 20 patients per dose. We use four scenarios in this case: in the first three cases the power model is used with and , while is equal to (Power 1), (Linear) and (Power 2). In addition we provide one scenario, where an Emax model is the truth. The Emax scenario is added to investigate the behaviour under misspecification of the model. Each simulation scenario will be repeated 1000 times.
We will compare the functional uniform prior distribution to the uniform distribution on the parameters and to the Jeffreys prior distribution. For the uniform prior distribution approach uniform prior distributions were assumed for all parameters, and the nonlinear parameter was assumed to be within to ensure integrability. The same bounds are used for the two other approaches for comparability. For the functional uniform prior approach, uniform priors are used for and , while for the functional uniform prior will be used on the function space defined by . The prior can be calculated to be . For the Jeffreys prior approach we used a prior proportional to , within the imposed parameter bounds. For analysis we used MCMC based on the HITRO algorithm, which is an MCMC sampler that combines the hit and run algorithm with the ratio of uniforms transformation. It does not need tuning and is hence well suited for a simulation study. The sampler is implemented in the Runuran package (Leydold and Hörmann, 2010), computations were performed with R (R Development Core Team, 2011). 10000 MCMC samples are used from the corresponding posterior distributions in each case, using a burnin phase of 1000 a thinning of 2.
| Prior | Model | MAE1 | MAE2 | CP | ILE |
|---|---|---|---|---|---|
| Uniform | Linear | 0.082 | 0.062 | 0.819 | 0.259 |
| Power 1 | 0.079 | 0.056 | 0.816 | 0.255 | |
| Power 2 | 0.066 | 0.067 | 0.881 | 0.220 | |
| Emax | 0.073 | 0.056 | 0.780 | 0.226 | |
| Jeffreys | Linear | 0.058 | 0.065 | 0.900 | 0.233 |
| Power 1 | 0.054 | 0.056 | 0.901 | 0.220 | |
| Power 2 | 0.056 | 0.073 | 0.895 | 0.227 | |
| Emax | 0.056 | 0.055 | 0.845 | 0.196 | |
| Func. Unif. | Linear | 0.060 | 0.060 | 0.892 | 0.240 |
| Power 1 | 0.057 | 0.053 | 0.893 | 0.226 | |
| Power 2 | 0.057 | 0.070 | 0.912 | 0.240 | |
| Emax | 0.059 | 0.054 | 0.834 | 0.203 |
In Table 1 one can observe the estimation results in terms of the mean absolute estimation error for the dose-response function, , where is the underlying true function and is either the point wise posterior median (corresponding to MAE1) or the prediction corresponding to the posterior mode for the parameters (MAE2), the posterior mode for the uniform prior is equal to the maximum likelihood estimate. The values displayed in Table 1 are the average over 1000 repetitions. In addition for each simulation the 0.9 credibility intervals at the dose-levels have been calculated. The number given in the Table is , where is the average coverage probability of the 0.9 credibility interval at dose over 1000 simulation runs. In addition the average length of the credibility intervals has been calculated as , where is the average length of the 0.9 credibility interval at dose over 1000 simulation runs. For estimation of the dose-response Jeffreys prior and the functional uniform prior improve upon the uniform prior distribution, while the Jeffreys prior and the functional uniform prior are close, with slight advantages for the Jeffreys prior. In terms of the credibility intervals the functional uniform and Jeffreys prior roughly keep their nominal level for the linear, and the power model cases, while the uniform prior probability does not. None of the priors achieves the nominal level for the Emax model, which is probably due to the fact that the Emax model is too different from the power model. Interestingly the credibility intervals of the uniform prior are larger than those of the other two priors, but lead to a smaller coverage probability.
Table 2 provides the estimation results with respect to parameter estimation. The main message here is that all priors perform roughly equal for estimation of the linear parameters and . For the nonlinear parameters, Jeffreys prior distribution and the functional uniform prior perform better than the uniform disribution.
In summary the functional uniform prior hence performs roughly equally well as the Jeffreys prior in these simulations. However, the functional uniform prior has the pragmatic and conceptual advantages that it does not depend on the observed covariates, and can thus be used for example for calculation of a Bayesian optimal design, or in sequential situations.
| Uniform Prior | Functional Uniform Prior | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario | MAE1 | MAE2 | CP | ILE | MAE1 | MAE2 | CP | ILE | |
| Sig. Emax 1 | 125 | 0.256 | 0.277 | 0.903 | 1.098 | 0.230 | 0.270 | 0.914 | 1.028 |
| Sig. Emax 2 | 0.278 | 0.283 | 0.895 | 1.144 | 0.258 | 0.278 | 0.909 | 1.089 | |
| Sig. Emax 3 | 0.243 | 0.275 | 0.902 | 1.014 | 0.251 | 0.262 | 0.898 | 1.030 | |
| Linear | 0.266 | 0.291 | 0.901 | 1.100 | 0.241 | 0.289 | 0.918 | 1.057 | |
| Quadratic | 0.272 | 0.278 | 0.880 | 1.109 | 0.242 | 0.276 | 0.898 | 1.038 | |
| Sig. Emax 1 | 250 | 0.185 | 0.214 | 0.908 | 0.818 | 0.167 | 0.209 | 0.920 | 0.768 |
| Sig. Emax 2 | 0.196 | 0.206 | 0.908 | 0.850 | 0.187 | 0.201 | 0.910 | 0.811 | |
| Sig. Emax 3 | 0.174 | 0.202 | 0.913 | 0.738 | 0.170 | 0.188 | 0.912 | 0.744 | |
| Linear | 0.200 | 0.209 | 0.891 | 0.831 | 0.189 | 0.211 | 0.900 | 0.794 | |
| Quadratic | 0.201 | 0.215 | 0.881 | 0.839 | 0.185 | 0.216 | 0.886 | 0.782 | |
3.3 Bayesian optimal design for exponential regression
In this section we will use the prior distribution for the exponential regression model derived in Section 2.2 to calculate a Bayesian optimal design. When assuming a homoscedastic normal model, the Fisher information is . Hence minimizing will lead to a design with most information. Unfortunately the expression depends on , which is of course unknown before the experiment. One way of dealing with this uncertainty are Bayesian optimal designs, where one optimizes the design criterion averaged with respect to a prior distribution: . In this situation we will use the uniform and functional uniform prior distribution (see Figures 1 and 3) both on the interval for calculation of the optimal design. Restricting the design space to and only performing the optimization up to 5 design points, one ends up with the weights on the design points , for the uniform prior, while the functional uniform prior distribution leads to a design of the form and . The design corresponding to the functional uniform prior hence spreads its allocation weights more uniformly on the design range, whereas the uniform prior results in essentially one major design point.
One way of comparing the two calculated designs is to look at the efficiency , of the calculated designs, with respect to the design that is locally optimal for the parameter value , for a range of different shapes. In Figure 5 we plot the efficiency for the different shapes on the functional shape scale.
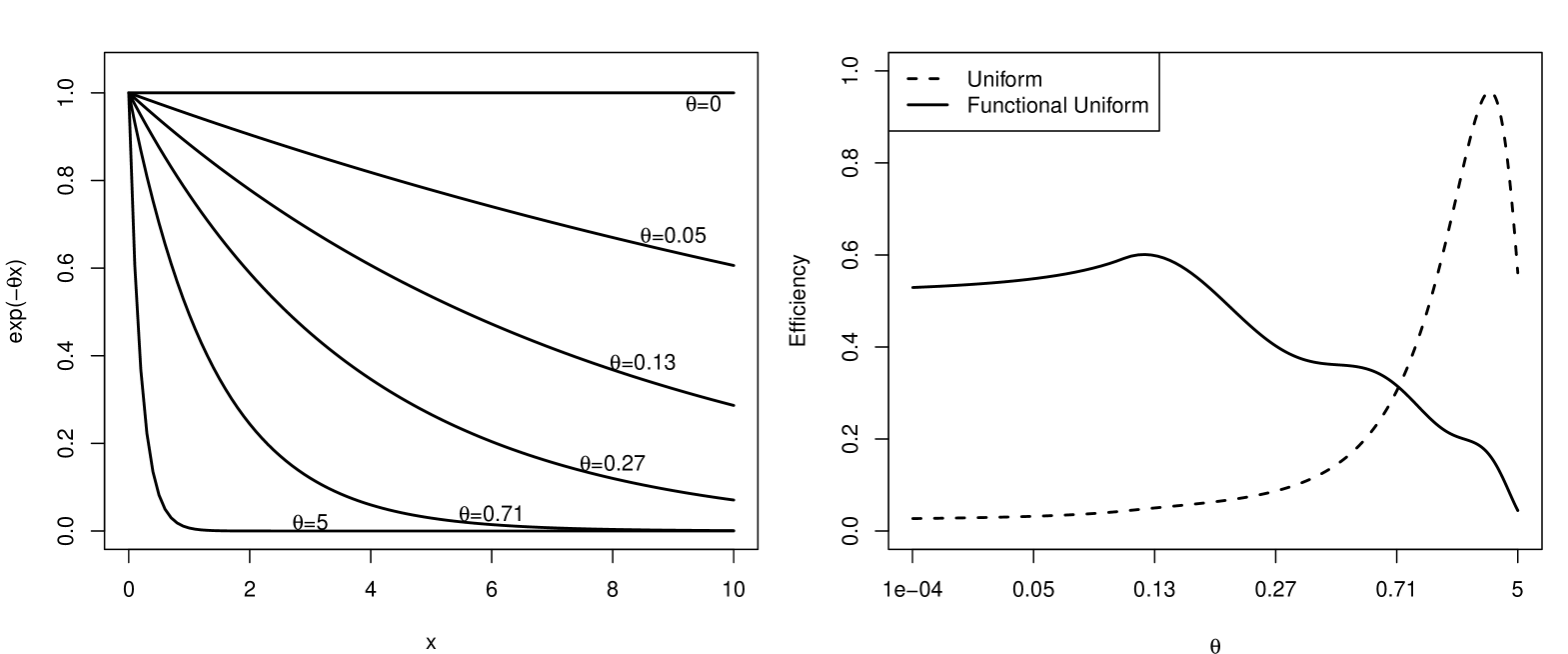
One can observe that the uniform prior design is only efficient for the sharply decreasing shapes with , but otherwise has very low efficiency. The functional uniform prior improves quite a bit over the uniform prior distribution for most of the functional shape space, and provides at least a reasonable efficiency for most shapes.
4 Conclusions
A main motivation for this work is the practical limitation of the classical Jeffreys prior that it cannot be used in nonlinear regression settings, where the prior needs to be specified before data collection, for example when one wants to calculate a Bayesian optimal design or in adaptive dose-finding trials. For this purpose the functional uniform distribution has been introduced, which imposes a distribution on the parameters, so that it is uniform in the functional shapes underlying the nonlinear regression function. This was achieved by using a general framework for constructing uniform distributions based on earlier work by Dembski (1990) and Ghosal et al. (1997). We investigated the functional uniform prior for nonlinear regression in a real example, a simulation study and an optimal design problem where it showed very satisfactory performance.
There is no reason to call the priors proposed in this article globally uninformative, because one needs to choose the space and in particular the metric , where to impose the uniform distribution. The priors derived from the theory in Section 2.1 might then be considered uninformative in the particular aspect that reflects. In the case of nonlinear regression we argue that the uniform distribution on the space of functional shapes is often, depending of course on the considered application, a reasonable assumption for nonlinear regression when particular prior information is lacking. However, this also does not apply generally: A situation, where the functional uniform prior might not be adequate, occurs, for example, when the considered nonlinear model is extremely flexible, containing virtually all continuous functions for example (as neural network models). In this case it is often more adequate to concentrate most prior probability on a reasonable subset of the function space (e.g., smooth functions), rather than building a uniform distribution on all potential shapes, including shapes that might be implausible a-priori.
The theory outlined in Section 2 might be of interest to formulate functional uniform priors also for other type of models with a nonlinear aspect. In quite a few modelling situations one might be able to find a space , where imposing a uniform distribution is plausible and then back-transform this distribution to the parameter scale. Ghosal et al. (1997) employ this idea, when is a space of densities and define priors for nonparametric density estimation. Another application could be the estimation of covariance matrices: Dryden et al. (2009) discuss the use of more adequate non-Euclidean distance metrics for covariance matrices, which would in our framework define the metric space for imposing the uniform distribution. Paulo (2005) derives default priors for Gaussian process interpolation, which are rather time consuming to evaluate. In this situation might choose the space of the covariance functions as .
Appendix A Proof of Theorem 1
Ghosal et al. (1997) prove a closely related result, when the underlying metric is the Hellinger distance and the space of residual densities. We review their proof and adapt to metrics of the form (1) and proceed in two parts. Part A summarizes the proof of Ghosal et al. (1997) for completeness and part B provides additional Lemmas needed in our situation.
Part A
The proof starts by covering with hypercubes and inner
hypercubes placed inside these cubes. Let be the
intersections of with the hypercubes and be the
intersections of with the inner hypercubes. Now separate the
hypercubes and inner hypercubes so that each inner hypercube is at
least apart from any other in the metric (this is
possible, when the results proved in Lemma 1 hold). By the
sub-additivity of packing numbers one then has
and , where and denote the intersection with the
hypercubes and inner hypercubes.
Now an upper an lower bound for is derived based on the local Euclidean approximation (1) to the metric . For a Euclidean metric one can calculate the packing number explicitly, see Kolmogorov and Tihomirov (1961). Up to proportionality is given by , consequently for a metric of form with a fixed positive definite matrix the packing number is up to proportionality . Using the local Euclidean approximation (1) and Lemma 2 one can derive lower and upper bounds for and in terms of and . and similarly for and thus for . As the size of the hypercubes goes to zero the bounds become sharper (see Lemma 2) and lower and upper bound converge to , see Ghosal et al. (1997) for the details of this argument.
Part B
Without loss of generality we focus on setting in
(1) for what follows.
Lemma 1
For symmetric, positive definite there exist for so that
Proof:
Now by an eigendecomposition and the compactness of and continuity of one knows that there exist so that
So that in total we get a lower and upper bound by , where , and similarly lower bounded.
Lemma 2
For lying in a hypercube we obtain
where and for , when the side length of converges to 0.
Proof:
Now is continuous, so one can lower and upper bound the second summand on . It converges to zero and hence the bounds towards each other when the size of the hypercubes shrinks (and by this ). Upper and lower bounding implies the desired result.
Appendix B Proof of Theorem 2
Consider the distance metric . To show invariance of the proposed procedure, the uniform distribution derived from needs to be , which is the distribution derived from using a change of variables.
A second order Taylor expansion of in leads to an approximation of the form where element of is given by , where and . When evaluating this expression in the expansion point the second summand vanishes as the gradient is zero. Hence one obtains , which results in the density
References
- Balasubramanian (1997) Balasubramanian, V. (1997). Statistical inference, Occam’s razor, and statistical mechanics on the space of probability distributions. Neural Computation 9, 349–369.
- Bates and Watts (1988) Bates, D. M. and Watts, D. G. (1988). Nonlinear Regression Analysis and Applications. John Wiley and sons, New York.
- Berger et al. (2009) Berger, J. O., Bernardo, J. M., and Sun, D. (2009). The formal definition of reference priors. Annals of Statistics 37, 905–938.
- Bornkamp (2011) Bornkamp, B. (2011). Approximating probability densities by iterated Laplace approximations. Journal of Computational and Graphical Statistics 00, 00–00.
- Bornkamp and Ickstadt (2009) Bornkamp, B. and Ickstadt, K. (2009). A note on B-splines for semiparametric elicitation. The American Statistician 63, 373–377.
- Bornkamp et al. (2010) Bornkamp, B., Pinheiro, J., and Bretz, F. (2010). DoseFinding: Planning and Analyzing Dose Finding experiments. R package version 0.4-1.
- Daniels (1999) Daniels, M. J. (1999). A prior for the variance in hierarchical models. Canadian Journal of Statistics 27, 567–578.
- Dembski (1990) Dembski, W. A. (1990). Uniform probability. Journal of Theoretical Probability 3, 611–626.
- Dragalin et al. (2010) Dragalin, V., Bornkamp, B., Bretz, F., Miller, F., Padmanabhan, S. K., Patel, N., Perevozskaya, I., Pinheiro, J., and Smith, J. R. (2010). A simulation study to compare new adaptive dose-ranging designs. Statistics in Biopharmaceutical Research 2, 487–512.
- Dryden et al. (2009) Dryden, I. L., Koloydenko, A., and Zhou, D. (2009). Non-Euclidean statistics for covariance matrices with applications to diffusion tensor imaging. Annals of Applied Statistics 3, 1102–1123.
- Ghosal et al. (1997) Ghosal, S., Ghosh, J. K., and Ramamoorthi, R. V. (1997). Non-informative priors via sieves and packing numbers. In Panchapakesan, S. and Balakrishnan, N., editors, Advances in Statistical Decision Theory and Applications, pages 119–132. Birkhäuser, Boston.
- Ghosh et al. (2006) Ghosh, J. K., Delampady, M., and Samanta, T. (2006). An Introduction to Bayesian Analysis: Theory and Methods. Springer, New York.
- Jeffreys (1961) Jeffreys, H. (1961). Theory of Probability. Oxford University Press.
- Jones et al. (2010) Jones, D. S., Plank, M. J., and Sleeman, B. D. (2010). Differential Equations and Mathematical Biology. Chapman and Hall, Boca Raton.
- Kass and Wasserman (1996) Kass, R. E. and Wasserman, L. (1996). The selection of prior distributions by formal rules. Journal of the American Statistical Association 91, 1343–1370.
- Kolmogorov and Tihomirov (1961) Kolmogorov, A. N. and Tihomirov, V. M. (1961). entropy and capacity of sets in function spaces. American Mathematics Society Translations Ser. 2 17, 277–364.
- Leydold and Hörmann (2010) Leydold, J. and Hörmann, W. (2010). Runuran: R interface to the UNU.RAN random variate generators. R package version 0.15.0.
- Lindsey (2001) Lindsey, J. K. (2001). Nonlinear Models for Medical Statistics. Oxford University Press, Oxford.
- Müller et al. (2006) Müller, P., Berry, D. A., Grieve, A. P., and Krams, M. (2006). A Bayesian decision-theoretic dose-finding trial. Decision Analysis 3, 197–207.
- Neuenschwander et al. (2010) Neuenschwander, B., Capkun-Niggli, G., Branson, M., and Spiegelhalter, D. J. (2010). Summarizing historical information on controls in clinical trials. Clinical Trials 7, 5–18.
- O’Hagan et al. (2006) O’Hagan, A., Buck, C., Daneshkhah, A., Eiser, R., Garthwaite, P., Jenkinson, D., Oakley, J., and Rakow, T. (2006). Uncertain Judgements: Eliciting Expert Probabilities. John Wiley and Sons Inc.
- O’Hagan and Forster (2004) O’Hagan, A. and Forster, J. (2004). Kendall’s Advanced Theory of Statistics, Volume 2B: Bayesian Inference. Arnold, London, 2nd edition.
- Paulo (2005) Paulo, R. (2005). Default priors for Gaussian processes. Annals of Statistics 33, 556–582.
- Pennec (2006) Pennec, X. (2006). Intrinsic statistics on Riemannian manifolds: Basic tools for geometric measurements. Journal of Mathematical Imaging and Vision 25, 127–154.
- R Development Core Team (2011) R Development Core Team (2011). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0.