Galactic Cosmic-Rays in a Breeze
Abstract
We study a scenario in which the Fermi bubbles are formed through a Galactocentric outflow of gas and pre-accelerated cosmic-rays (CR). We take into account CR energy losses due to proton-proton interactions with the gas present in the bubbles, and calculate the associated gamma-ray emission. We find that CRs diffusing and advecting within a breeze outflow result in an approximately flat surface brightness profile of the gamma-ray emission, as observed by Fermi satellite. Finally, we apply similar outflow profiles to larger Galactocentric radii, and investigate their effects on the CR spectrum and boron-to-carbon ratio. Hardenings can appear in the spectrum, even in cases with equal CR diffusion coefficients in the disk and halo [1].
keywords:
cosmic rays , galactic wind , Fermi bubbles1 Introduction
A number of indications that the center of our Galaxy feeds a wind has been found over the last few decades. This body of evidence has been provided from observations in a broad energy range: radio HI [2], infrared (IR) [3], and X-rays [4]. IR observations have also indicated that this wind continues further away [5], and that it may be responsible for the larger structures observed out of the Galactic plane. Absorption line features in the spectra of Active Galactic Nuclei (AGN) can be used as a probe of the structure of the gas flow: See Reference [6], whose results indicate the presence of a coherent gas flow, consistent with an outflow being directed away from the Galactic plane.
More recent gamma-ray and radio observations have shown the presence of extended non-thermal particle populations in bubble-like structures in the halo, both above and below the Galactic center (GC), see References [7, 8, 9, 10]. The current picture seems to indicate that cosmic-rays (CR) and hot gas are conveyed out from the GC region into the halo within a Galactocentric outflow.
As for the velocity of this outflow, values of km/s have been suggested in the region close to the Galactic disk (within a couple of kiloparsecs), from the weakness of the X-ray features associated with the edge of the bubbles [7, 11, 12, 13]. At distances kpc and kpc away of the Galactic plane, observations of high velocity clouds suggest velocities of about km/s, cf. Reference [6]. Further out, towards the edges, velocities are km/s. In radio [10], the bending observed in the outflow at high latitudes may be related to the motion of our Galaxy towards Andromeda (relative velocity km/s).
In the present work, we study the secondary signatures produced by CRs embedded in outflows.
2 Fermi bubbles: CRs and gamma-rays associated with a Galactocentric Outflow
A description for the propagation of cosmic rays in a turbulent region in which an advective flow is present is provided by,
| (1) |
where denotes the CR density per unit of particle momentum , at spatial position . Here is the cosmic-ray source term, is the cosmic-ray diffusion coefficient, and is the cosmic-ray lifetime in the system.
For the advective flow of the gas, as motivated by observations, a divergence free velocity field is adopted, of the form
| (2) |
where km s-1, kpc, and is the distance to the Galactic plane. This profile broadly encapsulates the velocity profile of a “breeze” solution for the isothermal outflow problem [15, 16].
With regards the energy source driving this outflow, both a past AGN outburst event (see e.g. [17, 18, 19]), and a starburst phase or a sustained outflow driven by star formation in the Galactic centre (e.g. [20]) have been previously proposed. However, reference [21] claims that the present velocity data are not conclusive on the type of source responsible for this outflow. Energetically, the starburst-driven outflow luminosity is estimated to be erg s-1 [20]. The present level of AGN activity from the GC (of Sgr A*) is considerably below this ( erg s-1), but there is a growing body of evidence that its level in the recent past was significantly higher [22, 23]. It therefore currently seems plausible for either energy source to be driving the outflow. We here choose to keep the discussion general, adopting instead the velocity profile of Eq. (2) as the starting point in our calculations.
We adopt a Monte Carlo approach to solve Eq. (1). Our results with this technique have been compared with those obtained using an explicit differential equation solver. We found excellent agreement in all cases.
We assume that the source term is located at the GC region and constant in time. The copresence of the resultant accumulated CRs with the ambient gas gives rise to gamma-ray bubble emission through production generated in proton-proton interactions. This emission may potentially account for the observed gamma-rays from the bubbles, as has previously been proposed by other authors [24].
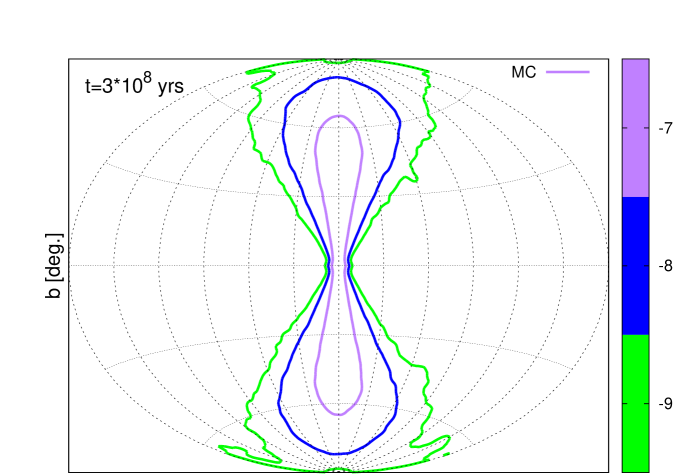
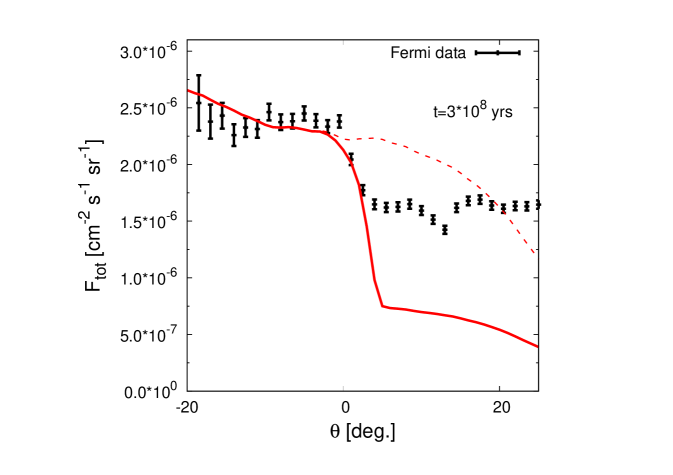
We determine the level of this emission by convolving the accumulated CR density throughout the outflow region with the target gas density in the outflow. As motivated on theoretical [25], and observational [12] grounds, we adopt a constant gas density within the bubbles at the level cm-3. In Fig. 1, we show a gamma-ray density map and a comparison of the gamma-ray bubble-edge profile with Fermi measurement. For these calculations, we took a CR luminosity of erg/s for the central source. In Fig. 1 (right panel), the origin of the diffuse gamma-ray emission in the region is assumed purely galactic in origin. Should some component of the emission from this region be extragalactic, a reduction of the GC luminosity or bubble gas density would be required in order to account for such a reduction in required -ray emission intensity.
As can be seen in Fig. 1, a flat surface brightness profile for the bubbles is obtained when assuming that the velocity profile in the bubbles is described by Eq. (2). We note, however, that in reality a range of velocity profiles can provide such a uniform brightness, see for example [26]. In general, we find that for the case of a constant density ambient gas description, the current gamma-ray data can be said to prefer decelerating profiles. For decreasing gas density profiles, a sharper fall-off in the velocity profile, than that used in Eq. (2), would be required.
Although the cutoff at the edge of the bubbles is not well described by the simple constant density gas model (see red dashed line in Fig. 1), a steeper cutoff in the -ray profile can be achieved by an abrupt change in the gas density at the bubble edge (see red solid line), as motivated in certain models [20]. Another motivation for such an origin for the bubble edges comes from a comparison of their morphology as seen in gamma-rays [7] and in radio [10]. If GeV protons (resp. electrons) give rise to the -ray (resp. radio) emission, it would be surprising that the electrons extend out to larger latitudes than the protons. Such a difference between the morphologies of the -ray and radio data disfavours simple leptonic scenarios for the -ray bubbles. However, despite these challenges, more involved diffuse acceleration models supporting a scenario in which both the radio and gamma-ray emission are leptonic in origin are currently viable [27].


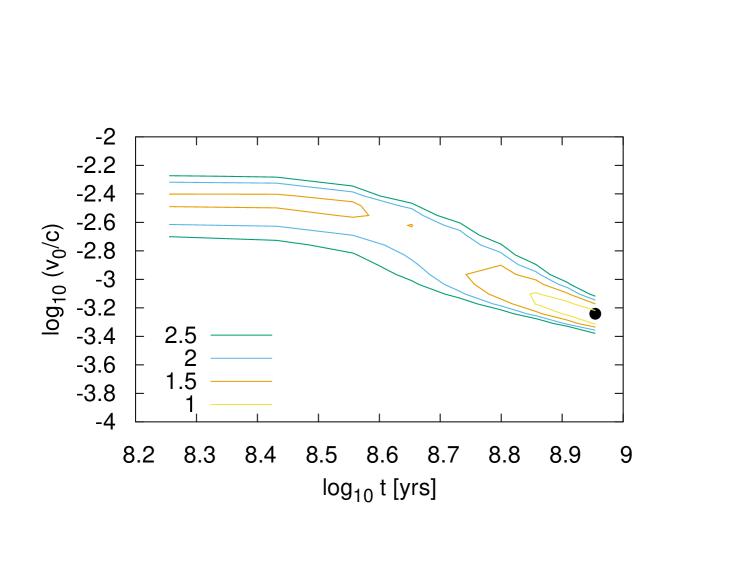
One simple explanation for the difference in the latitudinal profiles of the radio and gamma-ray emissions is that both protons and electrons possess extended distributions, and that the difference in morphology of their secondary emissions is due to differing distributions of target gas and magnetic fields. A potential association of IceCube high energy neutrinos [28], with the bubbles and beyond [29], allows such a hadronic origin scenario for the gamma-rays to be tested in the near future.
With regards the parameter , which dictates the turnover distance in the outflow velocity profile described by Eq. (2), a comparison of the fits to the radial gamma-ray profile of the Fermi bubbles is provided in Fig. 2, through a consideration of the contours. The upper plot in this figure shows that for the majority of the parameter space, small values of are problematic, with the large values obtained reflecting the fact that such values lead to centrally brightened profiles, incompatible with the flat profile suggested by the data. However, the middle and lower panels show that the results for such intermediate and “large” values of both show considerable regions of parameter space able to provide sufficiently flat profiles in agreement with that measured.
3 Local Outflow and CR Fluxes at Earth
In this Section, we study the impact that an outflow at larger Galactocentric radii would have on CR observables in the disk. The impacts of winds with either constant velocities [30, 31, 32] or velocities increasing with height in the halo [33, 34, 35, 36] have already been studied extensively in the literature. In the present work, we decide instead to study the case of outflows whose become negative above a given height . As far as we know, such a case has not been studied yet, with the exception of Reference [1]. We note that such velocity profiles do not correspond to those expected for winds driven by cosmic-rays. For such winds, at all , see Refs. [37, 38, 39, 40, 41, 42, 43, 36], as well as the numerical simulations of Refs. [44, 45, 46, 47]. However, the case of an outflow decelerating in the halo is worth studying for, at least, two reasons. First, some studies have argued that some galaxies may fail to produce “successful”, accelerating winds with a positive at all heights in the halo, for instance because of ram pressure from infalling material: See e.g. Reference [48]. Second, such a profile is preferred for the Fermi bubbles, as argued in the previous Section. It is unclear at the present time whether a breeze profile may apply to larger Galactocentric radii or not. Therefore, it is interesting to provide possible signatures that could confirm or rule out such a scenario.
As a first approximation, we assume in the following that variations of CR propagation or source parameters along the direction of the galactocentric radius can be ignored. We then assume that only depends on . We wrote a code which solves numerically Equation (1) in planar 1D, for any arbitrary profiles of and . This code was presented and tested in [1]. In particular, we checked that it reproduces correctly the expected CR density profiles in the halo for the known cases of V=constant [30] and [35], which are respectively constant and decreasing with . On the contrary, the profiles we consider below result in an increase of CR density above . Hereafter, we set at as a boundary condition, where denotes the size of the halo. The CR density then decreases again when , due to CR escape. Such boundary conditions are widely used in Galactic CR propagation codes, and may correspond to the height above which the magnetic field is too weak to confine cosmic-rays. We stress however that, in general, the use of such conditions is not guaranteed to be justified, and may not be a good proxy for the actual physical picture: For instance, if a strong wind is present up to large , see e.g. Refs. [37, 43]. In the latter case, the effective “halo size” seen by GeV–PeV CRs corresponds instead to the (energy-dependent) height above which CR advection wins over CR diffusion. In the following, for our breeze profiles, is small at large , and we stick to the aforementioned boundary condition at .
We calculate the steady-state distributions for CR protons, and for boron and carbon nuclei. We calculate the production and destruction of boron as described in Ref. [1], and we use the cross-section values quoted there. For the density profile of the target gas, , we take: cm-3 at , and cm-3 otherwise. The source term for primary nuclei is set to:
| (5) |
where denotes the fraction of nuclei emitted at the sources. The disk width is set to pc. For clarity, we assume below that there are no sources of primary boron. See e.g. [32] for a non-zero . We will not study here the hypothetical case where CR trapping around their sources contributes significantly to the boron-to-carbon ratio, e.g. [49]. In such a scenario, this ratio would contain little information on CR propagation on large scales in our Galaxy, and hence little constraints on a local outflow. For clarity, we assume below that does not depend on . We express it as:
| (6) |
for nuclei of charge . We set and , which correspond to the best fit values of Ref. [32] for kpc. Ref. [50] also suggested the same value for . We verified that our code reproduces the expected boron-to-carbon ratios both for the cases of “no wind”, and “wind velocity constant with ”.
In the static regime (), the boron current in the halo is (). Therefore, in the static regime, the boron-to-carbon ratio is
| (7) |
where indices “0” mean “at ”, and are the production and destruction cross-sections for boron. With the parameter values we take here, the diffusion term “” dominates over the “” term only around the last couple of points in the AMS-02 data [51], which is why the slope in the data, at GeV/nucl, looks flatter than 0.44. This calls for a better knowledge of cross-sections, as also noted by [32].
In the hypothetical case of a wind with a velocity constant with , the “” term in Eq. (7) must be replaced with “”, cf. Ref. [32]. Let us denote , the distance beyond which advection dominates over diffusion. In this particular setup, low-energy CRs with advect to the boundary, whereas higher-energy CRs diffuse to the boundary. This introduces a flattening in the boron-to-carbon ratio at low energies ( for constant). A value of larger than a few tens of km/s for kpc is incompatible with the data. This excludes a strong “ constant” wind. However, the current boron-to-carbon data does not exclude the presence of a strong wind in general, as other wind profiles with constant, such as , are allowed by the data. For winds with , . For a CR spectrum at the sources , the slope of the CR flux at Earth then tends to /2, cf. Reference [35].
From now on, we focus on profiles that decrease above a height in the halo. In Figure 3, we show eight profiles (lower panel) and their impact on the CR spectrum (upper panel) and boron-to-carbon ratio (middle panel) at . For reference, we also plot results for the “benchmark fit” of [32] for (thin black line). The boron-to-carbon ratio measurements from AMS-02 experiment coincide with this line. Our goal here is not to provide a fit of the data. Instead, we take “caricatural” examples of profiles with rather extreme parameter values, so as to make the impact of these parameters more visible. In some cases, changing the values of some of the parameters would provide a reasonable fit to the data.
We set the CR spectral index at the sources to . We do not vary , , , or , so as to help the reader distinguish between the contributions from the different wind parameters. For all eight profiles, at , then increases up to at , and then decreases on a typical length scale :
| (11) |
Each of these scenarios is represented by the same line type and colour in each panel of Fig. 3. Let us denote by A (resp. B) the thick (resp. thin) red solid lines in Fig. 3, C (resp. D) the thick (resp. thin) green dashed lines, E (resp. F) the thick (resp. thin) magenta dotted lines, and G (resp. H) the dark (resp. light) blue dashed-dotted lines. We take pc for {A,B,C,D}, and 2 kpc otherwise. kpc for {A,B,C,D}, 2.8 kpc for {E,F}, and 10 kpc for {G,H}. km/s for {A,B}, and 600 km/s otherwise. kpc for {A,C,E}, 5 kpc for H, and 20 kpc otherwise. kpc for {A,C,E}, and 50 kpc otherwise.
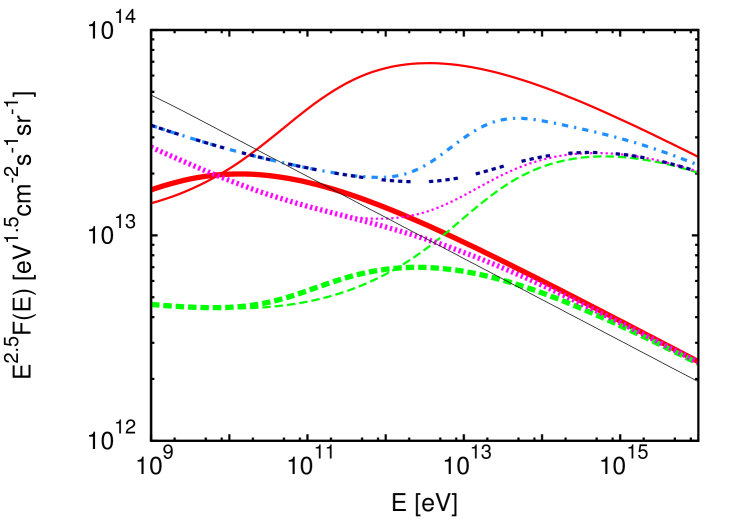
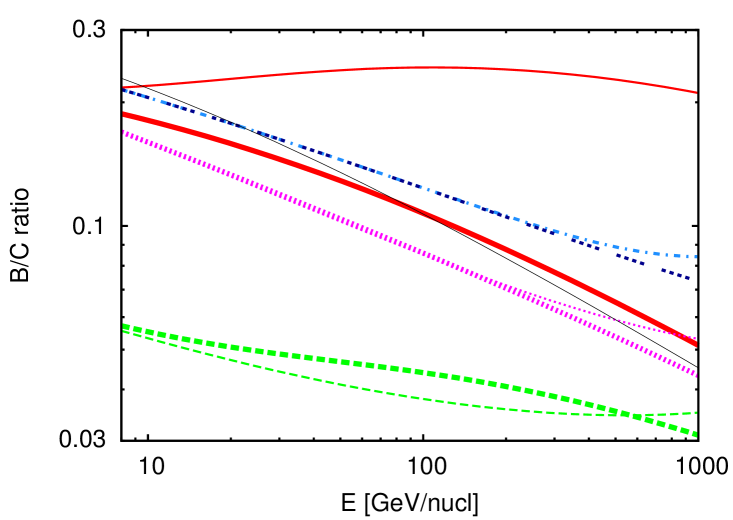
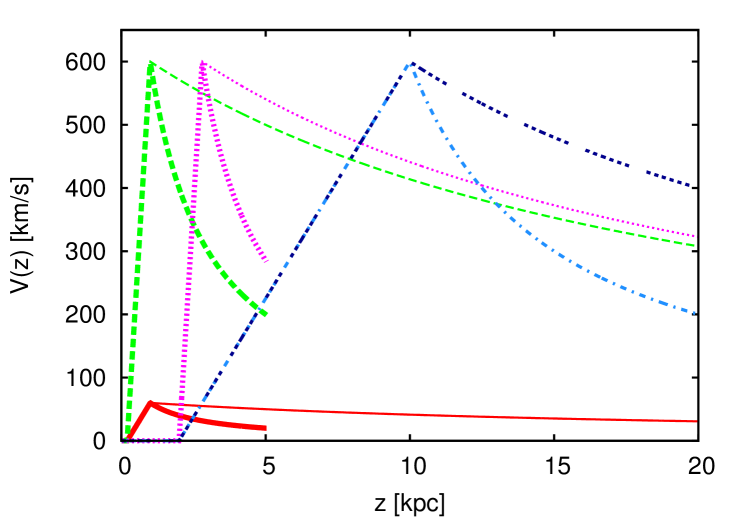
In all cases, when the CR energy is sufficiently high for diffusion to win over advection at all , the problem simplifies to a basic leaky-box with homogeneous diffusion coefficient. Spectra (upper panel) then all tend to , e.g. above GeV (resp. PeV) for A (resp. G). Case A shows that a weak outflow with such a profile introduces a turnover in the CR spectrum at low energies. This might explain the turnover measured below GeV from molecular clouds. The outflow reduces the “box” (in which low-energy CRs diffuse and can come back to ) to an effective size , where is the height where advection wins over diffusion. For these low-energy CRs, advection dominates in the region of large around . This region then acts as a bottleneck for them. A small turnover also occurs in the boron-to-carbon ratio. When increasing the extent of the wind, and then the size of the region in the halo in which is greater than a fraction of , the turnover is shifted to higher energy: Indeed, in this case, a larger is required for diffusion to win over advection, see curves B. The CR flux at high energies in case B is ten times larger than in case A, because we kept fixed in these examples, and did not rescale it with .
Increasing also increases the energy of the aforementioned feature, see C and D. More interestingly, CRs below this energy that can come back to , probe the part of the wind, because for them. Since in C and D, this results in a “” scenario [35], and the CR spectrum (resp. boron-to-carbon ratio) slope tends to /2 (resp. /2) at low energy, see green lines in Fig. 3. On the contrary, if one increases the altitude of the launching of the wind, the CR spectrum (resp. boron-to-carbon ratio) slope tends to (resp. ), as for the “” scenario: See the magenta lines for the cases E and F. This is due to the fact that, at these low energies, . Therefore, low-energy CRs see a small, energy-independent, effective leaky-box of height . In the cases E and F, , and, with increasing CR energy, there is a “quick” transition to a bigger box of effective size : The slopes of the magenta CR spectra are both at low and high energies in the energy range displayed in the upper panel.
For the case G, there is a hint of a smooth transition, at low energy, from a to a /2 slope. Indeed, has the same large value as in case F, but, for G, is not small compared to . It is interesting to note that G and H are not far from fitting the existing experimental data for the boron-to-carbon ratio, despite having velocity profiles very different from the profile of the “benchmark fit” (thin black line). The impact of on the CR spectrum is visible by comparing G with H. H, the profile with a faster fall off at high , achieves the transition between the two limiting regimes in a smaller energy interval. A hardening (upturn) is also present in the boron-to-carbon ratio for the cases D, F, and H.
Green, magenta, and blue lines show a hardening in the CR spectrum around eV, due to the launching of a wind in the halo. For some parameter values, it is possible to make it coincide better with the one measured at 200 GV in the CR spectra by PAMELA, CREAM and AMS-02 experiments. Thence, even in the limiting case of equal in the disk and in the halo, such a hardening may arise from the launching of a breeze or wind. This argument is valid for cases with above too. As noted above, similar hardenings also appear in the boron-to-carbon ratio. This does not contradict the experimental data, provided that the hardening is concealed at higher energies, or remains within the systematics of the detectors. Regarding the second of these possibilities, conflicts in secondary to primary ratios have been reported in existing data sets, cf. Ti/Fe ratio by HEAO-3-C3 [52], ATIC-2 [53], and comparison to the boron-to-carbon ratio [51].
4 Conclusions and perspectives
We presented in Section 2 a hadronic model of the Fermi bubbles. Assuming that they result from a Galactocentric outflow carrying pre-accelerated cosmic-rays, we calculated the gamma-ray emission produced by the CRs interacting with the gas present in the bubbles. We showed that outflows decelerating with distance to the Galactic disk can reproduce the flat gamma-ray surface brightness of the bubbles, in accordance with the measurements from Fermi satellite. Our description for the outflow profile is enclosed in breeze solutions of isothermal winds.
Motivated by the above findings, we studied in Section 3 the impacts that similar types of outflow profiles would have on the CR spectra at Earth, should such outflows exist at larger Galactocentric radii. Competition between CR diffusion and advection in the halo can produce an inflection point in the CR spectrum at . A hardening can appear in the CR spectrum due to the launching of a wind or breeze in the halo, even in the hypothetical, limiting case of equal CR diffusion coefficients in the halo and disk.
Although a breeze outflow scenario is currently only motivated for the outflow from the GC region, we conclude from the above results that future observations should be able to test its presence or absence at larger radii, thanks to local CR observables.
Acknowledgments
AT acknowledges a Schroedinger fellowship at DIAS.
References
- [1] A. M. Taylor, G. Giacinti, Cosmic rays in a galactic breeze, Phys. Rev. D 95 (2) (2017) 023001. arXiv:1607.08862, doi:10.1103/PhysRevD.95.023001.
- [2] F. J. Lockman, The H I halo in the inner galaxy, ApJ 283 (1984) 90–97. doi:10.1086/162277.
- [3] M. Morris, E. Serabyn, The Galactic Center Environment, Annu. Rev. Astron. Astrophys. 34 (1996) 645–702. doi:10.1146/annurev.astro.34.1.645.
- [4] L. X. Cheng, M. Leventhal, D. M. Smith, W. R. Purcell, J. Tueller, A. Connors, D. Dixon, R. L. Kinzer, J. G. Skibo, A Maximum Entropy Map of the 511 keV Positron Annihilation Line Emission Distribution Near the Galactic Center, ApJL 481 (1997) L43–L46. doi:10.1086/310638.
- [5] J. Bland-Hawthorn, M. Cohen, The Large-Scale Bipolar Wind in the Galactic Center, ApJ 582 (2003) 246–256. arXiv:astro-ph/0208553, doi:10.1086/344573.
- [6] B. A. Keeney, C. W. Danforth, J. T. Stocke, S. V. Penton, J. M. Shull, K. R. Sembach, Does the Milky Way Produce a Nuclear Galactic Wind?, ApJ 646 (2006) 951–964. arXiv:astro-ph/0604323, doi:10.1086/505128.
- [7] M. Su, T. R. Slatyer, D. P. Finkbeiner, Giant Gamma-ray Bubbles from Fermi-LAT: Active Galactic Nucleus Activity or Bipolar Galactic Wind?, ApJ 724 (2010) 1044–1082. arXiv:1005.5480, doi:10.1088/0004-637X/724/2/1044.
- [8] R.-z. Yang, F. Aharonian, R. Crocker, The Fermi bubbles revisited, Astron. Astrophys. 567 (2014) A19. arXiv:1402.0403, doi:10.1051/0004-6361/201423562.
- [9] M. Ackermann, A. Albert, W. B. Atwood, L. Baldini, J. Ballet, G. Barbiellini, D. Bastieri, R. Bellazzini, E. Bissaldi, R. D. Blandford, et al., The Spectrum and Morphology of the Fermi Bubbles, ApJ 793 (2014) 64. arXiv:1407.7905, doi:10.1088/0004-637X/793/1/64.
- [10] E. Carretti, R. M. Crocker, L. Staveley-Smith, M. Haverkorn, C. Purcell, B. M. Gaensler, G. Bernardi, M. J. Kesteven, S. Poppi, Giant magnetized outflows from the centre of the Milky Way, Nature 493 (2013) 66–69. arXiv:1301.0512, doi:10.1038/nature11734.
- [11] J. Kataoka, M. Tahara, T. Totani, Y. Sofue, L. Stawarz, Y. Takahashi, Y. Takeuchi, H. Tsunemi, M. Kimura, Y. Takei, C. C. Cheung, Y. Inoue, T. Nakamori, Suzaku Observations of the Diffuse X-Ray Emission across the Fermi Bubbles’ Edges, ApJ 779 (2013) 57. arXiv:1310.3553, doi:10.1088/0004-637X/779/1/57.
- [12] T. Fang, X. Jiang, High Resolution X-Ray Spectroscopy of the Local Hot Gas along the 3C 273 Sightline, ApJL 785 (2014) L24. arXiv:1403.2028, doi:10.1088/2041-8205/785/2/L24.
- [13] A. J. Fox, R. Bordoloi, B. D. Savage, F. J. Lockman, E. B. Jenkins, B. P. Wakker, J. Bland-Hawthorn, S. Hernandez, T.-S. Kim, R. A. Benjamin, D. V. Bowen, J. Tumlinson, Probing the Fermi Bubbles in Ultraviolet Absorption: A Spectroscopic Signature of the Milky Way’s Biconical Nuclear Outflow, ApJL 799 (2015) L7. arXiv:1412.1480, doi:10.1088/2041-8205/799/1/L7.
- [14] A. A. Abdo, M. Ackermann, M. Ajello, W. B. Atwood, L. Baldini, J. Ballet, G. Barbiellini, D. Bastieri, B. M. Baughman, K. Bechtol, Fermi LAT Collaboration, Spectrum of the Isotropic Diffuse Gamma-Ray Emission Derived from First-Year Fermi Large Area Telescope Data, Physical Review Letters 104 (10) (2010) 101101. arXiv:1002.3603, doi:10.1103/PhysRevLett.104.101101.
- [15] J. W. Chamberlain, On the Existence of Slow Solutions in Coronal Hydrodynamics., ApJ 141 (1965) 320. doi:10.1086/148119.
- [16] E. N. Parker, Dynamical Properties of Stellar Coronas and Stellar Winds, IV. The Separate Existence of Subsonic and Supersonic Solutions., ApJ 141 (1965) 1463. doi:10.1086/148235.
- [17] F. Guo, W. G. Mathews, The Fermi Bubbles. I. Possible Evidence for Recent AGN Jet Activity in the Galaxy, ApJ 756 (2012) 181. arXiv:1103.0055, doi:10.1088/0004-637X/756/2/181.
- [18] F. Guo, W. G. Mathews, G. Dobler, S. P. Oh, The Fermi Bubbles. II. The Potential Roles of Viscosity and Cosmic-Ray Diffusion in Jet Models, ApJ 756 (2012) 182. arXiv:1110.0834, doi:10.1088/0004-637X/756/2/182.
- [19] M. V. Barkov, V. Bosch-Ramon, Formation of large-scale magnetic structures associated with the Fermi bubbles, Astron. Astrophys. 565 (2014) A65. arXiv:1311.6722, doi:10.1051/0004-6361/201322743.
- [20] R. M. Crocker, G. V. Bicknell, A. M. Taylor, E. Carretti, A Unified Model of the Fermi Bubbles, Microwave Haze, and Polarized Radio Lobes: Reverse Shocks in the Galactic Center’s Giant Outflows, ApJ 808 (2015) 107. arXiv:1412.7510, doi:10.1088/0004-637X/808/2/107.
- [21] K. C. Sarkar, B. B. Nath, P. Sharma, Supernovae vs. AGN: Clues to the origin of Fermi Bubbles from OVIII/OVII line ratio, ArXiv e-printsarXiv:1610.00719.
- [22] G. Ponti, R. Terrier, A. Goldwurm, G. Belanger, G. Trap, Discovery of a Superluminal Fe K Echo at the Galactic Center: The Glorious Past of Sgr A* Preserved by Molecular Clouds, ApJ 714 (2010) 732–747. arXiv:1003.2001, doi:10.1088/0004-637X/714/1/732.
- [23] R. Terrier, G. Ponti, G. Bélanger, A. Decourchelle, V. Tatischeff, A. Goldwurm, G. Trap, M. R. Morris, R. Warwick, Fading Hard X-ray Emission from the Galactic Center Molecular Cloud Sgr B2, ApJ 719 (2010) 143–150. arXiv:1005.4807, doi:10.1088/0004-637X/719/1/143.
- [24] R. M. Crocker, F. Aharonian, Fermi Bubbles: Giant, Multibillion-Year-Old Reservoirs of Galactic Center Cosmic Rays, Physical Review Letters 106 (10) (2011) 101102. arXiv:1008.2658, doi:10.1103/PhysRevLett.106.101102.
- [25] R. Feldmann, D. Hooper, N. Y. Gnedin, Circum-galactic Gas and the Isotropic Gamma-Ray Background, ApJ 763 (2013) 21. arXiv:1205.0249, doi:10.1088/0004-637X/763/1/21.
- [26] K. C. Sarkar, B. B. Nath, P. Sharma, Multiwavelength features of Fermi bubbles as signatures of a Galactic wind, MNRAS 453 (2015) 3827–3838. arXiv:1505.03634, doi:10.1093/mnras/stv1806.
- [27] P. Mertsch, S. Sarkar, Fermi Gamma-Ray “Bubbles” from Stochastic Acceleration of Electrons, Physical Review Letters 107 (9) (2011) 091101. arXiv:1104.3585, doi:10.1103/PhysRevLett.107.091101.
- [28] IceCube Collaboration, Evidence for High-Energy Extraterrestrial Neutrinos at the IceCube Detector, Science 342 (2013) 1242856. arXiv:1311.5238, doi:10.1126/science.1242856.
- [29] A. M. Taylor, S. Gabici, F. Aharonian, Galactic halo origin of the neutrinos detected by IceCube, Phys. Rev. D 89 (10) (2014) 103003. arXiv:1403.3206, doi:10.1103/PhysRevD.89.103003.
- [30] A. J. Owens, J. R. Jokipii, Cosmic rays in a dynamical halo. I - Age and matter traversal distributions and anisotropy for nuclei. II - Electrons, ApJ 215 (1977) 677–689. doi:10.1086/155401.
- [31] F. C. Jones, The dynamical halo and the variation of cosmic-ray path length with energy, ApJ 229 (1979) 747–752. doi:10.1086/157010.
- [32] Y. Genolini, A. Putze, P. Salati, P. D. Serpico, Theoretical uncertainties in extracting cosmic-ray diffusion parameters: the boron-to-carbon ratio, Astron. Astrophys. 580 (2015) A9. arXiv:1504.03134, doi:10.1051/0004-6361/201526344.
- [33] I. Lerche, R. Schlickeiser, On the transport and propagation of cosmic rays in galaxies. I - Solution of the steady-state transport equation for cosmic ray nucleons, momentum spectra and heating of the interstellar medium, MNRAS 201 (1982) 1041–1072. doi:10.1093/mnras/201.4.1041.
- [34] V. A. Dogiel, The cosmic-ray halo - Insight from gamma rays and cosmic-ray observations, in: H. Bloemen (Ed.), The Interstellar Disk-Halo Connection in Galaxies, Vol. 144 of IAU Symposium, 1991, pp. 175–186.
- [35] J. B. G. M. Bloemen, V. A. Dogiel, V. L. Dorman, V. S. Ptuskin, Galactic diffusion and wind models of cosmic-ray transport. I - Insight from CR composition studies and gamma-ray observations, Astron. Astrophys. 267 (1993) 372–387.
- [36] S. Recchia, P. Blasi, G. Morlino, Cosmic ray driven Galactic winds, MNRAS 462 (2016) 4227–4239. arXiv:1603.06746, doi:10.1093/mnras/stw1966.
- [37] V. S. Ptuskin, H. J. Voelk, V. N. Zirakashvili, D. Breitschwerdt, Transport of relativistic nucleons in a galactic wind driven by cosmic rays., Astron. Astrophys. 321 (1997) 434–443.
- [38] D. Breitschwerdt, V. A. Dogiel, H. J. Völk, The gradient of diffuse gamma -ray emission in the Galaxy, Astron. Astrophys. 385 (2002) 216–238. arXiv:astro-ph/0201345, doi:10.1051/0004-6361:20020152.
- [39] A. Socrates, S. W. Davis, E. Ramirez-Ruiz, The Eddington Limit in Cosmic Rays: An Explanation for the Observed Faintness of Starbursting Galaxies, ApJ 687 (2008) 202–215. arXiv:astro-ph/0609796, doi:10.1086/590046.
- [40] J. E. Everett, E. G. Zweibel, R. A. Benjamin, D. McCammon, L. Rocks, J. S. Gallagher, III, The Milky Way’s Kiloparsec-Scale Wind: A Hybrid Cosmic-Ray and Thermally Driven Outflow, ApJ 674 (2008) 258–270. arXiv:0710.3712, doi:10.1086/524766.
- [41] S. Samui, K. Subramanian, R. Srianand, Cosmic ray driven outflows from high-redshift galaxies, MNRAS 402 (2010) 2778–2791. arXiv:0909.3854, doi:10.1111/j.1365-2966.2009.16099.x.
- [42] E. A. Dorfi, D. Breitschwerdt, Time-dependent galactic winds. I. Structure and evolution of galactic outflows accompanied by cosmic ray acceleration, Astron. Astrophys. 540 (2012) A77. arXiv:1304.1311, doi:10.1051/0004-6361/201118082.
- [43] V. N. Zirakashvili, Cosmic ray propagation and interactions in the Galaxy, Nuclear Physics B Proceedings Supplements 256 (2014) 101–106. arXiv:1412.0863, doi:10.1016/j.nuclphysbps.2014.10.012.
- [44] M. Hanasz, H. Lesch, T. Naab, A. Gawryszczak, K. Kowalik, D. Wóltański, Cosmic Rays Can Drive Strong Outflows from Gas-rich High-redshift Disk Galaxies, ApJL 777 (2013) L38. arXiv:1310.3273, doi:10.1088/2041-8205/777/2/L38.
- [45] T. Peters, P. Girichidis, A. Gatto, T. Naab, S. Walch, R. Wünsch, S. C. O. Glover, P. C. Clark, R. S. Klessen, C. Baczynski, Impact of Supernova and Cosmic-Ray Driving on the Surface Brightness of the Galactic Halo in Soft X-Rays, ApJL 813 (2015) L27. arXiv:1510.06563, doi:10.1088/2041-8205/813/2/L27.
- [46] P. Girichidis, T. Naab, S. Walch, M. Hanasz, M.-M. Mac Low, J. P. Ostriker, A. Gatto, T. Peters, R. Wünsch, S. C. O. Glover, R. S. Klessen, P. C. Clark, C. Baczynski, Launching Cosmic-Ray-driven Outflows from the Magnetized Interstellar Medium, ApJL 816 (2016) L19. arXiv:1509.07247, doi:10.3847/2041-8205/816/2/L19.
- [47] C. M. Simpson, R. Pakmor, F. Marinacci, C. Pfrommer, V. Springel, S. C. O. Glover, P. C. Clark, R. J. Smith, The Role of Cosmic-Ray Pressure in Accelerating Galactic Outflows, ApJL 827 (2016) L29. arXiv:1606.02324, doi:10.3847/2041-8205/827/2/L29.
- [48] Y. Dubois, R. Teyssier, On the onset of galactic winds in quiescent star forming galaxies, Astron. Astrophys. 477 (2008) 79–94. arXiv:0707.3376, doi:10.1051/0004-6361:20078326.
- [49] M. D’Angelo, P. Blasi, E. Amato, Grammage of cosmic rays around Galactic supernova remnants, Phys. Rev. D 94 (8) (2016) 083003. arXiv:1512.05000, doi:10.1103/PhysRevD.94.083003.
- [50] C. Evoli, H. Yan, Cosmic Ray Propagation in Galactic Turbulence, ApJ 782 (2014) 36. arXiv:1310.5732, doi:10.1088/0004-637X/782/1/36.
- [51] A. Collaboration, Precision Measurement of the Cosmic Ray Boron-to-Carbon Ratio with AMS, International Cosmic Ray Conference.
- [52] V. Vylet, J. C. Waddington, R. W. Binns, L. T. Garrard, H. M. Israel, J. Klarmann, M. Metzger, Energy Spectra Between 10 and Several Hundred GeV/Nucleon for Elements From 18Ar to 23V: Results from HEAO-3, International Cosmic Ray Conference 3 (1990) 19.
- [53] V. I. Zatsepin, A. D. Panov, N. V. Sokolskaya, J. H. Adams, H. S. Ahn, G. L. Bashindzhagyan, J. Chang, M. Christl, A. R. Fazely, T. G. Guzik, J. B. Isbert, K. C. Kim, E. N. Kouznetsov, M. Panasyuk, E. S. Seo, J. Watts, J. P. Wefel, J. Wu, Energy dependence of Ti/Fe ratio in the Galactic cosmic rays measured by the ATIC-2 experiment, Astronomy Letters 35 (2009) 338–342. arXiv:0905.0049, doi:10.1134/S1063773709050089.