Galaxy Optical Variability of Virgo Cluster: New Tracer for Environmental Influences on Galaxies

The Virgo cluster, the closest large cluster to our local group, is reported as a cool core and cooling flow cluster (Fabian, 1994; Hudson et al., 2010). Binggeli et al. (1985) identifies 1277 member galaxies and 574 possible member galaxies for the Virgo cluster, their Virgo Cluster Catalog (VCC). Our galaxy sample comes from this catalog. Also, 245 galaxies are reported by Binggeli et al. (1985) as background galaxies and these are distributed as part of VCC. We use these galaxies as a control sample for comparison purposes in our work.

Virgo cluster is reported to be 16.5 Mpc away (Mei et al., 2007). The member galaxies from Binggeli et al. (1985) distribute within a radius of 1.6 Mpc from the cluster centre. The most distant background galaxy in our control sample is 1.4 Mpc away from the cluster centre. The largest clustercentric distances of both member and background galaxies in our sample are close to the virial radius of the Virgo cluster (i.e. 1.72Mpc; Hoffman et al., 1980).

The Palomar Transient Factory is a time-domain sky survey, employing the 48 inch Samuel Oschin Telescope with an 8 square degree camera (Law et al., 2009). The exposure time for the PTF survey is 60 seconds, with limiting magnitudes of $m_{g^{{}^{\prime}}}$ $\sim$ 21.3 and $m_{R}\sim$ 20.6. The source extraction and data reduction are performed by an automated pipeline in the Infrared Processing and Analysis centre (IPAC; Laher et al., 2014). In our work, we aim to use R band data due to the greater number of observations. The PTF data have been well-utilized by other authors (e.g. Pian et al., 2017; Kao et al., 2016). The conditions under which we use the data are similar to those in the work of Cook et al. (2019).

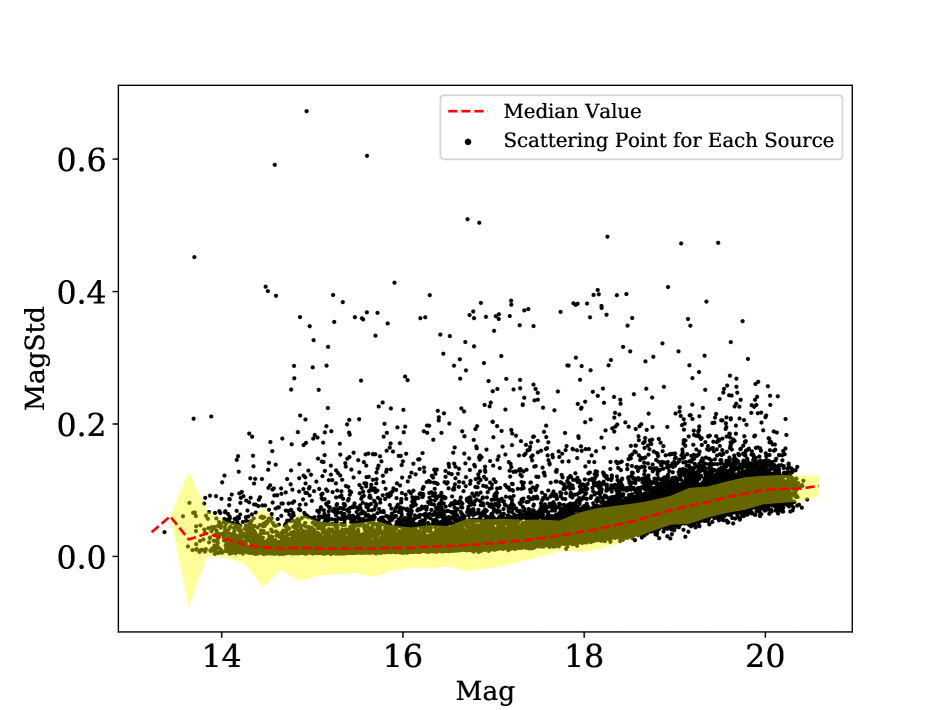
As our work is based on the estimation of galaxy optical variability, an assessment of the PTF photometry uncertainty is necessary. To this end, we choose 10⁵ stars in the SDSS Stripe 82 Standard Catalog (Ivezić et al., 2007). The standard deviations of magnitude of these standard stars indicate the statistical error of the PTF photometry (shown in Figure 1). In the range of 14 to 20 magnitude, the standard deviation is less than 0.1 mag.

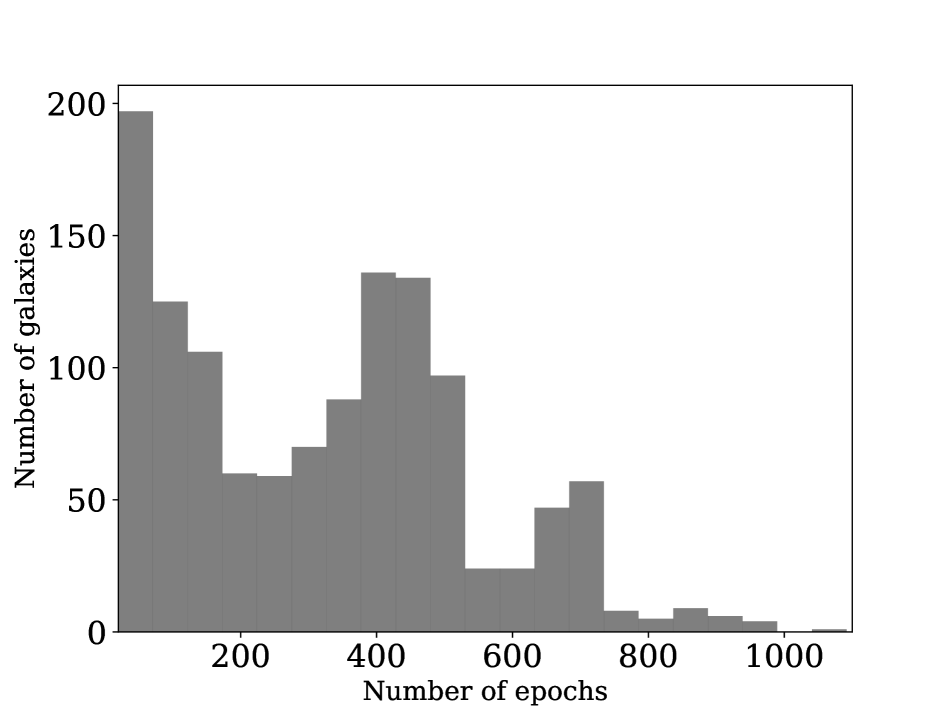
The VCC galaxies were crossed matched with the Palomar Transient Factory (PTF) data base^***https://irsa.ipac.caltech.edu/cgi-bin/Gator/nph-scan?submit=Select&projshort=PTF. We retrieved 554 confirmed member galaxies with 169258 observations, 260 possible members with 61005 observations, and 217 background galaxies with 55921 observations. During cross-matching, we required the number of observational epochs for each source to be greater than 20, with magnitudes in the range of 14 to 18. The histogram of observation times for PTF VCC galaxies is given in Figure 2.

The optical galaxy variability comes intrinsically from the activity of galactic nuclei. Optical variability has been proven to be an important criterion for AGN detection (Trevese et al., 2008; Villforth et al., 2010; De Cicco et al., 2015; Prakash et al., 2019). The standard deviation of a galaxy brightness is a combination of the galaxy intrinsic brightness variability and the observational uncertainties of the measurements. In PTF data, the observational error is connected to the brightness as shown in Figure 1. To investigate the physical properties of galaxy variability, we have to remove the influence of observational error. e.g. the uncertainty dependency upon brightness.

Thus we define galaxy optical variability in our work as the ratio between the standard deviation of the galaxy flux among all the measurements taken of a galaxy ($\sigma_{single}$) and the mean value of the standard deviation in the flux bin enclosing the magnitude of the galaxy ($\sigma_{flux}$). Mathematically, the definition can be explained by considering the following error propagation equation.

$\sigma_{galaxy}$ indicates the galaxy intrinsic variability. $\xi$ is a random variable indicating the ratio between the standard deviation of one galaxy caused by photometry uncertainty and $\sigma_{flux}$. The flux is derived from photometry magnitude according to the Flux-Apparent Magnitude Relationship. The brightness bin here is set to be 0.2 in the unit of mag. We also performed tests with bin sizes of 0.1, 0.5 which gave negligible differences.

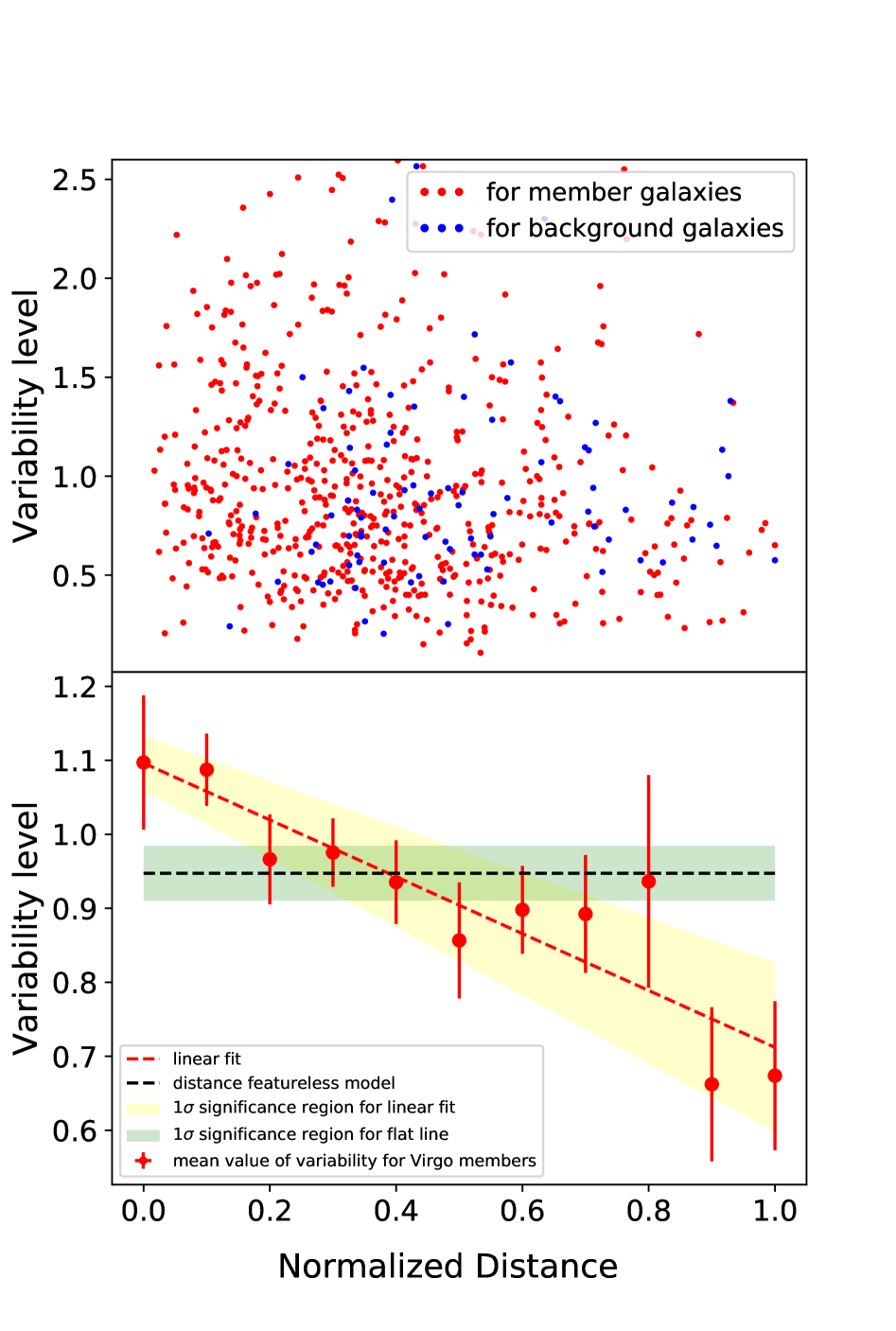
Using the variability estimates from the previous sections, we display the radial distribution of the galaxy variability for the Virgo Cluster in Figure 3. The plot shows a large scatter due to the combination of the diversity of galaxy variability and observational uncertainty.

The points are not uniformly distributed across the plot with the points in the upper right corner being particularly sparse. This can be explained by the fact that some galaxies in the inner part of the cluster present optical variability due to AGN. Theses sources have higher statistical variability levels and thus occupy the space in the upper left corner of the plot. We also give the variability of background galaxies for comparison (see Figure 3). The background galaxy variability gives a more uniform distribution.

To determine the statistical properties of the variability distribution, we calculate the mean value of the scattered points in radius bins (in Figure 3). The error bars are derived according to standard error propagation rules and are the ratio between the standard deviation of the points in the bin and the square root of the numbers of points in the bin. Any undersampling if present will be reflected in higher error bars.

The binned values indicate a monotonically decreasing variability with increasing clustercentric distance. The variability level in the cluster centre is higher than that outside at a significance level of 3.2$\sigma$. The values in all the distance bins are within 1$\sigma$ uncertainty to the fit prediction.

We fitted the binned values with a linear function as well as a flat line for comparison (in Figure 3). The best-fitting linear function gives us a reduced chi-square of 0.49 indicating that a linear fit with a negative slope is a good fit to the data, but the large uncertainties may indicate some degeneracy. The flat line fit to the data gives a reduced chi-square of 3.64 which means that a ’distance-independent’ model is rejected by the data.

We compare the optical variability-distance relation with samples consisting of background galaxies in the vicinity of the Virgo cluster, as well as Monte Carlo simulated galaxies.

Background galaxies in the Virgo cluster neighborhood are also taken from VCC as discussed in sections 2.1 and 2.2. The binned variability shows no significant relation to the distance from the cluster centre as shown in Figure 4. When we fit the data with a linear fit function, the slope is -0.06$\pm$0.10 which shows no significant difference from 0.00. The difference in chi-square between the linear fit (2.88) and the distance-independent fit (2.92) is negligible. The results show no compelling clustercentric distance-dependent relation for background galaxy variability. The background galaxies imply that the clustercentric-dependent variability is a cluster intrinsic property rather than due to some photometry measurement bias in the Virgo Cluster vicinity.

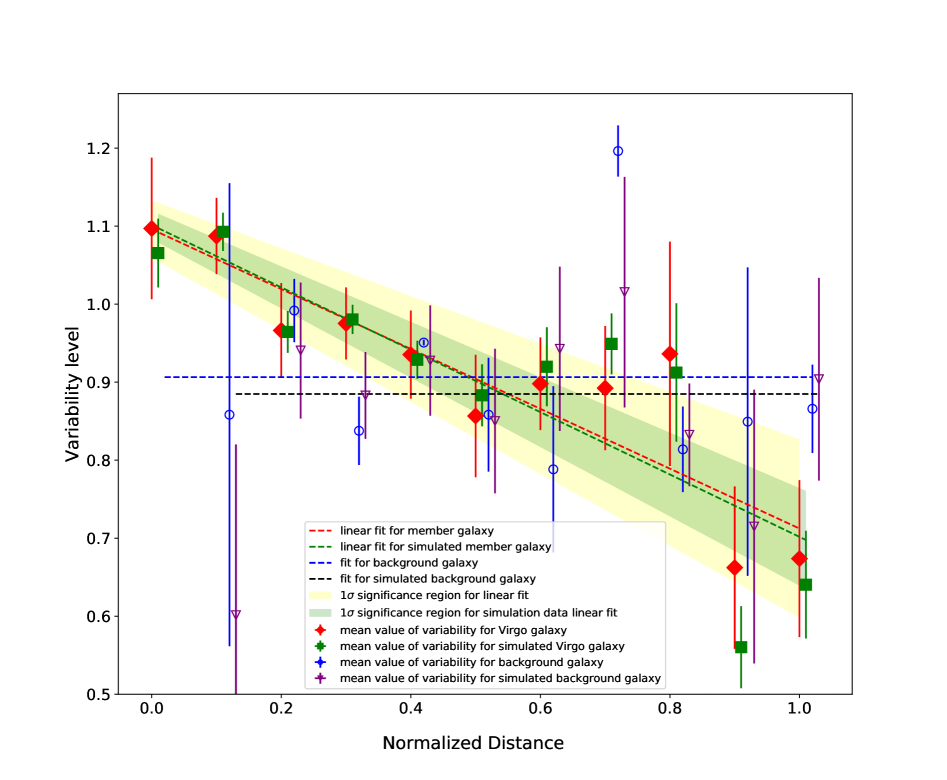
The relation was also investigated with simulated data. The simulation sampled the brightness distribution for every galaxy. We built a Gaussian distribution for every photometry epoch based on the magnitude and its error. This photometry was then sampled using the Gaussian distribution. In this manner, we obtained a new sample of simulated galaxy brightnesses and calculated the mean value of the variability. The procedure was repeated for 1000 times, both for Virgo member galaxies and background galaxies.

The binned galaxy variability from simulated data was then co-added. The median value was treated as the result of the whole simulation (as shown in Figure 4). The standard deviation of the binned variability among all the simulations is set as the error. The variability for member galaxies shows a consistent monotonically decreasing trend comparable to the real data. The results from background galaxies yield no significant relation.

By comparison, the simulation result for background galaxies gives a different data structure than real data. A constant function is a better fit than a linear function with a significant slope for the simulation data. The reduced chi-square is 0.65 for the constant fit and 0.98 for the linear fit. The inconsistent structure for background galaxies, even though both show a distance-independent relation, comes from the limited number of data sets. In contrast, the stable distribution for the member galaxies indicates that the relationship is not due to the data randomly walking within the photometry precision.

Galaxy variability presents a decreasing trend from the cluster centre outwards. The cluster-size feature of galaxy variability is a tracer of the environmental influences on galaxies. A precise description of how galaxies are affected is not clear due to limited observational evidence. There are a number of possible explanations but they are not fully conclusive. For example, more massive galaxies in the cluster centre might present more nuclear activity, according to the correlation between AGN luminosity and host galaxy mass (Fabian, 2012). However, the AGN fraction is reported to statistically decrease in the cluster centre (Miller et al., 2003; Kauffmann et al., 2004) which indicates that the increase of variability towards the cluster centre is specific to the Virgo cluster rather than for clusters in general. Another possibility is that the galaxies may be disturbed with gas provided by galaxy mergers (Hopkins et al., 2006). However, whether a merger is dry or wet differs in observations (Heckman & Best, 2014). Here, we present one possibility to explain the cluster scale galaxy variability distribution according to the best of our knowledge.

The Virgo cluster is reported as a cooling flow cluster (Hudson et al., 2010) in which group member galaxies show increasing star formation towards the cluster centre (Peterson et al., 2003). The central giant elliptical galaxy M87 is also known to present a high star formation rate due to the accretion of cooling intracluster gas (Fabian et al., 1982). Hillel & Soker (2014) states that some dense cool clumps are not fully heated by the feedback. Some of the cool gas falls in and feeds the central supermassive black hole. If the cooling gas in the Virgo cluster behaves accordingly to the theory by Hillel & Soker (2014), the gas will provide fuel for AGN activity which is consistent with our observations. The explanation fits but more observations, e.g. a comprehensive investigation of the variability of member galaxies for different types of galaxy clusters, would shed light on the underlying physical processes.