Gamow-Teller strength distributions of 18O and well-deformed nuclei 24,26Mg by deformed QRPA
Abstract
We investigate the Gamow-Teller (GT) transition strength distributions of strongly deformed nuclei, 24,26Mg, as well as of 18O. The calculations are performed within a deformed quasi-particle random phase approximation (DQRPA) which explicitly includes the deformation degree of freedom in the Skyrme-Hartree-Fock (SHF) and RPA calculations. The residual particle-particle () interaction as well as the particle-hole () interaction are extracted from Brückner -matrix calculations. The residual interaction dependence of the low-lying GT strength of these strongly deformed nuclei is examined by changing the strength of the residual and interactions. We have found that the low-lying GT peaks are quite similar in energy to those found in spherical and nuclei near magic shells, but the configurations of 24,26Mg are largely mixed by the pairing correlations and the deformation. Our results are compared to the experimental GT transition data by (, 3He) and (3He, ) reactions, and found to reproduce the main features of GT strength distributions.
pacs:
23.40.Hc, 21.60.Jz, 26.50.+xI Introduction
The Gamow-Teller (GT) excitation is one of the key transitions when studying the weak interaction of nuclei through charge-exchange (CEX) (or charged-current (CC)) reactions, beta decays, and electron or muon capture reactions. Recent remarkable progresses in the study of supernova (SN) neutrinos reveal that the GT transition is a key transition in the neutrino-induced reactions relevant to the neutrino processes Taka2015 ; Bala2015 ; Taka2013 ; Cheoun2012 ; Moha2023 ; Suzuki2023 ; Cheoun2023 . For example, the GT transition turns out to be dominant among various multipole transitions in the neutrino-nucleus (-A) reaction, according to recent theoretical calculations Taka2015 ; Bala2015 . However, we do not have enough data to confirm the reliability of theoretical models. Only limited data for the neutrino-induced reactions are available until now, despite many discussions about the possibility of low-energy neutrino sources Sato2005 ; Shin2016 . The recent progress in JSNS2 experiments JSNS2 could provide valuable low-energy neutrino beams on nuclear targets.
In this respect, neutrino reaction data at LSND LSND1 ; LSND2 , and recent successful CEX reaction data by proton or neutron beam at RIKEN or NSCL Sasano2011 ; Sasano2012 , triton and 3He beam at RCNP Freke2016 , and other light nuclei beams at other facilities, are greatly helpful for understanding the neutrino-induced reactions in the following aspects. First, the main contribution to the neutrino-induced reaction, namely, the GT transition, can be studied experimentally by the CEX reaction. Second, the quenching factor can be deduced from the GT data. Here, we should note that recent ab initio calculations have explained the quenching factor in a number of light- and medium-mass nuclei by the combined effect of two-body currents as well as by strong correlations Gysb2019 ; Heiko2020 . Third, some high-lying GT excitations, which contribute to the neutrino-induced reactions, can be investigated by the CEX reactions. These CEX data may also provide important information for the -process nucleosynthesis study, because additional protons and/or neutrons in cosmological nucleosynthesis sites may change the nuclear species by means of CEX reactions. For example, Gamow-Teller (+) transitions from 24Mg affect the electron capture rates in the O+Ne+Mg cores of stars, but theoretical results in Refs. Full1982 ; Jame2007 show some inconsistency among them. The understanding of decay branching ratios of the excited 24Mg states are also important for 12C + 12C fusion reactions Muns2017 ; Tumi2018 ; Monp2022 . The GT results for 18O are an important input for astrophysical calculations such as the CNO cycle Moha2023 , and also for neutrino detection due to the admixture of 18O in natural water at Hyper-Kamiokande Abe2021 .
From the nuclear physics viewpoint, the GT transition is an allowed spin-isospin excitation of a nucleus, and the transition operator is one of the simplest. Consequently, it may give invaluable information of the nuclear spin-isospin structure. However, there still remain some ambiguities, that prevent us from having a full quantitative understanding of GT excitations throughout the nuclear chart; the same issues prevent us from knowing precisely the matrix elements for 2 and 0 decays. In this work, we focus on one of the ambiguities, or open questions, regarding the GT strength in deformed nuclei: we study the deformation effects on the GT strength, by using Deformed Quasi-particle Random Phase Approximation (DQRPA) calculations.
Many nuclei in the nuclear chart are considered to be deformed, which can be verified from the E2 transition data as well as the rotational band structure. In particular, neutron-rich and neutron-deficient nuclei may be largely deformed, and these nuclei are among those that have strong low-energy GT strength or short -decay half-lives. Moreover, the deformation may produce unusual phenomena of shell evolution of protons and neutrons Ichik2019 , which make new sub-magic numbers and change to some extent the nature of particle-particle () and particle-hole () interactions. One of the practical but successful ways for properly describing the deformation is to start from the Nilsson model with the axial symmetry. Our previous calculations Ha2015a ; Ha2015b ; Ha2016 for the GT strength distribution of open shell nuclei by deformed QRPA showed that the deformation markedly alters the GT strength peaks obtained by a spherical QRPA.
The -QRPA model has been exploited using the Skyrme Hartree-Fock (SHF) plus BCS scheme developed by P. Sarrgiuren and co-workers Sarri2001 ; Sarri2001-b ; Sarri2005 ; Sarri2014 . They investigated the GT strength distribution in Zr and Mo isotopes Sarri2014 , the neutron-deficient Pb isotopes Sarri2005 , and the proton-rich Kr isotopes Sarri2001-b . For the neutron-rich nuclei, K. Yoshida also employed a model with Skyrme-type energy density functional (EDF) in the DQRPA Yoshi2008 ; Yoshi2013 .
The importance of the residual interaction was discussed in our early reports through calculations of both single- and double- decay transitions Ch93 ; pan . It should be noticed that these calculations were performed using spherical QRPA, which did not include the deformation explicitly. Primary aim of the present work is to perform the deformed QRPA (DQRPA) calculations with a realistic residual interaction, determined from the Brückner -matrix with the CD Bonn potential. We utilized as a starting point the Skyrme-type mean field (MF) Stoitsov instead of the Woods-Saxon potential employed in the previous calculations Ha2015a ; Ha2015b ; Ha2016 . Therefore, this work is an extension of our recent works Ha2015a ; Ha2015b for the DQRPA, in which all effects of the deformation are consistently treated in the QRPA framework based on the Woods-Saxon mean field Ha2015a .
As an application of the present DQRPA model, we choose the GT transitions of two Mg isotopes, 24Mg and 26Mg, because they are known as well-deformed nuclei. Moreover, there are precise GT experimental data by 3He and beams in these nuclei Zegers08 ; Madey87 ; Zegers06 . We perform also the study of an almost spherical nucleus 18O in DHF calculation as a counter example to strongly deformed nuclei. Our paper is organized as follows. In Sec. II, we briefly explain the formalism including the deformation. The applications to the GT transition strength distributions for Mg isotopes are performed in Sec. III with detailed discussions on the choice of necessary parameters for and residual interactions in the present formalism. Conclusions are drawn with a short perspective for future works in Sec. IV.
II formalism
Our calculation is carried out by using the QRPA Ha2015a , which adopts the SHF mean field Stoitsov for the mean field, and the residual interactions calculated by the Brückner -matrix based on the CD Bonn potential. On top of the mean field, the pairing correlations are taken into account in the BCS approximation. We refer to our previous papers for the detailed calculations of the BCS wave functions including the tensor force (TF) Ha18-1 ; Ha18-2 . Hereafter, we briefly summarize the DQRPA model, which will be applied for calculations of the GT strength distributions.
In the following, we adopt the standard QRPA formalism based on the equation of motion for the following phonon operator, acting on the BCS ground state Ha2015a :
| (1) |
where denotes the sign of the total angular momentum projection of the state for the reflection symmetry. Here, we have introduced pair creation and annihilation operators, composed by two quasiparticles and defined as
| (2) |
where is the quantum number associated with the projection of the intrinsic angular momentum on the symmetry axis, which is a good quantum number in the axially deformed nuclei. We note that parity is also treated as a good quantum number in the present approach. Here, indicates a set of quantum numbers to specify the single-particle-state (SPS). Isospin of the real particle is denoted by the Greek letter with prime (see Eqs. (II) and (II)). Since our formalism is constructed to include the pairing correlations composed of and contributions, we have two different types of quasiparticles, quasi-proton and quasi-neutron, and the isospin of the quasiparticles cannot be clearly defined Ha2015a . The quantum number corresponding to the quasi-isospin is denoted by , that is, with double-primes: in other words, these indices are and are used hereafter, instead of for neutrons and protons. Detailed discussion regarding the part has been done in our previous papers Ha18-1 ; Ha18-2 .
Within the quasi-boson approximation for the phonon operator, we obtain the following QRPA equation for describing the correlated DQRPA ground state:
| (11) | |||
| (30) |
where the amplitudes and in Eq. (11) stand for forward and backward going amplitudes from the state to the state Ha2015a ,
The and matrices in Eq. (11) are given by
where = 1 if and = , otherwise = Ch93 . The and coefficients are determined from the gap equations. The and stand for particle-particle and particle-hole renormalization factors for the residual interactions in Eqs. (II) and (II). The two-body interactions and are particle-particle and particle-hole matrix elements of the residual - interaction , respectively, which are calculated from the -matrix as solutions of the Bethe-Goldstone equation from the CD Bonn potential.
The two-body interactions and are, respectively, and matrix elements of the residual interaction in the deformed state. They are calculated from the -matrix in the spherical basis as follows
| (33) | |||||
Here and indicates spherical and deformed SPS, respectively. We note that the quasi-isospin and in the -matrix is replaced by total isospin ( or ) of the two-body interaction in the isospin representation. We use for . The expansion coefficient is defined as
| (34) |
with the Clebsch-Gordan coefficient , the spatial overlap integral , and the eigenvalues obtained from the total Hamiltonian in the deformed basis . Detailed formulas regarding the transformation of Eq. (7) can be found in Ref. Ha2015a .
Our DQRPA equation has a very general form because we include the deformation as well as two kinds of pairing correlations, and , in the model. If we switch off the pairing, all off-diagonal terms in the and matrices in Eq. (11) disappear with the replacement of 1 and 2 into and . Then the DQRPA equation is decoupled into DQRPA equations. QRPA can describe charge-conserving reactions such as the electromagnetic (EM) transitions, including magnetic dipole (M1) transition, between the initial and final states in the same nucleus, while QRPA describes charge-exchange reactions like the GT transitions between mother and daughter nuclei having different proton and neutron numbers, . If we assume spherical symmetry, our equations are reduced to the QRPA equations in Ref. Ch93 . If we neglect the pairing for the nuclei considered in this work, i.e. take only 1212 terms, Eq. (11) becomes the proton-neutron DQRPA as in Ref. saleh .
The GT transition operator is defined by
| (35) |
Detailed calculation for the transformation from the intrinsic frame to the nuclear laboratory system were presented in Ref. Ha2015a . The transition amplitudes from the ground state of an initial (parent) nucleus to the excited state of a final (daughter) nucleus, i.e. the one phonon state , are written as
| (36) | |||
where denotes the correlated QRPA ground state in the intrinsic frame and the nomalization factor is given as
Here, we use the following pairing interaction,
| (37) |
where the parameter for 18O is adjusted for fixing the GT peak position, and the other , and are taken from Ref. Stoitsov . The results of the parameters and the pairing gaps obtained with the pairing window associated with an energy cut-off of 60 MeV, are summarized in Table 1 for the Skyrme EDF parameter sets adopted in the present work.
| Nucleus | Skyrme EDF | [MeV] | [MeV] | |||
|---|---|---|---|---|---|---|
| 18O | SLy4 | -125 | 0.5 | 1.0 | 0.03 | 0.13 |
| 24Mg | SkP | -213 | 0.5 | 1.0 | 0.178 | 0.184 |
| 26Mg | SkP | -213 | 0.5 | 1.0 | 0.149 | 0.300 |
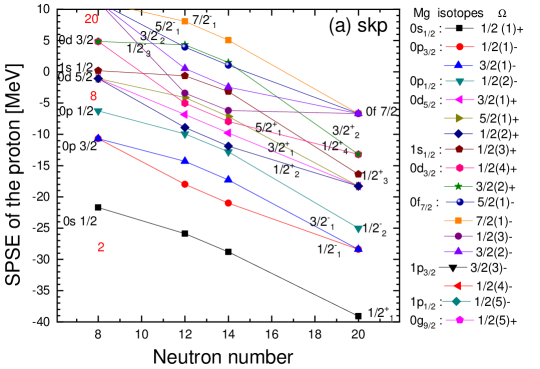
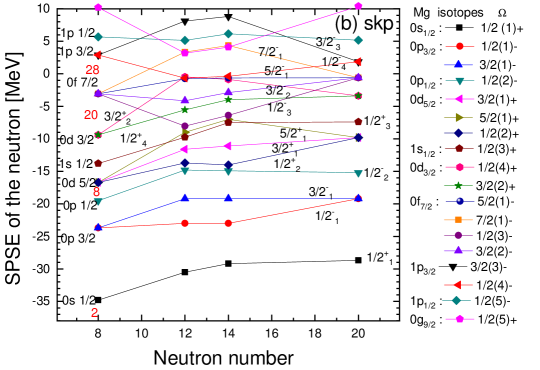
III Results and discussions
This study is based on the mean field obtained with the axially deformed Skyrme Hartree-Fock-Bogoliubov (SHFB) approach using a harmonic oscillator basis Stoitsov . The particle model space, for the nuclei considered here, includes states up to and , respectively, for the deformed and spherical basis. In the DQRPA, we adopt the wave functions and the SP energies from the SHFB equations. We utilize the SP energies from the deformed SHF mean field, and the -matrix for the two-body interaction in Eq. (II) and (II) is also calculated by using the wave functions from the deformed SHF.
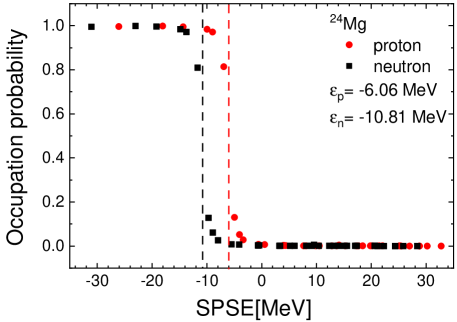
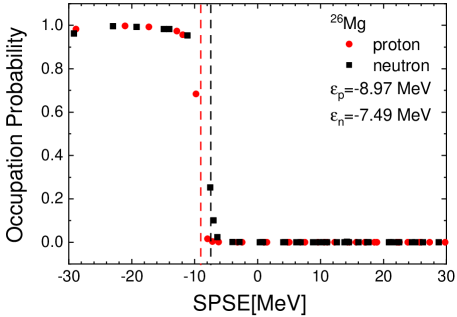
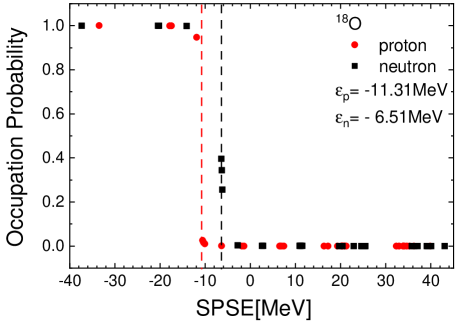
In Fig. 1, we illustrate the SPS evolution of protons and neutrons with the deformation. We note that the SP energy splitting of either the state or the state, induced by deformation in 24,26Mg, smears out the shell closures, and the magic numbers and 20 are disappeared. Instead, in the current work, appears as a proton quasi-magic number for Mg12 and Mg14 because of the relatively large energy gaps above the shell induced by the strong deformations as tabulated in Table 2. We note that the pairing interaction in Eq. (10) may smear the occupation probabilities, but the smearing is not significant, as shown in Fig. 4.
Another interesting point is that the SP energies of and orbitals are slightly higher in energy as the neutron number is increased while those of protons and orbitals are decreased. As a consequence, the Fermi energy gap of protons and neutrons for 26Mg and 16O is about 6 MeV, but for 24Mg it is about 1.5 MeV. Interestingly, in 24,26Mg, the three states, and as well as , are almost degenerate.
III.1 24Mg
| Nucleus | (MeV) | (MeV) | |
|---|---|---|---|
| 18O | 0.03 | - 6.51 | - 11.31 |
| 24Mg | 0.45 | - 10.81 | - 6.06 |
| 26Mg | 0.45 | - 7.49 | - 8.97 |


| configuration (spherical limit) | configuration type | ||
|---|---|---|---|
| SHFB+QRPA | , | 0.640 (0.022) | |
| , | 0.470 (0.019) | ||
| , | 0.450 (0.001) | ||
| , | 0.260 (0.007) | ||
| SHFB | , | 1.0 (0.0) |


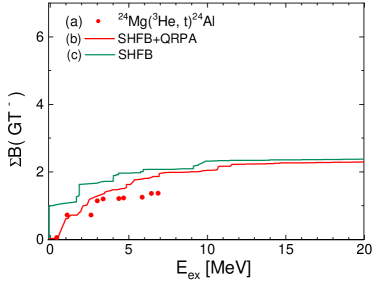
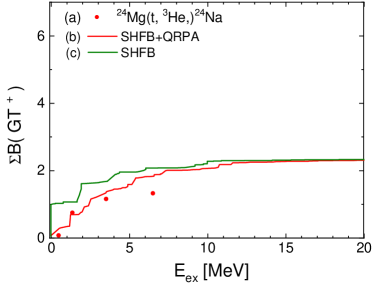
First, in Fig. 2, we present the results for 24Mg. The DQRPA explains GT(-) data as well as GT(+) data very well. Low energy GT peaks explicitly appear in the GT∓ strength distributions. It is interesting to see that both GT(-) and GT(+) strengths are concentrated in the low-energy region both in experiment and theory. The major configuration of the low-energy peak of the GT(-) strength is the excitation, while for the GT(+) peak, the excitation is dominant. This low-energy GT(-) strength may affect very much the -decay and electron capture reactions in the relevant nucleosynthesis processes in the stellar burning. A large low-lying GT(-) strength is also found in the doubly magic nucleus, 48Ca Ha2023 , where about 15 % of the sum rule strength is shifted to the low energy GT peak because of the attractive TF interaction between and states in the framework of the DQRPA based on the WS potential. Another interesting point to note is that the unperturbed configurations dictate the feature of low-lying strengths (see the panel (c) in Fig. 2), and the residual QRPA interactions scatter the main peaks obtained by the unperturbed SHF mean field calculations.
If we assume that 24Mg is a closed shell nucleus with the sub-magic number , the GT transition has to be dominated by the configurations and residual interaction. However some changes are induced by the smearing of the Fermi surface shown in Fig. 4, associated with the small pairing gap in Table 1. Thus, the assumed sub-magic shell is weakened and the effect of the interaction, associated with , also appears explicitly, as shown in Table 3. In Fig. 3, we examine the strength, or dependence of the GT strength distribution. The increase of slightly shifts the first peak to the higher energy region, and the change of makes a small change of the second peak strength, but the whole structure of the strength distribution is not changed. This is similar to the trend found in the case of double magic spherical nuclei like 48Ca, but the dominant interaction is a bit mixed with the interaction.
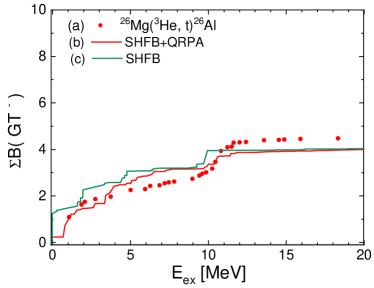
Fig. 5 shows the cumulated sum of the GT(∓) distributions for 24Mg. We use the quenching factor , which is taken from a shell model study of nuclear decay half-lives in and shell nuclei Kumar ; Kumar2 . This is somewhat smaller than the commonly used quenching factor Suzuki2023 . The adopted quenching factor reproduces well the gross feature of the cumulated sum, while the experimental data show further quenching than the calculated one.
III.2 26Mg

| configuration (spherical limit) | configuration type | ||
|---|---|---|---|
| SHFB+QRPA | , | 0.54 (0.16) | |
| , | 0.41 (0.14) | ||
| , | 0.28 (0.09) | ||
| SHFB | , | 1.0 (0.0) |
| configuration (spherical limit) | configuration type | ||
|---|---|---|---|
| SHFB+QRPA | , | 0.49 (0.0035) | |
| , | 0.44 (0.0009) | ||
| , | 0.43 (0.0019) | ||
| SHFB | , | 1.0 (0.0) |
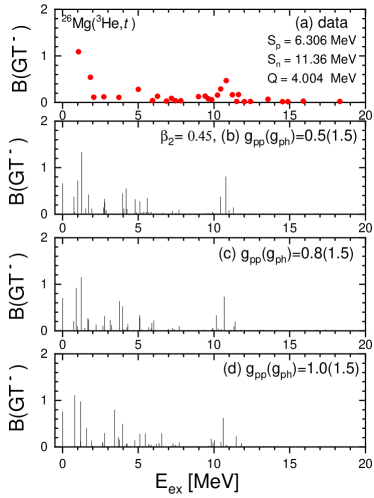
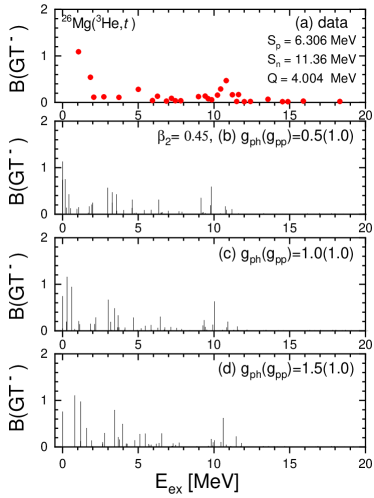
Hereafter, we discuss the results for 26Mg, where one can find a low-lying GT peak as well as the typical GTGR peak around 12 MeV as shown in Fig. 6(a). This strength distribution is similar to the case of 42Ca Ha2023 , i.e., a nucleus with .
Figure 6 (b) and (c) show numerical results for the B(GT(∓)) strength distribution for 26Mg: we remind its large deformation, associated with . The experimental data are described well by the present calculations. The main configurations for the first peak at MeV in Fig. 6 (b) and (c) are presented in Table 4. Compared with the 24Mg case, there are 2 extra neutrons above the semi-magic shell , which will create more type configurations than in 24Mg. However, because of the the smearing due to the pairing interaction as shown in Fig. 4, the interaction channels also play an important role as well as the one. This can be seen in Fig. 7, in which the effect of the variation of is similar to that induced by the change of : the lower energy strengths are changed appreciably, but the higher-energy peak is not so much changed by the increase of in the left panels of Fig. 7. A similar effect is also found in the right panels where the value is increased.
Now, we will discuss detailed features of the GT transitions in Tables 4 and 5. The first peak comes from two transitions between and , and and . We note that the low-lying GT transitions stem from the same states of protons and neutrons in the spherical limit, i.e., transitions within states as well as within spherical states.
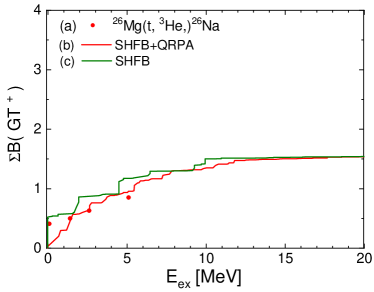
The main configurations of the high-lying GT state at MeV in Fig. 6 (b)-(d) are presented in Table 5, which shows the transition between different states i.e, and and and . It is interesting to notice that the negative parity configuration has also a large RPA amplitude to enhance the GT strength. The cumulated sum is shown in Fig. 8. The gross feature of the sum is reproduced by our calculations of SHFB+QRPA with the quenching factor =0.684.
III.3 18O
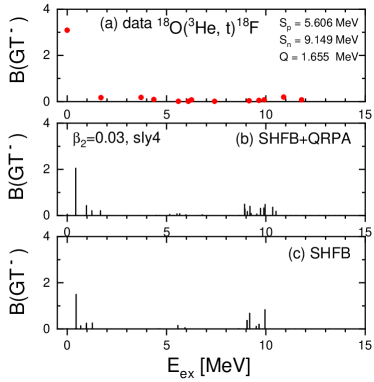
| configuration (spherical) | configuration type | ||
|---|---|---|---|
| SHFB+QRPA | , | 0.57 (0.08) | |
| , | 0.40 (0.07) | ||
| , | 0.29 (0.04) | ||
| , | 0.22 (0.06) | ||
| SHFB | , | 1.0 (0.0) |


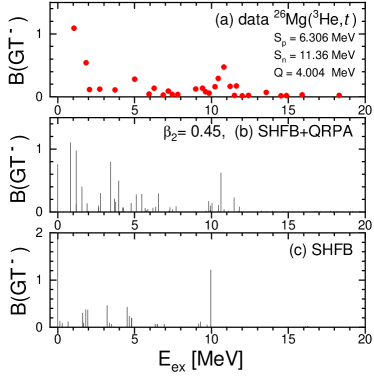
Finally, we discuss the results for 18O, which has a negligible intrinsic deformation in the DHF calculation and no rotational band structure was found experimentally, while the vibrational states are found Shukla . Therefore we consider the SHFB solution associated with in the following. We also expect that the GT strength distribution of 18O has low-lying GT peaks similar to those in 26Mg, because of the two extra neutrons on top of the magic number . Figure 9 shows results of the B(GT(-)) strength distribution for 18O. The results show low-lying peaks and also some GT strength around 10 MeV. The results are compatible with the experimental data.
The main configurations for the first peak at MeV in Fig. 9(b) are presented in Table 6. This peak comes, largely, from the configuration , under the influence of the attractive TF interaction. It turns out that a low-lying super-GT peak is also found in 18O similarly to other nuclei such as 42Ca Fujita2015 and 46Ti Adachi2006 . Since the GT results of the nuclei are sensitive to the strength we also provide the sensitivity tests to and in Fig. 10. They show clearly the dependence in the low-lying GT peaks in the left panels, while the dependence is almost invisible in the right panels. Another interesting point is that 18O does not show GTGR. It may come from the fact that the GTGR strength is fully shifted to low-lying GT states by a strong residual interaction, since the spin-orbit force is weaker than the case of 26Mg. However, there are some differences between data and theory in the MeV region. We note that the experiments may have strong background compared to those by reaction, and consequently, more careful analysis might be necessary to confirm the strength in the MeV region.
IV Summary and conclusion
We investigated the GT strength distributions of largely deformed s-d shell nuclei, 24Mg, 26Mg, and of an almost spherical nucleus, 18O, in the framework of Deformed QRPA (DQRPA). The present calculation adopts the SHF mean field with the residual interaction derived the -matrix calculation. We found that major part of the experimental data are better explained than in the previous calculations based on the Woods-Saxon potential Ha2016 . We found that 24Mg and 26Mg are strongly deformed, and a sub-magic shell at is found and plays an important role to describe the GT strength distributions of these nuclei. The cumulated sums of GT± strengths of 24Mg, 26Mg are studied in the low-energy region where the experimental data are available. Our SHFB+QRPA results give a good account of the sum rule values with a quenching factor for the GT operator.
We also confirmed similarities of the GT strength distributions of nuclei to those of nuclei. It implies that the low-lying GT states in nuclei are enhanced mainly by the () interaction, and relatively small GT strengths appear in the higher energy region in the case of the nuclei studied in this article. We argued that the strong deformation makes it so that the relevant residual interaction is a combination of and interactions, as shown in 24Mg and 26Mg, due to the smearing of Fermi surface by the pairing correlations. On the other hand, this phenomenon is not significant in the case of 18O nucleus, since it is almost spherical.
Finally, we note that the present DQRPA formalism is constructed to include the pairing on top of the pairing correlations, although the pairing is not considered in this work. In particular, a group of nuclei approximately with neutron number near the proton drip-line, such as 132Dy and 132Nd, have been reported to be good candidates for displaying both and pairing correlations, and consequently may have low-lying excitations associated with spin mixing, due to both isospin pairing correlations Alex2011 . Furthermore, recently -delayed spectroscopy from nuclei near the proton drip-line, for example, 56Zn, 48Fe and 60,62Ge, are available Sonj2023 . We leave the application of our formalism to the nuclei near proton drip-line as a future work.
Acknowledgement
This work was supported by the National Research Foundation of Korea (Grant Nos. NRF-2018R1D1A1B05048026). The work of MKC is supported by the National Research Foundation of Korea (Grant Nos. NRF-2021R1A6A1A03043957 and NRF-2020R1A2C3006177).
References
References
- (1)
- (2)
- (3) Toshitaka Kajino, Grant J. Mathews, Takehito Hayakawa, J. Phys. G 41, 044007 (2014).
- (4) K.G. Balasi, K. Langanke, G. Martinez-Pinedo, Prog. Part. Nucl. Phys. 85, 33 (2015).
- (5) T. Hayakawa, K. Nakamura, T. Kajino, S. Chiba, N. Iwamoto, M. K. Cheoun, G.J. Mathews, Astrophys. J. Lett. 779, L9 (2013).
- (6) Myung-Ki Cheoun, Eunja Ha, T. Hayakawa, Satoshi Chiba, Ko Nakamura, Toshitaka Kajino, Grant J. Mathews, Phys. Rev. C 85, 065807 (2012).
- (7) M. Mohammadzadeh, H. Khalili, A.R. Samana, M. dos Santos , C. A. Barbero4 S. B. Duarte, Eur. Phys. J. A 59, 31 (2023).
- (8) Myung-Ki Cheoun, K. Kim, E. Ha, H. Ko, D. Jang, Nuclear Physics Constraints on Neutrino Astrophysics, I. Tanihata, H. Toki, T. Kajino (eds), Handbook of Nuclear Physics, Springer, Singapore (2023).
- (9) Toshio Suzuki, Ken’ichiro Nakazato, Makoto Sakuda, Nucl. Phys. A 1038, 122719 (2023).
- (10) Joe Sato, Phys. Rev. Lett. 95, 131804 (2005).
- (11) J. Shin, Myung-Ki Cheoun, T.S. Park, T. Kajino, Phys. Rev. C 94, 045804 (2016).
- (12) D. H. Lee, S. Ajimura, M. K. Cheoun, J. H. Choi et al., arXiv:2308.02722v1 [hep-ex] (2023).
- (13) LSND Collaboration (C. Athanassopoulos et al.), Phys. Rev. C 55, 2078 (1997).
- (14) LSND Collaboration (L.B. Auerbach et al.), Phys. Rev. C 64, 065501 (2001).
- (15) M. Sasano, G. Perdikakis, R.G.T. Zegers, Sam M. Austin, D. Bazin, B.A. Brown, C. Caesar, A.L. Cole, J.M. Deaven, N. Ferrante, C.J. Guess, G.W. Hitt, R. Meharchand, F. Montes, J. Palardy, A. Prinke, L.A. Riley, H. Sakai, M. Scott, A. Stolz, L. Valdez, K. Yako, Phys. Rev. Lett. 107, 202501 (2011).
- (16) M. Sasano, G. Perdikakis, R.G.T. Zegers, Sam M. Austin, D. Bazin, B.A. Brown, C. Caesar, A.L. Cole, J.M. Deaven, N. Ferrante, C.J. Guess, G.W. Hitt, M. Honma, R. Meharchand, F. Montes, J. Palardy, A. Prinke, L.A. Ri ley, H. Sakai, M. Scott, A. Stolz, T. Suzuki, L. Valdez, K. Yako, Phys. Rev. C 86, 034324 (2012).
- (17) D. Frekers, M. Alanssari, T. Adachi, B.T. Cleveland, M. Dozono, H. Ejiri, S.R. Elliott, H. Fujita, Y. Fujita, M. Fu jiwara, K. Hatanaka, M. Holl, D. Ishikawa, H. Matsubara, H. Okamura, P. Puppe, K. Suda, A. Tamii, J. Thies, H. P. Yoshida, Phys. Rev. C 94, 014614 (2016).
- (18) P. Gysbers et al., Nature Physics 15, 428 (2019).
- (19) Heiko Hergert, Frontiers in Physics 8, 379 (2020).
- (20) G. M. Fuller, W. A. Fowler, and M. J. Newman, Astrophys. J. Suppl. 42, 447 (1980); 48, 279 (1982); Astrophys. J. 252, 715 (1982); 293, 1 (1985).
- (21) Jameel-Un Nabi and Muneeb-Ur Rahman, Phys. Rev. C 75, 035803 (2007).
- (22) J. M. Munson, E. B. Norman, J. T. Burke, R. J. Casperson et al. Phys. Rev. C 95, 015805 (2017).
- (23) A. Tumino, C. Spitaleri, M. La Cognata, S. Cherubini et al., Nature 557, 687 (2018).
- (24) E. Monpribat, S. Martinet, S. Courtin, M. Heine et al., Astronomy and Astrophysics 660, A47 (2022).
- (25) K. Abe et al., Hyper-Kamiokande Collaboration, Astrophys. J. 916 (2021) 15; K. Abe et al., Hyper-Kamiokande Design Report, arXiv:1805.04163, (2018).
- (26) Y. Ichikawa, H. Nishibata, Y. Tsunoda, A. Takamine et al., Nature Physics 15, 321 (2019).
- (27) Eunja Ha, Myung-Ki Cheoun, Nucl. Phys. A 934, 73 (2015).
- (28) Eunja Ha, Myung-Ki Cheoun, F. Simkovic, Phys. Rev. C 92, 044315 (2015).
- (29) Eunja Ha and Myung-Ki Cheoun, Phys. Rev. C 94, 054320 (2016).
- (30) P. Sarriguren, E. Moya de Guerra, A. Escuderos, and A. C. Carrizo, Nucl. Phys. A 635, 55 (1998); P. Sarriguren, E. Moya de Guerra, and A. Escuderos, ibid. A 658, 13 (1999); A691, 631 (2001).
- (31) P. Sarriguren, E. Moya de Guerra, and A. Escuderos, Phys. Rev. C 64, 064306 (2001).
- (32) P. Sarriguren, O. Moreno, R. Alvarez-Rodriguez, and E. Moya de Guerra, Phys. Rev. C 72, 054317 (2005).
- (33) P. Sarriguren, A. Algora, and J. Pereira, Phys. Rev. C 89, 034311 (2014).
- (34) Kenichi Yoshida and Nguyen Van Giai, Phys. Rev. C 78, 064316 (2008).
- (35) Kenichi Yoshida, Progress of Theoretical and Experimental Physics 2013, 113D02 (2013).
- (36) M. K. Cheoun, A. Bobyk, A. Faessler, F. imkovic, and G. Teneva, Nucl. Phys. A561, 74 (1993); A564, 329 (1993); M. K. Cheoun, A. Faessler, F. imkovic, G. Teneva, and A. Bobyk, ibid. A587, 301 (1995).
- (37) G. Pantis, F. imkovic, J. D. Vergados, and A. Faessler, Phys. Rev. C 53, 695 (1996).
- (38) S. Cwiok et al., Computer Physics Communications 46, 379 (1987).
- (39) Eunja Ha, Myung-Ki Cheoun, and H. Sagawa, Phys. Rev. C 97, 024320, (2018); ibid. 99, 064304 (2019).
- (40) Eunja Ha, Myung-Ki Cheoun, and H. Sagawa, W. Y. So, Phys. Rev. C 97, 064322, (2018).
- (41) R. G. T. Zegers et al., Phys. Rev. C 78, 014314 (2008).
- (42) R. Madey, et al., Phys. Rev. C 35, 2011 (1987).
- (43) R. G. T. Zegers et al., Phys. Rev. C 74, 024309 (2008).
- (44) Jouni Suhonen, From Nucleons to Nucleus (Springer-Verlag Berlin Heidelberg, 2007).
- (45) M. S. Yousef, V. Rodin, A. Faessler, and F. Simkovic, Phys. Rev. C 79, 014314 (2009).
- (46) S. Raman, C. W. Nestor Jr., P. Tikkanen, At. Data Nucl. Data Tables 78 (2001) 1.
- (47) Vikas Kumar, Anil Kumar, and Praveen C. Srivastava, Nucl. Phys. A 1017, 122344 (2022).
- (48) V. Kumar, P.C. Srivastava, H. Li, J. Phys. G, Nucl. Part. Phys., 43 105104 (2016).
- (49) Eunja Ha, Myung-Ki Cheoun, and H. Sagawa, arXiv 2402.01184 [nucl-th] (2023).
- (50) A Shukla, Sven Aberg, and S K Patra, J. Phys. G 38, 095103 (2011).
- (51) Y. Fujita et al., Phys. Rev. C 91, 064316 (2015).
- (52) T. Adachi et al., Phys. Rev. C 73, 024311 (2006).
- (53) M. E. Howard et al., Phys. Rev. C 78, 047302 (2008).
- (54) H. T. Chen and A. Goswami, Phys. Lett. 24B, 257 (1967).
- (55) H. H. Wolter, A. Faessler, and P. U. Sauer, Phys. Lett. 31B, 516 (1970).
- (56) A. Goodman, Phys. Rev. C 58, R3051 (1998).
- (57) F. imkovic, Ch. C. Moustakidis, L. Pacearescu, and A. Faessler, Phys. Rev. C 68, 054319 (2003).
- (58) Alexandros Gezerlis, G. F. Bertsch, and Y. L. Luo, Phys. Rev. Lett. 106, 252502 (2011).
- (59) E. Chabanat, P. Bonche, P. Haensel, J. Meyer and R. Schaeffer, Nucl. Phys. A 635, 231 (1998) Erratum: Nucl. Phys. A 643, 441 (1998).
- (60) Soonchul Choi, Ying Zhang, Myung-Ki Cheoun, Youngshin Kwon, Kyungsik Kim, Hungchong Kim, Phys. Rev. C 96, 024311 (2017).
- (61) M. Dutra, O. Lourenco, J. S. Sa Martins, A. Delfino, J. R. Stone, P. D. Stevenson, Phys. Rev. C 85, 035201 (2012).
- (62) P. -G. Reinhard and H. Flocard, Nucl. Phys. A 584, 467 (1995).
- (63) N. Van Giai and H. Sagawa, Phys. Lett. B 106, 379 (1981).
- (64) B. K. Agrawal, S. Shlomo and V. K. Au, Phys. Rev. C 72, 014310 (2005).
- (65) L. G. Cao, U. Lombardo, C. W. Shen and N. Van Giai, Phys. Rev. C 73, 014313 (2006).
- (66) A. W. Steiner, M. Prakash, J. M. Lattimer and P. J. Ellis, Phys. Rept. 411, 325 (2005)
- (67) M. Rashdan, Mod. Phys. Lett. A15, 1287 (2000).
- (68) Eunja Ha, Myung-Ki Cheoun, and H. Sagawa, Progress of Theoretical and Experimental Physics 2022, 043D01 (2022).
- (69) G. A. Lalazissis, S. Raman, P. Ring, At. Data and Nucl. Data tables 71, 1-40 (1999).
- (70) M. V. Stoitsov, J. Dobaczewski, W. Nazarewicz, P. Ring, Computer Physics Communications 167, 43-63 (2005).
- (71) Eunja Ha and Myung-Ki Cheoun, Phys. Rev. C 88, 017603 (2013).
- (72) P. Ring, Y. K. Gambhir, and G. A. Lalazissis, Comput. Phys. Commun. 105, 77 (1997). Phys. Rev. C 67, 044313 (2003).
- (73) A. Poves and G. Martinez-Pinedo, Phys. Lett. B 430, 203 (1998).
- (74) S. Baroni, A. O. Macchiavelli, and A. Schwenk, Phys. Rev. C 81, 064308 (2010).
- (75) S. G. Nilsson and I. Ragnarsson, Shapes and Shells in Nuclear Structure (Cambridge University Press, Cambridge, UK, 1995).
- (76) R. A. Eramzhyan, V. A. Kuz’min and T. V. Tetereva, Nucl. Phys. A 643, 428 (1998).
- (77) Eunja Ha, Myung-Ki Cheoun and K. S. Kim, J. Korean Phys. Soc., 67, 1142 (2015).
- (78) O. Civitarese, H. Muther, L. D. Skouras and Amand Faessler, J. Phys. G 17, 1363 (1991).
- (79) Alexandros Gezerlis, G. F. Bertsch, and Y. L. Luo, Phys. Rev. Lett. 106, 252502 (2011).
- (80) Sonja E. A. Orrigo1, Berta Rubio, and William Gelletly, EPJ Web of Conferences 290, 02018 (2023).