Gamow vectors formalism applied to the Loschmidt echo

As is well known, scattering resonances and quasi-stationary states are used to describe a scattering process in which a particle stays in the neighborhood of a center of forces –usually given by a potential– a time much longer than it would have remained if the center of forces were not present [8, 30]. Scattering resonances can be modeled using Hamiltonian pairs, $\{H_{0},H\}$, where $H_{0}$ is the unperturbed Hamiltonain and $H=H_{0}+V$, where $V$ is the potential responsible for the creation of the quasi-stationary states. The simplest model for resonances is the Friedrichs model, in which $H_{0}$ is given by

Here, $H_{0}$ has a pure absolutely and non-degenerate continuous spectrum, which is $\mathbb{R}^{+}\equiv[0,\infty)$ and an eigenvalue, $\omega_{0}>0$. Kets $|\omega\rangle$ are the eigenkets of $H_{0}$ with eigenvalues $\omega\in\mathbb{R}^{+}$, $H_{0}|\omega\rangle=\omega\,|\omega\rangle$. As in the case of plane waves, $|\omega\rangle$ are not normalizable states, which acquire meaning in suitable extensions of the Hilbert space called rigged Hilbert spaces or Gelfand triplets, for which there exists an extensive literature as mentioned in the Introduction. The eigenvector $|1\rangle$, $H|1\rangle=\omega_{0}\,|1\rangle$ belongs to Hilbert space and is normalized so that $\langle 1|1\rangle=1$. Notice that the eigenvalue $\omega_{0}$ is imbedded in the continuous spectrum of $H_{0}$.

The potential intertwines discrete and continuous spectrum of $H_{0}$ and it usually has the form

where $f(\omega)$ is a real function, usually square integrable, called form factor. Since bound states and scattering states are orthogonal to each other, we have that $\langle\omega|1\rangle=\langle 1|\omega\rangle=0$, for all $\omega\in\mathbb{R}^{+}$. In addition, $\langle\omega|\omega^{\prime}\rangle=\delta(\omega-\omega^{\prime})$ [49].

The total Hamiltonian has the form $H=H_{0}+\lambda\,V$, where $\lambda$ is a real coupling constant. The Hamiltonian $H$ has a pure simple absolutely continuous spectrum, so that

where $H|\omega^{\pm}\rangle=\omega\,|\omega^{\pm}\rangle$ are eigenkets for $\omega\in\mathbb{R}^{+}$, the continuous spectrum of $H$. The signs $\pm$ correspond to in and out states of scattering theory. More details can be found in [49].

This is the simplest possible Friedrichs model. The most straightforward generalization, is obtained by adding more bound states for $H_{0}$, so that

Thus, while $H_{0}$ has bound states, at least one, $H$ possesses none. What has happened with the bound states of $H_{0}$? To see it, we need a mathematical definition for resonances. A precise definition based in the analytic properties of the resolvent $(H-zI)^{-1}$ of $H$, where $z$ is a complex number, $z\in\mathbb{C}/\mathbb{R}^{+}$ and $I$ the identity operator, was given in [50], page 55. In the case of the simplest Friedrichs model, in which $H_{0}$ has only one bound state, it is sufficient to consider the analytic properties of the reduced resolvent function given by

Under mild conditions on the form factor $f(\omega)$ [51], the function $\eta(z)$ admits an analytic continuation with a pair of poles at the points $z_{0}=E_{R}-i\Gamma/2$ and $z_{0}^{*}=E_{R}+i\Gamma/2$, with $\Gamma>0$. In addition, and following the formulation of resonances in rigged Hilbert spaces [20, 21], there are two non-normalizable vectors $|f^{D}\rangle$ and $|f^{G}\rangle$, such that

Usually, $|f^{D}\rangle$ and $|f^{G}\rangle$ receive the names of decaying and growing Gamow vectors, respectively. Under mild assumptions, $z_{0}$ is analytic in the coupling constant $\lambda$ and has the property that $\lim_{\lambda\to 0}z_{0}=\omega_{0}$ [51].

In correspondence with the two spectral decompositions for $H$ given in (5), we have these other two:

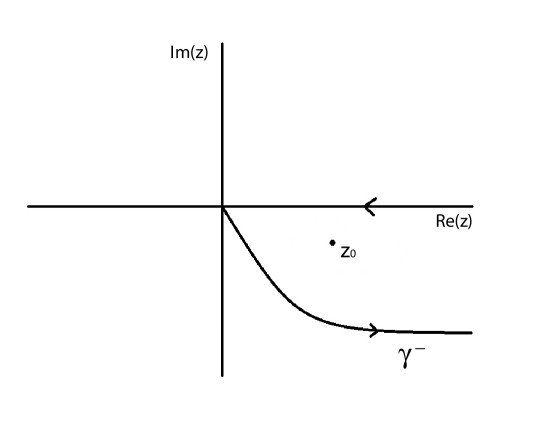
The meaning of the first spectral decomposition (10) is the following: let us assume that the functions $\varphi(\omega)=\langle\omega|\varphi\rangle$ and $\phi(\omega)=\langle\omega|\phi\rangle$ are analytically continuable to the upper and lower half of the complex plane, respectively. This, in particular, implies that $\varphi^{*}(\omega)=\langle\varphi|\omega\rangle$ admits analytic continuation to the lower half plane. The value of these functions at the point $z_{0}$ in the lower half plane is given by $\varphi^{*}(z_{0})=\langle\varphi|f^{D}\rangle$ and $\phi(z_{0})=\langle f^{G}|\phi\rangle$. The values of $\varphi^{*}(\omega)$ and $\phi(\omega)$ at the complex number $z$ with negative imaginary part are $\varphi^{*}(\omega)=\langle\varphi|z^{-}\rangle$ and $\phi(z)=\langle z^{+}|\phi\rangle$, respectively. Thus, what really has proper meaning is the value of $\langle\varphi|H|\phi\rangle$. Finally, $\gamma^{-}$ is a curve in the lower half plane, starting at the origin, that together with the positive semi-axis of the real line encloses the pole $z_{0}$ (see Fig. 1). Analogously, $\gamma^{+}$ is a curve in the upper half plane, starting at the origin, that together with the positive semi-axis of the real line encloses the pole $z^{*}_{0}$. The meaning of the second spectral decomposition in (10) is similar, but in the upper half plane.

A Friedrichs model with free Hamiltonian as in (6) and potential given by

The integral terms in (10) and (12) are responsible for the deviations of the exponential decay for very short (Zeno effect [3]) or very large values of time [4]. These effects are observable, although not easy to be observed [5, 6]. This means that, for the vast majority of experiments, they are not detected. Due to this reason, it makes sense to drop the integral term form (10) and (12), at least within a reasonable range of observations. Also, note that the spectral decompositions for $H$ either in (10) or in (12) are time reversal of each other, so that they are completely equivalent [34]. Therefore, one may take as an effective Hamiltonian, valid for the majority of observations, the following:

As in the case $N=1$, we have that $H|f^{D}_{k}\rangle=z_{k}\,|f_{k}^{D}\rangle$, for $k=1,\dots,N$. Along (3), this suggests that

Resonances may be considered as independent of each other, so that the Gamow vectors $|f_{1}^{D}\rangle,\dots,|f_{N}^{D}\rangle$ and $|f_{1}^{G}\rangle,\dots,|f_{N}^{G}\rangle$ may be assumed to be linearly independent. Then, we may assume that linear combinations of resonance states may belong either to the $N$ dimensional linear space, $\mathcal{H}_{N}^{D}$, spanned $|f_{1}^{D}\rangle,\dots,|f_{N}^{D}\rangle$ , or the space $\mathcal{H}_{N}^{G}$ spanned by $|f_{1}^{G}\rangle,\dots,|f_{N}^{G}\rangle$ or even to the $2N$ dimensional space, $\mathcal{H}_{2N}$, spanned by $|f_{1}^{D}\rangle,\dots,|f_{N}^{D}\rangle$ and $|f_{1}^{G}\rangle,\dots,|f_{N}^{G}\rangle$. Due to (14), the spaces $\mathcal{H}_{N}^{D}$ and $\mathcal{H}_{N}^{G}$ may be considered as duals of each other.

These ideas, along with (9), are the basis for the following comment. Assume that $|\psi\rangle$ and $|\varphi\rangle$ are arbitrary vectors in $\mathcal{\ H}_{N}^{D}$, so that

where the star denotes complex conjugation. The probability amplitude for the state $|\varphi(t)\rangle$ to be in the state $|\psi\rangle$ at time $t$ is given by

Instead, we may have considered the vectors $|\psi\rangle$ and $|\varphi\rangle$ to be in the space $\mathcal{H}_{2N}$, and follow a similar reasoning. Formally, the results would have been different, since to (20), we had to add a similar term. If this were the case,

In this section we study the Friedrichs model in terms of the creation and annihilation operators. Its construction has been proposed, for instance, in [28]. The idea is the following: Let us assume that $a$ and $a^{\dagger}$ are the annihilation and creation of $|1\rangle$ in (3), respectively, and that $b_{\omega}$ and $b^{\dagger}_{\omega}$ play the same role in relation to $|\omega\rangle$. Then, the Friedrichs free Hamiltonian $H_{0}$ written in terms of these operators is a contribution of two terms $H_{0}=H_{A}+H_{R}$, where [28],

and the interaction is now written as

where $\lambda$ is the coupling constant and $f(\omega)$ the form factor. Again, the total Hamiltonian is $H=H_{0}+H_{I}=H_{A}+H_{R}+H_{I}$. The function

is analytic with a branch cut on the positive semi-axis $[0,\infty)$. We denote its limits on this semi-axis from above to below and from below to above as $\eta^{+}(\omega):=\eta(\omega+i0)$ and $\eta^{-}(\omega):=\eta(\omega-i0)$, respectively. Then, a “diagonalization” of the total Hamiltonian $H$ is given by [28]

Here, $(A^{\dagger})_{\mathrm{in}}$ and $A_{\mathrm{out}}$ are the creation and annihilation of the Gamow state from a vacuum $|0\rangle$, so that

while $(\tilde{B}^{\dagger}_{\omega})_{\mathrm{in}}$ and $(\tilde{B}_{\omega})_{\mathrm{out}}$ are creation and annihilation operators of states in the continuum, which were defined in [28]. The latter do not have here any interest for us, as we are solely interested in the resonance behavior. The subscripts “in” and “out” come from scattering theory and do not play any role in our discussion here, so that we will omit them. Thus, the effective Hamiltonian, which concerns only to the presence of resonances is given by $H=z_{0}\,A^{\dagger}\,A$ in our notation.

Now, rename $|f_{1}^{D}\rangle:=|f^{D}\rangle$ and define $|f_{n}^{D}\rangle:=(A^{\dagger})^{n}\,|f_{1}^{D}\rangle$. If we denote by $N:=A^{\dagger}\,A$, it readily comes that

which formally yields

In the next section, we are going to apply the formalism of Gamow vectors to the Loschmidt echo.

For systems having an infinite number of resonances, it is possible in principle to define coherent resonance states. This states should have the following form for each complex number $z\in\mathbb{C}$:

Unfortunately, up to our knowledge, nobody has constructed a solvable Friedrichs model with an infinite number of resonance poles. Let us assume that we have $N+1$ resonances with decaying Gamow vectors $|f_{0}^{D}\rangle,\dots,|f_{N}^{D}\rangle$. By definition, a quasi coherent state at time $t=0$ is a vector of the form:

where $\alpha_{1}(0)$ is a given complex number. Note that for $N$ going to infinity (38) acquires the form (37), hence the name of quasi-coherent state. Analogously, for any other complex number $\alpha_{2}(0)$, we have

After a time $t>0$, the state becomes

The expression in the second row in (4.1) contains four terms. The sum of the second and third terms is called the non-diagonal part that we intend to analyze next.

Let us denote the sum of the second and third term in (4.1) as $\rho^{\mathrm{ND}}(t)$. Under the condition of macroscopicity, which is introduced below, the non-diagonal terms in (4.1) approximately satisfy the following relation:

This is not true in the general case as one may check by a direct calculation on $|\alpha_{1}(t)\rangle\langle\alpha_{2}(t)|=e^{-itH}\,|\alpha_{1}(0)\rangle\langle\alpha_{2}(0)|\,e^{itH}$.

In order to show (43), we should make the hypothesis of the macroscopicity condition, which means that the peaks of both approximate Gaussians are far from each other. This means that $|\alpha_{1}^{*}(0)-\alpha_{2}(0)|$ is very large (we will consider $\alpha_{1}(0)$ as a real value). Notice that, under this hypothesis, the states of the preferred basis $\{|\alpha_{1}(0)\rangle,|\alpha_{2}(0)\rangle\}$ are approximately orthogonal or quasi-orthogonal, which means that

where $\rho(t)$ has been introduced in (4.1), from which we have that

so that,