General analysis of polarization effects in coherent pseudoscalar mesons photo– and electroproduction on deuteron

G. I. Gakh National Science Centre, Kharkov Institute of Physics and Technology,
61108 Akademicheskaya 1, Kharkov, and V. N. Karazin Kharkov National University, Dept. of Physics and Technology, 31 Kurchatov, 61108, Kharkov, Ukraine A. G. Gakh V. N. Karazin Kharkov National University, Dept. of Physics and Technology, 31 Kurchatov, 61108, Kharkov, Ukraine E. Tomasi–Gustafsson egle.tomasi@cea.fr IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette Cedex, France

Abstract

General expressions for the unpolarized differential cross section and for various polarization observables in the coherent pseudoscalar meson photo- and electroproduction on the deuteron target have been obtained in one-photon-exchange approximation. The spin structure of the matrix element is explicitly derived in terms of structure functions. The correspondence with the helicity amplitudes is given. The polarization effects have been investigated for the case of a longitudinally polarized electron beam and vector or tensor polarized deuteron target. The polarization (vector or tensor) of the scattered deuteron for the case of unpolarized or a longitudinally polarized electron beam is also considered. In the case of the photoproduction reaction, we consider linearly, circularly or elliptically polarized photon beam. Numerical estimations have been done for the unpolarized differential cross section and for some polarization observables.

pacs:

13.40-f,13.40.Gp,13.88+e

I Introduction

The complete characterization of meson photo- and electroproduction on nuclei requires the detection of the neutron which must rely on meson production by real or virtual photons from light nuclei. The well known nuclear structure of the deuteron makes it a most suitable nuclear target, in comparison to other nuclei. Experiments with deuteron targets have been done and are being performed. A recent status of the study of the meson photoproduction can be found in the review Krusche and Schadmand (2003).

Besides the experiments on the electromagnetic production of the isovector mesons ( $\pi$ -meson), a series of precise measurements of breakup and coherent isoscalar meson ( $\eta$ -meson) photoproduction from the deuteron target have been performed during the last few years. The inclusive cross section of the reactions $d(\gamma,\eta)X$ are presented in Refs. Krusche et al. (1995); Weiss et al. (2003). The exclusive reaction with detection of the recoil nucleons was also investigated for the deuteron target Weiss et al. (2003); Hoffmann-Rothe et al. (1997); Hejny et al. (1999). The data on coherent $\eta$ -meson photoproduction off the deuteron are given in Refs. Hoffmann-Rothe et al. (1997); Weiss et al. (2001).

The combination of $4\pi$ detectors (as it can be recently done in Bonn and Mainz) with linearly and circularly polarized photon beams as well as polarized targets will provide the measurement of various polarization observables. These new observables can give us an additional information on resonance properties and the details of the reaction mechanism.

In the last decade the progress in the investigation of the meson production by the electromagnetic probes has been substantial and we moved forward in the understanding of the resonance properties.

The differential cross sections for the reaction on coherent and incoherent $\pi^{0}$ -meson photoproduction from the deuteron have been measured at MAMI (Mainz) in the energy range $140$ MeV $<E_{\gamma}<306$ MeV Siodlaczek et al. (2001). Earlier, the total and differential cross sections covering the full angular range have been obtained for coherent and incoherent single $\pi^{0}$ -meson photoproduction from the deuteron in the second resonance region (200 MeV $<E_{\gamma}<792$ MeV) at Mainz Krusche et al. (1999). It was found that final-state interaction effects for the incoherent process are much more important than for coherent reaction. In the last case these effects are not very large and different models do not agree about the main final-state interaction mechanism. Therefore, no final conclusion about these mechanisms can be reached.

The data on pion production in coherent electron-deuteron collisions are scarce. The experimental study of this reaction is now possible, at Mainz and JLab, due to the high-duty cycle of the electron machines. Threshold $\pi^{0}$ -meson electroproduction on protons and deuteron has been investigated by the A1 collaboration at Mainz Distler et al. (1998); Ewald et al. (2001) at small four momentum transfer squared $Q^{2}\leq 0.1$ GeV². The first experimental results for the coherent $\pi^{0}$ -meson electroproduction off the deuteron at large $Q^{2}$ , $1.1<Q^{2}<1.8$ GeV², from the threshold to 200 MeV excitation energy in the $d\pi^{0}$ system, are reported in Ref. Tomasi-Gustafsson et al. (2003). The data were collected during the $t_{20}$ experiment, the primary aim of which was the measurement of the deuteron tensor polarization in elastic electron-deuteron scattering Abbott et al. (2000).

A general theoretical study of pion electroproduction on deuterons was first developed in Ref. Rekalo et al. (2002) for the unpolarized case. The reaction $e+d\to e+d+\pi^{0}$ involves the study of the deuteron structure and of the reaction mechanism, and requires the knowledge of the neutron and proton elementary amplitudes, $\gamma^{*}+n,p\to n,p+\pi^{0}$ .

The experimental investigation of the nucleon resonance properties by means of the meson production processes can be used to verify and constrain the models of the hadron structure. The production of the neutral mesons by real or virtual photons is of special interest since,in these reactions, the background contributions are suppressed due to the weak coupling of the photon with neutral mesons.

In this work, we follow the formalism of Ref. Rekalo et al. (2002). We focus on the polarization observables, giving the general expressions for the case of a longitudinally polarized electron beam and vector or tensor polarized deuteron target (or scattered deuteron), in the one-photon exchange approximation and neglecting the lepton mass. In the case of the photoproduction reaction, we consider linearly, circularly or elliptically polarized photon beam. A numerical application and illustration of the observables is shown, on the basis of impulse approximation and the elementary model previously developed in Ref. Rekalo et al. (2002).

Not only high intensity polarized electron beams are available, and vector and tensor polarized targets are currently used, but also the principle of measuring the vector and tensor deuteron polarization in the GeV range from backward elastic scattering, has been proved to be feasible Tomasi-Gustafsson et al. (1999).

II Matrix element and differential cross section

The general structure of the differential cross section for the reaction

e^{-}(k_{1})+d(p_{1})\to e^{-}(k_{2})+d(p_{2})+\pi^{0}(q),

(1)

(the four–momenta of the corresponding particles are indicated in the brackets) can be written in the frame of the one–photon–exchange mechanism. The formalism in this section is based on the most general symmetry properties of the hadron electromagnetic interaction, such as the gauge invariance (the conservation of the hadronic and leptonic electromagnetic currents), $P$ –invariance (the invariance with respect to the space reflections) and does not depend on the deuteron structure and on the details of the reaction mechanism.

In the one–photon–exchange approximation, the matrix element for the process of the coherent $\pi^{0}$ –meson electroproduction on the deuteron can be written as

M(ed\to ed\pi^{0})=\frac{e^{2}}{k^{2}}j_{\mu}J_{\mu},

(2)

with

j_{\mu}=\bar{u}(k_{2})\gamma_{\mu}u(k_{1}),\ \ J_{\mu}=<d\pi^{0}|\hat{J}_{\mu}|d>,

(3)

where $k=k_{1}-k_{2}$ is the virtual–photon four–momentum and $J_{\mu}$ is the electromagnetic current describing the transition $\gamma^{*}+d\to d+\pi^{0}$ ( $\gamma^{*}$ is the virtual photon).

The electromagnetic structure of nuclei, as probed by elastic and inelastic electron scattering by nuclei, can be characterized by a set of response functions or structure functions Donnelly and Raskin (1986); Boffi et al. (1944). Each of these structure functions is determined by different combinations of the longitudinal and transverse components of the electromagnetic current $J_{\mu}$ , thus providing different pieces of information about the nuclear structure or possible mechanisms of the reaction under consideration. The components which are determined by the real parts of the bilinear combinations of the reaction amplitudes, are nonzero in the impulse approximation, the other ones, which originate from the imaginary part of structure functions, vanish if the final state interaction is absent.

The formalism of the structure functions is especially convenient for the investigation of polarization phenomena for the reaction (1).

Using the conservation of the leptonic $j_{\mu}$ and hadronic $J_{\mu}$ electromagnetic currents $(k\cdot j=k\cdot J=0)$ , one can rewrite the matrix element (2) in terms of the space components of these currents only

M(ed\to ed\pi^{0})=\frac{e^{2}}{k^{2}}{\vec{e}}\cdot{\vec{J}},\ \ {\vec{e}}=\frac{{\vec{j}}\cdot{\vec{k}}}{k_{0}^{2}}{\vec{k}}-{\vec{j}},

(4)

where $k=(k_{0},{\vec{k}})$ and $k_{0}({\vec{k}})$ is the energy (three–momentum) of the virtual photon in CMS of the $\gamma^{*}+d\to d+\pi^{0}$ reaction. All observables are determined by bilinear combinations of the space components of the hadronic current ${\vec{J}}$ : $H_{ab}=J_{a}J_{b}^{*}.$ As a result, we obtain the following general structure of the differential cross section for the reaction (1), when the scattered electron and $\pi^{0}$ –meson are detected in coincidence, and the electron beam is longitudinally polarized (the polarization states of the deuteron target and scattered deuteron can be any)

$\displaystyle\frac{d^{3}\sigma}{dE^{\prime}d\Omega_{e}d\Omega_{P}}$	$\displaystyle=$	$\displaystyle N\biggl{[}H_{xx}+H_{yy}+\varepsilon\cos(2\varphi)(H_{xx}-H_{yy})+\varepsilon\sin(2\varphi)(H_{xy}+H_{yx})$	(5)
		$\displaystyle-2\varepsilon\frac{k^{2}}{k_{0}^{2}}H_{zz}-\frac{\sqrt{-k^{2}}}{k_{0}}\sqrt{2\varepsilon(1+\varepsilon)}\cos\varphi(H_{xz}+H_{zx})-$
		$\displaystyle-\frac{\sqrt{-k^{2}}}{k_{0}}\sqrt{2\varepsilon(1+\varepsilon)}\sin\varphi(H_{yz}+H_{zy})$
		$\displaystyle\mp i\lambda\sqrt{(1-\varepsilon^{2})}(H_{xy}-H_{yx})\mp i\lambda\frac{\sqrt{-k^{2}}}{k_{0}}\sqrt{2\varepsilon(1-\varepsilon)}\cos\varphi(H_{yz}-H_{zy})\pm$
		$\displaystyle\pm i\lambda\frac{\sqrt{-k^{2}}}{k_{0}}\sqrt{2\varepsilon(1-\varepsilon)}\varphi(H_{xz}-H_{zx})\biggr{]},$
		$\displaystyle N=\frac{\alpha^{2}}{64\pi^{3}}\frac{E^{\prime}}{E}\frac{\|{\vec{q}}\|}{MW}\frac{1}{1-\varepsilon}\frac{1}{(-k^{2})},\|{\vec{k}}\|=\frac{1}{2W}\sqrt{(W^{2}+M^{2}-k^{2})^{2}-4M^{2}W^{2}},$
		$\displaystyle\|{\vec{q}}\|=\frac{1}{2W}\sqrt{(W^{2}+M_{P}^{2}-M^{2})^{2}-4M_{P}^{2}W^{2}},\ \varepsilon^{-1}=1-2\frac{{\vec{k}}^{2}_{Lab}}{k^{2}}\tan^{2}(\frac{\theta_{e}}{2}).$

The $z$ axis is directed along the virtual photon momentum ${\vec{k}}$ , the momentum of the detected $P$ –meson ${\vec{q}}$ lies in the $xz$ plane (reaction plane); $E(E^{\prime})$ is the energy of the initial (scattered) electron in the deuteron rest frame (laboratory (Lab) system); $\theta_{e}$ is the electron scattering angle (the angle between the momenta of the initial and scattered electrons) in the Lab system; $d\Omega_{e}$ is the solid angle of the scattered electron in the Lab system, $d\Omega_{P}(q)$ is the solid angle (value of the three-momentum) of the detected $P$ –meson in the $Pd$ –pair center–of–mass system (CMS), $M_{P},M$ are the masses of the $P$ –meson, deuteron, respectively; $\varphi$ is the azimuthal angle between the electron scattering plane and the plane where the detected $P$ –meson lies $(xz)$ , $k_{0}=(W^{2}+k^{2}-M^{2})/2W$ is the virtual photon energy in the $Pd$ –pair CMS, $W$ is the invariant mass of the final hadrons, $W^{2}=M^{2}+k^{2}+2M(E-E^{\prime})$ ; $\lambda$ is the degree of the electron longitudinal polarization, $\varepsilon$ is the degree of the linear polarization of the virtual photon. The upper (bottom) sign in this formula corresponds to the electron (positron) scattering. This expression is valid for zero electron mass. Below we will neglect it wherever possible.

Let us introduce, for convenience and simplification of the following calculations of the polarization observables, the orthonormal system of basic unit vectors ${\vec{m}},{\vec{n}}$ , and $\hat{\vec{k}}$ which are built from the momenta of the particles participating in the reaction under consideration

\hat{\vec{k}}=\frac{{\vec{k}}}{|{\vec{k}}|},\ \ {\vec{n}}=\frac{{\vec{k}}\times{\vec{q}}}{|{\vec{k}}\times{\vec{q}}|},\ \ {\vec{m}}={\vec{n}}\times\hat{\vec{k}}.

The unit vectors $\hat{\vec{k}}$ and ${\vec{m}}$ define the $\gamma^{*}+d\to d+\pi^{0}$ reaction $xz$ –plane ( $z$ axis is directed along the three–momentum of the virtual photon ${\vec{k}}$ , and $x$ axis is directed along the unit vector ${\vec{m}}$ ), and the unit vector ${\vec{n}}$ is perpendicular to the reaction plane.

First of all, let us establish the spin structure of the matrix element for the $\gamma^{*}+d\to d+\pi^{0}$ reaction without any constraint on the kinematical conditions.

The amplitude spin structure can be parameterized by different (and equivalent) methods, but for the analysis of the polarization phenomena the choice of the transverse amplitudes is sometimes preferable. Taking into account the $P$ –invariance of the hadron electromagnetic interaction, the dependence of the $\gamma^{*}+d\to d+\pi^{0}$ amplitude on the virtual–photon polarization vector and polarization three vectors ${\vec{U}}_{1}$ and ${\vec{U}}_{2}$ of the initial and final deuterons is given by Rekalo et al. (2002):

$\displaystyle F(\gamma^{*}d\to dP)$	$\displaystyle=$	$\displaystyle{\vec{e}}\cdot{\vec{m}}(g_{1}{\vec{m}}\cdot{\vec{U}}_{1}{\vec{n}}\cdot{\vec{U}}_{2}^{}+g_{2}\hat{\vec{k}}\cdot{\vec{U}}_{1}{\vec{n}}\cdot{\vec{U}}_{2}^{}+g_{3}{\vec{n}}\cdot{\vec{U}}_{1}{\vec{m}}\cdot{\vec{U}}_{2}^{}+g_{4}{\vec{n}}\cdot{\vec{U}}_{1}\hat{\vec{k}}\cdot{\vec{U}}_{2}^{})+$	(6)
		$\displaystyle+{\vec{e}}\cdot{\vec{n}}\bigl{(}g_{5}{\vec{m}}\cdot{\vec{U}}_{1}{\vec{m}}\cdot{\vec{U}}_{2}^{}+g_{6}{\vec{n}}\cdot{\vec{U}}_{1}{\vec{n}}\cdot{\vec{U}}_{2}^{}+g_{7}\hat{\vec{k}}\cdot{\vec{U}}_{1}\hat{\vec{k}}\cdot{\vec{U}}_{2}^{*}+$
		$\displaystyle+g_{8}{\vec{m}}\cdot{\vec{U}}_{1}\hat{\vec{k}}\cdot{\vec{U}}_{2}^{}g_{9}\hat{\vec{k}}\cdot{\vec{U}}_{1}{\vec{m}}\cdot{\vec{U}}_{2}^{})+{\vec{e}}\cdot\hat{\vec{k}}(g_{10}{\vec{m}}\cdot{\vec{U}}_{1}{\vec{n}}\cdot{\vec{U}}_{2}^{*}+$
		$\displaystyle+g_{11}\hat{\vec{k}}\cdot{\vec{U}}_{1}{\vec{n}}\cdot{\vec{U}}_{2}^{}+g_{12}{\vec{n}}\cdot{\vec{U}}_{1}{\vec{m}}\cdot{\vec{U}}_{2}^{}+g_{13}{\vec{n}}\cdot{\vec{U}}_{1}\hat{\vec{k}}\cdot{\vec{U}}_{2}^{*}\bigr{)},$

where $g_{i}(i=1-13)$ are the scalar amplitudes, depending on three variables $k^{2}$ , $W$ and $\vartheta$ ( $\vartheta$ is the angle between the virtual photon and $\pi^{0}$ –meson momenta in the $\gamma^{*}+d\to d+\pi^{0}$ reaction CMS), which completely determine the reaction dynamics. If we single out the virtual–photon polarization vector ${\vec{e}}$ , we can write the amplitude ${\it F}$ as follows

{\it F}={\it F_{i}}e_{i}

and the hadronic tensor can be written in terms of ${\it F_{i}}$ as

H_{ij}={\it F_{i}}{\it F_{j}^{*}}.

The process $\gamma^{*}+d\to d+P$ is described by a set of nine amplitudes for the absorption of a virtual photon with transverse polarization and four amplitudes for the absorption of a virtual photon with longitudinal polarization. These numbers are dictated by the values of the spins of the particles and by the $P$ –invariance of hadron electrodynamics. Therefore, the complete experiment requires, at least, the measurement of 25 observables. Let us mention in this respect specific properties of polarization phenomena for inelastic electron–hadron scattering: in exclusive $e^{-}+d\to e^{-}+d+P$ processes the virtual photon has a nonzero linear polarization, even for the scattering of unpolarized electrons by an unpolarized deuteron target.

III Polarized deuteron target

Let us consider the dependence of the observables on the polarization state of the deuteron target, which is described by the spin density matrix. We use the following general expression for the deuteron spin density matrix in the coordinate representation Schildknecht (1965, 1967)

\rho_{\mu\nu}=-\frac{1}{3}(g_{\mu\nu}-\frac{p_{1\mu}p_{1\nu}}{M^{2}})-\frac{i}{2M}\varepsilon_{\mu\nu\alpha\beta}s_{\alpha}p_{1\beta}+S_{\mu\nu},

(7)

where $s_{\alpha}$ is the four–vector describing the vector polarization of the target, $s^{2}=-1,$ $s\cdot p_{1}=0$ and $S_{\mu\nu}$ is the tensor describing the tensor (quadrupole) polarization of the target, $S_{\mu\nu}=S_{\nu\mu},$ $p_{1\mu}S_{\mu\nu}=0,$ $S_{\mu\mu}=0$ (due to these properties the tensor $S_{\mu\nu}$ has only five independent components). In Lab system all time components of the tensor $S_{\mu\nu}$ are zero and the tensor polarization of the target is described by five independent space components $(S_{ij}=S_{ji},S_{ii}=0,i,j=x,y,z).$ The four–vector $s_{\alpha}$ is related to the unit vector ${\vec{\xi}}$ of the deuteron vector polarization in its rest system by:

s_{0}=-{\vec{k}}{\vec{\xi}}/M,\ {\vec{s}}={\vec{\xi}}+{\vec{k}}({\vec{k}}{\vec{\xi}})/M(M+E_{1}),

(8)

where $E_{1}$ is the deuteron–target energy in the $\gamma^{*}+d\to d+\pi^{0}$ reaction CMS.

The hadronic tensor $H_{ij}(i,j=x,y,z)$ depends linearly on the target polarization and can be written as

H_{ij}=H_{ij}(0)+H_{ij}(\xi)+H_{ij}(S),

(9)

where the term $H_{ij}(0)$ corresponds to the case of unpolarized deuteron target, and the term $H_{ij}(\xi)(H_{ij}(S))$ corresponds to the case of vector (tensor)-polarized target.

III.1 Unpolarized deuteron target

The general structure of the part of the hadronic tensor which corresponds to the unpolarized deuteron target has following form:

H_{ij}(0)=h_{1}m_{i}m_{j}+h_{2}n_{i}n_{j}+h_{3}\hat{k}_{i}\hat{k}_{j}+h_{4}\{m,\hat{k}\}_{ij}+ih_{5}[m,\hat{k}]_{ij},

(10)

where $\{a,b\}_{ij}=a_{i}b_{j}+a_{j}b_{i},\ [a,b]_{ij}=a_{i}b_{j}-a_{j}b_{i}$ and the real structure functions $h_{i}$ depend on three invariant variables $s=W^{2}=(k+p_{1})^{2}$ , $k^{2}$ and $t=(k-p_{1})^{2}$ . The structure functions $h_{1}-h_{4}$ determine the cross section for the $e^{-}+d\to e^{-}+d+P$ reaction with unpolarized particles. Let us emphasize that the structure function $h_{5}$ (the so–called fifth structure function) determines the asymmetry of longitudinally polarized electrons scattered by an unpolarized target. It is determined by the strong interaction effects of the $P$ –meson and deuteron in the final state and it vanishes for the pole (Born) diagram contribution in all kinematic range (independently on the particular parametrization of the $\gamma^{*}N\to NP$ amplitude and $dnp-$ vertex). This is true for the nonrelativistic approach and for the relativistic one as well describing the $\gamma^{*}+d\to d+P$ reaction. The scattering of longitudinally polarized electrons by unpolarized deuteron target allows to determine the $h_{5}$ contribution. Then the corresponding asymmetry is determined only by the strong interaction effects. More exactly, it is determined by the effects arising from non-pole mechanisms of various nature: meson exchange currents can induce nonzero asymmetry, dibaryon resonances, if they exist, lead also to nonzero asymmetry.

In the chosen coordinate system, the different hadronic tensor components, entering in the expression of the cross section (4), are related to the structure functions $h_{i}(i=1-5)$ by:

	$\displaystyle H_{xx}\pm H_{yy}$	$\displaystyle=$	$\displaystyle h_{1}\pm h_{2},\ \ H_{zz}=h_{3},\ \ H_{xz}+H_{zx}=2h_{4},$
	$\displaystyle H_{xz}-H_{zx}$	$\displaystyle=$	$\displaystyle 2ih_{5},\ \ H_{xy}\pm H_{yx}=0,\ \ H_{yz}\pm H_{zy}=0.$		(11)

The expressions for the structure functions $h_{i}$ (i=1-5) in terms of the reaction amplitudes $g_{i}(i=1-13)$ are given in Appendix I. The expressions of the reaction amplitudes $g_{i}(i=1-13)$ depend on the underlying model. Their explicit form as function of the deuteron inelastic form factors in impulse approximation can be found in Ref. Rekalo et al. (2002).

In the one–photon–exchange approximation, the general structure of the differential cross section for the reaction $d({\vec{e}},e^{\prime}P)d$ (in the case of longitudinally polarized electron beam and unpolarized deuteron target) can be written in terms of five independent contributions

\frac{d^{3}\sigma}{dE^{\prime}d\Omega_{e}d\Omega_{P}}=N\biggl{[}\sigma_{T}+\varepsilon\sigma_{L}+\varepsilon\cos(2\varphi)\sigma_{P}+\sqrt{2\varepsilon(1+\varepsilon)}\cos\varphi\sigma_{I}+\lambda\sqrt{2\varepsilon(1-\varepsilon)}\varphi\sigma^{\prime}_{I}\biggr{]},

(12)

where the individual contributions are related to the structure functions $h_{i}$ of the spin–independent hadronic tensor, Eq. (10), by:

\sigma_{T}=h_{1}+h_{2},~\sigma_{P}=h_{1}-h_{2},~\sigma_{L}=-2\frac{k^{2}}{k_{0}^{2}}h_{3},\sigma_{I}=-2\frac{\sqrt{-k^{2}}}{k_{0}}h_{4},~\sigma^{\prime}_{I}=-2\frac{\sqrt{-k^{2}}}{k_{0}}h_{5}.

(13)

One can see from this equation that it exists a single–spin asymmetry due to the longitudinal polarization of the electron beam and it is defined as:

\Sigma_{e}(\varphi)=\frac{d\sigma(\lambda=+1)-d\sigma(\lambda=-1)}{d\sigma(\lambda=+1)+d\sigma(\lambda=-1)}=

(14)

=\frac{sin\varphi\sqrt{2\varepsilon(1-\varepsilon)}\sigma^{\prime}_{I}}{\sigma_{T}+\varepsilon\sigma_{L}+\varepsilon\cos(2\varphi)\sigma_{P}+\sqrt{2\varepsilon(1+\varepsilon)}\cos\varphi\sigma_{I}}.

Due to the $\varphi$ –dependence, this asymmetry has to be measured in noncoplanar geometry (out–of–plane kinematics).

For the case of unpolarized particles, one can determine the so called left–right asymmetry

A_{LR}=\frac{d\sigma(\varphi=0^{0})-d\sigma(\varphi=180^{0})}{d\sigma(\varphi=0^{0})+d\sigma(\varphi=180^{0})}=\frac{\sqrt{2\varepsilon(1+\varepsilon)}\sigma_{I}}{\sigma_{T}+\varepsilon(\sigma_{L}+\sigma_{P})}.

(15)

We see that the $\Sigma_{e}(\varphi)$ asymmetry is determined by the structure function $h_{5}$ which is defined by the interference of the reaction amplitudes characterizing the absorption of virtual photons with nonzero longitudinal and transverse components of the electromagnetic current corresponding to the process $\gamma^{*}+d\to d+\pi^{0}$ . One finds that $h_{5}\sim\sin\vartheta$ ( $\vartheta$ is the angle between three–momenta of the virtual photon and the P-meson in the CMS of the $\gamma^{*}+d\to d+\pi^{0}$ reaction) for any reaction mechanism of the considered reaction. It vanishes in collinear kinematics, i.e., at $\pi^{0}$ –meson emission angles $\vartheta=0^{\circ}$ and $\vartheta=180^{\circ}$ due to the conservation of the total helicity of the interacting particles. The structure function $h_{5}$ is nonzero only if the complex amplitudes of the $\gamma^{*}+d\to d+P$ reaction have nonzero relative phases. This is a very specific observable, which has no counterpart in the process of the $P$ –meson photoproduction on the deuteron $\gamma+d\to d+\pi^{0}$ .

The study of the single–spin asymmetry $\Sigma_{e}$ was firstly suggested for the pion production in the electron–nucleon scattering, $e+N\to e+N+\pi$ Gehlen (1971). Afterwards this asymmetry has been dicussed for the hadron production in the exclusive processes of the type $A({\vec{e}},e^{\prime}h)X$ , where $A$ is a nucleus and $h$ is the detected hadron Boffi et al. (1985); Picklesimer et al. (1985). A number of experiments have measured the asymmetry $\Sigma_{e}$ Mandeville et al. (1994); Bartsch et al. (2002); Dolfini et al. (1995).

III.2 Vector polarized deuteron target

The part of the hadronic tensor depending on the deuteron vector polarization has the following general structure:

$\displaystyle H_{ij}(\xi)$	$\displaystyle=$	$\displaystyle{\vec{\xi}}{\vec{m}}(h_{6}\{m,n\}_{ij}+h_{7}\{\hat{k},n\}_{ij}+ih_{8}[m,n]_{ij}+ih_{9}[\hat{k},n]_{ij})+$	(16)
		$\displaystyle+{\vec{\xi}}{\vec{n}}(h_{10}m_{i}m_{j}+h_{11}n_{i}n_{j}+h_{12}\hat{k}_{i}\hat{k}_{j}+h_{13}\{m,\hat{k}\}_{ij}+ih_{14}[m,\hat{k}]_{ij})+$
		$\displaystyle+{\vec{\xi}}\hat{\vec{k}}(h_{15}\{m,n\}_{ij}+h_{16}\{\hat{k},n\}_{ij}+ih_{17}[m,n]_{ij}+ih_{18}[\hat{k},n]_{ij}).$

where one can see that , the dependence of the polarization observables on the deuteron vector polarization is determined by 13 structure functions. The expressions for these structure functions in terms of the reaction amplitudes $g_{i}$ , $(i=1-13)$ are given in Appendix I. On the basis of this formula one can make the following general conclusions:

If the deuteron is vector polarized and the polarization vector is perpendicular to the $\gamma^{*}+d\to d+P$ reaction plane, then the dependence of the differential cross section of the $e^{-}+d\to e^{-}+d+P$ reaction on the $\varepsilon$ and $\varphi$ variables is the same as in the case of the unpolarized target, and the nonvanishing components of the $H_{ij}(\xi)$ tensor are:

	$\displaystyle H_{xx}(\xi)\pm H_{yy}(\xi)$	$\displaystyle=$	$\displaystyle(h_{10}\pm h_{11}){\vec{\xi}}{\vec{n}},\ \ H_{zz}(\xi)=h_{12}{\vec{\xi}}{\vec{n}},$
	$\displaystyle H_{xz}(\xi)+H_{zx}(\xi)$	$\displaystyle=$	$\displaystyle 2h_{13}{\vec{\xi}}{\vec{n}},\ \ H_{xz}(\xi)-H_{zx}(\xi)=2ih_{14}{\vec{\xi}}{\vec{n}}.$		(17)

2.
If the deuteron target is polarized in the $\gamma^{*}+d\to d+\pi^{0}$ reaction plane (in the direction of the vector ${\vec{k}}$ or ${\vec{m}}$ ), then the dependence of the differential cross section of the $e^{-}+d\to e^{-}+d+\pi^{0}$ reaction on the $\varepsilon$ and $\varphi$ variables is:
- •
  
  for deuteron P-meson production by an unpolarized electron beam:
  
  $\varepsilon\sin(2\varphi),\ \ \sqrt{2\varepsilon(1+\varepsilon)}\sin\varphi,$ (18)
- •
  
  for deuteron P-meson production by a longitudinally polarized electron beam:
  
  $\pm i\lambda\sqrt{1-\varepsilon^{2}},\ \ \mp i\lambda\sqrt{2\varepsilon(1-\varepsilon)}\cos\varphi.$ (19)

The differential cross section of the reaction ${\vec{d}}({\vec{e}},e^{\prime}P)d$ , where the electron beam is longitudinally polarized and the deuteron target is vector polarized, can be written as follows:

\frac{d^{3}\sigma}{dE^{\prime}d\Omega_{e}d\Omega_{P}}=\sigma_{0}\biggl{[}1+\lambda\Sigma_{e}+(A_{x}^{d}+\lambda A_{x}^{ed})\xi_{x}+(A_{y}^{d}+\lambda A_{y}^{ed})\xi_{y}+(A_{z}^{d}+\lambda A_{z}^{ed})\xi_{z}\biggr{]},

(20)

where $\sigma_{0}$ coincides with the five-fold unpolarized differential cross section, Eq. (5), $\Sigma_{e}$ is the beam analyzing power (the asymmetry induced by the electron–beam polarization), $A_{i}^{d}(i=x,y,z)$ are the analyzing powers due to the vector polarization of the deuteron target, and $A_{i}^{ed}$ , $(i=x,y,z)$ are the spin–correlation parameters. The direction of the deuteron polarization vector is defined by the angles $\vartheta^{*}$ , $\varphi^{*}$ in the frame where the $z$ axis is along the direction of the three–momentum transfer ${\vec{k}}$ and the $y$ axis is defined by the vector product of the detected $\pi^{0}$ – meson and virtual photon momenta (along the unit vector ${\vec{n}}$ ). The target analyzing powers and spin–correlation parameters depend on the orientation of the deuteron polarization vector. The quantities $\Sigma_{e}$ and $A_{i}^{d}$ are T–odd observables and they are entirely determined by the reaction mechanisms beyond the impulse approximation, for example, by final–state interaction effects. On the contrary, the quantities $A_{i}^{ed}$ are T–even observables and they do not vanish even in the absence of final–state interaction effects.

The expressions of the $A_{i}^{d}$ and $A_{i}^{ed}$ asymmetries can be explicitly written as functions of the azimuthal angle $\varphi$ , of the virtual–photon linear polarization $\varepsilon$ , and of contributions of the longitudinal (L) and transverse (T) components (relative to the virtual–photon momentum ${\vec{k}}$ ) of the hadron electromagnetic current of $\gamma^{*}+d\to d+\pi^{0}$ :

$\displaystyle A_{x}^{d}\sigma_{0}$	$\displaystyle=$	$\displaystyle N\sin\varphi\biggl{[}\sqrt{2\varepsilon(1+\varepsilon)}A_{x}^{(LT)}+\varepsilon\cos\varphi A_{x}^{(TT)}\biggr{]},$
$\displaystyle A_{z}^{d}\sigma_{0}$	$\displaystyle=$	$\displaystyle N\sin\varphi\biggl{[}\sqrt{2\varepsilon(1+\varepsilon)}A_{z}^{(LT)}+\varepsilon\cos\varphi A_{z}^{(TT)}\biggr{]},$
$\displaystyle A_{y}^{d}\sigma_{0}$	$\displaystyle=$	$\displaystyle N\biggl{[}A_{y}^{(TT)}+\varepsilon A_{y}^{(LL)}+\sqrt{2\varepsilon(1+\varepsilon)}cos\varphi A_{y}^{(LT)}+\varepsilon cos(2\varphi)\bar{A}_{y}^{(TT)}\biggr{]},$
$\displaystyle A_{x}^{ed}\sigma_{0}$	$\displaystyle=$	$\displaystyle N\biggl{[}\sqrt{1-\varepsilon^{2}}B_{x}^{(TT)}+\sqrt{2\varepsilon(1-\varepsilon)}cos\varphi B_{x}^{(LT)}\biggr{]},$
$\displaystyle A_{z}^{ed}\sigma_{0}$	$\displaystyle=$	$\displaystyle N\biggl{[}\sqrt{1-\varepsilon^{2}}B_{z}^{(TT)}+\sqrt{2\varepsilon(1-\varepsilon)}cos\varphi B_{z}^{(LT)}\biggr{]},$
$\displaystyle A_{y}^{ed}\sigma_{0}$	$\displaystyle=$	$\displaystyle N\sqrt{2\varepsilon(1-\varepsilon)}\sin\varphi B_{y}^{(LT)},$	(21)

where $N$ is defined in Eq. (5) and the individual contributions to the considered asymmetries in terms of the structure functions $h_{i}$ are given by

$\displaystyle A_{x}^{(TT)}$	$\displaystyle=$	$\displaystyle 4h_{6},\ \ A_{y}^{(TT)}=h_{10}+h_{11},\ \ \bar{A}_{y}^{(TT)}=h_{10}-h_{11},\ \ A_{z}^{(TT)}=4h_{15},$
$\displaystyle A_{x}^{(LT)}$	$\displaystyle=$	$\displaystyle-2\frac{\sqrt{Q^{2}}}{k_{0}}h_{7},\ \ A_{y}^{(LT)}=-2\frac{\sqrt{Q^{2}}}{k_{0}}h_{13},\ \ A_{z}^{(LT)}=-2\frac{\sqrt{Q^{2}}}{k_{0}}h_{16},$
$\displaystyle A_{y}^{(LL)}$	$\displaystyle=$	$\displaystyle 2\frac{Q^{2}}{k_{0}^{2}}h_{12},\ \ B_{x}^{(TT)}=2h_{8},\ \ B_{z}^{(TT)}=2h_{17},$
$\displaystyle B_{x}^{(LT)}$	$\displaystyle=$	$\displaystyle-2\frac{\sqrt{Q^{2}}}{k_{0}}h_{9},\ \ B_{y}^{(LT)}=-2\frac{\sqrt{Q^{2}}}{k_{0}}h_{14},\ \ B_{z}^{(LT)}=-2\frac{\sqrt{Q^{2}}}{k_{0}}h_{18}.$	(22)

III.3 Tensor polarized deuteron target

The component of the hadronic tensor, $H_{ij}(S)$ , which depends on the deuteron tensor polarization has the following general structure:

$\displaystyle H_{ij}(S)$	$\displaystyle=$	$\displaystyle S_{ab}m_{a}m_{b}(h_{19}m_{i}m_{j}+h_{20}n_{i}n_{j}+h_{21}\hat{k}_{i}\hat{k}_{j}+h_{22}\{m,\hat{k}\}_{ij}+ih_{23}[m,\hat{k}]_{ij})+$	(23)
		$\displaystyle+S_{ab}n_{a}n_{b}(h_{24}m_{i}m_{j}+h_{25}n_{i}n_{j}+h_{26}\hat{k}_{i}\hat{k}_{j}+h_{27}\{m,\hat{k}\}_{ij}+ih_{28}[m,\hat{k}]_{ij})+$
		$\displaystyle+S_{ab}m_{a}\hat{k}_{b}(h_{29}m_{i}m_{j}+h_{30}n_{i}n_{j}+h_{31}\hat{k}_{i}\hat{k}_{j}+h_{32}\{m,\hat{k}\}_{ij}+ih_{33}[m,\hat{k}]_{ij})+$
		$\displaystyle+S_{ab}m_{a}n_{b}(h_{34}\{m,n\}_{ij}+h_{35}\{\hat{k},n\}_{ij}+ih_{36}[m,n]_{ij}+ih_{37}[\hat{k},n]_{ij})+$
		$\displaystyle+S_{ab}\hat{k}_{a}n_{b}(h_{38}\{m,n\}_{ij}+h_{39}\{\hat{k},n\}_{ij}+ih_{40}[m,n]_{ij}+ih_{41}[\hat{k},n]_{ij}).$

In this case, the dependence of the polarization observables on the deuteron tensor polarization is determined by 23 structure functions. The expressions for these structure functions in terms of the reaction amplitudes $g_{i}(i=1-13)$ are given in Appendix I.

From this expression one can conclude that:

1.

If the deuteron is tensor polarized so that only $S_{zz},\ S_{yy}$ and $(S_{xz}+S_{zx})$ components of the quadrupole polarization tensor are nonzero, then the dependence of the differential cross section of the $e^{-}+d\to e^{-}+P+d$ reaction on the parameter $\varepsilon$ and on the azimuthal angle $\varphi$ must be the same as in the case of the unpolarized target (more exactly, with similar $\varepsilon$ – and $\varphi$ – dependent terms).
2.

If the deuteron is polarized so that only the $(S_{xy}+S_{yx})$ and $(S_{yz}+S_{zy})$ components of the quadrupole polarization tensor are nonzero, then:

- for $P$ -meson production with unpolarized electron beam the typical terms follow $\sin\varphi$ and $\sin(2\varphi)$ dependencies;

- for $P$ -meson production with longitudinally polarized electron beam the terms do not depend on $\varepsilon$ , $\varphi$ , and $\cos\varphi$ .

In polarization experiments it is possible to prepare the deuteron target with definite spin projection on some quantization axis. The corresponding asymmetry is usually defined as

A=\frac{d\sigma(\lambda_{d}=+1)-d\sigma(\lambda_{d}=-1)}{d\sigma(\lambda_{d}=+1)+d\sigma(\lambda_{d}=-1)},

(24)

where $d\sigma(\lambda_{d})$ is the differential cross section of the $e^{-}+d\to e^{-}+P+d$ reaction when the quantization axis for the deuteron spin (in the $Pd$ –pair CMS) coincides with its momentum, i.e., the deuteron has helicity $\lambda_{d}$ . From an experimental point of view, the measurement of an asymmetry is more convenient than a measurement of a cross section, as most of systematic experimental errors and other multiplicative factors cancel in the ratio.

The general form of the hadron tensor $H_{ij}(\lambda_{d})$ , which determines the differential cross section of the process under consideration for the case of the deuteron with helicity $\lambda_{d}$ , can be written as

	$\displaystyle H_{ij}(\lambda_{d}$	$\displaystyle=$	$\displaystyle\pm 1)=\delta_{1}\hat{k}_{i}\hat{k}_{j}+\delta_{2}m_{i}m_{j}+\delta_{3}n_{i}n_{j}+\delta_{4}\{\hat{k},m\}_{ij}+i\delta_{5}[\hat{k},m]_{ij}\pm$		(25)
			$\displaystyle\pm\delta_{6}\{\hat{k},n\}_{ij}\pm i\delta_{7}[\hat{k},n]_{ij}\pm\delta_{8}\{m,n\}_{ij}\pm i\delta_{9}[m,n]_{ij}.$		(25)

The reaction amplitude is real in the Born (impulse) approximation. So, assuming the T-invariance of the hadron electromagnetic interactions, we can do the following statements, according to the deuteron polarization state:

The deuteron is unpolarized. Since, in this case, the hadronic tensor $H_{ij}(0)$ has to be symmetric (over the $i,j$ indices), the asymmetry in the scattering of longitudinally polarized electrons vanishes.

The deuteron is vector polarized. Since, in this case, the hadronic tensor $H_{ij}(\xi)$ has to be antisymmetric, then the deuteron vector polarization can manifest itself in the scattering of longitudinally polarized electrons. The perpendicular target polarization (normal to the $\gamma^{*}+d\rightarrow d+\pi^{0}$ reaction plane) leads to a correlation of the following type: $\pm i\lambda\sqrt{2\varepsilon(1-\varepsilon)}\sin\varphi.$ The longitudinal and transverse (along or perpendicular to the virtual–photon momentum) target polarization (lying in the $\gamma^{*}+d\rightarrow P+d$ reaction plane) leads to two correlations of the following type : $\mp i\lambda\sqrt{1-\varepsilon^{2}}$ and $\mp i\lambda\sqrt{2\varepsilon(1-\varepsilon)}\cos\varphi.$

The deuteron is tensor polarized. The hadronic tensor $H_{ij}(S)$ is symmetric in this case. In the scattering of longitudinally polarized electrons the contribution proportional to $\lambda S_{ab}$ vanishes. If the target is polarized so that only the $(S_{xy}+S_{yx})$ or $(S_{yz}+S_{zy})$ components of the quadrupole polarization tensor are nonzero, then in the differential cross section only the following two terms are present: $\varepsilon\sin(2\varphi)$ and $\sqrt{2\varepsilon(1+\varepsilon)}\sin\varphi.$ For all other target polarizations the following structures are present: a term which does not depend on $\varepsilon$ and $\varphi$ variables as well as terms with the following dependencies: $2\varepsilon$ , $\varepsilon cos(2\varphi)$ , and $\sqrt{2\varepsilon(1+\varepsilon)}cos\varphi.$

The differential cross section of the $P$ –meson production in the scattering of longitudinally polarized electrons by a tensor polarized deuteron target (in a coincidence experimental setup) has the following general structure

$\displaystyle\frac{d^{3}\sigma}{dE^{\prime}d\Omega_{e}d\Omega_{P}}$	$\displaystyle=$	$\displaystyle N\biggl{\{}\sigma_{T}+A_{xz}^{T}Q_{xz}+A_{xx}^{T}(Q_{xx}-Q_{yy})+A_{zz}^{T}Q_{zz}+$	(26)
		$\displaystyle+\varepsilon\biggl{[}\sigma_{L}+A_{xz}^{L}Q_{xz}+A_{xx}^{L}(Q_{xx}-Q_{yy})+A_{zz}^{L}Q_{zz}\biggr{]}+$
		$\displaystyle+\sqrt{2\varepsilon(1+\varepsilon)}\cos\varphi\biggl{[}\sigma_{I}+A_{xz}^{I}Q_{xz}+A_{xx}^{I}(Q_{xx}-Q_{yy})+A_{zz}^{I}Q_{zz}\biggr{]}+$
		$\displaystyle+\sqrt{2\varepsilon(1+\varepsilon)}\sin\varphi(A_{xy}^{I}Q_{xy}+A_{yz}^{I}Q_{yz}))+$
		$\displaystyle+\varepsilon\sin(2\varphi)(A_{xy}^{P}Q_{xy}+A_{yz}^{P}Q_{yz})+$
		$\displaystyle+\varepsilon\cos(2\varphi)\biggl{[}\sigma_{P}+A_{xz}^{P}Q_{xz}+A_{xx}^{P}(Q_{xx}-Q_{yy})+A_{zz}^{P}Q_{zz}\biggr{]}+$
		$\displaystyle+\lambda\sqrt{2\varepsilon(1-\varepsilon)}\sin\varphi\biggl{[}\sigma_{I}^{\prime}+\bar{A}_{xz}^{I}Q_{xz}+\bar{A}_{xx}^{I}(Q_{xx}-Q_{yy})+\bar{A}_{zz}^{I}Q_{zz}\biggr{]}+$
		$\displaystyle+\lambda\sqrt{2\varepsilon(1-\varepsilon)}\cos\varphi\biggl{[}\bar{A}_{xy}^{I}Q_{xy}+\bar{A}_{yz}^{I}Q_{yz}\biggr{]}+$
		$\displaystyle+\lambda\sqrt{1-\varepsilon^{2}}\cos\varphi\biggl{[}A_{xy}^{T}Q_{xy}+A_{yz}^{T}Q_{yz}\biggr{]}\biggr{\}},$

where the quantities $Q_{ij}(i,j=x,y,z)$ are the components of the quadrupole polarization tensor of the deuteron in its rest system (the coordinate system is specified similarly to the case of the $\pi^{0}d$ –pair CMS). These components satisfy to the following conditions: $Q_{ij}=Q_{ji}$ , $Q_{ii}=0$ . In the derivation of this formula we take into account that $Q_{xx}+Q_{yy}+Q_{zz}=0$ .

Thus, in the general case the exclusive cross section of the $P$ –meson production in the scattering of longitudinally polarized electrons by a tensor polarized deuteron target is determined by 23 independent asymmetries (16(7) ones in the scattering of unpolarized(longitudinally polarized) electrons) $A_{ij}^{m}(W,k^{2},\vartheta)$ , where $i,j=x,y,z;m=T,P,L,I$ . These asymmetries can be related to the structure functions $h_{i}$ which are the bilinear combinations of the 13 independent scalar amplitudes describing the $\gamma^{*}+d\to P+d$ reaction. These relations are:

$\displaystyle A_{xz}^{T}$	$\displaystyle=$	$\displaystyle\gamma_{1}(h_{29}+h_{30}),\ \ A_{xx}^{T}=\frac{1}{2}(h_{19}+h_{20}-h_{21}-h_{25}),\ \ A_{zz}^{T}=-\frac{1}{2}(h_{19}+h_{20}+h_{21}+h_{25}),$
$\displaystyle A_{xz}^{L}$	$\displaystyle=$	$\displaystyle-2\gamma_{1}\frac{k^{2}}{k_{0}^{2}}h_{31},\ \ A_{xx}^{L}=-\frac{k^{2}}{k_{0}^{2}}(h_{21}-h_{26}),\ \ A_{zz}^{L}=\frac{k^{2}}{k_{0}^{2}}(h_{21}+h_{26}),$
$\displaystyle A_{xz}^{I}$	$\displaystyle=$	$\displaystyle-2\gamma_{1}\frac{\sqrt{-k^{2}}}{k_{0}}h_{32},\ \ A_{xx}^{I}=-\frac{\sqrt{-k^{2}}}{k_{0}}(h_{22}-h_{27}),\ \ A_{zz}^{I}=\frac{\sqrt{-k^{2}}}{k_{0}}(h_{22}+h_{27}),$	(27)
$\displaystyle A_{xy}^{I}$	$\displaystyle=$	$\displaystyle-2\frac{\sqrt{-k^{2}}}{k_{0}}h_{35},\ \ A_{yz}^{I}=-2\gamma_{1}\frac{\sqrt{-k^{2}}}{k_{0}}h_{39},\ \ A_{xy}^{P}=2h_{34},\ \ A_{yz}^{P}=2\gamma_{1}h_{38},$
$\displaystyle A_{xz}^{P}$	$\displaystyle=$	$\displaystyle\gamma_{1}(h_{29}-h_{30}),\ \ A_{xx}^{P}=\frac{1}{2}(h_{19}-h_{20}-h_{24}+h_{25}),\ \ A_{zz}^{P}=-\frac{1}{2}(h_{19}-h_{20}+h_{24}-h_{25}),$
$\displaystyle\bar{A}_{xz}^{I}$	$\displaystyle=$	$\displaystyle-2\gamma_{1}\frac{\sqrt{-k^{2}}}{k_{0}}h_{33},\ \ \bar{A}_{xx}^{I}=-\frac{\sqrt{-k^{2}}}{k_{0}}(h_{23}-h_{28}),\ \ \bar{A}_{zz}^{I}=\frac{\sqrt{-k^{2}}}{k_{0}}(h_{23}+h_{28}),$
$\displaystyle\bar{A}_{xy}^{I}$	$\displaystyle=$	$\displaystyle-2\frac{\sqrt{-k^{2}}}{k_{0}}h_{37},\ \ \bar{A}_{yz}^{I}=-2\gamma_{1}\frac{\sqrt{-k^{2}}}{k_{0}}h_{41},\ \ A_{xy}^{T}=2h_{36},\ \ A_{yz}^{T}=2\gamma_{1}h_{40}.$

One can see from this formula that the scattering of unpolarized electrons by a tensor polarized deuteron target with components $Q_{xy}=Q_{yz}=0$ , is characterized by the same $\varphi$ – and $\varepsilon$ –dependences as in the case of the scattering of unpolarized electrons by the unpolarized deuteron target. If $Q_{xy}\neq 0,Q_{yz}\neq 0$ , then new terms of the type $\sqrt{2\varepsilon(1+\varepsilon)}\sin\varphi$ and $\varepsilon\sin(2\varphi)$ are present in the cross section. The asymmetries with upper indices $T,P(L)$ are determined only by the transverse (longitudinal) components of the electromagnetic current for the $\gamma^{*}+d\to P+d$ reaction, while the asymmetries with upper index $I$ are determined by the interference of the longitudinal and transverse components of the electromagnetic current.

Using the explicit form for the amplitude of the reaction under consideration it is easy to obtain the expression for the hadronic tensor $H_{ij}$ in terms of the scalar amplitudes $g_{i}\ (i=1,...,13).$ Appendix I contains the formulae for the structure functions $h_{i}$ in terms of the scalar amplitudes, which describe the polarization effects in the $e^{-}+d\to e^{-}+P+d$ reaction caused by the deuteron polarization.

Let us stress again that the results listed above have a general nature and are not related to a particular reaction mechanism. They are valid for the one–photon–exchange mechanism assuming P-invariance of the hadron electromagnetic interaction. Their general nature is due to the fact that the derivation of these formulae requires only the hadron electromagnetic current conservation and the fact that the photon has spin one.

IV Polarization state of scattered deuteron

Let us consider the general structure of the polarization effects related to the polarization of the scattered deuteron. The scattered deuteron spin density matrix can be written as

\rho^{s}_{\mu\nu}=-(g_{\mu\nu}-\frac{p_{2\mu}p_{2\nu}}{M^{2}})+\frac{i}{2M}\varepsilon_{\mu\nu\alpha\beta}\tilde{s}_{\alpha}p_{2\beta}+\tilde{S}_{\mu\nu},

(28)

where $\tilde{s}_{\alpha}$ is the four–vector describing the vector polarization of the scattered deuteron, $\tilde{s}^{2}=-1,$ $\tilde{s}\cdot p_{2}=0$ and $\tilde{S}_{\mu\nu}$ is the tensor describing the tensor (quadrupole) polarization of the scattered deuteron, $\tilde{S}_{\mu\nu}=\tilde{S}_{\nu\mu},$ $p_{2\mu}\tilde{S}_{\mu\nu}=0,$ $\tilde{S}_{\mu\mu}=0$ (due to these properties the tensor $\tilde{S}_{\mu\nu}$ has only five independent components).

In the scattered deuteron rest system all time components of the tensor $\tilde{S}_{\mu\nu}$ are zero and the tensor polarization of the scattered deuteron is described by five independent space components $(\tilde{S}_{ij}=\tilde{S}_{ji},\tilde{S}_{ii}=0,i,j=x,y,z).$ The four–vector $\tilde{s}_{\alpha}$ is related to the unit vector ${\vec{\zeta}}$ of the scattered deuteron vector polarization in its rest system by $\tilde{s}_{0}=-{\vec{q}}{\vec{\zeta}}/M,\$ ${\vec{\tilde{s}}}={\vec{\zeta}}+{\vec{q}}{\vec{q}}\cdot{\vec{\zeta}}/M(M+E_{2}),$ $E_{2}$ is the scattered deuteron energy in the $\gamma^{*}+d\to d+P$ reaction CMS.

The hadronic tensor $H_{ij}(i,j=x,y,z)$ has a linear dependence on the scattered deuteron polarization parameters and it can be represented as follows:

H_{ij}=H_{ij}(0)+H_{ij}(\zeta)+H_{ij}(\tilde{S}),

(29)

where the term $H_{ij}(0)$ corresponds to the case of the unpolarized deuteron target and scattered deuteron, and the term $H_{ij}(\zeta)(H_{ij}(\tilde{S}))$ corresponds to the case of the vector (tensor)-polarization of the scattered deuteron provided that target is unpolarized.

•

The scattered deuteron is unpolarized. The structure of the tensor $H_{ij}(0)$ is given by Eq. (10) with the same structure functions $h_{i},i=1-5$ .

•

The scattered deuteron is vector polarized. The structure of the tensor $H_{ij}(\zeta)$ is given by Eq. (16) where it is necessary to do the following change $\vec{\xi}\to\vec{\zeta}$ and the structure functions must be also changed $h_{i}\to\bar{h}_{i},i=6-18$ . Therefore, the dependence of the polarization observables on the vector polarization of the scattered deuteron is also determined by 13 structure functions. The expressions for the structure functions $\bar{h}_{i}$ in terms of the reaction amplitudes $g_{i}(i=1-13)$ are given in Appendix I. The differential cross section of the reaction $d({\vec{e}},e^{\prime}P){\vec{d}}$ , where the electron beam is longitudinally polarized and the scattered deuteron has vector polarization, can be written as follows:

\frac{d^{3}\sigma}{dE^{\prime}d\Omega_{e}d\Omega_{P}}=\sigma_{0}\left[1+\lambda\Sigma_{e}+(P_{x}^{d}+\lambda T_{x}^{ed})\zeta_{x}+(P_{y}^{d}+\lambda T_{y}^{ed})\zeta_{y}+(P_{z}^{d}+\lambda T_{z}^{ed})\zeta_{z}\right],

(30)

where $P_{i}^{d}(i=x,y,z)$ are the components of the vector polarization of the scattered deuteron, and $T_{i}^{ed}(i=x,y,z)$ are the coefficients of the polarization transfer from the longitudinal polarization of the electron beam to the vector polarization of the scattered deuteron. The quantities $\Sigma_{e}$ and $P_{i}^{d}$ are T–odd observables and they are completely determined by the reaction mechanism beyond the impulse approximation, for example, by the final–state interaction effects. On the contrary, the quantities $T_{i}^{ed}$ are T–even observables and they do not vanish in absence of final–state interaction effects.

The expressions of the $P_{i}^{d}$ and $T_{i}^{ed}$ polarization observables can be also explicitly written as functions of the azimuthal angle $\varphi$ , of the virtual photon linear polarization $\varepsilon$ , and of the contributions of the longitudinal (L) and transverse (T) components (relative to the virtual photon momentum ${\vec{k}}$ ) of the hadron electromagnetic current of the $\gamma^{*}+d\to d+P$ reaction. These expressions can be obtained from Eqs. (21,22) with the following substitutions: $A_{i}^{d}\to P_{i}^{d}$ , $A_{i}^{ed}\to T_{i}^{ed}$ , $A_{i}^{(IJ)}\to P_{i}^{(IJ)}$ and $B_{i}^{(IJ)}\to C_{i}^{(IJ)}$ , where $I,J=L,T$ .

The individual contributions to the components of the vector polarization and polarization transfer coefficients in terms of the structure functions $\bar{h_{i}}$ are given by Eq. (22) where it is necessary to change $h_{i}\to\bar{h_{i}}$ .

At this stage, the general model–independent analysis of the polarization observables in the reaction $d({\vec{e}},e^{\prime}P)\vec{d}$ , for the case of the vector-polarized scattered deuteron, is completed. To proceed further in the calculation of the observables, one needs a model for the reaction mechanism and for the deuteron structure.

•

The scattered deuteron is tensor polarized. The general structure of the tensor $H_{ij}(\tilde{S})$ is the same as given by Eq. (23) where it is necessary to do the following change $S_{ab}\to\tilde{S}_{ab}$ and $h_{i}\to\bar{h}_{i},i=19-41$ for the structure functions. Therefore, the dependence of the polarization observables on the tensor polarization of the scattered deuteron is also determined by 23 structure functions. The expressions for the structure functions $\bar{h}_{i}$ in terms of the reaction amplitudes $g_{i}(i=1-13)$ are given in Appendix I.

The differential cross section of the $P$ –meson production in the scattering of longitudinally polarized electrons by an unpolarized deuteron target, when the tensor polarization of the scattered deuteron is measured (in a coincidence experimental setup), has the following general structure:

$\displaystyle\frac{d^{3}\sigma}{dE^{\prime}d\Omega_{e}d\Omega_{P}}$	$\displaystyle=$	$\displaystyle N\biggl{\{}\sigma_{T}+P_{xz}^{T}\tilde{Q}_{xz}+P_{xx}^{T}(\tilde{Q}_{xx}-\tilde{Q}_{yy})+P_{zz}^{T}\tilde{Q}_{zz}+$	(31)
		$\displaystyle+\varepsilon\biggl{[}\sigma_{L}+P_{xz}^{L}\tilde{Q}_{xz}+P_{xx}^{L}(\tilde{Q}_{xx}-\tilde{Q}_{yy})+P_{zz}^{L}\tilde{Q}_{zz}\biggr{]}+$
		$\displaystyle+\sqrt{2\varepsilon(1+\varepsilon)}\cos\varphi\biggl{[}\sigma_{I}+P_{xz}^{I}\tilde{Q}_{xz}+P_{xx}^{I}(\tilde{Q}_{xx}-\tilde{Q}_{yy})+P_{zz}^{I}\tilde{Q}_{zz}\biggr{]}+$
		$\displaystyle+\sqrt{2\varepsilon(1+\varepsilon)}\sin\varphi(P_{xy}^{I}\tilde{Q}_{xy}+P_{yz}^{I}\tilde{Q}_{yz})+\varepsilon\sin(2\varphi)(P_{xy}^{P}\tilde{Q}_{xy}+P_{yz}^{P}\tilde{Q}_{yz})+$
		$\displaystyle+\varepsilon\cos(2\varphi)\biggl{[}\sigma_{P}+P_{xz}^{P}\tilde{Q}_{xz}+P_{xx}^{P}(\tilde{Q}_{xx}-\tilde{Q}_{yy})+P_{zz}^{P}\tilde{Q}_{zz}\biggr{]}+$
		$\displaystyle+\lambda\sqrt{2\varepsilon(1-\varepsilon)}\sin\varphi\biggl{[}\sigma_{I}^{\prime}+\bar{P}_{xz}^{I}\tilde{Q}_{xz}+\bar{P}_{xx}^{I}(\tilde{Q}_{xx}-\tilde{Q}_{yy})+\bar{P}_{zz}^{I}\tilde{Q}_{zz}\biggr{]}+$
		$\displaystyle+\lambda\sqrt{2\varepsilon(1-\varepsilon)}\cos\varphi\biggl{[}\bar{P}_{xy}^{I}\tilde{Q}_{xy}+\bar{P}_{yz}^{I}\tilde{Q}_{yz}\biggr{]}+$
		$\displaystyle+\lambda\sqrt{1-\varepsilon^{2}}\cos\varphi\biggl{[}P_{xy}^{T}\tilde{Q}_{xy}+P_{yz}^{T}\tilde{Q}_{yz}\biggr{]}\biggr{\}},$

where the quantities $\tilde{Q}_{ij}(i,j=x,y,z)$ are the components of the quadrupole polarization tensor of the scattered deuteron in the $Pd$ –pair CMS. These components satisfy to the following conditions:

\tilde{Q}_{ij}=\tilde{Q}_{ji},\ d\tilde{Q}_{zz}+u\tilde{Q}_{xx}+\gamma^{2}_{2}\tilde{Q}_{yy}-2z(1+\gamma_{2})\tilde{Q}_{xz}=0,

(32)

where $d=cos^{2}\vartheta+sin^{2}\vartheta\gamma^{2}_{2},\ u=sin^{2}\vartheta+cos^{2}\vartheta\gamma^{2}_{2},$ $z=(\gamma_{2}-1)cos\vartheta\sin\vartheta,\gamma_{2}=E_{2}/M$ . Eq. (31) takes into account the last condition.

Thus, in the general case the exclusive cross section of the $P$ –meson production in the scattering of longitudinally polarized electrons by unpolarized deuteron target, when the tensor polarization of the scattered deuteron is measured (in the coincidence experimental setup), is determined by 23 independent functions (16 (7) ones in the scattering of unpolarized (longitudinally polarized) electrons) $P_{ij}^{m}(W,k^{2},\vartheta)$ , where $i,j=x,y,z;m=T,P,L,I$ . These asymmetries can be related to the structure functions $\bar{h}_{i}$ which are the bilinear combinations of the 13 independent scalar amplitudes describing the $\gamma^{*}+d\to P+d$ reaction. These relations are:

$\displaystyle rP_{xz}^{T}$	$\displaystyle=$	$\displaystyle r(\bar{h}_{29}+\bar{h}_{30})-2z(1+\gamma_{2})(\bar{h}_{19}+\bar{h}_{20}+\bar{h}_{24}+\bar{h}_{25}),$
$\displaystyle rP_{xx}^{T}$	$\displaystyle=$	$\displaystyle u(\bar{h}_{24}+\bar{h}_{25})-\gamma^{2}_{2}(\bar{h}_{19}+\bar{h}_{20}),\ rP_{zz}^{T}=d(\bar{h}_{19}+\bar{h}_{20}+\bar{h}_{24}+\bar{h}_{25}),$
$\displaystyle rP_{xz}^{L}$	$\displaystyle=$	$\displaystyle 2\frac{Q^{2}}{k_{0}^{2}}[r\bar{h}_{31}-2z(1+\gamma_{2})(\bar{h}_{21}+\bar{h}_{26})],\ rP_{xx}^{L}=2\frac{Q^{2}}{k_{0}^{2}}(u\bar{h}_{26}-\gamma^{2}_{2}\bar{h}_{21}),$
$\displaystyle rP_{zz}^{L}$	$\displaystyle=$	$\displaystyle 2\frac{Q^{2}}{k_{0}^{2}}d(\bar{h}_{21}+\bar{h}_{26}),\ \ rP_{xz}^{I}=-2\frac{\sqrt{Q^{2}}}{k_{0}}[r\bar{h}_{32}-2z(1+\gamma_{2})(\bar{h}_{22}+\bar{h}_{27})],$
$\displaystyle rP_{xx}^{I}$	$\displaystyle=$	$\displaystyle-2\frac{\sqrt{Q^{2}}}{k_{0}}(u\bar{h}_{27}-\gamma^{2}_{2}\bar{h}_{22}),rP_{zz}^{I}=-2\frac{\sqrt{Q^{2}}}{k_{0}}d(\bar{h}_{22}+\bar{h}_{27}),\ \$	(33)
$\displaystyle P_{xy}^{I}$	$\displaystyle=$	$\displaystyle-2\frac{\sqrt{Q^{2}}}{k_{0}}\bar{h}_{35},\ \ P_{yz}^{I}=-2\frac{\sqrt{Q^{2}}}{k_{0}}\bar{h}_{39},\ \ P_{xy}^{P}=2\bar{h}_{34},\ P_{yz}^{P}=2\bar{h}_{38},$
$\displaystyle rP_{xz}^{P}$	$\displaystyle=$	$\displaystyle r(\bar{h}_{29}-\bar{h}_{30})-2z(1+\gamma_{2})(\bar{h}_{19}-\bar{h}_{20}+\bar{h}_{24}-\bar{h}_{25}),\ \$
$\displaystyle rP_{xx}^{P}$	$\displaystyle=$	$\displaystyle u(\bar{h}_{24}-\bar{h}_{25})-\gamma^{2}_{2}(\bar{h}_{19}-\bar{h}_{20}),$
$\displaystyle rP_{zz}^{P}$	$\displaystyle=$	$\displaystyle d(\bar{h}_{19}-\bar{h}_{20}+\bar{h}_{24}-\bar{h}_{25}),\ \ r\bar{P}_{xz}^{I}=-2\frac{\sqrt{Q^{2}}}{k_{0}}[r\bar{h}_{33}-2z(1+\gamma_{2})(\bar{h}_{23}+\bar{h}_{28})],$
$\displaystyle r\bar{P}_{xx}^{I}$	$\displaystyle=$	$\displaystyle-2\frac{\sqrt{Q^{2}}}{k_{0}}(u\bar{h}_{28}-\gamma^{2}_{2}\bar{h}_{23}),\ \ r\bar{P}_{zz}^{I}=-2\frac{\sqrt{Q^{2}}}{k_{0}}d(\bar{h}_{23}+\bar{h}_{28}),\ \$
$\displaystyle\bar{P}_{xy}^{I}$	$\displaystyle=$	$\displaystyle-2\frac{\sqrt{Q^{2}}}{k_{0}}\bar{h}_{37},\bar{P}_{yz}^{I}=-2\frac{\sqrt{Q^{2}}}{k_{0}}\bar{h}_{41},\ \ P_{xy}^{T}=2\bar{h}_{36},\ \ P_{yz}^{T}=2\bar{h}_{40},$

where $r=-(u+\gamma^{2}_{2})$ .

The results listed above have a general nature and are not related to a particular reaction mechanism. They are valid for the one–photon–exchange mechanism assuming P-invariance of the hadron electromagnetic interaction. Their general nature is due to the fact that derivation of these results requires only the hadron electromagnetic current conservation and the fact that the photon has spin one.

V Coherent production of pseudoscalar meson in deuteron photodisintegration process

Let us consider the particular case of the coherent photoproduction of the pseudoscalar meson on the deuteron target

\gamma(k)+d(p_{1})\to P(q)+d(p_{2}),

(34)

where the four–momenta of the particles are given in the brackets. Of course, all observables for this reaction can be obtained using the formulae presented above for the case of the virtual photon, but it is rather tedious procedure. So, it is worth to have the expressions for the differential cross section and various polarization observables which are suitable for the analysis of the data on this reaction.

The matrix element of this reaction can be written as

M=eA_{\mu}J_{\mu}=-eA_{i}J_{i},

(35)

where $A_{\mu}$ is the photon polarization four–vector and we use the transverse gauge: ${\vec{k}}\cdot{\vec{A}}=0$ ( ${\vec{k}}$ is the photon momentum),

The differential cross section in CMS (not averaged over the spins of the initial particles) can be written as

\frac{d\sigma}{d\Omega}=\frac{\alpha}{8\pi}\frac{q}{W}\frac{1}{W^{2}-M^{2}}\rho_{ij}H_{ij},

(36)

where $\rho_{ij}=A_{i}A_{j}^{*}$ and hadronic tensor is determined as $H_{ij}=J_{i}J_{j}^{*}$ . The quantities which are not redefined in this section have the same meaning as in the previous sections.

In the reaction CMS, the quantity $J_{i}$ can be represented as

J_{i}=m_{i}A+n_{i}B,

(37)

where

	$\displaystyle A$	$\displaystyle=$	$\displaystyle g_{1}{\vec{m}}\cdot{\vec{U}}_{1}{\vec{n}}\cdot{\vec{U}}_{2}^{}+g_{2}\hat{\vec{k}}\cdot{\vec{U}}_{1}{\vec{n}}\cdot{\vec{U}}_{2}^{}+g_{3}{\vec{n}}\cdot{\vec{U}}_{1}{\vec{m}}\cdot{\vec{U}}_{2}^{}+g_{4}{\vec{n}}\cdot{\vec{U}}_{1}\hat{\vec{k}}\cdot{\vec{U}}_{2}^{},$
	$\displaystyle B$	$\displaystyle=$	$\displaystyle g_{5}{\vec{m}}\cdot{\vec{U}}_{1}{\vec{m}}\cdot{\vec{U}}_{2}^{}+g_{6}{\vec{n}}\cdot{\vec{U}}_{1}{\vec{n}}\cdot{\vec{U}}_{2}^{}+g_{7}\hat{\vec{k}}\cdot{\vec{U}}_{1}\hat{\vec{k}}\cdot{\vec{U}}_{2}^{}+g_{8}{\vec{m}}\cdot{\vec{U}}_{1}\hat{\vec{k}}\cdot{\vec{U}}_{2}^{}+g_{9}\hat{\vec{k}}\cdot{\vec{U}}_{1}{\vec{m}}\cdot{\vec{U}}_{2}^{*}.$

In this case the nine scalar amplitudes depend on two variables $W$ and $\vartheta$ (energy and scattering angle) instead of three ones for the case of the pseudoscalar meson electroproduction ( $k^{2}\neq 0$ ).

The hadronic tensor $H_{ij}(i,j=x,y,z)$ can be also represented in the form given by Eq. (9) where each term corresponds to the definite polarization state of the deuteron target, provided that the scattered deuteron is unpolarized.

Let us consider the polarization observables of the $\gamma+d\to P+d$ reaction which correspond to each contribution of the hadronic tensor $H_{ij}$ .

•

The deuteron target is unpolarized. The general structure of the hadronic tensor for the case of unpolarized deuteron target has the following form

$H_{ij}(0)=h_{1}m_{i}m_{j}+h_{2}n_{i}n_{j},$ (38)

where the structure functions $h_{i}$ , for the case of the photoproduction of the P-meson on the deuteron, can be expressed in terms of the $\gamma+d\to P+d$ reaction scalar amplitudes $g_{i}(i=1-9)$ using the expressions in Appendix I, where it is necessary to cancel the four amplitudes $g_{i}(i=10-13)$ , since they correspond to the absorption of a virtual photon with longitudinal polarization.

Then the differential cross section of the $\gamma+d\to P+d$ reaction for the case of unpolarized particles can be written as:

$\frac{d\sigma_{un}}{d\Omega}=N(h_{1}+h_{2}),\ \ N=\frac{\alpha}{16\pi}\frac{q}{W}\frac{1}{W^{2}-M^{2}}.$ (39)

•

Let us consider the case when the photon beam is polarized. The general expression of the photon polarization vector is determined by two real parameters $\beta$ and $\delta$ and it can be written as Akhiezer and Berestetskii (1965)

{\vec{A}}=\cos\beta{\vec{m}}+\sin\beta\exp(i\delta){\vec{n}}.

(40)

If the parameter $\delta$ vanishes, $\delta=0$ , then this photon polarization vector describes the linear polarization state of the photon at an angle $\beta$ with respect to the $x$ axis. The parameters $\beta=\pi/4$ and $\delta=\pm\pi/2$ denote circular polarization of the photon. Arbitrary $\beta$ and $\delta$ correspond to the elliptic polarization of the photons.

The differential cross section when only the photon beam is polarized has the following form:

\frac{d\sigma}{d\Omega}=\frac{d\sigma_{un}}{d\Omega}(1+A_{\perp}\cos 2\beta),

(41)

where $A_{\perp}$ is the asymmetry due to the linear polarization of the photon beam. It is defined as:

A_{\perp}=\frac{d\sigma/d\Omega(\beta=0^{\circ})-d\sigma/d\Omega(\beta=90^{\circ})}{d\sigma/d\Omega(\beta=0^{\circ})+d\sigma/d\Omega(\beta=90^{\circ})},

(42)

and it has the following form in terms of the structure functions:

\frac{d\sigma_{un}}{d\Omega}A_{\perp}=N(h_{1}-h_{2})\ \ or\ \ A_{\perp}=\frac{h_{1}-h_{2}}{h_{1}+h_{2}}.

(43)

Note that the circular polarization of the photon beam does not contribute to the differential cross section due to the P–invariance of the hadron electromagnetic interaction.

•

The deuteron target is vector polarized. In the case of the pseudoscalar meson photoproduction, the part of the hadronic tensor which depends on the deuteron vector polarization is determined by six structure functions. It can be written as:

	$\displaystyle H_{ij}(\xi)$	$\displaystyle=$	$\displaystyle{\vec{\xi}}{\vec{m}}(h_{6}\{m,n\}_{ij}+ih_{8}[m,n]_{ij})+{\vec{\xi}}{\vec{m}}(h_{10}m_{i}m_{j}+h_{11}n_{i}n_{j})+$		(44)
			$\displaystyle{\vec{\xi}}\hat{\vec{k}}(h_{15}\{m,n\}_{ij}+ih_{17}[m,n]_{ij}).$		(44)

Therefore, for the $\gamma+d\to P+d$ reaction, the dependence of the polarization observables on the deuteron vector polarization is determined by six structure functions.

The part of the differential cross section of the $\gamma+d\to P+d$ reaction which depends on the deuteron vector polarization, for the case of arbitrarily polarized photon, can be written as

	$\displaystyle\frac{d\sigma_{v}}{d\Omega}$	$\displaystyle=$	$\displaystyle\frac{d\sigma_{un}}{d\Omega}\biggl{[}A_{y}\xi_{y}+C_{y}^{l}\cos 2\beta\xi_{y}+\sin 2\beta\cos\delta(C_{x}^{l}\xi_{x}+C_{z}^{l}\xi_{z})+$		(45)
			$\displaystyle+\sin 2\beta\sin\delta(C_{x}^{c}\xi_{x}+C_{z}^{c}\xi_{z})\biggr{]},$		(45)

where $A_{y}$ is the asymmetry due to the vector polarization of the deuteron target, provided that the photon is unpolarized (the so called single target asymmetry). This asymmetry is due to the normal (to the reaction plane) component of the polarization vector ${\vec{\xi}}$ describing the vector polarization of the target. If the reaction amplitudes are real functions (as, for example, in the impulse approximation), then this asymmetry is equal to zero. The quantities $C^{l}_{x,y,z}(C^{c}_{x,z})$ are the correlation coefficients due to the vector polarization of the deuteron target when the photon is linear (circularly) polarized. The correlation coefficients $C^{l}_{x,y,z}$ are zero when the amplitudes are real. The correlation coefficients $C^{c}_{x,z}$ are determined by the components of the polarization vector lying in the reaction plane and these coefficients are nonzero, in general, for real amplitudes. All these polarization observables can be expressed in terms of the structure functions $h_{i}$ and they are

$\displaystyle\frac{d\sigma_{un}}{d\Omega}A_{y}$	$\displaystyle=$	$\displaystyle N(h_{10}+h_{11}),\ \ \frac{d\sigma_{un}}{d\Omega}C_{y}^{l}=N(h_{10}-h_{11}),$
$\displaystyle\frac{d\sigma_{un}}{d\Omega}C_{x}^{l}$	$\displaystyle=$	$\displaystyle 2Nh_{6},\ \ \frac{d\sigma_{un}}{d\Omega}C_{z}^{l}=2Nh_{15},$
$\displaystyle\frac{d\sigma_{un}}{d\Omega}C_{x}^{c}$	$\displaystyle=$	$\displaystyle 2Nh_{8},\ \ \frac{d\sigma_{un}}{d\Omega}C_{z}^{c}=2Nh_{17}.$	(46)

•

The deuteron target is tensor polarized. The part of the hadronic tensor which depends on the tensor (quadrupole) polarization of the deuteron target is determined by 10 structure functions for the case of real photons and its general structure is

$\displaystyle H_{ij}(S)$	$\displaystyle=$	$\displaystyle S_{ab}m_{a}m_{b}(h_{19}m_{i}m_{j}+h_{20}n_{i}n_{j})+S_{ab}n_{a}n_{b}(h_{24}m_{i}m_{j}+h_{25}n_{i}n_{j})+$	(47)
		$\displaystyle+S_{ab}\hat{k}_{a}m_{b}(h_{29}m_{i}m_{j}+h_{30}n_{i}n_{j})+S_{ab}m_{a}n_{b}(h_{34}\{m,n\}_{ij}+$
		$\displaystyle+ih_{36}[m,n]_{ij})+S_{ab}\hat{k}_{a}n_{b}(h_{38}\{m,n\}_{ij}+ih_{40}[m,n]_{ij}).$

Thus, for the $\gamma+d\to P+d$ reaction, the dependence of the polarization observables on the deuteron tensor (quadrupole) polarization is completely determined by 10 structure functions.

For the case of arbitrarily polarized photons, the part of the differential cross section which depends on the deuteron tensor polarization, can be written as:

$\displaystyle\frac{d\sigma_{t}}{d\Omega}$	$\displaystyle=$	$\displaystyle\frac{d\sigma_{un}}{d\Omega}\biggl{\{}A_{zz}Q_{zz}+A_{xx}(Q_{xx}-Q_{yy})+A_{xz}Q_{xz}+\cos 2\beta\biggl{[}C^{l}_{zz}Q_{zz}+$	(48)
		$\displaystyle+C^{l}_{xx}(Q_{xx}-Q_{yy})+C^{l}_{xz}Q_{xz}\biggr{]}+\sin 2\beta\cos\delta(C^{l}_{xy}Q_{xy}+C^{l}_{yz}Q_{yz})+$
		$\displaystyle+\sin 2\beta\sin\delta(C^{c}_{xy}Q_{xy}+C^{c}_{yz}Q_{yz})\biggr{\}},$

where $A_{zz},A_{xx}$ and $A_{xz}$ are the asymmetries due to the tensor polarization of the deuteron target when the photon is unpolarized. These asymmetries are non-zero, in general case, if the reaction amplitudes are real functions (as, for example, in the impulse approximation) in contrast to the $A_{y}$ asymmetry. The quantities $C^{l}_{zz},C^{l}_{xx},C^{l}_{xz},C^{l}_{xy}$ and $C^{l}_{yz}$ are the correlation coefficients due to the tensor polarization of the deuteron target when the photon is linear polarized (they are also can be non–zero if the reaction amplitudes are the real functions). The quantities $C^{c}_{xy}$ and $C^{c}_{yz}$ are the correlation coefficients determined by the tensor polarization of the deuteron target and the circular polarization of the photon (they originate from reaction mechanisms beyond the impulse approximation, for example, by the final–state interaction effects). All these polarization observables can be expressed in terms of the structure functions $h_{i}$ and they are:

$\displaystyle\sigma A_{zz}$	$\displaystyle=$	$\displaystyle-\frac{N}{2}(h_{19}+h_{20}+h_{24}+h_{25}),$
$\displaystyle\sigma A_{xx}$	$\displaystyle=$	$\displaystyle\frac{N}{2}(h_{19}+h_{20}-h_{24}-h_{25}),$
$\displaystyle\sigma A_{xz}$	$\displaystyle=$	$\displaystyle N\gamma_{1}(h_{29}+h_{30}),$
$\displaystyle\sigma C^{l}_{zz}$	$\displaystyle=$	$\displaystyle\frac{N}{2}(h_{29}+h_{25}-h_{19}-h_{24}),$
$\displaystyle\sigma C^{l}_{xx}$	$\displaystyle=$	$\displaystyle\frac{N}{2}(h_{19}+h_{25}-h_{20}-h_{24}),$
$\displaystyle\sigma C^{l}_{xz}$	$\displaystyle=$	$\displaystyle N\gamma_{1}(h_{29}-h_{30}),$
$\displaystyle\sigma C^{l}_{xy}$	$\displaystyle=$	$\displaystyle 2Nh_{34},\ \ \sigma C^{l}_{yz}=2N\gamma_{1}h_{38},$
$\displaystyle\sigma C^{c}_{xy}$	$\displaystyle=$	$\displaystyle 2Nh_{36},\ \ \sigma C^{c}_{yz}=2N\gamma_{1}h_{40},$	(49)

with

\gamma_{1}=\frac{W^{2}+M^{2}}{2MW},~\sigma=\displaystyle\frac{d\sigma_{un}}{d\Omega}=N(h_{1}+h_{2}).

VI Helicity amplitudes

Sometimes it is more convenient to use the helicity amplitudes formalism. Let us introduce the set of helicity amplitudes $f_{\lambda\lambda^{\prime}}(k^{2},W,\vartheta)$ (where $\lambda$ and $\lambda^{\prime}$ are the helicities of the initial ( $\gamma^{*}+d$ ) and final ( $d+P$ ) states) and define the amplitudes

h_{\lambda\lambda^{\prime}}=<\lambda_{\Delta},\lambda_{N}|T|\lambda_{\gamma},\lambda_{d}>={\vec{\chi}}_{2}^{*}(\lambda_{\Delta}){\vec{F}}(\lambda_{\gamma},\lambda_{d})\chi_{1}^{c}(\lambda_{N}),

(50)

where $\lambda_{\gamma},\lambda_{d},\lambda^{\prime}_{d}$ are the helicities of the virtual photon, initial and scattered deuteron respectively, with $\lambda=\lambda_{\gamma}-\lambda_{d}$ and $\lambda^{\prime}=\lambda^{\prime}_{d}$ . We choose the following convention:

$\displaystyle f_{1}$	$\displaystyle=$	$\displaystyle<+\|T\|++>=\frac{i}{2\sqrt{2}}[g_{1}+g_{6}+\cos\vartheta(g_{5}-g_{3})+\sin\vartheta(g_{4}-g_{8})],$
$\displaystyle f_{2}$	$\displaystyle=$	$\displaystyle<-\|T\|++>=\frac{i}{2\sqrt{2}}[g_{1}+g_{6}-\cos\vartheta(g_{5}-g_{3})-\sin\vartheta(g_{4}-g_{8})],$
$\displaystyle f_{3}$	$\displaystyle=$	$\displaystyle<0\|T\|++>=\frac{i}{2}\frac{E_{2}}{M}[\sin\vartheta(g_{5}-g_{3})+\cos\vartheta(g_{8}-g_{4})],$
$\displaystyle f_{4}$	$\displaystyle=$	$\displaystyle<+\|T\|+->=\frac{i}{2\sqrt{2}}[g_{6}-g_{1}-\cos\vartheta(g_{3}+g_{5})+\sin\vartheta(g_{4}+g_{8})],$
$\displaystyle f_{5}$	$\displaystyle=$	$\displaystyle<-\|T\|+->=\frac{i}{2\sqrt{2}}[g_{6}-g_{1}+\cos\vartheta(g_{3}+g_{5})-\sin\vartheta(g_{4}+g_{8})],$
$\displaystyle f_{6}$	$\displaystyle=$	$\displaystyle<0\|T\|+->=-\frac{i}{2}\frac{E_{2}}{M}[\sin\vartheta(g_{3}+g_{5})+\cos\vartheta(g_{4}+g_{8})],$
$\displaystyle f_{7}$	$\displaystyle=$	$\displaystyle<+\|T\|+0>=\frac{i}{2}\frac{E_{1}}{M}[g_{2}-\sin\vartheta g_{7}+\cos\vartheta g_{9}],$
$\displaystyle f_{8}$	$\displaystyle=$	$\displaystyle<-\|T\|+0>=\frac{i}{2}\frac{E_{1}}{M}[g_{2}+\sin\vartheta g_{7}-\cos\vartheta g_{9}],$
$\displaystyle f_{9}$	$\displaystyle=$	$\displaystyle<0\|T\|+0>=\frac{i}{\sqrt{2}}\frac{E_{1}E_{2}}{M^{2}}[\cos\vartheta g_{7}+\sin\vartheta g_{9}],$
$\displaystyle f_{10}$	$\displaystyle=$	$\displaystyle<+\|T\|0+>=-\frac{i}{2}\frac{k_{0}}{\sqrt{Q^{2}}}[g_{10}-\cos\vartheta g_{12}+\sin\vartheta g_{13}],$
$\displaystyle f_{11}$	$\displaystyle=$	$\displaystyle<-\|T\|0+>=-\frac{i}{2}\frac{k_{0}}{\sqrt{Q^{2}}}[g_{10}+\cos\vartheta g_{12}-\sin\vartheta g_{13}],$
$\displaystyle f_{12}$	$\displaystyle=$	$\displaystyle<0\|T\|0+>=\frac{i}{\sqrt{2}}\frac{E_{2}}{M}\frac{k_{0}}{\sqrt{Q^{2}}}[\cos\vartheta g_{13}+\sin\vartheta g_{12}],$
$\displaystyle f_{13}$	$\displaystyle=$	$\displaystyle<+\|T\|00>=-\frac{i}{\sqrt{2}}\frac{E_{1}}{M}\frac{k_{0}}{\sqrt{Q^{2}}}g_{11}.$	(51)

where $E_{2}=(W^{2}-M_{P}^{2}+M^{2})/2W$ is the energy of the scattered deuteron in the reaction CMS.

At this stage, the general model–independent analysis of the polarization observables for pseudoscalar meson photo–production is completed. To proceed further in the calculation of the observables, one needs a model for the reaction mechanism and for the deuteron structure.

VII Model, kinematics, and results

In order to illustrate the derived formalism with numerical results it is necessary to calculate the elementary amplitudes in frame of a model describing the structure of the involved hadrons. Following Ref. Rekalo et al. (2002) we use the impulse approximation for the deuteron, and consider a model for the interaction of the virtual photon with the nucleon. The neutron and proton structure is parametrized in terms of electromagnetic form factors and deuteron wave functions. The Bonn Machleidt (2001) or the Paris Lacombe et al. (1980) nucleon-nucleon potentials, were considered in Ref. Rekalo et al. (2002) as they give the most different values for the observables. It was shown that other recent potentials based on the Argonne Wiringa et al. (1984) and Reid Reid (1968) potentials give indeed intermediate values. The photon interaction is described in frame of an effective Lagrangian model, considering nucleon and $\Delta$ -exchange in $s$ -channel, nucleon exchange in $t$ -channel and $\pi$ , $\rho$ and $\omega$ -mesons exchange in $u$ -channel. The details of the model are given in Ref. Rekalo et al. (2002). In principle, in the near threshold region, for $\gamma(\gamma^{*})+d\to d+\pi^{0}$ , rescattering effects may play an important role, for pion S-state electroproduction. However, it has been shown in a model independent way based only on the Pauli principle, that the main rescattering contribution from the two step process: $\gamma+d\to p+p+\pi^{-}(\mbox{and}~n+n+\pi^{+})\to d+\pi^{0}$ vanishes, when the two nucleons in the $NN\pi$ -intermediate state are on mass shell Rekalo and Tomasi-Gustafsson (2002).

As stated in the introduction, the main purpose of this paper is the general and model independent derivation of polarized and unpolarized observables for pion electro and photo-production on the deuteron. Therefore, we give an example of the behavior of some of the observables and do not discuss in extent their dependence on the ingredients of the model.

The experimental detection of the pion and the scattered electron, for a definite beam energy, allows to fully determine the kinematics of the $e+d\to e+d+\pi^{0}$ reaction, i.e., $\gamma^{*}+d\to d+\pi^{0}$ , that depends on three kinematical variables. Let us choose

•

$k^{2}$ : the four momentum squared of the $\gamma^{*}$ ,
•

$s=W^{2}=(k+p_{1})^{2}=(q+p_{2})^{2}$ : the total energy in CMS of the $\gamma^{*}d$ system,
•

$\vartheta$ : the $\pi^{0}$ emission angle in the CMS of the reaction $\gamma^{*}+d\to d+\pi^{0}$ .

As shown above, there are 13 independent amplitudes for the reaction $\gamma^{*}+d\to d+\pi^{0}$ : $g_{i}(k^{2},W,\vartheta),i=1-13$ , that are functions of these three variables.

In the assumption of impulse approximation, the $\gamma^{*}$ interacts on the bare nucleon inside the deuteron either the proton or the neutron, while the other nucleon stays as a spectator. There are six amplitudes for the reaction $\gamma^{*}+N\to N+\pi^{0}$ , depending also on three variables that can not be connected in a unique way to the previous set. The problem is that one has to make an assumption how the momentum $Q^{2}$ is transferred to one of the nucleons inside the deuteron, while this nucleon have itself a Fermi momentum.

It seems reasonable to calculate these amplitudes at the same values of the two variables, $k^{2}$ and $t$ . The choice is open for the total energy, $s=(k+p_{1})^{2}=(k+M)^{2}\neq s_{1}=(k+p_{N})^{2}=(k+m)^{2}$ . The value of the $\pi^{0}$ emission angle in the CMS of the reaction $\gamma^{*}+N\to N+\pi^{0}$ , $\theta_{\pi}$ , calculated from $s_{1}$ may fall outside the kinematical limits. However, one can increase $s_{1}$ , what can be physically understood taking into account the Fermi-motion of the nucleon in the deuteron (see discussion in Ref. Rekalo et al. (2002), page 11).

Therefore the six independent amplitudes for $\gamma^{*}+N\to N+\pi^{0}$ , depend on three kinematical variables: $f^{N}_{i}(k^{2},W_{N},\theta_{\pi}),$ i=1-6, where $s_{N}=W_{N}^{2}$ is the total energy of the $\gamma^{*}N$ (or $\pi^{0}N$ ).

In Ref. Rekalo et al. (2002) the structure functions and the observables have been calculated as a function of these last variables, because it was straightforward to implement the nucleon electro-production model. However, the experimentalists will measure the electron, deuteron and pion in the Lab system. They will have access to $t,W,\cos\vartheta,\cos\theta$ but not to: $s_{N}$ , and in general to the participant nucleon.

Therefore we choose to fix $\vec{p}_{1}+\vec{k}$ =0, $s_{1}=k_{0}+m$ in a near threshold kinematics, where all phase space is available for the proton: s=4.1 GeV, $0.5\leq t\leq 2.5$ GeV² and calculate the structure functions and some polarization observables as a function of the pion angle in CMS of $\gamma^{*}d$ system, $\cos\vartheta$ .

Let us stress that this application is given as an example. The general formalism derived in this paper allows to calculate the observables for any energy and for any kinematics, in frame of the one photon exchange approximation, implementing any suitable model for the deuteron structure and for the reaction.

VII.1 Numerical results

We choose to illustrate the results as a function of $\cos\vartheta$ , at the total energy $W$ =2.5 GeV for four values of the momentum transfer in the range $0.5\leq-k^{2}\leq 2$ GeV². These conditions do not violate the energy and momentum conservation in the $\gamma^{*}d$ and $\gamma^{*}p$ systems in the kinematical range of all the variables considered here. The numerical calculations are done for the Paris potential, for the dipole parametrization of the proton form factor, whereas the electric neutron form factor is set to zero.

VII.2 Unpolarized Structure Functions

The four structure functions that define the unpolarized cross section are shown in Fig. 1. From top to bottom each plot corresponds to $-k^{2}$ = 0.5, 1, 1.5 and 2 GeV², $H_{xx}+H_{yy}$ , $H_{xx}-H_{yy}$ , $H_{zz}$ and $H_{xz}+H_{zx}$ . The different lines illustrate the considered contributions to $\pi^{0}$ production: $\Delta$ (green, dotted line), $\Delta+s+u$ (blue, dash-dotted line), $\Delta+s+u-\omega$ (red, dashed line), $\Delta+s+u+\omega$ (black, solid line).

Refer to caption — Figure 1: $\vartheta$ -dependence of the functions $H_{xx}+H_{yy}$ , $H_{xx}-H_{yy}$ , $H_{zz}$ and $H_{xz}+H_{zx}$ (respectively from left to right) for $W$ =2.5 GeV. From top to bottom each plot corresponds to $-k^{2}$ = 0.5, 1, 1.5 and 2 GeV². The different lines illustrate the considered contributions for $\pi^{0}$ production: $\Delta$ (green, dotted line), $\Delta+s+u$ (blue, dash-dotted line), $\Delta+s+u-\omega$ (red, dashed line), $\Delta+s+u+\omega$ (black, solid line).

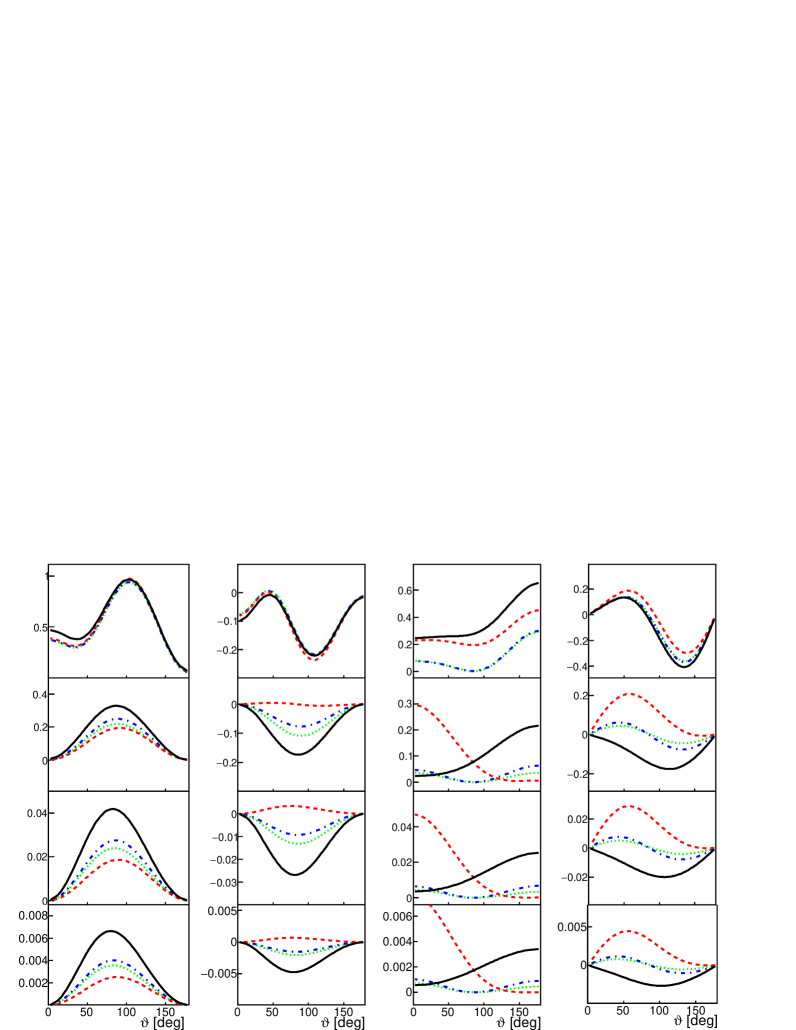
VII.3 Observables for a polarized deuteron target

The asymmetries for a vector polarized target can be expressed as a function of longitudinal and transverse components, as in Eq. (22). In Fig. 2 the transverse components, i.e., the functions $A_{x}^{(TT)}$ , $A_{y}^{(TT)}$ , $\bar{A}_{y}^{(TT)}$ and $A_{z}^{(TT)}$ (respectively from left to right) are illustrated in terms of the $\pi^{0}$ angle in the CMS of the $\gamma^{*}d$ system, and the longitudinal components, $A_{x}^{(LT)}$ , $A_{y}^{(LT)}$ , $A_{z}^{(LT)}$ and $A_{y}^{(LL)}$ are shown in Fig. 3. In Fig. 4 the $\vartheta$ -dependence of the functions $B_{x}^{(TT)}$ , $B_{z}^{(TT)}$ , $B_{x}^{(LT)}$ $B_{y}^{(LT)}$ and $B_{z}^{(LT)}$ is shown.

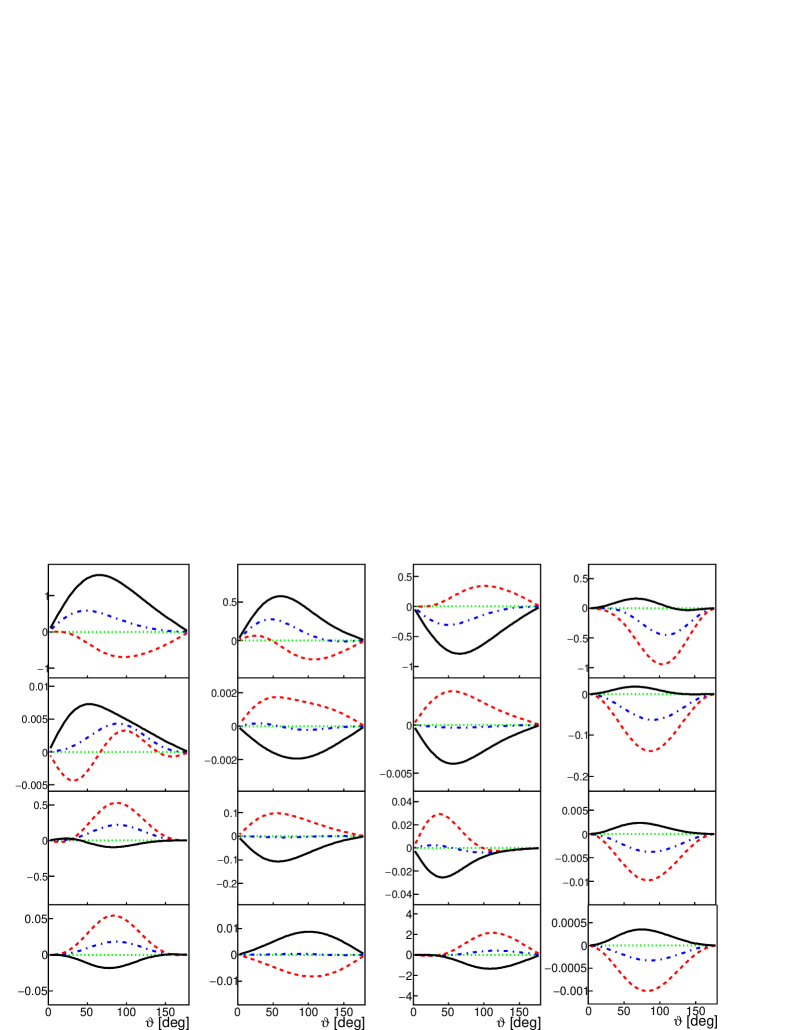
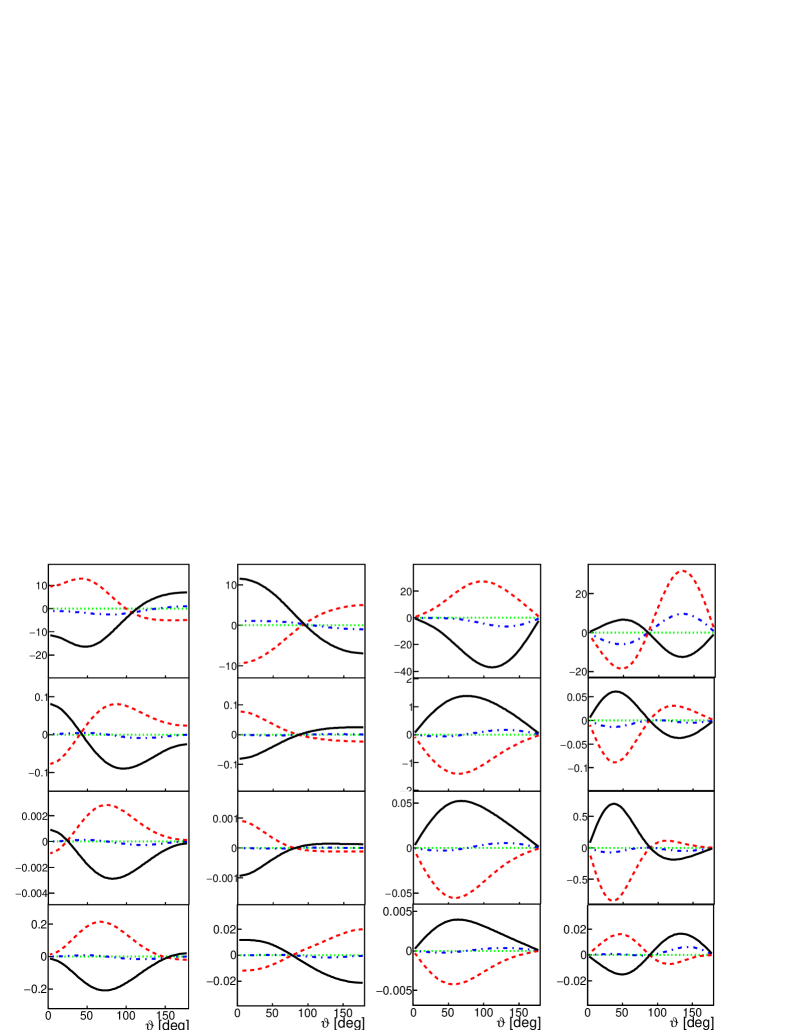
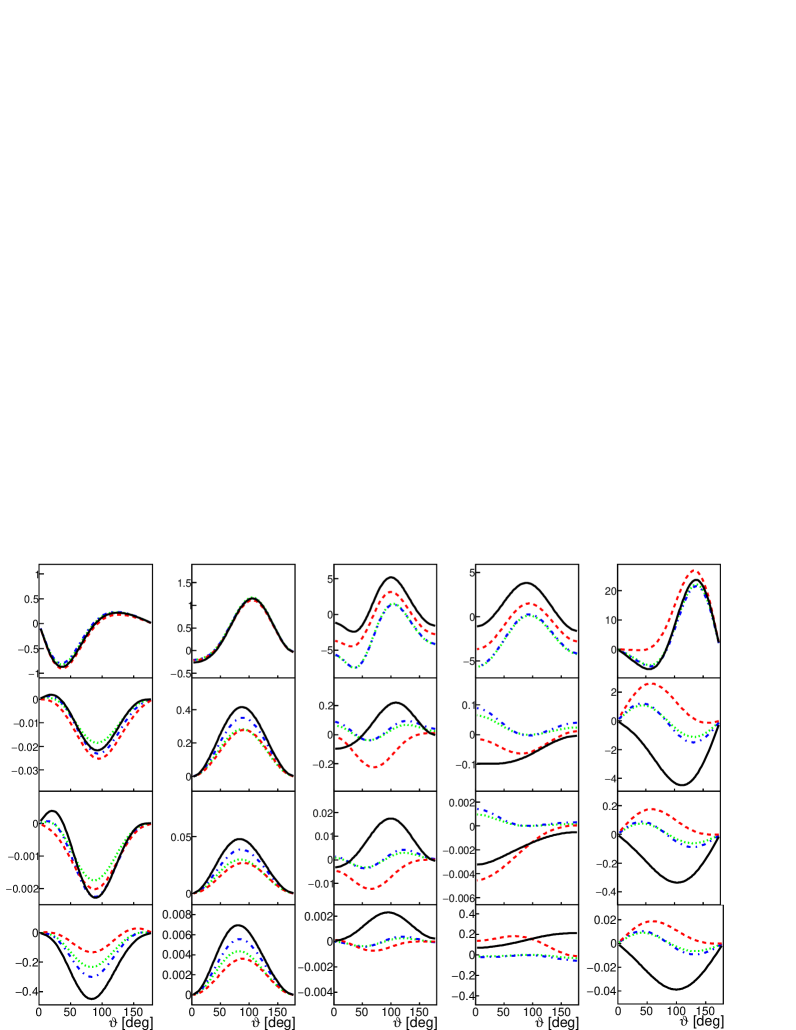
As an example of tensor observables, the $\vartheta$ -dependence of the functions $A_{zz}^{T}$ , $A_{zz}^{L}$ , $A_{zz}^{I}$ , $A_{zz}^{P}$ and $\bar{A}_{zz}^{I}$ (from left to right) is shown in Fig. 5.

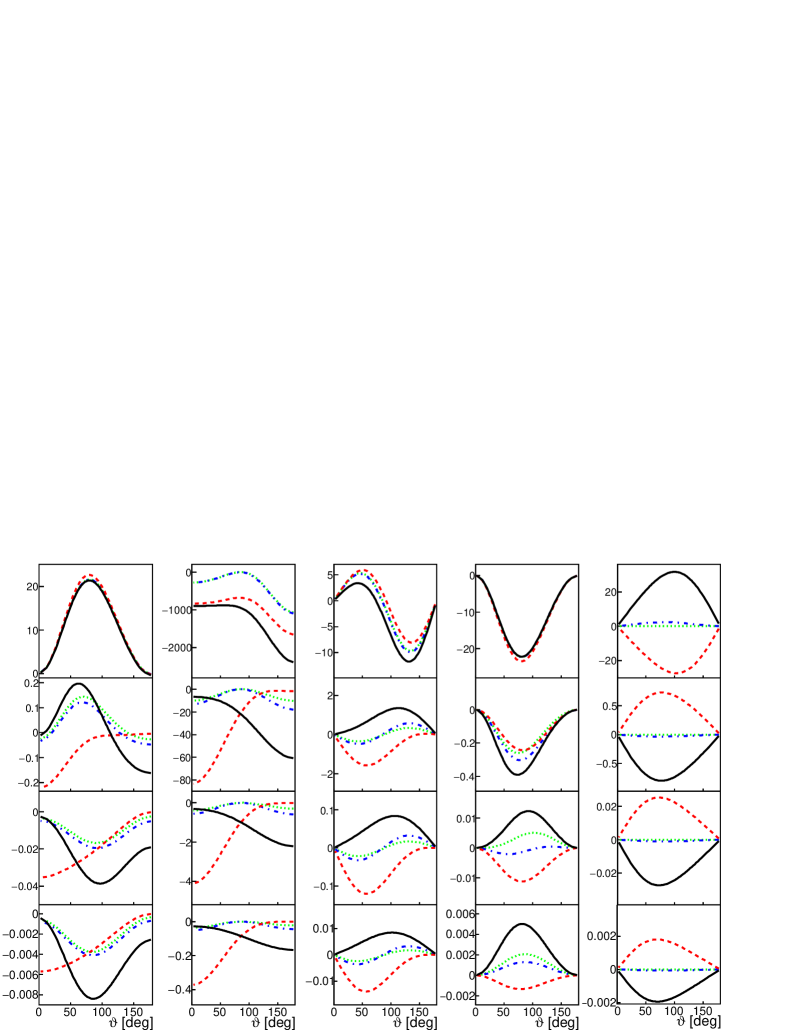
We can see that all observables have a strong angular dependence, they become smaller when $k^{2}$ increases, they may change shape and also the sign.

VIII Conclusions

This work give general expressions for various polarization observables in the coherent pseudoscalar meson photo- and electroproduction on the deuteron target assuming one-photon-exchange approximation. It completes and generalizes a previous work on the unpolarized differential cross section. The spin structure of the matrix element is explicitly derived in terms of structure functions. The correspondence with the helicity amplitudes is given. The polarization effects have been investigated for the case of a longitudinally polarized electron beam and vector or tensor polarized deuteron target. In the case of the photoproduction reaction, we consider linearly, circularly or elliptically polarized photon beam. The asymmetries arising from the polarization of the particles in the initial state have been discussed as well as the measurable observables related to the scattered deuteron polarization.

Numerical estimations for the unpolarized differential cross section and for some polarization observables have been done in the frame of the simple model developed in Ref. Rekalo et al. (2002).

The purpose of this paper is focussed on model independent expressions, that depend on the elementary amplitudes. This formalism is applicable to all phenomenological models developed in frame of a definite picture of the deuteron, and is useful to bridge the experimental information and the theoretical background.

IX Acknowledgments

This work was partially supported by the Ministry of Education and Science of Ukraine (projects no. 0115U000474 and no. 0117U004866). The research is carried on in the frame of the France-Ukraine IDEATE International Associated Laboratory (LIA).

X Appendix I: explicit expressions for the amplitudes $h$

We present here the expressions for the structure functions $h_{i}$ and $\bar{h}_{i}$ (i=1-41) in terms of the scalar amplitudes $g_{i}$ (i=1-13) describing the $\gamma^{*}+d\to d+P$ reaction.

The structure functions $h_{i}$ describe the polarization observables in the $\gamma^{*}+d\to d+P$ reaction for the case of different polarization states of the deuteron target.

•

The deuteron target is unpolarized. The structure functions $h_{1}-h_{5}$ corresponding to the interaction of the virtual photon with an unpolarized deuteron target can be written as

$\displaystyle h_{1}$	$\displaystyle=$	$\displaystyle\frac{1}{3}\biggl{[}\|g_{1}\|^{2}+\gamma_{1}^{2}\|g_{2}\|^{2}+a\|g_{3}\|^{2}+b\|g_{4}\|^{2}+2cReg_{3}g_{4}^{*}\biggr{]},$
$\displaystyle h_{2}$	$\displaystyle=$	$\displaystyle\frac{1}{3}\biggl{[}\|g_{6}\|^{2}+a(\|g_{5}\|^{2}+\gamma_{1}^{2}\|g_{9}\|^{2})+b(\|g_{8}\|^{2}+\gamma_{1}^{2}\|g_{7}\|^{2})+2cRe(g_{5}g_{9}^{}+\gamma_{1}^{2}g_{7}g_{9}^{})\biggr{]},$
$\displaystyle h_{3}$	$\displaystyle=$	$\displaystyle\frac{1}{3}\biggl{[}\|g_{10}\|^{2}+\gamma_{1}^{2}\|g_{11}\|^{2}+a\|g_{12}\|^{2}+b\|g_{13}\|^{2}+2cReg_{12}g_{13}^{*}\biggr{]},$
$\displaystyle h_{4}$	$\displaystyle=$	$\displaystyle ReA_{1},\ \ h_{5}=ImA_{1},$
$\displaystyle A_{1}$	$\displaystyle=$	$\displaystyle\frac{1}{3}\biggl{[}g_{1}g_{10}^{}+\gamma_{1}^{2}g_{2}g_{11}^{}+ag_{3}g_{12}^{}+bg_{4}g_{13}^{}+c(g_{3}g_{13}^{}+g_{4}g_{12}^{})\biggr{]},$
$\displaystyle\gamma_{1}$	$\displaystyle=$	$\displaystyle\frac{E_{1}}{M},\ \ a=1+\frac{{\vec{q}}^{2}}{M^{2}}\sin^{2}\vartheta,\ \ b=1+\frac{{\vec{q}}^{2}}{M^{2}}\cos^{2}\vartheta,\ \ c=\frac{{\vec{q}}^{2}}{M^{2}}\cos\vartheta\sin\vartheta,$	(52)

where ${\vec{q}}(E_{1})$ is the $P-$ meson momentum (energy) in the $\gamma^{*}+d\to P+d$ reaction CMS and $\vartheta$ is the angle between the pseudoscalar meson and virtual photon momenta in this system, $E_{1}=(W^{2}-k^{2}+M^{2})/2W.$

•

The deuteron target is a vector polarized. The structure functions $h_{6}-h_{18}$ which describe the effects of the vector polarization of the deuteron target can be written as

$\displaystyle h_{6}$	$\displaystyle=$	$\displaystyle-\frac{\gamma_{1}}{2}ImA_{2},\ \ h_{7}=-\frac{\gamma_{1}}{2}ImA_{3},\ \ h_{8}=\frac{\gamma_{1}}{2}ReA_{2},\ \ h_{9}=-\frac{\gamma_{1}}{2}ReA_{3},$
$\displaystyle A_{2}$	$\displaystyle=$	$\displaystyle g_{2}g_{6}^{}-ag_{3}g_{9}^{}-bg_{4}g_{7}^{}-c(g_{3}g_{7}^{}+g_{4}g_{9}^{*}),$
$\displaystyle A_{3}$	$\displaystyle=$	$\displaystyle-g_{6}g_{11}^{}+ag_{9}g_{12}^{}+bg_{7}g_{13}^{}+c(g_{9}g_{13}^{}+g_{7}g_{12}^{*}),$
$\displaystyle h_{10}$	$\displaystyle=$	$\displaystyle-\gamma_{1}Img_{1}g_{2}^{},~h_{11}=\gamma_{1}Im\biggl{[}-ag_{5}g_{9}^{}+bg_{7}g_{8}^{}-c(g_{5}g_{7}^{}+g_{8}g_{9}^{*})\biggr{]},$
$\displaystyle h_{12}$	$\displaystyle=$	$\displaystyle-\gamma_{1}Img_{10}g_{11}^{},h_{13}=-\frac{\gamma_{1}}{2}Im(g_{1}g_{11}^{}-g_{2}g_{10}^{}),~h_{14}=\frac{\gamma_{1}}{2}Re(g_{1}g_{11}^{}-g_{2}g_{10}^{*}),$
$\displaystyle h_{15}$	$\displaystyle=$	$\displaystyle-\frac{1}{2}ImA_{4},\ \ h_{16}=-\frac{1}{2}ImA_{5},h_{17}=\frac{1}{2}ReA_{4},\ \ h_{18}=-\frac{1}{2}ReA_{5},$
$\displaystyle A_{4}$	$\displaystyle=$	$\displaystyle-g_{1}g_{6}^{}+ag_{3}g_{5}^{}+bg_{4}g_{8}^{}+c(g_{3}g_{8}^{}+g_{4}g_{5}^{*}),$
$\displaystyle A_{5}$	$\displaystyle=$	$\displaystyle g_{6}g_{10}^{}-ag_{5}g_{12}^{}-bg_{8}g_{13}^{}-c(g_{5}g_{13}^{}+g_{8}g_{12}^{*}).$	(53)

•

The deuteron target is tensor polarized. The structure functions $h_{19}-h_{41}$ which describe the effects of the tensor polarization of the deuteron target can be written as

$\displaystyle h_{19}$	$\displaystyle=$	$\displaystyle\|g_{1}\|^{2}-\gamma_{1}^{2}\|g_{2}\|^{2},~h_{20}=a\|g_{5}\|^{2}+b\|g_{8}\|^{2}+2cReg_{5}g_{8}^{*}-$
		$\displaystyle\gamma_{1}^{2}\biggl{[}a\|g_{9}\|^{2}+b\|g_{7}\|^{2}+2cReg_{7}g_{9}^{*}\biggr{]},$
$\displaystyle h_{21}$	$\displaystyle=$	$\displaystyle\|g_{10}\|^{2}-\gamma_{1}^{2}\|g_{11}\|^{2},h_{22}=Re(g_{1}g_{10}^{}-\gamma_{1}^{2}g_{2}g_{11}^{}),$
$\displaystyle h_{23}$	$\displaystyle=$	$\displaystyle Im(g_{1}g_{10}^{}-\gamma_{1}^{2}g_{2}g_{11}^{}),~h_{24}=a\|g_{3}\|^{2}+b\|g_{4}\|^{2}+2cReg_{3}g_{4}^{*}-\gamma_{1}^{2}\|g_{2}\|^{2},$
$\displaystyle h_{25}$	$\displaystyle=$	$\displaystyle\|g_{6}\|^{2}-\gamma_{1}^{2}\biggl{[}a\|g_{9}\|^{2}+b\|g_{7}\|^{2}+2cReg_{7}g_{9}^{*}\biggr{]},$
$\displaystyle h_{26}$	$\displaystyle=$	$\displaystyle a\|g_{12}\|^{2}+b\|g_{13}\|^{2}+2cReg_{12}g_{13}^{*}-\gamma_{1}^{2}\|g_{11}\|^{2},$
$\displaystyle h_{27}$	$\displaystyle=$	$\displaystyle ReA_{6},\ \ h_{28}=ImA_{6},~A_{6}=ag_{3}g_{12}^{}+bg_{4}g_{13}^{}+c(g_{3}g_{13}^{}+g_{4}g_{12}^{})-\gamma_{1}^{2}g_{2}g_{11}^{*},$
$\displaystyle h_{29}$	$\displaystyle=$	$\displaystyle 2Reg_{1}g_{2}^{},~h_{30}=2Re\biggl{[}ag_{5}g_{9}^{}+bg_{7}g_{8}^{}+c(g_{5}g_{7}^{}+g_{8}g_{9}^{*})\biggr{]},$
$\displaystyle h_{31}$	$\displaystyle=$	$\displaystyle 2Reg_{10}g_{11}^{},~h_{32}=Re(g_{2}g_{10}^{}+g_{1}g_{11}^{}),~h_{33}=Im(g_{2}g_{10}^{}+g_{1}g_{11}^{*}),$
$\displaystyle h_{34}$	$\displaystyle=$	$\displaystyle ReA_{7},\ \ h_{35}=ReA_{8},\ \ h_{36}=ImA_{7},\ \ h_{37}=-ImA_{8},$
$\displaystyle A_{7}$	$\displaystyle=$	$\displaystyle ag_{3}g_{5}^{}+bg_{4}g_{8}^{}+c(g_{3}g_{8}^{}+g_{4}g_{5}^{})+g_{1}g_{6}^{*},$
$\displaystyle A_{8}$	$\displaystyle=$	$\displaystyle g_{5}g_{12}^{}+bg_{8}g_{13}^{}+c(g_{5}g_{13}^{}+g_{8}g_{12}^{})+g_{6}g_{10}^{*},$
$\displaystyle h_{38}$	$\displaystyle=$	$\displaystyle ReA_{9},\ \ h_{39}=ReA_{10},\ \ h_{40}=ImA_{9},\ \ h_{41}=-ImA_{10},$
$\displaystyle A_{9}$	$\displaystyle=$	$\displaystyle ag_{3}g_{9}^{}+bg_{4}g_{7}^{}+c(g_{3}g_{7}^{}+g_{4}g_{9}^{})+g_{2}g_{6}^{*},$
$\displaystyle A_{10}$	$\displaystyle=$	$\displaystyle ag_{9}g_{12}^{}+bg_{7}g_{13}^{}+c(g_{9}g_{13}^{}+g_{7}g_{12}^{})+g_{6}g_{11}^{*}.$	(54)

The structure functions $\bar{h}_{i}$ describe the polarization observables in the $\gamma^{*}+d\to d+P$ reaction for the case of the polarized scattered deuteron.

•

The scattered deuteron is vector polarized. The structure functions $\bar{h}_{6}-\bar{h}_{18}$ which describe the effects of the vector polarization of the scattered deuteron can be written as

$\displaystyle\bar{h}_{6}$	$\displaystyle=$	$\displaystyle\frac{1}{6}[xIm(g_{4}g_{6}^{}-g_{1}g_{8}^{}-\gamma^{2}_{1}g_{2}g_{7}^{})-zIm(g_{1}g_{5}^{}-g_{3}g_{6}^{}+\gamma^{2}_{1}g_{2}g_{9}^{}),$
$\displaystyle\bar{h}_{7}$	$\displaystyle=$	$\displaystyle-\frac{1}{6}[zIm(g_{6}g_{12}^{}-g_{5}g_{10}^{}-\gamma^{2}_{1}g_{9}g_{11}^{})-xIm(g_{8}g_{10}^{}-g_{6}g_{13}^{}+\gamma^{2}_{1}g_{7}g_{11}^{}),$
$\displaystyle\bar{h}_{8}$	$\displaystyle=$	$\displaystyle\frac{1}{6}[-xRe(g_{4}g_{6}^{}-g_{1}g_{8}^{}-\gamma^{2}_{1}g_{2}g_{7}^{})+zRe(g_{1}g_{5}^{}-g_{3}g_{6}^{}+\gamma^{2}_{1}g_{2}g_{9}^{}),$
$\displaystyle\bar{h}_{9}$	$\displaystyle=$	$\displaystyle-\frac{1}{6}[zRe(g_{6}g_{12}^{}-g_{5}g_{10}^{}-\gamma^{2}_{1}g_{9}g_{11}^{})-xRe(g_{8}g_{10}^{}-g_{6}g_{13}^{}+\gamma^{2}_{1}g_{7}g_{11}^{}),$
$\displaystyle\bar{h}_{10}$	$\displaystyle=$	$\displaystyle\frac{1}{3}\gamma_{2}Img_{3}g_{4}^{},\ \ \bar{h}_{11}=\frac{1}{3}\gamma_{2}Im(g_{5}g_{8}^{}-\gamma^{2}_{1}g_{7}g_{9}^{}),\ \ \bar{h}_{12}=\frac{1}{3}\gamma_{2}Img_{12}g_{13}^{},$
$\displaystyle\bar{h}_{13}$	$\displaystyle=$	$\displaystyle\frac{1}{6}\gamma_{2}Im(g_{3}g_{13}^{}-g_{4}g_{12}^{}),\ \ \bar{h}_{14}=-\frac{1}{6}\gamma_{2}Re(g_{3}g_{13}^{}-g_{4}g_{12}^{}),$
$\displaystyle\bar{h}_{15}$	$\displaystyle=$	$\displaystyle-\frac{1}{6}[zIm(g_{4}g_{6}^{}-g_{1}g_{8}^{}-\gamma^{2}_{1}g_{2}g_{7}^{})-yIm(g_{1}g_{5}^{}-g_{3}g_{6}^{}+\gamma^{2}_{1}g_{2}g_{9}^{}),$
$\displaystyle\bar{h}_{16}$	$\displaystyle=$	$\displaystyle-\frac{1}{6}[zIm(g_{8}g_{0}^{}-g_{6}g_{13}^{}+\gamma^{2}_{1}g_{7}g_{11}^{})-yIm(g_{6}g_{12}^{}-g_{5}g_{10}^{}-\gamma^{2}_{1}g_{9}g_{11}^{}),$
$\displaystyle\bar{h}_{17}$	$\displaystyle=$	$\displaystyle\frac{1}{6}[zRe(g_{4}g_{6}^{}-g_{1}g_{8}^{}-\gamma^{2}_{1}g_{2}g_{7}^{})-yRe(g_{1}g_{5}^{}-g_{3}g_{6}^{}+\gamma^{2}_{1}g_{2}g_{9}^{}),$
$\displaystyle\bar{h}_{18}$	$\displaystyle=$	$\displaystyle-\frac{1}{6}[zRe(g_{8}g_{0}^{}-g_{6}g_{13}^{}+\gamma^{2}_{1}g_{7}g_{11}^{})-yRe(g_{6}g_{12}^{}-g_{5}g_{10}^{}-\gamma^{2}_{1}g_{9}g_{11}^{}),$	(55)