Generalized Josephson effect in an asymmetric double-well potential
at finite temperatures

In what follows we want to keep our considerations as general as possible, making them applicable to a wide range of potentials that can be realized in experiment. For convenience we will restrict our analysis to one spatial dimension, assuming that the confinement in the other two directions is sufficiently strong, such that excitations of perpendicular modes are highly suppressed (see Appendix A).

We assume a symmetric, time-independent potential $V(x)=V(-x)$ without further specification of its explicit shape. This potential enters the single-particle Hamiltonian

$$\hat{H}_{0}=-\frac{\hbar^{2}}{2m}\partial_{x}^{2}+V(x)\,.$$

(1)

The corresponding eigenvalue problem $\hat{H}_{0}\phi(x)=E\phi(x)$ can be solved in terms of orthogonal basis functions $\phi_{n}(x)$ with energies $E_{n}$. We assume that the Hamiltonian has at least two normalized eigenstates: the ground state $\phi_{0}(x)$ and the first excited state $\phi_{1}(x)$. Since the potential $V(x)$ is symmetric, the ground state is necessarily symmetric as well, while the first excited state must be anti-symmetric, as visualized in Fig. 1a. From these states we want to construct proper left and right states $\phi_{L/R}(x)$, which describe the quantum particle being in the left or right part of the potential. To do this we linearly combine the energy eigenstates in the form

	$\displaystyle\phi_{L}(x)$	$\displaystyle=$	$\displaystyle\cos\xi\,\phi_{0}(x)+\sin\xi\,\phi_{1}(x)$		(2)
	$\displaystyle\phi_{R}(x)$	$\displaystyle=$	$\displaystyle\sin\xi\,\phi_{0}(x)-\cos\xi\,\phi_{1}(x)\,$

with a parameter $\xi$ that needs to be determined hereafter. To investigate these states, we now introduce the left- and right-side scalar products

$$\langle\,\cdot\,|\,\cdot\,\rangle_{L}+\langle\,\cdot\,|\,\cdot\,\rangle_{R}=\langle\,\cdot\,|\,\cdot\,\rangle\,,$$

(3)

which imply an integral over all negative or positive $x$, respectively, such that their sum gives the standard scalar product. Calculating the left- and right-side scalar products of the left and right states (2) we obtain

	$\displaystyle\langle\phi_{R}|\phi_{R}\rangle_{R}=\langle\phi_{L}|\phi_{L}\rangle_{L}$	$\displaystyle=$	$\displaystyle 1/2+\sin(2\xi)\langle\phi_{0}|\phi_{1}\rangle_{L}$
	$\displaystyle\langle\phi_{R}|\phi_{R}\rangle_{L}=\langle\phi_{L}|\phi_{L}\rangle_{R}$	$\displaystyle=$	$\displaystyle 1/2-\sin(2\xi)\langle\phi_{0}|\phi_{1}\rangle_{L}\,.$		(4)

In this calculation we use $\langle\phi_{0}|\phi_{0}\rangle_{L/R}=\langle\phi_{1}|\phi_{1}\rangle_{L/R}=1/2$, which is clear by symmetry considerations. The scalar product $\langle\phi_{0}|\phi_{1}\rangle_{L}=-\langle\phi_{0}|\phi_{1}\rangle_{R}$ can be chosen real and positive by adapting the phases of the energy eigenstates. Recalling that the scalar products (4) represent the probabilities to find the particles of state $\phi_{L/R}(x)$ in the left or right part of the potential, we can maximize this probability by the choice $\xi=\pi/4$, leading to the states

	$\displaystyle\phi_{L}(x)$	$\displaystyle=$	$\displaystyle\frac{1}{\sqrt{2}}[\phi_{0}(x)+\phi_{1}(x)]$
	$\displaystyle\phi_{R}(x)$	$\displaystyle=$	$\displaystyle\frac{1}{\sqrt{2}}[\phi_{0}(x)-\phi_{1}(x)]\,$		(5)

as the best fitting left and right states in the potential $V(x)$, shown in Fig. 2a. The explicit shape of this potential now only enters our consideration via the scalar product $\langle\phi_{0}|\phi_{1}\rangle_{L}$, which is a measure of how good the states $\phi_{L/R}(x)$ actually represent a particle at the left or right side of the potential. In particular, we will call all such potentials a symmetric double-well, in which $\langle\phi_{0}|\phi_{1}\rangle_{L}=1/2-\epsilon$ with a sufficiently small $\epsilon>0$, such that

	$\displaystyle\langle\phi_{R}|\phi_{R}\rangle_{R}=\langle\phi_{L}|\phi_{L}\rangle_{L}$	$\displaystyle=$	$\displaystyle 1-\epsilon$
	$\displaystyle\langle\phi_{R}|\phi_{R}\rangle_{L}=\langle\phi_{L}|\phi_{L}\rangle_{R}$	$\displaystyle=$	$\displaystyle\epsilon\,,$		(6)

and the $\phi_{L/R}(x)$ appropriately describe a single quantum particle in a left or right well state.

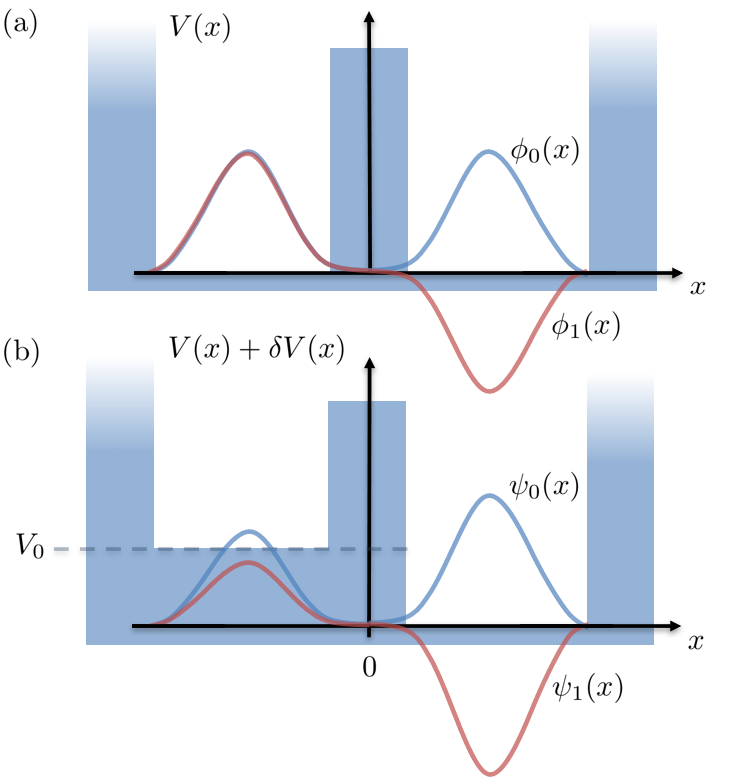
In the next section, we will use these definitions for the symmetric double-well to extend our analysis to a double-well potential with an additional potential step.

To describe a particle in an asymmetric double-well potential we extend the Hamiltonian

$$\hat{H}=\hat{H}_{0}+\delta V(x)$$

(7)

by a small potential step

$$\delta V(x)=\left\{\begin{array}[]{ll}V_{0}&\quad x<0\\ 0&\quad\mathrm{elsewhere}\,\,.\end{array}\right.\,$$

(8)

The solutions of the corresponding eigenvalue problem

$$\hat{H}\psi_{n}(x)=\tilde{E}_{n}\psi_{n}(x)$$

(9)

can be obtained in the framework of first order perturbation theory, up to linear order in $V_{0}/E$, where $E=(E_{0}+E_{1})/2$. For that we use the states from Sec. II.1 and treat $\delta V(x)$ as a small perturbation of the symmetric double-well.

It is well known that in perturbation theory, states strongly affect each other when they have similar energies. For the symmetric double-well (6) the separation of the ground and excited state from other possible states is in the order of $E$. In contrast, their own energies are much closer to each other, i.e., $E_{1}-E_{0}=\Delta E\ll E$. This is due to the fact that the scalar product $\langle\phi_{0}|\phi_{1}\rangle_{L}=1/2-\epsilon$ only slightly deviates from $1/2$, such that the states $\phi_{0}(x)\approx\phi_{1}(x)$ closely resemble each other for $x<0$, as also can be seen in Fig. 1a. In consequence, acting on them with the Hamiltonian $\hat{H}_{1}$ gives similar energy eigenvalues $E_{0}\approx E_{1}$, which become degenerated in the ultimate case $\epsilon=0$. We, thus, can restrict our investigation to the corrections of $\phi_{0}(x)$ by $\phi_{1}(x)$ and vise versa, while we have to deal with the perturbation theory for nearly degenerated states [31]. For that we make the ansatz ${\psi}_{n}(x)=c^{0}_{n}\phi_{0}(x)+c^{1}_{n}\phi_{1}(x)$ in Eq. (9) and integrate this equation with the states $\phi^{*}_{0}(x)$ and $\phi^{*}_{1}(x)$, respectively. This, together with the normalization of the corrected states, yields six equations for the six constants $c^{0}_{n}$, $c^{1}_{n}$, and $\tilde{E}_{n}$ with $n=0,1$. The only non-trivial, linearly independent solution is given by

	$\displaystyle\psi_{0}(x)$	$\displaystyle=$	$\displaystyle\mathcal{C}\left(\phi_{0}(x)-\frac{V_{0}}{\Delta E+\sqrt{\Delta E^{2}+V_{0}^{2}}}\,\phi_{1}(x)\right)$		(10)
	$\displaystyle\psi_{1}(x)$	$\displaystyle=$	$\displaystyle\mathcal{C}\left(\phi_{1}(x)+\frac{V_{0}}{\Delta E+\sqrt{\Delta E^{2}+V_{0}^{2}}}\,\phi_{0}(x)\right)\,$

with $\mathcal{C}=\frac{1}{\sqrt{2}}\left(1+\Delta E/\sqrt{\Delta E^{2}+V_{0}^{2}}\right)^{1/2}$. Those states satisfy Eq. (9) to linear order in $V_{0}/E$ for the corrected energies

$$\tilde{E}_{0/1}=E+\frac{V_{0}}{2}\mp\frac{1}{2}\sqrt{\Delta E^{2}+V_{0}^{2}}\,,$$

(11)

where we assume that $\epsilon V_{0}/E$ can be neglected, cf. Eq. (6). The $\psi_{0/1}(x)$, hence, are energy eigenstates of the asymmetric double-well, illustrated in Fig. 1b.

As for the symmetric double-well in the last section, we now can define the left and right well states $\psi_{L/R}(x)$ in the case of the asymmetric double-well potential

	$\displaystyle\psi_{L}(x)$	$\displaystyle=$	$\displaystyle\cos\xi\,\psi_{0}(x)+\sin\xi\,\psi_{1}(x)$
	$\displaystyle\psi_{R}(x)$	$\displaystyle=$	$\displaystyle\sin\xi\,\psi_{0}(x)-\cos\xi\,\psi_{1}(x)\,$		(12)

in total analogy to Eq. (2), but this time using the energy eigenstates $\psi_{0/1}(x)$ as a basis.

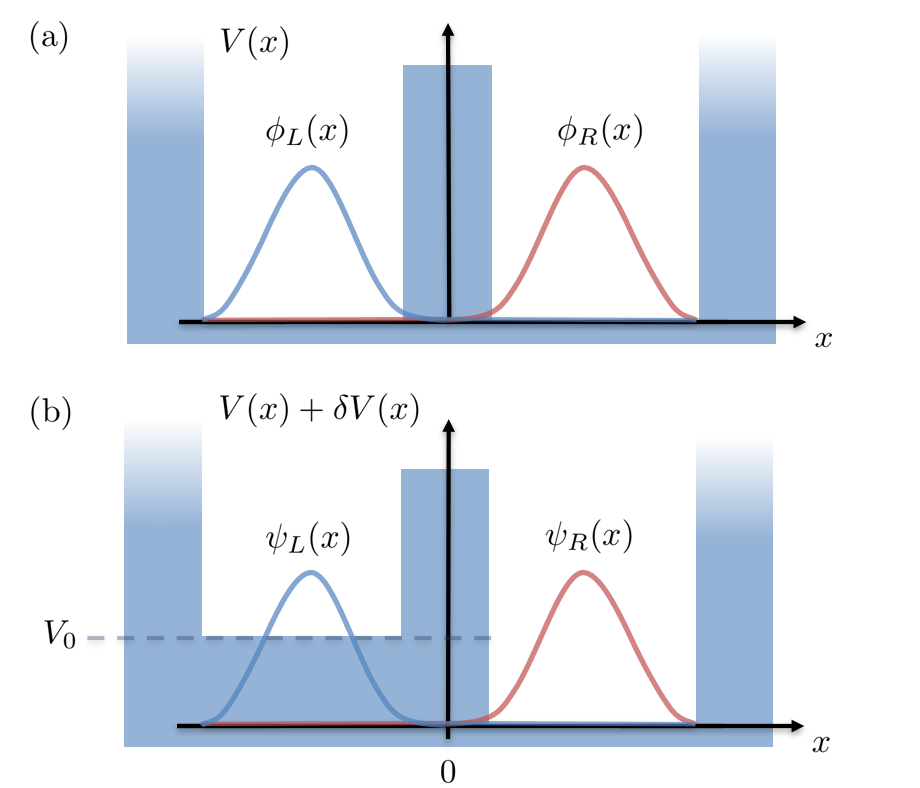
We now again ask for the optimal states that maximize $\langle\psi_{R}|\psi_{R}\rangle_{R}$ and $\langle\psi_{L}|\psi_{L}\rangle_{L}$. Inserting Eq. (10) into Eq. (12) we can formulate this question in the basis $\phi_{0/1}(x)$ of the symmetric double-well problem. In this basis the optimal states $\phi_{L/R}(x)$ are already known and given by Eq. (5). Therefore, we find that those states are optimal for both, the symmetric and the asymmetric case, i.e, $\psi_{L}(x)=\phi_{L}(x)$ and $\psi_{R}(x)=\phi_{R}(x)$, see Fig. 2. In Eq. (12) this is achieved by the choice

$$\xi=\arcsin\left[\frac{1}{\sqrt{2}}\left(1+V_{0}/\sqrt{\Delta E^{2}+V_{0}^{2}}\right)^{1/2}\right]\,,$$

(13)

which for $V_{0}=0$ recovers the symmetric case $\xi=\pi/4$.

Having found the optimal left and right states for the asymmetric double-well potential, we can investigate their dynamics, which is governed by the Hamiltonian operator (7). With $\psi_{L/R}(x)$ being a superposition of energy eigenstates, it is clear that they do not satisfy an eigenvalue equation for a particular energy. Instead, we obtain the coupled equations

	$\displaystyle\hat{H}\psi_{L}(x)$	$\displaystyle=$	$\displaystyle E_{L}\psi_{L}(x)+K\psi_{R}(x)$
	$\displaystyle\hat{H}\psi_{R}(x)$	$\displaystyle=$	$\displaystyle E_{R}\psi_{R}(x)+K\psi_{L}(x)\,,$		(14)

with the newly introduced constants

$$E_{L}=E+V_{0}\,,\quad E_{R}=E\,,\quad K=-\frac{\Delta E}{2}\,.$$

(15)

With that we find a coupling $\sim\Delta E$ between the left and right state, which vanishes when the energies $E_{0/1}$ degenerate, as it is the case when the wells are seperated by a very high potential barrier. Moreover, the difference $E_{L}-E_{R}=V_{0}$ coincides with the potential step (8), which is a well known feature of a Josephson junction [32].

In the last section we analyzed the eigenvalue equation $\hat{H}\psi_{0/1}=\tilde{E}_{0/1}\psi_{0/1}$, holding for the time-dependent, but stationary states $\psi_{0/1}(x,t)=\exp(-i\tilde{E}_{0/1}t/\hbar)\psi_{0/1}(x)$. From the spatial wave functions $\psi_{0}(x)$ and $\psi_{1}(x)$ the left and right states $\psi_{L}(x)$ and $\psi_{R}(x)$ were constructed, cf. Eqs. (12). Now we want to investigate the evolution of the states $\psi_{L}(x,t)$ and $\psi_{R}(x,t)$, which are not stationary states of a particular energy $E_{L/R}$, solely, as becomes clear in Eqs. (14). Instead, we can assume a time-dependent superposition of $\psi_{L}(x)$ and $\psi_{R}(x)$, giving rise to a single wave-function

$$\psi(x,t)=w_{L}(t)\psi_{L}(x)+w_{R}(t)\psi_{R}(x)\,.$$

(16)

By using the action (14) of the one-particle Hamiltonian $\hat{H}$ on the left and right well states, as well as the orthogonality relation $\langle\psi_{L}|\psi_{R}\rangle=0$, we obtain

	$\displaystyle i\hbar\dot{w}_{L}(t)$	$\displaystyle=$	$\displaystyle E_{L}w_{L}(t)+Kw_{R}(t)$
	$\displaystyle i\hbar\dot{w}_{R}(t)$	$\displaystyle=$	$\displaystyle E_{R}w_{R}(t)+Kw_{L}(t).$

These equations describe the evolution of the coefficients $w_{L/R}(t)$, where $|w_{L/R}(t)|^{2}$ represent the time-dependent probabilities to find the particle in the left or right well, respectively. Here, the normalization condition would be given by $|w_{L}(t)|^{2}+|w_{R}(t)|^{2}=1$.

While, so far we have applied the wave function (16) to describe a single particle, it can also be used to represent a many-particle system, as long as that system behaves coherently, i.e, is in a pure state. In this case, we only need to renormalize Eq. (16) to obtain $|w_{L}(t)|^{2}+|w_{R}(t)|^{2}=N$, where $N$ is the total number of bosons. Then, the $|w_{L/R}(t)|^{2}=N_{L/R}(t)$ represent the population of the left and right well, respectively.

Staying with the many-particle interpretation and by defining $w_{L/R}(t)=\sqrt{N_{L/R}(t)}e^{i\theta_{L/R}(t)}$ we find the coupled differential equations

	$\displaystyle\hbar\dot{Z}$	$\displaystyle=$	$\displaystyle 2K\sqrt{1-Z^{2}}\sin\theta$		(17)
	$\displaystyle\hbar\dot{\theta}$	$\displaystyle=$	$\displaystyle E_{L}-E_{R}-\frac{2KZ\cos\theta}{\sqrt{1-Z^{2}}},$		(18)

for the fractional population imbalance $Z(t)=(N_{L}(t)-N_{R}(t))/N$ and the phase difference $\theta(t)=\theta_{R}(t)-\theta_{L}(t)$. These are standard Josephson equations, as they are used in literature to describe the standard Josephson effect [20, 21, 22, 23, 24, 25, 26]. As we recapitulate in Appendix B, the general solution of these equations leads to oscillations of the observable population imbalance $Z(t)$ with the frequency $\sqrt{\Delta E^{2}+V_{0}^{2}}/\hbar$.

Having found these familiar expressions for a many-particle system in a pure state, in what follows we will investigate what happens when the pure state assumption is not initially made. We will show, that this leads to a generalization of Josephson equations, opening up a way to investigate many-particle dynamics in the double-well beyond the regime of global coherence.

In this section we will reformulate the description of a many-particle system by the density matrix (20) in terms of an effective density matrix in the basis of the one-particle states $|\psi_{0}\rangle$ and $|\psi_{1}\rangle$, which appear as the two lowest states in the double-well potential. In the following we are particularly interested in the occupation probabilities of these states, needed to investigate the Josephson effect.

For this purpose, we consider a generic single-particle operator

$$\hat{\mathcal{O}}=\underbrace{\hat{O}\oplus\mathbb{1}\oplus\dots\oplus\mathbb{1}}_{N\textnormal{-times}}+\mathbb{1}\oplus\hat{O}\oplus\dots\oplus\mathbb{1}+\dots{\\[-8.5359pt] }+\mathbb{1}\oplus\mathbb{1}\oplus\dots\oplus\hat{O}$$

in the $N$-particle Hilbert space, constructed from the operator $\hat{O}$, acting on a single-particle state. For instance, the occupation number operator $\hat{N}_{0/1}$ is given by the particular choice $\hat{O}=|\psi_{0/1}\rangle\langle\psi_{0/1}|$ in the formula above. The expectation value of a many-particle operator then reads

$$\langle\hat{\mathcal{O}}\rangle_{\rho}=\mathrm{tr}(\hat{\rho}\hat{\mathcal{O}})=\sum_{N_{1}=0}^{N}\sum_{\tilde{N}_{1}=0}^{N}p_{N_{1}\tilde{N}_{1}}\langle\psi_{\tilde{N}_{1}}|\hat{\mathcal{O}}|\psi_{N_{1}}\rangle\\ =\sum_{N_{1}=0}^{N}p_{N_{1}N_{1}}[N_{1}\langle\psi_{1}|\hat{O}|\psi_{1}\rangle+(N-N_{1})\langle\psi_{0}|\hat{O}|\psi_{0}\rangle]\\ +\sum_{N_{1}=0}^{N-1}\sqrt{(N_{1}+1)(N-N_{1})}[p_{N_{1}+1,N_{1}}\langle\psi_{0}|\hat{O}|\psi_{1}\rangle\\ +p_{N_{1},N_{1}+1}\langle\psi_{1}|\hat{O}|\psi_{0}\rangle],$$

(22)

cf. [35]. In front of the expectation values $\langle\psi_{i}|\hat{O}|\psi_{j}\rangle$ we now can read off the coefficients $\alpha_{ij}$, which contain all information accessible by the measurement of one-particle observables:

	$\displaystyle\alpha_{00}$	$\displaystyle=$	$\displaystyle\sum_{N_{1}=0}^{N}(N-N_{1})p_{N_{1}N_{1}}$
	$\displaystyle\alpha_{11}$	$\displaystyle=$	$\displaystyle\sum_{N_{1}=0}^{N}N_{1}p_{N_{1}N_{1}}$
	$\displaystyle\alpha_{01}$	$\displaystyle=$	$\displaystyle\sum_{N_{1}=0}^{N-1}\sqrt{(N_{1}+1)(N-N_{1})}p_{N_{1}+1,N_{1}}$
	$\displaystyle\alpha_{10}$	$\displaystyle=$	$\displaystyle\alpha^{*}_{01}.$

We now formally rearrange Eq. (22) and introduce the effective density matrix $\hat{\rho}_{\mathrm{e}}$:

$$\langle\hat{\mathcal{O}}\rangle_{\rho}=\begin{bmatrix}\langle\psi_{0}|&\langle\psi_{1}|\\ \end{bmatrix}\begin{bmatrix}\alpha_{00}&\alpha_{01}\\ \alpha_{10}&\alpha_{11}\\ \end{bmatrix}\hat{O}\begin{bmatrix}|\psi_{0}\rangle\\ |\psi_{1}\rangle\\ \end{bmatrix}=\mathrm{tr}(\hat{\rho}_{\mathrm{e}}\hat{O})\,.$$

(23)

As we show in Appendix C, this effective density matrix, which we obtained from the calculation of one-particle expectation values, coincides with the reduced density matrix of a single particle in a bath of all the other $N-1$ bosons [36]. It therefore can be interpreted as a description of the many-particle ensemble by an average boson.

Further, we are interested in the population of the left and right potential wells rather than the occupation of the global ground and excited states $|\psi_{0/1}\rangle$. Therefore, in the following we will describe the system in the basis of left and right well states $|\psi_{L/R}\rangle$, introduced in Sec. II. Here this is done by the matrix transformation

$$\begin{bmatrix}|\psi_{L}\rangle\\ |\psi_{R}\rangle\\ \end{bmatrix}=\begin{bmatrix}\cos\xi|\psi_{0}\rangle+\sin\xi|\psi_{1}\rangle\\ \sin\xi|\psi_{0}\rangle-\cos\xi|\psi_{1}\rangle\\ \end{bmatrix}=\hat{T}\begin{bmatrix}|\psi_{0}\rangle\\ |\psi_{1}\rangle\\ \end{bmatrix}\,,$$

(24)

where the parameter $\xi$ is given by Eq. (13) for the asymmetric double-well potential. The matrix $\hat{T}$ now can be used to express the effective density matrix $\hat{\rho}_{eLR}=\hat{T}\hat{\rho}_{e}\hat{T}^{-1}$ in the left and right well basis. In general, this hermitian $2\times 2$ matrix can be parameterized by

$$\hat{\rho}_{\mathrm{e}LR}=\begin{bmatrix}N_{L}(t)&A(t)e^{i\theta(t)}\\ A(t)e^{-i\theta(t)}&N_{R}(t)\\ \end{bmatrix},$$

(25)

where $N_{L}(t)$ and $N_{R}(t)$ are the occupation numbers of the left and right well, respectively. Moreover, by $\mathrm{tr}(\hat{\rho}_{\mathrm{e}LR})=N=N_{L}(t)+N_{R}(t)$ the total number of particles is conserved. The non-diagonal complex matrix elements describe the interference between left and right well states and therefore induce the coupling between the wells by a mixing parameter $A(t)$ and the phase difference $\theta(t)$ between them.

In what follows, we will derive the equations of motion for $\hat{\rho}_{\mathrm{e}LR}$, which will generalize the standard Josephson equations (17) and (18) to the case where the system is not described by a single wave-function.

With the help of the effective density matrix (25), we can go beyond the description of a many-particle system by a pure state. This will give us the opportunity to consider a wider range of physical setups. For instance, this will enable us to describe bosonic systems at finite temperatures.

The evolution of the effective density matrix is given by the Liouville equation

$$i\hbar\frac{\partial}{\partial t}\hat{\rho}_{\mathrm{e}LR}=[\hat{\mathcal{H}}_{\mathrm{e}LR},\hat{\rho}_{\mathrm{e}LR}],$$

(26)

with the Hamiltonian operator $\hat{\mathcal{H}}_{\mathrm{e}LR}=\hat{H}|\psi_{L}\rangle\langle\psi_{L}|+\hat{H}|\psi_{R}\rangle\langle\psi_{R}|$, where the single-particle Hamiltonian $\hat{H}$ is given by Eq. (7). By using the action of $\hat{H}$ on the left and right well states $|\psi_{L/R}\rangle$ given in Eq. (14), the Liouville equation reduces to the three coupled differential equations

	$\displaystyle\hbar\dot{Z}$	$\displaystyle=$	$\displaystyle 4\frac{K}{N}A\sin\theta$		(27)
	$\displaystyle\hbar\dot{\theta}$	$\displaystyle=$	$\displaystyle E_{L}-E_{R}-\frac{KNZ}{A}\cos\theta$		(28)
	$\displaystyle\frac{\dot{A}}{A}$	$\displaystyle=$	$\displaystyle\left[\dot{\theta}+\frac{E_{R}-E_{L}}{\hbar}\right]\tan\theta\,.$		(29)

In what follows we want to draw attention to the additional physical effects that are described by the generalized Josephson equations (27) - (29) in comparison to the standard ones (17),(18). For this purpose, we use the fact that these equations can be rewritten in the form

	$\displaystyle\hbar\dot{Z}$	$\displaystyle=$	$\displaystyle 2K\sqrt{f^{2}-Z^{2}}\sin\theta$		(30)
	$\displaystyle\hbar\dot{\theta}$	$\displaystyle=$	$\displaystyle E_{L}-E_{R}-\frac{2KZ\cos\theta}{\sqrt{f^{2}-Z^{2}}},$		(31)

as we show in Appendix D. The structure of these equations is obtained by formally integrating Eq. (29) for $A(t)$ and eliminating the mixing parameter in the Josephson equations (27) and (28) for $Z(t)$ and $\theta(t)$. The representation (30),(31) of the generalized Josephson equations only deviates from the standard ones by the newly introduced constant parameter $f$. At the level of the effective density matrix, $f$ is fixed by the initial condition $\hat{\rho}_{\mathrm{e}LR}(t=0)$.

For $f=1$ we recover the standard Josephson equations, i.e., dynamics in the pure state regime. At the level of the effective density matrix this corresponds to the special choice $A(t)=\sqrt{N_{L}(t)N_{R}(t)}=N\sqrt{1-Z(t)^{2}}/2$. In this case the effective density matrix is a projector $|\psi\rangle\langle\psi|$ to one of its eigenvectors, representing a globally coherent state, such that $\langle\hat{\mathcal{O}}\rangle_{\rho}=\langle\psi|\hat{\mathcal{O}}|\psi\rangle$. In this regime the system can be described by the single wave function $\psi$, given by Eq. (16).

For general values of $f$ the eigenvalues of the effective density matrix $\hat{\rho}_{\mathrm{e}}$ are given by $N(1\pm f)/2$, see Appendix D. Recalling the interpretation of the effective density matrix as the reduced density matrix for an average boson, these eigenvalues have to be non-negative, to ensure non-negative probabilities. This leads to the restriction $|f|\leq 1$. Following the discussion of BEC fragmentation, given in [37, 38], we choose $f>0$ and use the term degree of fragmentation for the $1-f$ parameter, implying $f=1$ for a non-fragmented globally coherent state and $f=0$ for two incoherent fragmented states. The $f$ parameter can be associated with the commonly used degree of coherence, or coherence factor, which defines the visibility of interference fringes in an interference experiment with fragmented BECs [3]. However, notice that the same terms are used differently in the studies of quantum fluctuations in BECs [39, 40], where a strongly interacting system is discussed (see also Appendix D).

In the following, we want to describe a closed many-particle bosonic system in thermal equilibrium of finite temperature $T$. In thermodynamics and statistical physics this is typically done by assuming a canonical ensemble with the density matrix

$$\hat{\rho}=\mathcal{Z}^{-1}e^{-\beta\hat{H}}\,,$$

(32)

where we introduced $\beta=1/k_{\mathrm{B}}T$, and $\hat{H}$ is given by Eq. (19) [34]. Moreover, the partition function $\mathcal{Z}=\mathrm{tr}(e^{-\beta\hat{H}})$ ensures the normalization $\mathrm{tr}\hat{\rho}=1$.

Projecting the density operator (32) to the basis of states $|\Psi_{N_{1}}\rangle$, as done in Eq. (20), we can read off the density matrix elements

	$\displaystyle p_{N_{1}\tilde{N}_{1}}$	$\displaystyle=$	$\displaystyle\langle\Psi_{N_{1}}|\mathcal{Z}^{-1}e^{-\beta\hat{H}}|\Psi_{\tilde{N}_{1}}\rangle$
		$\displaystyle=$	$\displaystyle\mathcal{Z}^{-1}e^{-\beta(N-N_{1}){\tilde{E}}_{0}-\beta N_{1}{\tilde{E}}_{1}}\delta_{N_{1},\tilde{N_{1}}}\,.$

We find that the original density matrix $\hat{\rho}$ is diagonal, which also results in a diagonal effective density matrix $\hat{\rho}_{\mathrm{e}}$ in the $|\psi_{0/1}\rangle$ basis with

	$\displaystyle\alpha_{00}$	$\displaystyle=$	$\displaystyle\mathcal{Z}^{-1}\sum_{N_{1}=0}^{N}(N-N_{1})e^{-\beta{\tilde{E}}_{1}N_{1}-\beta{\tilde{E}}_{0}(N-N_{1})}$		(33)
		$\displaystyle=$	$\displaystyle\frac{1+Ne^{(N+1)\beta\Delta{\tilde{E}}}-(N+1)e^{N\beta\Delta{\tilde{E}}}}{(1-e^{-\beta\Delta{\tilde{E}}})(e^{(N+1)\beta\Delta{\tilde{E}}}-1)}$
	$\displaystyle\alpha_{11}$	$\displaystyle=$	$\displaystyle\mathcal{Z}^{-1}\sum_{N_{1}=0}^{N}N_{1}e^{-\beta{\tilde{E}}_{1}N_{1}-\beta{\tilde{E}}_{0}(N-N_{1})}$		(34)
		$\displaystyle=$	$\displaystyle\frac{e^{(N+1)\beta\Delta{\tilde{E}}}+N-(N+1)e^{\beta\Delta{\tilde{E}}}}{(e^{\beta\Delta{\tilde{E}}}-1)(e^{(N+1)\beta\Delta{\tilde{E}}}-1)}$
	$\displaystyle\alpha_{01}$	$\displaystyle=$	$\displaystyle\alpha_{10}=0,$		(35)

where $\Delta{\tilde{E}}={\color[rgb]{0,0,0}\sqrt{\Delta E^{2}+V_{0}^{2}}}$, cf. Eq. (11), and consistently $\alpha_{00}+\alpha_{11}=N$. This gives rise to the effective density matrix

$$\hat{\rho}_{\mathrm{e}}=\begin{bmatrix}\alpha_{00}&0\\ 0&\alpha_{11}\\ \end{bmatrix}$$

(36)

as the starting point for our investigation of the generalized Josephson effect in thermal equilibrium.

In this work we assume a Bose gas with negligibly small interactions. In such a system the establishment of thermal equilibrium takes a very long time $\Delta t_{\mathrm{th}}\gg\hbar/\Delta E$ that is much larger than the typical time scale of dynamics in the double-well potential (see also Appendix A). In this section, we assume that the system has already undergone this thermalization process and reached thermal equilibrium. Then the elements of the effective density matrix $\hat{\rho}_{\mathrm{e}}$ are given by Eqs. (33)-(35) and we are ready to apply our formalism to describe the generalized Josephson effect in this regime.

For that purpose we consider the effective density matrix in the left and right well basis. Applying the transformation $\hat{T}$ from Eq. (24) to Eq. (36), we obtain

$${\color[rgb]{0,0,0}\hat{\rho}_{\mathrm{e}LR}(V_{0})=\frac{N}{2}\begin{bmatrix}1&0\\ 0&1\\ \end{bmatrix}+\frac{\delta N_{01}}{2\sqrt{\Delta E^{2}+V_{0}^{2}}}\begin{bmatrix}-V_{0}&\Delta E\\ \Delta E&V_{0}\\ \end{bmatrix},}$$

(37)

where we introduced the population imbalance $\delta N_{01}(N,\beta\Delta{\tilde{E}})=\alpha_{00}-\alpha_{11}$ between ground and excited state. Using Eq. (37) as a specific initial condition for these solutions we find

$${\color[rgb]{0,0,0}Z(t)=-\frac{V_{0}}{\Delta\tilde{E}}\frac{\delta N_{01}}{N}\,\,,\quad A(t)=\frac{\Delta E}{\Delta\tilde{E}}\frac{\delta N_{01}}{2}\,\,,\quad\theta(t)=0\,,}$$

(38)

such that no oscillations between the wells occur. In consequence, Eq. (37) is not only the initial condition but a static solution for the effective density matrix, i.e., for the dynamics of the system. We recognize that Eqs. (38) represent the unique solution of the generalized Josephson equations for $N$ particles in a given double-well geometry at temperature $T$.

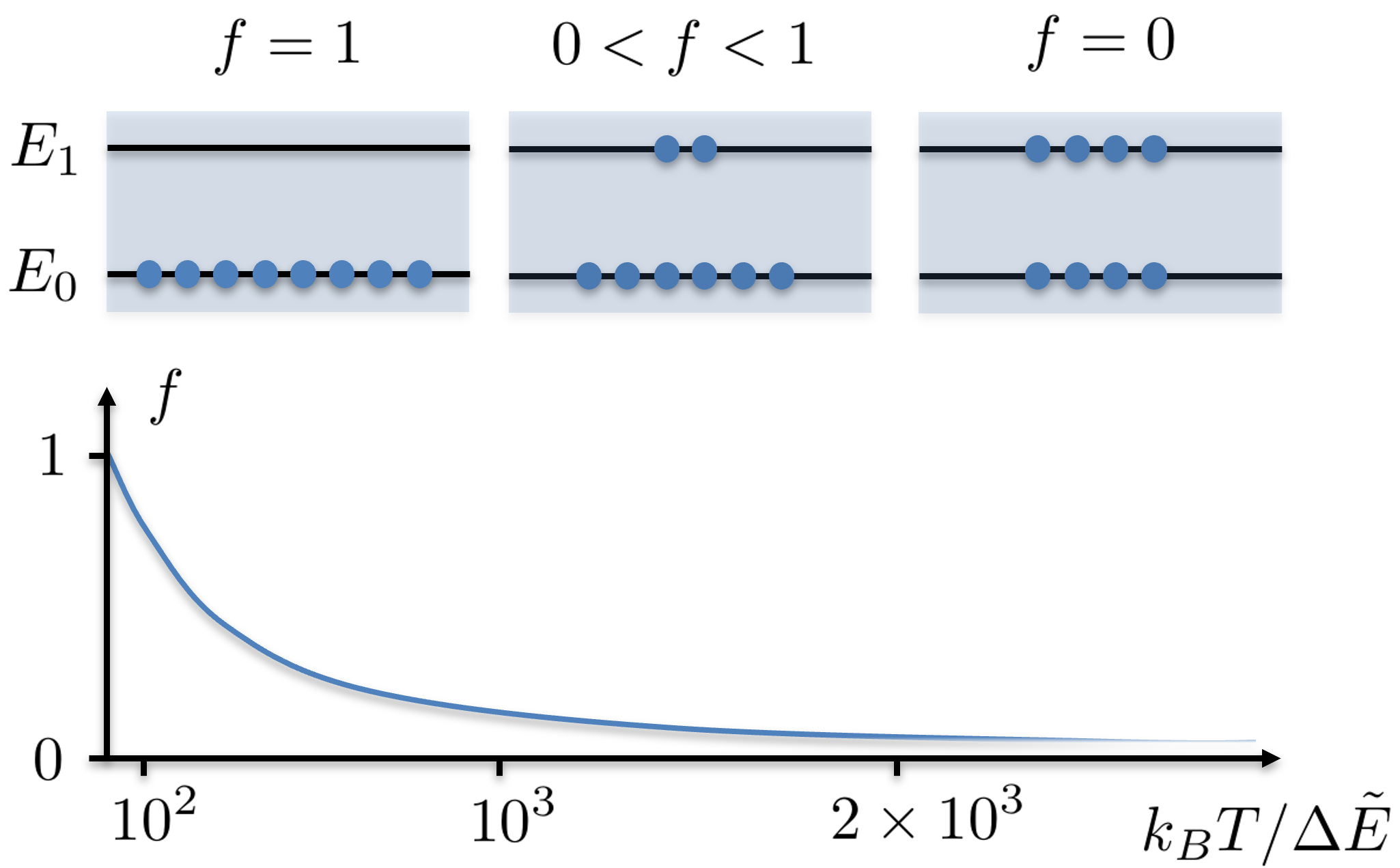
From the solution (37) we find, that in thermal equilibrium, the degree of fragmentation $1-f=1-\delta N_{01}/N$ equals the population imbalance between the excited state $|\psi_{1}\rangle$ and the ground state $|\psi_{0}\rangle$. In this case $f$ reaches from $f=0$ for $k_{\mathrm{B}}T\gg\Delta{\tilde{E}}$ to $f=1$ for $k_{\mathrm{B}}T\ll\Delta{\tilde{E}}$, as shown in Fig. 3. The latter particularly holds true for $T=0$, where $\alpha_{00}=N$, such that the bosons form a global BEC in the double-well system. Hence, in thermal equilibrium $f\in[0,1]$ can be interpreted as the degree of condensation. In the literature such a parameter is also used to introduce $T\neq 0$ effects in the Gross-Pitaevskii equation phenomenologically [41]. However, in our model it arises from first principles of statistics of a many-particle quantum system and has a wider interpretation in the non-equilibrium case.

We can summarize the findings of this section with the evident statement that in the case of thermal equilibrium the solutions of the generalized Josephson equations are static and the system exhibits no Josephson oscillations. However, the insights from this section will be of great value also for the study of the non-equilibrium case in the next section.

We now will discuss how Josephson oscillations appear as an out-of-equilibrium phenomenon in a particular experimental scenario [42]. First a cloud of atoms is thermalized to the equilibrium configuration with some population imbalance between the wells, induced by the energy difference $E_{L}-E_{R}=V_{0}^{i}$. Then, the potential step between the wells is instantly lowered to a new value $V_{0}^{f}<V_{0}^{i}$, bringing the system out of equilibrium. Directly after that, the system evolves according to Eqs. (27)-(29), but with $E_{L}-E_{R}=V_{0}^{f}$. The initial conditions for the system are given by $\hat{\rho}_{\mathrm{e}LR}(V_{0}^{i})$ from Eq. (37). Plugging that into the general solutions to the generalized Josephson equations we present in Appendix E, we obtain the population imbalance

$$Z(t)=-\frac{V_{0}^{f}}{\sqrt{\Delta E^{2}+(V_{0}^{i})^{2}}}\frac{\delta N_{01}^{i}}{N}\\ -\frac{V_{0}^{i}-V_{0}^{f}}{\sqrt{\Delta E^{2}+(V_{0}^{i})^{2}}}\frac{\delta N_{01}^{i}}{N}\cos\left(\frac{\Delta Et}{\hbar}\right),$$

(39)

showing an oscillatory behavior. Here, for the sake of simplicity we only consider terms to linear order in the parameter $V_{0}^{f}/\Delta E$, which is assumed to be small in our further discussion. This includes the case considered in Ref. [42], where the final double-well is symmetric $V_{0}^{f}=0$.

As can be seen in Eq. (39), the amplitude of oscillations is proportional to the difference between the initial and final potential step $V_{0}^{i}-V_{0}^{f}$, which also quantifies how far the system is from the initial equilibrium state. In the limit $V_{0}^{i}\gg\Delta E$ we observe the maximum possible amplitude of oscillations $\delta N_{01}^{i}/N$ for given $N$, $\Delta E$ and $T$, see Fig. 4 for particular temperatures. In the opposite case if $V_{0}^{i}\ll\Delta E$ the amplitude of Josephson oscillations is proportional to a small ratio $(V_{0}^{i}-V_{0}^{f})/\Delta E$.

The $f$ parameter in the non-equilibrium regime reads $f=\delta N_{01}^{i}/N$, where $\delta N_{01}^{i}=\alpha_{00}^{i}-\alpha_{11}^{i}$ is the initial population imbalance between the ground and first excited state with the energies $\tilde{E}_{0}^{i}$ and $\tilde{E}_{1}^{i}$, respectively. Moreover, the $f$ parameter remains independent of the new potential step $V_{0}^{f}$ and is preserved from the initial thermal equilibrium condition, discussed in Sec. IV.2. In general the values $V_{0}^{i}$, $V_{0}^{f}$ and $\Delta E$ are known from the experimental setup [42], which allows us to deduce $f$ from the oscillation amplitude. The $f$ parameter depends only on the number of bosons $N$ and $\Delta\tilde{E}^{i}/(k_{B}T)$. Thus, by the measurement of the amplitude of Josephson oscillations in the Bose gas it is possible to determine the thermodynamic temperature it had before the potential step was lowered $V_{0}^{i}\to V_{0}^{f}$.

The pure state case $f=1$, for which standard Josephson equations hold, is realized for $k_{B}T\ll\Delta\tilde{E}^{i}$, allowing for the maximum possible oscillation amplitude. The opposite regime of $f=0$ can be achieved either in the case of high temperatures or in the case of nearly degenerated initial energy levels $\tilde{E}_{0/1}^{i}$ in the double-well, i.e, $\Delta\tilde{E}^{i}\approx 0$. Nearly degenerated energy levels appear for very high potential barriers between the two wells. In such a geometry the populations of each well become weakly coupled, as can be seen in the Eqs. (14) and (15). This is exactly the regime, where the system can be seen as two separate, weakly interacting systems (often referred to as coupled BECs), as it is done, e.g., in the Bose-Hubbard model [3, 23].

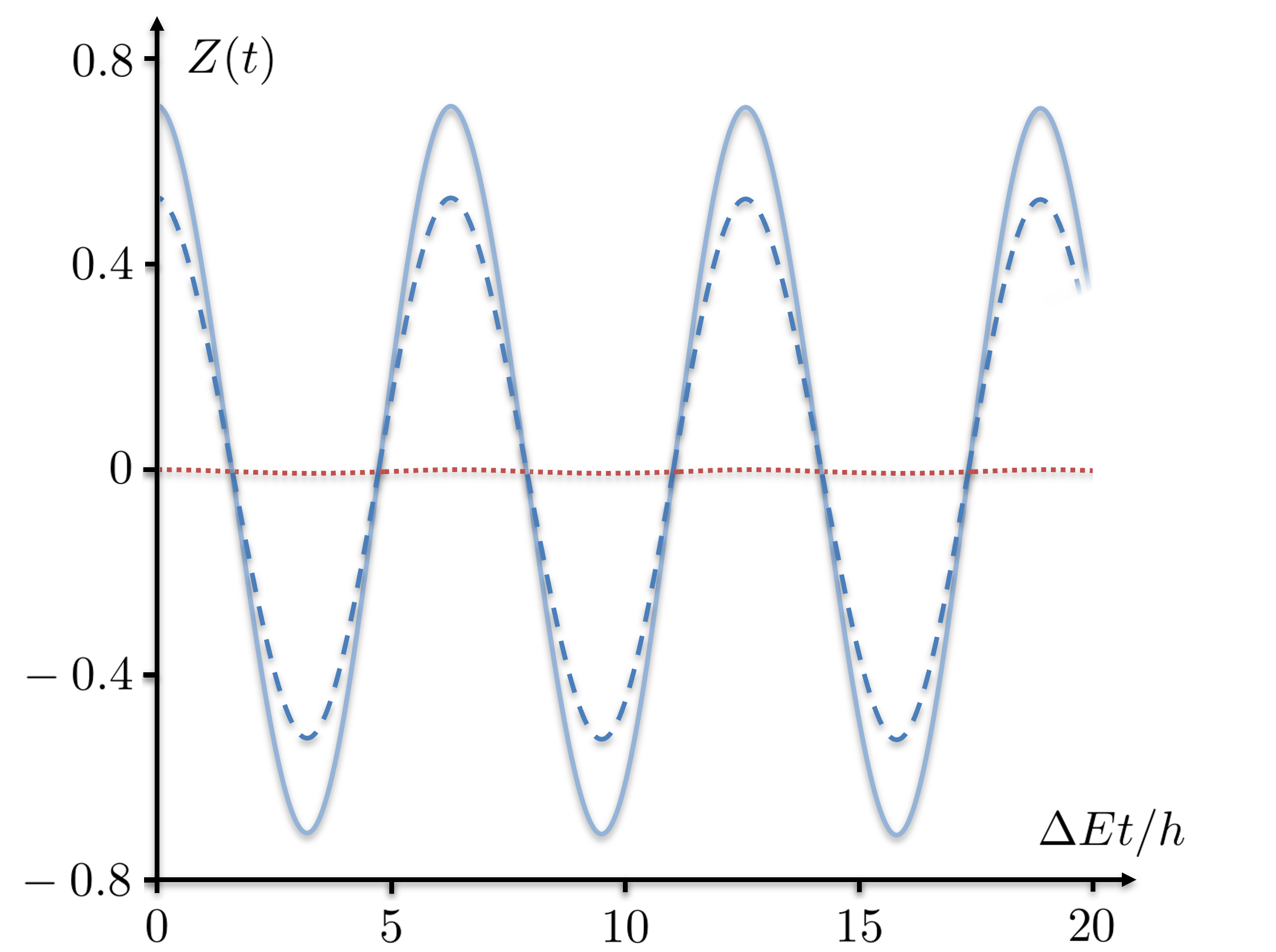
The equilibrium position of the oscillations (39) is given by the averages $\langle Z(t)\rangle_{t}=-V_{0}^{f}/\sqrt{\Delta E^{2}+(V_{0}^{i})^{2}}\times\delta N_{01}^{i}/N$ and $\langle\theta(t)\rangle_{t}=0$ over one period of oscillations. We see that this equilibrium position depends on the initial value of potential step $V_{0}^{i}$, implying that the system ‘remembers’ the initial condition. By direct comparison with the Eqs. (38) we find that this equilibrium position does not represent a static thermal equilibrium solution of the generalized Josephson equations for the new double-well with the potential step $V_{0}^{f}$. Thus, to reach the new static equilibrium the system must ‘forget’ its initial condition during the process of thermalization. Therefore, this process must not only cause a damping of the oscillations but also has to shift the equilibrium position to the position of a, yet undefined, new static thermal equilibrium. While this process itself is not accessible within our model directly (see also Appendix A), we can deduce some conclusions about its final state. The exact nature of the thermalization process defines to which final thermal equilibrium state the system tends to. All these possible final thermal equilibrium states are labeled by their degree of fragmentation $1-f$. For each of those $f\in[0,1]$ there is a unique static solution of the generalized Josephson equations (30) - (31) and the degree of fragmentation for the final equilibrium state does not necessarily coincides with the initial one. Assuming a fixed degree of fragmentation $1-f=1-\delta N_{01}^{i}/N$, inherited from the initial condition, one would need to allow for a loss of energy. Otherwise, assuming the energy to be conserved, one has to account for an increase of the degree of fragmentation to allow for thermalization to happen. This means that the system is less coherent after an adiabatic thermalization process.

A more detailed analysis of the thermalization mechanism in dependence of the underlying physical processes can be an interesting future perspective of our study.

In what follows, we consider an $N$-particle system of initial temperature $T$ and discuss the implications of our model for different experimental setups. In Table 1 we give the upper limit for the amplitude of Josephson oscillations (39), determined by the initial degree of condensation $f=\delta N_{01}^{i}/N$ for experimentally relevant scenarios, related to typical temperatures and cooling techniques [43]. The corresponding oscillations for $N=10^{3}$ and different temperatures are visualized in Fig. 4.

On its way to ultra-cold temperatures the many-particle bosonic system undergoes different cooling stages of characteristic temperatures. The first stage is the formation of a longitudinal supersonic beam with a narrow velocity distribution (about $T\propto 8$ K) [44].

If lower temperatures are pursued, the beam can be placed in a magneto-optical trap (MOT) and can be laser-cooled to temperatures of $T\propto 2.5\times 10^{-4}$ K [45]. In this regime the $f$ parameter sensitively depends on the particle number, ranging from $N\propto 10^{3}-10^{6}$ in typical experiments [7, 18, 17, 21, 29, 23, 42]. While for $10^{3}$ particles we see that the amplitude of Josephson oscillations is restricted to maximally $0.5\%$ of all particles, for $10^{6}$ this amplitude is barely restricted.

At the next cooling stage the atoms are placed in an optical dipole trap reaching typical temperatures in the range of $T\propto 10^{-6}$ K [46]. For low particle numbers $\propto 10^{3}$, in this regime, it is necessary to use not the standard, but the generalized Josephson equations with a degree of fragmentation of $1-f\approx 0.25$ (see Table 1). To describe such a cold (but not yet ultra-cold) Bose gas correctly is of interest for modern precision metrology [6].

Finally, evaporative cooling and adiabatic expansion can lead to the BEC formation at $T\propto 10^{-8}$ K [4] with almost all particles condensed in the ground state, such that $\delta N^{i}_{01}\approx N$. In this regime the system is almost fully coherent and can be represented by a single wave-function to good approximation. Here, the standard Josephson equations are sufficient to describe the dynamics of the many-particle system. In the BEC regime our model puts no significant restriction on the amplitude of Josephson oscillations, in agreement with the experimental observations [7, 17, 29, 23, 42].