This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Generalized torsion elements in the fundamental groups of 3-manifolds obtained by the 0-surgeries along some double twist knots

Nozomu Sekino
Abstract

We consider the 3-manifold obtained by the 0-surgery along a double twist knot. We construct a candidate for a generalized torsion element in the fundamental group of the surged manifold, and see that there exists the cases where the candidate is actually a generalized torsion element. For a proof, we use the JSJ-decomposition of the surged manifold. We also prove that the fundamental group of the 3-manifold obtained from the 0-surgery along a double twist knot is bi-orderable if and only if it admits no generalized torsion elements. We also list some examples of the surged manifolds whose fundamental groups admit generalized torsion elements.

1 Introduction

A non-trivial element of a group is called a generalized torsion element if some products of conjugates of it is the identity element. The existence of a generalized torsion element prevents the group from being bi-orderable. Thus for a group, admitting no generalized torsion elements is a necessary condition for the group being bi-orderable. In general, there exists a group which is not bi-orderable and has no generalized torsion elements. See Chapter 4 of [18] and [1], for example.

However, in [16], it is conjectured that if FF is a 3-manifold group i.e the fundamental group of a compact 3-manifold, then non-existence of generalized torsion elements on FF implies the bi-orderability of FF. There are many works toward this conjecture [16], [10] [19]. For example, this conjecture is verified for the fundamental groups of non-hyperbolic geometric 3-manifolds [16], for those of 3-manifolds obtained by some Dehn surgeries along some knots [10] and for those of once punctured torus bundles [19].

According to this conjecture, sometimes a question whether a given (3-manifold) group admits a generalized torsion element arises. In general it is difficult to find a generalized torsion element. There are also many works for this question, for some knot groups and link groups [21] [6] [5] [22] [23] [17], for the fundamental groups of the 3-manifolds obtained by some Dehn surgeries along some knots [10].

In this paper, we focus on the fundamental groups of the 3-manifolds obtained by the 0-surgeries along double twist knots. The double twist knot of type (p,q)(p,q), denoted by Kp,qK_{p,q} in this paper, is the knot represented as C​[2​p,2​q]C[2p,2q] in the Conway notation. For example, K1,1K_{1,1} is the figure eight knot and K1,−1K_{1,-1} is the right-handed trefoil. Note that the bridge number of each double twist knot is two. By using a part of the result of [5], we see that the knot group i.e the fundamental group of the complement of the knot of Kp,qK_{p,q} is not bi-orderable if p​qpq is negative, and that of K1,qK_{1,q} is bi-orderable if qq is positive. A generalized torsion element of the knot group of K1,qK_{1,q} for negative qq is constructed [22]. To the author’s knowledge, it is unknown whether the knot group of Kp,qK_{p,q} with positive p​qpq is bi-orderable and whether the knot group of Kp,qK_{p,q} with negative p​qpq other than that of K1,qK_{1,q} admits a generalized torsion element.

About Dehn surgeries along a double twist knot Kp,qK_{p,q}, the generalized torsion element of the fundamental group π1​(Kp,q​(r))\pi_{1}(K_{p,q}(r)) of the 3-manifold Kp,q​(r)K_{p,q}(r) obtained by the rr-surgery along Kp,qK_{p,q} is constructed in [10] with condition on rr in terms of pp and qq. Since it is known that a finitely generated bi-orderable group must surject onto ℤ\mathbb{Z}, the only possible surgery along a knot in the 3-sphere producing a 3-manifold whose fundamental group may be bi-orderable is the 0-surgery. About the 0-surgeries, it is known that π1​(K1,1​(0))\pi_{1}(K_{1,1}(0)) is bi-orderable and π1​(K1,−1​(0))\pi_{1}(K_{1,-1}(0)) admits a generalized torsion element. In this paper, we construct a candidate for a generalized torsion element in other π1​(Kp,q​(0))\pi_{1}(K_{p,q}(0)), and we see that there exists some (p,q)(p,q) such that this candidate is actually a generalized torsion element:

Theorem 1.1.

Let (p,q)(p,q) and (p′,q′)(p^{\prime},q^{\prime}) be two pairs of non-zero integers such that p​q=p′​q′pq=p^{\prime}q^{\prime} and p≠±p′,±q′p\neq\pm p^{\prime},\pm q^{\prime}. Then at least one of π1​(Kp,q​(0))\pi_{1}\left(K_{p,q}(0)\right) and π1​(Kp′,q′​(0))\pi_{1}(K_{p^{\prime},q^{\prime}}(0)) admits a generalized torsion element.

Note that only by Theorem 1.1 we cannot know whether π1​(Kp,q​(0))\pi_{1}(K_{p,q}(0)) admits a generalized torsion element for a given (p,q)(p,q). We also give computation which judges whether the candidate is a generalized torsion element for some (p,q)(p,q) in the last section. Moreover, we see that there is a generalized torsion element in π1​(Kp,q​(0))\pi_{1}\left(K_{p,q}(0)\right) for every double twist knot Kp,qK_{p,q} with negative p​qpq:

Theorem 1.2.

Let (p,q)(p,q) be a pair of non-zero integers such that p​q<0pq<0. Then there is a generalized torsion element in π1​(Kp,q​(0))\pi_{1}\left(K_{p,q}(0)\right).

As stated above, the knot group of Kp,qK_{p,q} with negative p​qpq is not bi-orderable and this implies that there exists a generalized torsion element in the group if the conjecture above is true. However, we cannot find a generalized torsion element in the group so far. A generalized torsion element constructed at the proof of Theorem 1.2 is obtained through the 0-surgery. Moreover, we have the following, which implies that the conjecture above is true for the fundamental groups of the 3-manifolds obtained by the 0-surgeries along double twist knots:

Theorem 1.3.

Let (p,q)(p,q) be a pair of non-zero integers. Then π1​(Kp,q​(0))\pi_{1}\left(K_{p,q}(0)\right) is bi-orderable if and only if it admits no generalized torsion elements.

The rest of this paper is constructed as follows. In Section 2, we give some definitions and lemmas about generalized torsion elements that are needed later. In Section 3, we consider the double twist knots, their complements and the 3-manifolds obtained by the 0-surgeries along these knots. We give some presentations of the fundamental groups of such 3-manifolds. In Section 4, we consider the JSJ-decompositions of the 3-manifolds obtained by the 0-surgeries along double twist knots. Using this, we see that two double twist knots give homeomorphic 3-manifolds by the 0-surgeries if and only if these knots are equivalent. In Section 5, we give a proof of Theorem 1.1 using the results above. A candidate for a generalized torsion element is constructed there. In Section 6, we give a proof of Theorem 1.2 using some computation. In Section 7, we give a proof of Theorem 1.3. Assuming there are no generalized torsion elements, we give a bi-order. In Section 8, we give some results of computation which judges whether the candidate is a generalized torsion element.

Acknowledgements

The author would like to thank professor Nozaki for giving him many helpful advices for computations.

Notation

We give some notations about elements of group. The conjugate h−1​g​hh^{-1}gh of gg with hh is represented by the notation ghg^{h}. The commutator g−1​h−1​g​hg^{-1}h^{-1}gh of gg and hh is represented by the notation [g,h][g,h].

2 Terminologies and Lemmas for generalized torsion elements

In this section, we define some terminologies and prove lemmas about generalized torsion elements which are needed in later. In this section FF denotes a group.

Definition 2.1.

(Generalized torsion elements)
A non-trivial element g∈Fg\in F is called a generalized torsion element if there exists a positive integer nn and h1,…,hn∈Fh_{1},\dots,h_{n}\in F such that gh1⋅gh2​⋯​ghn=1Fg^{h_{1}}\cdot g^{h_{2}}\cdots g^{h_{n}}=1_{F} holds. Minimal such nn is called the order of gg.

A group FF is called bi-orderable if it admits a total order << such that a​g​b<a​h​bagb<ahb holds for any g,h,a,b∈Fg,h,a,b\in F whenever g<hg<h holds i.e the order << is invariant under multiplying elements from left and right. Such an order is called bi-order. Suppose that FF has a generalized torsion element gg and take h1,…,hnh_{1},\dots,h_{n} in the definition. If FF admitted a bi-order <<, then ghk<1Fg^{h_{k}}<1_{F} for all kk or ghk>1Fg^{h_{k}}>1_{F} for all kk would hold. This would imply that gh1⋅gh2​⋯​ghn<1Fg^{h_{1}}\cdot g^{h_{2}}\cdots g^{h_{n}}<1_{F} or gh1⋅gh2​⋯​ghn>1Fg^{h_{1}}\cdot g^{h_{2}}\cdots g^{h_{n}}>1_{F} would hold. This leads a contradiction. Hence existing of a generalized torsion element prevents a group from being bi-orderable.

Definition 2.2.

For an element g∈Fg\in F, the semigroup consisting of non-empty finite products of conjugates of gg is denoted by ⟨⟨g⟩⟩+\left<\left<g\right>\right>^{+}. It can be checked easily that a non-trivial element gg is a generalized torsion element if and only if 1F∈⟨⟨g⟩⟩+1_{F}\in\left<\left<g\right>\right>^{+}.

Lemma 2.1.

(Lemma 4.1 in [10])
Let g,hg,h and xx be elements of FF. Then the following holds.

  1. 1.

    gn​hn∈⟨⟨g​h⟩⟩+g^{n}h^{n}\in\left<\left<gh\right>\right>^{+} for all n>0n>0.

  2. 2.

    If g​h∈⟨⟨x⟩⟩+gh\in\left<\left<x\right>\right>^{+}, then gn​hn∈⟨⟨x⟩⟩+g^{n}h^{n}\in\left<\left<x\right>\right>^{+} for all n>0n>0.

  3. 3.

    If [g,h]∈⟨⟨x⟩⟩+[g,h]\in\left<\left<x\right>\right>^{+}, then [gn,hm]∈⟨⟨x⟩⟩+[g^{n},h^{m}]\in\left<\left<x\right>\right>^{+} for all n,m>0n,m>0.

Proof.

(From [10])
The first follows from the equality gn​hn=(g​h)g−(n−1)​(g​h)g−(n−2)​⋯​(g​h)g^{n}h^{n}=(gh)^{g^{-(n-1)}}(gh)^{g^{-(n-2)}}\cdots(gh).
The second follows from the first and the fact that if g​h∈⟨⟨x⟩⟩+gh\in\left<\left<x\right>\right>^{+}, then ⟨⟨g​h⟩⟩+⊂⟨⟨x⟩⟩+\left<\left<gh\right>\right>^{+}\subset\left<\left<x\right>\right>^{+}.
For the third, assume that [g,h]=g−1​(h−1​g​h)∈⟨⟨x⟩⟩+[g,h]=g^{-1}(h^{-1}gh)\in\left<\left<x\right>\right>^{+}. Apply the second to see that (g−n​h−1​gn)​h=g−n​(h−1​gn​h)∈⟨⟨x⟩⟩+(g^{-n}h^{-1}g^{n})h=g^{-n}(h^{-1}g^{n}h)\in\left<\left<x\right>\right>^{+}. Then apply the second again to see that [gn,hm]=g−n​h−m​gn​hm=(g−n​h−m​gn)​hm∈⟨⟨x⟩⟩+[g^{n},h^{m}]=g^{-n}h^{-m}g^{n}h^{m}=(g^{-n}h^{-m}g^{n})h^{m}\in\left<\left<x\right>\right>^{+}. □\Box

Lemma 2.2.

Let gg and hh be elements of FF, and nn and mm positive integers.
Then {(h​g)−m​(g​h)m}n​{(h​g)m​(g​h)−m}n∈⟨⟨[g​h,h​g]⟩⟩+\{(hg)^{-m}(gh)^{m}\}^{n}\{(hg)^{m}(gh)^{-m}\}^{n}\in\left<\left<[gh,hg]\right>\right>^{+}.

Proof.

By the third of Lemma 2.1, we have

(h​g)−m​(g​h)m​(h​g)m​(g​h)−m=[(h​g)m,(g​h)−m]∈⟨⟨[h​g,(g​h)−1]⟩⟩+=⟨⟨(g​h)​[g​h,h​g]​(g​h)−1⟩⟩+=⟨⟨[g​h,h​g]⟩⟩+.\displaystyle(hg)^{-m}(gh)^{m}(hg)^{m}(gh)^{-m}=[(hg)^{m},(gh)^{-m}]\in\left<\left<[hg,(gh)^{-1}]\right>\right>^{+}=\left<\left<(gh)[gh,hg](gh)^{-1}\right>\right>^{+}=\left<\left<[gh,hg]\right>\right>^{+}.

Moreover, by the second of Lemma 2.1, we have {(h​g)−m​(g​h)m}n​{(h​g)m​(g​h)−m}n∈⟨⟨[g​h,h​g]⟩⟩+\{(hg)^{-m}(gh)^{m}\}^{n}\{(hg)^{m}(gh)^{-m}\}^{n}\in\left<\left<[gh,hg]\right>\right>^{+}. □\Box

3 Double twist knots and their 0-surgeries

3.1 Double twist knots

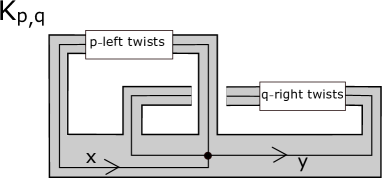
For non-zero integers pp and qq, Kp,qK_{p,q} denotes the knot which is represented as C​[2​p,2​q]C[2p,2q] in the Conway notation. This Kp,qK_{p,q} is called the double twist knot of type (p,q)(p,q). See Figure 1, which we call the standard diagram of Kp,qK_{p,q}. In Figure 1, (−n)(-n)-left twists (or right twists) represents nn-right twists (or left twists, respectively). For example, K1,1K_{1,1} is the figure eight knot and K1,−1K_{1,-1} is the right-handed trefoil. Note that Kp,qK_{p,q} is isotopic to K−q,−pK_{-q,-p}, that Kp,qK_{p,q} is the mirror of K−p,−qK_{-p,-q} and Kq,pK_{q,p} (see Figure 2), that the bridge number of Kp,qK_{p,q} is two and that the genus of Kp,qK_{p,q} is one.

Refer to caption
Figure 1: left: the standard diagram of Kp,qK_{p,q},    right: K3,2K_{3,2}
Refer to caption
Figure 2: Correspondence among Kp,qK_{p,q}, K−p,−qK_{-p,-q}, K−p,−qK_{-p,-q} and Kq,pK_{q,p}.

In the standard diagram of Kp,qK_{p,q}, we fix a Seifert surface T′T^{\prime} of genus one as the shaded surface in Figure 3. Let Ep,qE_{p,q} denote the closure of the complement of Kp,qK_{p,q} in S3S^{3}. There is a useful presentation of the fundamental group of Ep,qE_{p,q}, so called the Lin presentation:

π1​(Ep,q)=⟨a,b,t∣t​ap​t−1=b−1​ap,t​b−q​a−1​t−1=b−q⟩\displaystyle\pi_{1}(E_{p,q})=\left<a,b,t\mid ta^{p}t^{-1}=b^{-1}a^{p},\ tb^{-q}a^{-1}t^{-1}=b^{-q}\right> (1)

In this presentation, aa, bb and tt are based loops in Ep,qE_{p,q} as in Figure 4. This presentation is obtained by noting that the complement of the Seifert surface T′T^{\prime} is a handlebody whose fundamental group is generated by loops aa and bb, that the push ups of loops xx and yy on T′T^{\prime} is apa^{p} and b−q​a−1b^{-q}a^{-1}, respectively and that the push downs of loops xx and yy on T′T^{\prime} is b−1​apb^{-1}a^{p} and b−qb^{-q}, respectively. In this presentation, the meridian of Kp,qK_{p,q} corresponds to tt and the canonical longitude of it corresponds to [bq,ap][b^{q},a^{p}].

Refer to caption
Figure 3: Seifert surface T′T^{\prime} of Kp,qK_{p,q} and based loops on T′T^{\prime}
Refer to caption
Figure 4: the generators of the Lin presentation of π1​(Ep,q)\pi_{1}(E_{p,q})

3.2 The 0-surgeries along double twist knots

Let Kp,q​(0)K_{p,q}(0) denote the 3-manifold obtained by the 0-surgery along Kp,qK_{p,q}. In Kp,q​(0)K_{p,q}(0), the boundary of the (minimal genus) Seifert surface T′T^{\prime} is capped-off by a disk. We call this resultant closed torus TT. According to [7], Kp,q​(0)K_{p,q}(0) is irreducible and TT is incompressible. From the presentation (1), the fundamental group of Kp,q​(0)K_{p,q}(0), denoted by Gp,qG_{p,q}, can be computed as:

Gp,q=π1​(Kp,q​(0))=⟨a,b,t∣t​ap​t−1=b−1​ap,t​b−q​a−1​t−1=b−q,[bq,ap]=1⟩.\displaystyle G_{p,q}=\pi_{1}\left(K_{p,q}(0)\right)=\left<a,b,t\mid ta^{p}t^{-1}=b^{-1}a^{p},\ tb^{-q}a^{-1}t^{-1}=b^{-q},\ [b^{q},a^{p}]=1\right>. (2)

Moreover, we consider Kp,q​(0)∖T¯\overline{K_{p,q}(0)\setminus T}, the closure of the complement of TT in Kp,q​(0)K_{p,q}(0). This is obtained from the closure of the complement of the Seifert surface T′T^{\prime} of Kp,qK_{p,q} in S3S^{3}, which is a handlebody of genus two by attaching a 22-handle along the longitude of Kp,qK_{p,q}. Following this construction, the fundamental group of Kp,q​(0)∖T¯\overline{K_{p,q}(0)\setminus T}, denoted by Γp,q\Gamma_{p,q}, can be computed as:

Γp,q=π1​(Kp,q​(0)∖T¯)=⟨a,b∣[bq,ap]=1⟩.\displaystyle\Gamma_{p,q}=\pi_{1}\left(\overline{K_{p,q}(0)\setminus T}\right)=\left<a,b\mid[b^{q},a^{p}]=1\right>. (3)

The boundary of Kp,q​(0)∖T¯\overline{K_{p,q}(0)\setminus T} consists of two tori. We call the one coming from the front side of T′T^{\prime} T+T_{+} and call the other T−T_{-}. We fix presentations of π1​(T±)\pi_{1}(T_{\pm}), denoted by Γ±\Gamma_{\pm} as follows, where X±X_{\pm} and Y±Y_{\pm} are coming from xx and yy in Figure 3.

Γ+\displaystyle\Gamma_{+} =π1​(T+)=⟨X+,Y+∣[X+,Y+]=1⟩\displaystyle=\pi_{1}(T_{+})=\left<X_{+},Y_{+}\mid[X_{+},Y_{+}]=1\right> (4)
Γ−\displaystyle\Gamma_{-} =π1​(T−)=⟨X−,Y−∣[X−,Y−]=1⟩\displaystyle=\pi_{1}(T_{-})=\left<X_{-},Y_{-}\mid[X_{-},Y_{-}]=1\right> (5)

Then we take homomorphisms ι+:Γ+⟶Γ\iota_{+}:\Gamma_{+}\longrightarrow\Gamma and ι−:Γ−⟶Γ\iota_{-}:\Gamma_{-}\longrightarrow\Gamma which are induced by the inclusions such that ι+​(X+)=ap\iota_{+}(X_{+})=a^{p}, ι+​(Y+)=b−q​a−1\iota_{+}(Y_{+})=b^{-q}a^{-1}, ι−​(X−)=b−1​ap\iota_{-}(X_{-})=b^{-1}a^{p} and ι−​(Y−)=b−q\iota_{-}(Y_{-})=b^{-q} hold. Note that since Kp,q​(0)K_{p,q}(0) is irreducible and TT is incompressible, Kp,q​(0)∖T¯\overline{K_{p,q}(0)\setminus T} is irreducible and has incompressible boundary.

3.3 Another presentation

For our use, we give another presentations of the fundamental groups of Ep,qE_{p,q} and Kp,q​(0)K_{p,q}(0). By changing the presentation (1) as follows, we get a presentation of the fundamental groups of Ep,qE_{p,q}.

π1​(Ep,q)\displaystyle\pi_{1}(E_{p,q}) =⟨a,b,t∣t​ap​t−1=b−1​ap,t​b−q​a−1​t−1=b−q⟩\displaystyle=\left<a,b,t\mid ta^{p}t^{-1}=b^{-1}a^{p},\ tb^{-q}a^{-1}t^{-1}=b^{-q}\right>
=⟨a,b,t∣t​ap​t−1=b−1​ap,a=t−1​bq​t​b−q⟩\displaystyle=\left<a,b,t\mid ta^{p}t^{-1}=b^{-1}a^{p},\ a=t^{-1}b^{q}tb^{-q}\right>
=⟨b,t∣t​(t−1​bq​t​b−q)p​t−1=b−1​(t−1​bq​t​b−q)p⟩\displaystyle=\left<b,t\mid t(t^{-1}b^{q}tb^{-q})^{p}t^{-1}=b^{-1}(t^{-1}b^{q}tb^{-q})^{p}\right>
=⟨b,t,x,y∣t​(t−1​bq​t​b−q)p​t−1=b−1​(t−1​bq​t​b−q)p,x=b​t,y=t−1⟩\displaystyle=\left<b,t,x,y\mid t(t^{-1}b^{q}tb^{-q})^{p}t^{-1}=b^{-1}(t^{-1}b^{q}tb^{-q})^{p},\ x=bt,\ y=t^{-1}\right>
=⟨b,t,x,y∣t​(t−1​bq​t​b−q)p​t−1=b−1​(t−1​bq​t​b−q)p,b=x​y,t=y−1⟩\displaystyle=\left<b,t,x,y\mid t(t^{-1}b^{q}tb^{-q})^{p}t^{-1}=b^{-1}(t^{-1}b^{q}tb^{-q})^{p},\ b=xy,\ t=y^{-1}\right>
=⟨x,y∣y−1{(yx)q(xy)−q)}py=y−1x−1{(yx)q(xy)−q)}p⟩\displaystyle=\left<x,y\mid y^{-1}\{(yx)^{q}(xy)^{-q})\}^{p}y=y^{-1}x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p}\right>
=⟨x,y∣{(yx)q(xy)−q)}py=x−1{(yx)q(xy)−q)}p⟩\displaystyle=\left<x,y\mid\{(yx)^{q}(xy)^{-q})\}^{p}y=x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p}\right> (6)

In the deformation above, the meridian tt is changed into y−1y^{-1} and the longitude [bq,ap][b^{q},a^{p}] is changed into {(yx)−q(xy)q)}p{(yx)q(xy)−q)}p\{(yx)^{-q}(xy)^{q})\}^{p}\{(yx)^{q}(xy)^{-q})\}^{p}. Then we get another presentation of Gp,qG_{p,q}, the fundamental group of Kp,q​(0)K_{p,q}(0) as follows.

Gp,q=⟨x,y∣{(yx)q(xy)−q)}py=x−1{(yx)q(xy)−q)}p,{(yx)−q(xy)q)}p{(yx)q(xy)−q)}p=1⟩\displaystyle G_{p,q}=\left<x,y\mid\{(yx)^{q}(xy)^{-q})\}^{p}y=x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p},\ \{(yx)^{-q}(xy)^{q})\}^{p}\{(yx)^{q}(xy)^{-q})\}^{p}=1\right> (7)
Remark 3.1.

The presentations (6) and (7) are obtained directly by noting that the tunnel number of Kp,qK_{p,q} is one.

Lemma 3.1.

Let pp be a positive integer and qq a non-zero integer. Then in Gp,qG_{p,q} with presentation (7), 1∈⟨⟨[x​y,y​x]⟩⟩+1\in\left<\left<[xy,yx]\right>\right>^{+} holds.

Proof.

For positive qq, considering the second relation of (7) and applying Lemma 2.2 by replacing gg and hh with xx and yy respectively, we have

1={(yx)−q(xy)q)}p{(yx)q(xy)−q)}p∈⟨⟨[xy,yx]⟩⟩+.\displaystyle 1=\{(yx)^{-q}(xy)^{q})\}^{p}\{(yx)^{q}(xy)^{-q})\}^{p}\in\left<\left<[xy,yx]\right>\right>^{+}.

For negative qq, considering the second relation of (7) and applying Lemma 2.2 by replacing gg and hh with y−1y^{-1} and x−1x^{-1} respectively, we have

1\displaystyle 1 ={(yx)−q(xy)q)}p{(yx)q(xy)−q)}p={(x−1y−1)q(y−1x−1)−q)}p{(x−1y−1)−q(y−1x−1)q)}p\displaystyle=\{(yx)^{-q}(xy)^{q})\}^{p}\{(yx)^{q}(xy)^{-q})\}^{p}=\{(x^{-1}y^{-1})^{q}(y^{-1}x^{-1})^{-q})\}^{p}\{(x^{-1}y^{-1})^{-q}(y^{-1}x^{-1})^{q})\}^{p}
∈⟨⟨[y−1​x−1,x−1​y−1]⟩⟩+=⟨⟨[(x​y)−1,(y​x)−1]⟩⟩+=⟨⟨[x​y,y​x]⟩⟩+.\displaystyle\in\left<\left<[y^{-1}x^{-1},x^{-1}y^{-1}]\right>\right>^{+}=\left<\left<[(xy)^{-1},(yx)^{-1}]\right>\right>^{+}=\left<\left<[xy,yx]\right>\right>^{+}.

□\Box

Note that the lemma above does not imply that [x​y,y​x][xy,yx] is a generalized torsion element. It may be the trivial element.

4 The JSJ-decompositions of 3-manifolds obtained by the 0-surgeries along double twist knots

Let MM be a prime compact 3-manifold with (possibly empty) incompressible boundary. There exists a set 𝒯\mathcal{T} consisting of pairwise non-parallel disjoint essential tori in MM such that

  • •

    each component obtained by cutting along the tori in 𝒯\mathcal{T} is either a Seifert manifold or an atoroidal manifold, and

  • •

    there are no proper subset of 𝒯\mathcal{T} satisfying the above condition.

This decomposition is called the JSJ-decomposition of MM [12] [14]. It is known that the set 𝒯\mathcal{T} is unique for a given MM. In this section, we give the JSJ-decomposition of the 3-manifold Kp,q​(0)K_{p,q}(0) obtained by the 0-surgery along the double twist knot Kp,qK_{p,q}.

4.1 Components for the decomposition

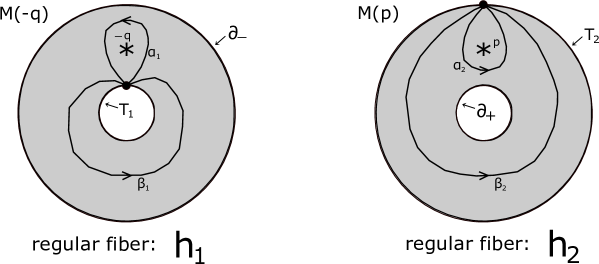
We will define 3-manifolds M​(k)M(k), which appear in the JSJ-decompositions of 3-manifolds obtained by the 0-surgeries along double twist knots for a non-zero integer kk. Let AA be an annulus. Take a point ∗∈IntA*\in{\rm Int}A, in the interior of AA. Consider 3-manifold A×S1A\times S^{1}. For a non-zero integer kk, M​(k)M(k) denotes the 3-manifold obtained by kk-surgery along {∗}×S1\{*\}\times S^{1} from A×S1A\times S^{1}. We take a longitude of {∗}×S1\{*\}\times S^{1} for the surgery such that it is isotopic to {∗′}×S1\{*^{\prime}\}\times S^{1} for {∗′}∈A∖{∗}\{*^{\prime}\}\in A\setminus\{*\} in (A∖{∗})×S1\left(A\setminus\{*\}\right)\times S^{1}. Note that M​(k)M(k) is a Seifert manifold whose regular fiber comes from the S1S^{1} factor of A×S1A\times S^{1}, that the base orbifold of this fiber structure is annulus with one (or zero) exceptional point, and that M​(k)M(k) is irreducible and has incompressible boundary. Moreover, note that M​(±1)M(\pm 1) is S1×S1×[0,1]S^{1}\times S^{1}\times[0,1] and that M​(k)M(k) admits the unique fiber structure unless k=±1k=\pm 1. See [13] for example.

Lemma 4.1.

For non-zero integers k1k_{1} and k2k_{2}, M​(k1)M(k_{1}) and M​(k2)M(k_{2}) are homeomorphic if and only if |k1|=|k2||k_{1}|=|k_{2}|.

Proof.

“If” part is clear. Note that if k1=−k2k_{1}=-k_{2}, the homoeomorphism may be orientation reversing. We prove “only if” part. Suppose that M​(k1)M(k_{1}) and M​(k2)M(k_{2}) are homeomorphic. If one of k1k_{1} and k2k_{2} is ±1\pm 1, then the manifold is S1×S1×[0,1]S^{1}\times S^{1}\times[0,1] and the other is also ±1\pm 1. If neither k1k_{1} nor k2k_{2} is ±1\pm 1, then the manifolds admit the unique fiber structures. Thus the homeomorphism sends regular and singular fibers to regular and singular fibers, respectively. Note that in M​(k1)M(k_{1}), a regular fiber near the singular fiber spirals around the singular fiber |k1||k_{1}| times and that in M​(k2)M(k_{2}), a regular fiber near the singular fiber spirals around the singular fiber |k2||k_{2}| times. Thus |k1|=|k2||k_{1}|=|k_{2}| must hold. □\Box

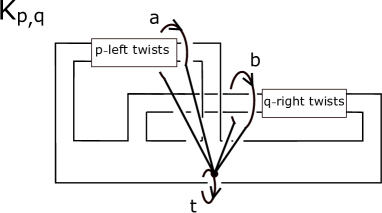
Let Xp,qX_{p,q} be a manifold obtained by gluing M​(−q)M(-q) and M​(p)M(p) as follows: Take base points and based loops in M​(−q)M(-q) and M​(p)M(p) as in Figure 5. In Figure 5, h1h_{1} and h2h_{2} are based loops which are also regular fibers in M​(−q)M(-q) and M​(p)M(p) pointing into the front side of this paper, and T1T_{1}, T2T_{2}, ∂+\partial_{+} and ∂−\partial_{-} are boundary tori. We can see that π1​(M​(−q))=⟨α1,β1,h1∣[α1,h1]=[β1,h1]=h1​α1−q=1⟩\pi_{1}\left(M(-q)\right)=\left<\alpha_{1},\beta_{1},h_{1}\mid[\alpha_{1},h_{1}]=[\beta_{1},h_{1}]=h_{1}{\alpha_{1}}^{-q}=1\right> and
π1​(M​(p))=⟨α2,β2,h2∣[α2,h2]=[β2,h2]=h2​α2p=1⟩\pi_{1}\left(M(p)\right)=\left<\alpha_{2},\beta_{2},h_{2}\mid[\alpha_{2},h_{2}]=[\beta_{2},h_{2}]=h_{2}{\alpha_{2}}^{p}=1\right>. Paste M​(−q)M(-q) and M​(p)M(p) along T1T_{1} and T2T_{2} so that the pair (β1,h1)(\beta_{1},h_{1}) is identified with (h2,β2−1)(h_{2},{\beta_{2}}^{-1}). This resultant manifold is denoted by Xp,qX_{p,q}. The boundary of Xp,qX_{p,q} coming from ∂±\partial_{\pm} is also denoted by ∂±\partial_{\pm}. Note that Xp,qX_{p,q} is also irreducible and has incompressible boundary.

Refer to caption
Figure 5: M​(−q)M(-q) and M​(p)M(p)

Set GG, G+G_{+} and G−G_{-} to be the fundamental groups of Xp,qX_{p,q}, ∂+\partial_{+} and ∂−\partial_{-}, respectively. Let j±:G+⟶Gj_{\pm}:G_{+}\longrightarrow G be (some) homomorphisms induced by the inclusions. Then we can compute and fix presentations of GG and G±G_{\pm} as follows.

G\displaystyle G =⟨α1,β1,h1,α2,β2,h2∣[α1,h1]=[β1,h1]=h1​α1−q=[α2,h2]=[β2,h2]=h2​α2p=β1​h2−1=β2​h1=1⟩\displaystyle=\left<\alpha_{1},\beta_{1},h_{1},\alpha_{2},\beta_{2},h_{2}\mid[\alpha_{1},h_{1}]=[\beta_{1},h_{1}]=h_{1}{\alpha_{1}}^{-q}=[\alpha_{2},h_{2}]=[\beta_{2},h_{2}]=h_{2}{\alpha_{2}}^{p}=\beta_{1}{h_{2}}^{-1}=\beta_{2}h_{1}=1\right>
=⟨α1,α2∣[α1q,α2p]=1⟩\displaystyle=\left<\alpha_{1},\alpha_{2}\mid[{\alpha_{1}}^{q},{\alpha_{2}}^{p}]=1\right> (8)
G+\displaystyle G_{+} =⟨x+,y+∣[x+,y+]=1⟩\displaystyle=\left<x_{+},y_{+}\mid[x_{+},y_{+}]=1\right> (9)
G−\displaystyle G_{-} =⟨x−,y−∣[x−,y−]=1⟩\displaystyle=\left<x_{-},y_{-}\mid[x_{-},y_{-}]=1\right> (10)

We take x±x_{\pm} and y±y_{\pm} so that j+(x+)=(β2α2−1=)α1−qα2−1j_{+}(x_{+})=(\beta_{2}{\alpha_{2}}^{-1}=){\alpha_{1}}^{-q}{\alpha_{2}}^{-1}, j+(y+)=(h2=)α2−pj_{+}(y_{+})=(h_{2}=){\alpha_{2}}^{-p}, j−(x−)=(α1β1=)α1α2−pj_{-}(x_{-})=(\alpha_{1}\beta_{1}=)\alpha_{1}{\alpha_{2}}^{-p} and j−(y−)=(h1=)α1qj_{-}(y_{-})=(h_{1}=)\alpha_{1}^{q} hold.

Lemma 4.2.

Kp,q​(0)∖T¯\overline{K_{p,q}(0)\setminus T} is homeomorphic to Xp,qX_{p,q}.

Proof.

Recall that GG is the fundamental group of Xp,qX_{p,q} and that Γ\Gamma is that of Kp,q∖T¯\overline{K_{p,q}\setminus T}. We use the presentation (3) for Γ\Gamma. Set ϕ\phi, ϕ+\phi_{+}, ϕ−\phi_{-} and ff to be isomorphisms satisfying:

  • •

    ϕ:G⟶Γ\phi:G\longrightarrow\Gamma maps α1\alpha_{1} and α2\alpha_{2} to b−1b^{-1} and a−1a^{-1} respectively,

  • •

    ϕ+:G+⟶Γ+\phi_{+}:G_{+}\longrightarrow\Gamma_{+} maps x+x_{+} and y+y_{+} to Y+−1{Y_{+}}^{-1} and X+X_{+} respectively,

  • •

    ϕ−:G−⟶Γ−\phi_{-}:G_{-}\longrightarrow\Gamma_{-} maps x−x_{-} and y−y_{-} to X−X_{-} and Y−Y_{-} respectively, and

  • •

    f:Γ⟶Γf:\Gamma\longrightarrow\Gamma maps aa and bb to aa and a−1​b​aa^{-1}ba respectively.

Then the following two diagrams are commute, where i​dΓid_{\Gamma} denotes the identity map of Γ\Gamma.

Γ+\textstyle{\Gamma_{+}\ignorespaces\ignorespaces\ignorespaces\ignorespaces}ι+\scriptstyle{\iota_{+}}Γ\textstyle{\Gamma\ignorespaces\ignorespaces\ignorespaces\ignorespaces}f\scriptstyle{f}Γ\textstyle{\Gamma}Γ−\textstyle{\Gamma_{-}\ignorespaces\ignorespaces\ignorespaces\ignorespaces}ι−\scriptstyle{\iota_{-}}Γ\textstyle{\Gamma\ignorespaces\ignorespaces\ignorespaces\ignorespaces}i​dΓ\scriptstyle{id_{\Gamma}}Γ\textstyle{\Gamma}G+\textstyle{G_{+}\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}ϕ+\scriptstyle{\phi_{+}}j+\scriptstyle{j_{+}}G\textstyle{G\ignorespaces\ignorespaces\ignorespaces\ignorespaces}ϕ\scriptstyle{\phi}G−\textstyle{G_{-}\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces\ignorespaces}ϕ−\scriptstyle{\phi_{-}}j−\scriptstyle{j_{-}}G\textstyle{G\ignorespaces\ignorespaces\ignorespaces\ignorespaces}ϕ\scriptstyle{\phi}

Therefore, ϕ\phi (with other isomorphisms) is an isomorphism preserving the peripheral structure. Note that Xp,qX_{p,q} and Kp,q​(0)∖T¯\overline{K_{p,q}(0)\setminus T} are irreducible and that they have essential surfaces since 3-manifold whose boundary component other than spheres are not empty has an essential surface. By a result of Waldhausen [25], this isomorphism is induced by a homeomorphism between Xp,qX_{p,q} and Kp,q​(0)∖T¯\overline{K_{p,q}(0)\setminus T}. □\Box

Lemma 4.3.

Xp,qX_{p,q} is not a Seifert manifold unless p=±1p=\pm 1 or q=±1q=\pm 1.

Proof.

Suppose that p≠±1p\neq\pm 1 and q≠±1q\neq\pm 1. Suppose that Xp,qX_{p,q} is a Seifert manifold for the contrary. Xp,qX_{p,q} has an incompressible torus T~\tilde{T}, which is coming from the attaching torus of M​(p)M(p) and M​(−q)M(-q). It is known that (see [13]) if FF is a connected incompressible surfaces in a Seifert manifold MM, then either

  • •

    FF is a boundary parallel annulus,

  • •

    MM is a surface bundle over S1S^{1} and FF is a fiber surface,

  • •

    FF splits MM into two 3-manifolds M1M_{1} and M2M_{2}, both of which are twisted II-bundles over non-orientable surfaces or

  • •

    FF is annulus or torus and isotopic to the one foliated by Seifert fibers of MM

holds. Apply this fact to T~\tilde{T}. Since T~\tilde{T} is a closed torus and Xp,qX_{p,q} has boundary, the first and the second cannot hold. Torus T~\tilde{T} splits Xp,qX_{p,q} into M​(p)M(p) and M​(−q)M(-q). Note that the boundary of each split component consists of two tori. Suppose that M​(p)M(p) is a twisted II-bundle over a non-orientable surface NN. Note that NN must have boundary since M​(p)M(p) has boundary. Then the Euler number of the boundary of M​(p)M(p) is twice as many as that of NN. Thus NN is a Mo¨{\rm\ddot{o}}bius band. However the twisted II-bundle over a Mo¨{\rm\ddot{o}}bius band is a solid torus, not M​(p)M(p). Thus the third cannot hold. If T~\tilde{T} can be foliated by Seifert fibers of Xp,qX_{p,q}, then the fiber structure descends to the split components M​(p)M(p) and M​(−q)M(-q), and the foliations on the cut ends coming from T~\tilde{T} are identical. Since p≠±1p\neq\pm 1 and q≠±1q\neq\pm 1, these fiber structures are the same as the ones defined in the construction of M​(k)M(k). However, in the construction of Xp,qX_{p,q}, the foliations on T~\tilde{T} are not identical. Thus the fourth cannot hold, and we conclude that Xp,qX_{p,q} is not a Seifert manifold unless p=±1p=\pm 1 or q=±1q=\pm 1. □\Box

4.2 The JSJ-decompositions of 3-manifolds obtained by the 0-surgeries along double twist knots

Proposition 4.1.

(The JSJ-decomposition of Kp,q​(0)K_{p,q}(0))
Let pp and qq be non-zero integers. The set of decomposing tori 𝒯\mathcal{T} of the JSJ-decomposition of Kp,q​(0)K_{p,q}(0) is

  • •

    empty if (p,q)=(1,−1)(p,q)=(1,-1) or (−1,1)(-1,1), and then Kp,q​(0)K_{p,q}(0) is a Seifert manifold,

  • •

    {T}\{T\}, where TT is the result of capping off the Seifert surface T′T^{\prime} of Kp,qK_{p,q} in Figure 3 if p=±1p=\pm 1 or q=±1q=\pm 1 and (p,q)(p,q) is neither (1,−1)(1,-1) nor (−1,1)(-1,1), and then the resulting component of splitting is homeomorphic to a Seifert manifold M​(p​q)M(pq), and

  • •

    {T,T~}\{T,\tilde{T}\}, where T~\tilde{T} is the torus in Xp,qX_{p,q}, homeomorpic to Kp,q​(0)∖T¯\overline{K_{p,q}(0)\setminus T}, splitting it into Seifert manifolds M​(p)M(p) and M​(−q)M(-q) if p≠±1p\neq\pm 1 and q≠±1q\neq\pm 1.

Proof.

In [9], it is proved that a Montesinos knot admits a Dehn surgery yielding a troidal Seifert 3-manifold if and only if the knot is trefoil and the surgery slope is 0. Thus we know that Kp,q​(0)K_{p,q}(0) is a Seifert manifold and the set of decomposing tori is empty if (p,q)=(1,−1)(p,q)=(1,-1) or (−1,1)(-1,1) and a non-Seifert manifold otherwise. Assume that (p,q)(p,q) is neither (1,−1)(1,-1) nor (−1,1)(-1,1). Then Kp,q​(0)K_{p,q}(0) is a non-Seifert manifold and having essential torus TT, and the set of decomposing tori must contain TT. By Lemma 4.2, the result of cutting Kp,q​(0)K_{p,q}(0) along TT is homeomorphic to Xp,qX_{p,q}. This Xp,qX_{p,q} is a Seifert manifold homeomorphic to M​(p​q)M(pq) if p=±1p=\pm 1 or q=±1q=\pm 1, and otherwise a non-Seifert manifold by Lemma 4.3 and having essential torus T~\tilde{T}, which splits Xp,qX_{p,q} into two Seifert manifolds M​(p)M(p) and M​(−q)M(-q). This completes the proof. □\Box

Using the JSJ-decomposition above, we get the following:

Proposition 4.2.

Let Kp,qK_{p,q} and Kp′,q′K_{p^{\prime},q^{\prime}} be two double twist knots. Then Kp,q​(0)K_{p,q}(0) and Kp′,q′​(0)K_{p^{\prime},q^{\prime}}(0) are homeomorphic if and only if (p′,q′)=(p,q)(p^{\prime},q^{\prime})=(p,q), (q,p)(q,p), (−p,−q)(-p,-q) or (−q,−p)(-q,-p).

Proof.

“If” part is clear since Kp′,q′K_{p^{\prime},q^{\prime}} is isotopic to Kp,qK_{p,q} or its mirror in such condition of (p′,q′)(p^{\prime},q^{\prime}). We prove “only if” part. Since the 0-surgery of a knot determines the Alexander polynomial of the knot and the Alexander polynomial ΔKp,q​(t)\Delta_{K_{p,q}}(t) of Kp,qK_{p,q} is −p​q​t2+(2​p​q+1)​t−p​q-pqt^{2}+(2pq+1)t-pq, the equation p​q=p′​q′pq=p^{\prime}q^{\prime} must hold. If (p,q)(p,q) is (1,−1)(1,-1) or (−1,1)(-1,1), the set of decomposing tori of Kp,q​(0)K_{p,q}(0) is empty. This also holds for that of Kp′,q′​(0)K_{p^{\prime},q^{\prime}}(0). By Proposition 4.1, this implies that (p′,q′)=(1,−1)(p^{\prime},q^{\prime})=(1,-1) or (−1,1)(-1,1). We assume that (p,q)(p,q) is neither (1,−1)(1,-1) nor (−1,1)(-1,1). If p=±1p=\pm 1 or q=±1q=\pm 1, the set of decomposing tori consists of one element. This also holds for that of Kp′,q′​(0)K_{p^{\prime},q^{\prime}}(0). By Proposition 4.1, this implies that p′=±1p^{\prime}=\pm 1 or q′=±1q^{\prime}=\pm 1. Combining this with the equation p​q=p′​q′pq=p^{\prime}q^{\prime}, we conclude that (p′,q′)=(p,q)(p^{\prime},q^{\prime})=(p,q), (q,p)(q,p), (−p,−q)(-p,-q) or (−q,−p)(-q,-p). Assume that p≠±1p\neq\pm 1 and q≠±1q\neq\pm 1 next. Then the set of decomposing tori for Kp,q​(0)K_{p,q}(0) consists of two tori and this also holds for that of Kp′,q′​(0)K_{p^{\prime},q^{\prime}}(0). Moreover, the sets {M​(p),M​(−q)}\{M(p),M(-q)\} and {M​(p′),M​(−q′)}\{M(p^{\prime}),M(-q^{\prime})\} of the resulting pieces of splitting must identical. By Lemma 4.1, p=±p′p=\pm p^{\prime} or ±q′\pm q^{\prime}. Combining this with the equation p​q=p′​q′pq=p^{\prime}q^{\prime}, we conclude that (p′,q′)=(p,q)(p^{\prime},q^{\prime})=(p,q), (q,p)(q,p), (−p,−q)(-p,-q) or (−q,−p)(-q,-p). □\Box

Remark 4.1.

There are many inequivalent knots which produce homeomorphic 3-manifolds by the 0-surgeries [4] [20] [24] [15]. On the other hand, there are many knots such that the 0-surgery along them never homeomorphic to those along inequivalent knots [2] [3]. In these cases, it is said that 0 is the characterizing slope for the knot. Note that the proposition above does not state that 0 is the characterizing slope for a double twist knot. There may be a knot in a class of knots other than double twist knots a surgery along which produces 3-manifold homeomorphic to the 3-manifold obtained by the 0-surgery along a double twist knot.

5 A proof of Theorem 1.1

Take two pair of non-zero integers (p,q)(p,q) and (p′,q′)(p^{\prime},q^{\prime}) such that p​q=p′​q′pq=p^{\prime}q^{\prime} and p≠±p′,±q′p\neq\pm p^{\prime},\pm q^{\prime}. Recall that Kp,qK_{p,q} is the mirror of K−p,−qK_{-p,-q}. And note that the knot group of a knot is isomorphic to that of the mirror of the knot and that this isomorphism extends to an isomorphism between the fundamental groups of the 3-manifolds obtained by the 0-surgeries along the knot and its mirror. Thus we assume that pp and p′p^{\prime} are positive. We use the presentations of type (7) for Gp,qG_{p,q} and Gp′,q′G_{p^{\prime},q^{\prime}}, the fundamental groups of Kp,q​(0)K_{p,q}(0) and Kp′,q′​(0)K_{p^{\prime},q^{\prime}}(0) respectively. As stated at Lemma 3.1, [x​y,y​x][xy,yx] is a generalized torsion element in Gp,qG_{p,q} unless [x​y,y​x]=1[xy,yx]=1 holds. Suppose that [x​y,y​x]=1[xy,yx]=1 holds in Gp,qG_{p,q} i.e x​yxy and y​xyx commute in Gp,qG_{p,q}. Then we can deform the presentation (7) as follows. Note that the second relation of the presentation (7) follows from [x​y,y​x]=1[xy,yx]=1 by Lemma 3.1.

Gp,q\displaystyle G_{p,q} =⟨x,y∣{(yx)q(xy)−q)}py=x−1{(yx)q(xy)−q)}p,{(yx)−q(xy)q)}p{(yx)q(xy)−q)}p=1⟩\displaystyle=\left<x,y\mid\{(yx)^{q}(xy)^{-q})\}^{p}y=x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p},\ \{(yx)^{-q}(xy)^{q})\}^{p}\{(yx)^{q}(xy)^{-q})\}^{p}=1\right>
=⟨x,y∣{(yx)q(xy)−q)}py=x−1{(yx)q(xy)−q)}p,{(yx)−q(xy)q)}p{(yx)q(xy)−q)}p=1,[xy,yx]=1⟩\displaystyle=\left<x,y\mid\{(yx)^{q}(xy)^{-q})\}^{p}y=x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p},\ \{(yx)^{-q}(xy)^{q})\}^{p}\{(yx)^{q}(xy)^{-q})\}^{p}=1,\ [xy,yx]=1\right>
=⟨x,y∣{(yx)q(xy)−q)}py=x−1{(yx)q(xy)−q)}p,[xy,yx]=1⟩\displaystyle=\left<x,y\mid\{(yx)^{q}(xy)^{-q})\}^{p}y=x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p},\ [xy,yx]=1\right>
=⟨x,y∣{(yx)(xy)−1)}p​qy=x−1{(yx)(xy)−1)}p​q,[xy,yx]=1⟩\displaystyle=\left<x,y\mid\{(yx)(xy)^{-1})\}^{pq}y=x^{-1}\{(yx)(xy)^{-1})\}^{pq},\ [xy,yx]=1\right>

Similarly, if [x​y,y​x]=1[xy,yx]=1 holds in Gp′,q′G_{p^{\prime},q^{\prime}}, then we have the following presentation.

Gp′,q′\displaystyle G_{p^{\prime},q^{\prime}} =⟨x,y∣{(yx)(xy)−1)}p′​q′y=x−1{(yx)(xy)−1)}p′​q′,[xy,yx]=1⟩\displaystyle=\left<x,y\mid\{(yx)(xy)^{-1})\}^{p^{\prime}q^{\prime}}y=x^{-1}\{(yx)(xy)^{-1})\}^{p^{\prime}q^{\prime}},\ [xy,yx]=1\right>

Therefore, if [x​y,y​x]=1[xy,yx]=1 holds simultaneously in Gp,qG_{p,q} and Gp′,q′G_{p^{\prime},q^{\prime}}, then Gp,qG_{p,q} and Gp′,q′G_{p^{\prime},q^{\prime}} are isomorphic. Note that Kp,q​(0)K_{p,q}(0) and Kp′,q′​(0)K_{p^{\prime},q^{\prime}}(0) is irreducible and have essential surfaces, which are obtained by capping off a Seifert surfaces of minimal genus. By a result of Waldhausen [25] (for closed 3-manifold), stating that every isomorphism between the fundamental groups of closed 3-manifolds which have essential surfaces is induced by a homeomorphism between the 3-manifolds, we know that Kp,q​(0)K_{p,q}(0) and Kp′,q′​(0)K_{p^{\prime},q^{\prime}}(0) are homeomorphic. However, this is impossible in our condition of (p,q)(p,q) and (p′,q′)(p^{\prime},q^{\prime}) by Proposition 4.2. Therefore, [x​y,y​x]≠1[xy,yx]\neq 1 in at least one of Gp,qG_{p,q} and Gp′,q′G_{p^{\prime},q^{\prime}}.

Remark 5.1.

As one can see in the proof above, we say that [x​y,y​x][xy,yx] is not a generalized torsion element in at most one of Gp,qG_{p,q} and Gp′,q′G_{p^{\prime},q^{\prime}}. There may be another generalized torsion element in Gp,qG_{p,q} even if [x​y,y​x][xy,yx] is not a generalized torsion element. Later we construct an (at most) infinite family of elements in Gp,qG_{p,q}. And show that if Gp,qG_{p,q} admits a generalized torsion element, then Gp,qG_{p,q} admits a torsion element or admits a generalized torsion element in the constructed family. For the family of elements, see the last paragraph of Section 6 for p​q<0pq<0 and Remark 7.2 for p​q>0pq>0.

6 A proof of Theorem 1.2

In this section, we search a generalized torsion element in the fundamental group Gp,−qG_{p,-q} of the 3-manifold Kp,−q​(0)K_{p,-q}(0) obtained by the 0-surgery along a double twist knot Kp,−qK_{p,-q} for positive integers pp and qq. For p=1p=1, the generalized torsion element in the knot group of K1,−qK_{1,-q} constructed in [22] remains to be a generalized torsion element after the 0-surgery. Though we cannot find a generalized torsion element in the knot group of Kp,−qK_{p,-q} for general pp so far, we can see that there exists a generalized torsion element in Gp,−qG_{p,-q}. We use the presentation (2) for Gp,−qG_{p,-q}.

Gp,−q=π1​(Kp,−q​(0))=⟨a,b,t∣t​ap​t−1=b−1​ap,t​bq​a−1​t−1=bq,[b−q,ap]=1⟩\displaystyle G_{p,-q}=\pi_{1}\left(K_{p,-q}(0)\right)=\left<a,b,t\mid ta^{p}t^{-1}=b^{-1}a^{p},\ tb^{q}a^{-1}t^{-1}=b^{q},\ [b^{-q},a^{p}]=1\right>

By the third of Lemma 2.1, we have 1=[b−q,ap]∈⟨⟨[b−1,a]⟩⟩+1=[b^{-q},a^{p}]\in\left<\left<[b^{-1},a]\right>\right>^{+} in Gp,−qG_{p,-q}. Thus [b−1,a][b^{-1},a] is a generalized torsion element in Gp,−qG_{p,-q} unless [b−1,a]=1[b^{-1},a]=1 holds i.e aa and bb commute in Gp,−qG_{p,-q}. In the following, we suppose that aa and bb commute in Gp,−qG_{p,-q} and prove that aa (and bb) are generalized torsion elements in Gp,−qG_{p,-q} under this assumption.

Under the assumption, we have t​ap​t−1=ap​b−1ta^{p}t^{-1}=a^{p}b^{-1} and t​a−p​bp​q​t−1=t​(a−1​bq)p​t−1=bp​qta^{-p}b^{pq}t^{-1}=t\left(a^{-1}b^{q}\right)^{p}t^{-1}=b^{pq}. Thus “informally”, the representation matrix AA of the action of t​(⋅)​t−1t(\cdot)t^{-1} on the subgroup of Gp,−qG_{p,-q} generated by aa and bb under a basis {a,b}\{a,b\} is A=(11q−1p1−1p​q)A=\left(\begin{array}[]{cc}1&\frac{1}{q}\\ -\frac{1}{p}&1-\frac{1}{pq}\\ \end{array}\right). Note that since we have ap=t−1​b−1​ap​ta^{p}=t^{-1}b^{-1}a^{p}t and bq​a−1=t−1​bq​tb^{q}a^{-1}=t^{-1}b^{q}t from the presentation, the representation matrix of the action of t−1​(⋅)​tt^{-1}(\cdot)t on this group under the same basis is A−1=(1−1p​q−1q1p1)A^{-1}=\left(\begin{array}[]{cc}1-\frac{1}{pq}&-\frac{1}{q}\\ \frac{1}{p}&1\\ \end{array}\right). The word “informally” is used because the result of the action t​(⋅)​t−1t(\cdot)t^{-1} is not necessary closed in the subgroup generated by aa and bb. However, for an element of the subgroup whose exponents of both of aa and bb are multiples of p​qpq, the result of the action t​(⋅)​t−1t(\cdot)t^{-1} is in the subgroup: For a(p​q)​s​b(p​q)​la^{(pq)s}b^{(pq)l} where ss and ll are integers, we have

t​(a(p​q)​s​b(p​q)​l)​t−1\displaystyle t\left(a^{(pq)s}b^{(pq)l}\right)t^{-1} =t​(ap​q​s+p​l)​t−1⋅t​(a−p​l​bp​q​l)​t−1\displaystyle=t\left(a^{pqs+pl}\right)t^{-1}\cdot t\left(a^{-pl}b^{pql}\right)t^{-1}
=t​(ap)q​s+l​t−1⋅t​(a−1​bq)p​l​t−1\displaystyle=t\left(a^{p}\right)^{qs+l}t^{-1}\cdot t\left(a^{-1}b^{q}\right)^{pl}t^{-1}
=(ap​b−1)q​s+l⋅(bq)p​l\displaystyle=\left(a^{p}b^{-1}\right)^{qs+l}\cdot\left(b^{q}\right)^{pl}
=ap​q​s+p​l​b−q​s+(p​q−1)​l\displaystyle=a^{pqs+pl}b^{-qs+(pq-1)l}

This is represented as A​((p​q)​s(p​q)​l)=(11q−1p1−1p​q)​((p​q)​s(p​q)​l)=(p​q​s+p​l−q​s+(p​q−1)​l)A\begin{pmatrix}(pq)s\\ (pq)l\end{pmatrix}=\left(\begin{array}[]{cc}1&\frac{1}{q}\\ -\frac{1}{p}&1-\frac{1}{pq}\\ \end{array}\right)\begin{pmatrix}(pq)s\\ (pq)l\end{pmatrix}=\begin{pmatrix}pqs+pl\\ -qs+(pq-1)l\end{pmatrix}. Similarly, for non-negative integer kk, the exponents of aa and bb in tk​(a(p​q)k​s​b(p​q)k​l)​t−kt^{k}\left(a^{(pq)^{k}s}b^{(pq)^{k}l}\right)t^{-k} are obtained from Ak​((p​q)k​s(p​q)k​l)A^{k}\begin{pmatrix}(pq)^{k}s\\ (pq)^{k}l\end{pmatrix} and those of t−k​(a(p​q)k​s​b(p​q)k​l)​tkt^{-k}\left(a^{(pq)^{k}s}b^{(pq)^{k}l}\right)t^{k} are obtained from A−k​((p​q)k​s(p​q)k​l)A^{-k}\begin{pmatrix}(pq)^{k}s\\ (pq)^{k}l\end{pmatrix} .

We use the following Lemma:

Lemma 6.1.

Let M∈G​L2​(ℝ)M\in GL_{2}(\mathbb{R}) be a matrix such that one of whose eigenvalues λ\lambda is in ℂ∖{1}\mathbb{C}\setminus\{1\}, has length |λ|\left|\lambda\right| one and the real part Re​(λ){\rm Re}(\lambda) of λ\lambda is in ℚ\mathbb{Q}. Then there exist positive integers kk, nn and mm such that n​Mk+m​I2+n​M−k=O2nM^{k}+mI_{2}+nM^{-k}=O_{2} holds, where I2I_{2} and O2O_{2} are the 2×22\times 2 identity and zero matrices, respectively.

Proof.

We regard MM as in G​L2​(ℂ)GL_{2}(\mathbb{C}) through the natural inclusion. Since the characteristic polynomial of MM has real coefficients, the other eigenvalue is the conjugate of λ\lambda and this is λ−1\lambda^{-1} since |λ|=1|\lambda|=1. Let 𝒱\mathcal{V} and 𝒱′\mathcal{V}^{\prime} be eigenvectors of λ\lambda and λ−1\lambda^{-1}, respectively. Note that 𝒱\mathcal{V} and 𝒱′\mathcal{V}^{\prime} are linearly independent. Since λ≠1\lambda\neq 1 and |λ|=1\left|\lambda\right|=1, there is some positive integer kk such that Re​(λk)<0{\rm Re}(\lambda^{k})<0. Note that Re​(λ−k)=Re​(λk){\rm Re}(\lambda^{-k})={\rm Re}(\lambda^{k}). Moreover, since |λ|=1\left|\lambda\right|=1, Re​(λk)=Tk​(Re​(λ)){\rm Re}(\lambda^{k})=T_{k}\left({\rm Re}(\lambda)\right) holds, where Tk​(⋅)T_{k}(\cdot) is the kk-th Chebyshev polynomial. We see that Re​(λk){\rm Re}(\lambda^{k}) is in ℚ\mathbb{Q} since Re​(λ){\rm Re}(\lambda) also is in and TkT_{k} has integer coefficients. Thus there exist positive integers mm and nn such that mn=−2​R​e​(λk)\frac{m}{n}=-2{\rm Re}(\lambda^{k}). Then

(n​Mk+n​M−k)​𝒱=(n​λk+n​λ−k)​𝒱=2​n​Re​(λk)​𝒱=−m​𝒱=−m​I2​𝒱.\displaystyle\left(nM^{k}+nM^{-k}\right)\mathcal{V}=\left(n\lambda^{k}+n\lambda^{-k}\right)\mathcal{V}=2n{\rm Re}(\lambda^{k})\mathcal{V}=-m\mathcal{V}=-mI_{2}\mathcal{V}.

Similarly, the equation obtained by replacing 𝒱\mathcal{V} in the above equation with 𝒱′\mathcal{V}^{\prime} also holds with the same kk, mm and nn. Since 𝒱\mathcal{V} and 𝒱′\mathcal{V}^{\prime} span ℂ2\mathbb{C}^{2}, the equation n​Mk+m​I2+n​M−k=O2nM^{k}+mI_{2}+nM^{-k}=O_{2} holds. □\Box

One of the eigenvalues of AA is 2​p​q−12​p​q+4​p​q−12​p​q​−1\frac{2pq-1}{2pq}+\frac{\sqrt{4pq-1}}{2pq}\sqrt{-1}, which is a complex number of length one and whose real part is rational. Hence we can apply Lemma 6.1 and we get positive integers kk, nn and mm such that n​Ak+m​I2+n​A−k=O2nA^{k}+mI_{2}+nA^{-k}=O_{2} holds. Using this equation, we have:

(n​Ak+m​I2+n​A−k)​((p​q)k0)=(00)⟺(tk​a(p​q)k​t−k)n⋅(a(p​q)k)m⋅(t−k​a(p​q)k​tk)n=1.\displaystyle\left(nA^{k}+mI_{2}+nA^{-k}\right)\begin{pmatrix}(pq)^{k}\\ 0\end{pmatrix}=\begin{pmatrix}0\\ 0\end{pmatrix}\Longleftrightarrow\left(t^{k}a^{(pq)^{k}}t^{-k}\right)^{n}\cdot\left(a^{(pq)^{k}}\right)^{m}\cdot\left(t^{-k}a^{(pq)^{k}}t^{k}\right)^{n}=1.

This implies that 1∈⟨⟨a⟩⟩+1\in\left<\left<a\right>\right>^{+}. This aa is actually a generalized torsion element. For a contradiction, suppose that a=1a=1 holds in Gp,−qG_{p,-q}. Then we have Gp,−q≅ℤG_{p,-q}\cong\mathbb{Z} from the presentation at the beginning of this section. However, Gp,−q=π1​(Kp,−q​(0))G_{p,-q}=\pi_{1}\left(K_{p,-q}(0)\right) has ℤ2\mathbb{Z}^{2} as a subgroup since Kp,−q​(0)K_{p,-q}(0) has an incompressible torus, which is obtained by capping off a Seifert surface of minimal genus. This leads a contradiction. Therefore, aa is a generalized torsion element in Gp,−qG_{p,-q} under the assumption of the commutativity of aa and bb. Note that by the same argument, we see that bb is also a generalized torsion element in Gp,−qG_{p,-q} under the assumption.

As a result, at least one of aa and [b−1,a][b^{-1},a] is a generalized torsion element in Gp,−q=π1​(Kp,−q​(0))G_{p,-q}=\pi_{1}\left(K_{p,-q}(0)\right). This finishes a proof of Theorem 1.2.

7 A proof of Theorem 1.3

For negative p​qpq, the group Gp,qG_{p,q} admits a generalized torsion element, and thus is not bi-orderable as in Theorem 1.2. In the following, we assume pp and qq are positive and Gp,qG_{p,q} admits no generalized torsion elements. We will give a bi-order. The following transformation of a presentation of π1​(Ep,q)\pi_{1}(E_{p,q}) indicates the isomorphisms among π1​(Ep,q)\pi_{1}(E_{p,q}), π1​(E−q,−p)\pi_{1}(E_{-q,-p}) and π1​(Eq,p)\pi_{1}(E_{q,p}). We give some of the presentations names for readability, although some of these already are given names before. This transformation holds even if we do not impose the positivity of pp and qq:

π1​(Ep,q)\displaystyle\pi_{1}(E_{p,q}) =⟨x,y∣{(yx)q(xy)−q)}py=x−1{(yx)q(xy)−q)}p⟩\displaystyle=\left<x,y\mid\{(yx)^{q}(xy)^{-q})\}^{p}y=x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p}\right> (11)
=⟨x,y,b,t∣{(yx)q(xy)−q)}py=x−1{(yx)q(xy)−q)}p,b=xy,t=y−1⟩\displaystyle=\left<x,y,b,t\mid\{(yx)^{q}(xy)^{-q})\}^{p}y=x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p},\ b=xy,\ t=y^{-1}\right>
=⟨b,t∣t​(t−1​bq​t​b−q)p​t−1=b−1​(t−1​bq​t​b−q)p⟩\displaystyle=\left<b,t\mid t(t^{-1}b^{q}tb^{-q})^{p}t^{-1}=b^{-1}(t^{-1}b^{q}tb^{-q})^{p}\right>
=⟨a,b,t∣t​(t−1​bq​t​b−q)p​t−1=b−1​(t−1​bq​t​b−q)p,a=t−1​bq​t​b−q⟩\displaystyle=\left<a,b,t\mid t(t^{-1}b^{q}tb^{-q})^{p}t^{-1}=b^{-1}(t^{-1}b^{q}tb^{-q})^{p},\ a=t^{-1}b^{q}tb^{-q}\right>
=⟨a,b,t∣t​ap​t−1=b−1​ap,t​b−q​a−1​t−1=b−q⟩\displaystyle=\left<a,b,t\mid ta^{p}t^{-1}=b^{-1}a^{p},\ tb^{-q}a^{-1}t^{-1}=b^{-q}\right> (12)
=⟨a,b,t,A,B,T∣t​ap​t−1=b−1​ap,t​b−q​a−1​t−1=b−q,A=b−1,B=a−1,T=t−1⟩\displaystyle=\left<a,b,t,A,B,T\mid ta^{p}t^{-1}=b^{-1}a^{p},\ tb^{-q}a^{-1}t^{-1}=b^{-q},\ A=b^{-1},\ B=a^{-1},\ T=t^{-1}\right>
=⟨A,B,T∣T−1​B−p​T=A​B−p,T−1​Aq​B​T=Aq⟩\displaystyle=\left<A,B,T\mid T^{-1}B^{-p}T=AB^{-p},\ T^{-1}A^{q}BT=A^{q}\right>
=⟨A,B,T∣T​A(−q)​T−1=B−1​A(−q),T​B−(−p)​A−1​T−1=B−(−p)⟩\displaystyle=\left<A,B,T\mid TA^{(-q)}T^{-1}=B^{-1}A^{(-q)},\ TB^{-(-p)}A^{-1}T^{-1}=B^{-(-p)}\right> (13)
=⟨B,T∣{T−1​B(−p)​T​B−(−p)}−q​T−1=T−1​B−1​{T−1​B(−p)​T​B−(−p)}−q⟩\displaystyle=\left<B,T\mid\{T^{-1}B^{(-p)}TB^{-(-p)}\}^{-q}T^{-1}=T^{-1}B^{-1}\{T^{-1}B^{(-p)}TB^{-(-p)}\}^{-q}\right>
=⟨B,T,X,Y∣{T−1​B(−p)​T​B−(−p)}−q​T−1=T−1​B−1​{T−1​B(−p)​T​B−(−p)}−q,X=B​T,Y=T−1⟩\displaystyle=\left<B,T,X,Y\mid\{T^{-1}B^{(-p)}TB^{-(-p)}\}^{-q}T^{-1}=T^{-1}B^{-1}\{T^{-1}B^{(-p)}TB^{-(-p)}\}^{-q},\ X=BT,\ Y=T^{-1}\right>
=⟨X,Y∣{(Y​X)−p​(X​Y)−(−p)}−q​Y=X−1​{(Y​X)−p​(X​Y)−(−p)}−q⟩\displaystyle=\left<X,Y\mid\{(YX)^{-p}(XY)^{-(-p)}\}^{-q}Y=X^{-1}\{(YX)^{-p}(XY)^{-(-p)}\}^{-q}\right> (14)
=⟨X,Y∣Y​{(Y​X)−p​(X​Y)p}q={(Y​X)−p​(X​Y)p}q​X−1⟩\displaystyle=\left<X,Y\mid Y\{(YX)^{-p}(XY)^{p}\}^{q}=\{(YX)^{-p}(XY)^{p}\}^{q}X^{-1}\right>
=⟨X,Y,𝕏,𝕐∣Y​{(Y​X)−p​(X​Y)p}q={(Y​X)−p​(X​Y)p}q​X−1,𝕏=Y−1,𝕐=X−1⟩\displaystyle=\left<X,Y,\mathbb{X},\mathbb{Y}\mid Y\{(YX)^{-p}(XY)^{p}\}^{q}=\{(YX)^{-p}(XY)^{p}\}^{q}X^{-1},\ \mathbb{X}=Y^{-1},\ \mathbb{Y}=X^{-1}\right>
=⟨𝕏,𝕐∣{(𝕐​𝕏)p​(𝕏​𝕐)−p}q​𝕐=𝕏−1​{(𝕐​𝕏)p​(𝕏​𝕐)−p}q⟩\displaystyle=\left<\mathbb{X},\mathbb{Y}\mid\{(\mathbb{YX})^{p}(\mathbb{XY})^{-p}\}^{q}\mathbb{Y}=\mathbb{X}^{-1}\{(\mathbb{YX})^{p}(\mathbb{XY})^{-p}\}^{q}\right> (15)
=⟨𝕏,𝕐,𝔹,𝕋∣{(𝕐​𝕏)p​(𝕏​𝕐)−p}q​𝕐=𝕏−1​{(𝕐​𝕏)p​(𝕏​𝕐)−p}q,𝔹=𝕏​𝕐,𝕋=𝕐−1⟩\displaystyle=\left<\mathbb{X},\mathbb{Y},\mathbb{B},\mathbb{T}\mid\{(\mathbb{YX})^{p}(\mathbb{XY})^{-p}\}^{q}\mathbb{Y}=\mathbb{X}^{-1}\{(\mathbb{YX})^{p}(\mathbb{XY})^{-p}\}^{q},\ \mathbb{B}=\mathbb{XY},\ \mathbb{T}=\mathbb{Y}^{-1}\right>
=⟨𝔹,𝕋∣𝕋​(𝕋−1​𝔹p​𝕋​𝔹−p)q​𝕋−1=𝔹−1​(𝕋−1​𝔹p​𝕋​𝔹−p)q⟩\displaystyle=\left<\mathbb{B},\mathbb{T}\mid\mathbb{T}\left(\mathbb{T}^{-1}\mathbb{B}^{p}\mathbb{T}\mathbb{B}^{-p}\right)^{q}\mathbb{T}^{-1}=\mathbb{B}^{-1}\left(\mathbb{T}^{-1}\mathbb{B}^{p}\mathbb{T}\mathbb{B}^{-p}\right)^{q}\right>
=⟨𝔸,𝔹,𝕋∣𝕋​(𝕋−1​𝔹p​𝕋​𝔹−p)q​𝕋−1=𝔹−1​(𝕋−1​𝔹p​𝕋​𝔹−p)q,𝔸=𝕋−1​𝔹p​𝕋​𝔹−p⟩\displaystyle=\left<\mathbb{A},\mathbb{B},\mathbb{T}\mid\mathbb{T}\left(\mathbb{T}^{-1}\mathbb{B}^{p}\mathbb{T}\mathbb{B}^{-p}\right)^{q}\mathbb{T}^{-1}=\mathbb{B}^{-1}\left(\mathbb{T}^{-1}\mathbb{B}^{p}\mathbb{T}\mathbb{B}^{-p}\right)^{q},\ \mathbb{A}=\mathbb{T}^{-1}\mathbb{B}^{p}\mathbb{T}\mathbb{B}^{-p}\right>
=⟨𝔸,𝔹,𝕋∣𝕋​𝔸q​𝕋−1=𝔹−1​𝔸q,𝕋​𝔹−p​𝔸−1​𝕋−1=𝔹−p⟩\displaystyle=\left<\mathbb{A},\mathbb{B},\mathbb{T}\mid\mathbb{T}\mathbb{A}^{q}\mathbb{T}^{-1}=\mathbb{B}^{-1}\mathbb{A}^{q},\ \mathbb{T}\mathbb{B}^{-p}\mathbb{A}^{-1}\mathbb{T}^{-1}=\mathbb{B}^{-p}\right> (16)

Tracing the above transformation, we see that 𝔹\mathbb{B} and 𝕋\mathbb{T} in (16) correspond to aa and a−1​t−1a^{-1}t^{-1} in (12) respectively, and bb in (12) corresponds to 𝔸−1\mathbb{A}^{-1} in (16). Thus [𝔹p,𝔸q][\mathbb{B}^{p},\mathbb{A}^{q}] in (16) corresponds to [ap,b−q]=bq​[bq,ap]​b−q[a^{p},b^{-q}]=b^{q}[b^{q},a^{p}]b^{-q} in (12). This implies that under the 0-surgery, the relations [bq,ap]=1[b^{q},a^{p}]=1 and [𝔹p,𝔸q]=1[\mathbb{B}^{p},\mathbb{A}^{q}]=1 are equivalent. We pick up presentations of Gp,q=π1​(Kp,q​(0))G_{p,q}=\pi_{1}\left(K_{p,q}(0)\right) we needed.

Gp,q\displaystyle G_{p,q} =⟨a,b,t∣t​ap​t−1=b−1​ap,t​b−q​a−1​t−1=b−q,[bq,ap]=1⟩\displaystyle=\left<a,b,t\mid ta^{p}t^{-1}=b^{-1}a^{p},\ tb^{-q}a^{-1}t^{-1}=b^{-q},\ [b^{q},a^{p}]=1\right> (17)
=⟨x,y∣{(yx)q(xy)−q)}py=x−1{(yx)q(xy)−q)}p,{(yx)−q(xy)q)}p{(yx)q(xy)−q)}p=1⟩\displaystyle=\left<x,y\mid\{(yx)^{q}(xy)^{-q})\}^{p}y=x^{-1}\{(yx)^{q}(xy)^{-q})\}^{p},\ \{(yx)^{-q}(xy)^{q})\}^{p}\{(yx)^{q}(xy)^{-q})\}^{p}=1\right> (18)
=⟨𝕏,𝕐∣{(𝕐𝕏)p(𝕏𝕐)−p}q𝕐=𝕏−1{(𝕐𝕏)p(𝕏𝕐)−p}q,{(𝕐𝕏)−p(𝕏𝕐)p)}q{(𝕐𝕏)p(𝕏𝕐)−p)}q=1⟩\displaystyle=\left<\mathbb{X},\mathbb{Y}\mid\{(\mathbb{YX})^{p}(\mathbb{XY})^{-p}\}^{q}\mathbb{Y}=\mathbb{X}^{-1}\{(\mathbb{YX})^{p}(\mathbb{XY})^{-p}\}^{q},\ \{(\mathbb{YX})^{-p}(\mathbb{XY})^{p})\}^{q}\{(\mathbb{YX})^{p}(\mathbb{XY})^{-p})\}^{q}=1\right> (19)
=⟨𝔸,𝔹,𝕋∣𝕋​𝔸q​𝕋−1=𝔹−1​𝔸q,𝕋​𝔹−p​𝔸−1​𝕋−1=𝔹−p,[𝔹p,𝔸q]=1⟩\displaystyle=\left<\mathbb{A},\mathbb{B},\mathbb{T}\mid\mathbb{T}\mathbb{A}^{q}\mathbb{T}^{-1}=\mathbb{B}^{-1}\mathbb{A}^{q},\ \mathbb{T}\mathbb{B}^{-p}\mathbb{A}^{-1}\mathbb{T}^{-1}=\mathbb{B}^{-p},\ [\mathbb{B}^{p},\mathbb{A}^{q}]=1\right> (20)

By Lemma 3.1 and the assumption of admitting no generalized torsion elements, we have [x​y,y​x]=1[xy,yx]=1 holds in (18), which corresponds to [b,t−1​b​t]=1[b,t^{-1}bt]=1 in (17). Similarly, [𝕏​𝕐,𝕐​𝕏]=1[\mathbb{XY},\mathbb{YX}]=1 holds in (19), which corresponds to [𝔹,𝕋−1​𝔹​𝕋]=1[\mathbb{B},\mathbb{T}^{-1}\mathbb{BT}]=1 in (20).

Proposition 7.1.

For every integer nn, the relations [b,t−n​b​tn]=1[b,t^{-n}bt^{n}]=1 and [𝔹,𝕋−n​𝔹​𝕋n]=1[\mathbb{B},\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{n}]=1 hold in (17) and (20), respectively, under the assumption of admitting no generalized torsion elements and the positivity of pp and qq.

Proof.

Note that since tn​[b,t−n​b​tn]​t−n=[tn​b​t−n,b]t^{n}[b,t^{-n}bt^{n}]t^{-n}=[t^{n}bt^{-n},b], it is enough to prove for non-negative nn. We prove by induction on nn. The case n=0n=0 is trivial and the case n=1n=1 is stated above.
Let nn is a positive integer and assume that [b,t−k​b​t−k]=1[b,t^{-k}bt^{-k}]=1 and [𝔹,𝕋−k​𝔹​𝕋k]=1[\mathbb{B},\mathbb{T}^{-k}\mathbb{B}\mathbb{T}^{k}]=1 hold in (17) and (20), respectively, for every integer kk such that |k|≤n|k|\leq n. The element [𝔹−1,𝕋−n​𝔹−1​𝕋n]=[𝔹,𝕋n]−1⋅[𝔹,𝕋−n​𝔹​𝕋n]⋅[𝔹,𝕋n][\mathbb{B}^{-1},\mathbb{T}^{-n}\mathbb{B}^{-1}\mathbb{T}^{n}]=[\mathbb{B},\mathbb{T}^{n}]^{-1}\cdot[\mathbb{B},\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{n}]\cdot[\mathbb{B},\mathbb{T}^{n}] is represented as follows in (17):

1\displaystyle 1 =[𝔹−1,𝕋−n​𝔹−1​𝕋n]\displaystyle=[\mathbb{B}^{-1},\mathbb{T}^{-n}\mathbb{B}^{-1}\mathbb{T}^{n}]
=[a−1,(t​a)n​a−1​(t​a)−n]\displaystyle=[a^{-1},(ta)^{n}a^{-1}(ta)^{-n}]
=[bq​t−1​b−q​t,(bq​t​b−q)n⋅bq​t−1​b−q​t⋅(bq​t​b−q)−n]\displaystyle=[b^{q}t^{-1}b^{-q}t,(b^{q}tb^{-q})^{n}\cdot b^{q}t^{-1}b^{-q}t\cdot(b^{q}tb^{-q})^{-n}]
=[bq⋅t−1​b−q​t,(bq​tn​b−q)⋅bq​t−1​b−q​t⋅(bq​t−n​b−q)]\displaystyle=[b^{q}\cdot t^{-1}b^{-q}t,(b^{q}t^{n}b^{-q})\cdot b^{q}t^{-1}b^{-q}t\cdot(b^{q}t^{-n}b^{-q})]
=[[b−1,t]q,bq​tn−1​b−q​t​bq​t−n​b−q]\displaystyle=\left[[b^{-1},t]^{q},b^{q}t^{n-1}b^{-q}tb^{q}t^{-n}b^{-q}\right]
=[[b−1,t]q,bq⋅tn−1​b−q​t−(n−1)⋅tn​bq​t−n⋅b−q]\displaystyle=\left[[b^{-1},t]^{q},b^{q}\cdot t^{n-1}b^{-q}t^{-(n-1)}\cdot t^{n}b^{q}t^{-n}\cdot b^{-q}\right]
=[[b−1,t]q,tn−1​b−q​t−(n−1)⋅tn​bq​t−n]\displaystyle=\left[[b^{-1},t]^{q},t^{n-1}b^{-q}t^{-(n-1)}\cdot t^{n}b^{q}t^{-n}\right]
=[[b−1,t]q,tn−1⋅b−q⋅t​bq​t−1⋅t−(n−1)]\displaystyle=\left[[b^{-1},t]^{q},t^{n-1}\cdot b^{-q}\cdot tb^{q}t^{-1}\cdot t^{-(n-1)}\right]
=[[b−1,t]q,(tn−1⋅[b,t−1]⋅t−(n−1))q]\displaystyle=\left[[b^{-1},t]^{q},\left(t^{n-1}\cdot[b,t^{-1}]\cdot t^{-(n-1)}\right)^{q}\right]

Note that [b,t−k​b​tk]=1[b,t^{-k}bt^{k}]=1 implies [b−1,t−k​b​tk]=1[b^{-1},t^{-k}bt^{k}]=1 and so on. By the third of Lemma 2.1, we have 1∈⟨⟨[[b−1,t],tn−1⋅[b,t−1]⋅t−(n−1)]⟩⟩+1\in\left<\left<\left[[b^{-1},t],t^{n-1}\cdot[b,t^{-1}]\cdot t^{-(n-1)}\right]\right>\right>^{+}. Since Gp,qG_{p,q} admits no generalized torsion elements, we have [[b−1,t],tn−1⋅[b,t−1]⋅t−(n−1)]=1\left[[b^{-1},t],t^{n-1}\cdot[b,t^{-1}]\cdot t^{-(n-1)}\right]=1. We compute as follows:

1\displaystyle 1 =[[b−1,t],tn−1⋅[b,t−1]⋅t−(n−1)]\displaystyle=\left[[b^{-1},t],t^{n-1}\cdot[b,t^{-1}]\cdot t^{-(n-1)}\right]
=(t−1​b​t​b−1)​(tn​b−1​t−1​b​t−(n−1))​(b​t−1​b−1​t)​(tn−1​b−1​t​b​t−n)\displaystyle=\left(t^{-1}btb^{-1}\right)\left(t^{n}b^{-1}t^{-1}bt^{-(n-1)}\right)\left(bt^{-1}b^{-1}t\right)\left(t^{n-1}b^{-1}tbt^{-n}\right)
=(t−1​b​t)​b−1​(tn​b−1​t−n)​(tn−1​b​t−(n−1))​b​(t−1​b−1​t)​(tn−1​b−1​t−(n−1))​(tn​b​t−n)\displaystyle=(t^{-1}bt)b^{-1}(t^{n}b^{-1}t^{-n})(t^{n-1}bt^{-(n-1)})b(t^{-1}b^{-1}t)(t^{n-1}b^{-1}t^{-(n-1)})(t^{n}bt^{-n})
=(t−1​b​t)​(tn​b−1​t−n)​(tn−1​b​t−(n−1))​(t−1​b−1​t)​(tn−1​b−1​t−(n−1))​(tn​b​t−n)\displaystyle=(t^{-1}bt)(t^{n}b^{-1}t^{-n})(t^{n-1}bt^{-(n-1)})(t^{-1}b^{-1}t)(t^{n-1}b^{-1}t^{-(n-1)})(t^{n}bt^{-n})
=(t−1​b​t)​(tn​b−1​t−n)⋅t−1​(tn​b​t−n)​(b−1)​t⋅(tn−1​b−1​t−(n−1))​(tn​b​t−n)\displaystyle=(t^{-1}bt)(t^{n}b^{-1}t^{-n})\cdot t^{-1}(t^{n}bt^{-n})(b^{-1})t\cdot(t^{n-1}b^{-1}t^{-(n-1)})(t^{n}bt^{-n})
=(t−1​b​t)​(tn​b−1​t−n)⋅t−1​(b−1)​(tn​b​t−n)​t⋅(tn−1​b−1​t−(n−1))​(tn​b​t−n)\displaystyle=(t^{-1}bt)(t^{n}b^{-1}t^{-n})\cdot t^{-1}(b^{-1})(t^{n}bt^{-n})t\cdot(t^{n-1}b^{-1}t^{-(n-1)})(t^{n}bt^{-n})
=(t−1​b​t)​(tn​b−1​t−n)⋅(t−1​b−1​t)​(tn−1​b​t−(n−1))⋅(tn−1​b−1​t−(n−1))​(tn​b​t−n)\displaystyle=(t^{-1}bt)(t^{n}b^{-1}t^{-n})\cdot(t^{-1}b^{-1}t)(t^{n-1}bt^{-(n-1)})\cdot(t^{n-1}b^{-1}t^{-(n-1)})(t^{n}bt^{-n})
=(t−1​b​t)​(tn​b−1​t−n)​(t−1​b−1​t)​(tn​b​t−n)\displaystyle=(t^{-1}bt)(t^{n}b^{-1}t^{-n})(t^{-1}b^{-1}t)(t^{n}bt^{-n})
=t−1​b​tn+1​b−1​t−(n+1)​b−1​tn+1​b​t−n\displaystyle=t^{-1}bt^{n+1}b^{-1}t^{-(n+1)}b^{-1}t^{n+1}bt^{-n}
=t−1​[b−1,tn+1​b​t−(n+1)]​t\displaystyle=t^{-1}[b^{-1},t^{n+1}bt^{-(n+1)}]t

This implies [b,t−(n+1)​b​tn+1]=1[b,t^{-(n+1)}bt^{n+1}]=1.

To get [𝔹,𝕋−(n+1)​𝔹​𝕋n+1]=1[\mathbb{B},\mathbb{T}^{-(n+1)}\mathbb{B}\mathbb{T}^{n+1}]=1, we introduce the following claim:

Claim 7.1.

Under the assumption that [𝔹,𝕋−k​𝔹​𝕋k]=1[\mathbb{B},\mathbb{T}^{-k}\mathbb{B}\mathbb{T}^{k}]=1 holds for any integer kk such that |k|≤n|k|\leq n, the equation 𝔹​𝕋−1​𝔹−1​𝕋⋅(𝔹​𝕋)m=(𝔹​𝕋)m⋅𝕋−m​𝔹​𝕋−1​𝔹−1​𝕋m+1\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}\cdot\left(\mathbb{BT}\right)^{m}=\left(\mathbb{BT}\right)^{m}\cdot\mathbb{T}^{-m}\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}^{m+1} holds for any non-negative integer mm such that m≤nm\leq n.

Proof.

We prove by induction. The case m=0m=0 is trivial. Assume that the statement holds for some m<nm<n. Then

𝔹​𝕋−1​𝔹−1​𝕋⋅(𝔹​𝕋)m+1\displaystyle\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}\cdot\left(\mathbb{BT}\right)^{m+1} =(𝔹​𝕋)m⋅𝕋−m​𝔹​𝕋−1​𝔹−1​𝕋m+1⋅(𝔹​𝕋)\displaystyle=\left(\mathbb{BT}\right)^{m}\cdot\mathbb{T}^{-m}\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}^{m+1}\cdot\left(\mathbb{BT}\right)
=(𝔹​𝕋)m⋅(𝕋−m​𝔹​𝕋m)⋅(𝕋−(m+1)​𝔹−1​𝕋m+1)⋅𝔹⋅𝕋\displaystyle=\left(\mathbb{BT}\right)^{m}\cdot\left(\mathbb{T}^{-m}\mathbb{B}\mathbb{T}^{m}\right)\cdot\left(\mathbb{T}^{-(m+1)}\mathbb{B}^{-1}\mathbb{T}^{m+1}\right)\cdot\mathbb{B}\cdot\mathbb{T}
=(𝔹​𝕋)m⋅𝔹⋅(𝕋−m​𝔹​𝕋m)⋅(𝕋−(m+1)​𝔹−1​𝕋m+1)⋅𝕋\displaystyle=\left(\mathbb{BT}\right)^{m}\cdot\mathbb{B}\cdot\left(\mathbb{T}^{-m}\mathbb{B}\mathbb{T}^{m}\right)\cdot\left(\mathbb{T}^{-(m+1)}\mathbb{B}^{-1}\mathbb{T}^{m+1}\right)\cdot\mathbb{T}
=(𝔹​𝕋)m⋅𝔹​𝕋⋅(𝕋−(m+1)​𝔹​𝕋m+1)⋅(𝕋−(m+2)​𝔹−1​𝕋m+2)\displaystyle=\left(\mathbb{BT}\right)^{m}\cdot\mathbb{BT}\cdot\left(\mathbb{T}^{-(m+1)}\mathbb{B}\mathbb{T}^{m+1}\right)\cdot\left(\mathbb{T}^{-(m+2)}\mathbb{B}^{-1}\mathbb{T}^{m+2}\right)
=(𝔹​𝕋)m+1⋅𝕋−(m+1)​𝔹​𝕋−1​𝔹−1​𝕋m+2\displaystyle=\left(\mathbb{BT}\right)^{m+1}\cdot\mathbb{T}^{-(m+1)}\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}^{m+2}

This finishes the induction. □\Box

Using the claim above, we represent 1=[b,tn​b​t−n]1=[b,t^{n}bt^{-n}] in terms of {𝔹,𝕋}\{\mathbb{B},\mathbb{T}\} as follows:

1\displaystyle 1 =[b,tn​b​t−n]\displaystyle=[b,t^{n}bt^{-n}]
=[𝔸−1,(𝔹​𝕋)−n​𝔸−1​(𝔹​𝕋)n]\displaystyle=\left[\mathbb{A}^{-1},\left(\mathbb{BT}\right)^{-n}\mathbb{A}^{-1}\left(\mathbb{BT}\right)^{n}\right]
=[𝔹p​𝕋−1​𝔹−p​𝕋,(𝔹​𝕋)−n⋅𝔹p​𝕋−1​𝔹−p​𝕋⋅(𝔹​𝕋)n]\displaystyle=\left[\mathbb{B}^{p}\mathbb{T}^{-1}\mathbb{B}^{-p}\mathbb{T},\left(\mathbb{BT}\right)^{-n}\cdot\mathbb{B}^{p}\mathbb{T}^{-1}\mathbb{B}^{-p}\mathbb{T}\cdot\left(\mathbb{BT}\right)^{n}\right]
=[(𝔹​𝕋−1​𝔹−1​𝕋)p,(𝔹​𝕋)−n⋅(𝔹​𝕋−1​𝔹−1​𝕋)p⋅(𝔹​𝕋)n]\displaystyle=\left[\left(\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}\right)^{p},\left(\mathbb{BT}\right)^{-n}\cdot\left(\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}\right)^{p}\cdot\left(\mathbb{BT}\right)^{n}\right]
=[(𝔹​𝕋−1​𝔹−1​𝕋)p,(𝕋−n​𝔹​𝕋−1​𝔹−1​𝕋n+1)p]\displaystyle=\left[\left(\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}\right)^{p},\left(\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}^{n+1}\right)^{p}\right]

By the third of Lemma 2.1, we have 1∈⟨⟨[𝔹​𝕋−1​𝔹−1​𝕋,𝕋−n​𝔹​𝕋−1​𝔹−1​𝕋n+1]⟩⟩+1\in\left<\left<\left[\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T},\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}^{n+1}\right]\right>\right>^{+}. Since Gp,qG_{p,q} admits no generalized torsion elements, we have [𝔹​𝕋−1​𝔹−1​𝕋,𝕋−n​𝔹​𝕋−1​𝔹−1​𝕋n+1]=1\left[\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T},\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}^{n+1}\right]=1. We compute as follows:

1\displaystyle 1 =[𝔹​𝕋−1​𝔹−1​𝕋,𝕋−n​𝔹​𝕋−1​𝔹−1​𝕋n+1]\displaystyle=\left[\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T},\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}^{n+1}\right]
=𝕋−1​𝔹​𝕋​𝔹−1⋅𝕋−(n+1)​𝔹​𝕋​𝔹−1​𝕋n⋅𝔹​𝕋−1​𝔹−1​𝕋⋅𝕋−n​𝔹​𝕋−1​𝔹−1​𝕋n+1\displaystyle=\mathbb{T}^{-1}\mathbb{B}\mathbb{T}\mathbb{B}^{-1}\cdot\mathbb{T}^{-(n+1)}\mathbb{B}\mathbb{T}\mathbb{B}^{-1}\mathbb{T}^{n}\cdot\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}\cdot\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}^{n+1}
=(𝕋−1​𝔹​𝕋)⋅𝔹−1⋅(𝕋−(n+1)​𝔹​𝕋n+1)⋅(𝕋−n​𝔹−1​𝕋n)⋅𝔹⋅(𝕋−1​𝔹−1​𝕋)⋅(𝕋−n​𝔹​𝕋n)⋅(𝕋−(n+1)​𝔹−1​𝕋n+1)\displaystyle=\left(\mathbb{T}^{-1}\mathbb{B}\mathbb{T}\right)\cdot\mathbb{B}^{-1}\cdot\left(\mathbb{T}^{-(n+1)}\mathbb{B}\mathbb{T}^{n+1}\right)\cdot\left(\mathbb{T}^{-n}\mathbb{B}^{-1}\mathbb{T}^{n}\right)\cdot\mathbb{B}\cdot\left(\mathbb{T}^{-1}\mathbb{B}^{-1}\mathbb{T}\right)\cdot\left(\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{n}\right)\cdot\left(\mathbb{T}^{-(n+1)}\mathbb{B}^{-1}\mathbb{T}^{n+1}\right)
=𝔹−1⋅(𝕋−(n+1)​𝔹​𝕋n+1)⋅𝔹⋅(𝕋−(n+1)​𝔹−1​𝕋n+1)\displaystyle=\mathbb{B}^{-1}\cdot\left(\mathbb{T}^{-(n+1)}\mathbb{B}\mathbb{T}^{n+1}\right)\cdot\mathbb{B}\cdot\left(\mathbb{T}^{-(n+1)}\mathbb{B}^{-1}\mathbb{T}^{n+1}\right)
=[𝔹,𝕋−(n+1)​𝔹−1​𝕋n+1]\displaystyle=\left[\mathbb{B},\mathbb{T}^{-(n+1)}\mathbb{B}^{-1}\mathbb{T}^{n+1}\right]

In the above, we use the commutativity of 𝕋−1​𝔹​𝕋\mathbb{T}^{-1}\mathbb{BT} and 𝕋−(k+1)​𝔹​𝕋k+1\mathbb{T}^{-(k+1)}\mathbb{BT}^{k+1}, which is induced by that of 𝔹\mathbb{B} and 𝕋−k​𝔹​𝕋k\mathbb{T}^{-k}\mathbb{BT}^{k} for integer kk such that |k|≤n|k|\leq n. The above computation implies [𝔹,𝕋−(n+1)​𝔹​𝕋n+1]=1\left[\mathbb{B},\mathbb{T}^{-(n+1)}\mathbb{B}\mathbb{T}^{n+1}\right]=1, and this finishes the induction. □\Box

By Proposition 7.1, we have [t−m​b​tm,t−n​b​tn]=t−m​[b,t−(n−m)​b​tn−m]​tm=1[t^{-m}bt^{m},t^{-n}bt^{n}]=t^{-m}[b,t^{-(n-m)}bt^{n-m}]t^{m}=1 for all integers mm and nn. Moreover, [t−m​a​tm,t−n​b​tn]=1[t^{-m}at^{m},t^{-n}bt^{n}]=1 and [t−m​a​tm,t−n​a​tn]=1[t^{-m}at^{m},t^{-n}at^{n}]=1 hold for all integers mm and nn since a=t−1​bq​t​b−q=(t−1​b​t)q⋅b−qa=t^{-1}b^{q}tb^{-q}=(t^{-1}bt)^{q}\cdot b^{-q}. We give a lemma which will be used later:

Lemma 7.1.

Under the assumption of admitting no generalized torsion elements and the positivity of pp and qq, we have (t​bp​q​t−1)⋅b−(2​p​q+1)⋅(t−1​bp​q​t)=1\left(tb^{pq}t^{-1}\right)\cdot b^{-(2pq+1)}\cdot\left(t^{-1}b^{pq}t\right)=1 in Gp,qG_{p,q}.

Proof.

Under the assumption, we can use the commutativity in Proposition 7.1. Using the presentation (17) of Gp,qG_{p,q}, we have:

  • •

    t​bp​q​t−1=(t​bp​q​ap​t−1)⋅(t​a−p​t−1)=(t​b−q​a−1​t−1)−p⋅(t​ap​t−1)−1=(b−q)−p⋅(b−1​ap)−1=a−p​bp​q+1tb^{pq}t^{-1}=\left(tb^{pq}a^{p}t^{-1}\right)\cdot\left(ta^{-p}t^{-1}\right)=\left(tb^{-q}a^{-1}t^{-1}\right)^{-p}\cdot\left(ta^{p}t^{-1}\right)^{-1}=\left(b^{-q}\right)^{-p}\cdot(b^{-1}a^{p})^{-1}=a^{-p}b^{pq+1},

  • •

    t−1​bp​q​t=(t−1​b−q​t)−p=(b−q​a−1)−p=ap​bp​qt^{-1}b^{pq}t=\left(t^{-1}b^{-q}t\right)^{-p}=\left(b^{-q}a^{-1}\right)^{-p}=a^{p}b^{pq}.

Using the commutativity, we get the statement. □\Box

Injecting Gp,qG_{p,q} with the assumption into some group KK

We assume that pp and qq are positive, and Gp,qG_{p,q} admits no generalized torsion elements. We will construct some group KK and show that Gp,qG_{p,q} with our assumption injects into this KK, which will be shown to be bi-orderable later.

Consider a group HH with the following presentation.

H=⟨τ,xn​(n∈ℤ)∣[xi,xj]=1,xi+1p​q⋅xi−(2​p​q+1)⋅xi−1p​q=1,τ​xi​τ−1=xi+1​(i,j∈ℤ)⟩\displaystyle H=\left<\tau,\ x_{n}\ (n\in\mathbb{Z})\mid[x_{i},x_{j}]=1,\ x^{pq}_{i+1}\cdot x^{-(2pq+1)}_{i}\cdot x^{pq}_{i-1}=1,\ \tau x_{i}\tau^{-1}=x_{i+1}\ (i,j\in\mathbb{Z})\right> (21)
Lemma 7.2.

Under the assumption, Gp,qG_{p,q} is isomorphic to HH, where τ\tau and xnx_{n} in HH correspond to tt and tn​b​t−nt^{n}bt^{-n} in Gp,qG_{p,q}, respectively.

Proof.

Under the assumption, a map from HH to Gp,qG_{p,q} sending τ\tau and xnx_{n} to tt and tn​b​t−nt^{n}bt^{-n} sends every relation in (21) to the identity element in Gp,qG_{p,q} by Proposition 7.1 and Lemme 7.1, and this is a group homomorphism. For the other side, a map from Gp,qG_{p,q} to HH sending tt and bb to τ\tau and x0x_{0} sends every relation in (17) to the identity element in HH by noting that a=t−1​bq​t​b−qa=t^{-1}b^{q}tb^{-q}, the commutativity in Proposition 7.1 and the relation in Lemma 7.1 under the assumption, and this is also a group homomorphism. For the constructed two maps, one is the inverse of the other. Therefore Gp,qG_{p,q} and HH are isomorphic under the identification. □\Box

We identify HH with Gp,qG_{p,q}. Take the abelianization ρ:Gp,q⟶ℤ\rho:G_{p,q}\longrightarrow\mathbb{Z} such that ρ​(xn)=0\rho(x_{n})=0 for every n∈ℤn\in\mathbb{Z} and ρ​(τ)=1\rho(\tau)=1. Then we have the following:

Lemma 7.3.

Ker​(ρ){\rm Ker}(\rho) has the following presentation, where xnx_{n} is the same element of H=Gp,qH=G_{p,q} for every n∈ℤn\in\mathbb{Z}:

Ker​(ρ)=⟨xn​(n∈ℤ)∣[xi,xj]=1,xi+1p​q⋅xi−(2​p​q+1)⋅xi−1p​q=1​(i,j∈ℤ)⟩\displaystyle{\rm Ker}(\rho)=\left<x_{n}\ (n\in\mathbb{Z})\mid[x_{i},x_{j}]=1,\ x^{pq}_{i+1}\cdot x^{-(2pq+1)}_{i}\cdot x^{pq}_{i-1}=1\ (i,j\in\mathbb{Z})\right> (22)
Proof.

It is easy to see that Ker​(ρ){\rm Ker}(\rho) is generated by xnx_{n} (n∈ℤn\in\mathbb{Z}) in H=Gp,qH=G_{p,q}. Moreover, by using the relation of type τ​xi​τ−1=xi+1\tau x_{i}\tau^{-1}=x_{i+1}, we see that every conjugate of every relation in (21) in H=Gp,qH=G_{p,q} is equivalent to a conjugate of a relation (or its inverse) in (22). For example, τ​xk​[xi,xj]​xk−1​τ−1\tau x_{k}[x_{i},x_{j}]x^{-1}_{k}\tau^{-1} is equivalent to xk+1​[xi+1,xj+1]​xk+1−1x_{k+1}[x_{i+1},x_{j+1}]x^{-1}_{k+1}. This gives the presentation. □\Box

Remark 7.1.

The presentation (22) for Ker​(ρ){\rm Ker}(\rho) is also obtained by noting that H=Gp,qH=G_{p,q} has a structure of the HNN-extension of a group.

Definition 7.1.

Take a matrix A=(1−1q−1p1+1p​q)∈G​L2​(ℝ)A=\left(\begin{array}[]{cc}1&-\frac{1}{q}\\ -\frac{1}{p}&1+\frac{1}{pq}\\ \end{array}\right)\in GL_{2}(\mathbb{R}).
Define K=ℝ2⋊ℤK=\mathbb{R}^{2}\rtimes\mathbb{Z} as a group whose product is defined by

((s1l1),n1)∙((s2l2),n2)=((s1l1)+An1​(s2l2),n1+n2)\displaystyle\left(\begin{pmatrix}s_{1}\\ l_{1}\end{pmatrix},n_{1}\right)\bullet\left(\begin{pmatrix}s_{2}\\ l_{2}\end{pmatrix},n_{2}\right)=\left(\begin{pmatrix}s_{1}\\ l_{1}\end{pmatrix}+A^{n_{1}}\begin{pmatrix}s_{2}\\ l_{2}\end{pmatrix},n_{1}+n_{2}\right)

We will show that Gp,qG_{p,q} under the assumption is a subgroup of KK after some preparations. For every generator xnx_{n} in Ker​(ρ){\rm Ker}(\rho) with a presentation (22), we assign An​(01)∈ℝ2A^{n}\begin{pmatrix}0\\ 1\end{pmatrix}\in\mathbb{R}^{2}, which is denoted by r​(xn)r(x_{n}). Extend this map to a homomorphism r:Ker​(ρ)⟶ℝ2r:{\rm Ker}(\rho)\longrightarrow\mathbb{R}^{2}. An element w=∏k=ij(xnk)mk∈Ker​(ρ)w=\prod\limits_{k=i}^{j}\left(x_{n_{k}}\right)^{m_{k}}\in{\rm Ker}(\rho) for some integers i≤ji\leq j, nkn_{k}’s and mkm_{k}’s is sent to r​(w)=∑k=ij(mk​Ank​(01))∈ℝ2r(w)=\sum\limits_{k=i}^{j}\left(m_{k}A^{n_{k}}\begin{pmatrix}0\\ 1\end{pmatrix}\right)\in\mathbb{R}^{2}. Note that the order of the products in ww is not important since [xi,xj]=1[x_{i},x_{j}]=1 holds. Note also that r​(⋅)r(\cdot) is well-defined since r​(xi+1p​q⋅xi−(2​p​q+1)⋅xi−1p​q)=(p​q​Ai+1−(2​p​q+1)​Ai+p​q​Ai−1)​(01)=p​q​(A2−(2+1p​q)​A+I2)​Ai−1​(01)=(00)r\left(x^{pq}_{i+1}\cdot x^{-(2pq+1)}_{i}\cdot x^{pq}_{i-1}\right)=\left(pqA^{i+1}-(2pq+1)A^{i}+pqA^{i-1}\right)\begin{pmatrix}0\\ 1\end{pmatrix}=pq\left(A^{2}-(2+\frac{1}{pq})A+I_{2}\right)A^{i-1}\begin{pmatrix}0\\ 1\end{pmatrix}=\begin{pmatrix}0\\ 0\end{pmatrix} by the Cayley-Hamilton’s theorem.

Definition 7.2.

Let ϕ:Gp,q⟶K\phi:G_{p,q}\longrightarrow K be a map defined by ϕ​(g)=(r​(g⋅τ−ρ​(g)),ρ​(g))\phi(g)=\left(r\left(g\cdot\tau^{-\rho(g)}\right),\rho(g)\right) for g∈H=Gp,qg\in H=G_{p,q}. Note that this ϕ\phi is a homomorphism.

Proposition 7.2.

A map ϕ\phi defined above is injective.

Proof.

It is enough to show that r:Ker​(ρ)⟶Kr:{\rm Ker}(\rho)\longrightarrow K is injective. Suppose that r​(∏k=ij(xnk)mk)=∑k=ij(mk​Ank​(01))=(00)r\left(\prod\limits_{k=i}^{j}\left(x_{n_{k}}\right)^{m_{k}}\right)=\sum\limits_{k=i}^{j}\left(m_{k}A^{n_{k}}\begin{pmatrix}0\\ 1\end{pmatrix}\right)=\begin{pmatrix}0\\ 0\end{pmatrix} holds. Take eigenvectors V+=12​4​p​q+1​(−2​p1+4​p​q+1)V_{+}=\frac{1}{2\sqrt{4pq+1}}\begin{pmatrix}-2p\\ 1+\sqrt{4pq+1}\end{pmatrix} and V−=12​4​p​q+1​(−2​p1−4​p​q+1)V_{-}=\frac{1}{2\sqrt{4pq+1}}\begin{pmatrix}-2p\\ 1-\sqrt{4pq+1}\end{pmatrix} for eigenvalues λ+=(2​p​q+1)​4​p​q+12​p​q\lambda_{+}=\frac{(2pq+1)\sqrt{4pq+1}}{2pq} and λ−=(2​p​q+1)−4​p​q+12​p​q\lambda_{-}=\frac{(2pq+1)-\sqrt{4pq+1}}{2pq}, respectively for AA. Note that V+V_{+} and V−V_{-} are linearly independent, and (01)=V+−V−\begin{pmatrix}0\\ 1\end{pmatrix}=V_{+}-V_{-}. Then:

(00)\displaystyle\begin{pmatrix}0\\ 0\end{pmatrix} =∑k=ij(mk​Ank​(01))\displaystyle=\sum\limits_{k=i}^{j}\left(m_{k}A^{n_{k}}\begin{pmatrix}0\\ 1\end{pmatrix}\right)
=∑k=ij(mk​Ank​(V+−V−))\displaystyle=\sum\limits_{k=i}^{j}\left(m_{k}A^{n_{k}}\left(V_{+}-V_{-}\right)\right)
=∑k=ij(mk​(λ+nk​V+−λ−nk​V−))\displaystyle=\sum\limits_{k=i}^{j}\left(m_{k}\left(\lambda^{n_{k}}_{+}V_{+}-\lambda^{n_{k}}_{-}V_{-}\right)\right)
=(∑k=ijmk​λ+nk)​V+−(∑k=ijmk​λ−nk)​V−\displaystyle=\left(\sum\limits_{k=i}^{j}m_{k}\lambda^{n_{k}}_{+}\right)V_{+}-\left(\sum\limits_{k=i}^{j}m_{k}\lambda^{n_{k}}_{-}\right)V_{-}

This implies that a Laurent polynomial f​(x)=∑k=ijmk​xnkf(x)=\sum\limits_{k=i}^{j}m_{k}x^{n_{k}} with integer coefficients has roots λ+\lambda_{+} and λ−\lambda_{-}. Thus there exist a non-zero integer NN and a Laurent polynomial g​(x)g(x) with integer coefficients such that f​(x)=1N​(p​q​x2−(2​p​q+1)+p​q​x−1)​g​(x)f(x)=\frac{1}{N}\left(pqx^{2}-(2pq+1)+pqx^{-1}\right)g(x) holds. This implies that we can represent f​(x)f(x) as f​(x)=∑k=ijmk​xnk=1N​∑k=i′j′Mk​(p​q​xNk+1−(2​p​q+1)​xNk+p​q​xNk−1)f(x)=\sum\limits_{k=i}^{j}m_{k}x^{n_{k}}=\frac{1}{N}\sum\limits_{k=i^{\prime}}^{j^{\prime}}M_{k}\left(pqx^{N_{k}+1}-(2pq+1)x^{N_{k}}+pqx^{N_{k}-1}\right) for some integers i′≤j′i^{\prime}\leq j^{\prime}, NkN_{k}’s and MkM_{k}’s. Then we can represent (∏k=ij(xnk)mk)N\left(\prod\limits_{k=i}^{j}\left(x_{n_{k}}\right)^{m_{k}}\right)^{N} as:

(∏k=ij(xnk)mk)N\displaystyle\left(\prod\limits_{k=i}^{j}\left(x_{n_{k}}\right)^{m_{k}}\right)^{N} =∏k=i′j′((xNk+1)p​q⋅(xNk)−(2​p​q+1)⋅(xNk−1)p​q)Mk=1\displaystyle=\prod\limits_{k=i^{\prime}}^{j^{\prime}}\left(\left(x_{N_{k}+1}\right)^{pq}\cdot\left(x_{N_{k}}\right)^{-(2pq+1)}\cdot\left(x_{N_{k}-1}\right)^{pq}\right)^{M_{k}}=1

Thus ∏k=ij(xnk)mk\prod\limits_{k=i}^{j}\left(x_{n_{k}}\right)^{m_{k}} is a torsion element or the identity element in Ker​(ρ)◁H=Gp,q{\rm Ker}(\rho)\triangleleft H=G_{p,q}. In our assumption, there are no torsion elements in Gp,qG_{p,q}. Hence ∏k=ij(xnk)mk=1\prod\limits_{k=i}^{j}\left(x_{n_{k}}\right)^{m_{k}}=1, and r​(⋅)r(\cdot) is injective.

□\Box

A bi-order on KK

We construct a bi-order on KK by imitating the construction in [21]. Since Gp,qG_{p,q} with our assumption injects into KK by Proposition 7.2, this bi-order makes Gp,qG_{p,q} with our assumption bi-orderable.

Take eigenvectors V±V_{\pm} and eigenvalues λ±\lambda_{\pm} of AA defined in the proof of Proposition 7.2. Note that λ±\lambda_{\pm} are real and positive. Since V+V_{+} and V−V_{-} are linearly independent, every element of ℝ2\mathbb{R}^{2} is uniquely represented as a linear combination of V+V_{+} and V−V_{-}.

Definition 7.3.

Define an order << on K=ℝ2⋊ℤK=\mathbb{R}^{2}\rtimes\mathbb{Z} as follows, where a,b,ca,b,c and dd are real numbers:
(a​V++b​V−,n)<(c​V++d​V−,m)\left(aV_{+}+bV_{-},n\right)\ <\ \left(cV_{+}+dV_{-},m\right) if

  • •

    n<mn<m as integers,

  • •

    n=mn=m and a<ca<c as real numbers, or

  • •

    n=mn=m, a=ca=c and b<db<d as real numbers.

It is easy to check that the order << on KK defined above is invariant under the multiplying elements from left and right i.e << is bi-order. This finishes a proof of Theorem 1.3.

Remark 7.2.

As we see in the proof of Theorem 1.3 in this section, if Gp,qG_{p,q} with positive integers pp and qq are not bi-orderable, then there is a torsion element in Gp,qG_{p,q} (as in the proof of Proposition 7.2) or there is a generalized torsion element [b,t−n​b​tn][b,t^{-n}bt^{n}] in (17) or [𝔹,𝕋−n​𝔹​𝕋n][\mathbb{B},\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{n}] in (20) for some integer nn (as in the proof of Proposition 7.1). Moreover, if [b,t−n​b​tn][b,t^{-n}bt^{n}] in (17) or [𝔹,𝕋−n​𝔹​𝕋n][\mathbb{B},\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{n}] in (20) is a non-trivial element for some integer nn, then there exists an integer mm such that |m|≤|n||m|\leq|n| and [b,t−m​b​tm][b,t^{-m}bt^{m}] in (17) or [𝔹,𝕋−m​𝔹​𝕋m][\mathbb{B},\mathbb{T}^{-m}\mathbb{B}\mathbb{T}^{m}] in (20) is a generalized torsion element (as in the proof of Proposition 7.1).

8 Some computations

Unfortunately, we cannot know whether [x​y,y​x][xy,yx] is a generalized torsion element in Gp,qG_{p,q} under the presentation (7) for each (p,q)(p,q) by Theorem 1.1 only. In this section, we try to construct a homomorphism from Gp,qG_{p,q} to some symmetric group Sn+1S_{n+1} which maps [x​y,y​x][xy,yx] to a non-trivial element by using a computer. Note that the element [x​y,y​x][xy,yx] in the presentation (7) corresponds to [b,t−1​b​t][b,t^{-1}bt] in the presentation (2). As stated at Remark 7.2, if one of [b,t−n​b​tn][b,t^{-n}bt^{n}] in the presentation (17) or [𝔹,𝕋−n​𝔹​𝕋n][\mathbb{B},\mathbb{T}^{-n}\mathbb{B}\mathbb{T}^{n}] in the presentation (20) for some integer nn is a non-trivial element of Gp,qG_{p,q} for p​q>0pq>0, we can conclude that Gp,qG_{p,q} admits a generalized torsion element. Since Gp,qG_{p,q} is a 3-manifold group i.e. the fundamental group of a compact 3-manifold, it is residually finite ([8], for example). Thus the non-triviality of every non-trivial element of Gp,qG_{p,q} is detected by some homomorphism into some symmetric group. This detection is proposed to the author by Professor Nozaki. We list homomorphisms from Gp,qG_{p,q}’s to some symmetric groups which map [x​y,y​x][xy,yx]’s to non-trivial elements in Table 1. Note that when (p,q)=(1,1)(p,q)=(1,1) or (1,−1)(1,-1), the element [x​y,y​x][xy,yx] is always the identity element in the presentation (7). It is known that G1,1G_{1,1} admits no generalized torsion elements and that G1,−1G_{1,-1} admits a generalized torsion element. We impose on these homomorphisms the condition that xx is mapped to [1,2,…,n,0]∈Sn+1[1,2,\dots,n,0]\in S_{n+1} and nn is less than ten. This imposition is only due to the limitations of the author’s computer and his skill of programming. It may be true that except for (p,q)=±(1,1)(p,q)=\pm(1,1), the group Gp,q=π1​(Kp,q​(0))G_{p,q}=\pi_{1}\left(K_{p,q}(0)\right) admits a generalized torsion element.

Notation for symmetric groups

The symmetric group Sn+1S_{n+1} is a group consisting of bijections on a set {0,1,…,n}\{0,1,\dots,n\} for a non-negative integer nn. By [a0,…,an][a_{0},\dots,a_{n}], we represent a element of Sn+1S_{n+1} which maps ii to aia_{i}. For two elements aa and bb of Sn+1S_{n+1}, their product a​bab is a bijection obtained by composing aa and bb. In this paper, bb is carried out at first and aa is carried out at next in a​bab. For example, [2,0,1]⋅[1,0,2]=[0,2,1][2,0,1]\cdot[1,0,2]=[0,2,1].

Table 1: A homomorphisms from π1​(Kp,q​(0))\pi_{1}\left(K_{p,q}(0)\right) to some symmetric group which sends [x​y,y​x][xy,yx] to a non-trivial element
(p,q)(p,q) the symmetric group Sn+1S_{n+1} the image of xx the image of yy
(2,1)(2,1) S8S_{8} [1,2,3,4,5,6,7,0][1,2,3,4,5,6,7,0] [5,2,4,0,6,1,7,3][5,2,4,0,6,1,7,3]
(3,1)(3,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [3,0,5,2,6,4,1][3,0,5,2,6,4,1]
(4,1)(4,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [2,0,5,4,1,6,3][2,0,5,4,1,6,3]
(2,2)(2,2) S6S_{6} [1,2,3,4,5,0][1,2,3,4,5,0] [1,3,0,4,5,2][1,3,0,4,5,2]
(5,1)(5,1) ? ? ?
(6,1)(6,1) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [6,4,1,7,3,0,8,9,2,5][6,4,1,7,3,0,8,9,2,5]
(3,2)(3,2) S8S_{8} [1,2,3,4,5,6,7,0][1,2,3,4,5,6,7,0] [3,5,0,1,6,7,2,4][3,5,0,1,6,7,2,4]
(7,1)(7,1) ? ? ?
(8,1)(8,1) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [3,0,8,2,6,4,1,9,7,5][3,0,8,2,6,4,1,9,7,5]
(4,2)(4,2) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [4,2,6,0,1,7,8,3,9,5][4,2,6,0,1,7,8,3,9,5]
(9,1)(9,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [3,0,5,2,6,4,1][3,0,5,2,6,4,1]
(3,3)(3,3) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [1,2,4,0,5,6,3][1,2,4,0,5,6,3]
(10,1)(10,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [2,0,5,4,1,6,3][2,0,5,4,1,6,3]
(5,2)(5,2) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [1,3,4,5,0,6,2][1,3,4,5,0,6,2]
(11,1)(11,1) ? ? ?
(12,1)(12,1) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [5,4,3,0,7,8,1,2,9,6][5,4,3,0,7,8,1,2,9,6]
(6,2)(6,2) S6S_{6} [1,2,3,4,5,0][1,2,3,4,5,0] [1,3,0,4,5,2][1,3,0,4,5,2]
(4,3)(4,3) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [3,0,5,6,1,4,7,8,9,2][3,0,5,6,1,4,7,8,9,2]
(13,1)(13,1) ? ? ?
(14,1)(14,1) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [3,0,8,2,6,4,1,9,7,5][3,0,8,2,6,4,1,9,7,5]
(7,2)(7,2) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [3,8,6,5,1,4,0,9,7,2][3,8,6,5,1,4,0,9,7,2]
(15,1)(15,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [3,0,5,2,6,4,1][3,0,5,2,6,4,1]
(5,3)(5,3) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [3,4,5,1,6,0,2][3,4,5,1,6,0,2]
(16,1)(16,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [2,0,5,4,1,6,3][2,0,5,4,1,6,3]
(8,2)(8,2) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [1,3,4,5,0,6,2][1,3,4,5,0,6,2]
(4,4)(4,4) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [1,3,4,5,0,6,2][1,3,4,5,0,6,2]
(17,1)(17,1) ? ? ?
(18,1)(18,1) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [6,4,1,7,3,0,8,9,2,5][6,4,1,7,3,0,8,9,2,5]
(9,2)(9,2) S8S_{8} [1,2,3,4,5,6,7,0][1,2,3,4,5,6,7,0] [3,5,0,1,6,7,2,4][3,5,0,1,6,7,2,4]
(6,3)(6,3) S8S_{8} [1,2,3,4,5,6,7,0][1,2,3,4,5,6,7,0] [5,2,4,0,6,1,7,3][5,2,4,0,6,1,7,3]
(19,1)(19,1) ? ? ?
(20,1)(20,1) S10S_{10} [1,2,3,4,5,6,7,8,9,0][1,2,3,4,5,6,7,8,9,0] [3,0,8,2,6,4,1,9,7,5][3,0,8,2,6,4,1,9,7,5]
(10,2)(10,2) S6S_{6} [1,2,3,4,5,0][1,2,3,4,5,0] [1,3,0,4,5,2][1,3,0,4,5,2]
(21,1)(21,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [3,0,5,2,6,4,1][3,0,5,2,6,4,1]
(7,3)(7,3) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [3,4,5,1,6,0,2][3,4,5,1,6,0,2]
(22,1)(22,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [2,0,5,4,1,6,3][2,0,5,4,1,6,3]
(11,2)(11,2) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [1,3,4,5,0,6,2][1,3,4,5,0,6,2]
(23,1)(23,1) ? ? ?
(24,1)(24,1) ? ? ?
(12,2)(12,2) ? ? ?
(8,3)(8,3) ? ? ?
(6,4)(6,4) ? ? ?
(25,1)(25,1) S8S_{8} [1,2,3,4,5,6,7,0][1,2,3,4,5,6,7,0] [2,0,6,5,3,1,7,4][2,0,6,5,3,1,7,4]
(5,5)(5,5) S8S_{8} [1,2,3,4,5,6,7,0][1,2,3,4,5,6,7,0] [2,3,4,5,6,0,7,1][2,3,4,5,6,0,7,1]
(26,1)(26,1) S8S_{8} [1,2,3,4,5,6,7,0][1,2,3,4,5,6,7,0] [5,2,4,0,6,1,7,3][5,2,4,0,6,1,7,3]
(13,2)(13,2) S8S_{8} [1,2,3,4,5,6,7,0][1,2,3,4,5,6,7,0] [3,5,0,1,6,7,2,4][3,5,0,1,6,7,2,4]
(27,1)(27,1) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [3,0,5,2,6,4,1][3,0,5,2,6,4,1]
(9,3)(9,3) S7S_{7} [1,2,3,4,5,6,0][1,2,3,4,5,6,0] [1,2,4,0,5,6,3][1,2,4,0,5,6,3]

References

  • [1] A. Akhmedov and J. Thorne. Non-biorderable one-relator groups without generalized torsion. arXiv:2303.07499, 2023. 3
  • [2] J. A. Baldwin and S. Sivek. Characterizing slopes for 525_{2}. arXiv:2209.09805, 2022. 1,2,3,8
  • [3] J. A. Baldwin and S. Sivek. Zero-surger characterizes infinitely many knots. arXiv:2211.04280, 2022. 8
  • [4] W. R. Brakes. Manifolds with multiple knot-surgery descriptions. Math. Proc. Cambridge Philos. Soc., 87(3):443–448, 1980. 1
  • [5] A. Clay, C. Desmarais and P. Naylor. Testing bi-orderability of knot groups, Canad. Math. Bull. 59 (2016), no. 3, 472–482.
  • [6] A. Clay and D. Rolfsen. Ordered groups, eigenvalues, knots, surgery and L-spaces. Math. Proc. Cambridge Philos. Soc., 152(1):115–129, 2012.
  • [7] D. Gabai. Foliations and genera of links. Topology, Vol. 23, Issue 4, 1984, pp 381–394.
  • [8] J. Hempel. Residual finiteness for 3-manifolds. Combinatorial group theory and topology (Alta, Utah, 1984), pp. 379–396, Ann. of Math. Stud., 111, Princeton Univ. Press, Princeton, NJ, 1987.
  • [9] K. Ichihara and In Dae Jong. Totoidal Seifert fibered surgeries on Montesinos knots. Comm. Anal. Geom., 18(3):579–600, 2010. 5
  • [10] T. Ito, K. Motegi and M. Teragaito, Generalized torsion and Dehn filling. Topology and its Applications. Vol.301, 1 September 2021, 107515
  • [11] T. Ito, K. Motegi, and M. Teragaito, Generalized torsion and decomposition of 3-manifolds, Proc. Amer. Math. Soc. 147 (2019) 4999–5008.
  • [12] W. Jaco and P. Shalen, Seifert fibered spaces in 3-manifolds, Memorirs A. M. S. 21 (1979)
  • [13] W. Jaco. Lectures on Three Manifold Topology, Conference board of Math. No. 43, 1980
  • [14] K. Johannson, Homotopy equivalence of 3-manifolds with boundary, Lecture notes in Mathematics 761, Springer-Verlag, 1979
  • [15] C. Manolescu and L. Piccirillo. From zero surgeries to candidates for exotic definite four-manifolds. arXiv:2102.04391, 2021. 2
  • [16] K. Motegi and M. Teragaito. Generalized torsion elements and bi-orderability of 3-manifold groups. Canada. Math. Bull. 60 (2017), no. 4, 830–844.
  • [17] K. Motegi and M. Teragaito, Generalized torsion for knots with arbitrarily high genus. Canadian Mathematical Bulletin, 65(4) 867–881, Dec 13, 2022
  • [18] R. B. Mura and A. Rhemtulla. Orderable groups, Lecture Notes in Pure and Applied Mathematics, Vol. 27. Marcel Dekker, Inc., New York-Basel, 1997.
  • [19] N. Sekino. Generalized torsions in once punctured torus bundles. arXiv:2110.13411.
  • [20] J. K. Osoinach, Jr. Manifolds obtained by surgery on an infinite number of knots in S3S^{3}. Topology, 45(4):725–733, 2006. 1
  • [21] B. Perron and D. Rolfsen. On orderability of fibered knot groups. Math. Proc. Cambridge Philos. Soc., 135(1):147–153, 2003.
  • [22] M. Teragaito, Generalized torsion elements in the knot groups of twist knots, Proc. Amer. Math. Soc. 144 (2016), no.6, 2677–2682.
  • [23] M. Teragaito, Generalized torsion elements and hyperbolic links, J. Knot Theory Ramifications 29 (2020), no.11, 2050079 (9 pages).
  • [24] K. Yasui. Corks, exotic 4-manifolds and knot concordance. arXiv:1505.02551, 2015. 2
  • [25] F. Waldhausen. On irreducible 3-manifolds which are sufficiently large. Ann. of Math. vol.87 (1968), 56–88