Generation of spectrally factorable photon pairs via multi-order quasi-phase-matched spontaneous parametric downconversion
Abstract
For advanced quantum information technology, sources of photon pairs in quantum mechanically factorable states are of great importance for realizing high-fidelity photon-photon quantum gate operations. Here we experimentally demonstrate a technique to produce spectrally factorable photon pairs utilizing multi-order quasi-phase-matching (QPM) conditions in spontaneous parametric downconversion (SPDC). In our scheme, a spatial nonlinearity profile of a nonlinear optical crystal is shaped with current standard poling techniques, and the associated phase-matching function can be approximated to a Gaussian form. By the measurement of a phase-matching function and the second-order autocorrelation function, we demonstrate that telecom-band photon pairs produced by our custom-poled crystal are highly factorable with % single-photon purity.
I Introduction
Quantum photonics technology plays an important role in various quantum applications such as quantum computing O’Brien et al. (2009); Zhong et al. (2020), quantum communication Gisin et al. (2 03); Liao et al. (2017), quantum metrology Giovannetti et al. (2011), and bridging solid and atomic quantum systems at a distance Awschalom et al. (2021). One of the central requirements in the quantum photonics technology is to produce pure single photons. Most multi-photon applications rely on interference of independent single photons Hong et al. (1987), and only pure and indistinguishable photons can exhibit perfect interference. Photon-pair generation via spontaneous parametric downconversion (SPDC) has been widely accepted in quantum optics and photonic quantum information experiments Pan et al. (2012). Although a single SPDC source produces a photon pair only probabilistically, it is much easier to implement than single-emitter sources based on semiconductor Senellart et al. (2017) and atomic McKeever et al. (2004) systems that require cryogenic and/or ultra-high vacuum systems. Moreover, recently demonstrated multiplexing techniques Ma et al. (2011); Collins et al. (2013); Christensen et al. (2015); Joshi et al. (2018); Kaneda and Kwiat (2019) have overcome the probabilistic nature of SPDC, illustrating the possibility of the pseudo-on-demand generation of single photons.
For multi-photon quantum information applications, a joint state of an SPDC photon pair needs to be a spectrally factorable state, i.e., a product state of individual pure single photons. Such high-factorability sources can also be used as single-pass two-mode squeezed light sources, basic resources of a large-scale Gaussian boson sampler Zhong et al. (2020). A typical SPDC source has a certain amount of spectral correlation between a pair of photons, and thus does not generate spectrally factorable photon pairs. For spectral factorability of photon pairs, this type of source requires narrowband spectral filtering that is accompanied with the significant reduction of the source brightness and the probability of the coincident photon-pair collection and detection, i.e., the heralding efficiency.
In order to mitigate the spectral correlation of SPDC sources without spectral filtering, group-velocity-matching (GVM) condition Grice et al. (2001); Giovannetti et al. (2002); König and Wong (2004); Shimizu and Edamatsu (2009) of SPDC sources with appropriate broadband pump pulses have been demonstrated Mosley et al. (2008); Evans et al. (2010); Yabuno et al. (2012); Kaneda et al. (2016); Weston et al. (2016); Greganti et al. (2018). However, there remains residual spectral correlation in such a GVM-SPDC source due to the peripheral lobes of the sinc-shaped phase-matching function that is associated with a uniform longitudinal nonlinearity in a nonlinear optical crystal.
For tailoring a spectral shape of SPDC photons, quasi-phase matching (QPM) techniques via modulated periodic inversion of a nonlinear crystal have been demonstrated. While a standard QPM crystal with a single poling period is designed to satisfy one target QPM condition, such a modulated-poling crystal can achieve multiple QPMs in a single crystal, enabling to produce a variety of spectral shapes of photon pairs Nasr et al. (2008); Tanaka et al. (2012); Kaneda et al. (2019). For factorable photon-pair generation, several theoretical Brańczyk et al. (2011); Dixon et al. (2013); Dosseva et al. (2016) and experimental Chen et al. (2017); Graffitti et al. (2018); Pickston et al. (2021) works have demonstrated the usefulness of modulated periodic poling techniques to shape a phase-matching spectrum close to a Gaussian form, ideal for spectral factorability. However, most of the demonstrated schemes require high precision poling process and/or complicated numerical design. Since multi-photon quantum information applications require many indistinguishable single photons, an efficient and reproducible scheme with standard poling technology is desirable.
In this paper, we demonstrate the generation of spectrally factorable photon pairs with multi-order QPM conditions. A higher-order QPM condition is satisfied by a larger poling period of a nonlinear crystal, having a less effective nonlinearity. Therefore, a nonlinearity profile of a SPDC crystal can be engineered by utilizing large poling periods dependent on the position of the crystal without high-precision poling techniques. Multi-order QPM techniques for tailoring various forms of phase-matching functions has been proposed in Brańczyk et al. (2011). We show that our custom-poled crystal satisfying multi-order QPM and GVM conditions has an approximate Gaussian phase-matching function at the telecom C-band. This enables to generate high-factorability photon pairs incorporated with an optimal pump bandwidth. We characterize our CPKTP crystal using two different methods, i.e., the measurement of a phase-matching function and the second-order autocorrelation function, which consistently reveal high purity of produced single photons. We also discuss the possibility of further improvement to our SPDC source.
II Engineered phase-matching spectrum with multi-order QPM conditions
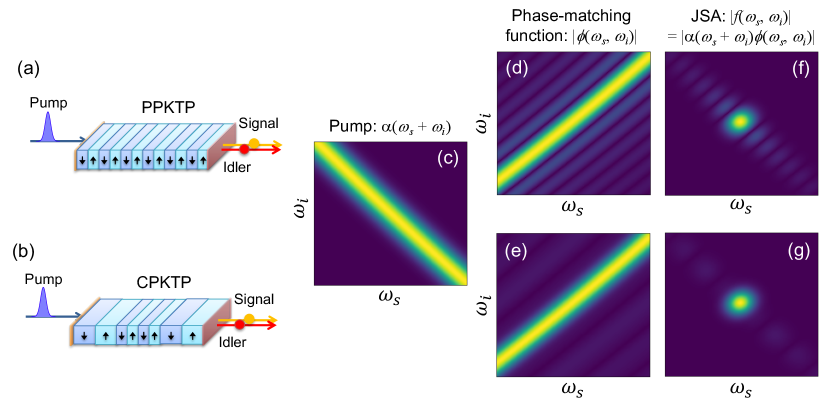
Conceptual diagrams of our scheme are depicted in Fig. 1. SPDC is a nonlinear optical process, where one high-frequency (pump) photon is split into two low-frequency (signal and idler) photons. With the plane-wave approximation, a SPDC two-photon joint spectral state is given by
| (1) |
Here, is the joint spectral amplitude (JSA), and denotes a photon-pair state with signal and idler frequencies and , respectively. For a collinear SPDC, the JSA is well approximated by
| (2) |
Here, is the pump envelope function. For a pump pulse with a Gaussian spectral distribution (that is a good approximation of a mode-locked laser pulse) can be described as
| (3) | ||||
| (4) |
where is the frequency detuning from the signal (idler) central frequency . The pump central frequency and bandwidth are respectively denoted by and . As shown in Eq. 3 and Fig. 1 (b,e), has a maximum value when energy-conservation condition is satisfied: .
The phase-matching function is given by
| (5) |
which is Fourier transform of a longitudinal nonlinearity profile . The phase mismatch represents the difference of the wavenumber of the pump (), signal (), and ilder () modes. Thus, the phase-matching function is essentially determined by the nonlinearity profile and the phase mismatch.
In order to generate a highly factorable JSA, the phase-matching function required to be a positively correlated () Gaussian function, since the pump envelope function has a negatively correlated () Gaussian form. A widely accepted method for producing a positively correlated phase-matching function is to utilize a Type-II QPM condition in a periodically-poled potassium titanyl phosphate (PPKTP) crystal Evans et al. (2010); Yabuno et al. (2012); Weston et al. (2016); Greganti et al. (2018), as shown in Fig. 1 (a). In this configuration, is well approximated by the first-order dispersion: , where is the inverse group velocity at the photon’s central frequency . In the case that the signal and idler photons are produced at a telecom band ( 1500-1600 nm), this SPDC process satisfies a GVM condition (), which result in with the positive spectral correlation , as shown in Fig. 1 (d). However, such a PPKTP crystal with a single poling period has a uniform nonlinearity profile, associated with a sinc-shaped phase-matching function. Therefore, due to peripheral lobes of the sinc distribution, the resulting JSA has a limited spectral factorability and a single-photon purity, as shown in Fig. 1 (f).
In our scheme, as shown in Fig. 1 (b), we use multiple orders of QPM conditions for shaping close to a Gaussian form. In general, a QPM condition is achieved by the periodic poling inversion of a nonlinear crystal that also periodically flips the sign of a nonlinearity. For the poling period and duty cycle of and , a nonlinearity profile can be written as the following Fourier components:
| (6) |
With this form, we see that a QPM conditions is satisfied for to produce SPDC photons. In other words, for a given phase mismatch, if a poling period satisfies a 1st-order QPM condition , its integer multiple also satisfies a -th order QPM: . Moreover, an amplitude of a Fourier component, i.e., effective nonlinearity, is decreased as absolute number of harmonic order (). Although inefficient higher-order QPM is not preferable in many classical optics applications, the -dependent nonlinearity can be utilized for shaping a nonlinearity profile.
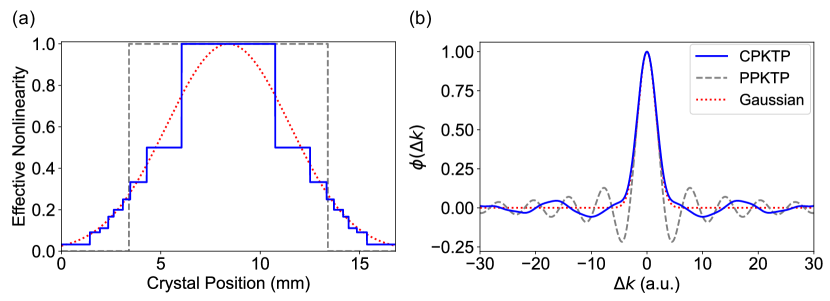
Figure 2 (a) shows a designed nonlinearity profile of our custom-poled KTP (CPKTP) crystal. We used eight different poling periods to achieve 1st- to 31st-order QPM conditions (m for the 1st-order QPM) for different regions of the crystal to approximate an effective nonlinearity profile to a Gaussian form with the full width at half maximum (FWHM) of 8 mm. An effective nonlinearity for each QPM condition is maximized by using the duty cycles and for odd- and even-order QPM conditions, respectively. (Note that one can use modulated poling duty cycles for engineering a nonlinearity profile, as demonstrated in Dixon et al. (2013); Chen et al. (2017). However, this approach also modulates central frequencies of SPDC photons and needs a high-precision poling technology.) A predicted phase-matching function of the CPKTP crystal is shown in Fig. 1 (e) and Fig. 2 (b). We see that our designed phase-matching function has smaller peripheral lobes than those of a 10-mm length PPKTP crystal that has the same phase-matching bandwidth at the main peak. As shown in Fig. 1 (g), this enables to generate a highly factorable JSA with a high single-photon purity (97.5%), comparable to the ones using more complicated, high spatial-resolution poling techniques Chen et al. (2017); Graffitti et al. (2018); Pickston et al. (2021). We also note that large spectral separation of the peripheral lobes and the main peak in our CPKTP crystal allows us to selectively eliminate the lobes by mild spectral filtering, as will be discussed later.
III Experiment
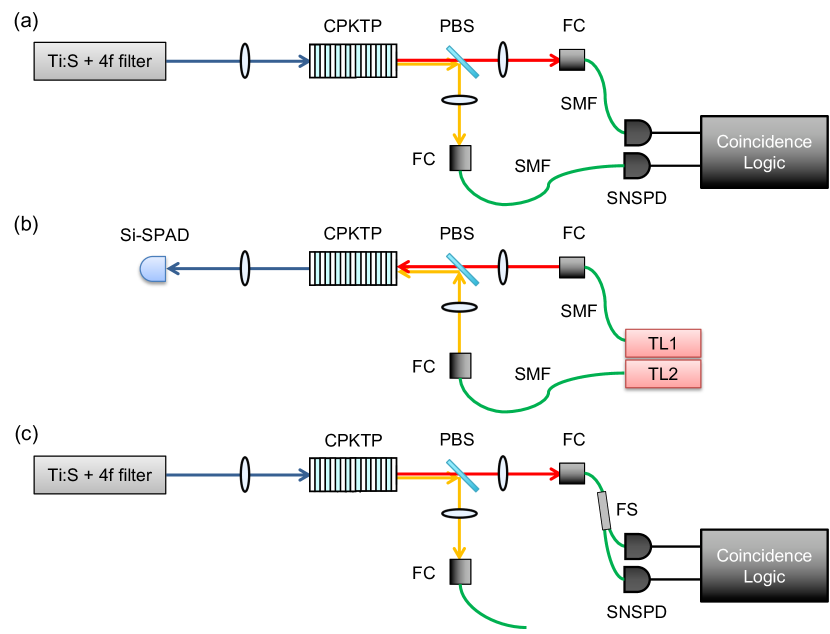
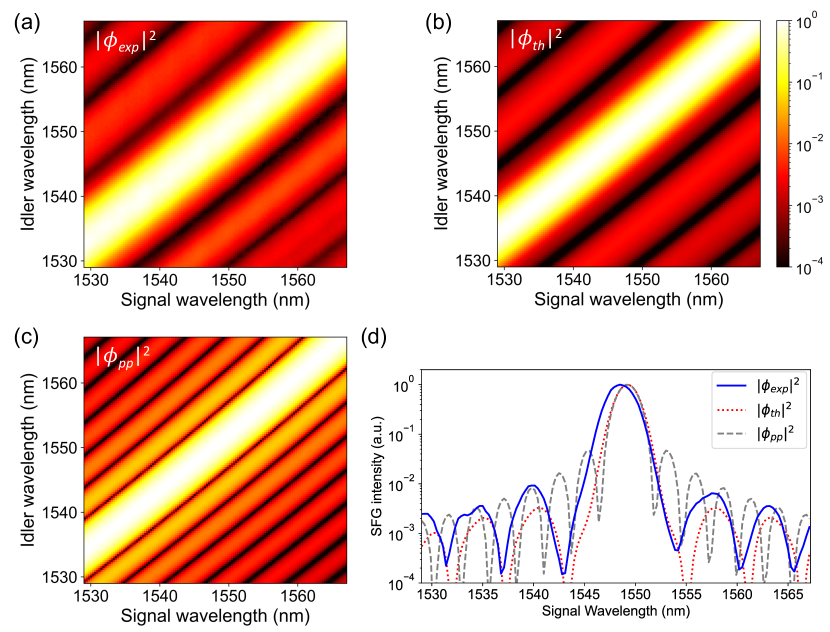
Figure 3 (a) shows the experimental setup for characterization of our SPDC source. Our CPKTP crystal designed as discussed above is fabricated by AdVR inc. We used Ti:S laser pulses (central wavelength nm, 4.6 nm FWHM) passed through a 4-f spectral filter as a bandwidth-tunable pump source (0.8-4.6 nm FWHM). Signal-idler photon pairs produced at 1550 nm are split by a polarizing beamsplitter (PBS) and then collected by independent single-mode optical fibers (SMF). For detecting SPDC photons we used superconducting nanowire single-photon detectors (SNSPDs) with % system detection efficiency Miki et al. (2017). With the pump power of 50 mW and the pump and photon-collection beam waist radii of 200 m and 180 m, we observed single and coincidence rates of cps and cps, respectively: note that the ratio of the single and coincidence rates, i.e., heralding efficiency (%) is lower than our theoretical prediction (%) Kaneda et al. (2016). We believe that this is in part due to rough surfaces of the crystal observed via optical microscope. Nonetheless, as will be demonstrated, the imperfect collection is not critical for the proof-of-concept demonstration of the spectral factorability that is essentially determined by the poling structure of our crystal and the time-frequency characteristics of the pump pulses.
In order to directly measure the phase-matching function of our CPKTP crystal, we performed frequency-resolved sum-frequency generation (SFG) measurement Kaneda et al. (2020), using a slightly modified setup as shown in Fig. 3 (b). A pair of tunable continuous-wave lasers (TL1 and TL2, the spectral linewidth of kHz, the center wavelength of 1530-1565 nm) coupled to the collection SMFs of the signal and idler modes are used to produce SFG photons. SFG photons are then detected by a Si single-photon avalanche diode (Si-SPAD). Since SFG is the reverse process of SPDC, a generation rate of SFG photons is proportional to the same phase-matching function . Thus, the phase-matching function of the CPKTP crystal can be revealed by the spectral distribution of SFG photons that can be measured by scanning the wavelengths of TL1 and TL2. For the measurement of the spectral factorability of photon pairs, we performed the second-order autocorrelation function measurement of the signal mode Christ et al. (2011) with a fiber-based Hanbury Brown-Twiss setup Brown and Twiss (1956), as shown in Fig. 3 (c).
IV Result and discussion
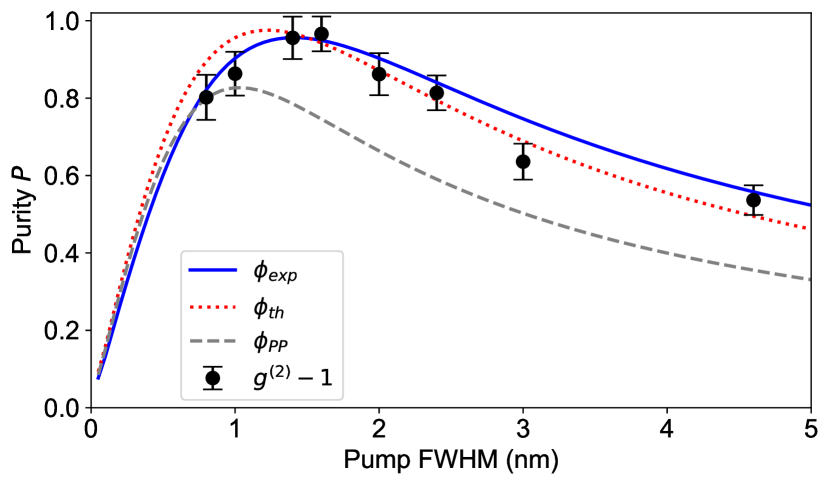
Figure 4 (a) is the observed phase-matching function for our CPKTP crystal (note that all the graphs in Fig. 4 show the phase-matching intensity distribution in log scale, while Fig. 1 and 2 shows the phase-matching amplitude distribution in linear scale). With the high-resolution (0.04 nm), high signal-to-noise ratio ( dB) SFG measurement, we confirm that is close to the predicted phase-matching function shown in Fig. 4 (b), where the Sellmeier equations König and Wong (2004) and our poling design (shown in Fig. 2) are taken into account. For comparison, in Fig. 4 (c), we also show the theoretical phase-matching function for a PPKTP crystal ( mm). Figure 4 (d) is cross sectional view of Figs. 5 (a)-(c), where the signal and idler wavelengths are anti-correlated: ( nm). We see that the ratio of the largest peripheral lobe and the main peak of our CPKTP crystal is 20 dB much larger than that for the PPKTP crystal (12 dB). Moreover, the phase-matching function of our CPKTP crystal has a larger spectral spacing between the main peak and lobes. As will be discussed, this allows us to use a mild spectral filtering to selectively eliminate the peripheral lobes. The slight difference in the center wavelengths of the observed and theoretical phase-matching functions may be caused by the difference of the actual indices of refraction of the CPKTP crystal and the Sellmeier equations. We also observed that has a wider bandwidth of the main peak and larger heights of the lobes compared to : this may be due to imperfect poling in some regions of the crystal.
We then estimated the single-photon spectral purity of our SPDC source. The spectral purity is estimated by Schmidt decomposition Eberly (2006) of a simulated JSA as a product of the phase-matching function observed by the frequency-resolved SFG measurement and a numerical Gaussian function in Eq. 3: . We assume that has no imaginary part and can be written as . Figure 5 shows the spectral purity versus the pump bandwidth (FWHM). Here we also show the purities of JSAs for the theoretical phase-matching functions and of the CPKTP and PPKTP crystals, respectively. The maximum purity for is % with the pump bandwidth of 1.4 nm, much higher than that for the PPKTP crystal (%). For the theoretical phase-matching function of the CPKTP crystal, the maximum purity is % with 1.2 nm pump bandwidth: The slight discrepancy for and is due to the larger peripheral lobes and the wider main peak of our experimental phase-matching function as observed in Fig. 4. The spectral purity was also characterized by the measurement of the second-order autocorrelation function for the signal mode Christ et al. (2011), shown as black circles in Fig. 5. We see that the purities obtained by the measurements () for several different pump bandwidths are in excellent agreement with our estimation based on the observed phase-matching function. Thus, the two different measurements consistently reveals the high-factorability photon pairs from our CPKTP crystal.
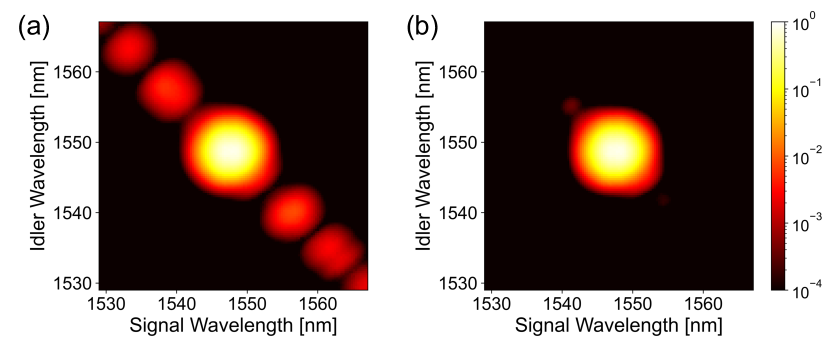
We note that the spectral factorability of our source can be further improved by mild spectral filtering. The predicted JSI with the optimal pump bandwidth (1.4 nm) is shown in Fig. 6 (a). The peripheral lobes are highly suppressed but still remain, resulting in the limited spectral purity. However, thanks to the large spectral spacing of the main peak and the peripheral lobes, one can selectively filter out the peripheral lobes with mild spectral filters. Figure 6 (b) shows the JSI with applied 13-nm band flat-top filters in the signal and idler modes. The spectral purity is enhanced to % with only 0.5% reduction in the spectral heralding efficiency. Thus, our multi-order QPM technique implemented with standard poling technique will be practically useful for producing high-purity, low-loss photon pairs, incorporated with efficient collection techniques of SPDC photons demonstrated in previous works Christensen et al. (2013); Kaneda et al. (2016); Pickston et al. (2021).
V Conclusion
We have demonstrated that the multi-order QPM technique is useful for producing spectrally factorable SPDC photon pairs. Our CPKTP crystal satisfying GVM and 1st- to 31st-order QPMs allow to produce photon pairs at the telecom C-band with the positively correlated, approximate Gaussian phase-matching function. Thanks to the highly suppressed peripheral lobes, we observed a high spectral purity (%) of individual SPDC photons via simulation of JSA with the measured phase-matching function and measurement of the second-order autocorrelation function. The obtained spectral purity can be further improved to % with a low (%) reduction of the spectral-mode heralding efficiency. We expect that our source incorporated with optimized photon collection optics and spectral filters will enable to produce low-loss, high-factorability photon pairs, an ideal resource for multi-photon quantum information applications.
Funding
JSPS KAKENHI Grant Number JP18H05949 and JP19H01815, MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) Grant Number JPMXS0118067581, Matsuo Academic Foundation, and Murata Academic Foundation.
Acknowledgments
We thank So-Young Baek for helpful discussions.
Disclosures
The authors declare no conflicts of interest.
References
- O’Brien et al. (2009) J. L. O’Brien, A. Furusawa, and J. Vučković, Nature Photonics 3, 687 (2009), 1003.3928 .
- Zhong et al. (2020) H.-S. Zhong, H. Wang, Y.-H. Deng, M.-C. Chen, L.-C. Peng, Y.-H. Luo, J. Qin, D. Wu, X. Ding, Y. Hu, P. Hu, X.-Y. Yang, W.-J. Zhang, H. Li, Y. Li, X. Jiang, L. Gan, G. Yang, L. You, Z. Wang, L. Li, N.-L. Liu, C.-Y. Lu, and J.-W. Pan, Science 370, 1460 (2020), 2012.01625 .
- Gisin et al. (2 03) N. Gisin, G. Ribordy, W. Tittel, and H. Zbinden, Reviews of Modern Physics 74, 145 (2002-03), quant-ph/0101098 .
- Liao et al. (2017) S.-K. Liao, W.-Q. Cai, W.-Y. Liu, L. Zhang, Y. Li, J.-G. Ren, J. Yin, Q. Shen, Y. Cao, Z.-P. Li, F.-Z. Li, X.-W. Chen, L.-H. Sun, J.-J. Jia, J.-C. Wu, X.-J. Jiang, J.-F. Wang, Y.-M. Huang, Q. Wang, Y.-L. Zhou, L. Deng, T. Xi, L. Ma, T. Hu, Q. Zhang, Y.-A. Chen, N.-L. Liu, X.-B. Wang, Z.-C. Zhu, C.-Y. Lu, R. Shu, C.-Z. Peng, J.-Y. Wang, and J.-W. Pan, Nature 549, 43 (2017), 1707.00542 .
- Giovannetti et al. (2011) V. Giovannetti, S. Lloyd, and L. Maccone, Nature Photonics 5, 222 (2011), 1102.2318 .
- Awschalom et al. (2021) D. Awschalom, K. K. Berggren, H. Bernien, S. Bhave, L. D. Carr, P. Davids, S. E. Economou, D. Englund, A. Faraon, M. Fejer, S. Guha, M. V. Gustafsson, E. Hu, L. Jiang, J. Kim, B. Korzh, P. Kumar, P. G. Kwiat, M. Lončar, M. D. Lukin, D. A. B. Miller, C. Monroe, S. W. Nam, P. Narang, J. S. Orcutt, M. G. Raymer, A. H. Safavi-Naeini, M. Spiropulu, K. Srinivasan, S. Sun, J. Vučković, E. Waks, R. Walsworth, A. M. Weiner, and Z. Zhang, PRX Quantum 2 (2021), 10.1103/prxquantum.2.017002, 1912.06642 .
- Hong et al. (1987) C. K. Hong, Z. Y. Ou, and L. Mandel, Physical Review Letters 59, 2044 (1987).
- Pan et al. (2012) J.-W. Pan, Z.-B. Chen, C.-Y. Lu, H. Weinfurter, A. Zeilinger, and M. Żukowski, Reviews of Modern Physics 84, 777 (2012), 0805.2853 .
- Senellart et al. (2017) P. Senellart, G. Solomon, and A. White, Nature Nanotechnology 12, 1026 (2017).
- McKeever et al. (2004) J. McKeever, A. Boca, A. D. Boozer, R. Miller, J. R. Buck, A. Kuzmich, and H. J. Kimble, Science 303, 1992 (2004).
- Ma et al. (2011) X.-s. Ma, S. Zotter, J. Kofler, T. Jennewein, and A. Zeilinger, Physical Review A 83, 043814 (2011), 1007.4798 .
- Collins et al. (2013) M. Collins, C. Xiong, I. Rey, T. Vo, J. He, S. Shahnia, C. Reardon, T. Krauss, M. Steel, A. Clark, and B. Eggleton, Nature Communications 4, 2582 (2013), 1305.7278 .
- Christensen et al. (2015) B. G. Christensen, F. Kaneda, H. S. Park, J. J. Wong, K. T. McCusker, and P. G. Kwiat, Optica 2, 1010 (2015), 1507.06052 .
- Joshi et al. (2018) C. Joshi, A. Farsi, S. Clemmen, S. Ramelow, and A. L. Gaeta, Nature Communications 9, 847 (2018), 1707.00048 .
- Kaneda and Kwiat (2019) F. Kaneda and P. G. Kwiat, Science Advances 5, eaaw8586 (2019).
- Grice et al. (2001) W. P. Grice, A. B. U’Ren, and I. A. Walmsley, Physical Review A 64, 063815 (2001).
- Giovannetti et al. (2002) V. Giovannetti, L. Maccone, J. H. Shapiro, and F. N. C. Wong, Physical Review A 66, 043813 (2002), quant-ph/0207009 .
- König and Wong (2004) F. König and F. N. C. Wong, Applied Physics Letters 84, 1644 (2004).
- Shimizu and Edamatsu (2009) R. Shimizu and K. Edamatsu, Optics Express 17, 16385 (2009).
- Mosley et al. (2008) P. J. Mosley, J. S. Lundeen, B. J. Smith, and I. A. Walmsley, New Journal of Physics 10, 093011 (2008), 0807.1409 .
- Evans et al. (2010) P. G. Evans, R. S. Bennink, W. P. Grice, T. S. Humble, and J. Schaake, Physical Review Letters 105, 253601 (2010), 1009.1609 .
- Yabuno et al. (2012) M. Yabuno, R. Shimizu, Y. Mitsumori, H. Kosaka, and K. Edamatsu, Physical Review A 86, 010302 (2012), 1112.2019 .
- Kaneda et al. (2016) F. Kaneda, K. Garay-Palmett, A. B. U’Ren, and P. G. Kwiat, Optics Express 24, 10733 (2016), 1603.08451 .
- Weston et al. (2016) M. M. Weston, H. M. Chrzanowski, S. Wollmann, A. Boston, J. Ho, L. K. Shalm, V. B. Verma, M. S. Allman, S. W. Nam, R. B. Patel, S. Slussarenko, and G. J. Pryde, Optics Express 24, 10869 (2016), 1603.03555 .
- Greganti et al. (2018) C. Greganti, P. Schiansky, I. A. Calafell, L. M. Procopio, L. A. Rozema, and P. Walther, Optics Express 26, 3286 (2018).
- Nasr et al. (2008) M. B. Nasr, S. Carrasco, B. E. A. Saleh, A. V. Sergienko, M. C. Teich, J. P. Torres, L. Torner, D. S. Hum, and M. M. Fejer, Physical Review Letters 100, 183601 (2008).
- Tanaka et al. (2012) A. Tanaka, R. Okamoto, H. H. Lim, S. Subashchandran, M. Okano, L. Zhang, L. Kang, J. Chen, P. Wu, T. Hirohata, S. Kurimura, and S. Takeuchi, Optics Express 20, 25228 (2012), 1210.6137 .
- Kaneda et al. (2019) F. Kaneda, H. Suzuki, R. Shimizu, and K. Edamatsu, Optics Express 27, 1416 (2019), 1810.02052 .
- Brańczyk et al. (2011) A. M. Brańczyk, A. Fedrizzi, T. M. Stace, T. C. Ralph, and A. G. White, Optics Express 19, 55 (2011), 1005.3086 .
- Dixon et al. (2013) P. B. Dixon, J. H. Shapiro, and F. N. C. Wong, Optics Express 21, 5879 (2013).
- Dosseva et al. (2016) A. Dosseva, Ł. Cincio, and A. M. Brańczyk, Physical Review A 93, 013801 (2016), 1410.7714 .
- Chen et al. (2017) C. Chen, C. Bo, M. Y. Niu, F. Xu, Z. Zhang, J. H. Shapiro, and F. N. C. Wong, Optics Express 25, 7300 (2017), 1701.01755 .
- Graffitti et al. (2018) F. Graffitti, P. Barrow, M. Proietti, D. Kundys, and A. Fedrizzi, Optica 5, 514 (2018), 1712.07140 .
- Pickston et al. (2021) A. Pickston, F. Graffitti, P. Barrow, C. L. Morrison, J. Ho, A. M. Brańczyk, and A. Fedrizzi, Optics Express 29, 6991 (2021).
- Miki et al. (2017) S. Miki, M. Yabuno, T. Yamashita, and H. Terai, Optics Express 25, 6796 (2017), 1701.07247 .
- Kaneda et al. (2020) F. Kaneda, J. Oikawa, M. Yabuno, F. China, S. Miki, H. Terai, Y. Mitsumori, and K. Edamatsu, Optics Express 28, 38993 (2020), 2010.07678 .
- Christ et al. (2011) A. Christ, K. Laiho, A. Eckstein, K. N. Cassemiro, and C. Silberhorn, New Journal of Physics 13, 033027 (2011), 1012.0262 .
- Brown and Twiss (1956) R. H. Brown and R. Q. Twiss, Nature 177, 27 (1956).
- Eberly (2006) J. H. Eberly, Laser Physics 16, 921 (2006), quant-ph/0508019 .
- Christensen et al. (2013) B. G. Christensen, K. T. McCusker, J. B. Altepeter, B. Calkins, T. Gerrits, A. E. Lita, A. Miller, L. K. Shalm, Y. Zhang, S. W. Nam, N. Brunner, C. C. W. Lim, N. Gisin, and P. G. Kwiat, Physical Review Letters 111, 130406 (2013), 1306.5772 .