^†^†thanks: This work was supported by the NWO VICI grant 639.043.201 “Optical Interferometry: A new Method for Studies of Extrasolar Planets” to A. Quirrenbach.

Geodetic Line at Constant Altitude above the Ellipsoid

Richard J. Mathar mathar@mpia-hd.mpg.de https://www.mpia-hd.mpg.de/˜mathar Max-Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany

(August 6, 2025)

Abstract

The two-dimensional surface of a bi-axial ellipsoid is characterized by the lengths of its major and minor axes. Longitude and latitude span an angular coordinate system across. We consider the egg-shaped surface of constant altitude above (or below) the ellipsoid surface, and compute the geodetic lines—lines of minimum Euclidean length—within this surface which connect two points of fixed coordinates. This addresses the common “inverse” problem of geodesics generalized to non-zero elevations. The system of differential equations which couples the two angular coordinates along the trajectory is reduced to a single integral, which is handled by Taylor expansion up to fourth power in the eccentricity.

geodesy; ellipsoid; eccentricity; geodetic line; inverse problem

pacs:

91.10.By, 91.10.Ws, 02.40.Hw

I Contents

The common three parameters employed to relate Cartesian coordinates to an ellipsoidal surface are the angles of latitude and longitude in a grid on the surface, plus an altitude which is a shortest (perpendicular) distance to the surface. The well-known functional relations (coordinate transformations) are summarized in Section II.

The inverse problem of geodesy is to find the line embedded in the ellipsoid surface which connects two fixed points subject to minimization of its length. We pose the equivalent problem for lines at constant altitude, as if one would ask for the shortest track of the center of a sphere of given radius which rolls on the ellipsoid surface and meets two points of the same, known altitude. In Section III, we formulate this in terms of the generic differential equations of geodesy parametrized by the Christoffel symbols.

In the main Section IV, the coupled system of differential equations of latitude and longitude as a function of path length is reduced to one degree of freedom, here chosen to be the direction along the path at one of the fixed terminal points, measured in the topocentric horizontal system, and dubbed the launching angle. Closed-form expressions of this parameter in terms of the coordinates of the terminal points have not been found; instead, the results are presented as series expansions up to fourth power in the eccentricity.

The standard treatment of this analysis is the projection on an auxiliary sphere; this technique is (almost) completely ignored but for the pragmatic aspect that the case of zero eccentricity is a suitable zeroth-order reference of series expansions around small eccentricities.

II Spheroidal Coordinates

II.1 Surface

The cross section of an ellipsis of equatorial radius $\rho_{e}>\rho_{p}$ with eccentricity $e$ in a Cartesian ( $x,z$ ) system is:

\rho_{p}^{2}=\rho_{e}^{2}(1-e^{2});\quad\frac{x^{2}}{\rho_{e}^{2}}+\frac{z^{2}}{\rho_{p}^{2}}=1.

(1)

The ellipsis defines a geocentric latitude $\phi^{\prime}$ and a geodetic latitude $\phi$ , the latter measured by intersection of the normal to the tangential plane with the equatorial plane (Figure 1).

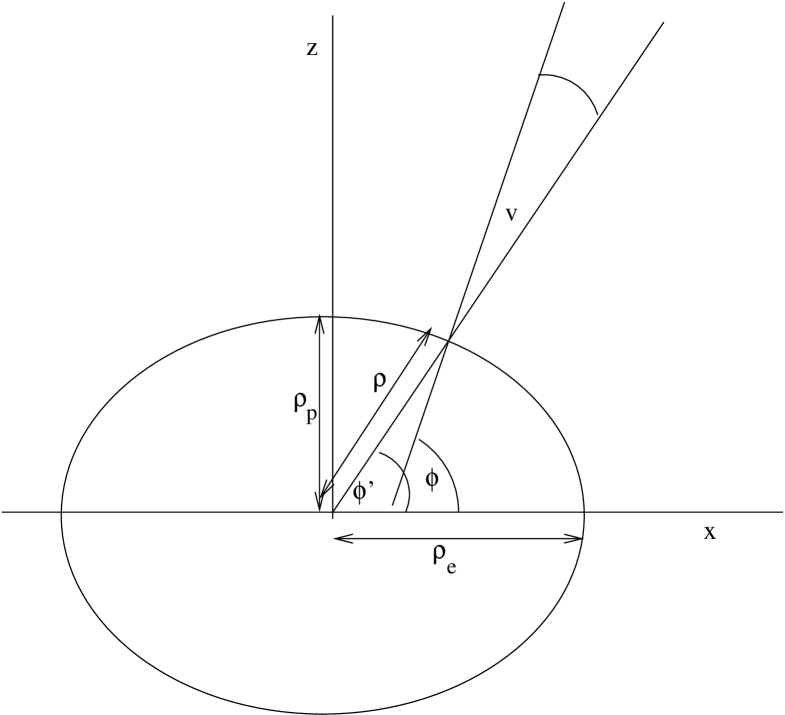
Refer to caption — Figure 1: Major semi-axis $\rho_{e}$ , minor semi-axis $\rho_{p}$ , straight distance to the center of coordinates $\rho$ , geocentric latitude $\phi^{\prime}$ , geodetic latitude $\phi$ , and their pointing difference $v$ .

On the surface of the ellipsoid [23, §IX][5][2, §140]:

\tan\phi=\frac{z}{x}\frac{\rho_{e}^{2}}{\rho_{p}^{2}};\quad\frac{z}{x}=\tan\phi^{\prime}=\frac{\rho_{p}^{2}}{\rho_{e}^{2}}\tan\phi.

(2)

Supposed $\rho$ denotes the distance from the center of coordinates to the point on the geoid surface, the transformation from $(x,z)$ to $\phi$ is

x=\rho\cos\phi^{\prime}=\frac{\rho_{e}\cos\phi}{\sqrt{1-e^{2}\sin^{2}\phi}},\quad z=\rho\sin\phi^{\prime}=\frac{\rho_{e}(1-e^{2})\sin\phi}{\sqrt{1-e^{2}\sin^{2}\phi}}.

(3)

$v=\phi-\phi^{\prime}$ defines the difference between the geodetic (astronomical) and the geocentric latitudes,

\tan v=\frac{e^{2}\sin(2\phi)}{2(1-e^{2}\sin^{2}\phi)}=\frac{m\sin(2\phi)}{1+m\cos(2\phi)}=m\sin(2\phi)-m^{2}\sin(2\phi)\cos(2\phi)+m^{3}\sin(2\phi)\cos^{2}(2\phi)+\cdots;

(4)

where the expansion of the denominator has been given in terms of the geometric series of the parameter

m\equiv\frac{e^{2}}{2-e^{2}}.

(5)

The Taylor series in powers of $\sin(2\phi)$ and in powers of $m$ are

	$\displaystyle v$	$\displaystyle=$	$\displaystyle\frac{m}{1+m}\sin(2\phi)+\frac{m^{2}(2+m)}{6(1+m)^{3}}\sin^{3}(2\phi)+\frac{m^{2}(5+25m+15m^{2}+3m^{3})}{40(1+m)^{5}}\sin^{5}(2\phi)+\cdots$		(6)
		$\displaystyle=$	$\displaystyle\sin(2\phi)m-\frac{1}{2}\sin(4\phi)m^{2}+\frac{1}{3}\sin(6\phi)m^{3}-\frac{1}{4}\sin(8\phi)m^{4}+\frac{1}{5}\sin(10\phi)m^{5}+\cdots.$		(7)

A flattening factor $f$ is also commonly defined [10][19, (3.14)],

f=\frac{\rho_{e}-\rho_{p}}{\rho_{e}}=1-\sqrt{1-e^{2}};\quad e^{2}=f(2-f).

(8)

The reference values of the Earth ellipsoid adopted in the WGS84 [16] are

f=1/298.257223563,\quad\rho_{e}=6378137.0\text{ m}.

(9)

II.2 General Altitude

If one moves along the direction of $\phi$ a distance $h$ away from the surface of the geoid, the new coordinates relative to (3) are [6, 28, 9, 18, 30, 8, 12]

x=\rho\cos\phi^{\prime}+h\cos\phi;\quad z=\rho\sin\phi^{\prime}+h\sin\phi,

(10)

which can be written in terms of a distance $N(\phi)$ ,

N(\phi)\equiv\frac{\rho_{e}}{\sqrt{1-e^{2}\sin^{2}\phi}}

(11)

x=(N+h)\cos\phi;\quad z=[N(1-e^{2})+h]\sin\phi.

(12)

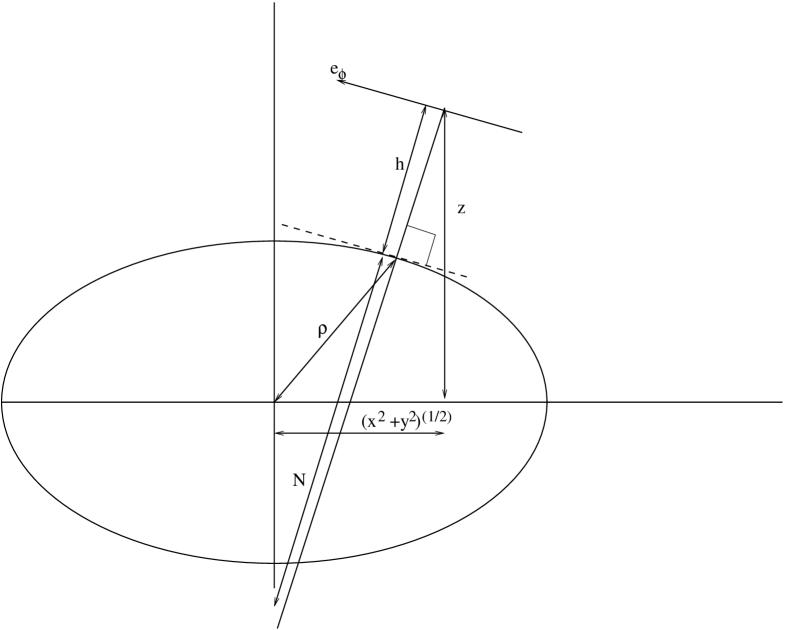
Rotation of (12) around the polar axis with geographic longitude $\lambda$ defines the full 3D transformation between $(x,y,z)$ and $(\lambda,\phi,h)$ ,

\left(\begin{array}[]{c}x\\ y\\ z\\ \end{array}\right)=\left(\begin{array}[]{c}\left[N(\phi)+h\right]\cos\phi\cos\lambda\\ \left[N(\phi)+h\right]\cos\phi\sin\lambda\\ \left[N(\phi)(1-e^{2})+h\right]\sin\phi\\ \end{array}\right).

(13)

The only theme of this paper is to generalize the geodetic lines of the literature [5, 24, 21, 25, 17, 3, 11, 14] to the case of finite altitude $h\neq 0$ . The physics of gravimetric or potential theory is not involved, only the mathematics of the geometry. It should be noted that points with constant, non-zero $h$ do not define a surface of an ellipsoid with effective semi-axes $\rho_{e,p}+h$ —otherwise the geodetic line could be deduced by mapping the problem onto an equivalent ellipsoidal surface [5].

III Inverse Problem of Geodesy

III.1 Topocentric Coordinate System

A line of shortest distance at constant height $h=$ const between two points 1 and 2 is defined by minimizing the Euclidean distance, the line integral

S=\int_{1}^{2}\sqrt{dx^{2}+dy^{2}+dz^{2}}=\int_{1}^{2}\sqrt{ds^{2}}\equiv\int_{1}^{2}{\cal L}ds

(14)

for some parametrization $\lambda(\phi)$ . The integrand is equivalent to a Lagrange function ${\cal L}(\phi,\lambda,d\lambda/d\phi)$ or ${\cal L}(\phi,\lambda,d\phi/d\lambda)$ .

The gradient of (13) with respect to $\lambda$ and $\phi$ defines the vectors ${\mathbf{e}}_{\lambda,\phi}$ that span the topocentric tangent plane

{\bf e}_{\lambda}=\left(\begin{array}[]{c}-\left[N(\phi)+h\right]\cos\phi\sin\lambda\\ \left[N(\phi)+h\right]\cos\phi\cos\lambda\\ 0\\ \end{array}\right);\quad{\bf e}_{\phi}=\left(\begin{array}[]{c}-\sin\phi\cos\lambda\left[M(\phi)+h\right]\\ -\sin\phi\sin\lambda\left[M(\phi)+h\right]\\ \cos\phi\left[M(\phi)+h\right]\\ \end{array}\right),

(15)

where a meridional radius of curvature [26][19, (3.87)]

M(\phi)\equiv\frac{\rho_{e}(1-e^{2})}{(1-e^{2}\sin^{2}\phi)^{3/2}}=N(\phi)\frac{1-e^{2}}{1-e^{2}\sin^{2}\phi}

(16)

is defined to simplify the notation. Building squares and dot products computes the three Gauss Fundamental parameters of the surface [20]

$\displaystyle{\bf e}_{\lambda}^{2}=E$	$\displaystyle=$	$\displaystyle(N+h)^{2}\cos^{2}\phi;$	(17)
$\displaystyle{\bf e}_{\lambda}\cdot{\bf e}_{\phi}=F$	$\displaystyle=$	$\displaystyle 0;$	(18)
$\displaystyle{\bf e}_{\phi}^{2}=G$	$\displaystyle=$	$\displaystyle\left[N\frac{1-e^{2}}{1-e^{2}\sin^{2}\phi}+h\right]^{2}=(M+h)^{2}.$	(19)

Specializing to $h=0$ we get the You formulae [29]. $E$ and $G$ provide the principal curvatures along the meridian and azimuth [4], and the coefficients of the metric tensor in the quadratic form of $ds^{2}$ ,

S=\int\sqrt{Ed\lambda^{2}+2Fd\lambda d\phi+Gd\phi^{2}}.

(20)

III.2 Christoffel Symbols

Christoffel symbols are the connection coefficients between differentials $d{\bf e}_{\epsilon}$ of the topocentric axis and of the positions $d{\bf x}^{\beta}$ , in a generic definition

d{\bf e}_{\epsilon}=\sum_{\alpha,\beta}{\bf e}_{\alpha}\Gamma_{\beta\epsilon}^{\alpha}d{\bf x}^{\beta}.

(21)

This format is matched by first computing the derivative of ${\bf e}_{\lambda}$ with respect to $\lambda$ and $\phi$ (at $h=const$ ):

d{\bf e}_{\lambda}=\left(\begin{array}[]{c}-(N+h)\cos\phi\cos\lambda\\ -(N+h)\cos\phi\sin\lambda\\ 0\\ \end{array}\right)d\lambda+\left(\begin{array}[]{c}(M+h)\sin\phi\sin\lambda\\ -(M+h)\sin\phi\cos\lambda\\ 0\\ \end{array}\right)d\phi

(22)

and of ${\bf e}_{\phi}$ with respect to $\lambda$ and $\phi$ :

d{\bf e}_{\phi}=\left(\begin{array}[]{c}(M+h)\sin\phi\sin\lambda\\ -(M+h)\sin\phi\cos\lambda\\ 0\\ \end{array}\right)d\lambda+\left(\begin{array}[]{c}\left[Ne^{2}\frac{\cos^{2}\phi}{1-e^{2}\sin^{2}\phi}-3Ne^{2}(1-e^{2})\frac{\sin^{2}\phi}{(1-e^{2}\sin^{2}\phi)^{2}}-(N+h)\right]\cos\phi\cos\lambda\\ \left[Ne^{2}\frac{\cos^{2}\phi}{1-e^{2}\sin^{2}\phi}-3Ne^{2}(1-e^{2})\frac{\sin^{2}\phi}{(1-e^{2}\sin^{2}\phi)^{2}}-(N+h)\right]\cos\phi\sin\lambda\\ \left[Ne^{2}(1-e^{2})\left(3\frac{\cos^{2}\phi}{(1-e^{2}\sin^{2}\phi)^{2}}-\frac{\sin^{2}\phi}{1-e^{2}\sin^{2}\phi}\right)-[N(1-e^{2})+h]\right]\sin\phi\\ \end{array}\right)d\phi.

(23)

The next step splits these two equations to the expanded version of (21),

	$\displaystyle d{\bf e}_{\lambda}$	$\displaystyle=$	$\displaystyle({\bf e}_{\lambda}\Gamma_{\lambda\lambda}^{\lambda}+{\bf e}_{\phi}\Gamma_{\lambda\lambda}^{\phi})d\lambda+({\bf e}_{\lambda}\Gamma_{\phi\lambda}^{\lambda}+{\bf e}_{\phi}\Gamma_{\phi\lambda}^{\phi})d\phi;$		(24)
	$\displaystyle d{\bf e}_{\phi}$	$\displaystyle=$	$\displaystyle({\bf e}_{\lambda}\Gamma_{\lambda\phi}^{\lambda}+{\bf e}_{\phi}\Gamma_{\lambda\phi}^{\phi})d\lambda+({\bf e}_{\lambda}\Gamma_{\phi\phi}^{\lambda}+{\bf e}_{\phi}\Gamma_{\phi\phi}^{\phi})d\phi.$		(25)

The eight $\Gamma$ are extracted by evaluating dot products of the four vector coefficients in (22)–(23) by ${\bf e}_{\lambda}$ and ${\bf e}_{\phi}$ ,

\Gamma_{\lambda\lambda}^{\lambda}=\Gamma_{\phi\lambda}^{\phi}=\Gamma_{\lambda\phi}^{\phi}=\Gamma_{\phi\phi}^{\lambda}=0;

(26)

\Gamma_{\lambda\lambda}^{\phi}=(N+h)\cos\phi\sin\phi\frac{1-e^{2}\sin^{2}\phi}{h(1-e^{2}\sin^{2}\phi)+N(1-e^{2})};

(27)

\Gamma_{\phi\lambda}^{\lambda}=\Gamma_{\lambda\phi}^{\lambda}=-\sin\phi\frac{h(1-e^{2}\sin^{2}\phi)+N(1-e^{2})}{(N+h)(1-e^{2}\sin^{2}\phi)\cos\phi};

(28)

\Gamma_{\phi\phi}^{\phi}=3Ne^{2}(1-e^{2})\sin\phi\cos\phi\frac{1}{[h(1-e^{2}\sin^{2}\phi)+N(1-e^{2})](1-e^{2}\sin^{2}\phi)}.

(29)

The Euler-Lagrange Differential Equations $\delta\int_{1}^{2}\sqrt{Ed\lambda^{2}+Gd\phi^{2}}=0$ for a stationary Lagrange density $\cal L$ (at $F=0$ ) become the differential equations of the geodesic [20], in the generic format

\frac{d^{2}x^{\epsilon}}{ds^{2}}+\sum_{\mu\nu}\Gamma_{\mu\nu}^{\epsilon}\frac{dx^{\mu}}{ds}\frac{dx^{\nu}}{ds}=0.

(30)

The explicit write-up

\frac{d^{2}\lambda}{ds^{2}}+\Gamma_{\lambda\lambda}^{\lambda}\frac{d\lambda}{ds}\frac{d\lambda}{ds}+\Gamma_{\lambda\phi}^{\lambda}\frac{d\lambda}{ds}\frac{d\phi}{ds}+\Gamma_{\phi\lambda}^{\lambda}\frac{d\phi}{ds}\frac{d\lambda}{ds}+\Gamma_{\phi\phi}^{\lambda}\frac{d\phi}{ds}\frac{d\phi}{ds}=0;

(31)

\frac{d^{2}\phi}{ds^{2}}+\Gamma_{\lambda\lambda}^{\phi}\frac{d\lambda}{ds}\frac{d\lambda}{ds}+\Gamma_{\lambda\phi}^{\phi}\frac{d\lambda}{ds}\frac{d\phi}{ds}+\Gamma_{\phi\lambda}^{\phi}\frac{d\phi}{ds}\frac{d\lambda}{ds}+\Gamma_{\phi\phi}^{\phi}\frac{d\phi}{ds}\frac{d\phi}{ds}=0,

(32)

simplifies with (26) to

	$\displaystyle\frac{d^{2}\lambda}{ds^{2}}+2\Gamma_{\lambda\phi}^{\lambda}\frac{d\lambda}{ds}\frac{d\phi}{ds}$	$\displaystyle=$	$\displaystyle 0;$		(33)
	$\displaystyle\frac{d^{2}\phi}{ds^{2}}+\Gamma_{\lambda\lambda}^{\phi}\left(\frac{d\lambda}{ds}\right)^{2}+\Gamma_{\phi\phi}^{\phi}\left(\frac{d\phi}{ds}\right)^{2}$	$\displaystyle=$	$\displaystyle 0.$		(34)

IV Reduction of the Differential Equations

IV.1 Separation of Angular Variables

Decoupling of the two differential equations (33)–(34) starts with the separation of variables in (33),

\frac{\frac{d^{2}\lambda}{ds^{2}}}{\frac{d\lambda}{ds}}=-2\Gamma_{\phi\lambda}^{\lambda}\frac{d\phi}{ds}.

(35)

Change of the integration variable on the right hand side from $s$ to $\phi$ allows to use the underivative of (28)

\int\Gamma_{\lambda\phi}^{\lambda}(\phi)d\phi=\log\left\{[N(\phi)+h]\cos\phi\right\}+const

(36)

to generate a first integral

\log\frac{d\lambda}{ds}=-2\log[(N+h)\cos\phi]+const.

(37)

Exponentiation yields

\frac{d\lambda}{ds}=c_{3}\frac{1}{(N+h)^{2}\cos^{2}\phi},

(38)

where

c_{3}\equiv\frac{d\lambda}{ds}_{\mid 1}(N_{1}+h)^{2}\cos^{2}\phi_{1}

(39)

is a constant for each geodesic; it plays the role of the Clairaut constant [22, 27], but has length units in our case. It has been defined with the azimuth $\phi_{1}$ and $N_{1}\equiv N(\phi_{1})$ at the start of the line, but could as well be associated with any other point or the end point $2$ . $c_{3}$ is positive for trajectories starting into eastwards direction, negative for the westwards heading, zero for routes to the poles. Moving the square of (38) into (34) yields

\frac{d^{2}\phi}{ds^{2}}+\frac{\sin\phi}{(N+h)^{3}\cos^{3}\phi}\,\frac{1-e^{2}\sin^{2}\phi}{h(1-e^{2}\sin^{2}\phi)+N(1-e^{2})}c_{3}^{2}+\frac{3Ne^{2}(1-e^{2})\sin\phi\cos\phi}{[h(1-e^{2}\sin^{2}\phi)+N(1-e^{2})](1-e^{2}\sin^{2}\phi)}\left(\frac{d\phi}{ds}\right)^{2}=0.

(40)

To solve this differential equation, we substitute the variable $\phi$ by its projection $\tau$ onto the polar axis,

\tau\equiv\sin\phi,

(41)

which implies transformations in the derivatives:

\frac{d\tau}{ds}=\cos\phi\frac{d\phi}{ds};

(42)

\frac{d^{2}\tau}{ds^{2}}=-\sin\phi\frac{d\phi}{ds}\frac{d\phi}{ds}+\cos\phi\frac{d^{2}\phi}{ds^{2}};

(43)

\cos\phi\frac{d^{2}\phi}{ds^{2}}=\frac{d^{2}\tau}{ds^{2}}+\tau\left(\frac{d\phi}{ds}\right)^{2}=\frac{d^{2}\tau}{ds^{2}}+\frac{\tau}{\cos^{2}\phi}\left(\frac{d\tau}{ds}\right)^{2}=\frac{d^{2}\tau}{ds^{2}}+\frac{\tau}{1-\tau^{2}}\left(\frac{d\tau}{ds}\right)^{2}.

(44)

We multiply (40) by $\cos\phi$ , then replace $d\phi/ds$ and $d^{2}\phi/ds^{2}$ as noted above,

\frac{d^{2}\tau}{ds^{2}}+\frac{\tau}{1-\tau^{2}}\left(\frac{d\tau}{ds}\right)^{2}+\frac{\tau}{(N+h)^{3}(1-\tau^{2})}\,\frac{1-e^{2}\tau^{2}}{h(1-e^{2}\tau^{2})+N(1-e^{2})}c_{3}^{2}+\frac{3Ne^{2}(1-e^{2})\tau}{[h(1-e^{2}\tau^{2})+N(1-e^{2})](1-e^{2}\tau^{2})}\left(\frac{d\tau}{ds}\right)^{2}=0;

\frac{d^{2}\tau}{ds^{2}}+\frac{\tau}{1-\tau^{2}}\,\frac{h(1-e^{2}\tau^{2})^{2}+N(1-4e^{2}\tau^{2}+2e^{2}+4e^{4}\tau^{2}-3e^{4})}{[h(1-e^{2}\tau^{2})+N(1-e^{2})][1-e^{2}\tau^{2}]}\left(\frac{d\tau}{ds}\right)^{2}\\ +\frac{\tau}{(N+h)^{3}(1-\tau^{2})}\,\frac{1-e^{2}\tau^{2}}{h(1-e^{2}\tau^{2})+N(1-e^{2})}c_{3}^{2}=0.

(45)

This is a differential equation with no explicit appearance of the independent variable $s$ ,

(1-\tau^{2})\frac{d^{2}\tau}{ds^{2}}+\frac{h(1-e^{2}\tau^{2})^{2}+N(1-e^{2})(1+3e^{2}-4e^{2}\tau^{2})}{[h(1-e^{2}\tau^{2})+N(1-e^{2})][1-e^{2}\tau^{2}]}\tau\left(\frac{d\tau}{ds}\right)^{2}+\frac{\tau c_{3}^{2}}{(N+h)^{3}}\,\frac{1-e^{2}\tau^{2}}{h(1-e^{2}\tau^{2})+N(1-e^{2})}=0,

and the standard way of progressing is the substitution

\frac{d\tau}{ds}\equiv p;\quad\frac{d^{2}\tau}{ds^{2}}=p\frac{dp}{d\tau};

(46)

(1-\tau^{2})p\frac{dp}{d\tau}+\frac{h(1-e^{2}\tau^{2})^{2}+N(1-e^{2})(1+3e^{2}-4e^{2}\tau^{2})}{[h(1-e^{2}\tau^{2})+N(1-e^{2})][1-e^{2}\tau^{2}]}\tau p^{2}+\frac{\tau c_{3}^{2}}{(N+h)^{3}}\,\frac{1-e^{2}\tau^{2}}{h(1-e^{2}\tau^{2})+N(1-e^{2})}=0.

(47)

This is transformed to a linear differential equation by the further substitution $P\equiv p^{2}$ , $dP/d\tau=2p\,dp/d\tau$ ,

\frac{1}{2}(1-\tau^{2})\frac{dP}{d\tau}+\frac{h(1-e^{2}\tau^{2})^{2}+N(1-e^{2})(1+3e^{2}-4e^{2}\tau^{2})}{[h(1-e^{2}\tau^{2})+N(1-e^{2})][1-e^{2}\tau^{2}]}\tau P+\frac{\tau c_{3}^{2}}{(N+h)^{3}}\,\frac{1-e^{2}\tau^{2}}{h(1-e^{2}\tau^{2})+N(1-e^{2})}=0.

(48)

The standard approach is to solve the homogeneous differential equation first,

\frac{dP}{d\tau}=-2\tau\frac{h(1-e^{2}\tau^{2})^{2}+N(1-e^{2})(1+3e^{2}-4e^{2}\tau^{2})}{[1-\tau^{2}][h(1-e^{2}\tau^{2})+N(1-e^{2})][1-e^{2}\tau^{2}]}P.

(49)

After division through $P$ , the left hand side is easily integrated, and the right hand side (incompletely) decomposed into partial fractions,

$\displaystyle\log P$	$\displaystyle=$	$\displaystyle-2\int\tau\frac{h(1-e^{2}\tau^{2})^{2}+N(1-e^{2})(1+3e^{2}-4e^{2}\tau^{2})}{[1-\tau^{2}][h(1-e^{2}\tau^{2})+N(1-e^{2})][1-e^{2}\tau^{2}]}d\tau$	(50)
	$\displaystyle=$	$\displaystyle\int\frac{-2\tau}{1-\tau^{2}}d\tau+3\int\frac{-2e^{2}\tau}{1-e^{2}\tau^{2}}d\tau+6he^{2}\int\frac{\tau}{h(1-e^{2}\tau^{2})+N(1-e^{2})}d\tau$
	$\displaystyle=$	$\displaystyle\log(1-\tau^{2})+3\log(1-e^{2}\tau^{2})-2\log\left[h(1-e^{2}\tau^{2})^{3/2}+\rho_{e}(1-e^{2})\right]+const.$

P=const\cdot\frac{(1-\tau^{2})(1-e^{2}\tau^{2})^{3}}{\left[h(1-e^{2}\tau^{2})^{3/2}+\rho_{e}(1-e^{2})\right]^{2}}=const\cdot\frac{(1-\tau^{2})(1-e^{2}\tau^{2})^{2}}{\left[h(1-e^{2}\tau^{2})+N(1-e^{2})\right]^{2}}=\frac{const\cdot(1-\tau^{2})}{G(\tau)}.

Solution of the inhomogeneous differential equation (48) proceeds with the variation of the constant, the ansatz

P=c(\tau)\cdot\frac{(1-\tau^{2})(1-e^{2}\tau^{2})^{2}}{\left[h(1-e^{2}\tau^{2})+N(1-e^{2})\right]^{2}}.

(51)

Back insertion into (48) leads to a first order differential equation for $c(\tau)$ ,

\frac{dc(\tau)}{d\tau}\frac{1-\tau^{2}}{G(\tau)}=-\frac{2\tau c_{3}^{2}}{(1-\tau^{2})(N+h)^{3}}\,\frac{1-e^{2}\tau^{2}}{h(1-e^{2}\tau^{2})+N(1-e^{2})},

which is decomposed into partial fractions

\frac{dc(\tau)}{d\tau}=c_{3}^{2}\left[eN\frac{2e\tau}{1-e^{2}\tau^{2}}\frac{1}{(N+h)^{3}}+\frac{-2\tau}{1-\tau^{2}}\frac{1}{(N+h)^{2}}\right]\frac{1}{1-\tau^{2}}.

The ensuing integral over $d\tau$ is solved by aid of the substitution $\tau^{2}=u$ ,

c(\tau)=-c_{3}^{2}\frac{1}{(N+h)^{2}(1-\tau^{2})}+const.

Back into (51)—using $const$ to indicate placement of any member of an anonymous bag of constants of integration,

$\displaystyle P$	$\displaystyle=$	$\displaystyle\left[const-\frac{1}{(N+h)^{2}(1-\tau^{2})}\right]\frac{c_{3}^{2}(1-\tau^{2})(1-e^{2}\tau^{2})^{2}}{\left[h(1-e^{2}\tau^{2})+N(1-e^{2})\right]^{2}}$	(52)
	$\displaystyle=$	$\displaystyle c_{5}\frac{(1-\tau^{2})(1-e^{2}\tau^{2})^{2}}{\left[h(1-e^{2}\tau^{2})+N(1-e^{2})\right]^{2}}-\frac{c_{3}^{2}(1-e^{2}\tau^{2})^{2}}{(N+h)^{2}\left[h(1-e^{2}\tau^{2})+N(1-e^{2})\right]^{2}}$	(53)
	$\displaystyle=$	$\displaystyle c_{5}\frac{1}{(h+M)^{2}}\left(1-\tau^{2}-\frac{c_{3}^{2}}{(N+h)^{2}}\right)=c_{5}\frac{1-\tau^{2}}{G(\tau)}\left(1-\frac{c_{3}^{2}}{E(\tau)}\right)=p^{2}.$	(54)

The subscript $1$ denotes values at the starting point of the curve,

	$\displaystyle P_{1}$	$\displaystyle=$	$\displaystyle c_{5}\frac{\cos^{2}\phi_{1}(1-e^{2}\sin^{2}\phi_{1})^{2}}{\left[h(1-e^{2}\sin^{2}\phi_{1})+N_{1}(1-e^{2})\right]^{2}}-\frac{c_{3}^{2}(1-e^{2}\sin^{2}\phi_{1})^{2}}{(N_{1}+h)^{2}\left[h(1-e^{2}\sin^{2}\phi_{1})+N_{1}(1-e^{2})\right]^{2}}=p_{1}^{2}$		(55)
		$\displaystyle=$	$\displaystyle c_{5}\frac{\cos^{2}\phi_{1}(1-e^{2}\sin^{2}\phi_{1})^{2}}{\left[h(1-e^{2}\sin^{2}\phi_{1})+N_{1}(1-e^{2})\right]^{2}}-\frac{(d\lambda/ds)_{1}^{2}(N_{1}+h)^{2}\cos^{4}\phi_{1}(1-e^{2}\sin^{2}\phi_{1})^{2}}{\left[h(1-e^{2}\sin^{2}\phi_{1})+N_{1}(1-e^{2})\right]^{2}}.$		(56)

Solving for $c_{5}$ yields

	$\displaystyle c_{5}$	$\displaystyle=$	$\displaystyle\left(\frac{d\lambda}{ds}_{\mid 1}\right)^{2}\cos^{2}\phi_{1}(N_{1}+h)^{2}+\frac{p_{1}^{2}\left[h(1-e^{2}\sin^{2}\phi_{1})+N_{1}(1-e^{2})\right]^{2}}{\cos^{2}\phi_{1}(1-e^{2}\sin^{2}\phi_{1})^{2}}=\left(\frac{d\lambda}{ds}_{\mid 1}\right)^{2}\cos^{2}\phi_{1}(N_{1}+h)^{2}+\frac{p_{1}^{2}}{\cos^{2}\phi_{1}}G_{1}$		(57)
		$\displaystyle=$	$\displaystyle\left(\frac{d\lambda}{ds}_{\mid 1}\right)^{2}E_{1}+\left(\frac{d\phi}{ds}_{\mid 1}\right)^{2}G_{1}=\frac{c_{3}^{2}}{(N_{1}+h)^{2}\cos^{2}\phi_{1}}+\left(\frac{d\phi}{ds}_{\mid 1}\right)^{2}(M_{1}+h)^{2}.$		(57)

Compared with the differential version of (20),

ds^{2}=Ed\lambda^{2}+Gd\phi^{2};\quad 1=E\left(\frac{d\lambda}{ds}\right)^{2}+G\left(\frac{d\phi}{ds}\right)^{2},

(58)

we must have $c_{5}=1$ . Note that (54) is essentially a write-up for $p^{2}\sim(d\phi/ds)^{2}$ and could be derived quickly by inserting (38) directly into (58).

The square root of (54) is

p=\pm\frac{1-e^{2}\tau^{2}}{h(1-e^{2}\tau^{2})+N(1-e^{2})}\sqrt{1-\tau^{2}-\frac{c_{3}^{2}}{(N+h)^{2}}}=\pm\frac{\sqrt{1-\tau^{2}-\frac{c_{3}^{2}}{(N+h)^{2}}}}{h+M(\tau)}=\frac{d\tau}{ds}.

(59)

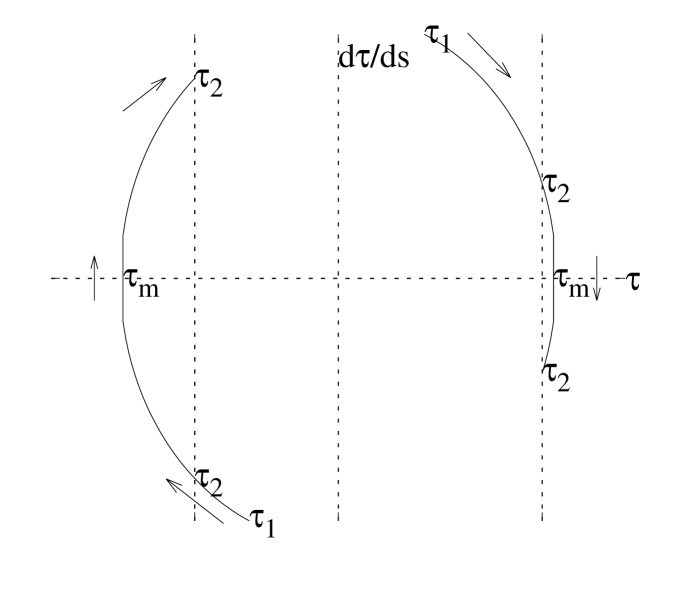
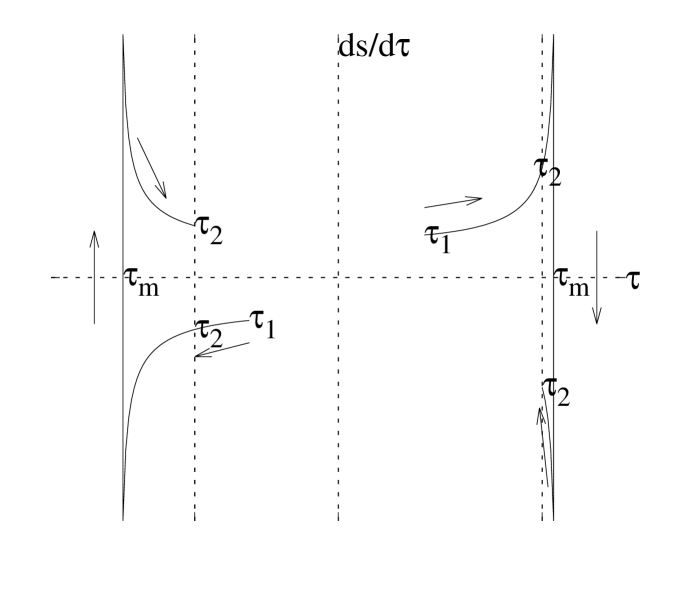
The sign in front of the square root is to be chosen positive for pieces of the trajectory with $d\tau/ds>0$ (northern direction), negative where $d\tau/ds<0$ (southern direction). The value in the square root may run through zero within one curve, $d\tau/ds=0$ at one point $\tau_{m}$ , such that the square root switches sign there (Figure 3). This happens whenever

(1-\tau_{m}^{2})[N(\tau_{m})+h]^{2}=c_{3}^{2}

(60)

yields a vanishing discriminant of the square root for some $(\lambda,\phi)$ , that is, whenever the difference $\lambda_{2}-\lambda_{1}$ is sufficiently large to create a point of minimum polar distance along the trajectory that is not one of the terminal points.

IV.2 Launching Direction

So far we have written the bundle of all geodesics through $(\lambda_{1},\phi_{1})$ in the format (59), which specifies the change of latitude as a function of distance traveled. The direction at point 1 in the topocentric system of coordinates is represented by $c_{3}$ . To address the inverse problem of geodesy, that is to pick the particular geodesics which also runs through the terminal point $(\lambda_{2},\phi_{2})$ in fulfillment of the Dirichlet boundary conditions, the associated change in longitude, some form of (38),

\frac{d\lambda}{ds}=c_{3}\frac{1}{(N+h)^{2}(1-\tau^{2})}=\frac{c_{3}}{E},

(61)

must obviously get involved. The strategy is to write down $\tau(\lambda)$ or $\lambda(\tau)$ with $c_{3}$ as a parameter, then to adjust $c_{3}$ to ensure with what would be called a shooting method that starting at point 1 at that angle eventually passes through point 2. Coupling of $\lambda$ to $\tau$ is done by division of (59) and (61),

\frac{d\tau}{d\lambda}=\frac{d\tau}{ds}\frac{ds}{d\lambda}=\frac{d\tau}{ds}/\frac{d\lambda}{ds}=\pm\frac{(N+h)^{2}(1-\tau^{2})\sqrt{1-\tau^{2}-\frac{c_{3}^{2}}{(N+h)^{2}}}}{c_{3}(h+M)}.

(62)

Separation of both variables yields

\pm\int_{1}d\tau\frac{c_{3}(h+M)}{(N+h)^{2}(1-\tau^{2})\sqrt{1-\tau^{2}-\frac{c_{3}^{2}}{(N+h)^{2}}}}=\lambda_{\mid 1}.

(63)

An approach of evaluating the integral by power series expansion in $h/\rho_{e}$ is proposed in [15].

For short paths, small $|\lambda_{2}-\lambda_{1}|$ , the integral is simply $\int_{\tau_{1}}^{\tau_{2}}$ . If one of the cases occurs, where the difference in $\lambda$ is too large for a solution, the additional path through the singularity $\tau_{m}$ is to be used [with some local extremum in the graph $\tau(s)$ ], and the integral is to be interpreted as $\int_{\tau_{1}}^{\tau_{m}}-\int_{\tau_{m}}^{\tau_{2}}$ . Taking the sign change and the symmetry of the integrand into account, this is $\int_{\tau_{1}}^{\tau_{2}}+2\int_{\tau_{2}}^{\tau_{m}}=\int_{\tau_{1}}^{\tau_{m}}+\int_{\tau_{2}}^{\tau_{m}}$ , twice the underivative at $\tau_{m}$ minus the sum of the underivative at $\tau_{1}$ and $\tau_{2}$ . In the right plot of Figure 3, the difference is in including or not including the loudspeaker shaped area between $\tau_{2}$ and $\tau_{m}$ .

$\tau_{m}$ is the solution of (60), the positive value of the solution taken if $d\tau/ds>0$ at $\phi_{1}$ , the negative value if $d\tau/ds<0$ at $\phi_{1}$ . The squared zero of $d\tau/ds$ , $\tau_{m}^{2}$ , is a root of the fourth-order polynomial which emerges by rewriting (60),

e^{4}h^{4}(\tau_{m}^{2})^{4}+2e^{2}h^{2}\left[\rho_{e}^{2}-h^{2}+e^{2}\left(c_{3}^{2}-h^{2}\right)\right](\tau_{m}^{2})^{3}\\ +\left[\left(\rho_{e}^{2}-h^{2}\right)^{2}+2e^{2}\left(2h^{4}-2c_{3}^{2}h^{2}-2\rho_{e}^{2}h^{2}-\rho_{e}^{2}c_{3}^{2}\right)+e^{4}\left(c_{3}^{2}-h^{2}\right)^{2}\right](\tau_{m}^{2})^{2}\\ +2\left[-\left(\rho_{e}^{2}-h^{2}\right)^{2}+c_{3}^{2}\left(\rho_{e}^{2}+h^{2}\right)+e^{2}\left(-\left(c_{3}^{2}-h^{2}\right)^{2}+\rho_{e}^{2}(c_{3}^{2}+h^{2})\right)\right]\tau_{m}^{2}\\ +\left[(\rho_{e}+h)^{2}-c_{3}^{2}\right]\left[(\rho_{e}-h)^{2}-c_{3}^{2}\right]=0.

(64)

Alternatively, $\tau_{m}$ admits a Taylor expansion by expanding the zero of (60) in orders of $e$ :

\pm\tau_{m}=\sqrt{1-\frac{c_{3}^{2}}{H^{2}}}+\frac{c_{3}^{2}\rho_{e}}{2H^{3}}\sqrt{1-\frac{c_{3}^{2}}{H^{2}}}e^{2}-\frac{3c_{3}^{2}\rho_{e}}{8H^{3}}\left[\left(\frac{\rho_{e}}{H}-\frac{c_{3}^{2}}{H^{2}}\right)^{2}-1\right]\sqrt{1-\frac{c_{3}^{2}}{H^{2}}}e^{4}+O(e^{6}),

(65)

where some maximum distance

H\equiv\rho_{e}+h

(66)

to the polar axis has been defined to condense the notation.

The integrand in (63) has a Taylor expansion in $e$ ,

\pm\int d\tau\left[\frac{c_{3}/(\rho_{e}+h)}{(1-\tau^{2})\sqrt{1-\tau^{2}-\frac{c_{3}^{2}}{(\rho_{e}+h)^{2}}}}-\frac{c_{3}\rho_{e}[(\rho_{e}+h)^{2}(2-\tau^{2})-2c_{3}^{2}]}{2(\rho_{e}+h)^{4}\left(1-\tau^{2}-\frac{c_{3}^{2}}{(\rho_{e}+h)^{2}}\right)^{3/2}}e^{2}+O(e^{4})\right]=\lambda_{\mid 1}.

(67)

We integrate the left hand side of (67) separately for each power of $e$ up to $O(e^{4})$ ,

\Big{[}\arctan\frac{\tau\frac{c_{3}}{H}}{\sqrt{T}}-\frac{c_{3}\rho_{e}}{2H^{2}}\left(\frac{\tau}{\sqrt{T}}+\arctan\frac{\tau}{\sqrt{T}}\right)e^{2}\\ -\frac{c_{3}\rho_{e}}{16H^{7}}\Big{(}\frac{\tau}{T^{3/2}}[-2H^{2}c_{3}^{2}\rho_{e}+4H^{2}c_{3}^{2}\rho_{e}T+2c_{3}^{4}\rho_{e}-6H^{3}c_{3}^{2}T+6H^{5}T-9H^{5}T^{2}-4H^{4}\rho_{e}T+6H^{4}\rho_{e}T^{2}]\\ +H^{2}[3H^{3}-2\rho_{e}H^{2}-3c_{3}^{2}H+4c_{3}^{2}\rho_{e}]\arctan\frac{\tau}{\sqrt{T}}\Big{)}e^{4}+O(e^{6})\Big{]}_{\tau_{1}}^{\tau_{2}}=\pm(\lambda_{2}-\lambda_{1}),

(68)

where

T\equiv 1-\tau^{2}-\left(\frac{c_{3}}{H}\right)^{2}

(69)

is some convenient definition of the trajectory’s distance to its solstice $\tau_{m}$ . The first term is not the principal value of the arc tangent but its steadily defined extension through the entire interval of $\tau$ -values, $|\tau|\leq\tau_{m}$ . It is an odd function of $\tau$ , and phase jumps are corrected as follows: the inclination at $\tau=0$ has (by inspection of the derivative above at $\tau=0$ ) the sign of $c_{3}$ . So whenever the triple product $\operatorname{sgn}\tau\operatorname{sgn}c_{3}\operatorname{sgn}(\arctan.)$ is negative, one must shift the branch of the arctan by adding multiples of $\pi\operatorname{sgn}\tau\operatorname{sgn}c_{3}$ to the principal value.

Whether this is to be taken between the limits $\tau_{2}$ and $\tau_{1}$ or as the sum of two components (see above) can be tested by integrating up to $\tau_{m}$ , $\int_{\tau_{1}}^{\tau_{m}}$ , where the value of the underivative at $\tau_{m}$ is given by $(1/2)\arctan 0$ , effectively $\frac{\pi}{2}\operatorname{sgn}\tau_{m}\operatorname{sgn}c_{3}$ after selecting the branch of the inverse trigonometric function as described above.

Equation (68) is solved numerically, where $c_{3}/H$ is the unknown, where $\tau_{1,2}$ and $\lambda_{1,2}$ are known from the coordinates of the two points that define the boundary value problem, and where $e$ and $H$ are constant parameters. The complexity of the equation suggests use of a Newton algorithm to search for the zero, starting from (118), $c_{3}/H\approx\cos\phi_{1}\cos\phi_{2}\sin(\lambda_{2}-\lambda_{1})/\sin Z$ , as the initial estimate.

An alternative is to insert the power series

c_{3}=c_{3}^{(0)}+c_{3}^{(2)}e^{2}+c_{3}^{(4)}e^{4}+\cdots

(70)

right into (63), integrate the orders of $e$ term-by-term, and to obtain the coefficients $c_{3}^{(2)}$ , $c_{3}^{(4)}$ etc. by comparison with the equivalent powers of the right hand side. $c_{3}^{(0)}$ is given by (118); the coefficients of the higher powers are recursively calculated from linear equations. $c_{3}^{(2)}$ , for example, is determined via

\left[\frac{\rho_{e}c_{3}^{(0)}}{H^{2}}\sqrt{1-\tau^{2}-\left(\frac{c_{3}^{(0)}}{H}\right)^{2}}\left[1-\frac{{c_{3}^{(0)}}^{2}}{H^{2}}\right]\arctan\frac{H\tau}{\sqrt{1-\tau^{2}-\left(\frac{c_{3}^{(0)}}{H}\right)^{2}}}+\frac{\rho_{e}c_{3}^{(0)}}{H^{2}}\left[\frac{1-{c_{3}^{(0)}}^{2}}{H^{2}}\right]\tau-2\frac{c_{3}^{(2)}}{H}\tau\right]_{\tau_{1}}^{\tau_{2}}=0.

(71)

The corresponding equation for $c_{3}^{(4)}$ is already too lengthy to be reproduced here, so no real advantage remains in comparison with solving the non-linear equation (67).

Once the parameter $c_{3}$ is known for a particular set of terminal coordinates, $\lambda(\phi)$ is given by replacing $\tau_{2}$ and $\lambda_{2}$ in (68) by any other generic pair of values. Two other variables of interest along the curve, the direction and integrated distance from the starting point, are then accessible with methods summarized in the next, final two sub-chapters.

IV.3 Nautical course

The nautical course at any point of the trajectory $\phi(\lambda)$ is the angle $\kappa$ in the topocentric coordinate system spanned by ${\bf e}_{\phi}$ (direction North) and ${\bf e}_{\lambda}$ (direction East), measured North over East,

\frac{d\bf r}{ds}=\cos\kappa\frac{{\bf e}_{\phi}}{|{\bf e}_{\phi}|}+\sin\kappa\frac{{\bf e}_{\lambda}}{|{\bf e}_{\lambda}|}=\sin\kappa\frac{{\bf e}_{\lambda}}{\sqrt{E}}+\cos\kappa\frac{{\bf e}_{\phi}}{\sqrt{G}}.

(72)

$d{\bf r}/ds$ is the differential of (13) with respect to $s$ , where $d/ds=(d\lambda/ds)(d/d\lambda)+(d\phi/ds)(d/d\phi)$ ,

\frac{d\bf r}{ds}\propto\frac{d\lambda}{ds}{\bf e}_{\lambda}+\frac{d\phi}{ds}{\bf e}_{\phi}.

(73)

The sign $\propto$ indicates that the left hand side of this equation is a vector normalized to unity, but not the right hand side.

\frac{\sin\kappa/\sqrt{E}}{\cos\kappa/\sqrt{G}}=\frac{d\lambda/ds}{d\phi/ds}=\frac{d\lambda}{d\phi}.

(74)

Insertion of (17), (19) and (42) yield

\frac{M+h}{(N+h)\cos\phi}\tan\kappa=\frac{1}{\frac{d\phi}{d\lambda}}=\frac{1}{\frac{d\phi}{d\tau}\frac{d\tau}{d\lambda}}=\frac{d\tau/d\phi}{\frac{d\tau}{d\lambda}}=\frac{\cos\phi}{\frac{d\tau}{d\lambda}}.

(75)

Mixing (62) into this yields the course, supposed $\phi$ and $c_{3}$ are known,

\tan\kappa=\pm\,\frac{c_{3}}{(N+h)\sqrt{\cos^{2}\phi-(\frac{c_{3}}{N+h})^{2}}}.

(76)

IV.4 Distance To Terminal Points

An implicit write-up for the distance from the origin ${\mathbf{s}}_{1}$ measured along the curve is given by separating variables in (59):

s=\pm\int_{\tau_{1}}d\tau\frac{h(1-e^{2}\tau^{2})+N(1-e^{2})}{(1-e^{2}\tau^{2})\sqrt{1-\tau^{2}-\frac{c_{3}^{2}}{(N+h)^{2}}}}.

(77)

Power series expansion of the integrand in powers of $e$ , then integration term-by-term, generate a Taylor series of the form

s=\pm(s^{(0)}+s^{(2)}e^{2}+s^{(4)}e^{4}+\ldots)\big{|}_{\tau_{1}}^{\tau}.

In the notation (69), the components of the underivative read:

s^{(0)}=H\arctan\frac{\tau}{\sqrt{1-\tau^{2}-c_{3}^{2}/H^{2}}}=H\arctan\frac{\tau}{\sqrt{T}};

(78)

s^{(2)}=-\frac{\rho_{e}}{4}\Big{[}(1+c_{3}^{2}/H^{2})\arctan\frac{\tau}{\sqrt{T}}+\tau\frac{3(1-\tau^{2})-c_{3}^{2}/H^{2}}{\sqrt{T}}\Big{]};

(79)

s^{(4)}=\frac{\rho_{e}}{64}\Big{\{}\left[9(c_{3}/H)^{4}-6(c_{3}/H)^{2}-12(c_{3}/H)^{4}(\rho_{e}/H)+4(c_{3}/H)^{2}(\rho_{e}/H)-3\right]\arctan\frac{\tau}{\sqrt{T}}\\ +\frac{\tau}{T^{3/2}}\Big{[}24T(c_{3}/H)^{4}-24T(c_{3}/H)^{2}+63T^{2}(c_{3}/H)^{2}-8(\rho_{e}/H)(c_{3}/H)^{6}+8(\rho_{e}/H)(c_{3}/H)^{4}\\ -8(\rho_{e}/H)T(c_{3}/H)^{4}+8(\rho_{e}/H)T(c_{3}/H)^{2}-12(\rho_{e}/H)T^{2}(c_{3}/H)^{2}-27T^{2}+30T^{3}\Big{]}\Big{\}}.

(80)

V Summary

Computation of the geodetic line within the iso-surface of constant altitude above the ellipsoid is of the same complexity as on its surface at zero altitude. Although the surface is no longer an ellipsoid, mathematics reaches an equivalent level of simplification at which one integral is commonly expanded in powers of the eccentricity or flattening factor. We have done this first for the parameter which provides a solution to the inverse problem, then for two of the basic functions, distance from the starting point and compass course.

Appendix A Reference: Spherical case

The limit of vanishing eccentricity, $e=0$ , simplifies the curved trajectories to arcs of great circles, and presents an easily accessible first estimate of the series expansions in orders of $e$ . The Cartesian coordinates of the two points to be connected then are

{\mathbf{s}}_{1}=(\rho_{e}+h)\left(\begin{array}[]{c}\cos\phi_{1}\cos\lambda_{1}\\ \cos\phi_{1}\sin\lambda_{1}\\ \sin\phi_{1}\\ \end{array}\right);\quad{\mathbf{s}}_{2}=(\rho_{e}+h)\left(\begin{array}[]{c}\cos\phi_{2}\cos\lambda_{2}\\ \cos\phi_{2}\sin\lambda_{2}\\ \sin\phi_{2}\\ \end{array}\right).

(81)

The angular separation $Z$ is derived from the dot product ${\bf s}_{1}\cdot{\bf s}_{2}=|{\bf s}_{1}||{\bf s}_{2}|\cos Z$ ,

\cos Z=\sin\phi_{1}\sin\phi_{2}+\cos\phi_{1}\cos\phi_{2}\cos(\lambda_{1}-\lambda_{2});\quad 0\leq Z\leq\pi.

(82)

Each point ${\bf s}$ on the great circle in between lies in the plane defined by the sphere center and the terminal points, and can therefore be written as a linear combination

{\bf s}=\alpha{\mathbf{s}}_{1}+\beta{\mathbf{s}}_{2},\quad 0\leq\alpha,\beta.

(83)

The square must remain normalized to the squared radius

s^{2}=\alpha^{2}{\mathbf{s}}_{1}^{2}+\beta^{2}{\mathbf{s}}_{2}^{2}+2\alpha\beta{\mathbf{s}}_{1}\cdot{\mathbf{s}}_{2}=\alpha^{2}(\rho_{e}+h)^{2}+\beta^{2}(\rho_{e}+h)^{2}+2\alpha\beta(\rho_{e}+h)^{2}\cos Z,

(84)

which couples the two expansion coefficients via

\alpha^{2}+\beta^{2}+2\alpha\beta\cos Z=1.

(85)

One reduction to a single parameter $\xi$ to enforce this condition is

\alpha=\frac{\cos\xi}{\sqrt{1+\sin(2\xi)\cos Z}};\quad\beta=\frac{\sin\xi}{\sqrt{1+\sin(2\xi)\cos Z}};\quad 0\leq\xi\leq\pi/2.

(86)

In summary, the point (83) on the great circle of radius $\rho_{e}+h$ between ${\mathbf{s}}_{1}$ and ${\mathbf{s}}_{2}$ has the Cartesian coordinates

	$\displaystyle{\mathbf{s}}$	$\displaystyle=$	$\displaystyle(\rho_{e}+h)\frac{\cos\xi}{\sqrt{1+\sin(2\xi)\cos Z}}\left(\begin{array}[]{c}\cos\phi_{1}\cos\lambda_{1}\\ \cos\phi_{1}\sin\lambda_{1}\\ \sin\phi_{1}\\ \end{array}\right)+(\rho_{e}+h)\frac{\sin\xi}{\sqrt{1+\sin(2\xi)\cos Z}}\left(\begin{array}[]{c}\cos\phi_{2}\cos\lambda_{2}\\ \cos\phi_{2}\sin\lambda_{2}\\ \sin\phi_{2}\\ \end{array}\right)$		(93)
		$\displaystyle\equiv$	$\displaystyle(\rho_{e}+h)\left(\begin{array}[]{c}\cos\phi(\xi)\cos\lambda(\xi)\\ \cos\phi(\xi)\sin\lambda(\xi)\\ \sin\phi(\xi)\\ \end{array}\right).$		(97)

The $z$ -component of this,

\sin\phi(\xi)=\frac{\cos\xi\sin\phi_{1}+\sin\xi\sin\phi_{2}}{\sqrt{1+\sin(2\xi)\cos Z}},

(98)

allows to convert $\xi$ into $\varphi$ . No ambiguity with respect to the branch of the $\arcsin$ arises since $-\pi/2\leq\phi\leq\pi/2$ . The ratio of the $y$ and $x$ -components demonstrates the dependence of $\lambda$ on $\xi$ ,

\tan\lambda(\xi)=\frac{\cos\xi\cos\phi_{1}\sin\lambda_{1}+\sin\xi\cos\phi_{2}\sin\lambda_{2}}{\cos\xi\cos\phi_{1}\cos\lambda_{1}+\sin\xi\cos\phi_{2}\cos\lambda_{2}},

(99)

where the $\arctan$ branch is defined by considering separately the numerator and denominator under the restrictions that no signs are canceled. The azimuth angle $\sigma$ between the points at $\xi=0$ and at $\xi$ follows from ${\mathbf{s}}\cdot{\mathbf{s}}_{1}=(\rho_{e}+h)^{2}\cos\sigma$ ,

	$\displaystyle\cos\sigma$	$\displaystyle=$	$\displaystyle\left(\frac{\cos\xi}{\sqrt{1+\sin(2\xi)\cos Z}}\left(\begin{array}[]{c}\cos\phi_{1}\cos\lambda_{1}\\ \cos\phi_{1}\sin\lambda_{1}\\ \sin\phi_{1}\\ \end{array}\right)+\frac{\sin\xi}{\sqrt{1+\sin(2\xi)\cos Z}}\left(\begin{array}[]{c}\cos\phi_{2}\cos\lambda_{2}\\ \cos\phi_{2}\sin\lambda_{2}\\ \sin\phi_{2}\\ \end{array}\right)\right)\cdot\left(\begin{array}[]{c}\cos\phi_{1}\cos\lambda_{1}\\ \cos\phi_{1}\sin\lambda_{1}\\ \sin\phi_{1}\\ \end{array}\right)$		(109)
		$\displaystyle=$	$\displaystyle\frac{\sin\xi\cos Z+\cos\xi}{\sqrt{1+\sin(2\xi)\cos Z}};\quad 0\leq\sigma\leq Z.$		(110)

The path length along the great circle perimeter is simply the radial distance $\rho_{e}+h$ to the center of coordinates times the azimuth angle $\sigma$ measured in radians,

s=\int_{1}\sqrt{ds^{2}}=(\rho_{e}+h)\sigma=(\rho_{e}+h)\arccos\frac{\sin\xi\cos Z+\cos\xi}{\sqrt{1+\sin(2\xi)\cos Z}};\quad 0\leq s\leq(\rho_{e}+h)Z.

(111)

To calculate the direction in the ${\mathbf{e}}_{\lambda}$ - ${\mathbf{e}}_{\phi}$ -plane at the starting point ${\mathbf{s}}_{1}$ , we employ $\xi$ as the parameter that mediates between $\lambda$ and $\phi$ :

\frac{d\lambda}{ds}=\frac{1}{\rho_{e}+h}\frac{d\lambda}{d\sigma}=\frac{1}{\rho_{e}+h}\frac{d\lambda}{d\xi}\,\frac{d\xi}{d\sigma}=\frac{1}{\rho_{e}+h}\frac{d\lambda}{d\xi}/\frac{d\sigma}{d\xi}.

(112)

To calculate $d\lambda/d\xi$ , use the derivative of (99) with respect to $\xi$ ,

	$\displaystyle\frac{1}{\cos^{2}\lambda}\frac{d\lambda}{d\xi}$	$\displaystyle=$	$\displaystyle\frac{-\sin\xi\cos\phi_{1}\sin\lambda_{1}+\cos\xi\cos\phi_{2}\sin\lambda_{2}}{\cos\xi\cos\phi_{1}\cos\lambda_{1}+\sin\xi\cos\phi_{2}\cos\lambda_{2}}$		(113)
			$\displaystyle-(\cos\xi\cos\phi_{1}\sin\lambda_{1}+\sin\xi\cos\phi_{2}\sin\lambda_{2})\frac{-\sin\xi\cos\phi_{1}\cos\lambda_{1}+\cos\xi\cos\phi_{2}\cos\lambda_{2}}{(\cos\xi\cos\phi_{1}\cos\lambda_{1}+\sin\xi\cos\phi_{2}\cos\lambda_{2})^{2}}.$		(113)

In particular at the starting point, where $\xi=0$ , $\lambda=\lambda_{1}$ and $\phi=\phi_{1}$ ,

\frac{1}{\cos^{2}\lambda_{1}}\frac{d\lambda}{d\xi}_{\mid 1}=\frac{\cos\phi_{2}\sin\lambda_{2}}{\cos\phi_{1}\cos\lambda_{1}}-\cos\phi_{1}\sin\lambda_{1}\frac{\cos\phi_{2}\cos\lambda_{2}}{(\cos\phi_{1}\cos\lambda_{1})^{2}}.

By multiplication with $\cos\phi_{1}\cos^{2}\lambda_{1}$

\cos\phi_{1}\frac{d\lambda}{d\xi}_{\mid 1}=\cos\phi_{2}\sin\lambda_{2}\cos\lambda_{1}-\sin\lambda_{1}\cos\phi_{2}\cos\lambda_{2}=\cos\phi_{2}\sin(\lambda_{2}-\lambda_{1}).

(114)

To calculate $d\sigma/d\xi$ , we convert the cosine in (110) to the sine,

\displaystyle\sin\sigma

\displaystyle=

\displaystyle\sqrt{1-\cos^{2}\sigma}=\frac{\sin\xi\sin Z}{\sqrt{1+\sin(2\xi)\cos Z}}.

(115)

The derivative of this with respect to $\xi$ is

\cos\sigma\frac{d\sigma}{d\xi}=\cos\xi\sin Z\frac{1}{\sqrt{1+\sin(2\xi)\cos Z}}-\frac{1}{2}\sin\xi\sin Z\frac{2\cos(2\xi)\cos Z}{(1+\sin(2\xi)\cos Z)^{3/2}},

in particular at the starting point, $\sigma=\xi=0$ ,

\frac{d\sigma}{d\xi}_{\mid 1}=\sin Z.

(116)

Insert this derivative and (114) back into (112)

\frac{d\lambda}{ds}_{\mid 1}=\frac{1}{\rho_{e}+h}\frac{\cos\phi_{2}\sin(\lambda_{2}-\lambda_{1})}{\cos\phi_{1}}\frac{1}{\sin Z},

(117)

to obtain the master parameter $c_{3}$ for the spherical case with (39),

c_{3}^{(0)}=(\rho_{e}+h)\frac{\cos\phi_{1}\cos\phi_{2}\sin(\lambda_{2}-\lambda_{1})}{\sin Z};\quad(e=0).

(118)

Appendix B Notations

$c_{5},c_{3}$	constants of integration
$E,E_{1}$	Gauss parameter eq. (17) and its value at curve origin $(\lambda_{1},\phi_{1},h)$
$E(.\setminus.)$	Incomplete Elliptic Integral of the Second Kind in the Abramowitz-Stegun notation [1, §17]
$e$	eccentricity of the ellipsoid, eq. (1)
${\mathbf{e}}_{\lambda,\phi}$	horizontal topocentric coordinate vectors at ( $\lambda,\phi,h$ )
$f$	flattening, eq. (8)
$F$	Gauss parameter, eq. (18)
$G,G_{1}$	Gauss parameter, eq. (19) and its value at curve origin
$\Gamma_{..}^{.}$	Christoffel symbols in $(\lambda,\phi,h)$ coordinates
$h$	vertical distance to surface of ellipsoid
$H$	maximum distance to polar axis (in the equatorial plane), eq. (66)
$\kappa$	nautical angle, North over East in the topocentric tangential plane
$\lambda$	longitude
$M$	a radius of curvature on the ellipsoid surface, eq. (16)
$N$	a radius of curvature on the ellipsoid surface, eq. (11)
$\rho$	distance ellipsoid center to foot point on the surface
$\rho_{e,p}$	equatorial, polar radius of ellipsoid, eq. (1)
$s$	distance along geodetic line measured from curve origin
${\mathbf{s}}$	vector from ellipsoid center to point on geodetic line
$S$	length of curved geodetic trajectory; equals $s_{2}$ at $(\lambda_{2},\phi_{2},h)$
$\operatorname{sgn}$	sign function, $\pm 1$ or $0$
$\sigma$	azimuth along great circle, eq. (111)
$T$	normalized distance from closest polar approach, eq (69)
$\tau,\tau_{1}$	$\sin\phi$ and its value at start of curve, eq. (41)
$v$	geodetic minus geocentric latitude
$\phi$	geodetic latitude
$\phi^{\prime}$	geocentric latitude
$x,y,z$	Cartesian coordinates from ellipsoid center, eq. (13)
$\xi$	parametrization of great circle (spherical case), eq. (93)
$Z$	cone angle of circular section (spherical case), eq. (82)

Appendix C FEM implementation

C.1 Compilation

The simplest numerical solution of the inverse problem without restriction on the eccentricity could be a finite-element (FEM) integration of (63) and iterative adjustment of the single free parameter $c_{3}$ . The Java program in the anc directory implements this approach. It is either compiled with

cd anc ; make

on Linux systems or by manually executing the compiler steps in anc/Makefile . It is then called with

•
```
java -jar Geod.jar
```
which will query the parameters interactively
•

or providing all parameters with

java -jar Geod.jar [-e $e$ ] [-R $\rho_{e}$ ] [-h h ] [-s $N_{s}$ ] [-u $N_{2}$ ] $\phi_{1}$ $\lambda_{1}$ $\phi_{2}$ $\lambda_{2}$

on the command line. The last four parameters are the geodetic angles of the start and final point in degrees. $N_{s}$ is the positive integer number of finite elements in the interval $\lambda$ -interval in the approximation, and $N_{2}$ in the range 1… $N_{s}$ (and typically a divisor of $N_{s}$ ) is the small positive integer subsampling number of the results along the trajectory which are actually printed to the standard output. The square brackets above indicate that the switches are optional because they have default values; the square brackets are not part of the command line syntax.
•

or calling the program as

java -cp Geod.jar org.nevec.rjm.GeodGUI

which allows to type the parameters in fields of a graphical user interface (GUI); the purpose of that wrapper is to embed the program in web applications that support the Java Network Launch Protocol (JNLP).

The output lines contain the information on the trajectory: the first three values are the $x$ , $y$ and $z$ Cartesian coordinates of the subsampled points, the next three values are $\phi$ , $\lambda$ and $\kappa$ at these points in degrees, and the last value is the length $s$ travelled from the start point.

C.2 Overview of Functions

Member functions in overview: the constructors Geod define a surface from the parameters $\rho_{e}$ , $e$ and $h$ in which the geodetic line is embedded. getCartesian computes the vector (13). curvN computes (11). dNdtau computes

\frac{dN}{d\tau}=N(\tau)\frac{e^{2}\tau}{1-e^{2}\tau^{2}}.

(119)

flatt computes (8). curvM computes (16). dMdtau computes

\frac{dM}{d\tau}=3M(\tau)\frac{e^{2}\tau}{1-e^{2}\tau^{2}}.

(120)

d2Mdtau2 computes

\frac{d^{2}M}{d\tau^{2}}=3M(\tau)\frac{e^{2}(1+4e^{2}\tau^{2})}{(1-e^{2}\tau^{2})^{2}}.

(121)

GaussE computes (17). dEdtau computes

\frac{dE}{d\tau}=-2\tau(N+h)(M+h).

(122)

d2Edtau2 computes the next higher derivative, $d^{2}E/d\tau^{2}$ . GaussG computes (19). dtaudlambda computes $d\tau/d\lambda$ via (62), referencing one factor to (59). dsdlambda is $ds/d\lambda$ , the inverse of (61). discrT computes $1-\tau^{2}-c_{3}^{2}/(N+h)^{2}$ , which generalizes (69) to nonzero $e$ . Its derivatives

	$\displaystyle\frac{d}{d\tau}\left[1-\tau^{2}-\frac{c_{3}^{2}}{[N(\tau)+h]^{2}}\right]$	$\displaystyle=$	$\displaystyle 2\tau\left[\frac{Ne^{2}c_{3}^{2}}{(N+h)^{3}(1-e^{2}\tau^{2})}-1\right];$		(123)
	$\displaystyle\frac{d^{2}}{d\tau^{2}}\left[1-\tau^{2}-\frac{c_{3}^{2}}{[N(\tau)+h]^{2}}\right]$	$\displaystyle=$	$\displaystyle-2\left[1-\frac{Nc_{3}^{2}e^{2}}{(N+h)^{3}(1-e^{2}\tau^{2})}\left(1+\frac{3he^{2}\tau^{2}}{(N+h)(1-e^{2}\tau^{2})}\right)\right],$		(124)

are implemented in dTdtau and d2Tdtau2. dtauds calculates (59). d2taudlambda2 calculates the derivative of (62),

\frac{d^{2}\tau}{d\lambda^{2}}=\frac{d}{d\lambda}\frac{E(\tau)\sqrt{1-\tau^{2}-c_{3}^{2}/(N+h)^{2}}}{c_{3}(h+M)}=\frac{d\tau}{d\lambda}\frac{d}{d\tau}\frac{E(\tau)\sqrt{1-\tau^{2}-c_{3}^{2}/(N+h)^{2}}}{c_{3}(h+M)}.

(125)

d3taudlambda3 is the next higher order application of Bruno di Faà’s formula to relegate derivatives $d/d\lambda$ to derivatives $d/d\tau$ , [7, 0.430],

\frac{d^{3}\tau}{d\lambda^{3}}=\frac{d^{2}\tau}{d\lambda^{2}}\frac{d}{d\tau}\frac{E(\tau)\sqrt{1-\tau^{2}-c_{3}^{2}/(N+h)^{2}}}{c_{3}(h+M)}+\left(\frac{d\tau}{d\lambda}\right)^{2}\frac{d^{2}}{d\tau^{2}}\frac{E(\tau)\sqrt{1-\tau^{2}-c_{3}^{2}/(N+h)^{2}}}{c_{3}(h+M)}.

(126)

d2sdlambda2 calculates

\frac{d^{2}s}{d\lambda^{2}}=\frac{d}{d\lambda}\frac{E}{c_{3}}=\frac{1}{c_{3}}\,\frac{d\tau}{d\lambda}\,\frac{d}{d\tau}E.

(127)

d3sdlambda3 calculates

\frac{d^{3}s}{d\lambda^{3}}=\frac{d^{2}}{d\lambda^{2}}\frac{E}{c_{3}}=\frac{1}{c_{3}}\left[(\frac{d\tau}{d\lambda})^{2}\,\frac{d^{2}}{d\tau^{2}}E+\frac{d^{2}\tau}{d\lambda^{2}}\,\frac{d}{d\tau}E\right].

(128)

c3Sphere returns the estimate (118). dtaudsSignum returns the sign of $d\tau/ds$ at $\tau_{1}$ , obtained by considering the sign of the derivative of (98) with respect to $\xi$ . adjLambdaEnd modifies $\phi_{2}$ modulo $2\pi$ to select the smallest value of $|\phi_{2}-\phi_{1}|$ . nautAngle computes $\kappa$ from (76).

tauShoot walks along a geodetic line on a discrete mesh of width $\Delta\lambda$ by extrapolating

\tau_{\lambda+\Delta\lambda}\approx\tau_{\lambda}+\frac{d\tau}{d\lambda}\Delta\lambda+\frac{1}{2}\frac{d^{2}\tau}{d\lambda^{2}}(\Delta\lambda)^{2}+\frac{1}{6}\frac{d^{3}\tau}{d\lambda^{3}}(\Delta\lambda)^{3}+\frac{1}{24}\frac{d^{4}\tau}{d\lambda^{4}}(\Delta\lambda)^{4},

(129)

initialized at $\lambda_{1},\phi_{1}$ , given $c_{3}$ . The equivalent formula is used to build up $s_{\lambda+\Delta\lambda}$ . c3shoot calls tauShoot four times to adjust $c_{3}$ such that the error by which $\phi_{2}$ was missed—returned by tauShoot—is minimized. The first call assumes (118), the second takes an arbitrary small offset, and the third and fourth estimates are from linear and quadratic interpolations in the earlier calls to zoom into a root of this error as a function of $c_{3}$ . The last of these runs tabulates the Cartesian coordinates (13), $\lambda$ , $\phi$ , $\kappa$ and $s$ on a subgrid of the $\lambda$ -mesh. main collects some adjustable parameters plus the pairs $(\lambda_{1},\phi_{1})$ and $(\lambda_{2},\phi_{2})$ , and calls c3shoot to solve the inverse problem of geodetics.

References

Abramowitz and Stegun [1972] Abramowitz, M., and I. A. Stegun (eds.), 1972, Handbook of Mathematical Functions (Dover Publications, New York), 9th edition, ISBN 0-486-61272-4.
Bouasse [1919] Bouasse, H., 1919, Geographie Mathématique (Librairie Delagrave, Paris).
Bowring [1983] Bowring, B. R., 1983, Bull. Geod. 57(1–4), 109.
Dorrer [1999] Dorrer, E., 1999, in Quo vadis geodesia…?, edited by F. Krumm and V. S. Schwarze (Universität Stuttgart), Technical Reports of Geodesy and GeoInformatics, ISSN 0933-2839.
Dufour [1958] Dufour, H. M., 1958, Bull. Geod. 32(2), 26.
Fukushima [2006] Fukushima, T., 2006, J. Geod. 79(12), 689.
Gradstein and Ryshik [1981] Gradstein, I., and I. Ryshik, 1981, Summen-, Produkt- und Integraltafeln (Harri Deutsch, Thun), 1st edition, ISBN 3-87144-350-6.
Hradilek [1976] Hradilek, L., 1976, Bull. Geod. 50(4), 301.
Jones [2004] Jones, G. C., 2004, J. Geod. 76(8), 437.
Kaplan [2006] Kaplan, G. H., 2006, arXiv:astro-ph/0602086 eprint astro-ph/0602086.
Karney [2013] Karney, C. F. F., 2013, J. Geod. 87, 43.
Keeler and Nievergelt [1998] Keeler, S. P., and Y. Nievergelt, 1998, SIAM Review 40(2), 300.
Long [1975] Long, S. A. T., 1975, Cel. Mech. 12(2), 225.
Mai [2010] Mai, E. ., 2010, J. Appl. Geodesy 4, 145.
Mathar [2010] Mathar, R. J., 2010, arXiv:1005.3790 [math.CA] .
National Imagery and Mapping Agency [2000] National Imagery and Mapping Agency, 2000, Department Of Defense World Geodetic System 1984, Technical Report TR8350.2, NIMA, URL http://earth-info.nga.mil/GandG/publications/tr8350.2/tr8350_2.html.
Ölander [1952] Ölander, V. R., 1952, Bull. Geod. 26(3), 337.
Pollard [2002] Pollard, J., 2002, J. Geod. 76(1), 36.
Rapp [1991] Rapp, R. H., 1991, Geometric Geodesy Part 1 (Ohio State University, Columbus, Ohio).
Reichardt [1957] Reichardt, H., 1957, Vorlesungen über Vektor- und Tensorrechnung, volume 34 of Hochschulbücher für Mathematik (Deutscher Verlag der Wissenschaften, Berlin).
Saito [1970] Saito, T., 1970, Bull. Geod. 44(4), 341.
Sjöberg [2012] Sjöberg, L. E., 2012, J. Geod. Sci. 2(3), 162.
Smart [1949] Smart, W. M., 1949, Text-book on Spherical Astronomy (Cambridge University Press, Cambridge), 4th edition.
Sodano [1958] Sodano, E. M., 1958, Bull. Geod. 32(2), 13.
Thomas [1965] Thomas, P. D., 1965, J. Geophys. Res. 70(14), 3331.
Tienstra [1951] Tienstra, J. M., 1951, Bull. Geod. 25(1), 7.
Tseng [2014] Tseng, W.-K., 2014, J. Navig. 67(5), 825.
Vermeille [2004] Vermeille, H., 2004, J. Geod. 78(1–2), 94.
You [1999] You, R.-J., 1999, in Quo vadis geodesia…?, edited by F. Krumm and V. S. Schwarze (Universität Stuttgart), Technical Reports of Geodesy and GeoInformatics, ISSN 0933-2839.
Zhang et al. [2005] Zhang, C.-D., H. T. Hsu, X. P. Wu, S. S. Li, Q. B. Wang, H. Z. Chai, and L. Du, 2005, J. Geod. 79(8), 413.