Geometric Properties of Partial Sums of Univalent Functions

The $n$th partial sum (or $n$th section) of the function $f$, denoted by $f_{n}$, is the polynomial defined by

The second partial sum $f_{2}$ of the Koebe function $k$ is given by

It is easy to check directly (or by using the fact that $|f_{2}^{\prime}(z)-1|<1$ for $|z|<1/4$) that this function $f_{2}$ is univalent in the disk $\mathbb{D}_{1/4}$ but, as $f_{2}^{\prime}(-1/4)=0$, not in any larger disk. This simple example shows that the partial sums of univalent functions need not be univalent in $\mathbb{D}$.

The second partial sum of the function $f(z)=z+\sum_{k=2}^{\infty}a_{k}z^{k}$ is the function $f_{2}(z)=z+a_{2}z^{2}$. If $a_{2}=0$, then $f_{2}(z)=z$ and its properties are clear. Assume that $a_{2}\neq 0$. Then the function $f_{2}$ satisfies, for $|z|\leq r$, the inequality

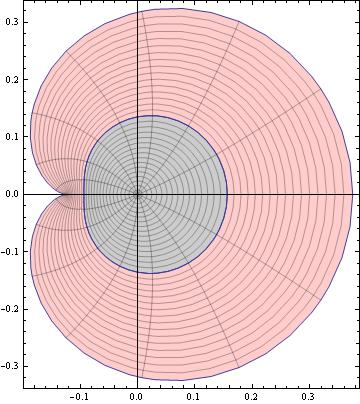
provided $r<1/(2|a_{2}|)$. Thus the radius of starlikeness of $f_{2}$ is $1/(2|a_{2}|)$. Since $f_{2}$ is convex in $|z|<r$ if and only if $zf_{2}^{\prime}$ is starlike in $|z|<r$, it follows that the radius of convexity of $f_{2}$ is $1/(4|a_{2}|)$. If $f$ is univalent or starlike univalent, then $|a_{2}|\leq 2$ and therefore the radius of univalence of $f_{2}$ is 1/4 and the radius of convexity of $f_{2}$ is 1/8. (See Fig. 1 for the image of $\mathbb{D}_{1/4}$ and $\mathbb{D}_{1/8}$ under the function $z+2z^{2}$.) For a convex function $f$ as well as for functions $f$ whose derivative has positive real part in $\mathbb{D}$, $|a_{2}|\leq 1$ and so the radius of univalence for the second partial sum $f_{2}$ of these functions is 1/2 and the radius of convexity is 1/4. In [25], the starlikeness and convexity of the initial partial sums of the Koebe function $k(z)=z/(1-z)^{2}$ and the function $l(z)=z/(1-z)$ are investigated.

It is therefore of interest to determine the largest disk $\mathbb{D}_{\rho}$ in which the partial sums of the univalent functions are univalent. Szegö also wrote a survey [50] on partial sums in 1936. In the present survey, the various results on the partial sums of functions belonging to the subclasses of univalent functions are given. However, Cesàro means and other polynomials approximation of univalent functions are not considered in this survey.

The second partial sum of the Koebe function indicates that the partial sums of univalent functions cannot be univalent in a disk of radius larger than 1/4. Indeed, by making use of Koebe’s distortion theorem and Löwner’s theory of univalent functions, Szegö [49] in 1928 proved the following theorem.

Using an inequality of Goluzin, Jenkins [14] (as well as Ilieff [12], see Duren [4, §8.2, pp. 241–246]) found a simple proof of this result and also shown that the partial sums of odd univalent functions are univalent in $\mathbb{D}_{1/\sqrt{3}}$. The number $1/\sqrt{3}$ is shown to be the radius of starlikeness of the partial sums of the odd univalent functions by He and Pan [10]. Iliev [13] investigated the radius of univalence for the partial sums $\sigma^{(k)}_{n}(z)=z+c^{(k)}_{1}z^{k+1}+\cdots+c^{(k)}_{n}z^{nk+1}$, $n=1,2,\dotsc$, of univalent function of the form $f_{k}(z)=z+c^{(k)}_{1}z^{k+1}+\cdots$. For example, it is shown that $\sigma^{(2)}_{n}$ is univalent in $|z|<1/\sqrt{3}$, and $\sigma^{(3)}_{n}$ is univalent in $|z|<\root 3 \of{3}/2$, for all $n=1,2,\dotsc$. He has also shown that $\sigma^{(1)}_{n}(z)$ is univalent in $|z|<1-4(\ln n)/n$ for $n\geq 15$. Radii of univalence are also determined for $\sigma^{(2)}_{n}$ and $\sigma^{(3)}_{n}$, as functions of $n$, and for $\sigma^{(k)}_{1}$ as a function of $k$.

Szegö’s theorem that the partial sums of univalent functions are univalent in $\mathbb{D}_{1/4}$ was strengthened to starlikeness by Hu and Pan [11]. Ye [53] has shown that the partial sums of univalent functions are convex in $\mathbb{D}_{1/8}$ and that the number 1/8 is sharp. Ye [53] has proved the following result.

Ruscheweyh gave an extension of Szegö’s theorem that the $n$th partial sums $f_{n}$ are starlike in $\mathbb{D}_{1/4}$ for functions belonging not only to $\mathcal{S}$ but also to the closed convex hull of $\mathcal{S}$.

Let $\mathcal{F}=\operatorname{clco}\{\sum_{k=1}^{n}x^{k-1}z^{k}:|x|\leq 1\}$ where $\operatorname{clco}$ stands for the closed convex hull. Convolution of two analytic functions $f(z)=z+\sum_{k=2}^{\infty}a_{k}z^{k}$ and $g(z)=z+\sum_{k=2}^{\infty}b_{k}z^{k}$ is the function $f*g$ defined by

Ruscheweyh [33] proved the following theorem.

In particular, for $g(z)=z+z^{2}+\cdots+z^{n}$, Theorem 2.3 reduces to the following result.

The class $\mathcal{F}$ contains the following two subsets:

and

Since the class $\mathcal{C}$ of convex functions is a subset of $\mathcal{R}_{1/2}$, it is clear that $\mathcal{S}^{*}\subset\mathcal{C}\subset\mathcal{F}$. For $g(z)=z/(1-z)^{2}\in\mathcal{S}^{*}$, Theorem 2.3 reduces to the following:

We remark that Suffridge [48] has shown that the partial sums of the function $e^{1+z}$ are all convex. More generally, Ruscheweyh and Salinas [35] have shown that the functions of the form $\sum_{k=0}^{\infty}a_{k}(1+z)^{k}/k!$, $a_{0}\geq a_{1}\geq\dots\geq 0$ are either constant or convex univalent in the unit disk $\mathbb{D}$. Let $F(z)=z+\sum_{1}^{\infty}a_{k}z^{-k}$ be analytic $|z|>1$. Reade [27] obtained the radius of univalence for the partial sums $F_{n}(z)=z+\sum_{1}^{n}a_{k}z^{-k}$ when $F$ is univalent or when $\operatorname{Re}F^{\prime}(z)>0$ in $|z|>1$.

Szegö [49] showed that the partial sums of starlike (respectively convex) functions are starlike (respectively convex) in the disk $\mathbb{D}_{1/4}$ and the number $1/4$ cannot be replaced by a larger one. If $n$ is fixed, then the radius of starlikeness of $f_{n}$ can be shown to depend on $n$. Motivated by a result of Von Victor Levin that the $n$th partial sum of univalent functions is univalent in $D_{\rho}$ where $\rho=1-6(\ln n)/n$ for $n\geq 17$, Robertson [28] determined $R_{n}$ such that the $n$th partial sum $f_{n}$ to have certain property $P$ in $\mathbb{D}_{R_{n}}$ when the function $f$ has the property $P$ in $\mathbb{D}$. He considered the function has one of the following properties: $f$ is starlike, $f/z$ has positive real part, $f$ is convex, $f$ is typically-real or $f$ is convex in the direction of the imaginary axis and is real on the real axis. An error in the expression for $R_{n}$ was later corrected in his paper [29] where he has extended his results to multivalent starlike functions.

The radius of starlikeness of the $n$th partial sum of starlike function is given in the following theorem.

An analytic function $f(z)=z^{p}+\sum_{k=1}^{\infty}a_{p+k}z^{p+k}$ is $p$-valently starlike [29, p. 830] if $f$ assumes no value more than $p$ times, at least one value $p$ times and

For $p$-valently starlike functions, Robertson [29, Theorem A, p. 830] proved that the radius of $p$-valently starlikeness of the $n$th partial sum $f_{n}(z)=z^{p}+\sum_{k=1}^{n}a_{p+k}z^{p+k}$ is at least $1-(2p+2)\log n/n$. Ruscheweyh [32] has given a simple proof that the partial sums $f_{n}$ of $p$-valently starlike (or close-to-convex) function is $p$-valently starlike (or respectively close-to-convex) in $|z|<1/(2p+2)$.

Kobori [16] proved the following theorem and Ogawa [23] gave another proof of this result.

In view of the above theorem, the $n$th partial sum of Koebe function $z/(1-z)^{2}$ is convex in $|z|<1/8$. A verification of this fact directly can be used to give another proof of this theorem by using the fact [34] that the convolution of two convex function is again convex. It is also known [34] that $\operatorname{Re}(f(z)/f_{n}(z))>1/2$ for a function $f$ starlike of order 1/2. This result was extended by Singh and Paul [45] in the following theorem.

For a convex function $f\in\mathcal{C}$, it is well-known that $\operatorname{Re}(f(z)/z)>1/2$. Extending this result, Sheil-Small [36] proved the following theorem.

As a consequence of this theorem, he has shown that the function $Q_{n}$ given by $Q_{n}(z)=\int_{0}^{z}(f_{n}(\eta)/\eta)d\eta$ is a close-to-convex univalent function. In fact, the inequality (4.1) holds for $f\in\mathcal{S}^{*}(1/2)$ as shown in [34]. The inequality (4.1) also holds for odd starlike functions as well as for functions whose derivative has real part greater than 1/2 [46].

Recall once again that [49] the partial sums of convex functions are convex in the disk $\mathbb{D}_{1/4}$ and the number $1/4$ cannot be replaced by a larger one. A different proof of this result can be given by using results about convolutions of convex functions. In 1973, Ruscheweyh and Shiel-Small proved the Polya-Schoenberg conjecture (of 1958) that the convolution of two convex univalent functions is again convex univalent. Using this result, Goodman and Schoenberg gave another proof of the following result of Szegö [49].

Let $P_{\alpha,n}$ denote the class of functions $p(z)=1+c_{n}z^{n}+\cdots\ (n\geq 1)$ analytic and satisfying the condition $\text{Re}\,p(z)>\alpha\ (0\leq\alpha<1)$ for $z\in\mathbb{D}$. Bernardi [3] proved that the sharp inequality

holds for $p(z)\in P_{\alpha,n}$, $|z|=r<1$, and $n=1,2,3,\dotsc$. He has also shown that, for any complex $\mu$, $\text{Re}\,\mu=\beta>0$,

For a convex function $f$, he deduced the sharp inequality

Making use of this inequality, he proved the following theorem.

The above theorem with a weaker conclusion that $f_{n}$ is univalent was obtained earlier by Ruscheweyh [31]. Singh [44] proved that the $n$th partial sum $f_{n}$ of a starlike function of order 1/2 is starlike in $|z|<r_{n}$ where $r_{n}$ is given in Theorem 4.3. He has also shown that the conclusion of Theorem 4.3 can be strengthened to convexity if one assumes that $f$ is a convex function of order 1/2. In addition, for a convex function $f$ of order 1/2, he has shown that $\operatorname{Re}(f_{n}(z)/z)>1/2$ and 1/2 is sharp. It is also known that all the partial sums of a convex function $f$ of order 1/2 are close-to-convex with respect to $f$ itself and that there are convex functions of order $\alpha<1/2$ whose partial sums are not univalent [30]. Singh and Puri [46] have however shown that each of the partial sums of an odd convex function $f$ is close-to-convex with respect to $f$.

Silverman [38] also proved Theorem 4.3 by finding the radius of starlikeness (of order $\alpha$) of the $n$th partial sums of the function $z/(1-z)$. The result then follows from the fact that the classes of convex and starlike functions are closed under convolution with convex functions.

Silverman [38, Corollary 2, pp. 1192] also proved that the $n$th partial sum $f_{n}$ of a convex function $f$ is starlike in $|z|<\sqrt{23/71}$ for $n\geq 3$ and the radius $\sqrt{23/71}$ is sharp. For a convex function $f$, its $n$th partial sum $f_{n}$ is shown to be starlike of order $\alpha$ in $|z|<(1-\alpha)/(2-\alpha)$, convex of order $\alpha$ in $|z|<(1-\alpha)/(2(2-\alpha))$ and the radii are sharp.

A function $f\in\mathcal{S}$ is uniformly convex, written $f\in\mathcal{UCV}$, if $f$ maps every circular arc $\gamma$ contained in $\mathbb{D}$ with center $\zeta\in\mathbb{D}$ onto a convex arc. The class $\mathcal{S}_{P}$ of parabolic starlike functions consists of functions $f\in\mathcal{A}$ satisfying

In other words, the class $\mathcal{S}_{P}$ consists of functions $f=zF^{\prime}$ where $F\in\mathcal{UCV}$. A survey of these classes can be found in [1].

Nabetani [20] noted that Theorem 5.1 holds even if the inequality $|f^{\prime}(z)|\leq M$ is replaced by the inequality

He has shown that the radii of starlikeness and convexity of functions $f$ satisfying the inequality

are respectively the positive root of the equations

and

For functions whose derivative has positive real part, MacGregor [18] proved the following result.