Giant plateau in the THz Faraday angle in gated Bi₂Se₃

In two-dimensional quantum Hall systems, one-dimensional edge states are topologically protected quantum states characterized by integer Chern numbers. Three dimensional topological insulators are characterized by a quantized magneto-electric term appearing in the effective Lagrangian, quantized in units of the fine structure constant $\alpha=\frac{e^{2}}{\hbar c}$.Volkov and Mikhailov (1985); Hasan and Kane (2010); Qi and Zhang (2011); Maciejko et al. (2010); Tse and MacDonald (2010) The quantization condition of this magneto-electric term stems from a Chern-Simons form of the Berry phase, known as the axion angle in particle physics.Wilczek (1987); Qi et al. (2008) In the non-trivial case, the axion angle attains odd-multiple values of $\pi$ resulting in two dimensional topologically protected surface states that are spin polarized. By breaking time reversal symmetry, these singly-occupied two dimensional Dirac states are predicted to exhibit a $1/2$-quantized Hall step near the Dirac point, a smoking gun signature of the topological origin of the surface state.Qi et al. (2008) Kerr or Faraday terahertz (THz) measurements offer a method to cleanly measure this quantized step since no contacts to the sample are required alleviating complications that can occur from gating a sample with no edges.Jenkins et al. (2012); Jenkins et al. (2010a)

Bi₂Se₃ has a single surface-state Dirac cone whose Dirac point is well above the valence band. The material has one of the largest bulk band gaps of all known topological insulators allowing access to the Dirac cone over a large range of Fermi energies. However, Bi₂Se₃ is susceptible to n-type bulk doping from defects as well as environmental surface doping.Butch et al. (2010); Jenkins et al. (2010a); Kong et al. (2011); Checkelsky et al. (2011); Analytis et al. (2010); Steinberg et al. (2010); Kim et al. (2012) High quality epitaxially grown thin films of Bi₂Se₃ have relatively low n-type bulk doping,Bansal et al. (2011a) and subsequent capping with In₂Se₃ further lowers the Fermi level of the surface states allowing conventional gating to reach the Dirac point.Jenkins et al. (2012)

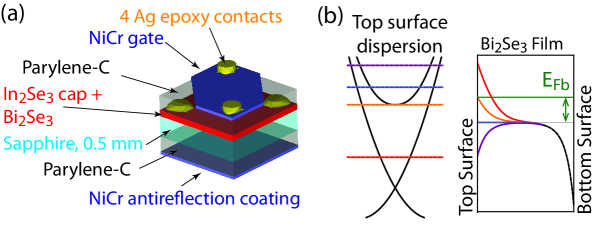
No previous optical probe has been reported that attempts to measure the quantized Hall effect on a topological insulator as a function of gate voltage.Jenkins et al. (2012); Jenkins et al. (2010a); Sushkov et al. (2010); Brune et al. (2011); Hancock et al. (2011); Kvon et al. (2012); Schafgans et al. (2012); Valdes Aguilar et al. (2012) We report Faraday angle and transmission measurements performed at a fixed laser frequency of $\omega/2\pi=0.74$ THz as a function of gate voltage at discrete magnetic fields up to $8$ T on two topological insulating films. These Bi₂Se₃ thin films, $40$ and $60$ quintuple layers thick (1 QL $\approx$ 1 nm), were grown epitaxially onto $0.5$ mm thick sapphire substrates and capped with $10$ nm thick In₂Se₃ layers without breaking vacuum.Bansal et al. (2011a, b) As depicted in Figure 1(a), the dielectric Parylene-C was deposited encasing the sample to a thickness of $590$ nm ($620$ nm) for the 60 (40) QL film. A NiCr top gate and a NiCr antireflection coating were evaporated onto the Parylene-C. For the 60 QL device, the gate moves a charge density of $2.6\times 10^{10}e/\text{cm}^{2}$ per volt on or off the Bi₂Se₃ film.

The Faraday angle is related to the off-axis conductivity $\sigma_{xy}$ of a thin film by $\theta_{F}\approx Z\sigma_{xy}/(1+Z\sigma_{xx})$ where $Z=Z_{0}/(n_{s}+1)$, and $n_{s}$ is the substrate index of refraction, $Z_{0}$ is the impedance of free space, and $\sigma_{xx}$ is the longitudinal conductivity.Jenkins et al. (2010b); Jenkins et al. (2012) Considering the case where the cyclotron frequency $\omega_{c}$ is large compared to the scattering rate $\gamma$ and radiation frequency $\omega$, and $Z\sigma_{xx}$ is small compared with $1$, crossing a Landau level results in $\Delta\theta_{F}\approx 2\alpha/(n_{s}+1)$. Under very specific geometric conditions, the substrate properties can be ignored and $\Delta\theta_{F}$ is quantized exactly in units of $\alpha$.O’Connell and Wallace (1982); Volkov and Mikhailov (1985); Maciejko et al. (2010); Tse and MacDonald (2010) More generally, the quantization of $\Delta\theta_{F}$ from step-to-step is scaled by the material properties of the substrate and any longitudinal conductivity contributions (like a conducting gate or other dissipation channels), as well as corrections from non-zero $\gamma$ and $\omega$.Morimoto et al. (2009); Stier et al. (2011)

The complex Faraday angle measurement at THz frequencies utilizes polarization-modulated fixed-frequency laser radiation, a technique detailed elsewhere.Jenkins et al. (2010b) The beam is normally incident on the film held at $10$ K that is maintained in a normally applied magnetic field. The transmission through the film is measured concurrently. The differential Faraday angle $\Delta\theta_{F}$ and the differential transmission $\Delta T$ are differences between the optical signals measured at a fixed gate voltage $V_{g}^{0}=+170$ V and the signals measured at a variable gate voltage $V_{g}$.

The differential Faraday angle $\Delta\theta_{F}$ and differential transmission $\Delta T$ as a function of gate voltage at fixed fields for the two devices are reported in Figure 2. Measurements performed at THz frequencies on the same 60 quintuple layer (QL) device, but as a function of magnetic field, are reported in reference 8. The gate sweeps at fixed magnetic field presented here offer better signal-to-noise than previous measurements. $Re(\Delta\theta_{F})$ is measured to within a standard deviation of the mean of $30$ $\mu$rad without systematic drift effects associated with changing the magnetic field. With this additional sensitivity, $Re(\Delta\theta_{F})$ of the $60$ QL film shows an extraordinarily flat response over a tremendous span of gate voltages, from $+170$ V to $+70$ V.

The previous THz measurements on the 60 QL film provide an overview of the characteristics of the film. The salient features of the THz data are captured utilizing two gate dependent Drude terms in the conductivity: the first term is primarily associated with the bulk carriers of the gate-modulated screened region near the top surface (MTB), and the second term is the top topological surface state (TSS). The conception of the model is based upon the Thomas-Fermi band bending in the film, depicted in Figure 1(b). All carrier contributions in the film were measured to be n-type. Based on the small measured cyclotron mass $m_{c}=\hbar k_{F}/v_{F}$ at high negative gate voltages, the Dirac point is estimated to be in the vicinity of $-170$ V. The conduction band edge (CBE) voltage location is $V_{g}=-70$ V deduced from a sudden increase in the measured surface state scattering rate, interpreted as the optical signature where surface state carriers begin scattering into bulk channels, and is demarcated by the green vertical dashed lines in Figure 2.Jenkins et al. (2012) This corresponds to a CBE that is 80 meV above the Dirac point, whereas the vacuum/Bi₂Se₃ interface CBE characterized by surface probes is at 190 meVXia et al. (2009); Zhu et al. (2011); Bahramy et al. (2012) implying a shift in the Dirac point due to the In₂Se₃/Bi₂Se₃ interface properties.Jenkins et al. (2012) With regard to the plateau region, this is a minor point since top surface bulk carriers are degenerate with the surface state carriers over the full range of the plateau whether the CBE location is 80 or 190 meV above the Dirac point (as discussed in more detail in the Appendix).

There are a number of important observations associated with the plateau in the $Re(\Delta\theta_{F})$ shown in Figure 2(a) and (g). The first is the degree of flatness. Such an extremely flat response is very difficult to reproduce invoking non-quantized behavior. In the simplest view, a gate moves electrons to the film with increasingly positive gate voltage, predictably lowering the transmission as reported in Figure 2(c), yet the real part of the Faraday angle remains constant over a large range of voltages.

A slightly more sophisticated approach using the same multi-fluid Drude model that reproduced the features of all the data reported in reference 8 does not reproduce the extremely flat behavior of the $Re(\Delta\theta_{F})$ gate sweeps in fixed magnetic field, as shown in Figure 2(i). The gate dependent scattering rates of the TSS and MTB Drude terms give rise to an extremum in the modelled response of Figure 2(i). The observation in Figure 2(g) of such a flat response over such a large range of gate voltages is irreconcilable with two gate-dependent n-type Drude terms while maintaining consistency with previous optical data. The data suggests the existence of localized states associated with $\sigma_{xy}$ which absorb the transferred charge from the gate but give no additional contribution to $Re(\theta_{F})$.

The formation of Landau levels is one way that can provide localized states. Although we currently do not have a complete explanation for the observed plateau, recent dc Hall measurements on highly doped $\gtrsim 10^{19}$ cm^-3 Bi₂Se₃ bulk crystals, performed on many different samples spanning four orders of magnitude in thickness, appear to support the scenario that an extraordinary bulk quantum Hall effect (QHE) occurs in which each pair of QLs contribute a distinct Landau Level to the Hall response.Cao et al. (2012) These Landau levels appear to act in unison such that the step-to-step height $\Delta\sigma_{xy}=\text{(\# of QLs)}\frac{e^{2}}{h}$. However, $\rho_{xx}$ oscillates but does not go to zero, remaining comparable with $\rho_{xy}$ even within plateaus, indicating appreciable dissipation. Within this context, we discuss the character of the observed plateau in the $Re(\Delta\theta_{F})$ shown in Figure 2(g).

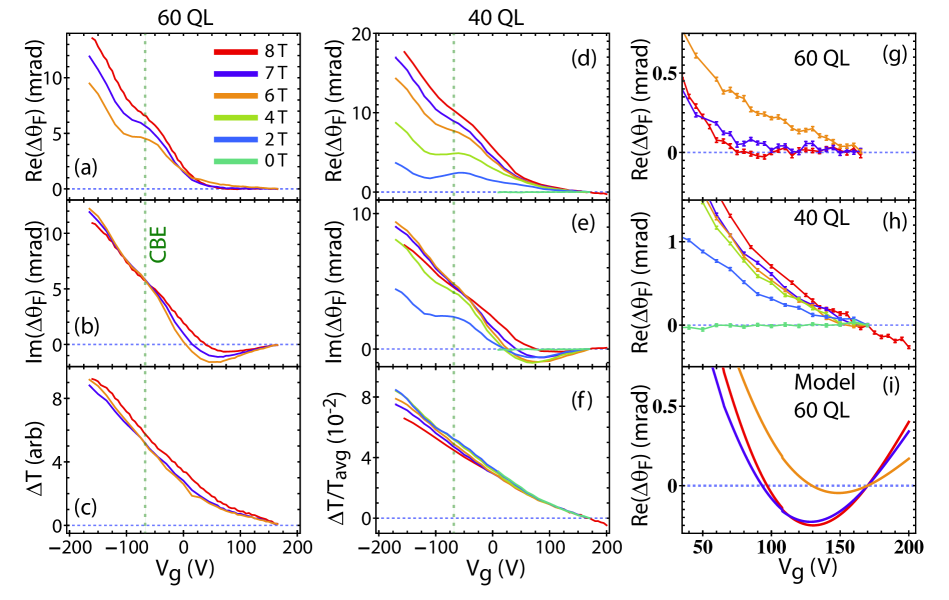
For small longitudinal conductivity ($Z\,\sigma_{xx}<<1)$ and large cyclotron frequency $\omega_{c}>>\gamma,\,\omega$, the finite-frequency off-axis conductivity $\sigma_{xy}=\Omega_{0}\omega_{c}/((\gamma-\imath\omega)^{2}+\omega_{c}^{2})$ reduces to $\sigma_{xy}=ne/B$ since the spectral weight $\Omega_{0}=ne^{2}/m$ and the cyclotron frequency $\omega_{c}=eB/m_{c}$. The electron density $n$ changes by $B/(h/e)$ when the Fermi level sweeps through a single Landau Level at fixed magnetic field $B$, so $Z_{0}\Delta\sigma_{xy}=2\alpha$. Since sapphire has an index of refraction of $n\approx 3$, $Z_{0}/R\approx 1$ for the NiCr gate, and $Z_{0}\sigma_{xx}\approx 1$, the change in the real part of the Faraday angle upon stepping through a Landau Level is expected to be $Re(\Delta\theta_{F})\approx\alpha/3=2.4$ mrad in the low frequency limit. In this limit, the $Re(\Delta\theta_{F})$ at $8$ T is flat over a range of at least $100$ V to within 1/80 of the expected step size from a single Landau level. The expected step size for a 2DEG has been predicted to increase from this estimate due to the finite probe frequency ($\omega=4.6$ THz) and scattering rate ($1/\tau\approx 5$ THz) in comparison to the cyclotron frequency ($\omega_{c}=6.4$ THz at $8$ T).Morimoto et al. (2009)

The plateau at positive gate voltage decreases in width with decreasing magnetic field qualitatively consistent with Landau level behavior. The surface state is degenerate with surface accumulated bulk carriers over the full range of the plateau. The step-like feature at $-70$ V at the CBE location is a result of the changing surface state scattering rate.Jenkins et al. (2012) This feature does not display the expected behavoir by a quantized Hall step upon changing the magnetic field.

The width of the positive-voltage plateau is much larger than expected from a single Landau level. The gate moves $2.6\times 10^{12}$ $e$/cm² over $100$ V, and each Landau level is occupied by an electron density of $B/(h/e)=1.9\times 10^{11}$ cm^-2 in $8$ T. At least $14$ Landau levels are traversed over the span of the plateau.

Given that no Landau level steps are discernable in the data at negative gate voltages, and the topological surface state is singly occupied contributing at most 1 Landau level of charge, the conclusion is that the plateau must primarily be a bulk effect.

Figure 2(d-f) and (h) show gated THz measurements performed on a 40 QL Bi₂Se₃ film. Although the qualitative behavior is very similar to the 60 QL film, there are no plateaus in the $Re(\Delta\theta_{F})$ response. The Thomas-Fermi screening length is estimated to be about $11$ nm based upon dc measurements of bulk densities of similarly prepared films performed over a wide range of thicknesses (see Appendix). Gating the top surface of the $40$ nm film will affect the accumulated bottom surface layer much more than the thicker $60$ nm film. An additional gate dependent conductivity channel associated with the bottom surface accumulation layer can give rise to a different behavior. Study of thicker films is necessary to verify this thickness effect.

The gate dependence of $\Delta T$ and Im($\Delta\theta_{F}$) of the 60 QL film over the same voltage range where the plateau exists indicates dissipation in the $\sigma_{xx}$ and $\sigma_{xy}$ channels. In this regard, the similarities between the reported dc measured bulk QHECao et al. (2012) and the gated THz measurements are striking. These dc data show plateaus in the Hall conductivity, consistent with the sum of many Landau level contributions, in the presence of significant dissipative channels.

However, even the highest positive applied gate voltage of $+170$ V, which causes the conduction band to bend downward at the surface as depicted in Figure 1(b), only results in a Fermi level of $\sim 40$ meV above the conduction band edge at the surface (see Appendix). This Fermi level translates into a bulk density of $\sim 3\times 10^{18}$ cm^-3, about an order of magnitude less than the dc measurements on bulk crystals reporting bulk QHE.Cao et al. (2012)

More important, the most significant difference between the THz and dc experiments is associated with the gradient of the potential from band bending effects in the film produced by the applied gate. In the case of the dc measurements, identical independent two-dimensional layers exhibiting the QHE are known to summate in the expected way, corresponding to a single Landau level but with a degeneracy corresponding to the number of layers.Haavasoja et al. (1984) However, if the potential varies appreciably from layer to layer, the Landau levels would not remain degenerate nor give well defined large steps. In our case, screening effects are expected to cause such a misalignment of Landau levels. At $+170$ V, the bands are bent downward by $\sim 30$ meV over $\sim 14$ QL (the screening length), producing $\sim 2$ meV change in potential energy from QL to QL. The Landau level spacing (cyclotron frequency) in $8$ T is only $\sim 4$ meV, so one might expect the variation of potential would wipe out any additive effect from independent Landau levels that could produce a wide Hall plateau.

This may indicate that the contributing Landau levels are not independent, but interact in a way that tends to lock the levels together. For the dc measured bulk QHE of reference 31, the scenario put forth was that the quintuple layers of Bi₂Se₃ decouple, forming independent 2-DEGs. Many questions remain about the nature of this decoupling since Shubnikov-de Haas measurements show a 3-D Fermi surface.Kohler (1973); Eto et al. (2010) It is also puzzling how the QHE survives the large measured $\sigma_{xx}$ in the Hall plateaus.Cao et al. (2012) Similarly in this paper we report the phenomenology of an extremely flat Hall response observed at sub-THz frequencies, manifesting in the real part of the Faraday angle that is flat to within 1/80 of the expected low-frequency quantized step size for a single Landau level. This plateau extends over a large range of gate induced carrier density change of $\sim 3\times 10^{12}\text{cm}^{-2}$, occurring above the conduction band edge, corresponding to more than $14$ occupied Landau levels. A full understanding of this plateau is likely tied to understanding the bulk QHE, which currently remains elusive.

The authors thank M. S. Fuhrer, T. D. Stanescu, and S. Das Sarma for helpful conversations. The work at the University of Maryland is supported by NSF (DMR-1104343) and CNAM. The Rutgers work is supported by IAMDN of Rutgers University, National Science Foundation (NSF DMR-0845464,) and Office of Naval Research (ONR N000140910749).