Gluon distributions and mass decompositions of the pion and kaon
Abstract
We present the gluon distribution functions of pion and kaon in small- and large- regions, and compare them with the results obtained from lattice QCD and continuum Schwinger function methods. Whether in the small- region or the large- region, our gluon distribution of pion is consistent with the results of lattice QCD and continuum Schwinger function method. In addition, the first four moments of gluon distributions of pion and kaon at different scales are calculated. Furthermore, we present the mass decompositions of pion and kaon with the dynamical parton distribution functions calculated by the DGLAP equation with parton-parton recombination corrections. The mass structures of pion and kaon are totally different from that of the proton.
I Introduction
The pion, the lightest bound state in quantum chromodynamics (QCD), plays an important role in nuclear physics as it is a Nambu-Goldstone boson Nambu (1960); Goldstone (1961) with dynamical chiral symmetry breaking (DCSB). For the kaon meson, although it was discovered in the 1950s Rochester and Butler (1947), little is known about its structure. The studies of the structures of pion and kaon can reflect the physics of DCSB, which is helpful to reveal the relative influence of DCSB on the chiral symmetry breaking of the quark masses, and it is of great significance to understand the non-perturbative QCD. Studying the pion and kaon parton distribution functions (PDFs) is not only for characterizing their structures but also for further understanding of DCSB and non-perturbative QCD. At present, people know less about the pion and kaon PDFs than the nucleon PDFs, for the experimental data are scarce, especially for the gluon distributions.
Most of the global analyses of pion PDFs mostly rely on Drell-Yan data. In our previous global QCD analysis Han et al. (2021), studies of pion and kaon PDFs were based mostly on pion-induced Drell-Yan data Badier et al. (1980, 1983); Betev et al. (1985); Conway et al. (1989), and the leading-neutron deep inelastic scattering (DIS) data of collision at HERA Chekanov et al. (2002); Aaron et al. (2010). There are some recent studies, including the work of Bourrely and Soffer Bourrely and Soffer (2019) that extract the pion parton distributions from the Drell-Yan + data with quantum statistical approach. JAM Collaboration Barry et al. (2018); Cao et al. (2021) performed the first Monte Carlo global QCD analysis of the Drell-Yan A data and the leading-neutron DIS data from HERA to reach the low- region. This Monte Carlo global QCD analysis of pion PDFs by the JAM Collaboration reveals that the gluons carry significantly higher momentum fraction than that only inferred from Drell-Yan data. The xFitter developers’ team Novikov et al. (2020) used their open source QCD fitting framework to promote a PDF extraction from the Drell-Yan A and photon production data. It is found that these data can well constrain the valence distribution, but they are not sensitive enough to the accurate determination of sea and gluon distributions. Chang et al.Chang et al. (2020) show that the pion-induced production data can impose useful additional constraints on pion PDFs, especially for the gluon distribution of the pion in the large- region.
As we know, the studies of pion and kaon gluon distributions from a theoretical perspective can provide useful information for experiments. Most theoretical model calculations only predict the valence quark distribution of pion Nam (2012); Watanabe et al. (2016, 2018); Hutauruk et al. (2016); de Teramond et al. (2018); Watanabe et al. (2020); Han et al. (2020); Chang et al. (2014); Chang and Thomas (2015); Chen et al. (2016); Shi et al. (2018); Bednar et al. (2020); Ding et al. (2020), while gluon and sea PDFs are predicted by the Dyson-Schwinger equation (DSE) continuum method with QCD evolution Watanabe et al. (2018). The description of the pion gluon PDF that based on the Rainbow-Ladder truncation of DSE is consistent with the pion gluon PDF results of JAM Collaboration Barry et al. (2018); Cao et al. (2021) within two sigma. Recently, Fan and Lin present the -dependent gluon distribution of pion from lattice-regularised QCD (LQCD) with the pseudo-PDF approach Fan and Lin (2021) for the first time.
In this work, we present our -dependent pion gluon distribution from a global QCD analysis of the available experimental data Han et al. (2021) and compare it with the results of LQCD calculations, continuum Schwinger function methods (CSMs), and other theoretical calculations. The -dependent gluon distribution of kaon is also presented under a certain scale . In addition, the first four moments of gluon distributions of pion and kaon at different scales are calculated and compared with some model results of DSE Cui et al. (2020a), JAM Barry et al. (2018); Cao et al. (2021), xFitter Novikov et al. (2020) and LQCD Salas-Chavira et al. (2022) respectively. Furthermore, according to the hadron mass decomposition which is based on the structure of the QCD energy-momentum tensor and the pion and kaon PDFs from our global QCD analysis, we study the mass structures of the pion and kaon.
II Gluon Distributions of Pion and Kaon
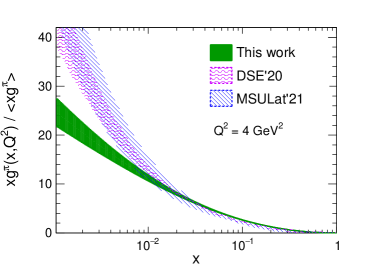
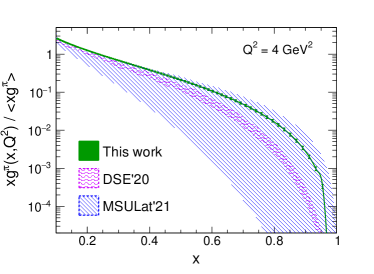
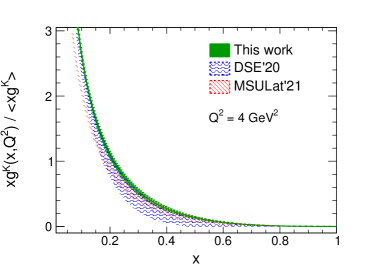
Fan and Lin recently showed the determination of the -dependent pion gluon distribution from LQCD using the pseudo-PDF approach Fan and Lin (2021). Besides, Cui et al. predicted the pion’s gluon distribution with CSMs Cui et al. (2020a). In this work, we present pion and kaon PDFs with uncertainties from a global QCD analysis of the experimental data within the framework of dynamical parton model Han et al. (2021). Figure 1 displays the normalized pion gluon distribution at = 4 GeV2 from us, compared with the LQCD Fan and Lin (2021) and DSE Cui et al. (2020a, 2021) calculations. The top pad in Fig.1 shows the gluon distribution in the small- region, and the bottom pad in Fig.1 shows the gluon distribution in the large- region. There shows agreements among the three results of gluon distribution on the entire depicted domain. Judged by the agreement between our work and other theoretical predictions (LQCD and CSMs) for the pion gluon distribution in Fig.1, our pion gluon distribution obtained from global QCD analysis is also reliable.
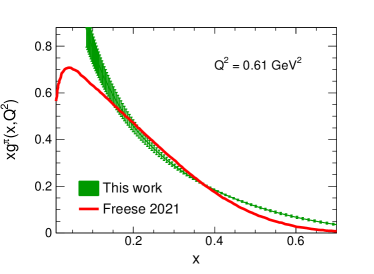
The pion gluon distribution we calculated at = 0.61 GeV2 is shown in Fig. 2, compared with the gluon distribution from the dressed quark Freese et al. (2021) in the pion. By comparison, one sees that our result based on the dynamical parton model is consistent with Freese’s result. The dressing-gluon is derived from the constituent quarks, thus when , the distribution of dressing-gluon decreases. For our result, most of the gluons generated under the dynamical parton model are from parton splitting process, thus when , our dynamical parton model still has the gluons which are not related to the dressed quarks.
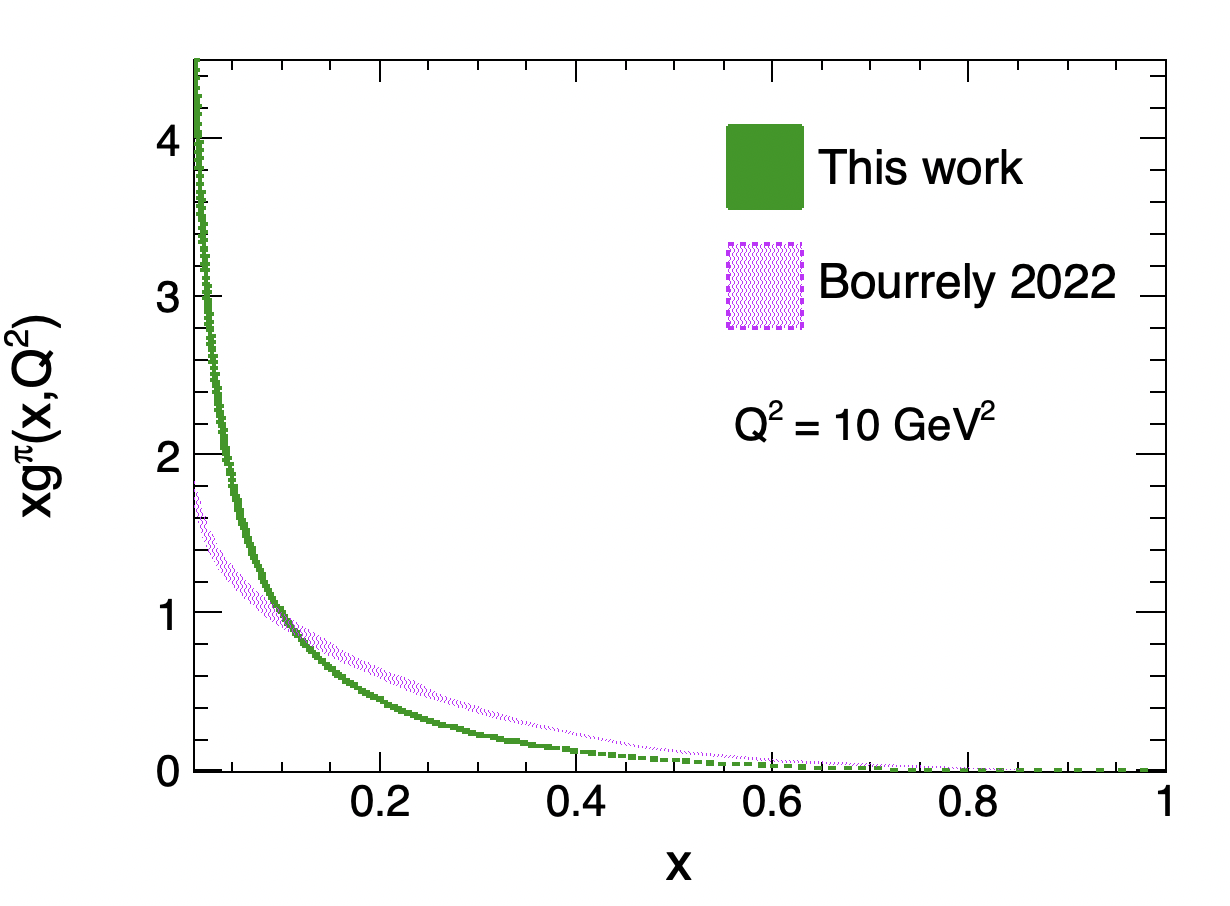
Figure 3 shows our pion gluon distribution at = 10 GeV2, compared to the pion gluon distribution from the framework of a statistical model fitted to the pion-induced Drell-Yan data and J/ production data of the pion Bourrely et al. (2022).
Figure 4 shows our normalized gluon distribution of the kaon in the large- region at = 4 GeV2. By comparing the kaon gluon distributions, one sees that our result is consistent with the DSE’20 Cui et al. (2020a) in the scheme and the lattice QCD calculation Salas-Chavira et al. (2022).
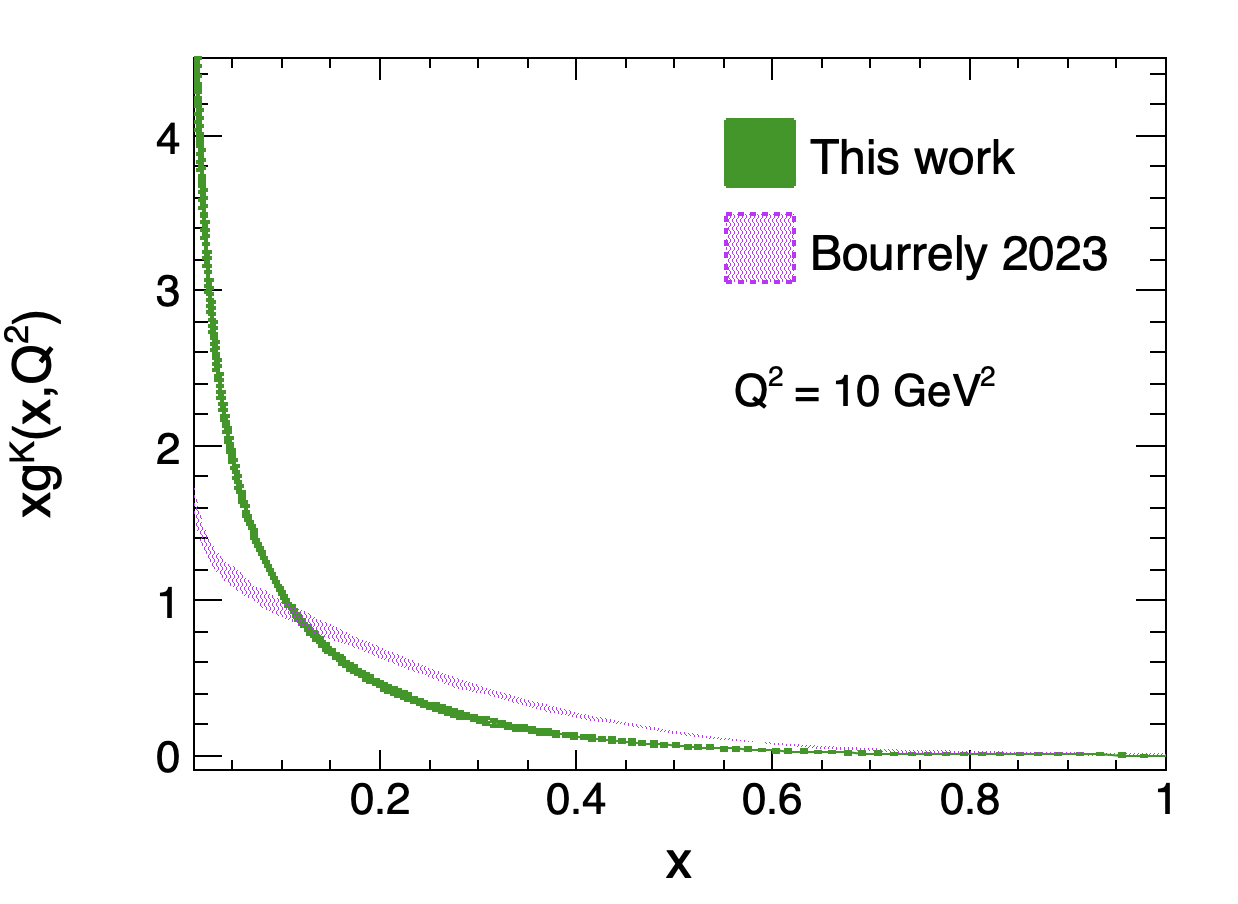
Our kaon gluon distribution at = 10 GeV2 from a global QCD analysis is shown in Fig. 5, compared with Bourrely’s result from an analysis of meson-induced Drell-Yan and quarkonium production data within a statistical model Bourrely et al. (2023).
In order to compare with more other theoretical calculations, we calculate the first four moments of the pion and kaon gluon distributions at different Q2. The moments of the gluon distribution is defined as follows,
| (1) |
where is the gluon distribution.
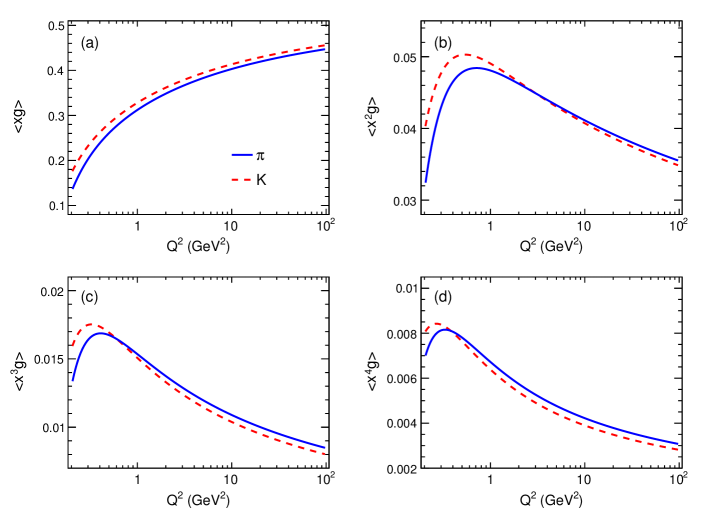
Figure 6 shows the first four moments of pion and kaon gluon distributions as a function of scale. The blue solid and red dashed curves show the evolutions of the first four moments of pion and kaon gluon distributions, respectively. The (a), (b), (c), and (d) pads present the first-order moment, second-order moment, third-order moment, and fourth-order, respectively.
The first moments of the gluon distributions of pion and kaon are listed in Table 1. Our and predictions agree well with the other model calculations. It is worth noting that LQCD and DSE are two main nonperturbative approaches derived directly from the QCD theory.
| Model | Model | ||
|---|---|---|---|
| DSE Cui et al. (2020a) | 0.076 | DSE Cui et al. (2020a) | 0.075 |
| JAM Barry et al. (2018); Cao et al. (2021) | 0.103 | LQCD Salas-Chavira et al. (2022) | 0.078 |
| xFitter Novikov et al. (2020) | 0.158 | This work | 0.087 |
| LQCD Salas-Chavira et al. (2022) | 0.092 | ||
| This work | 0.117 | ||
| Model | Model | ||
| DSE Cui et al. (2020a) | 0.015 | DSE Cui et al. (2020a) | 0.015 |
| JAM Barry et al. (2018); Cao et al. (2021) | 0.024 | LQCDSalas-Chavira et al. (2022) | 0.019 |
| LQCD Salas-Chavira et al. (2022) | 0.048 | This work | 0.021 |
| This work | 0.033 |
III Mass structures of the pion and kaon
The mass structure of pion is very interesting. According to Goldstone theorem, the pion is essentially different from other ordinary hadrons, which is a collective mode in QCD vacuum. We will see that the mass structure does reflect that. The QCD structure of hadron mass can be decomposed into four different parts:
| (2) |
in which is the quark energy contribution, is the gluon energy contribution, is the quark mass contribution and is the trace anomaly contribution.
| (3) | |||
These four mass terms mainly depend on the momentum fraction carried by all the quarks from our analysis Han et al. (2021), QCD trace anomaly parameter calculated via chiral perturbation theory Ji (1995) and the quark mass anomalous dimension . The quark mass anomalous dimension Baikov et al. (2014) is predicted by perturbative QCD as follows:
| (4) |
where , and denotes the renormalized strong coupling constant. It is worth noticing that the anomalous dimension defined by Ji Ji (1995) is -2 times Wang et al. (2020) that defined in Ref. Baikov et al. (2014). For the running coupling constant , we adopted Cui’s latest parametrization of the effective charge from lattice QCD Cui et al. (2020b). The adopted running coupling constant including the gluon mass effect of dynamical chiral symmetry breaking is written as:
| (5) |
In general, the matrix element in Eq. (3) can be deduced from the quark distributions that are measured in -N Drell-Yan process. The matrix element is the momentum faction carried by the quarks in the pion, which is given by,
| (6) |
Here and are the quark and anti-quark distributions with flavor in the pion. In this work, we use the pion PDFs from our recent global QCD analysis of the experimental data to evaluate the matrix element .
For the trace anomaly parameter in Eq. (3), it can be derived from the pion mass in the chiral perturbation theory. The first-order chiral perturbation theory gives a clean prediction of the trace anomaly parameter to be = 0.5 Ji (1995).
Here we provide a brief explanation of the criteria for estimating the trace anomaly parameter . First, according to the original derivation of mass decomposition and the requirement of Lorentz covariance Ji (1995), is viewed to be a scale-invariant quantity which has been discussed in many previous studies Ji (1995); Wang et al. (2020); Kou et al. (2022); Duran et al. (2023); Kou and Chen (2024). Two estimates of trace anomaly parameter of proton in the limits of chiral SU(3) and heavy strange quark are = 0.17 and = 0.11 provided by Ji Ji (1995). Wang et al. firstly present an extraction of the QCD trace anomaly parameter to be = 0.07 0.17 Wang et al. (2020) from the experimental data of near-threshold photoproduction cross section from GlueX at JLab. Recently, Kou et al. analyze the updated differential cross-section data from Hall C and GlueX Collaborations Duran et al. (2023); Adhikari et al. (2023), and obtain a new value of trace anomaly parameter = 0.52 0.09 Kou and Chen (2024), which is close to the trace anomaly parameter for the pion estimated in the chiral perturbation theory Gasser and Leutwyler (1982). But this does not necessarily prove that is independent of the hadrons. Second, the mass decomposition of different hadrons should be different. Therefore, the trace anomaly parameter could be different for different hadrons. Third, we assume that in the chiral limit, the first-order chiral perturbation theory under SU(3) gives the same mass formula for the pion and the kaon. This is due to the fact that the vacuum condensations of quarks with three flavors are treated equally Gasser and Leutwyler (1982). Therefore the parameter of the kaon is also taken to be = 0.5 in this work.
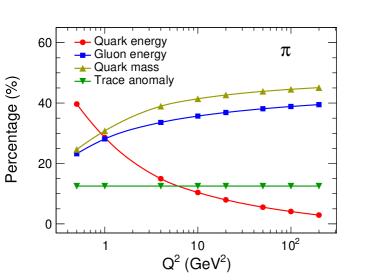
Using the trace anomaly parameter explained above, we calculated the mass decompositions of pion and kaon at different scales. Figure 7 shows the pion mass decomposition as a function of , where the different markers indicate the percentages of different contributions to the pion mass. By comparing to the mass decomposition of the proton Wang et al. (2020), it is found that the proportion of the quark mass contribution in the pion is smaller than that in the proton, while the proportion of the trace anomaly contribution in the pion is larger than that in the proton. The reason for the large difference between the mass decompositions of the pion and the proton is that the trace anomaly parameter 0.1 of the proton Wang et al. (2020); Ji (1995) is much smaller than that of the pion. Quark mass plays a more important role in the pion mass comparing to the proton, as the chiral-limit mass of the pion is zero while the chiral-limit mass of the proton is huge. Moreover, the proportion of quark energy in the pion is smaller than that in the proton, especially at high scale. The quark energy is the sum of kinetic energy and potential energy. The reason for the smaller proportion of in the pion is that the quark potential energy in the pion is lower compared to that in the proton. In addition to the small proportion of to the pion mass, the small proportion of may be another reason why the pion mass is so light. Figure 8 shows the kaon mass decompositions at different scales, where the different markers indicate the percentages of different contributions to the kaon mass.
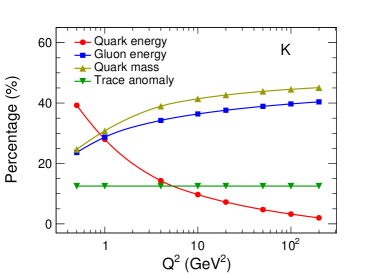
The -dependences of different mass origins in the pion or kaon mass decomposition are discussed. Firstly, we emphasize that the trace anomaly is scale-invariant, which is governed by the symmetry of QCD energy-momentum tensor. In other words, the trace anomaly parameter is scale-invariant and it is associated with the hadron’s scalar charge Ji (1995). Secondly, the quark mass term depends on the anomalous dimension and this gives the -dependence of . Thirdly, the -dependence of the quark energy term depends on the momentum fraction carried by all quarks , and the traditional DGLAP evolution tells us that decreases as increases. This is the main reason why the quark energy term is negatively correlated with the scale. Fourthly, the gluon energy term increases with increasing , and it is also governed by the DGLAP evolution equation. With the increasing , the parton splitting processes radiate more and more gluons, resulting in a decrease of quark kinetic energy, and an increase of gluon kinetic energy, which is in Fig. 6. In whole description of the hadron mass decomposition, the anomalous dimension only affects the terms related to quarks, as the gluon is massless. The gluon contributions to the hadron mass only depends on the trace anomaly and the momentum fraction carried by the gluons.
IV Summary
The pion and kaon gluon distributions from our previous global QCD analysis applying DGLAP equations with parton recombination corrections are basically consistent with the DSE and LQCD calculations in both small- and large- regions. The future experimental measurements will provide excellent chances to verify these predictions. Additionally, the first four moments of the gluon distributions of pion and kaon at different scales are predicted, which agree well with some theoretical models.
We also give the mass structures of pion and kaon at different scales, according to the mass decomposition of QCD energy-momentum tensor. The mass of the pion or the kaon can be decomposed into four parts in this work. For the pion and the kaon, the quark mass contribution is the largest one contributed to the meson mass at high . Compared to the proton, the trace anomaly contribution of pion or kaon is small. These four origins of the hadron mass depend on the momentum fraction by the quarks, the trace anomaly parameter , and the quark mass anomalous dimension . In this work, we find some apparent differences between the mass decompositions of the pion and the proton Wang et al. (2020). Besides the trace anomaly contribution , we notice that the quark energy contribution , the gluon energy contribution , and the quark mass contribution all have obvious dependence on .
The US Electron Ion Collider (EIC) Aschenauer et al. (2017); Aguilar et al. (2019); Arrington et al. (2021) under the construction and the proposed Electron-Ion Collider in China (EicC) Anderle et al. (2021); Chen (2018); Chen et al. (2020) provide great opportunities to deepen our understanding on the meson structures through the measurements of Sullivan process Aguilar et al. (2019); Wang et al. (2023); Xie et al. (2022). These high-energy projects will surely increase our knowledge about the pion and kaon gluon distributions and the emergence of the meson mass.
Acknowledgements.
This work is supported by the National Natural Science Foundation of China under the Grant No. 12305127, the International Partnership Program of the Chinese Academy of Sciences under the Grant No. 016GJHZ2022054FN, the Strategic Priority Research Program of Chinese Academy of Sciences under Grant No. XDB34030301 and the Guangdong Major Project of Basic and Applied Basic Research No. 2020B0301030008.References
- Nambu (1960) Y. Nambu, Phys. Rev. 117, 648 (1960).
- Goldstone (1961) J. Goldstone, Nuovo Cim. 19, 154 (1961).
- Rochester and Butler (1947) G. D. Rochester and C. C. Butler, Nature 160, 855 (1947).
- Han et al. (2021) C. Han, G. Xie, R. Wang, and X. Chen, Eur. Phys. J. C 81, 302 (2021), arXiv:2010.14284 [hep-ph] .
- Badier et al. (1980) J. Badier et al. (Saclay-CERN-College de France-Ecole Poly-Orsay), Phys. Lett. B 93, 354 (1980).
- Badier et al. (1983) J. Badier et al. (NA3), Z. Phys. C 18, 281 (1983).
- Betev et al. (1985) B. Betev et al. (NA10), Z. Phys. C 28, 9 (1985).
- Conway et al. (1989) J. S. Conway et al., Phys. Rev. D 39, 92 (1989).
- Chekanov et al. (2002) S. Chekanov et al. (ZEUS), Nucl. Phys. B 637, 3 (2002), arXiv:hep-ex/0205076 .
- Aaron et al. (2010) F. D. Aaron et al. (H1), Eur. Phys. J. C 68, 381 (2010), arXiv:1001.0532 [hep-ex] .
- Bourrely and Soffer (2019) C. Bourrely and J. Soffer, Nucl. Phys. A 981, 118 (2019), arXiv:1802.03153 [hep-ph] .
- Barry et al. (2018) P. C. Barry, N. Sato, W. Melnitchouk, and C.-R. Ji, Phys. Rev. Lett. 121, 152001 (2018), arXiv:1804.01965 [hep-ph] .
- Cao et al. (2021) N. Y. Cao, P. C. Barry, N. Sato, and W. Melnitchouk (Jefferson Lab Angular Momentum), Phys. Rev. D 103, 114014 (2021), arXiv:2103.02159 [hep-ph] .
- Novikov et al. (2020) I. Novikov et al., Phys. Rev. D 102, 014040 (2020), arXiv:2002.02902 [hep-ph] .
- Chang et al. (2020) W.-C. Chang, J.-C. Peng, S. Platchkov, and T. Sawada, Phys. Rev. D 102, 054024 (2020), arXiv:2006.06947 [hep-ph] .
- Nam (2012) S.-i. Nam, Phys. Rev. D 86, 074005 (2012), arXiv:1205.4156 [hep-ph] .
- Watanabe et al. (2016) A. Watanabe, C. W. Kao, and K. Suzuki, Phys. Rev. D 94, 114008 (2016), arXiv:1610.08817 [hep-ph] .
- Watanabe et al. (2018) A. Watanabe, T. Sawada, and C. W. Kao, Phys. Rev. D 97, 074015 (2018), arXiv:1710.09529 [hep-ph] .
- Hutauruk et al. (2016) P. T. P. Hutauruk, I. C. Cloet, and A. W. Thomas, Phys. Rev. C 94, 035201 (2016), arXiv:1604.02853 [nucl-th] .
- de Teramond et al. (2018) G. F. de Teramond, T. Liu, R. S. Sufian, H. G. Dosch, S. J. Brodsky, and A. Deur (HLFHS), Phys. Rev. Lett. 120, 182001 (2018), arXiv:1801.09154 [hep-ph] .
- Watanabe et al. (2020) A. Watanabe, T. Sawada, and M. Huang, Phys. Lett. B 805, 135470 (2020), arXiv:1910.10008 [hep-ph] .
- Han et al. (2020) C. Han, H. Xing, X. Wang, Q. Fu, R. Wang, and X. Chen, Phys. Lett. B 800, 135066 (2020), arXiv:1809.01549 [hep-ph] .
- Chang et al. (2014) L. Chang, C. Mezrag, H. Moutarde, C. D. Roberts, J. Rodríguez-Quintero, and P. C. Tandy, Phys. Lett. B 737, 23 (2014), arXiv:1406.5450 [nucl-th] .
- Chang and Thomas (2015) L. Chang and A. W. Thomas, Phys. Lett. B 749, 547 (2015), arXiv:1410.8250 [nucl-th] .
- Chen et al. (2016) C. Chen, L. Chang, C. D. Roberts, S. Wan, and H.-S. Zong, Phys. Rev. D 93, 074021 (2016), arXiv:1602.01502 [nucl-th] .
- Shi et al. (2018) C. Shi, C. Mezrag, and H.-s. Zong, Phys. Rev. D 98, 054029 (2018), arXiv:1806.10232 [nucl-th] .
- Bednar et al. (2020) K. D. Bednar, I. C. Cloët, and P. C. Tandy, Phys. Rev. Lett. 124, 042002 (2020), arXiv:1811.12310 [nucl-th] .
- Ding et al. (2020) M. Ding, K. Raya, D. Binosi, L. Chang, C. D. Roberts, and S. M. Schmidt, Phys. Rev. D 101, 054014 (2020), arXiv:1905.05208 [nucl-th] .
- Fan and Lin (2021) Z. Fan and H.-W. Lin, Phys. Lett. B 823, 136778 (2021), arXiv:2104.06372 [hep-lat] .
- Cui et al. (2020a) Z.-F. Cui, M. Ding, F. Gao, K. Raya, D. Binosi, L. Chang, C. D. Roberts, J. Rodríguez-Quintero, and S. M. Schmidt, Eur. Phys. J. C 80, 1064 (2020a).
- Salas-Chavira et al. (2022) A. Salas-Chavira, Z. Fan, and H.-W. Lin, Phys. Rev. D 106, 094510 (2022), arXiv:2112.03124 [hep-lat] .
- Cui et al. (2021) Z.-F. Cui, M. Ding, F. Gao, K. Raya, D. Binosi, L. Chang, C. D. Roberts, J. Rodriguez-Quintero, and S. M. Schmidt, Eur. Phys. J. A 57, 5 (2021), arXiv:2006.14075 [hep-ph] .
- Freese et al. (2021) A. Freese, I. C. Cloët, and P. C. Tandy, Phys. Lett. B 823, 136719 (2021), arXiv:2103.05839 [hep-ph] .
- Bourrely et al. (2022) C. Bourrely, W.-C. Chang, and J.-C. Peng, Phys. Rev. D 105, 076018 (2022), arXiv:2202.12547 [hep-ph] .
- Bourrely et al. (2023) C. Bourrely, F. Buccella, W.-C. Chang, and J.-C. Peng, (2023), arXiv:2305.18117 [hep-ph] .
- Gluck et al. (1992) M. Gluck, E. Reya, and A. Vogt, Z. Phys. C 53, 651 (1992).
- Shanahan and Detmold (2019) P. E. Shanahan and W. Detmold, Phys. Rev. D 99, 014511 (2019), arXiv:1810.04626 [hep-lat] .
- Ji (1995) X.-D. Ji, Phys. Rev. D 52, 271 (1995), arXiv:hep-ph/9502213 .
- Baikov et al. (2014) P. A. Baikov, K. G. Chetyrkin, and J. H. Kühn, JHEP 10, 076 (2014), arXiv:1402.6611 [hep-ph] .
- Wang et al. (2020) R. Wang, J. Evslin, and X. Chen, Eur. Phys. J. C 80, 507 (2020), arXiv:1912.12040 [hep-ph] .
- Cui et al. (2020b) Z.-F. Cui, J.-L. Zhang, D. Binosi, F. de Soto, C. Mezrag, J. Papavassiliou, C. D. Roberts, J. Rodríguez-Quintero, J. Segovia, and S. Zafeiropoulos, Chin. Phys. C 44, 083102 (2020b), arXiv:1912.08232 [hep-ph] .
- Kou et al. (2022) W. Kou, R. Wang, and X. Chen, Eur. Phys. J. A 58, 155 (2022), arXiv:2103.10017 [hep-ph] .
- Duran et al. (2023) B. Duran et al., Nature 615, 813 (2023), arXiv:2207.05212 [nucl-ex] .
- Kou and Chen (2024) W. Kou and X. Chen, Phys. Rev. D 109, 036034 (2024), arXiv:2311.08789 [hep-ph] .
- Adhikari et al. (2023) S. Adhikari et al. (GlueX), Phys. Rev. C 108, 025201 (2023), arXiv:2304.03845 [nucl-ex] .
- Gasser and Leutwyler (1982) J. Gasser and H. Leutwyler, Phys. Rept. 87, 77 (1982).
- Aschenauer et al. (2017) E.-C. Aschenauer et al., Eur. Phys. J. A 53, 71 (2017), arXiv:1410.8831 [hep-ph] .
- Aguilar et al. (2019) A. C. Aguilar et al., Eur. Phys. J. A 55, 190 (2019), arXiv:1907.08218 [nucl-ex] .
- Arrington et al. (2021) J. Arrington et al., J. Phys. G 48, 075106 (2021), arXiv:2102.11788 [nucl-ex] .
- Anderle et al. (2021) D. P. Anderle et al., Front. Phys. (Beijing) 16, 64701 (2021), arXiv:2102.09222 [nucl-ex] .
- Chen (2018) X. Chen, PoS DIS2018, 170 (2018), arXiv:1809.00448 [nucl-ex] .
- Chen et al. (2020) X. Chen, F.-K. Guo, C. D. Roberts, and R. Wang, Few Body Syst. 61, 43 (2020), arXiv:2008.00102 [hep-ph] .
- Wang et al. (2023) R. Wang, G. Xie, W. Xiong, Y. Liang, and X. Chen, Few Body Syst. 64, 28 (2023).
- Xie et al. (2022) G. Xie, C. Han, R. Wang, and X. Chen, Chin. Phys. C 46, 064107 (2022), arXiv:2109.08483 [hep-ph] .