Goos-Hänchen effect singularities in transdimensional plasmonic films
Abstract
We identify and classify topologically protected singularities for the reflection coefficient of transdimensional plasmonic systems. Originating from nonlocal electromagnetic response due to vertical electron confinement in the system, such singularities lead to lateral (angular) Goos-Hänchen shifts on the millimeter (milliradian) scale in the visible range, greatly exceeding those reported previously for artificially designed metasurfaces, offering new opportunities for quantum material development.
It has been known that the reflection of a linearly polarized optical beam of finite transverse extent incident on a plane surface does not exactly follow the Snell’s law of geometrical optics [1, 2]. Instead, the reflected beam experiences slight lateral in-plane displacement and angular deflection in the plane of incidence—the phenomenon commonly referred to as the Goos-Hänchen (GH) effect. Originating from the spatial dispersion of reflection or transmission coefficients due to the finite transverse size of the beam (and so nonlocal in its nature), the GH effect occurs for both reflected and refracted light in realistic optical systems. It was observed in a variety of systems (see Ref.[2]) including plasmonic metamaterials [3], graphene [4] and even neutron scattering experiments [5]. These days the effect attracts much attention as well [6, 7, 8] due to the new generation of materials being available—quantum nanomaterials of reduced dimensionality, materials that can enhance nonlocal subwalength light propagation to offer new directions for quantum optics, quantum nanophotonics, and quantum computing application development [9, 10].
Plasmonic transdimensional (TD) quantum materials are atomically-thin metal (or semiconductor) films of precisely controlled thickness [11]. Currently available due to great progress in nanofabrication techniques [12, 13, 14, 15], such materials offer high tailorability of their electronic and optical properties not only by altering their chemical and/or electronic composition (stoichiometry, doping) but also by merely varying their thickness (number of monolayers) [16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]. They provide a new regime—transdimensional, in between three (3D) and two (2D) dimensions, turning into 2D as the film thickness tends to zero. In this regime the strong vertical quantum confinement makes the linear electromagnetic (EM) response of the TD film nonlocal, or spatially dispersive, and the degree of nonlocality can be controlled by varying the film thickness [19, 23]. That is what makes plasmonic TD films indispensable for studies of the nonlocal light-matter interactions at the nanoscale [25, 26, 27, 28, 29, 30].
The properties of the TD plasmonic films can be explained by the confinement-induced nonlocal EM response theory [19, 20] built on the Keldysh-Rytova (KR) electron interaction potential [31]. The theory is verified experimentally in a variety of settings [13, 32, 28]. It accounts for vertical electron confinement due to the presence of substrate and superstrate of dielectric permittivities less than that of the film, whereby the thickness of the film becomes a parameter to control its nonlocal EM response. The KR model covers both ultrathin films of thickness less than the half-wavelength of incoming light radiation and conventional films as thick as a few optical wavelengths [19, 20]. The nonlocal EM response of TD plasmonic systems enables a variety of new effects such as thickness-controlled plasma frequency red shift [13], low-temperature plasma frequency dropoff [32], plasma mode degeneracy lifting [23], a series of quantum-optical [25, 33] and nonlocal magneto-optical effects [20] as well as thermal and vacuum field fluctuation effects responsible for near-field heat transfer [27, 28] and Casimir interaction phenomena [29, 30].
Here, we focus on the confinement-induced nonlocality of the EM response of the TD plasmonic film to study theoretically the GH effect for an incident laser beam. Using the nonlocal KR model, analytical calculations and numerical analysis, we identify and classify topologically protected singularities for the nonlocal reflection coefficient of the system. Such singularities are shown to lead to giant lateral and angular GH shifts in the millimeter and milliradian range, respectively, to greatly exceed those of microscale reported for beams of finite transverse extent with no material-induced nonlocality [2, 3, 4, 5, 6, 7]. They appear in TD materials with broken in-plane reflection symmetry (substrate and superstrate of different dielectric permittivities) where due to the confinement-induced nonlocality the eigenmode degeneracy is lifted to create the points of topological darkness in the visible range not existing in standard local Drude materials.
The theory of the GH shift was originally formulated by Artmann back in 1948 [34]. The geometry of the effect is shown in Fig. 1. After reflectance at an interface, the lateral and angular shifts of an incoming -polarized wave in medium (refractive index ) are given by [34, 36, 2, 35]
| (1) |
and
| (2) |
respectively. Here, is the wavevector in-plane projection, is the angle of incidence, , and is the angular spread of an incident Gaussian light beam of waist . The -wave reflection coefficient is written as in the complex exponential form. Both shifts can be seen being spatially dispersive, with being sensitive to reflectivity phase jumps and to zero reflection itself so that large effects are highly likely for all kinds of zero reflection modes in the system. Phase jumps and singularities make the phase ill-defined, in which case the reflection coefficient absolute value must go to zero for causality reasons. In nonlocal materials such as our TD plasmonic films, phase jumps and singularities come from material spatial dispersion in addition to that of the light beam itself. This is precisely what we study here. The respective extra terms are derived for the structure in Fig. 1 and can be found elsewhere [37]. Expressions similar to Eqs. (1) and (2) can be written for -polarized waves as well. However, as they show no peculiarities such as those we are about to discuss, we leave them out [37]. The derivations of relevance can also be found in Refs. [36, 2].
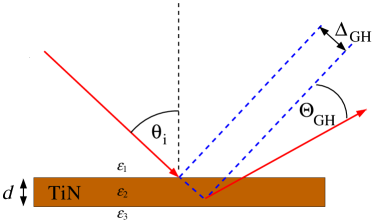
For a free standing plasmonic film of thickness in air (Fig. 1), the -polarized wave reflection coefficient is [38]
| (3) |
with medium 1 (superstrate) and medium 3 (substrate) having the same permittivities . For medium 2 (film) we use taking a TiN example of TD material that surpasses noble metals such as Au and Ag [39]. The latter have exceptional plasmonic properties but relatively low melting temperatures making them incompatible with semiconductor fabrication technologies. On the contrary, transition metal nitrides have low-loss plasmonic response, high melting point and structural stability that makes them capable of forming stoichiometrically perfect TD films down to nm in thickness at room temperature [13, 40]. The Fresnel reflection coefficients () for interfaces between medium 1 and 2 and between medium 2 and 3 are defined as follows
| (4) |
where are the wave vectors components normal to the interface. Here, as , in which case zeroes of are determined by the Brewster mode (BM) condition at the film-air interface, whereby , leading to the dispersion relation
| (5) |
Also, zeros of can come from the film standing wave (SW) condition, , in which case
| (6) |
Here, and . Lastly, zero reflection can also occur at the Christiansen point (CP) where . If one uses the local Drude model (a ’workhorse’ routinely used in plasmonics), then comes out of it for any angle of incidence, whereas in the nonlocal KR model used here the confinement-induced nonlocality of the EM response function makes the CP depend on and thus on the incidence angle. The comparison of the two as well as generally accepted TiN material parameters we use can be found elsewhere [37].
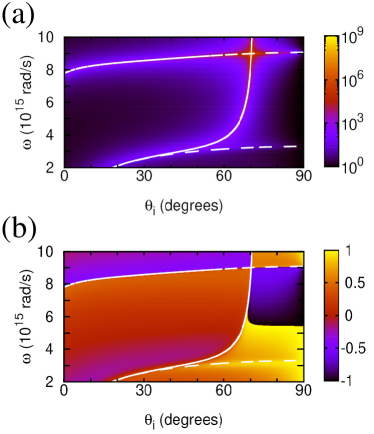
Figure 2 shows the inverse reflectivity function and reflection phase calculated from Eqs. (3) and (4) for an example of the 40 nm thick free standing TiN slab with nonlocal EM response. Reflectivity reduction and phase jumps can be seen when the SW, BM or CP mode are excited in the system. The BM still exists below the bulk TiN plasma frequency , making the GH shifts observable for , including the visible range that is impossible to access with local Drude-like plasmonic materials. Figure 3, calculated from Eqs. (1) and (2) for the same example, shows strong lateral and angular GH shifts when the BM is excited, up to and , respectively. TD plasmonic materials thereby open access to the GH effect observation with visible light due to their remarkable property of the confinement-induced nonlocal EM response.
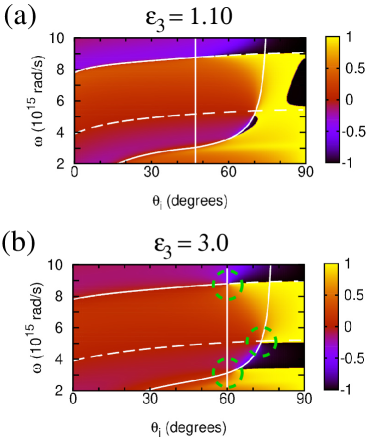
For TD plasmonic films sandwiched between superstrates and substrates with , the in-plane reflection symmetry is broken and top-bottom interface mode degeneracy is lifted. Figure 4 shows the birth and development of phase singularities in this case as with (air) the substrate permittivity rises up to (MgO typically used in TiN thin film systems [13]). It can be seen that just a slight substrate-superstrate dielectric permittivity difference gives birth to the two phase singularities close to the BM phase jump. They have opposite winding numbers (topological charges)
| (7) |
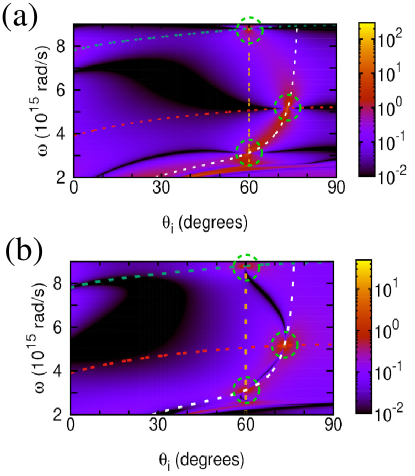
where is a closed integration path around the phase singularity point. There is also another phase singularity on the SW branch, which moves for larger substrate permittivities close to the SW and BM crossing point. Such singularities result in zero reflection previously reported as ’points of topological darkness’ for specially designed metasurfaces [42, 43] and ultrathin multilayer nanostructures [44, 45]. Here, we observe these topologically protected singularity points in mere nonlocal TD films. Remarkably, though, due to the plasma frequency decrease with thickness in our case [37, 13], the gap in Fig. 4 between the low-frequency opposite topological charge singularities widens in thinner films (not shown), to red-shift the lower- and blue-shift the higher-frequency singularity points, respectively. By reducing in a controllable way in our case it can therefore be possible to access the low frequency phase singularity point with He-Ne laser at () to observe an enhanced GH effect in the visible range. This remarkable feature is only offered by the TD plasmonic films due to their confinement-induced nonlocality and can never be realized with local Drude-like materials.
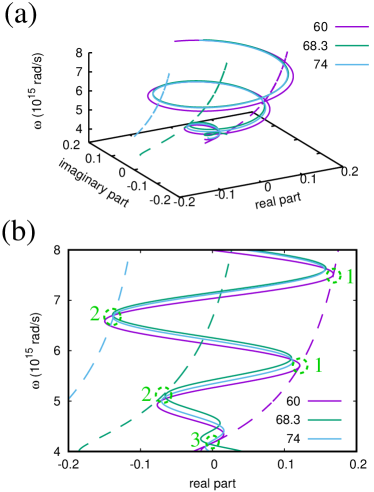
To understand the origin of the topological singularities discussed, it is instructive to represent the condition in the form
| (8) |
with dissipation temporarily neglected. In this case the interface reflection coefficients are real numbers for all where (and accordingly) so that our TD film behaves as a dielectric. The LHS of this equation makes a circle in the complex plane of radius with phase , while the RHS is a real number varying between and as and change. This is why the equality can only be achieved if the LHS is a real number as well, yielding two cases for Eq. (8) to fulfill. They are: (1) , and (2) , . Here, the first equations are the SW condition and its alternative . Both of them lead to the same dispersion relation of Eq. (6), but the former for and the latter for describing SWs with multiples of a quarter wavelength and so to be referred to as standing quarter waves (SQW), accordingly. The second equation of case 1 is per Eq. (4) fulfilled if
| (9) |
This is the substrate-superstrate interface BM condition, which can only be realized hypothetically for , and so to be refereed to as zero-thickness BM (zBM). Similarly, the second equation of case (2) is fulfilled if
| (10) |
For this reduces to the symmetric in-plane interface condition leading to the BM dispersion relation of Eq. (5). However, since it also holds for a broken in-plane reflection symmetry with , we refer to the solution of this equation as the generalized BM (gBM).
The two simultaneous equations of cases 1 and 2 are represented by the lines in the 2D configuration space spanned by frequency and angle of incidence. The solutions to Eq. (8) are given by the intersection of these lines. This is where the phase singularity points come from that we obtain at certain frequencies and incident angles. Additionally, there is a singularity coming from the trivial solution of Eq. (8), to give case 3 where , or and simultaneously. This leads to the phase singularity at the intersection of the air-TiN and TiN-MgO interface BMs, or more generally, at the intersection of zBM and gBM lines in the configuration space. A complimentary analysis of the Christiansen points can be found elsewhere [37].
Figure 5 (a) shows the real and imaginary parts of Eq. (8) calculated for a thicker TiN film of nm (to include more solution points) as functions of frequency for a few incident angles fixed. In Fig. 5 (b) that presents a projection of (a), solution cases 1, 2 and 3 discussed above are marked accordingly. Here, case 1 can be seen to generate an infinite number of discrete solution points for a single 60∘ incident angle as and in Eq. (9) are frequency independent constants. Case 2 yields the solution points at different incident angles 68.3∘, 74∘, and 76∘ (not shown), etc. (also an infinite number, in principle) due to the strong gBM frequency dependence in Eq. (10). The case 3 solution point can be seen at the intersection of the two lines of the 60∘ incidence angle, to yield the phase singularity point that can be shifted down to the visible for thinner films (see below) due to the confinement-induced nonlocal EM response.
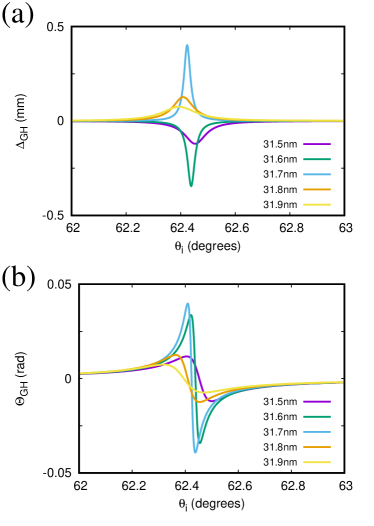
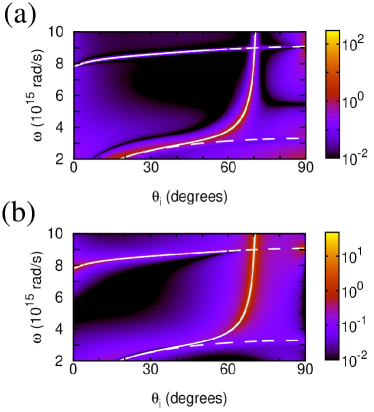
The impact of phase singularities on the GH shifts is shown in Fig. 6 for the air/TiN/MgO system of the nm thick TiN film with dissipation neglected. Comparing to Fig. 4 (b), the GH shifts can be seen to be very pronounced at the phase singularity points, which move with dissipation just slightly (not shown), for all three cases discussed. Using thinner TD films with broken in-plane symmetry it is even possible to make these GH shift singularities observable in the visible range under He-Ne laser excitation (). Figure 7 shows the GH shifts under such excitation with angle of incidence varied around for the same air/TiN/MgO system (dissipation included [37]) with TiN film thickness varied around to encounter the case 3 phase singularity point. For slightly thicker or thinner than that the singularity shows up slightly red- or blue-shifted, depending on its topological charge, making of Eq. (1) change its sign as decreases. Similarly, the sign of of Eq. (2) changes as the incidence angle varies around of the case 3 phase singularity point. Most important though is that both lateral and angular GH shifts shown are extremely large, in the millimeter and a few tens of millirad range, respectively, over an order of magnitude greater than those shown in Fig. 3 for a similar in-plane symmetric TD film system.
To summarize, we show that the TD plasmonic films with broken in-plane reflection symmetry can feature an extraordinarily large GH effect in the visible range due to the topologically protected phase singularities of their reflection coefficient. This stems from the confinement-induced EM response nonlocality of the system, with plasma frequency decreasing as the film gets thinner [13]. The remarkable opportunity to bring the GH effect to the visible range comes from the nonlocal plasma frequency which can be red-shifted not only by thickness but also by in-plane momentum reduction through the incident angle change. Previous studies reported an overall GH shift of by coupling incident light to a surface plasmon polariton of a plasmonic film [35], as well as lateral and angular GH shifts as large as times incident wavelength and , respectively, for artificially designed metasurface structures [41]. Our analysis reveals even greater lateral and angular GH shifts mm (632 times the wavelength) and mrad for visible He-Ne laser light with simple TD plasmonic films, indicating that such systems could provide a new flexible quantum material platform to offer new opportunities for quantum optics, quantum computing and biosensing application development.
Acknowledgements.
This research was supported in part by grant NSF PHY-2309135 to the Kavli Institute for Theoretical Physics (KITP). I.V.B. gratefully acknowledges support from the U.S. Army Research Office under award No. W911NF2310206.References
- [1] J.D.Jackson, Classical Electrodynamics, 3rd edn. (Wiley, 1999) [see also refs. therein].
- [2] K.Y.Bliokh and A.Aiello, Goos-Hänchen and Imbert-Fedorov beam shifts: an overview, J. Opt. 15, 014001 (2013).
- [3] I.V.Shadrivov, A.A.Zharov, and Yu.S.Kivshar, Giant Goos-Hänchen effect at the reflection from left-handed metamaterials, Appl. Phys. Lett. 83, 2713 (2003).
- [4] C.W.J.Beenakker, R.A.Sepkhanov, A.R.Akhmerov, and J.Tworzydlo, Quantum Goos-Hänchen effect in graphene, Phys. Rev. Lett. 102, 146804 (2009).
- [5] V.O.de Haan, J.Plomp, T.M.Rekveldt, W.H.Kraan, et al., Observation of the Goos-Hänchen shift with neutrons, Phys. Rev. Lett. 104, 010401 (2010).
- [6] S.Zhu, R.Jaffiol, A.Crunteanu, C.Vézy, et al., Label-free biosensing with singular-phase-enhanced lateral position shift based on atomically thin plasmonic nanomaterial, Light: Science & Applications 13, 2 (2024).
- [7] R.-G.Wan and M.S.Zubairy, Tunable and enhanced Goos-Hänchen shift via surface plasmon resonance assisted by a coherent medium, Optics Express 28, 6036 (2020).
- [8] Q.You, Y.Shan, S.Gan, Y.Zhao, X.Dai, and Y.Xiang, Giant and controllable Goos-Hänchen shifts based on surface plasmon resonance with graphene-MoS2 heterostructure, Optical Mater. Express 8, 3036 (2018).
- [9] F.Schlawin, D.M.Kennes, and M.A.Sentef, Cavity quantum materials, Appl. Phys. Rev. 9, 011312 (2022).
- [10] A.Gonzáles-Tudela, A.Reiserer, J.J.García-Ripoll, and F.J.García-Vidal, Light-matter interactions in quantum nanophotonic devices, Nature Rev. Phys. 6, 166 (2024).
- [11] A.Boltasseva and V.M.Shalaev, Transdimensional photonics, ACS Photon. 6, 1 2019.
- [12] C.Pan, Y.Tong, H.Qian, A.V.Krasavin, et al., Large area single crystal gold of single nanometer thickness for nanophotonics, Nature Commun. 15, 2840 (2024).
- [13] D.Shah, M.Yang, Z.Kudyshev, X.Xu, et al., Thickness-dependent Drude plasma frequency in transdimensional plasmonic TiN, Nano Lett. 22, 4622 (2022).
- [14] Z.M.Abd El-Fattah, V.Mkhitaryan, J.Brede, L.Fernández, et al., Plasmonics in atomically thin crystalline silver films, ACS Nano 13, 7771 (2019).
- [15] J.Halim, S.Kota, M.R.Lukatskaya, M.Naguib, et al., Synthesis and characterization of 2D molybdenum carbide (MXene), Adv. Funct. Mater. 26, 3118 (2016).
- [16] A.Manjavacas and F.J.Garcia de Abajo, Tunable plasmons in atomically thin gold nanodisks, Nature Commun. 5, 3548 (2014).
- [17] F.J.Garcia de Abajo and A.Manjavacas, Plasmonics in atomically thin materials, Faraday Discuss. 178, 87 (2015).
- [18] X.Liu, J.-H.Kang, H.Yuan, J.Park, et al., Electrical tuning of a quantum plasmonic resonance, Nature Nanotechn. 12, 866 (2017).
- [19] I.V.Bondarev and V.M.Shalaev, Universal features of the optical properties of ultrathin plasmonic films, Optical Mater. Express 7, 3731 (2017).
- [20] I.V.Bondarev, H.Mousavi, and V.M.Shalaev, Optical response of finite-thickness ultrathin plasmonic films, MRS Commun. 8, 1092 (2018).
- [21] I.V.Bondarev, Finite-thickness effects in plasmonic films with periodic cylindrical anisotropy [Invited], Optical Mater. Express 9, 285 (2019).
- [22] R.A.Maniyara, D.Rodrigo, R.Yu, J.Canet-Ferrer, et al., Tunable plasmons in ultrathin metal films, Nature Photon. 13, 328 (2019).
- [23] I.V.Bondarev, H.Mousavi, and V.M.Shalaev, Transdimensional epsilon-near-zero modes in planar plasmonic nanostructures, Phys. Rev. Research 2, 013070 (2020).
- [24] I.V.Bondarev and C.M.Adhikari, Collective excitations and optical response of ultrathin carbon-nanotube films, Phys. Rev. Applied 15, 034001 (2021).
- [25] I.V.Bondarev, Controlling single-photon emission with ultrathin transdimensional plasmonic films, Ann. Phys. (Berlin) 535, 2200331 (2023).
- [26] L.Zundel, P.Gieri, S.Sanders, and A.Manjavacas, Comparative analysis of the near- and far-field optical response of thin plasmonic nanostructures, Adv. Optical Mater. 10, 2102550 (2022).
- [27] S.-A.Biehs and I.V.Bondarev, Far- and near-field heat transfer in transdimensional plasmonic film systems, Adv. Optical Mater. 11, 2202712 (2023).
- [28] H.Salihoglu, J.Shi, Z.Li, Z.Wang, et al., Nonlocal near-field radiative heat transfer by transdimensional plasmonics, Phys. Rev. Lett. 131, 086901 (2023).
- [29] I.V.Bondarev, M.D.Pugh, P.Rodriguez-Lopez, L.M. Woods, and M.Antezza, Confinement-induced nonlocality and Casimir force in transdimensional systems, Phys. Chem. Chem. Phys. 25, 29257 (2023).
- [30] P.Rodriguez-Lopez, D.-N.Le, I.V.Bondarev, M.Antezza, and L.M.Woods, Giant anisotropy and Casimir phenomena: The case of carbon nanotube metasurfaces, Phys. Rev. B 109, 035422 (2024).
- [31] L.V.Keldysh, Coulomb interaction in thin semiconductor and semimetal films, Pis’ma Zh. Eksp. Teor. Fiz. 29, 716 (1979) [Engl. translation: JETP Lett. 29, 658 (1980)]; N.S.Rytova, Screened potential of a point charge in a thin film, Moscow University Physics Bulletin 3, 30 (1967).
- [32] L.Vertchenko, L.Leandro, E.Shkondin, O.Takayama, et al., Cryogenic characterization of titanium nitride thin films, Optical Mater. Express 9, 2117 (2019).
- [33] M.D.Pugh, SK.F.Islam and I.V.Bondarev, Anisotropic photon emission enhancement near carbon nanotube metasurfaces, Phys. Rev. B 109, 235430 (2024).
- [34] K.Artmann, Berechnung der Seitenversetzung des totalreflektierten Strahles, Ann. Phys. 437, 87 (1948).
- [35] C.M.Olaya, N.Hayazawa, N.Hermosa, and T.Tanaka, Angular Goos-Hänchen shift sensor using a gold film enhanced by surface plasmon resonance, J. Phys. Chem. A 125, 451 (2021).
- [36] A.Aiello, M.Merano, and J.P.Woerdman, Duality between spatial and angular shift in optical reflection. Phys. Rev. A 2009, 80, No. 061801].
- [37] S.-A.Biehs and I.V.Bondarev, Supplementary information file for this article.
- [38] P.Yeh, Optical waves in layered media (Wiley, 2005).
- [39] A.Boltasseva and H.A.Atwater, Low-loss plasmonic metamaterials, Science 331, 290 (2011).
- [40] P.Das, S.Rudra, D.Rao, S.Banerjee, et al., Electron confinement-induced plasmonic breakdown in metals, Science Adv. 10, eadr2596 (2024).
- [41] V.J.Yallapragada, A.P.Ravishankar, G.L.Mulay, G.S. Agarwal, and V.G.Achanta, Observation of giant Goos-Hänchen and angular shifts at designed metasurfaces, Sci. Rep. 6, 19319 (2016).
- [42] L.Malassis, P.Masse, M.Treguer-Delapierre, S.Mornet, et al., Topological darkness in self-assembled plasmonic metamaterials, Adv. Mater. 26, 324 (2014).
- [43] V.G.Kravets, F.Schedin, R.Jalil, L.Britnell, et al., Singular phase nano-optics in plasmonic metamaterials for label-free single-molecule detection, Nature Mater. 12, 305 (2014).
- [44] K.V.Sreekanth, S.Sreejith, S.Han, X.Chen, et al., Biosensing with the singular phase of an ultrathin metal-dielectric nanophotonic cavity, Nature Commun. 9, 369 (2018).
- [45] G.Ermolaev, K.Voronin, D.G.Baranov, V.Kravets, et al., Topological phase singularities in atomically thin high-refractive-index materials, Nature Commun. 13, 2049 (2022).