Graph Spectral Embedding using the Geodesic Betweeness Centrality
Abstract
We introduce the Graph Sylvester Embedding (GSE), an unsupervised graph representation of local similarity, connectivity, and global structure. GSE uses the solution of the Sylvester equation to capture both network structure and neighborhood proximity in a single representation. Unlike embeddings based on the eigenvectors of the Laplacian, GSE incorporates two or more basis functions, for instance using the Laplacian and the affinity matrix. Such basis functions are constructed not from the original graph, but from one whose weights measure the centrality of an edge (the fraction of the number of shortest paths that pass through that edge) in the original graph. This allows more flexibility and control to represent complex network structure and shows significant improvements over the state of the art when used for data analysis tasks such as predicting failed edges in material science and network alignment in the human-SARS CoV-2 protein-protein interactome.
1 Introduction
Analysis of networks arising in social science, material science, biology and commerce, relies on both local and global properties of the graph that represents the network. Local properties include similarity of attributes among adjacent nodes, and global properties include the structural role of nodes or edges within the graph, as well as similarity among distant nodes. Graph representations based on the eigenvectors of the standard Graph Laplacian have limited expressivity when it comes to capturing local and structural similarity, which we wish to overcome.
We propose an unsupervised approach to learn embeddings that exploit both the Laplacian and the affinity matrix combined into a Sylvester equation. However, to better capture local as well as structural similarity, we consider the Laplacian and the affinity matrix not of the original graph, but rather of a modified betweenness centrality graph derived from it. Centrality is a statistic (a function of) the topology of the graph that is not captured in the original edge weights. The node embeddings are the Spectral Kernel Descriptors of the solution of the Sylvester equation.
The key to our approach is three-fold: (i) The betweeness centrality of edges, defined as the fraction of shortest paths going through that edge, to capture semi-global structure in the original graph; (ii) The use of both the Laplacian and the affinity matrix of the centrality graph, to modulate the effect of local and global structure; (iii) The use of the Sylvester equation as a natural way of combining these two graph properties into a single basis. Any number of descriptors could be built on this basis, we just choose the Spectral Kernel Descriptor for simplicity.
Our approach is related to uncertainty principles of graph harmonic analysis, that explore the extent in which signals can be represented simultaneously in the vertex and spectral domains. We extend this approach to characterize the relation between the spectral and non-local graph domain spread of signals defined on the nodes.
We illustrate the use of our method in multiple unsupervised learning tasks including node classification in social networks, network alignment in protein-to-protein interaction (PPI) for the human-SARS-CoV-2 protein-protein interactome, and forecasting failure of edges in material science.
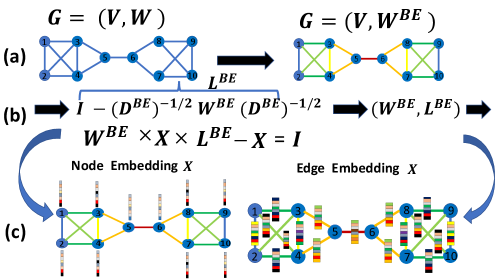
2 Related Work
For a graph with vertices in the set and edge weights in , where denotes the weight of an edge between nodes and , we measure the centrality of an edge by the fraction of the number of shortest paths that pass through that edge, called edge betweenness centrality (EBC). From the betweenness centrality of the edges of , we construct a modified graph with the same connectivity of , but edges weighted by their EBC value. The result is called edge betweeness centrality graph (BCG), or centrality graph for short, and denoted by , which measures the importance of edges given the adjacency matrix.
Graph centrality based measurements, such as vertex centrality, eigenvector centrality [20], and edge betweeness centrality [28] have been widely used in network analysis and its diverse applications [7, 10]. There is a large body of work that focus on graph embedding methods that, similar to our approach, aims to learn a function from the graph nodes into a vector space [23, 1, 30, 40]. Such methods construct graph representations that are based on either local or structural similarities.
Graph convolutional networks [24, 11, 39] are among the most popular methods for graph based feature learning, combining the expressiveness of neural networks with the graph structures. Typically, these methods assume that node features or attributes are available, while we focus on problems where only the graph network is available. There is also a large body of work that focus on graph embedding methods that, similar to our approach, only assumes that the affinity matrix is given as an input. Such methods construct graph representations that are based on either local or structural similarities [23, 1, 30, 40].
Uncertainty principles in graphs have been explored by [2, 37], extending traditional uncertainty principles of signal processing to more general domains such as irregular and unweighted graphs [32]. [2] provides definitions of graph and spectral spreads, where the graph spread is defined for an arbitrary vertex, and studies to what extent a signal can be localized both in the graph and spectral domains.
Other related work includes different approaches in manifold learning [31, 5, 38], manifold regularization [21, 17, 13, 16, 12, 18, 14, 15], graph diffusion kernels [9] and kernel methods widely used in computer graphics [3, 36] for shape detection. Most methods assume that signals defined over the graph nodes exhibit some level of smoothness with respect to the connectivity of the nodes in the graph and therefore are biased to capture local similarity.
The Sylvester equation was previously employed in a variety of graph mining applications such as network alignment and subgraph matching [41, 19]. Most previous works used the continuous Sylvester equation with two input affinity matrices corresponding to the input affinity matrices. We propose a different approach, where we solve the discrete-time Sylvester equation using the affinity matrix and its associated Laplacian.
3 Preliminaries and Definitions
Consider an undirected, weighted graph . The degree of a node is the sum of the weights of edges connected to it. The combinatorial graph Laplacian is denoted by , and defined as , with the diagonal degree matrix with entries . The eigenvalues and eigenvectors of are denoted by and , respectively. The normalized Laplacian is defined as and its real eigenvalues are in the interval . In this work we use the normalized Laplacian , which from now on we refer to as for simplicity.
3.1 Centrality Graph
The edge betweeness centrality (EBC) is defined as
| (1) |
where is the number of the shortest distance paths from node to node and is the number of those paths that includes the edge . Since we do not use other forms of centrality in this work, we refer to EBC simply as centrality. Accordingly, the (edge betweenness) centrality graph BCG is defined as which shares the same connectivity but modifies the edges of to be . Formally, the similarity matrix representing the connectivity of is
| (2) |
Note that while and share the same connectivity, their spectral representation given by the eigensystem of the graph Laplacian , the eigenvalues and their associated eigenvectors and , are rather different. Importantly, the eigenvectors provide a different realization of the graph structure in comparison to the eigenvectors of an unweighted graph, that is captured by a different diffusion process around each vertex. We denote with the matrices corresponding to the eigenvector decomposition of respectively.
3.2 Structural and local similarity trade-off Via Total Vertex and Spectral Spreads
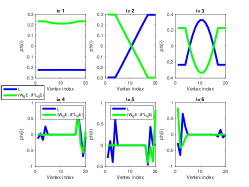
The eigensystem of the Laplacian and the affinity matrix provides two alternative basis functions that capture different properties of the graph structure (see Fig. 2 for an illustration). One way to study the basis functions’ different characterizing network structure and local structure is using the vertex and spectral spreads (see their definitions below).
Definition 1
(Total vertex domain spread)
The global spread of a non zero signal with respect to a matrix (corresponding to an arbitrary affinity matrix) is defined as
| (3) |
where corresponds to vertices connected in the similarity graph .
Definition 2
(Spectral spread) [2]
The spectral spread of a non zero signal with respect to a similarity affinity matrix is defined as
| (4) |
where
| (5) |
is the graph Fourier transform of the signal with respect to the eigenvalue .
The trade-off can be realized by characterizing the domain enclosing all possible pairs of vertex and spectral spreads of the BCG.
Definition 3
Feasibility domain of
| (6) |
where .
Specifically, searching for the lower boundary of the feasibility domain of the vertex and spectral spreads of is shown to yield a generalized eigenvalue problem, whose corresponding eigenvectors produce a representation which trades off local and structural node similarity. We can write the generalized eigenvalue problem (17) using the matrix pencil
| (7) |
where
| (8) |
where the eigenvector solving (17) is also a minimizer for (15) (see the appendix for additional details).
The scalar controls the trade-off between the total vertex and spectral spreads, as illustrated in the barbell graph ) in Fig.2 (a) and (b) using = -200, and = -0.2, respectively. Functions colored with green correspond to the eigenvectors of ), functions colored with blue correspond to the eigenvectors of . As can be seen, when is large, the eigenvectors of ) reveal structure which is similar to the eigenvectors of , while small values of produce structure which is similar to those corresponding to .
4 Proposed Graph Sylvester Embedding
We suggest an embedding that goes beyond the scalar modulation of the generalized Laplacian Eq.(17) by using a linear mapping between the subspaces and . We exploit the fact that the correspondence between the nodes represented by the two basis functions of and is known, i.e., it is the identity map, with for each (i.e., the column index corresponding to each node in is the same in ). We propose using the solution of a Sylvester equation as the node feature representation, which is also the mapping between the nodes’ representations. The resulting embedding is given by the solution to the discrete Sylvester equation (or the singular value decomposition associated with the solution) will be composed of two hybrid representations associated with the graph networks and local connectivity. The proposed method is coined Graph Sylvester Embedding (GSE).
The discrete-time Sylvester operator is used to express the eigenvalues and eigenvectors of and using a single operator , where we solve
| (9) |
using , ( is the identity matrix), .
Let , , and , be the corresponding eigenvectors and eigenvalues of and , respectively.
We will assume that the eigenvalues of and satisfy that , , hence the operator is non-singular and has matrix eigenvalues and eigenvectors. Note that the Sylvester equation has a unique solution for any if and only if is non-singular, which occurs if and only if . By choosing and ordering the columns in and based on the identity map, we obtain that each column in provides a node representation to its corresponding node .
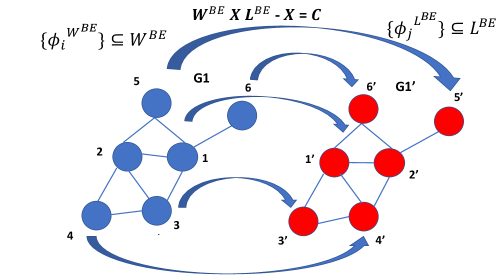
Note that we can also express the solution to the Sylvester equation Eq.(9) using the Kronecker product :
| (10) |
where we vectorize and to obtain its equivalent vector representation = vec and = vec. Since the Sylvester equation can be written using the Kronecker product, then all known properties of the Kronecker product are carried on to the proposed graph Sylvester embedding. One important property is invariance to permutations.
Proposition 1
Suppose that is a permutation matrix, , and , and assume that are two solutions to the discrete-time Sylvester equation Eq.(24) with the associate matrices and , respectively, and , , then
| (11) |
Proof: See Appendix.
The resulting solution of can be described using the following conditions. Assume that , and that the graph representation encoded in and has the same order based on the identity map, and . Then the solution to the discrete-time Sylvester system Eq.(9) is unique where
| (12) |
where . See proof in the appendix.
Remark 1: Eq. (12) shows the analytical solution to the Sylvester equation. In practice, one can use fast iterative methods [26]. Also note that under the assumptions that , the solution is unique [26]. We note that Sylvester’s equation can be generalized to include multiple terms, thus allowing one to incorporate multiple basis functions. We illustrate the concept with two bases, to capture local and global statistics of the topology of the network, and leave extension to additional bases, that can be specific to particular domains or tasks, for future work.
Remark 2: One can view the solution to the Sylvester equation as a polynomial of the matrices and ([22]), where using higher-order polynomials in , can be interpreted as imposing smoothness in the embedding space.
4.1 Spectral Representation of GSE
By our specific construction of matrices in the Sylvester equation Eq.( 12) we have that the th row of the solution captures local and global statistics of the topology of the network with respect to the node . This is an important property which was achieved by our choice of , and using the same order of the graph representation encoded in and . It is now possible to construct graph embedding from . We employ graph embedding using the spectral decomposition of .
Given the Singular Value Decomposition and equally spaced scales , we compute a node embedding for each node using the Spectral Kernel descriptor of using
| (13) |
where , and correspond to the left and right singular eigenvectors, and singular values, respectively, is to the number of the largest eigenvalues and eigenvectors used in the SVD decomposition, and are normalizing constants.
Remark: Note that the spectral kernel descriptor in Eq.(13) is similar to the WKS descriptor [3] proposed to describe the spectral signature of the Laplace- Beltrami operator (LBO). For applications using Sylvester embedding shown in this work, we find the descriptor in Eq.(13) effective as it weighs the eigenvalues equally and separates the influence between different eigenvalues.
| (14) |
5 Experimental Results
We evaluate our method on real-world networks in several applications including material science and network alignment of Protein-Protein interactions (PPIs) networks using a recent dataset that has been used to study Covid-19, the SARS-CoV-2. We compare GSE to known and existing state of the art methods in the respective applications. There are a number of benchmarks to evaluate network embeddings built using at least partial supervision, for instance for node classification relative to a given ground truth. Our method does not require any, and therefore we focus our attention on unsupervised benchmarks. Extension of our method to graph classification, or other graph analysis tasks that can exploit supervision is beyond the scope of this paper and will be considered in future work.
Evaluation metrics: In the problem of network alignment we use the percentage of correct node correspondence found to evaluate our method, based on the known ground truth correspondence between the two networks. In detecting failure edges in material science we measure the success rate using sensitivity.
To detect failured edges, we use the graph embedding obtained by each method to cluster the data into two approximately equal size clusters using spectral clustering .
We then choose the cluster with the largest betweenness centrality mean value.
For further validation, we test the statistical significance of each method by computing the values using hyper-geometric distribution (see the Appendix).
Comparison with other methods: Our baseline for comparison with the proposed Graph Sylvester Embedding is using the concatenated spectral embedding corresponding to both the Laplacian and the affinity matrix. We coin the concatenated bases as St.(). We compare to the spectral Wave Kernel Descriptor signature (WKS) [3] (coined desc.).
in the Tables indicates methods that failed to converge or provided meaningless results.
We compare with a representative of graph embeddings methods including Laplacian Eigenmaps [5], node2vec [1], and NetMF [23].
We also test against methods that were specifically tailored to this applications we explored including methods for graph alignments [41, 42] and methods based on betweenness centrality for detecting failured edges [7].
5.1 Detect Failed Edges in Material Sciences
Forecasting fracture locations in a progressively failing disordered structure is a crucial task in structural materials [7]. Recently, networks were used to represent 2 dimensional (2D) disordered lattices and have been shown a promising ability to detect failures locations inside 2D disordered lattices.
Due to the ability of BC edges that are above the mean to predict failed behaviors [7], we expect the edge embedding based on EBC to be effective. As shown in the experimental results below, our proposed edge embedding improves robustness in comparison to simpler methods such as the one employed in [7] or methods that are based on ”standard” Laplacian embedding. We first describe how to employ edge embedding (proposed node embedding detailed in Sect. 4) for this task.
Edge Embedding using GSE: Edge embedding is constructed by first applying our node embedding and then using the concatenated nodes features to construct the edge embeddings. To forecast the failed edges, we construct a new graph where nodes correspond to the edge embedding features and then apply spectral clustering to cluster the edges into two groups. We apply the same strategy to test spectral descriptors which are based on the graph Laplacian.
Dataset: The set of disordered structures was derived from experimentally determined force networks in granular materials [6]. The network data is available in the Dryad repository [8].
We tested 6 different initial networks, with mean degrees , 3.0, 3.6, following the same datasets corresponding to different initial granular configurations.
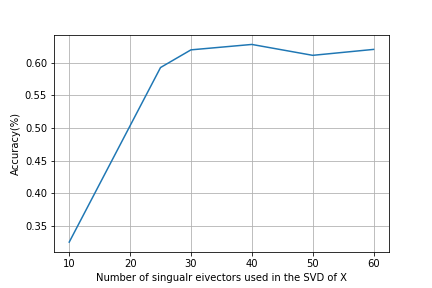
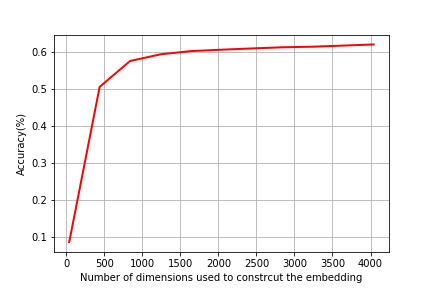
Implementation Details: In all experiments, we used , for all , corresponds to the coefficients in the wave kernel signature WKS (Eq (15)). We used a fixed number of total 800 scales in all experiments. We measure the success rate in detecting failure edges in terms of the sensitivity (true positive rate). We report experimental results for a varying number of singular eigenvectors in the SVD of the solution to the Sylvester equation, which is then employed to compute edge embeddings (as described above, based on the node embeddings detailed in Algorithm 1 ).
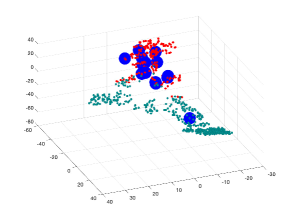
Table 1 shows a comparison of our method where we report the results using for all methods which are based on eigensystem computation (this the same number of eigenvectors and associated eigenvalues computed for the spectral methods which are based on graph Laplacian such as LE and spectral descriptors). Fig.4 (b) show visualization using t-SNE of our proposed methods for edge embedding. The points colored in red correspond to the edges whose values are above the mean EBC, while the points colored in turquoise correspond to edges bellow the mean EBC. The blue enlarged dots correspond to the failed edges in the system which were successfully detected by each method. In the examples illustrated, our proposed embeddeding successfully forecast all failed edges, which were mapped to the same cluster including edges whose EBC value was below the mean value.
| Method /Network | Mean deg. | Mean deg. | Mean deg. | Mean deg. | Mean deg. | Mean deg. | Avg. std | |
|---|---|---|---|---|---|---|---|---|
| (2.4) | (2.6) | (3.35) | (2.55) | (3) | (3.6) | |||
| FL[7] | 85.7 | 70 | 60 | 58.3 | 48.4 | 58.1 | 63.4 11.7 | |
| NetMF | 28 | 40 | 72 | 45 | 93.9 | 90.0 | 61.4 25.2 | |
| node2vec | 64.2 | 55 | 40 | 79.0 | 69.6 | 37.2 | 61.4 15.1 | |
| LE | 64.2 | 75 | 68.0 | 66.6 | 63.6 | 83.7 | 70.1 6.5 | |
| desc. | 57.1 | 45 | 84.0 | 45.0 | 54.5 | 37.2 | 53.8 15 | |
| St.() | 64.2 | 75.0 | 80.0 | 75.0 | 78.7 | 79.0 | 75.3 27.6 | |
| GSE | 92.8 | 80 | 76.0 | 75.0 | 72.2 | 83.7 | 79.9 6.8 |
5.2 Network Alignment on PPI networks with human protein interactors of SARS-CoV-2
Effective representation of nodes with similar network topology is important for network alignment applications, where the network structure around each node provides valuable information for matching and aligning the networks. Network alignment of Protein-protein interactions (PPIs) networks is considered as an important first step for the analysis of biological processes in computational biology. Typically, popular methods in this domain gather statistics about each node in the graph (e.g: node degree) followed by an optimization methods to align the network. For PPI networks, it is assumed that a protein in one PPI network is a good match for a protein in another network if their respective neighborhood topologies are a good match [33]. In this case, features or nodes attributes are in general not available which makes this task of network alignment and finding node correspondence more challenging, with only the graph network to rely on.
Dataset: We test using the STRING network from the STRING database, a PPI network that consists of 18,886 nodes and 977,789 edges. The STRING network includes 332 human proteins that physically interact with SARS-CoV-2. It is likely to have both false positives and false negatives edges. We aim to find network alignment between two copies of the STRING network, using an additional STRING network which is created by randomly removing 10 of the network edges. We also test on the Lung network [35], which is a more recent PPI networks with known human protein interactors of SARS-CoV-2 proteins that consists of 8376 nodes, 48522 edges, and 252 human proteins that physically interact with SARS-CoV-2.
Implementation details: Given the node correspondence of the protein interactors of SARS-CoV-2, we connect each pair of nodes corresponding to the same human protein interactors of SARS-CoV-2 with an edge, which is resulted in a network composed of the two STRING networks. We then apply the proposed GSE to generate node embeddings. We used 5-fold cross validation, where in each experiment we used 50 of the known human proteins in the STRING and Lung networks.
We compare to network alignment methods, such as Isorank [33], Final [41] and iNEAT [42]. For the network alignments methods, we provide as an input the corresponding affinity graphs and a matrix with the known correspondence between the nodes that correspond to human proteins that physically interact with SARS-CoV-2. Additionally, we also tested graph embeddings including Laplacian Eigenmaps (LE) [4], Locally Linear Embedding (LLE) [31], Hope [29], and node2vec [1] which are given the same input network. Graph embedding methods are not effective for this task and thus some of the results are omitted. Network alignments methods perform better, while our proposed GSE outperforms all competing methods.
Table 2 shows the percentage of nodes whose nearest neighbor corresponds to its true node correspondence using GSE in the STRING and Lung networks. Our proposed GSE outperforms all competing methods.
| Method/Data | STRING (s) | Lung | |
|---|---|---|---|
| node2vec | 10.4 % | - % | |
| Isorank | 23 % | 44.2 % | |
| Isorank using | 20 % | 44.2 % | |
| Final | 36 % | 50.5 % | |
| iNeat | 37.0 % | 53.5 % | |
| St.() | 25.3 % | 53.2 % | |
| GSE | 61.2 | 55.0 % |
6 Discussion
We have presented an embedding to represent local and global structure of a graph network, constructed without the need for any supervision nor explicit annotation. Besides the cost of time and effort, annotating data can create privacy and security risks. Our focus is on developing expressive and flexible representations that can be used in a variety of downstream tasks without human intervention. Flexibility is exercised through the choice of bases, that are combined through Sylvester’s equation. In the specific cases we have experimented, the bases are chosen to capture local and structural similarity across the graph network.
The implementation of our approach is computationally intensive, with most of the burden falling on the computation of the BCG, which is where is the total number of edges and is the total number of nodes, thus approximately for sparse graphs. The execution time of our method with Python code implementation using Intel Core i7 7700 Quad-Core 3.6GHz with 64B Memory on the Cora dataset with approximately 2700 nodes takes 24.9 seconds.
Computing BC measurements on large graphs is computationally heavy ( for sparse graphs), and developing fast methods for BC measurements is an ongoing research area. With significant progress that has been made in recent years (e.g: [27]) we can foresee extensions to scale our approach to networks with millions of nodes. In addition, the effectiveness of BC measurements degrades on larger graphs due to noise (for example when the graph includes a large number of nodes with clustering coefficient close to zero). Applying our approach to small sub-graphs or “Network motifs” before aggregating it to to the entire graph may be one foreseeable solution.
In our study, we found that spectral embedding by solving the Sylvester equation of the edge betweeness centrality graph reveals the node’s network structure, which is not necessarily possible with the original graph weights. It is also possible to compute edge betweenness centrality in a way that takes into account the original weight information. For example, by looking into the path evaluation function that assesses a path between two nodes that is combining both the sum of edge weights and the number of shortest distance path as was proposed in [34]. Another possible direction is to solve a generalized Sylvester equation which would incorporate both matrices corresponding to the original weight information and the edge betweenness centrality. Other future work includes expanding our approach to address applications which include dynamic graphs and multi-layer graphs, which would include solving Sylvester equation with time-varying coefficients.
References
- [1] node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining, 2016.
- [2] Ameya Agaskar and Yue M. Lu. A spectral graph uncertainty principle. IEEE Transactions on Information Theory, 59(7):4338–4356, 2013.
- [3] Mathieu Aubry, Ulrich Schlickewei, and Daniel Cremers. The wave kernel signature: A quantum mechanical approach to shape analysis. In ICCV Workshops, pages 1626–1633. IEEE Computer Society, 2011.
- [4] M. Belkin and P. Niyogi. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Computation, 15(6):1373–1396, 2003.
- [5] Mikhail Belkin and Partha Niyogi. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Computation, 2003.
- [6] Estelle Berthier, Jonathan E. Kollmer, Silke E. Henkes, Kuang Liu, J. M. Schwarz, and Karen E. Daniels. Rigidity percolation control of the brittle-ductile transition in disordered networks. Phys. Rev. Materials, 2019.
- [7] Estelle Berthier, Mason A. Porter, and Karen E. Daniels. Forecasting failure locations in 2-dimensional disordered lattices. Proceedings of the National Academy of Sciences, 116(34):16742–16749, Aug 2019.
- [8] Estelle et al Berthier. Rigidity percolation control of the brittle-ductile transition in disordered networks dryad, dataset,. Phys. Rev. Materials, 2019.
- [9] R. R. Coifman, S. Lafon, A. B. Lee, M. Maggioni, B. Nadler, F. Warner, and S. W. Zucker. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. Proceedings of the National Academy of Sciences of the United States of America, 2005.
- [10] MIHAI CUCURINGU, PUCK ROMBACH, SANG HOON LEE, and MASON A. PORTER. Detection of core–periphery structure in networks using spectral methods and geodesic paths. European Journal of Applied Mathematics, page 846–887, 2016.
- [11] Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in Neural Information Processing Systems 29. 2016.
- [12] Shay Deutsch, Andrea L. Bertozzi, and Stefano Soatto. Zero shot learning with the isoperimetric loss. In AAAI 2020.
- [13] Shay Deutsch, Soheil Kolouri, Kyungnam Kim, Yuri Owechko, and Stefano Soatto. Zero shot learning via multi-scale manifold regularization. CVPR, 2017.
- [14] Shay Deutsch and Gerard Medioni. Intersecting manifolds: Detection, segmentation, and labeling. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, 2015.
- [15] Shay Deutsch and Gerard Medioni. Unsupervised learning using the tensor voting graph. In Scale Space and Variational Methods in Computer Vision (SSVM), 2015.
- [16] Shay Deutsch and Gérard G. Medioni. Learning the geometric structure of manifolds with singularities using the tensor voting graph. Journal of Mathematical Imaging and Vision, 57(3):402–422, 2017.
- [17] Shay Deutsch, Antonio Ortega, and Gerard Medioni. Manifold denoising based on spectral graph wavelets. International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2016.
- [18] Shay Deutsch, Antonio Ortega, and Gérard G. Medioni. Robust denoising of piece-wise smooth manifolds. In 2018 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP 2018, Calgary, AB, Canada, April 15-20, 2018, pages 2786–2790, 2018.
- [19] Boxin Du and Hanghang Tong. Fasten: Fast sylvester equation solver for graph mining. KDD ’18, page 1339–1347, 2018.
- [20] L. Freeman. A set of measures of centrality based on betweenness. Sociometry, 1977.
- [21] M. Hein and M. Maier. Manifold denoising. pages 561–568, 2007.
- [22] Qingxi Hu Hu and Daizhan Cheng. The polynomial solution to the sylvester matrix equation. Applied Mathematics Letters, 2006.
- [23] Qiu Jiezhong, Dong Yuxiao, Ma Hao, Kuansan Jian, and Tang Jie. Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec. In Proceedings of the Eleventh International Conference on Web Search and Data Mining, WSDM, 2018.
- [24] Thomas N. Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations, ICLR ’17, 2017.
- [25] Jeffrey N Law, Kyle Akers, Nure Tasnina, Catherine M Della Santina, Shay Deutsch, Meghana Kshirsagar, Judith Klein-Seetharaman, Mark Crovella, Padmavathy Rajagopalan, Simon Kasif, and T M Murali. Interpretable network propagation with application to expanding the repertoire of human proteins that interact with sars-cov-2. 12 2021.
- [26] Tiexiang Li, Peter Chang-Yi Weng, Eric King-Wah Chu, and Wen-Wei Lin. Large-scale stein and lyapunov equations, smith method, and applications. Numer. Algorithms, 2013.
- [27] S. Maurya, Xin Liu, and T. Murata. Fast approximations of betweenness centrality with graph neural networks. Proceedings of the 28th ACM International Conference on Information and Knowledge Management, 2019.
- [28] M E Newman. Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 2002.
- [29] Mingdong Ou, Peng Cui, Jian Pei, Ziwei Zhang, and Wenwu Zhu. Asymmetric transitivity preserving graph embedding. In KDD, 2016.
- [30] Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. Deepwalk. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD ’14, 2014.
- [31] S. Roweis and L. Saul. Nonlinear dimensionality reduction by locally linear embedding. SCIENCE, 290:2323–2326, 2000.
- [32] D.I. Shuman, S.K. Narang, P. Frossard, A. Ortega, and P. Vandergheynst. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Processing Magazine, 2013.
- [33] Rohit Singh, Jinbo Xu, and Bonnie Berger. Global alignment of multiple protein interaction networks with application to functional orthology detection. Proceedings of the National Academy of Sciences, 2008.
- [34] Jadwiga Sosnowska and Oskar Skibski. Path evaluation and centralities in weighted graphs - an axiomatic approach. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI-18, pages 3856–3862. International Joint Conferences on Artificial Intelligence Organization, 7 2018.
- [35] Alexey Stukalov, Virginie Girault, Vincent Grass, Valter Bergant, Ozge Karayel, Christian Urban, Darya A. Haas, Yiqi Huang, Lila Oubraham, Anqi Wang, Sabri M. Hamad, Antonio Piras, Maria Tanzer, Fynn M. Hansen, Thomas Enghleitner, Maria Reinecke, Teresa M. Lavacca, Rosina Ehmann, Roman Wölfel, Jörg Jores, Bernhard Kuster, Ulrike Protzer, Roland Rad, John Ziebuhr, Volker Thiel, Pietro Scaturro, Matthias Mann, and Andreas Pichlmair. Multi-level proteomics reveals host-perturbation strategies of sars-cov-2 and sars-cov. bioRxiv, 2020.
- [36] Jian Sun, Maks Ovsjanikov, and Leonidas Guibas. A concise and provably informative multi-scale signature based on heat diffusion. Computer Graphics Forum, 2009.
- [37] O. Teke and P. P. Vaidyanathan. Uncertainty principles and sparse eigenvectors of graphs. IEEE Transactions on Signal Processing, 65(20):5406–5420, 2017.
- [38] J. Tenenbaum, V. de Silva, and J. Langford. A global geometric framework for nonlinear dimensionality reduction. Science, 2000.
- [39] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. Graph Attention Networks. International Conference on Learning Representations, 2018.
- [40] Xiao Wang, Peng Cui, Jing Wang, Jian Pei, Wenwu Zhu, and Shiqiang Yang. Community preserving network embedding. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, AAAI’17, 2017.
- [41] Si Zhang and Hanghang Tong. Final: Fast attributed network alignment. In KDD, 2016.
- [42] Si Zhang, Hanghang Tong, Jie Tang, Jiejun Xu, and Wei Fan. Incomplete network alignment: Problem definitions and fast solutions. ACM Trans. Knowl. Discov. Data, 14(4), 2020.
- [43] Dengyong Zhou and B. Schölkopf. A regularization framework for learning from graph data. In ICML 2004, 2004.
7 Appendix
7.1 Graph Differentiation
The lower boundary of the curve enclosing the feasibility domain of the spreads , with respect to a unit norm vector is defined as
| (15) |
To solve (15), we use the Lagrangian
| (16) |
with . Differentiating and comparing to zero, we obtain the following eigenvalue problem:
| (17) |
where the eigenvector solving (17) is also a minimizer for (15). Denoting
| (18) |
we can write the generalized eigenvalue problem (17) using the matrix pencil
| (19) |
The scalar controls the trade-off between the total vertex and spectral spreads, as illustrated in the barbell graph ) in Fig.2 (a) and (b) using = -200, and = -0.2, respectively. Functions colored with green correspond to the eigenvectors of ), functions colored with blue correspond to the eigenvectors of .
As can be seen, when is large, the eigenvectors of ) reveal structure which is similar to the eigenvectors of , while small values of produce structure which is similar to those corresponding to .
The analysis above yields the generalized graph Laplacian in Eq.(17) whose solutions can be used for graph embedding. One could use different scaling coefficients for the two matrix coefficients, thus giving different weight to the Laplacian and affinity terms in the resulting embedding. The embedding (coined GSSE), obtained by solving Eq.(18), is composed of solutions to the generalized eigenvalue problem that characterize the relationships between these two quantities, specifically the lower bound of their feasibility domain.
7.2 Node Embeddings using Total Vertex and Spectral Spreads (GSSE)
We present an additional embedding method which is based on the analysis in section 4.2 (Graph Differentiation) which derived the generalized Laplacian in Eq.(10). In order to employ for analysis and practical considerations it is often useful to encode the network captured in using a semi positive definite operator. For practical consideration, we transform into a semi positive definite matrix using a simple perturbation matrix , where , , where is the smallest eigenvalue of , and is the identity matrix. Setting
| (20) |
ensures that is semi positive definite (SPD) matrix. Letting and be the eigenvalues corresponding to and , respectively, we can see that the choice made in (20) ensures that the original spacing in eigenvalues of is preserved in . The embedding method proposed using is coined Graph Spectral Spread Embedding (GSSE). Note that there is a geometric interpretation which is related to the way was obtained from the lower boundary curve enclosing the feasibility domain ; Setting instead another perturbation matrix with and defining
| (21) |
where corresponds to the minimum eigenvalue of . we have that
| (22) |
which defines a half plane in .
Properties: The feasibility domain is a bounded set since
| (23) |
where corresponds to the largest eigenvalue of the affinity graph.
7.3 Forecasting failures edges: additional details and comparisons
We report additional experimental results on the granular material datasets [7]. In all experiments, we used , for all , corresponds to the coefficients in the wave kernel signature WKS (Eq.(13)). We used a fixed number of 800 scales and a fixed and number of singular eigenvectors corresponding to the number of points. The experiments reported in Table 3) test the statistical significant of each method by computing the values using hyper-geometric probability distribution. Specifically, the total number of edges corresponds to the total population size parameter in the hyper-geometric distribution with the feature that contains K failed edges, the size of the cluster is the number of draws and the number of observed successes corresponds to the number of edges correctly classified as failed edges.
| Method /Network | Mean deg. | Mean deg. | Mean deg. | Mean deg. | Mean deg. | Mean deg. | |
|---|---|---|---|---|---|---|---|
| (2.4) | (2.6) | (3.35) | (2.55) | (3) | (3.6) | ||
| node2vec | 3 | ||||||
| NetMF | |||||||
| LE | |||||||
| desc. | |||||||
| desc. | 9.9 | ||||||
| St.() | |||||||
| GSE |
8 Network Alignment
We report additional results and details in the problem of network alignment using the STRING network from the STRING database. In the experimental results we used all 332 human proteins known to interact with the Sars-Cov-2 as the available node correspondence between the two networks we tested on network alignment. From the 18,886 node of the String network we extract the 1000 nodes which corresponds to the nodes with the largest diffusion scores and the 332 nodes corresponding the human proteins known to interact with the Sars-Cov-2, based on the method suggested in [25]. Alignment is performed between two copies of the STRING network, where 10 and 20 edges were removed from the sub-network consisting of a total of 1332 nodes. It is evident that graph embedding methods such as LLE and LE, which are rooted in manifold learning that is biased to local similarity and heavily relies on the graph smoothness are not effective for this task.
| Method/noisy edges percentage | 10 | 20 |
|---|---|---|
| LE [4] | 5.38 | - |
| LLE [31] | 1.5 | 1.3 |
| RL [43] | 1 | - |
| HOPE [29] | 2 | - |
| Isorank [33] | 41 | 40 |
| Final [41] | 58.2 | 56.6 |
| iNEAT [42] | 63.8 | 56.1 |
| GSSE | 48 | 20.21 |
| GSE | 76.4 | 60 |
9 The Sylvester operator
The discrete-time Sylvester operator is used to express the eigenvalues and eigenvectors of and using a single operator , where we solve
| (24) |
using , ( is the identity matrix), .
Proposition 2
Suppose that is a permutation matrix, , , and assume that are two solutions to the discrete-time Sylvester equation Eq.(24) with the associate matrices and , respectively, then
| (25) |
Proof: For a permutation matrix , let
, and .
Let are two solutions to the discrete-time Sylvester equation Eq.(24) with the associate matrices and , respectively, and .
Next note that . Since is a permutation matrix, we have that and by multiplying and from the left hand and right hand side, respectively, we obtain . Denoting , under the assumptions that is a unique solution, then .
The resulting solution of is described in the next Lemma below. Note that since we have and that are diagonalizable, (with the matrices corresponding to the associated eigenvectors of , respectively).
Lemma 1
Let , and in the Sylvester equation (24), with . Let , , and , be the corresponding eigenvectors and eigenvalues of and , respectively. Assume that , and that the graph representation encoded in and have the same order based on the identity map , with for each . Then, if , the solution to the discrete-time Sylvester system (24) is
| (26) |
where
Proof: Using we have that and are diagonalizable, and where and . Since the matrices are orthogonal, we have
| (27) |
Multiplying by and we obtain
| (28) |
Setting and using , we have
| (29) |
Since is a diagonal matrix, we have that the th row of is times the th row of and since is a diagonal matrix, then the th column of is times the th column of . Combining the two properties, we obtain that for the entry
hence:
, with .
The next Proposition is a result of Lemma 2.1 in [22], showing the solution to the Sylvester equation as a polynomial of the matrices and [22], where in our case using higher-order polynomials in , can be interpreted as imposing smoothness in the embedding space.
Proposition 3
Given , and , where do not share eigenvalues (i.e., ). Let and , then
| (30) |
Moreover, the solution to the Sylvester equation can be represented as a polynomial in for , :
| (31) |
where and is the characteristic polynomial of .
Proof: Let be a solution to Eq (24), we assume that and are symmetric matrices with the same dimensionality, and that . By Lemma 2.1 in [22] is unique and
| (32) |
for any . Taking , we have that . Since then . Substituting and with and , respectively, then by similar arguments to Proposition 2.3. in [22] can be represented as a polynomial of and using the Cayley–Hamilton Theorem with , where is the characteristic polynomial of .