Gravitational bremsstrahlung from spinning binaries
in the post-Minkowskian expansion

Consider the case of two spinning bodies approaching one another from infinity, and suppose that their distance of closest approach remains much larger than their individual radii. In this scenario, the details of their scattering encounter are well described by an EFT in which the two bodies are treated as point particles traveling along the worldlines of their respective centers of energy. Their dynamics are conveniently described by a Routhian [65, 105, 106, 107], which for each body of mass $m$ reads

The translational degrees of freedom (d.o.f.s) of this body are encoded in four worldline coordinates $x^{\mu}(\tau)$, which chart the integral curve of the four-velocity ${\mathcal{U}^{\mu}\equiv\text{d}x^{\mu}/\text{d}\tau}$. Only three of these are needed to specify the position of the body uniquely, however, and so we remove the remaining unphysical d.o.f. by imposing the constraint ${\mathcal{U}_{\mu}\mathcal{U}^{\mu}=1}$ [43, 65]. Meanwhile, the body’s rotational d.o.f.s are encoded in the antisymmetric spin tensor $\mathcal{S}_{ab}$, which notably is defined in a locally flat frame with coordinates $\{y^{a}\}$. Tensors defined in the general coordinate frame $\{x^{\mu}\}$ are transformed into the former by way of the vielbein ${e_{\mu}^{a}\equiv\partial y^{a}/\partial x^{\mu}}$ (e.g., ${\mathcal{U}^{a}\equiv e^{a}_{\mu}\mathcal{U}^{\mu}}$), which also defines for us the spin connection ${\omega_{\mu}^{ab}\coloneq g^{\rho\sigma}\!e^{b}_{\sigma}\nabla_{\!\mu}^{\vphantom{a}}e^{a}_{\rho}}$. Only three of the six components in $\mathcal{S}_{ab}$ are needed to specify the spin of the body uniquely; hence, the other three d.o.f.s are to be removed by imposing a spin supplementary condition (SSC) [108, 109, 110, 111]. Given the relativistic nature of the problem, the covariant SSC, ${\,\mathcal{U}^{a}\mathcal{S}_{ab}=0+O(\mathcal{S}^{3})}$ [111], proves to be the most convenient choice.

The first three terms in Eq. (1) are universal, in the sense that they apply to any body with a mass monopole and spin dipole. Higher-order multipole moments, however, are sensitive to the body’s internal structure, and this is why the final term in Eq. (1), which describes the self-induced quadrupole moment of the rotating body (${E_{\mu\nu}\equiv R_{\mu\rho\nu\sigma}\mathcal{U}^{\rho}\mathcal{U}^{\sigma}}$), is accompanied by the Wilson coefficient $C_{E}$. Kerr black holes have ${C_{E}=1}$ [106], although this value can be larger for objects like neutron stars [112, 113]. Infinitely many more terms can be appended to Eq. (1) should we wish to include even higher-order multipoles [114], or other finite-size effects like tidal deformations [115, 74], but these all come with higher powers of either the curvature tensors or the spin, and so are irrelevant to our purposes here.

As the Routhian behaves like a Lagrangian from the point of view of the translational d.o.f.s, but like a Hamiltonian with regards to the rotational d.o.f.s, the equations of motion for each body follow from a mixture of Euler-Lagrange and Hamilton equations [116]; namely,

The only nontrivial Poisson bracket we require is [105]

where $\eta^{ab}$ is the Minkowski metric with a mostly minus signature. Note that the aforementioned constraints on $\mathcal{U}^{\mu}$ and $\mathcal{S}_{ab}$ should be imposed only after all functional derivatives and Poisson brackets have been evaluated.

To fully specify our EFT, we must also endow the metric $g_{\mu\nu}$ with its own dynamics; hence, we take the full effective action to be ${S=S_{\text{EH}}+S_{\text{FP}}+\sum_{A=1}^{2}\int\text{d}\tau_{A}\mathcal{R}_{A}}$, where $S_{\text{EH}}$ is the Einstein-Hilbert action, $S_{\text{FP}}$ is a Faddeev-Popov term that enforces the de Donder gauge, and the label ${A\in\{1,2\}}$ is used to distinguish between the binary’s two constituents.

As a precursor to computing the radiated four-momentum, we first determine the stress-energy tensor $T^{\mu\nu}$ for the binary as a whole. This object is sourced by the multipolar moments of the two bodies, as well as by the energy stored in nonlinear interactions of the gravitational field, and can be obtained perturbatively from our EFT with the help of Feynman diagrams once we expand the action in powers of ${\kappa h_{\mu\nu}\coloneq g_{\mu\nu}-\eta_{\mu\nu}}$, with ${\kappa\equiv\sqrt{32\pi G}}$. Crucially, since

in this expansion, Greek and Latin indices are now indistinct. The spin tensors are, nonetheless, still defined in their respective locally flat frames [65].

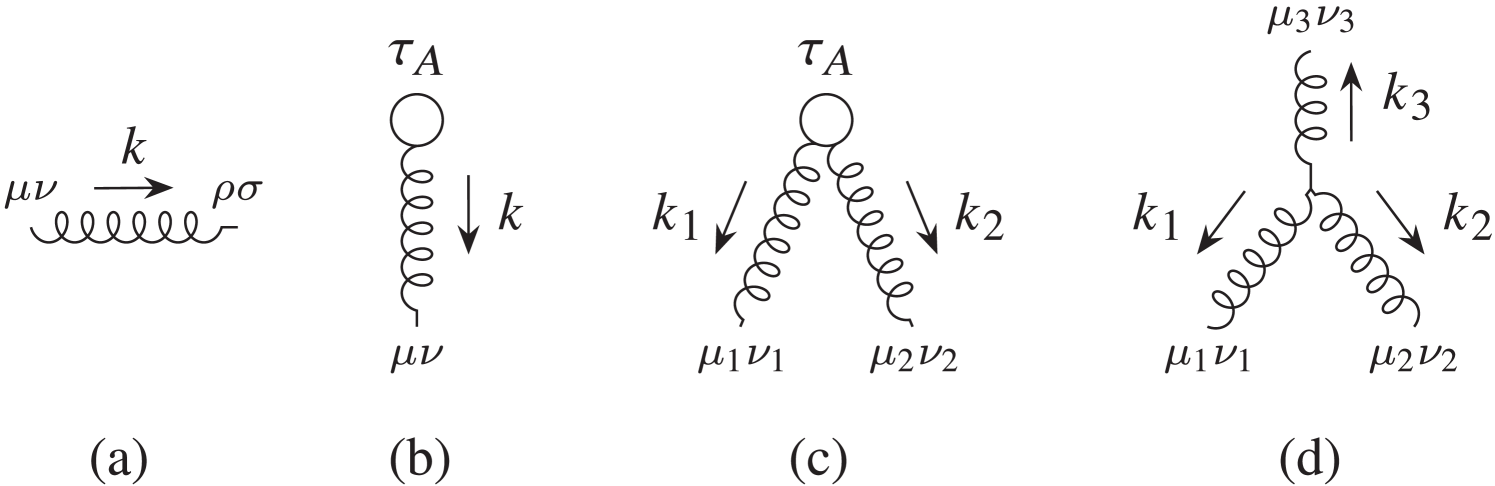
Only the Feynman rules shown in Fig. 1 are required at the order in $G$ to which we are working. In $d$-dimensional momentum space (we work in $d$ dimensions for added generality), the graviton propagator in Fig. 1(a) is $iP_{\mu\nu\rho\sigma}/k^{2}$, with ${P_{\mu\nu\rho\sigma}=\eta_{\mu(\rho}\eta_{\sigma)\nu}+\eta_{\mu\nu}\eta_{\rho\sigma}/(d-2)}$ (an $i\epsilon$ prescription is unnecessary at this order because the loop integrals never hit the poles at ${k^{2}=0}$ [83]), while the worldline vertex for single-graviton emission is

Expressions for the two remaining vertices, which are much lengthier, are presented in the Supplemental Material [104].

In addition to making the weak-field expansion above, we must also expand the body variables ${X_{A}\equiv(x_{A},\mathcal{U}_{A},\mathcal{S}_{A})}$ about their initial straight-line trajectories in order to achieve manifest power counting in $G$. We therefore write [43, 65]

where $\delta^{(n)}X_{A}$ is the $O(G^{n})$ deflection away from the initial trajectory $\overline{X}_{A}$ due to the gravitational pull of the other body. The 1PM deflections $\delta^{(1)}X_{A}$, which we will need later in our calculation, were previously computed using Eq. (2) in Refs. [43, 65]. (They are reproduced in the Supplemental Material [104] for completeness.) As for $\overline{X}_{A}$, we write

where the constant vectors $u_{A}^{\mu}$ and $b_{A}^{\mu}$ are the initial velocity and orthogonal displacement of the $A$th body, respectively, while the constant tensor $s_{A}^{\mu\nu}$ describes its initial spin per unit mass. Note that ${s_{A}^{\mu\nu}u_{A\,\nu}=0}$ as per the covariant SSC, while the impact parameter ${b^{\mu}_{\mathstrut}\coloneq b_{1}^{\mu}-b_{2}^{\mu}}$ satisfies ${b\cdot u_{A}=0}$ [43].

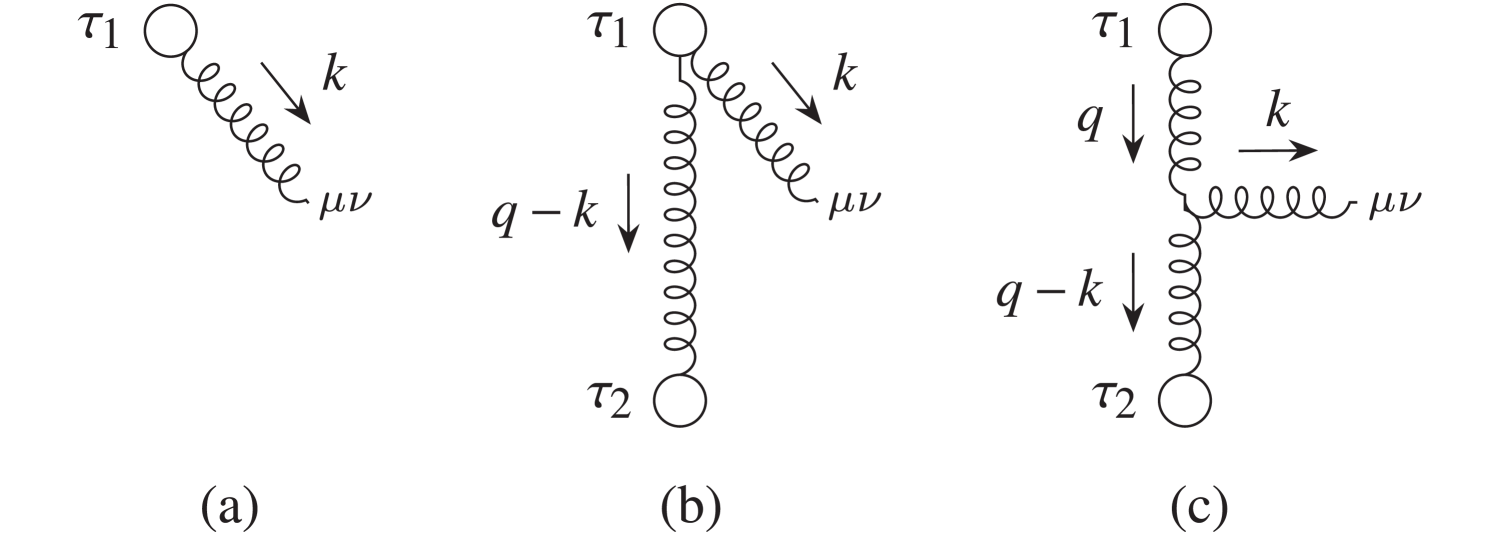
We now use these rules to compute the (tree-level) expectation value ${{\langle h_{\mu\nu}(k)\rangle}\equiv\kappa P_{\mu\nu\rho\sigma}T^{\rho\sigma}(k)/(2k^{2})}$, from which the (classical) stress-energy tensor $T^{\mu\nu}$ may be extracted. At leading order in $G$, only the diagram in Fig. 2(a), with $X_{A}$ replaced by $\overline{X}_{A}$, contributes. The result is

where the delta function ${\text{\smash{\raisebox{2.58334pt}{--}}\kern-4.73611pt$\delta$}(x)\equiv 2\pi\delta(x)}$ comes from having performed the integral over $\tau_{A}$ in Eq. (5).

All three diagrams in Fig. 2 contribute at next-to-leading order in $G$. From Fig. 2(a), we extract the $O(G)$ part of the diagram by expanding $X_{A}$ up to 1PM, whereas for Figs. 2(b) and 2(c), it suffices to replace $X_{A}$ by $\overline{X}_{A}$. The total result is

where ${M=m_{1}+m_{2}}$ is the binary’s total mass, ${\nu=m_{1}m_{2}/M^{2}}$ is its symmetric mass ratio, ${\int_{q}\!\equiv\!\int\text{d}^{d}q/(2\pi)^{d}}$, and $\Delta_{12}(q,k)\coloneq\,\text{\smash{\raisebox{2.58334pt}{--}}\kern-4.73611pt$\delta$}(q\cdot u_{1})\,\text{\smash{\raisebox{2.58334pt}{--}}\kern-4.73611pt$\delta$}((k-q)\cdot u_{2})$. An explicit expression for the object $t^{\mu\nu}$, accurate to $O(s^{2})$, is presented in the Supplemental Material [104].

Given the above, we may now compute the radiated four-momentum via the definition [117]

where ${\text{\smash{\raisebox{2.58334pt}{--}}\kern-4.73611pt$\delta$}_{+}(k^{2})\,\text{d}^{d}k/(2\pi)^{d}}$ is the Lorentz-invariant phase-space measure for the emission of on shell gravitons. Observe that because the delta functions in Eq. (8) have compact support away from ${k^{2}=0}$, $T^{\mu\nu}_{\text{LO}}$ is nonradiative and so does not contribute to $P^{\mu}_{\text{rad}}$. It therefore suffices to substitute Eq. (9) into Eq. (10) when working to leading order in $G$. We then find

Next, we define new momentum variables ${q=q_{1}-q_{2}}$, ${\ell_{1}=-q_{2}}$, and ${\ell_{2}=q_{1}-k}$ [73] in order to write

The radiated four-momentum may thus be viewed as the inverse Fourier transform of some object $Q^{\mu}$, which is expressible as a sum of terms in which $q^{\mu}$, $u_{A}^{\mu}$, and $s_{A}^{\mu\nu}$ are contracted amongst themselves and with the two-loop integrals

Following Ref. [90], we define $\rho_{2}={-2\ell_{1}\cdot u_{2}}$, $\rho_{3}={-2\ell_{2}\cdot u_{1}}$, ${\rho_{5}=\ell_{1}^{2}}$, ${\rho_{6}=\ell_{2}^{2}}$, ${\rho_{8}=(\ell_{1}-q)^{2}}$, and ${\rho_{9}=(\ell_{2}-q)^{2}}$, while the underlined variables are used to denote the presence of delta functions; i.e., ${2/\underline{\rho}{}_{1}=\text{\smash{\raisebox{2.58334pt}{--}}\kern-4.73611pt$\delta$}(\ell_{1}\cdot u_{1})}$, ${2/\underline{\rho}{}_{4}=\text{\smash{\raisebox{2.58334pt}{--}}\kern-4.73611pt$\delta$}(\ell_{2}\cdot u_{2})}$, and ${1/\underline{\rho}{}_{7}=\text{\smash{\raisebox{2.58334pt}{--}}\kern-4.73611pt$\delta$}_{+}(k^{2})}$ with ${k\equiv q-\ell_{1}-\ell_{2}}$. All of the integrals in $Q^{\mu}$ have $n_{1}=n_{4}={n_{7}=1}$. Reverse unitarity then allows us to treat these delta functions as cut propagators [91, 92, 93, 94].

The tensor-valued nature of these integrals make them cumbersome to evaluate as is, but fortunately they can all be reduced to scalar-valued ones via a suitable basis decomposition [85]. Specifically, we expand each of the loop momenta $\ell_{A}^{\mu}$ (${A\in\{1,2\}}$) in the numerator as

where ${\check{u}_{1}^{\mu}\coloneq(u_{1}^{\mu}-\gamma u_{2}^{\mu})/(1-\gamma^{2})}$ and ${\check{u}_{2}^{\mu}\!\coloneq\check{u}_{1}^{\mu}|_{1\leftrightarrow 2}}$ are the dual vectors to the two initial velocities (${\check{u}_{A}\cdot u_{B}=\delta_{AB}}$), ${\gamma\equiv u_{1}\cdot u_{2}}$ is the Lorentz factor for the relative velocity $v$, and $\ell_{A\bot}^{\mu}$ is the part of $\ell_{A}^{\mu}$ that is orthogonal to $u_{1}$, $u_{2}$, and $q$ [the delta functions in Eq. (12) guarantee that ${q\cdot u_{A}=0}$]. The three inner products in Eq. (14) are then easily rewritten in terms of the variables $\rho_{i}$ and $q^{2}$ only.

As for $\ell_{A\bot}^{\mu}$, the fact that the denominator of Eq. (13) is invariant under $(\ell_{1\bot},\ell_{2\bot})\mapsto-(\ell_{1\bot},\ell_{2\bot})$ implies that any term in the numerator with $i$ powers of $\ell_{1\bot}$ and $j$ powers of $\ell_{2\bot}$ will integrate to zero if ${i+j}$ is odd. If instead ${i+j=2}$, then rotational invariance on the hypersurface orthogonal to $u_{1}$, $u_{2}$, and $q$ allows us to replace

under the integral, where the metric on this hypersurface is ${\bot^{\mu\nu}=\eta^{\mu\nu}-\check{u}_{1}{}^{\mu}u_{1}{}^{\nu}-\check{u}_{2}{}^{\mu}u_{2}{}^{\nu}-q^{\mu}q^{\nu}/q^{2}}$, and note that the inner product ${(\ell_{A}^{\mathstrut\rho}\bot_{\rho\sigma}\ell_{B}^{\mathstrut\sigma})}$ is easily rewritten solely in terms of the variables $\rho_{i}$, $q^{2}$, and $\gamma$. Analogous replacement rules can be derived for the ${i+j=4}$ case by positing the ansatz $\ell_{A\bot}^{\mathstrut\mu}\ell_{B\bot}^{\mathstrut\nu}\ell_{C\bot}^{\mathstrut\rho}\ell_{D\bot}^{\mathstrut\sigma}\mapsto{c_{1}\bot^{\mu\nu}\bot^{\rho\sigma}}+{c_{2}\bot^{\mu\rho}\bot^{\nu\sigma}}+{c_{3}\bot^{\mu\sigma}\bot^{\rho\nu}}$ and then solving for the coefficients ${\{c_{1},c_{2},c_{3}\}}$ by taking appropriate contractions. The same can be done for all ${i+j\in 2\mathbb{Z}}$, although in practice we encounter only integrals with ${i+j\leq 5}$.

The object $Q^{\mu}$ is now a sum of terms in which different combinations of $q^{\mu}$, $u_{A}^{\mu}$, and $s_{A}^{\mu\nu}$ are contracted with one another and multiplied by one of the scalar-valued integrals $G_{n_{1}\cdots\,n_{9}}$. At this stage, $3100$ different scalar integrals enter into $Q^{\mu}$, but not all of them are independent. After using the LiteRed software package [118, 119] to identify nontrivial integration by parts relations between the different integrals [95, 96, 97], we find that they reduce to a set of only four master integrals; the same four as in Eqs. (4.13)–(4.16) of Ref. [73]. These are solved via differential equation methods [98, 99, 100, 101, 102, 103]; see Ref. [73] for details.

All that remains is to compute the Fourier transform in Eq. (12). We do so by using another family of master integrals,

whose scalar-valued member evaluates to

with ${\bot_{12}^{\mu\nu}=\eta^{\mu\nu}_{\mathstrut}-\check{u}_{1}^{\mathstrut\mu}u_{1}^{\mathstrut\nu}-\check{u}_{2}^{\mathstrut\mu}u_{2}^{\mathstrut\nu}}$ [67]. Its tensor-valued cousins follow from differentiation; e.g., ${I^{\mu}_{n}=-i\partial I_{n}/\partial b_{\mu}}$.

Now specializing to four dimensions, it becomes convenient to decompose our final result into components along the basis vectors $\{u_{1},u_{2},\hat{b},\hat{l}\}$, where ${\hat{b}^{\mu}\coloneq b^{\mu}/b}$ ${(b\equiv\sqrt{-b_{\mu}b^{\mu}})}$ and ${\hat{l}_{\mu}\coloneq\epsilon_{\mu\nu\rho\sigma}u_{1}^{\mathstrut\nu}u_{2}^{\mathstrut\rho}\hat{b}^{\mathstrut\sigma}_{\mathstrut}/\sqrt{\gamma^{2}-1}}$ are the unit vectors pointing along the impact parameter and orbital angular momentum, respectively. After also eliminating the spin tensors in favor of the Pauli-Lubanski spin vectors ${s_{A}^{\mu}\coloneq\epsilon^{\mu}_{\mathstrut}{}_{\nu\rho\sigma}u_{A}^{\mathstrut\nu}s_{A}^{\mathstrut\rho\sigma}/2}$, we find that we can write

The components $\mathcal{C}_{V}$, with ${V\in\{u_{1},u_{2},\hat{b},\hat{l}\}}$, are dimensionless functions of only the Lorentz factor $\gamma$, the two Wilson coefficients $C_{E_{A}}$, and the six inner products $(s_{A}\cdot V)/b$. (There are only six because ${s_{A}\cdot u_{A}=0}$ by definition.)

The fact that $P^{\mu}_{\text{rad}}$ is a polar vector strongly constrains which inner products can appear at any given order, and in which combinations. For instance, because $\mathcal{C}_{u_{1}}$, $\mathcal{C}_{u_{2}}$, and $\mathcal{C}_{\hat{b}}$ must all be even under parity, they can only depend on $(s_{A}\cdot\hat{l})/b$ at linear order in the spins. Indeed, we find explicitly that

while ${\mathcal{C}_{\hat{b}}=0+O(s^{2})}$. The remaining component $\mathcal{C}_{u_{2}}$ can be obtained from $\mathcal{C}_{u_{1}}$ by swapping the body labels ${1\leftrightarrow 2}$, since $P^{\mu}_{\text{rad}}$ must be symmetric under this interchange. As an added consequence, $\mathcal{C}_{\hat{b}}$ and $\mathcal{C}_{\hat{l}}$ must be odd and even under this interchange, respectively.

The four functions ${\{f_{\text{I}},\,\dots,f_{\text{IV}}\}}$ in Eq. (19) depend purely on $\gamma$ and are presented in Table 1 [$f_{\text{I}}$, which appears at $O(s^{0})$, was previously determined in Refs. [70, 71, 72, 73], but is reproduced here for completeness]. An additional 21 functions of $\gamma$, with similar analytic structures, appear at $O(s^{2})$. These are presented in the Supplemental Material [104]. Notice that $\mathcal{C}_{\hat{b}}$ and $\mathcal{C}_{\hat{l}}$ both vanish when the spins are aligned along $\hat{l}$ (or, indeed, when they are zero); hence, for so-called “aligned-spin” configurations, for which the binary’s motion is confined to a plane, we see that momentum is lost only in the direction of the relative velocity.

To validate Eq. (18) against the existing literature, we compare results for the energy $\Delta E$ radiated in the center-of-mass frame. This is computed in our approach as ${\Delta E=(P_{\text{rad}}\cdot p_{\text{tot}})/E}$, where ${p^{\mu}_{\text{tot}}=m_{1}^{\mathstrut}u_{1}^{\mu}+m_{2}^{\mathstrut}u_{2}^{\mu}}$ and ${E^{2}=p_{\text{tot}}^{2}=M^{2}[1+2\nu(\gamma-1)]}$. Since $\hat{b}^{\mu}$ and $\hat{l}^{\mu}$ are purely spatial in this frame, ${s_{A}\cdot\hat{b}}$ and ${s_{A}\cdot\hat{l}}$ are equivalent to the three-dimensional dot products ${-\,\mathbf{s}_{A}\cdot\hat{\vphantom{b}}\kern-1.4pt\mathbf{b}}$ and ${-\,\mathbf{s}_{A}\cdot\hat{\mathbf{l}}}$, respectively, and note that ${s_{1}\cdot u_{2}\simeq\mathbf{s}_{1}\cdot\mathbf{v}}$ while ${s_{2}\cdot u_{1}\simeq-\,\mathbf{s}_{2}\cdot\mathbf{v}}$ after expanding to first order in the relative 3-velocity $\mathbf{v}$. Having done so, our result for $\Delta E$ agrees with that of Ref. [85], which is accurate to leading order in $\mathbf{v}$ and to quadratic order in the spins, once we also replace $(\mathbf{b},\mathbf{s}_{A},C_{E_{A}})\mapsto(-\mathbf{b},-\mathbf{s}_{A},1-C_{E_{A}})$ to account for differing conventions.

As a second consistency check, we use analytic continuation by way of the boundary-to-bound (B2B) map [15, 16, 17] to convert our result for $\Delta E$ into the energy $\Delta E_{\text{ell}}$ radiated during one period of ellipticlike motion. This is accomplished in three steps. Owing to current limitations of the B2B map, we first specialize to aligned-spin configurations. Next, we must transform from the covariant SSC to the canonical (Newton-Wigner) SSC [110] for the map to work. This generally entails transforming $(\mathbf{b},\mathbf{s}_{A})$ to new canonical variables $(\mathbf{b}_{\text{c}},\mathbf{s}_{A\,\text{c}})$ [59, 60], but ${\mathbf{s}_{A}\equiv\mathbf{s}_{A\,\text{c}}}$ in the aligned-spin case; hence, only the magnitude of the impact parameter must be transformed. The rule is

where ${p_{\infty}=M^{2}\nu\sqrt{\gamma^{2}-1}/E}$ is the initial momentum of either body in the center-of-mass frame, ${a_{\pm}=(\mathbf{s}_{1}\!\pm\mathbf{s}_{2})\cdot\hat{\mathbf{l}}}$, and we may define ${L_{\text{c}}=b_{\text{c}}p_{\infty}}$ as the canonical orbital angular momentum. Finally, we obtain $\Delta E_{\text{ell}}$ from $\Delta E$ via [17]

having eliminated $\gamma$ in favor of ${\mathcal{E}\equiv(E-M)/(M\nu)}$. The left-hand side follows after analytic continuation from positive to negative values of $\mathcal{E}$. Expanded in powers of $\mathcal{E}$, we find that our result, which is valid in the large-angular-momentum limit [17], agrees with the overlapping terms from PN theory up to 3PN in Ref. [17], and up to 4PN in Refs. [120, 121].