Gravitationally sensitive structured x-ray optics using nuclear resonances

The Pound–Rebka experiment [6] has demonstrated a unique system for probing the gravitational red-shift effect by exploiting an extremely narrow nuclear linewidth in combination of a high x-ray energy in the Mössbauer effect [7]. Moreover, advances in modern x-ray light sources and optics have raised the field of x-ray-nuclei interactions to a new level of accuracy where coherent quantum control comes into play [8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21]. A combination of nuclear quantum coherence and its sensitivity to gravity will potentially lead to a new type of x-ray optics whose performance depends on the gravitational red-shift in addition to the typical Zeeman shift [8, 12] and Doppler shift [14, 17, 18, 19]. In this context, we investigate a system that emulates the Schrödinger equation [22] and is sensitive to gravity. The present scheme allows for a systematic generation of structured x rays [23, 24, 25, 26] via changing the altitude, the x-ray photon energy, or the external magnetic field of a our system for a given waveguide structure.

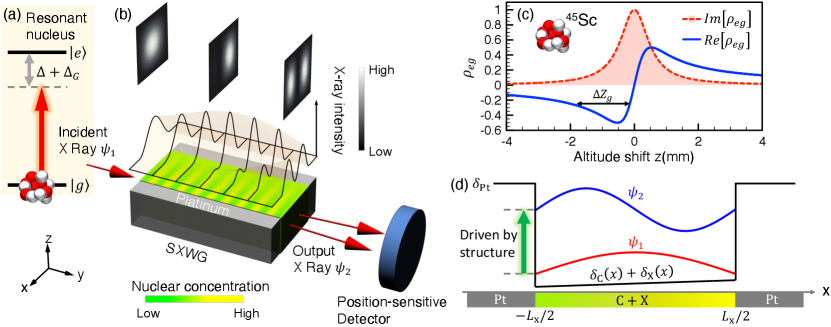
The system is depicted in Figure 1 with the description as follows. An x ray drives a nuclear transition from the ground state $|g\rangle$ to the excited state $|e\rangle$ with the total detuning $\Delta_{t}\Gamma=\left(\Delta_{G}+\Delta\right)\Gamma$ in Fig. 1(a). We emphasize that the gravitational red shift $\Delta_{G}\simeq-zE_{t}GM_{E}/\left(\hbar\Gamma c^{2}R_{E}^{2}\right)$ has to be taken into account when the system is located at different altitude $z$ relative to where x rays are emitted. Here $E_{t}$ is the nuclear transition energy, $G$ is the gravitational constant, $M_{E}$ is the mass of the Earth, and $R_{E}$ is the average radius of the Earth. $\Delta\Gamma$ is the x-ray detuning, and $\Gamma$ the spontaneous decay rate of the excited state $|e\rangle$. Our system of nuclear resonant scattering of x rays can be described by the optical-Bloch equation [9, 21]:

where $\rho_{eg}$ is the coherence of a nuclear two-level system, $E$ is the x-ray electric field strength, $\hbar$ is the reduced Planck constant, $k$ is the x-ray wavenumber, and $n_{e}$ is the index of refraction from electrons. Further, we denote the transverse Laplacian $\nabla_{\perp}^{2}=\partial^{2}_{x}+\partial^{2}_{z}$, and the coupling constant $\eta=2\hbar\Gamma\xi/\left(PL\right)$, where $L$ the length of the waveguide, $P$ is the nuclear transition dipole moment, and $\xi$ is the nuclear resonant thickness. The steady state of Eqs. (1-2) leads to the analytic solution $\rho_{eg}=PE\left(i-2\Delta_{t}\right)/\left[\hbar\Gamma\left(1+4\Delta_{t}^{2}\right)\right]$ and the optical Schrödinger equation [22] (see supplemental information)

with the effective mass $m_{e}=\hbar k/c$. Equation (3) suggests a structured x-ray waveguide (SXWG) system composed of resonant nuclei, as depicted in Fig. 1(b), with a high degree of freedom for simulating different quantum systems via spatial engineering of $n_{e}$ and $\xi$. Fig. 1(c) displays the altitude dependent real part $Re\left[\rho_{eg}\right]$ (blue-solid) and imaginary part $Im\left[\rho_{eg}\right]$ (red-dashed line) of $\rho_{eg}$ with $\Delta=0$ for the isotope ⁴⁵Sc. $Re\left[\rho_{eg}\right]$ describes the refractive index from nuclei and results in the gravitational effects in our system as revealed by the last term of Eq. (3). In cantrast, $Im\left[\rho_{eg}\right]$ of Lorentzian line shape represents the nuclear absorption of x rays and leads to the Pound–Rebka experiment [6].

In the following, we use the SXWG to simulate Rabi oscillations of x ray in a finite square well of width $L_{x}$. As illustrated in Fig. 1(d), we introduce a platinum cladding $n_{e}=1-\delta_{\mathrm{Pt}}+i\beta_{\mathrm{Pt}}$ for $|x|>L_{x}/2$ to constitute a finite square well potential, which provides with a transverse confinement to the x ray propagation direction [21]. The cladding material leads to the energy eigenfunctions of the $E$ field in Eq. (3) which read as (see supplemental information)

with the eigen angular frequencies $\omega_{n}=n^{2}\pi^{2}c/\left(2kL_{x}^{2}\right).$ Inside the square well $|x|\leq L_{x}/2$, we perturb the system by a periodic (gradient) particle distribution of isotope $X$ and carbon along the y direction (x direction), where $\xi\left(x,y\right)=\left(\varrho/2\right)\left[1+\left(2x/L_{x}\right)\sin\left(k_{d}y\right)\right]$ and $n_{e}\left(x,y\right)=1-\delta_{\mathrm{C}}\left(x,y\right)+i\beta_{\mathrm{C}}\left(x,y\right)-\delta_{\mathrm{X}}\left(x,y\right)+i\beta_{\mathrm{X}}\left(x,y\right)$ (see supplemental information for the form of $n_{e}$). In Fig. 1(d) subscripts Pt, C, and X represent platinum, carbon and resonant nucleus, respectively. We list other relevant material parameters in Table 1. With the above density modulation, the last term in Eq. (3) effectively becomes the electric dipole Hamiltonian in an oscillating field which perturbes the square well potential. This plays the key role to drive the x-ray Rabi oscillation with gravitational sensitivity. When the resonant condition $ck_{d}=\omega_{n+1}-\omega_{n}$ is fulfilled, the periodic structure of the refractive index drives the dipole transition $\psi_{n}\rightarrow\psi_{n+1}$ with the effective Rabi frequency (see supplemental information)

A propagating x ray experiences a constant SXWG-induced Rabi frequency, and the condition for having a $m\pi$ pulse is $|\Omega_{n}|L/c=m\pi$. We use $m=2$ to demonstrate the Rabi oscillation between the x-ray ground state $\psi_{1}$ and the first excited state $\psi_{2}$ by numerically solving Eq. (3).

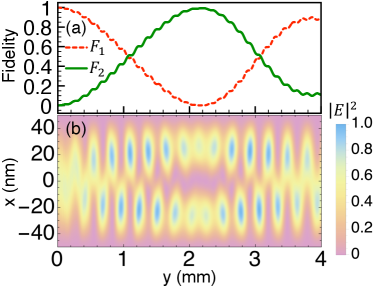
The solution of Eq. (3) in Fig. 2 represents an x ray which propagates through an SXWG with with $X=^{45}$Sc, $\varrho=26.25$, natural scandium particle density $N=3.99\times 10^{28}$m^-3, nuclear resonance absorption cross section $\sigma_{0}=12.6$(kbarn), $L_{x}=100$nm, $L=4$mm, $k_{d}=22.778\times 10^{3}$rad/m, $\Delta=4\Gamma$, and $\Delta_{G}=0$. The process is visualized in terms of the fidelity $F_{n}\left(y\right)=|\int_{-\infty}^{\infty}\psi_{n}^{\ast}\left(x\right)E\left(x,y\right)dx|^{2}/\int_{-\infty}^{\infty}|E\left(x,y\right)|^{2}dx$ in Fig. 2(a), and the normalized intra-waveguide x-ray intensity distribution $|E\left(x,y\right)|^{2}/\int_{-\infty}^{\infty}|E\left(x,y\right)|^{2}dx$ in Fig. 2(b). The alternation of $F_{1}$ and $F_{2}$ in Fig. 2(a) clearly demonstrates that the ground-state x ray enters the SXWG at $y=0$, and is then coherently promoted to the first excited state when approaching $y=2$mm. After that, the x ray returns to the ground state and finishes a full Rabi cycle at $y=4$mm. One can also observe the same phenomenon at the intra-waveguide x-ray intensity which evolves back and forth between states $\psi_{1}$ and $\psi_{2}$ in Fig.2(b).

The above x-ray Rabi oscillation suggests a systematic way to generate the $\psi_{n}$ mode with a sequence of SXWGs driving $\Delta n=1$ transitions, where one can raise the quantum number one by one. Specifically, one can connect two different SXWGs to accomplish a $\psi_{1}\rightarrow\psi_{3}$ transition, where the upstream SXWG drives a $\psi_{1}\rightarrow\psi_{2}$ transition, and the downstream SXWG achieves a $\psi_{2}\rightarrow\psi_{3}$ promotion. Moreover, one can even design multiple SXWG modules for $\Delta n=2$ or any dipole forbidden transitions. Thus, all combinations of SXWG modules open the capability to generate high order x-ray modes starting from the ground state $\psi_{1}$. It is worth mentioning another possible application using dual SXWGs with a gap in between as an x-ray interferometer. While the upstream SXWG causes the $\psi_{1}\rightarrow\psi_{2}$ transition as a beam splitter, the downstream SXWG leads to the return of $\psi_{2}\rightarrow\psi_{1}$ as a beam combiner. Furthermore, in the gap between two SXWGs one can introduce a phase modulator to impose a phase shift at one branch of the split state $\psi_{2}$, e.g., $x>0$ at $y=2$mm in Fig. 2. A controllable interference due to the phase modulation is expected to happen at the end of the downstream SXWG.

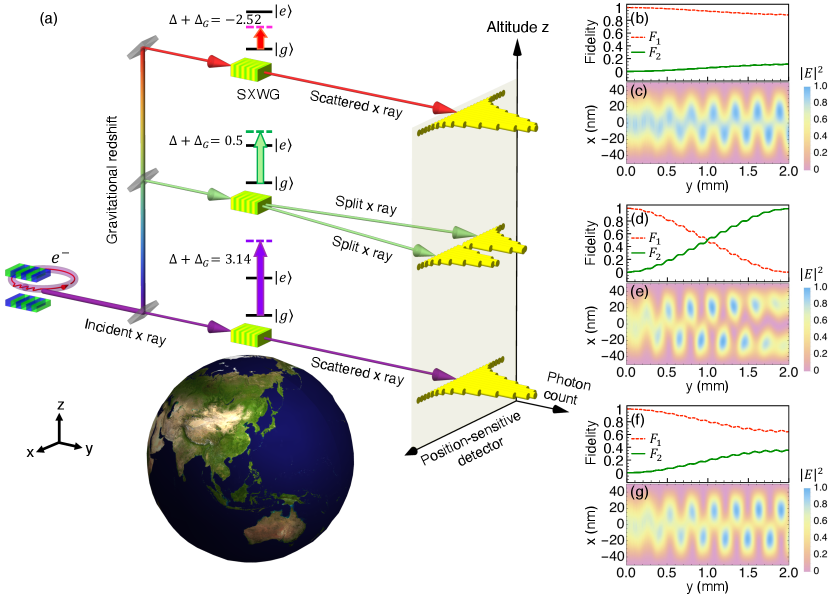
We are ready to demonstrate the Earth’s gravitational effect on our SXWG system. Given that the gravitational redshift $\Delta_{G}$ significantly changes the nuclear coherence $\rho_{eg}$ and Rabi frequency $\Omega_{n}$ in Eq. (5) in two millimeter on Earth as demonstrated in Fig. 1(c), this sensitivity potentially allows for turning gravity into a practical use, e.g., gravitationally sensitive x-ray optics. For illustrating the effect, we numerically solve Eq. (3) and use the isotope ⁴⁵Sc in an SXWG with parameters $\varrho=8.38$, $L_{x}=100$nm, $L=2$mm, $k_{d}=23.778\times 10^{3}$rad/m, and $\Delta=19.36$ to show the gravitational effect. Fig. 4(a) illustrates three cases where the above discussed SXWG is located at $z=2.32$cm, $z=2$cm, and $z=1.72$cm from the top down. An incident x ray with the transverse mode $\psi_{1}$ is deflected upward and experiences a gravitational redshift (vertical upward arrow with color gradient). The $\Delta_{G}$ will change when the x ray illuminates the SXWG at different altitudes. The total detuning for each case is specified at the level-scheme plot, namely, $\Delta+\Delta_{G}=-2.52$, $\Delta+\Delta_{G}=0.5$, and $\Delta+\Delta_{G}=3.14$ from the top down. We emphasize that the periodic particle density modulation effectively plays the role of a resonant field, and it always resonantly drives a transition between the x-ray modes in a cladding waveguide for three cases. However, various $\Delta_{G}$ change the effective coupling strength $\Omega_{n}$ and result in different outputs. The scattered/split x rays reflect the output mode and can be measured by a downstream position-sensitive detector. The $x$-dependent photon number counts show the output $|E\left(x,L\right)|^{2}$ and reveal the Earth’s gravitational effect. We depict the normalized $|E\left(x,y\right)|^{2}$ for $z=2.32$cm, $z=2$cm, and $z=1.72$cm in Fig. 4(c, e, and g), respectively. The intra-waveguide intensity shows that the x ray significantly gets split in Fig. 4(e) under a half Rabi cycle $\psi_{1}\rightarrow\psi_{2}$ in the SXWG at $z=2$cm. In contrast, Fig. 4(c and g) depicts only a transverse broadening of the x ray due to a small $|\Omega_{1}|$. Fig. 4(b,d, and f) illustrate $F_{1}\left(y\right)$ (red-dashed line) and $F_{2}\left(y\right)$ (green-solid line) for $z=2.32$cm, $z=2$cm, and $z=1.72$cm, respectively. One can clearly see that the x ray experiences Rabi flopping and becomes $\psi_{2}$ at the resonant altitude $z=2$cm as also pointed out by Fig. 4(d and e). Given that $|\Omega_{1}|$ decreases when the SXWG leaves the resonant altitude, the x ray mostly remains in the initial mode $\psi_{1}$, namely, $F_{1}\left(y\right)>F_{2}\left(y\right)$ at $z=2.32$cm and $z=1.72$cm. We depict the output altitude-dependent $F_{2}$ at $y=2$mm in Fig. 4(a). As a result, different x-ray splitting is expected to occur when lifting an SXWG composed of ⁴⁵Sc at only a millimeter altitude change.

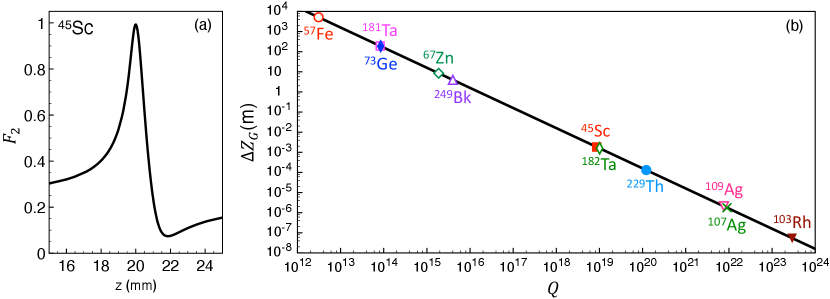
We quantify the gravitational sensitivity of the SXWG by the full altitude width $\Delta Z_{G}$ at the half maximum $Re\left[\rho_{eg}\right]$

as indicated by the black-horizontal double arrow in Fig. 1(c). The introduced $\Delta Z_{G}$ is a measure for the sensitivity of the x-ray-nucleus coupling to the change of the SXWG vertical location. With the definition of the quality factor of a nuclear resonance $Q=E_{t}/\left(\hbar\Gamma\right)$, we can see that $\Delta Z_{G}$ is proportional to $1/Q$. Fig. 4(b) exemplifies the implication of Eq. (6) for our system on Earth in a double-logarithmic plot, where we mark the isotopes ⁴⁵Sc, ⁵⁷Fe, ⁶⁷Zn, ⁷³Ge, ¹⁰³Rh, ¹⁰⁷Ag, ¹⁰⁹Ag, ¹⁸¹Ta, ¹⁸²Ta, ²²⁹Th, and ²⁴⁹Bk, according their $Q$ factor. Some of the nuclear parameters are listed in Table 1. Remarkably, the advantage of a very high $Q\sim 10^{19}$ of ⁴⁵Sc or ¹⁸²Ta nuclear resonance endues an SXWG with a gravitational sensitivity to only millimeter altitude change. Notably, it is also possible to get sub-millimeter $\Delta Z_{G}$ using ²²⁹Th whose $Q\sim 10^{20}$ [29], and micron $\Delta Z_{G}$ with ¹⁰⁷Ag and ¹⁰⁹Ag whose $Q\sim 10^{22}$. It deserves to mention that ¹⁰³Rh whose $Q>10^{23}$ [27] even results in a nanometer $\Delta Z_{G}$, and it may lead to gravitational application in mesoscopic scale.

In conclusion we have put forward a controllable SXWG system that potentially turns gravity into an application of x-ray optics. A periodic intra-waveguide structure, e.g., nuclear optical lattice ⁵⁷Fe/⁵⁶Fe bilayers in Ref.[30], can drive a transition between x-ray modes. The x-ray transverse mode experiences Rabi oscillation when propagating in an SXWG. Our scheme allows for applications like a systematic production of structured x rays and an x-ray interferometer without any beam splitter. Remarkably, a significant change of a gravitionally induced splitting of x rays could happen by lifting our SXWG made of, e.g., ⁴⁵Sc or ¹⁸²Ta, at only a millimeter scale.

S.-Y. L. and W.-T. L. are supported by the National Science and Technology Council of Taiwan (Grant No. 110-2112-M-008-027-MY3, 110-2639-M-007 -001-ASP, 111-2923-M-008-004-MY3 & 111-2639-M-007-001-ASP). S. A. is supported by National Science Foundation of China (Grant No. 11975155).