GRBs luminosity function synthesized from Swift/BAT, Fermi/GBM and Konus-Wind data
Abstract
We study the luminosity function of long gamma-ray bursts (LGRBs) using the peak flux obtained from three LGRB samples with known redshifts: (a) a sample of 251 LGRBs from the Swift/BAT satellite/instrument; (b) a sample of 37 LGRBs from the Fermi/GBM telescope; (c) a sample of 152 GRBs from the Konus-Wind instrument. For the Swift/BAT and Fermi/GBM samples, we use data available on the Swift Burst Analyser websites (http://www.swift.ac.uk/burst˙analyser; (Evans, P. A. et al., 2010)) and (http://swift.gsfc.nasa.gov/archive/grb/table/) and on the Fermi website (https://heasarc.gsfc.nasa.gov/W3Browse/fermi/fermigbrst.html; (Gruber et al., 2014; von Kienlin et al., 2014; Bhat et al., 2016)) to calculate the luminosity at the peak of the flux by using a cut-off power-law spectrum (CPL). For the Konus-Wind sample, we use the Yonetoku correlation relationship (Yonetoku et al., 2010) to determine the isotropic luminosity from the energy at the peak of the flux measured in the source frame (Minaev and Pozanenko, 2019). With these three samples (totalling 439 GRBs), we use the Monte Carlo method to synthesize 10,000 “artificial” GRBs similar to each real GRB by considering that each physical quantity observed obeys a normal distribution, where the tabulated value and uncertainty represent the mean and the error. The results obtained for the luminosity function from our data samples are consistent with those published in previous works.
Keywords gamma-rays bursts; luminosity function; statistical methods
1 Introduction
Gamma-ray bursts (GRBs) are extremely powerful explosions that involve either the death of massive stars or the merger of compact stellar objects. The equivalent isotropic energy of GRBs can exceed erg, and their nonthermal spectra peak between 10 and keV (e.g. Atteia et al. (2017)). Their light curves display intense pulses that can last anywhere from less than a second to hundreds of seconds, they are often irregular and sometimes include multiple pulses. Although the radiation emitted by GRBs is believed to come out mainly through jets (with collisions inside), the precise formation mechanism behind these jets is not fully understood (e.g. Le and Mehta (2017)).
Given the complex nature of their occurrence and unfolding, it is not surprising that GRBs are among the most studied topics and phenomena in astrophysics today, both theoretically and observationally. Many theoretical models have been proposed to try and explain this very spectacular phenomenon; but, unsurprisingly given the astounding amount of energy involved and the short time scales of these explosions, none of these models has been fully successful ((Dainotti et al., 2019)).
There are currently many observation missions, both from the ground and from space, that are involved in the study of GRBs in the different bands of the electromagnetic spectrum. Furthermore, a new observational tool has recently emerged, namely gravitational waves, which are produced by the merger of neutron stars or black holes. This new tool is already providing insight into the formation mechanisms of short, merger-type GRBs and has become an integral part of the multi-messenger approach to studying GRBs (Abbott and al. 2017, Drago et al. 2018, Mészáros 2019, and others).
The study of the luminosity function (LF), which is defined as the number of bursts per unit interval of luminosity, is part of the verification and validation of the theoretical models of the physical processes involved in the occurrence of GRBs. It allows us, among other things, to predict the production rates of GRBs and the probability of detecting gravitational waves associated with some of them. Furthermore, it can provide insights into the star-formation rate.
Previous research on luminosity functions has been done on different data samples, most of which contained a limited number of gamma-ray bursts (Schmidt, 1999, 2001; Sethi and Bhargavi, 2001; Yonetoku et al., 2004; Liang et al., 2007; Virgili et al., 2009; Butler et al., 2010; Cao et al., 2011; Salvaterra et al., 2012; Wanderman and Piran, 2015; Amaral-Rogers et al., 2016; Paul, 2017; Kinugawa et al., 2019; Lan et al., 2019). Our present work uses three larger data samples from three satellites/instruments, namely Swift/BAT (251 GRBs), Konus/Wind (152 GRBs), and Fermi/BAT (37 GRBs), and then enlarges the data set with simulated (artificial) GRBs.
In Section 2, we describe how we select our samples. Sections 3 and 4 provide details of how we calculate the luminosities and the luminosity functions (for each sample), respectively. In Section 5, We present our results and then discuss them in Section 6, ending with concluding remarks and a mention of future research prospects in Section 7.
2 Sample Selection
2.1 The Swift/BAT sample
We use the Swift GRBs data that is published on the satellite’s official websites111http://swift.gsfc.nasa.gov/archive/grb/table/,,222http://www.swift.ac.uk/burst˙analyser. The first one presents the observational results characterizing each detected GRB in several aspects: peak flux, fluence, duration, redshift, host galaxy, as well as data on afterglows (successive emission down the electromagnetic spectrum: X-ray, UV, visible, infrared, radio). The second website provides more details on the energy spectrum and the light curve (time profile) in different energy bands, with different time resolutions. The data are all provided with their uncertainties (error bars).
As of 14/08/2020, Swift/BAT had observed 379 GRBs with measured redshifts. We have eliminated five GRBs which redshifts were determined with poor precision: 060708, 090814A, 060116, 110726A, and 050904. Nine GRBs have no peak flux value in the published data: 050408, 130518A, 140614A, 150101B, 150821A, 151027B, 160117B, 170405A, and 170607A. Three bursts were removed due to the lack of one of the spectral parameters characterizing the cut-off power-law: 090516A, 140311A, and 071112C. With this filtering, we are left with 359 GRBs. Then, considering the Swift/BAT energy band between 15 keV and 350 keV and following the same approach as Daigne et al. (2006) and Campisi et al. (2010) in taking the lower limit of the peak flux as , we have a sample of 261 GRBs. However, considering the uncertainty on the edges of the energy band interval, it was possible to add three bursts: 120521C, 090715B, and 050416A. We get a sample of 265 GRBs (251 long GRBs and 15 short GRBs). Our final sample is then composed of 251 LGRBs, which full data (redshift, duration, spectral parameters) we present in Table (LABEL:tabSwift).
2.2 The Fermi/GBM sample
We have used the spectral data for Fermi/GBM GRBs given on the official website333https://heasarc.gsfc.nasa.gov/W3Browse/fermi/fermigbrst.html (Gruber et al., 2014; von Kienlin et al., 2014; Bhat et al., 2016). Since we need GRBs with redshifts, we take the set given by Minaev and Pozanenko (2019) and its references, as well as GCN (Gamma-ray Coordination Network) alerts. This gives us a total of 37 LGRBs, which we present in Table (LABEL:tabFermi).
2.3 The Konus-Wind sample
The Konus-Wind satellite has observed 152 LGRBs (Svinkin et al., 2016; Tsvetkova et al., 2017; Cano et al., 2017; Minaev and Pozanenko, 2019; Frederiks et al., 2019). In this sample, we know the bursts’ redshifts and energies at the peak . We present this data in Table (LABEL:tabKW) to facilitate future research.
2.4 Representativeness of the GRB sample (with known redshifts)
Before we perform our calculations, we must ensure that the GRB samples (with known redshifts) that we will be using are representative of the whole population of long gamma-ray bursts (with or without known redshifts).
We first analyze the bursts in the Swift/ BAT sample. Our approach consists in comparing the distributions of the three physical quantities: the duration, , the energy at the peak flux, , and the flux at the peak. Taking into account the lower limit of the peak flux as ) and the energy band of Swift/BAT (15-350 keV), the full sample, denoted by A (for All), is reduced to 870 LGRBs. The second sample, denoted by B (bursts of Known redshift z), consists of 251 GRBs (there are thus 619 LGRBs without known redshifts). For each of the above physical quantities, a comparison is made between its distribution for the full sample and that for the B sample (of bursts with known redshifts).
We present a visual comparison of the distributions by graphical representation in the figures (1: a, b and c).

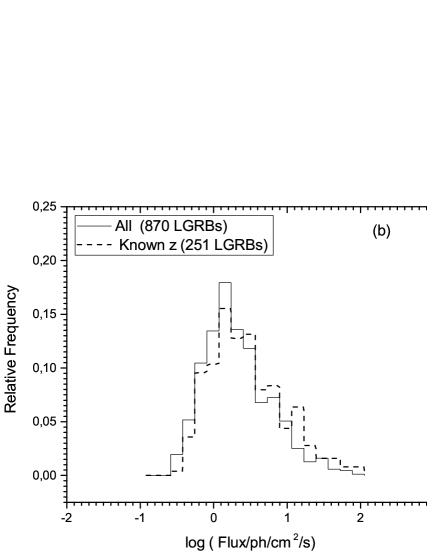
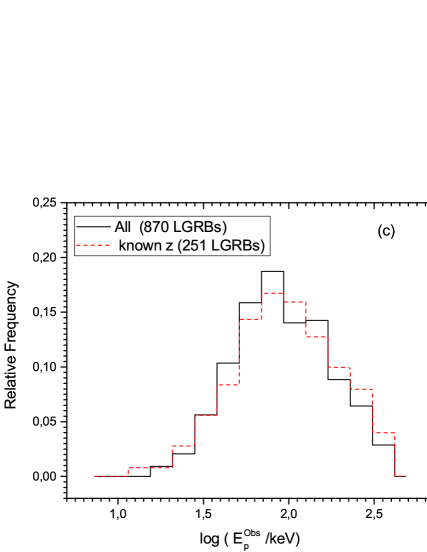
Our statistical analysis starts with a check of the normality of each of the six distributions (three for each sample). We adopted the Kolmogorov Smirnov test and applied it to each of the distributions, taking the logarithm of the physical quantities. The results obtained for each sample are presented in the two tables (4). We should note that the graphical representation was made on the normalized distributions, while the statistical tests were made on the actual ones.
| Statistic | p-value | Decision at 5% level |
Sample of 870 LGRBs (A: All)
0.0445
0.063
can’t reject normality
0.0723
0.0002
reject normality
0.0322
0.328
can’t reject normality
Sample of 251 LGRBs (B: Known z)
0.041
0.864
can’t reject normality
0.077
0.098
can’t reject normality
0.039
0.929
can’t reject normality
As the normality of the two quantities ( and was not rejected at a 5% significance level for the two samples, we proceeded to an F-test to check for the null hypothesis of equality of variances (), and a t-test to check for the null hypothesis of equality of means ).The results are presented in the table (5).
Hypothesis of equal variance
F-Statistic
p-value
Decision at 5% level
0.916
0.377
can’t reject
0.869
0.156
can’t reject
Hypothesis of equal means
t-Statistic
p-value
Decision at 5% level
-1.223
0.221
can’t reject
-0.52
0.60
can’t reject
We conclude that for the two quantities and the distributions given by the two samples are not significantly different at the 0.05 level.
For the distribution of the logarithm of the flux, we performed a nonparametric Kolmogorov-Smirnov (KS) test, which rejected the null hypothesis (equality of the two distributions representing the two samples) at a 0.05 significance level, but not at a 0.005 level (p-value = 0.0059). On the other hand, a Mann-Whitney test concluded that the two distributions are significantly different at a level of 0.005 (p-value = ).
We should also note that in this analysis, we did not take the uncertainties on the measured quantities into account; perhaps if the uncertainties are considered, the distributions of flux could also have an acceptable non-significant difference.
It can be concluded from this statistical analysis that the two samples A and B can be considered as drawn from the same population of LGRBs.
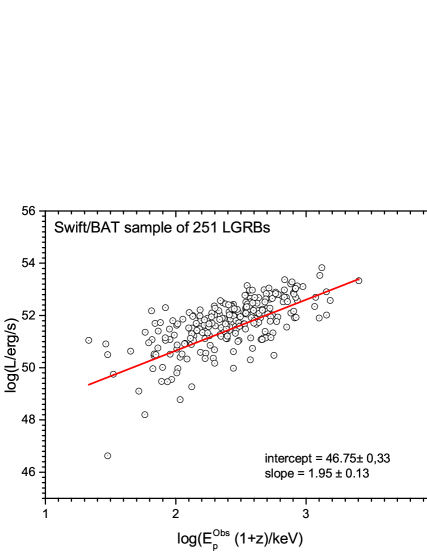
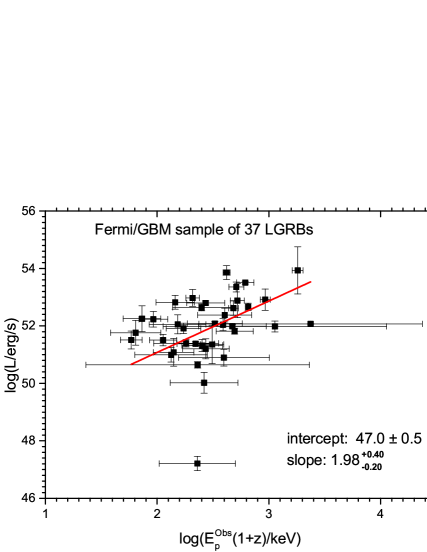
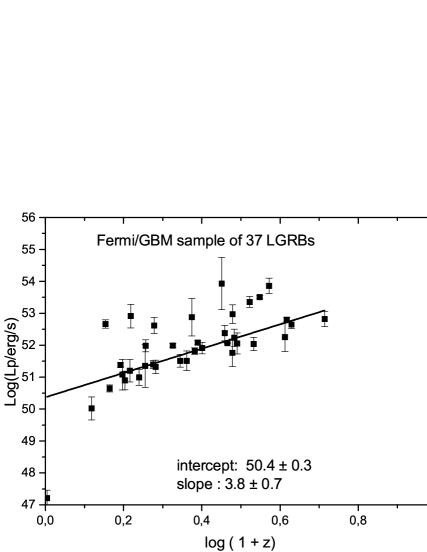
For our sample of Fermi/GBM bursts with known redshifts, due to their limited number (37 LGRBs), we found it useful to validate its representativeness by checking the Yonetoku relation on this sample, as this correlation is widely assumed to be true for all long bursts; it has been studied by a number of researchers and for several samples. We also tested it on our Swift/BAT sample (251 LGRBs), for which we found parameters (intercept and slope) very close to the original values published in Yonetoku et al. (2004). Our results are presented graphically in figure 2(top). For the Fermi sample (37 long GRBs), the values we obtained for the intercept and slope parameters are within the error bars of those of the original relation. This is shown graphically in figure 2(bottom). For a clear comparison with the ( and q) parameters of the relation (6), we present the table below(6):
| Swift | ||
|---|---|---|
| Fermi | ||
| Ref1 | ||
| Ref2 |
For the Konus-Wind sample, which consists of 152 LGRBs with known redshifts, we first check for the normality of the distributions of the duration and the observed energy at the peak flux, ; the (normalized) distributions (of the logarithms of each quantity) are shown in the figures (3 a and b). For this, we have performed a Kolmogorov Smirnov test on the data; the results we obtained are presented in the table (7).


| Statistic | p-value | Decision at 5% level | |
|---|---|---|---|
| 0.0406 | 0.99 | can’t reject normality | |
| 0.0327 | 0.99 | can’t reject normality |
Now to check for the representativeness of the Konus-Wind sample data, we use a comparison test of our sample against referenced values for the mean and variance as typically adopted for LGRBs. We use a t-test for the means and a -test for the variance at a significance level of 0.05. The distribution of of BATSE LGRBs (bright and faint) studied by Nava et al. (2011) is characterized by (, ). Taking these values as a reference and comparing with our Konus-Wind sample data, the t-test gives a p-value =0.012 for the means, and the -test gives a p-value = 0.012 for the variance. In both tests the null hypothesis is rejected at a significance level of 0.05 but is not for 0.01. In the same way, The distribution of of the Fermi LGRBs (bright and faint) studied by Nava et al. (2011) is characterized by (, ). The t-test gives a p-value =0.09 for the means, and the -test gives a p-value = 0.50 for the variance. In both tests the null hypothesis ( and ) is not rejected at a significance level of 0.05.
The duration distribution was studied by Tarnopolski, M. (2015) for 1566 long Fermi bursts; he found a normal distribution for characterized by (). In the same way as for , a t-test on the means gave us a p-value = 0.23, while a -test of the variance gave a p-value = 0.048. The duration distribution was also studied by Shahmoradi (2013) considering 1366 long Fermi bursts; he found (). In the same manner, we find p-value = 0.53 in a t-test on the means and p-value = 0.225 in a -test on the variance. In both tests the null hypothesis ( and ) is not rejected at a significance level of 0.05, considering the error bars.
Finally, the Konus-Wind sample’s representativeness could not be tested for the photon flux, as this parameter is not given among the satellite/detector’s data for all the LGRBs of our KW sample ; nor could we utilize the Yonetoku relation, since we use it to derive the luminosity (again because the Yonetoku relation is widely assumed to be true for all long bursts).
From the above statistical tests, we conclude that our samples of LGRBs with known redshifts are mostly, if imperfectly, representative of the general populations of LGRBs (with or without known redshifts) with their physical parameters (duration, energy at the peak of the flux, flux at the peak) as recorded by the Swift, Fermi, and Konus-Wind satellites.
3 Luminosity calculation
For the Swift/BAT and Fermi/GBM samples, the luminosity at the peak of the flux can be calculated using the spectral data of each burst, characterized by a known redshift. The 1-second photon flux at the peak can be found in the Swift/BAT and data Fermi/GBM. This flux gives the total number of photons per unit area and per unit time, regardless of their individual energies. The Swift/BAT energy spectrum is divided into four bands: 15-25 keV, 25-50 keV, 50-100 keV, 100-350 keV. The Fermi/GBM covers the wider band 10-1000 keV. In this work, we use a cut-off power-law (Band et al., 1992), which is characterized by two spectral parameters: the observed peak energy, , and the spectral index alpha ():
| (1) |
where .
The bolometric luminosity of the 1-second isotropic peak flux, denoted by , is the maximum energy radiated per unit time in all space. It is calculated by integrating the function in the energy band corresponding to the observed gamma radiation band in the source’s frame, i.e. = 1 keV to = keV. And because of cosmological effects, the corresponding observed energy band is: to .
Thus, the k-corrected is calculated via:
| (2) |
Here is k-corrected with the method developed by (Bloom et al., 2001), and is the peak flux expressed as . The k-correction factor is defined by (Yonetoku et al., 2004; Rossi et al., 2008; Elliott et al., 2012) as:
| (3) |
The cosmological distance is given by the equation:
| (4) |
where we adopt the following cosmological parameters: = 0.27, = 0.73, and = 70 (Komatsu et al., 2009).
These integrals are performed numerically using the time-resolved spectral parameters given by Swift/BAT and Fermi/GBM.
With this data, as explained above, we calculate the luminosity of each burst, taking into account the error on each quantity used. The results of this calculation are presented in Tables LABEL:tabSwift and LABEL:tabFermi. The errors are evaluated using the Monte Carlo method. The quantities needed in the calculation of the luminosity (, , flux) are assumed to follow a normal distribution. For each GRB, by making N random draws from these distributions, we obtain the two extremum values of the luminosity. The subtraction of these two values from the calculated value without uncertainty gives the errors.
For the Konus Wind sample, given the difficulty of obtaining the spectral parameters (, ) for all the bursts, we preferred to use the correlation relation of Yonetoku et al. (2004), which relates the luminosity to . We used the data for z and given in Minaev and Pozanenko (2019). We also used the improved Yonetoku et al. (2004) correlation relation:
| (5) |
In our Monte Carlo simulation, we draw values of using the following relation (which is the same as (5)):
| (6) |
where and are the luminosity and the energy corresponding to the jth GRB in our data table. To estimate the error on , we assume that and are random quantities obeying a normal distribution, such that: and . We also assume that the peak energy is normally distributed. The results of this calculation are presented in Table LABEL:tabKW.
4 Method for calculating the luminosity function
The total number of gamma-ray bursts observed by a telescope within an aperture solid angle and during an effective period of of activity T (in years) is:
| (7) |
where is the luminosity function and is the rate of occurrence of GRBs at redshift z expressed in . The factor (1+z) introduces the cosmological expansion factor and is the variation of the volume of the universe as a function of the redshift z, given by the equation :
| (8) |
The GRB luminosity function is usually defined as the number of bursts per unit of luminosity (Sethi and Bhargavi, 2001; Daigne et al., 2006; Zitouni et al., 2008; Cao et al., 2011; Amaral-Rogers et al., 2016; Paul, 2017):
| (9) |
To predict the total number of gamma-ray bursts that will be observed by a telescope, we need to know the rate of occurrence of GRBs and their luminosity function . The rate is very poorly known despite the fact that there are several attempts based on broad assumptions.
In the present work, we assume that the rate of long gamma-ray bursts is proportional to the star formation rate (SFR). Indeed, it is now accepted that long gamma-ray bursts are due to the collapse of massive stars, thus the burst rate should be proportional to the supernova rate through a constant k parameter (Porciani and Madau, 2001; Daigne et al., 2006):
| (10) |
where is the Type II supernova comoving rate. Moreover, these authors assume that the rate of supernovae is proportional to the rate of massive star formation:
| (11) |
where is the star formation rate, which is determined by observations only up to a redshift . Beyond this value, several hypotheses are made in the literature, from which we retain the three most common ones: , where the star formation rate decreases beyond ; , where the rate remains constant beyond ; and , where the rate continues to increase beyond (Daigne et al., 2006). These three hypotheses are expressed by the following relations (Porciani and Madau, 2001):
| (12) |
| (13) |
| (14) |
In our work, we have found it useful to use an equivalent form of the luminosity function presented by Butler et al. (2010). This form can be considered as a scale-free function (Sethi and Bhargavi, 2001). Moreover, we are interested in determining the parameters (detailed below) that characterize this luminosity function, so we will use a form of normalized luminosity function defined as follows:
| (15) |
To calculate the GRB luminosity function, we use the samples of GRBs (and their data) from the Swift/BAT, the Fermi/GBM, and the Konus/Wind satellites/instruments. With the exception of the redshift, all the parameters used in our calculations are given with their respective uncertainties. We have assumed that each parameter value is a normally distributed quantity characterized by the density function:
| (16) |
where represents the mean value of the measured quantity, and corresponds to its uncertainty, both given in Table 8. For example, for each GRB, the energy at the peak given in the table corresponds to and the corresponds to .
5 Results
5.1 Luminosity versus redshift
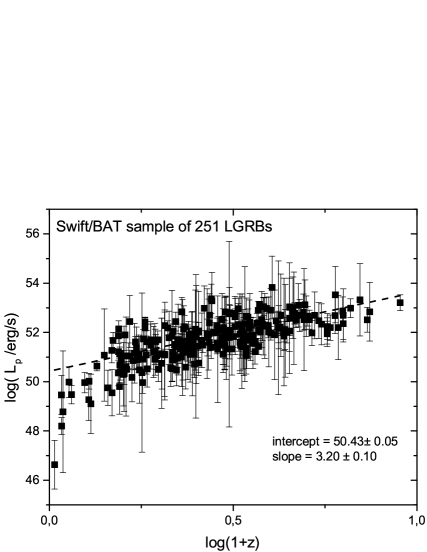
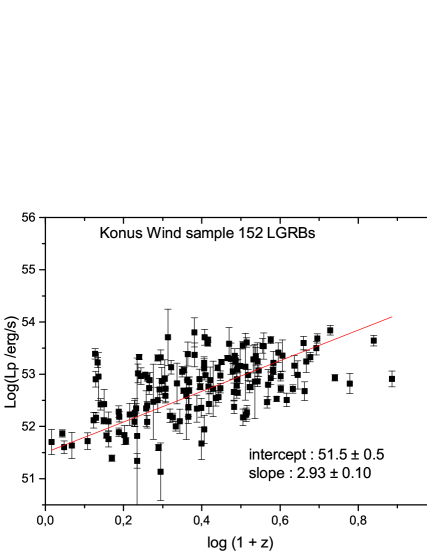
We study the variation of the luminosity observed as a function of the redshift for the three samples. We represent these results graphically in Figures (4, 5, 6), representing each instrument and its GRBs. Several previous works have shown the existence of a relationship between the luminosity L and the redshift z in the form:
| (17) |
where is the slope (in log-log), and is the intercept at z near 0. From the figures (4, 5, 6), one can notice that the data can indeed be fitted by a relation such as given in equation (2), although there is significant scatter, especially for Konus-Wind. The numerical results of this fit are presented in Table 8. Some values obtained from other references are also presented.
| Swift | ||
|---|---|---|
| Fermi | ||
| Konus/Wind | ||
| Ref1 | ||
| Ref2 | ||
| Ref3 | ||
| Ref4 | ||
| Ref5 |
A luminosity evolution has been suggested by some authors, e.g. (Lloyd-Ronning et al., 2002; Firmani et al., 2004; Matsubayashi et al., 2005; Kocevski and Liang, 2006; Salvaterra et al., 2009; Wanderman and Piran, 2010) with or without GRB rate evolution. Some of these authors used a sample of long bursts with known redshifts and found evidence for luminosity evolution. Other works find self-consistency without luminosity evolution. Butler et al. (2010) conclude that a rigorous treatment of the largest available Swift data set allows for a firm conclusion in favor of rate evolution but not luminosity evolution. Deng et al. (2016) say that with the large uncertainty on the index derived from one’s simulation/analysis, one cannot convincingly argue for a robust evolution feature of the GRB luminosity.
5.2 Luminosity function
Based on the data from the three samples, we found that the luminosity function varies according to the broken power law form (Zitouni et al., 2008; Wanderman and Piran, 2010; Butler et al., 2010; Cao et al., 2011; Amaral-Rogers et al., 2016):
| (18) |
where is the luminosity at the break of the power law, and and are the exponents of each part of the function; corresponds to the value of the luminosity function at the break . is expressed in . Many authors have studied the evolution of the break luminosity and found that it varies with the redshift (Cao et al., 2011; Deng et al., 2016; Amaral-Rogers et al., 2016). The latter studies considered the evolution of the rate of formation of GRBs. For example, Amaral-Rogers et al. (2016) expressed the break luminosity as and found that varies between and if we consider all models. For , they found that it varies between and .
For the luminosity function (LF) we present results with two cases/hypotheses: with evolution and without evolution of the LF. The “unevolved” luminosity function is obtained in the same way that was done by Pescalli, A. et al. (2016), taking . The parameter k is obtained from the table 8 for each sample.
Using the likelihood method, we find the different parameters of the luminosity function for each sample and for each case ( evolution and non evolution of LF). The results are presented in Table 9 for the evolution case. For the Fermi sample, we could not get a fit with a broken power law.. These results are also represented graphically in the figures (7 a, b, c).
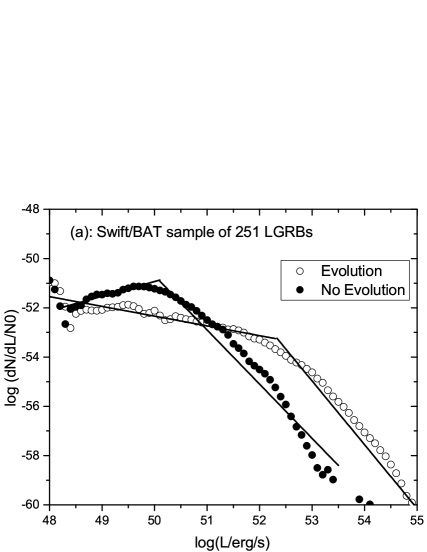

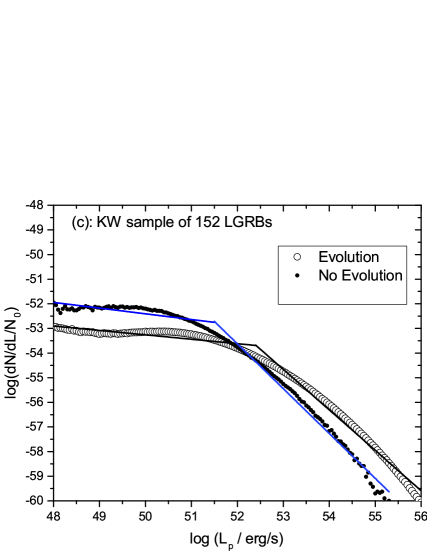
| No | evolution | ||
|---|---|---|---|
| Swift | |||
| Fermi | - | - | - |
| KW | |||
| Ref1 | |||
| Ref2 | |||
| Ref3 | |||
| Ref4 | |||
| With | evolution | ||
| Swift | |||
| Fermi | |||
| KW | |||
| Ref4 | |||
| Ref5 | |||
| Ref6 | |||
| Ref7 |
6 Discussion
Let us now compare and contrast our work and results to those of other researchers.
Like our own, the investigation by Wanderman and Piran (2015) involved a joint analysis of GRBs from different satellites, with data from Swift, Fermi, and CGRO-BATSE, aiming to determine the luminosity function and the formation rate of GRBs. However, unlike our study, their investigation was restricted to short GRBs, and more specifically to non-collapsar short bursts, having found that their short-GRBs sample was ”contaminated” by collapsars, which affected their data sample. With those restrictions, they obtained a luminosity function that was best fit with a broken power law with a break at , which is consistent with our results.
The investigation by Pescalli, A. et al. (2016) is most relevant to us because, like our study, theirs examines the luminosity function of GRBs and briefly explores whether GRBs undergo luminosity evolution. However, these authors restrict their data sample to long Swift GRBs, which reduces their sample to only 99 bursts compared to the 439 bursts in ours. Furthermore, our data is augmented by thousands of simulated ”artificial” bursts for simulation purposes. Despite these differences, Pescalli, A. et al. (2016) find that their data can be best fit with a broken power law with , which is consistent with what we obtain. However, although their high luminosity index is consistent with our value, their low luminosity index is not, indicating that the low-end of their luminosity function is steeper than ours. The difference could be due to their data sample being restricted to long GRBs taken from Swift only, whereas our sample consists of data combined three sub-samples. We should note that a close examination of our results reveals that among our three sub-samples, the value for the Swift sub-sample was significantly the steepest among the three, which is at least qualitatively in agreement with Pescalli, A. et al. (2016), and it might be hinting that the lower-end of the luminosity function is steeper for the Swift GRBs in particular. Moreover, like us, Pescalli, A. et al. (2016) found that there was a correlation between the luminosity and the redshift but concluded that this evolution should not be interpreted as being purely due to luminosity evolution. We agree with them, as the correlation with the redshift could be due to density evolution as well, and like Pescalli, A. et al. (2016) we admit that this issue needs further work, beyond the scope of our current study, because simulating both the luminosity and density evolutions and extricating the impact of each on the luminosity function and finding the extent and shape of its evolution is a separate and full-fledged topic. This is also the conclusion reached by Lan et al. (2019) who analyzed the same data sample used by Pescalli, A. et al. (2016) to investigate the GRB luminosity function and utilize it to determine the star-formation rate.
The investigation by Amaral-Rogers et al. (2016) takes a distinct approach from ours. These authors explore the pulse luminosity function for Swift GRBs. They use a sample of 118 bursts to generate a total of 607 pulses and then compute the pulse luminosity function by employing three different GRB formation rate models. Despite this markedly different approach that includes contributions from all fitted pulses and not just from the brightest ones, the best-fit parameters for their luminosity function, , , and , are consistent with our results, although once again their low-end luminosity function is somewhat steeper than what we obtain.
7 Conclusion
The investigation of the GRB luminosity function is an important issue in GRB research because it gives insight into the physics involved in the production mechanism of GRBs. Not only does it shed light on the range of luminosities that GRBs can have, it also reveals whether there is a ”scale” for GRB luminosities. The fact that all three sub-samples that we explored had a broken power-law luminosity function, with break luminosities consistent with one another, strongly indicates that the physics behind the formation of GRBs is not ”scaleless”, a result which can be useful when probing other physical aspects of GRBs.
In this study, we performed separate analyses of Swift/BAT, Fermi/GBM, and Konus/Wind data for all GRBs with known redshifts, in the aim of determining their luminosity functions. In doing that, we left out the formation rate of the GRBs from our considerations. We obtained the best parameters for the luminosity functions using the likelihood method. We found that they can be well represented by a broken power law -the so-called broken luminosity function.
The luminosity function expressed in log-log is well fit with a broken power-law with a break in the luminosity, which varies from to . The exponent-index of the low luminosity part, , varies between -0.23 and -0.47 and that of the high luminosity part, , varies between -1.79 and -2.68. These power law indices are consistent with those found in previous studies (values and references are given in Table 9).
In the future, we plan to look at both the density and luminosity evolution of GRBs, which is something that we only brushed briefly in this study. Such an investigation is important because it will cast light on several critical issues such as the star-formation rate, the degree to which GRBs can be utilized as ”standard candle”, and the evolution of the luminosity function itself.
Acknowledgements
The authors gratefully acknowledge the use of the online Swift/BAT table compiled by Taka Sakamoto and Scott D. Barthelmy and Evans, P. A. et al. (2010). The authors also aknowledge the use of the online Fermi/GMB table compiled by von Kienlin et al. (2014), Gruber et al. (2014) and Bhat et al. (2016). We thank the General Directorate of Scientific Research and Technological Development (DGRSDT), Algiers, Algeria for the financial support.
References
- Abbott and al. (2017) Abbott, B.P., al.: Phys. Rev. Lett. 119, 161101 (2017)
- Amaral-Rogers et al. (2016) Amaral-Rogers, A., Willingale, R., O’Brien, P.T.: Monthly Notices of the Royal Astronomical Society 464(2), 2000 (2016)
- Atteia et al. (2017) Atteia, J.-L., Heussaff, V., Dezalay, J.-P., Klotz, A., Turpin, D., Tsvetkova, A.E., Frederiks, D.D., Zolnierowski, Y., Daigne, F., Mochkovitch, R.: The Astrophysical Journal 837(2), 119 (2017). doi:10.3847/1538-4357/aa5ffa
- Band et al. (1992) Band, D., Matteson, J., Ford, L., Schaefer, B., Teegarden, B., Cline, T., Paciesas, W., Pendleton, G., Fishman, G., Meegan, C.: In: Paciesas, W.S., Fishman, G.J. (eds.) American Institute of Physics Conference Series. American Institute of Physics Conference Series, vol. 265, p. 169 (1992)
- Bhat et al. (2016) Bhat, P.N., Meegan, C.A., von Kienlin, A., Paciesas, W.S., Briggs, M.S., Burgess, J.M., Burns, E., Chaplin, V., Cleveland, W.H., Collazzi, A.C., Connaughton, V., Diekmann, A.M., Fitzpatrick, G., Gibby, M.H., Giles, M.M., Goldstein, A.M., Greiner, J., Jenke, P.A., Kippen, R.M., Kouveliotou, C., Mailyan, B., McBreen, S., Pelassa, V., Preece, R.D., Roberts, O.J., Sparke, L.S., Stanbro, M., Veres, P., Wilson-Hodge, C.A., Xiong, S., Younes, G., Yu, H.-F., Zhang, B.: The Astrophysical Journal Supplement Series 223(2), 28 (2016)
- Bloom et al. (2001) Bloom, J.S., Frail, D.A., Sari, R.: Astron. J. 121, 2879 (2001). astro-ph/0102371
- Butler et al. (2010) Butler, N.R., Bloom, J.S., Poznanski, D.: Astrophys. J. 711(1), 495 (2010). 0910.3341
- Campisi et al. (2010) Campisi, M.A., Li, L.-X., Jakobsson, P.: Monthly Notices of the Royal Astronomical Society 407(3), 1972 (2010)
- Cano et al. (2017) Cano, Z., Wang, S.-Q., Dai, Z.-G., Wu, X.-F.: Advances in Astronomy 2017, 1 (2017). doi:10.1155/2017/8929054
- Cao et al. (2011) Cao, X.-F., Yu, Y.-W., Cheng, K.S., Zheng, X.-P.: Monthly Notices of the Royal Astronomical Society 416(3), 2174 (2011)
- Daigne et al. (2006) Daigne, F., Rossi, E.M., Mochkovitch, R.: Monthly Notices of the Royal Astronomical Society 372(3), 1034 (2006)
- Dainotti et al. (2019) Dainotti, M., Petrosian, V., Bogdan, M., Miasojedow, B., Nagataki, S., Hastie, T., Nuyngen, Z., Gilda, S., Hernandez, X., Krol, D.: arXiv e-prints, 1907 (2019). 1907.05074
- Deng et al. (2016) Deng, C.-M., Wang, X.-G., Guo, B.-B., Lu, R.-J., Wang, Y.-Z., Wei, J.-J., Wu, X.-F., Liang, E.-W.: The Astrophysical Journal 820(1), 66 (2016)
- Drago et al. (2018) Drago, A., Pagliara, G., Traversi, S.: Mem. Soc. Astron. Italiana 89, 236 (2018). 1802.01696
- Elliott et al. (2012) Elliott, J., Greiner, J., Khochfar, S., Schady, P., Johnson, J.L., Rau, A.: Astron. Astrophys. 539, 113 (2012). 1202.1225
- Evans, P. A. et al. (2010) Evans, P. A., Willingale, R., Osborne, J. P., O’Brien, P. T., Page, K. L., Markwardt, C. B., Barthelmy, S. D., Beardmore, A. P., Burrows, D. N., Pagani, C., Starling, R. L. C., Gehrels, N., Romano, P.: A&A 519, 102 (2010)
- Firmani et al. (2004) Firmani, C., Avila-Reese, V., Ghisellini, G., Tutukov, A.V.: The Astrophysical Journal 611(2), 1033 (2004)
- Frederiks et al. (2019) Frederiks, D., Svinkin, D., Tsvetkova, A., Aptekar, R., Golenetskii, S., Kozlova, A., Lysenko, A., Ulanov, M.: arXiv e-prints, 1907 (2019). 1907.00402
- Gruber et al. (2014) Gruber, D., Goldstein, A., von Ahlefeld, V.W., Bhat, P.N., Bissaldi, E., Briggs, M.S., Byrne, D., Cleveland, W.H., Connaughton, V., Diehl, R., Fishman, G.J., Fitzpatrick, G., Foley, S., Gibby, M., Giles, M.M., Greiner, J., Guiriec, S., van der Horst, A.J., von Kienlin, A., Kouveliotou, C., Layden, E., Lin, L., Meegan, C.A., McGlynn, S., Paciesas, W.S., Pelassa, V., Preece, R.D., Rau, A., Wilson-Hodge, C.A., Xiong, S., Younes, G., Yu, H.-F.: The Astrophysical Journal Supplement Series 211(1), 12 (2014)
- Kinugawa et al. (2019) Kinugawa, T., Harikane, Y., Asano, K.: Astrophys. J. 878(2), 128 (2019). 1901.03516
- Kocevski and Liang (2006) Kocevski, D., Liang, E.: The Astrophysical Journal 642(1), 371 (2006)
- Komatsu et al. (2009) Komatsu, E., Dunkley, J., Nolta, M.R., Bennett, C.L., Gold, B., Hinshaw, G., Jarosik, N., Larson, D., Limon, M., Page, L., Spergel, D.N., Halpern, M., Hill, R.S., Kogut, A., Meyer, S.S., Tucker, G.S., Weiland, J.L., Wollack, E., Wright, E.L.: Astrophys. J. Suppl. Ser. 180, 330 (2009). 0803.0547
- Lan et al. (2019) Lan, G.-X., Zeng, H.-D., Wei, J.-J., Wu, X.-F.: Monthly Notices of the Royal Astronomical Society 488(4), 4607 (2019)
- Le and Mehta (2017) Le, T., Mehta, V.: The Astrophysical Journal 837(1), 17 (2017)
- Liang et al. (2007) Liang, E., Zhang, B., Virgili, F., Dai, Z.G.: Astrophys. J. 662(2), 1111 (2007)
- Lloyd-Ronning et al. (2002) Lloyd-Ronning, N.M., Fryer, C.L., Ramirez-Ruiz, E.: The Astrophysical Journal 574(2), 554 (2002)
- Matsubayashi et al. (2005) Matsubayashi, T., Yamazaki, R., Yonetoku, D., Murakami, T., Ebisuzaki, T.: Progress of Theoretical Physics 114(5), 983 (2005)
- Mészáros (2019) Mészáros, P.: Mem. Soc. Astron. Italiana 90, 57 (2019). 1904.10488
- Minaev and Pozanenko (2019) Minaev, P.Y., Pozanenko, A.S.: Monthly Notices of the Royal Astronomical Society 492(2), 1919 (2019)
- Nava et al. (2011) Nava, L., Ghirlanda, G., Ghisellini, G., Celotti, A.: Monthly Notices of the Royal Astronomical Society 415(4), 3153 (2011). doi:10.1111/j.1365-2966.2011.18928.x
- Paul (2017) Paul, D.: Monthly Notices of the Royal Astronomical Society 473(3), 3385 (2017)
- Pescalli, A. et al. (2016) Pescalli, A., Ghirlanda, G., Salvaterra, R., Ghisellini, G., Vergani, S. D., Nappo, F., Salafia, O. S., Melandri, A., Covino, S., Götz, D.: A&A 587, 40 (2016). doi:10.1051/0004-6361/201526760
- Porciani and Madau (2001) Porciani, C., Madau, P.: Astrophys. J. 548(2), 522 (2001). astro-ph/0008294. doi:10.1086/319027
- Rossi et al. (2008) Rossi, F., Guidorzi, C., Amati, L., Frontera, F., Romano, P., Campana, S., Chincarini, G., Montanari, E., Moretti, A., Tagliaferri, G.: Mon. Not. R. Astron. Soc. 388, 1284 (2008). 0802.0471
- Salvaterra et al. (2009) Salvaterra, R., Guidorzi, C., Campana, S., Chincarini, G., Tagliaferri, G.: Monthly Notices of the Royal Astronomical Society 396(1), 299 (2009)
- Salvaterra et al. (2012) Salvaterra, R., Campana, S., Vergani, S.D., Covino, S., D’Avanzo, P., Fugazza, D., Ghirlanda, G., Ghisellini, G., Melandri, A., Nava, L., Sbarufatti, B., Flores, H., Piranomonte, S., Tagliaferri, G.: Astrophys. J. 749(1), 68 (2012). 1112.1700
- Schmidt (1999) Schmidt, M.: Astrophys. J. Lett. 523(2), 117 (1999). astro-ph/9908206
- Schmidt (2001) Schmidt, M.: Astrophys. J. 552(1), 36 (2001). astro-ph/0101163
- Sethi and Bhargavi (2001) Sethi, S., Bhargavi, S.G.: Astron. Astrophys. 376, 10 (2001)
- Shahmoradi (2013) Shahmoradi, A.: The Astrophysical Journal 766(2), 111 (2013). doi:10.1088/0004-637x/766/2/111
- Svinkin et al. (2016) Svinkin, D.S., Frederiks, D.D., Aptekar, R.L., Golenetskii, S.V., Palshin, V.D., Oleynik, P.P., Tsvetkova, A.E., Ulanov, M.V., Cline, T.L., Hurley, K.: The Astrophysical Journal Supplement Series 224(1), 10 (2016)
- Tarnopolski, M. (2015) Tarnopolski, M.: A&A 581, 29 (2015). doi:10.1051/0004-6361/201526415
- Tsvetkova et al. (2017) Tsvetkova, A., Frederiks, D., Golenetskii, S., Lysenko, A., Oleynik, P., Pal’shin, V., Svinkin, D., Ulanov, M., Cline, T., Hurley, K., Aptekar, R.: Astrophys. J. 850(2), 161 (2017)
- Virgili et al. (2009) Virgili, F.J., Liang, E.-W., Zhang, B.: Mon. Not. R. Astron. Soc. 392(1), 91 (2009)
- von Kienlin et al. (2014) von Kienlin, A., Meegan, C.A., Paciesas, W.S., Bhat, P.N., Bissaldi, E., Briggs, M.S., Burgess, J.M., Byrne, D., Chaplin, V., Cleveland, W., Connaughton, V., Collazzi, A.C., Fitzpatrick, G., Foley, S., Gibby, M., Giles, M., Goldstein, A., Greiner, J., Gruber, D., Guiriec, S., van der Horst, A.J., Kouveliotou, C., Layden, E., McBreen, S., McGlynn, S., Pelassa, V., Preece, R.D., Rau, A., Tierney, D., Wilson-Hodge, C.A., Xiong, S., Younes, G., Yu, H.-F.: The Astrophysical Journal Supplement Series 211(1), 13 (2014)
- Wanderman and Piran (2010) Wanderman, D., Piran, T.: Monthly Notices of the Royal Astronomical Society 406(3), 1944 (2010)
- Wanderman and Piran (2015) Wanderman, D., Piran, T.: Mon. Not. R. Astron. Soc. 448(4), 3026 (2015). 1405.5878
- Yonetoku et al. (2004) Yonetoku, D., Murakami, T., Nakamura, T., Yamazaki, R., Inoue, A.K., Ioka, K.: Astrophys. J. 609(2), 935 (2004). astro-ph/0309217
- Yonetoku et al. (2010) Yonetoku, D., Murakami, T., Tsutsui, R., Nakamura, T., Morihara, Y., Takahashi, K.: Publ. Astron. Soc. Jpn. 62, 1495 (2010)
- Yu et al. (2015) Yu, H., Wang, F.Y., Dai, Z.G., Cheng, K.S.: The Astrophysical Journal Supplement Series 218(1), 13 (2015)
- Zitouni et al. (2008) Zitouni, H., Daigne, F., Mochkovich, R., Zerguini, T.H.: Monthly Notices of the Royal Astronomical Society 386(3), 1597 (2008)
| GRB | z | flux | ||||
|---|---|---|---|---|---|---|
| sec | keV | |||||
| GRB050126 | 1.29 | 24.80 | ||||
| GRB050223 | 0.59 | 22.50 | ||||
| GRB050315 | 1.95 | 95.60 | ||||
| GRB050318 | 1.44 | 32.00 | ||||
| GRB050319 | 3.24 | 152.50 | ||||
| GRB050401 | 2.90 | 33.30 | ||||
| GRB050406 | 2.44 | 5.40 | ||||
| GRB050416A | 0.65 | 2.50 | ||||
| GRB050505 | 4.27 | 58.90 | ||||
| GRB050525A | 0.61 | 8.80 | ||||
| GRB050802 | 1.71 | 19.00 | ||||
| GRB050814 | 5.30 | 150.90 | ||||
| GRB050908 | 3.35 | 19.40 | ||||
| GRB050915A | 2.53 | 52.00 | ||||
| GRB050922C | 2.20 | 4.50 | ||||
| GRB051001 | 2.43 | 189.10 | ||||
| GRB051006 | 1.06 | 34.80 | ||||
| GRB051016B | 0.94 | 4.00 | ||||
| GRB051109A | 2.35 | 37.20 | ||||
| GRB051109B | 0.08 | 14.30 | ||||
| GRB051117B | 0.48 | 9.00 | ||||
| GRB060108 | 2.03 | 14.30 | ||||
| GRB060124 | 2.30 | 13.42 | ||||
| GRB060206 | 4.04 | 7.60 | ||||
| GRB060210 | 3.91 | 255.00 | ||||
| GRB060218 | 0.03 | 2100.00 | ||||
| GRB060223A | 4.41 | 11.30 | ||||
| GRB060502A | 1.51 | 28.40 | ||||
| GRB060505 | 0.09 | 4.00 | ||||
| GRB060512 | 0.44 | 8.50 | ||||
| GRB060522 | 5.11 | 71.10 | ||||
| GRB060526 | 3.21 | 298.20 | ||||
| GRB060602A | 0.79 | 75.00 | ||||
| GRB060604 | 2.14 | 95.00 | ||||
| GRB060614 | 0.13 | 108.70 | ||||
| GRB060707 | 3.43 | 66.20 | ||||
| GRB060714 | 2.71 | 115.00 | ||||
| GRB060719 | 1.53 | 66.90 | ||||
| GRB060729 | 0.54 | 115.30 | ||||
| GRB060814 | 0.84 | 145.30 | ||||
| GRB060904B | 0.70 | 171.50 | ||||
| GRB060906 | 3.69 | 43.50 | ||||
| GRB060908 | 1.88 | 19.30 | ||||
| GRB060912A | 0.94 | 5.00 | ||||
| GRB060926 | 3.21 | 8.00 | ||||
| GRB060927 | 5.60 | 22.50 | ||||
| GRB061110A | 0.76 | 40.70 | ||||
| GRB061210 | 0.41 | 85.30 | ||||
| GRB061222A | 2.09 | 71.40 | ||||
| GRB061222B | 3.35 | 40.00 | ||||
| GRB070103 | 2.62 | 18.60 | ||||
| GRB070129 | 2.34 | 460.60 | ||||
| GRB070208 | 1.17 | 47.70 | ||||
| GRB070306 | 1.50 | 209.50 | ||||
| GRB070318 | 0.84 | 74.60 | ||||
| GRB070411 | 2.95 | 121.50 | ||||
| GRB070506 | 2.31 | 4.30 | ||||
| GRB070508 | 0.82 | 20.90 | ||||
| GRB070521 | 0.55 | 37.90 | ||||
| GRB070529 | 2.50 | 109.20 | ||||
| GRB070611 | 2.04 | 12.20 | ||||
| GRB070612A | 0.62 | 368.80 | ||||
| GRB070714B | 0.92 | 64.00 | ||||
| GRB070721B | 3.63 | 340.00 | ||||
| GRB070802 | 2.45 | 16.40 | ||||
| GRB070810A | 2.17 | 11.00 | ||||
| GRB071010A | 0.98 | 6.00 | ||||
| GRB071010B | 0.95 | 36.12 | ||||
| GRB071028B | 0.94 | 55.00 | ||||
| GRB071117 | 1.33 | 6.60 | ||||
| GRB071122 | 1.14 | 68.70 | ||||
| GRB080207 | 2.09 | 340.00 | ||||
| GRB080310 | 2.43 | 365.00 | ||||
| GRB080319C | 1.95 | 34.00 | ||||
| GRB080413A | 2.43 | 46.00 | ||||
| GRB080413B | 1.10 | 8.00 | ||||
| GRB080430 | 0.75 | 16.20 | ||||
| GRB080516 | 3.20 | 5.80 | ||||
| GRB080520 | 1.54 | 2.80 | ||||
| GRB080605 | 1.64 | 20.00 | ||||
| GRB080607 | 3.04 | 79.00 | ||||
| GRB080707 | 1.23 | 27.10 | ||||
| GRB080710 | 0.84 | 120.00 | ||||
| GRB080804 | 2.21 | 34.00 | ||||
| GRB080805 | 1.50 | 78.00 | ||||
| GRB080906 | 2.00 | 147.00 | ||||
| GRB080913 | 6.44 | 8.00 | ||||
| GRB080916A | 0.69 | 60.00 | ||||
| GRB080928 | 1.69 | 280.00 | ||||
| GRB081008 | 1.97 | 185.50 | ||||
| GRB081118 | 2.58 | 67.00 | ||||
| GRB081121 | 2.51 | 14.00 | ||||
| GRB081203A | 2.10 | 294.00 | ||||
| GRB081221 | 2.26 | 34.00 | ||||
| GRB081222 | 2.70 | 24.00 | ||||
| GRB090102 | 1.55 | 27.00 | ||||
| GRB090205 | 4.70 | 8.80 | ||||
| GRB090407 | 1.45 | 310.00 | ||||
| GRB090423 | 8.00 | 10.30 | ||||
| GRB090424 | 0.54 | 48.00 | ||||
| GRB090529 | 2.62 | 10.40 | ||||
| GRB090530 | 1.27 | 48.00 | ||||
| GRB090618 | 0.54 | 113.20 | ||||
| GRB090715B | 3.00 | 266.00 | ||||
| GRB090726 | 2.71 | 67.00 | ||||
| GRB090926B | 1.24 | 109.70 | ||||
| GRB090927 | 1.37 | 2.20 | ||||
| GRB091018 | 0.97 | 4.40 | ||||
| GRB091029 | 2.75 | 39.20 | ||||
| GRB091109A | 3.50 | 48.00 | ||||
| GRB091127 | 0.49 | 7.10 | ||||
| GRB091208B | 1.06 | 14.90 | ||||
| GRB100302A | 4.81 | 17.90 | ||||
| GRB100316B | 1.18 | 3.80 | ||||
| GRB100418A | 0.62 | 7.00 | ||||
| GRB100425A | 1.75 | 37.00 | ||||
| GRB100615A | 1.40 | 39.00 | ||||
| GRB100621A | 0.54 | 63.60 | ||||
| GRB100704A | 3.60 | 197.50 | ||||
| GRB100728B | 2.80 | 12.10 | ||||
| GRB100814A | 1.44 | 174.50 | ||||
| GRB100816A | 0.80 | 2.90 | ||||
| GRB100902A | 4.50 | 428.80 | ||||
| GRB100906A | 1.73 | 114.40 | ||||
| GRB101219B | 0.55 | 34.00 | ||||
| GRB110128A | 2.34 | 30.70 | ||||
| GRB110205A | 1.98 | 257.00 | ||||
| GRB110213A | 1.46 | 48.00 | ||||
| GRB110422A | 1.77 | 25.90 | ||||
| GRB110503A | 1.61 | 10.00 | ||||
| GRB110715A | 0.82 | 13.00 | ||||
| GRB110731A | 2.83 | 38.80 | ||||
| GRB110801A | 1.86 | 385.00 | ||||
| GRB110808A | 1.35 | 48.00 | ||||
| GRB111008A | 5.00 | 63.46 | ||||
| GRB111209A | 0.68 | 810.96 | ||||
| GRB111225A | 0.30 | 106.80 | ||||
| GRB111228A | 0.71 | 101.20 | ||||
| GRB111229A | 1.38 | 25.40 | ||||
| GRB120118B | 2.94 | 23.26 | ||||
| GRB120119A | 1.73 | 253.80 | ||||
| GRB120326A | 1.80 | 69.60 | ||||
| GRB120404A | 2.88 | 38.70 | ||||
| GRB120422A | 0.28 | 5.35 | ||||
| GRB120521C | 6.00 | 26.70 | ||||
| GRB120712A | 4.00 | 14.70 | ||||
| GRB120722A | 0.96 | 42.40 | ||||
| GRB120724A | 1.48 | 72.80 | ||||
| GRB120729A | 0.80 | 71.50 | ||||
| GRB120802A | 3.80 | 50.00 | ||||
| GRB120805A | 3.10 | 48.00 | ||||
| GRB120811C | 2.67 | 26.80 | ||||
| GRB120815A | 2.36 | 9.70 | ||||
| GRB120909A | 3.93 | 220.60 | ||||
| GRB121128A | 2.20 | 23.30 | ||||
| GRB121201A | 3.38 | 85.00 | ||||
| GRB121211A | 1.02 | 182.00 | ||||
| GRB130215A | 0.60 | 65.70 | ||||
| GRB130408A | 3.76 | 28.00 | ||||
| GRB130418A | 1.22 | 274.92 | ||||
| GRB130420A | 1.30 | 123.50 | ||||
| GRB130427B | 2.78 | 27.00 | ||||
| GRB130511A | 1.30 | 5.43 | ||||
| GRB130514A | 3.60 | 204.00 | ||||
| GRB130604A | 1.06 | 37.70 | ||||
| GRB130610A | 2.09 | 46.40 | ||||
| GRB130612A | 2.01 | 4.00 | ||||
| GRB130701A | 1.16 | 4.38 | ||||
| GRB130831A | 0.48 | 32.50 | ||||
| GRB130925A | 0.35 | 160.29 | ||||
| GRB131030A | 1.29 | 41.10 | ||||
| GRB131103A | 0.60 | 17.30 | ||||
| GRB131105A | 1.69 | 112.30 | ||||
| GRB131117A | 4.18 | 11.00 | ||||
| GRB131227A | 5.30 | 18.00 | ||||
| GRB140114A | 3.00 | 139.70 | ||||
| GRB140206A | 2.73 | 93.60 | ||||
| GRB140213A | 1.21 | 60.00 | ||||
| GRB140301A | 1.42 | 31.00 | ||||
| GRB140304A | 5.28 | 15.60 | ||||
| GRB140318A | 1.02 | 8.43 | ||||
| GRB140419A | 3.96 | 94.70 | ||||
| GRB140423A | 3.26 | 134.00 | ||||
| GRB140428A | 4.70 | 17.42 | ||||
| GRB140430A | 1.60 | 173.60 | ||||
| GRB140506A | 0.89 | 111.10 | ||||
| GRB140512A | 0.72 | 154.80 | ||||
| GRB140515A | 6.32 | 23.40 | ||||
| GRB140518A | 4.71 | 60.50 | ||||
| GRB140629A | 2.27 | 42.00 | ||||
| GRB140703A | 3.14 | 67.10 | ||||
| GRB140710A | 0.56 | 3.52 | ||||
| GRB140907A | 1.21 | 79.20 | ||||
| GRB141004A | 0.57 | 3.92 | ||||
| GRB141026A | 3.35 | 146.00 | ||||
| GRB141121A | 1.47 | 549.90 | ||||
| GRB141220A | 1.32 | 7.21 | ||||
| GRB150206A | 2.09 | 83.20 | ||||
| GRB150314A | 1.76 | 14.79 | ||||
| GRB150323A | 0.59 | 149.60 | ||||
| GRB150413A | 3.20 | 263.60 | ||||
| GRB150818A | 0.28 | 123.30 | ||||
| GRB150915A | 1.97 | 164.70 | ||||
| GRB151029A | 1.42 | 8.95 | ||||
| GRB151031A | 1.17 | 5.00 | ||||
| GRB151111A | 3.50 | 76.93 | ||||
| GRB151112A | 4.10 | 19.32 | ||||
| GRB151215A | 2.59 | 17.80 | ||||
| GRB160121A | 1.96 | 12.00 | ||||
| GRB160203A | 3.52 | 20.20 | ||||
| GRB160227A | 2.38 | 316.50 | ||||
| GRB160303A | 2.30 | 5.00 | ||||
| GRB160327A | 4.99 | 28.00 | ||||
| GRB160425A | 0.56 | 304.58 | ||||
| GRB160703A | 1.50 | 44.40 | ||||
| GRB160804A | 0.74 | 144.20 | ||||
| GRB161014A | 2.82 | 18.30 | ||||
| GRB161108A | 1.16 | 105.10 | ||||
| GRB161117A | 1.55 | 125.70 | ||||
| GRB161129A | 0.65 | 35.53 | ||||
| GRB161219B | 0.15 | 6.94 | ||||
| GRB170113A | 1.97 | 20.66 | ||||
| GRB170202A | 3.65 | 46.20 | ||||
| GRB170531B | 2.37 | 164.13 | ||||
| GRB170604A | 1.33 | 26.70 | ||||
| GRB170705A | 2.01 | 217.30 | ||||
| GRB170714A | 0.79 | 459.22 | ||||
| GRB170903A | 0.89 | 29.20 | ||||
| GRB171020A | 1.87 | 41.90 | ||||
| GRB171222A | 2.41 | 174.80 | ||||
| GRB180115A | 2.49 | 40.90 | ||||
| GRB180205A | 1.41 | 15.50 | ||||
| GRB180314A | 1.45 | 51.20 | ||||
| GRB180329B | 2.00 | 210.00 | ||||
| GRB180510B | 1.30 | 134.30 | ||||
| GRB180620B | 1.12 | 198.80 | ||||
| GRB180624A | 2.85 | 486.40 | ||||
| GRB180720B | 0.65 | 108.40 | ||||
| GRB181010A | 1.39 | 16.40 | ||||
| GRB181110A | 1.50 | 138.40 | ||||
| GRB181213A | 2.40 | 15.31 | ||||
| GRB190106A | 1.86 | 76.80 | ||||
| GRB190114A | 3.38 | 66.60 | ||||
| GRB190324A | 1.17 | 28.40 | ||||
| GRB190719C | 2.47 | 185.70 | ||||
| GRB190829A | 0.08 | 58.20 | ||||
| GRB191004B | 3.50 | 37.70 | ||||
| GRB191011A | 1.72 | 7.37 | ||||
| GRB191019A | 0.25 | 64.35 | ||||
| GRB191221B | 1.19 | 48.00 | ||||
| GRB 200205B | 1.465 | 458 |
| GRB | z | flux | ||||
|---|---|---|---|---|---|---|
| (sec) | (keV) | |||||
| GRB090902B | 1.82 | 19.33 | ||||
| GRB091003A | 0.90 | 20.22 | ||||
| GRB100414A | 1.37 | 26.50 | ||||
| GRB110402A | 0.81 | 35.65 | ||||
| GRB120712A* | 4.17 | 22.53 | ||||
| GRB120729A | 0.80 | 71.46 | ||||
| GRB120922A* | 3.10 | 182.28 | ||||
| GRB130215A | 0.60 | 143.75 | ||||
| GRB130420A* | 1.30 | 104.96 | ||||
| GRB130610A* | 2.09 | 21.76 | ||||
| GRB130612A* | 2.01 | 7.42 | ||||
| GRB131011A* | 1.87 | 77.06 | ||||
| GRB140206A* | 2.73 | 146.69 | ||||
| GRB140423A* | 3.26 | 95.23 | ||||
| GRB140620A* | 2.04 | 45.83 | ||||
| GRB140623A* | 1.92 | 111.10 | ||||
| GRB140703A* | 3.14 | 83.97 | ||||
| GRB140907A* | 1.21 | 35.84 | ||||
| GRB141004A | 0.57 | 2.56 | ||||
| GRB141028A* | 2.33 | 31.49 | ||||
| GRB141221A* | 1.45 | 23.81 | ||||
| GRB141225A* | 0.92 | 56.32 | ||||
| GRB150120A* | 0.46 | 3.33 | ||||
| GRB150301B* | 1.52 | 13.31 | ||||
| GRB150727A* | 0.31 | 49.41 | ||||
| GRB160804A* | 0.74 | 131.59 | ||||
| GRB161129A* | 0.65 | 36.10 | ||||
| GRB170214A* | 2.53 | 122.88 | ||||
| GRB170607A* | 0.56 | 20.93 | ||||
| GRB170705A* | 2.01 | 22.78 | ||||
| GRB170817A | 0.01 | 2.05 | ||||
| GRB170903A* | 0.89 | 25.60 | ||||
| GRB171222A* | 2.41 | 80.38 | ||||
| GRB180205A* | 1.41 | 15.36 | ||||
| GRB180620B* | 1.12 | 46.72 | ||||
| GRB180720B* | 0.65 | 48.90 | ||||
| GRB190114C | 0.42 | 170.94 |
| GRB | z | Log() | |
|---|---|---|---|
| 91018 | 0.971 | ||
| 970228 | 0.695 | ||
| 970828 | 0.958 | ||
| 971214 | 3.418 | ||
| 990123 | 1.600 | ||
| 990506 | 1.307 | ||
| 990510 | 1.619 | ||
| 990705 | 0.842 | ||
| 990712 | 0.433 | ||
| 991208 | 0.706 | ||
| 991216 | 1.020 | ||
| 000131 | 4.500 | ||
| 000210 | 0.846 | ||
| 000301C | 2.034 | ||
| 000418 | 1.118 | ||
| 000911 | 1.058 | ||
| 000926A | 2.037 | ||
| 010222 | 1.477 | ||
| 010921 | 0.450 | ||
| 011121 | 0.360 | ||
| 020405 | 0.690 | ||
| 020813 | 1.254 | ||
| 020819B | 0.411 | ||
| 030329 | 0.169 | ||
| 031203 | 0.105 | ||
| 041006 | 0.716 | ||
| 050401 | 2.899 | ||
| 050525A | 0.606 | ||
| 050603 | 2.821 | ||
| 050820 | 2.615 | ||
| 051008 | 2.770 | ||
| 051022 | 0.800 | ||
| 051109A | 2.346 | ||
| 060124 | 2.297 | ||
| 060418 | 1.489 | ||
| 060502A | 1.503 | ||
| 060814 | 1.923 | ||
| 060912A | 0.937 | ||
| 061007 | 1.261 | ||
| 061021 | 0.345 | ||
| 061121 | 1.314 | ||
| 061222A | 2.088 | ||
| 070125 | 1.547 | ||
| 070328 | 2.063 | ||
| 070508 | 0.820 | ||
| 070521 | 2.087 | ||
| 071003 | 1.604 | ||
| 071010B | 0.947 | ||
| 071020 | 2.146 | ||
| 071112C | 0.823 | ||
| 071117 | 1.331 | ||
| 080319B | 0.938 | ||
| 080319C | 1.949 | ||
| 080411 | 1.030 | ||
| 080413A | 2.433 | ||
| 080514B | 1.800 | ||
| 080602 | 1.820 | ||
| 080603B | 2.689 | ||
| 080605 | 1.640 | ||
| 080607 | 3.036 | ||
| 080721 | 2.591 | ||
| 080913 | 6.695 | ||
| 080916A | 0.689 | ||
| 080916C | 4.350 | ||
| 081121 | 2.512 | ||
| 081203A | 2.050 | ||
| 081221 | 2.260 | ||
| 081222 | 2.770 | ||
| 090102 | 1.547 | ||
| 090201 | 2.100 | ||
| 090323 | 3.570 | ||
| 090328 | 0.736 | ||
| 090424 | 0.544 | ||
| 090618 | 0.540 | ||
| 090709A | 1.800 | ||
| 090715B | 3.000 | ||
| 090812 | 2.452 | ||
| 090926A | 2.106 | ||
| 100606A | 1.554 | ||
| 100621A | 0.542 | ||
| 100728A | 1.567 | ||
| 100814A | 1.440 | ||
| 101213A | 0.414 | ||
| 110213B | 1.083 | ||
| 110422A | 1.770 | ||
| 110503A | 1.613 | ||
| 110715A | 0.820 | ||
| 110731A | 2.830 | ||
| 110918A | 0.984 | ||
| 111008A | 5.000 | ||
| 111228A | 0.716 | ||
| 120119A | 1.728 | ||
| 120624B | 2.197 | ||
| 120711A | 1.405 | ||
| 120716A | 2.486 | ||
| 120909A | 3.930 | ||
| 121128A | 2.200 | ||
| 130408A | 3.758 | ||
| 130427A | 0.340 | ||
| 130505A | 2.270 | ||
| 130514A | 3.600 | ||
| 130518A | 2.488 | ||
| 130606A | 5.913 | ||
| 130701A | 1.155 | ||
| 130831A | 0.479 | ||
| 130907A | 1.238 | ||
| 130925A | 0.347 | ||
| 131030A | 1.293 | ||
| 131105A | 1.686 | ||
| 131108A | 2.400 | ||
| 131231A | 0.644 | ||
| 140213A | 1.208 | ||
| 140226A* | 1.980 | ||
| 140419A | 3.956 | ||
| 140506A | 0.889 | ||
| 140508A | 1.027 | ||
| 140512A | 0.725 | ||
| 140606B | 0.384 | ||
| 140629A | 2.275 | ||
| 140801A | 1.320 | ||
| 140808A | 3.293 | ||
| 141109A | 2.993 | ||
| 141220A | 1.319 | ||
| 150206A | 2.087 | ||
| 150314A | 1.758 | ||
| 150323A | 0.593 | ||
| 150403A | 2.060 | ||
| 150413A | 3.139 | ||
| 150818A | 0.282 | ||
| 150821A | 0.755 | ||
| 151021A | 2.330 | ||
| 151027A | 0.810 | ||
| 160131A | 0.972 | ||
| 160509A | 1.170 | ||
| 160623A | 0.367 | ||
| 160625B | 1.406 | ||
| 160629A | 3.332 | ||
| 161014A | 2.823 | ||
| 161017A | 2.013 | ||
| 161023A | 2.708 | ||
| 161117A | 1.549 | ||
| 170202A | 3.645 | ||
| 170604A | 1.329 | ||
| 171010A | 0.329 | ||
| 171205A | 0.037 | ||
| 180325A | 2.248 | ||
| 180728A | 0.117 | ||
| 180914B* | 1.096 | ||
| 181020A | 2.938 | ||
| 181110A | 1.505 | ||
| 181201A | 0.450 |