Ground state phase diagram and the exotic phases in the spin- square lattice -- model
Abstract
The intricate interplay between frustration and spin chirality has the potential to give rise to unprecedented phases in frustrated quantum magnets. In this investigation, we examine the ground state phase diagram of the spin- square lattice -- model by employing critical level crossings and ground state fidelity susceptibility (FS) using exact diagonalization (ED) with full lattice symmetries. Our analysis reveals the evolution of highly symmetric energy levels as a function of at fixed . During a magnetic to non-magnetic phase transition, the precise identification of the phase boundary is achieved through critical level crossings between the gapless excitation of a magnetic phase and the quasi-degenerate ground state of a non-magnet phase. Conversely, a direct transition between two non-magnetic phases is characterized by a FS peak accompanied by an avoided ground state level crossing, serving as a distinctive signal. Within a substantial range of , we identify an anticipated chiral spin liquid (CSL) state and an adjacent nematic spin liquid (NSL) phase with a degeneracy of two on a cylinder. These two phases are demarcated by a nearly vertical boundary line at . Notably, this critical line terminates at the lower boundary of a magnetic ordered chiral spin solid (CSS) phase, which gains prominence with increasing from both the CSL and NSL phases. We validate the topological nature of the CSL using the modular matrix of the minimum entangled states (MES) on a torus, along with the entanglement spectra (ES) of even and odd sectors on a cylinder, employing an -symmetric density matrix renormalization group (DMRG) method. Furthermore, we delve into a comprehensive discussion on the nature of the NSL, exploring aspects such as ground state degeneracy, the local bond energy landscape, and the singlet and triplet gaps on various tori. These analysis provide substantial evidence supporting the nematic nature of the NSL.
I Introduction
Fractional Quantum Hall (FQH) states are among the most exotic phases of matter in strongly correlated quantum systems which exhibit fractionalized excitations and gapless edge modes Laughlin83 ; Haldane88 ; Moore91 . Interestingly topological flat bands of fermions or hard-core bosons can host similar physics without an external magnetic field Sheng11 ; Wang11 . In this scenario, the role of magnetic flux is emulated by a complex hopping phase Haldane88 ; Sheng11 ; Wang11 . In quantum spin system, chiral spin liquid (CSL) state, akin to the FQH state, is anticipated when introducing a scalar chirality term () expressed as . The interactions governed by break the time-reversal symmetry, playing a role analogous to that of a magnetic flux bauer_chiral_2014 ; Nielsen13 ; Wietek17 . Drawing a parallel to the electron filling quantized orbitals in a magnetic field, one can understand spin-up or spin-down states as akin to filled or vacant states of hard-core bosons. When the intricate interplay between competing phases of frustrated quantum magnets and chirality occurs, the potential arises for the generation of novel phases of matter huang_coexistence_2022 . This intersection poses a significant challenge in condensed matter theory, and demands thorough exploration and understanding.
In geometrically frustrated quantum spin systems, such as Kagome White11 ; Liao17 ; He17 and triangular ZhuZY15 ; Hu_triangulr_15 ; Saadatmand15 lattice Heisenberg models, the absence of a spin chirality term typically results in a ground state that maintains time reversal symmetry. In these cases, a non-chiral gapped White11 ; ZhuZY15 ; ZhuZY18 ; Hu_triangulr_15 or gapless Liao17 ; He17 quantum spin liquid (QSL) is commonly expected. However, with the introduction of a chiral interaction , topological CSL can be easily induced bauer_chiral_2014 ; Wietek17 , and they are energetically favored compared to their neighboring non-chiral counterparts Wietek17 .
Similarly, for a bipartite square lattice, a similar scenario is anticipated. Specifically, in the frustrated spin- square lattice - Antiferromagnetic Heisenberg model without , a gapless QSL has been identified adjacent to an Antiferromagnetic (AFM) state Gong14 ; Morita15 ; Wang18 ; Ferrari20 ; Nomura20 ; Schackleton21 , with no reported signs of a CSL. This model closely describes the magnetic interactions among within the copper oxide plane of high-Tc superconducting parent compounds. Recently experiments have observed an anomalous large thermal Hall signal close to the AFM phase in undoped and underdoped cuprate Grissonnanche19 . This experimental result was interpreted as proximity effects close to a CSL Samajdar19 . In this context, we undertake a study of the ground state phase diagram of the spin- square lattice -- Hamiltonian. Within a proper coupling range, it has been demonstrated to be the local parent Hamiltonian of the Kalmeyer-Laughlin (KL) state Kalmeyer87 , utilizing conformal field correlators’ relationships Nielsen12 ; Nielsen13 .
In the spin- square lattice -- model, the intricate interplay of frustration and chirality gives rise to a unique coexistence of non-abelian topological order and stripe magnetic order. This is substantiated by the simultaneous presence of distinctive features, such as the signature of chiral entanglement spectra (ES) LiES08 ; QiES12 and the existence of non-vanishing stripe magnetic order in the ground state (the topological vacuum state) huang_coexistence_2022 . Extending this investigation to the spin- counterpart of the -- model, our observations reveal a nematic spin liquid (NSL) adjacent to a KL type CSL. This finding corroborates the richness in phase diagram for the frustrated chiral quantum magnets.
A primary tool of our investigation is exact diagonalization (ED) on small tori Laflorencie04 ; Noack05 ; Weisse08 ; Lauchli11 ; Sandvik10ed . This method furnishes a rigorous set of symmetry quantum numbers for each eigenstate, enabling the deduction of ground state degeneracy and low-energy excitations. We leverage critical level crossing to precisely identify phase boundaries between magnetic and non-magnetic states. This involves observing a level order switch between a gapless magnetic excitation and a neighboring quasi-degenerate non-magnetic ground state while varying the coupling strength Wang18 ; Ferrari20 ; Nomura20 . However, when it comes to phase transitions between two non-magnetic phases, critical level crossings become inappropriate. In such instances, ground state fidelity susceptibility (FS) peaks GuFidelity10 ; You11 ; Wang10 , accompanied by an avoided ground state level crossing in the energy spectra, serve as signals indicative of a critical point.
Indeed at intermediate values we identify two novel gapped non-magnetic phases absent in the case. For a specific , on the relative small side, we observe an expected topological CSL reminiscent of the KL state. On the larger side, the disordered phase exhibits a two-fold ground state degeneracy and a strong bond anisotropy between the periodic and open boundary directions when placed on a cylinder, and a gapped magnetic excitation at momentum or on a torus. Employing an -symmetric density matrix renormalization group (DMRG) method, we analyze their bipartite entanglement spectra on a cylinder Wietek17 ; zhu_minimal_2013 ; huang_coexistence_2022 , where is the perimeter in the periodic direction. Additionally, we compute the topological modular matrix using the two symmetric ground states on a torus zhu_minimal_2013 for the CSL. All pieces of evidence consistently affirm that the topological CSL on the side belongs to the KL type. However, the disordered state on the side, despite its novel properties, has not been encountered in the literature before. Its characteristics point towards the intriguing concept of a nematic spin liquid.
The remainder of this paper is organized as follows. In Sec. II, we delve into the ground state phase diagram derived through critical level crossings and FS methods, utilizing results obtained from a 32-site fully symmetric periodic cluster. Sec. III focuses on local expectation values, encompassing various magnetic and valence bond orders across the entire parameter space. In Sec. IV, we uncover the topological nature of the CSL by examining the modular matrix and ES on both even and odd sectors of a cylinder. Section V employs the local bond energy landscape on a cylinder to showcase the two-fold ground state degeneracy, compares ES between the CSL and the NSL, highlighting their distinctions, and presents singlet and triplet gaps on various tori to confirm the existence of a finite magnetic gap. Finally, in Section VI, we provide a summary along with discussions and conclusions.
II Ground state phase diagram
The spin- -- model on a square lattice can be expressed as follows.
| (1) | |||||
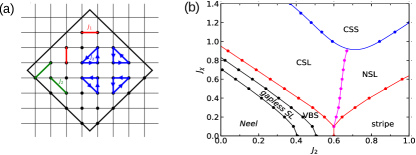
where and denote the nearest neighbor (NN) and the next nearest neighbor (NNN) pairs, while signifies any smallest triangle with its vertex sites arranged in a counter clockwise order. These Hamiltonian terms are also highlighted in Fig. 1(a). For the sake of simplicity, we fix throughout this paper and concentrate on the parameter space where and .
To determine the ground state phase diagram of this system, we employ ED Laflorencie04 ; Noack05 ; Weisse08 ; Lauchli11 ; Sandvik10ed with space group symmetry (rotation and translation to be specific), spin reflection symmetry (), and the particle number conservation symmetry (). Each eigenstate is labeled by a strict set of quantum numbers , where represents the total spin, , denote the momenta in the , directions, respectively, and signifies the phase acquired when applying a lattice rotation given or . In cases where , a “” symbol is assigned to , indicating that the rotation symmetry is not applicable to this quantum sector.
Within the ground state phase diagram, there exist several well-understood phases, see Fig. 1(b). Enumerating these phases, along with their respective ground state symmetry quantum numbers and low-energy magnetic excitations, aids in selecting the correct highly symmetric low-energy sectors for further analysis. In the regime of small and small , the ground state exhibits AFM order, with its finite size singlet ground state located at the quantum sector. The lowest two Anderson Tower collective excitations include a spin triplet with quantum numbers and a spin quintuplet with quantum numbers . As becomes large and remains small, the ground state becomes two-fold degenerate, representing collinear magnetic stripe states. These states feature antiferromagnetic spin correlation in one direction and ferromagnetic spin correlation in the other. The positive and negative superpositions of these differently oriented stripe patterns form highly symmetric ground states in the and quantum sectors, respectively. The low-energy magnetic excitations reveal the stripe nature and exhibit quantum numbers or . In the limit of very large , the ground state displays chiral spin solid (CSS) magnetic order Rabson . The gapless triplet excitations are situated at , , and in the Brillouin Zone huang_coexistence_2022 .
In the special case of , critical level crossings have already provided an accurate and compelling ground state phase diagram Wang18 ; Ferrari20 ; Nomura20 . Between the well-understood antiferromagnetic and collinear states, there exists a gapless QSL and a columnar VBS. The transition from the AFM to the gapless QSL is characterized by an energy level crossing between the quintuplet Anderson rotor state and a low-energy singlet excitation, signifying the disappearance of the AFM order. This singlet evolves continuously into the quasi-degenerate VBS ground state upon further increasing . The transition from the gapless QSL to the columnar VBS phase is identified by an energy level crossing between the lowest triplet excitation and the quasi-degenerate non-magnetic ground state of the columnar VBS phase. The VBS phase terminates through a direct first-order transition to the collinear phase at .
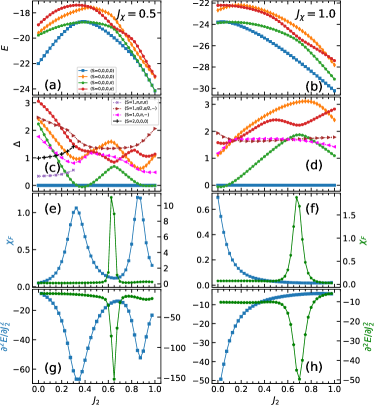
To examine relevant energy level evolutions as a function of with fixed , we partition the two-parameter space into a mesh with steps and to investigate critical level crossings. Fig. 2(a,b) illustrate two typical low-energy spectra taken at and while scanning for a 32-site, 45∘ tilted cluster, as depicted in Fig. 1(a). We present the two lowest states in the sector and another two lowest states in the sector (as marked in the figure), to which all finite-size ground states belong. Demonstrating the two lowest levels in each singlet sector is intended for resolving avoided ground state level crossings.
Various low-energy magnetic excitations in relevant magnetic ordered regions are displayed in Fig. 2(c,d), where energy gaps are defined relative to the “ground state” in the sector (not always being the lowest among all sectors). Identical symbols in different panels of Fig. 2 refer to the same state for a given . For the antiferromagnetic phase, they are the triplet level in the sector (in purple crosses) and the quintuplet level in the sector (in black pluses). For the collinear phase, it is the triplet in the sector (in violaceous left triangles). And for the CSS phase, it is the triplet in the sector (in brown right triangles). Their level crossings with the lowest singlet excitation signal continuous quantum phase transitions, as discussed in the case. Following the critical mechanism discussed previously in the case (also see Ref. Wang18 ; Ferrari20 ; Nomura20 ; Wang22 ), we determine the two black lines in the global phase diagram in Fig. 1(b), separating the AFM with the gapless QSL and the gapless QSL with the VBS, respectively. Other phase boundaries appearing in Fig. 1(b) will be discussed next, which are either driven by a similar magnetic to non-magnetic critical level crossing mechanism or by strong signals in the ground state FS and second-order energy derivatives.
FS is commonly used to detect phase transition accompanied by avoided ground state level crossing GuFidelity10 ; You11 ; Wang10 . Its definition is as following
| (2) |
where is the “ground state” of a given singlet sector at parameter . We compute FS in both and sectors. The energy second order derivative is defined as
| (3) |
The ground state FS for the sector (in blue squares) and sector (in green pentagons) are shown in Fig. 2(e,f). Their energy second order derivatives are shown in Fig. 2(g,h). At , we observe three quantum phase transitions, all associated with avoided (quasi-degenerate) ground state level crossings, which cause peaks in the ground state FS and energy derivatives GuFidelity10 . The first FS peak in sector governs the transition from the columnar VBS to the CSL phase. Remarkably, its accompanying avoided level crossing (between the lowest two levels within this sector) manifests as a clear dip in the gap in orange diamond at the transition point, as shown in Fig. 2(c). At , we observe another avoided level crossing happening in sector, which causes a much pronounced FS peak in Fig. 2(e), and it is where the CSL terminates. Finally, the third FS peak appears in sector at , driving the disordered phase into the collinear magnetic phase. A clear avoided ground state level crossing (between levels in blue squares and orange diamonds) can be associated with this peak too, as shown in Fig. 2(c). The energy second-order derivative (in Fig. 2(g,h)) seems to exactly reproduce the signals given by FS (in Fig. 2(e,f)) as the two definitions are closely related in a perturbative picture GuFidelity10 , suggesting the nature of these phase transitions is likely continuous. The locations of three FS peaks form three critical lines in Fig. 1(b) (two in red and one in violet). At , only one complete FS peak falls within the parameter range, as in Fig. 2(f); the other two are located beyond our parameter scope. However, this second FS peak is no longer associated with a phase transition at since the level in green pentagons is no longer a ground state in this region, which will be discussed next.
In Fig. 2(b), at and , we observe that two magnetic triplet excitations with quantum numbers and drop below all singlet excitations, as shown in Fig. 2(d). These magnetic excitations are associated with a CSS magnetic order, whose static structure factor peaks at the following eight points in momentum space: , , huang_coexistence_2022 . We, therefore, define the region in parameter space where these magnetic excitations become the lowest as the CSS phase, bounded by the blue line in Fig. 1(b). The transition is associated with a critical level crossing between magnetic and non-magnetic phases. Specifically, we choose crossing points between the triplet and singlet as the left and right boundaries of the CSS phase at a given , as seen in Fig. 2(d).
We present the ground state phase diagram of the -- model in Fig. 1(b), summarizing all previous results based on critical level crossings or ground state FS. All critical transitions seem to be continuous, except for the thick orange line, indicating a direct VBS to collinear transition. We observe three new phases, namely, the CSL, the NSL, and the magnetic CSS phases, in addition to the four known phases in the - model (the antiferromagnetic, the gapless QSL, the columnar VBS, and the collinear phases). Before discussing the topological nature of the two new non-magnetic phases, we first take a look at the local order parameters.
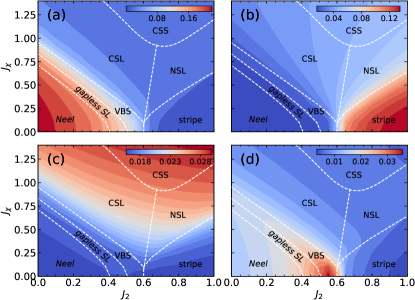
III Local order parameters
To illustrate the magnetic and valence bond ordered phases, we define following local order parameters. Magnetization square at momentum is defined as
| (4) |
where . For the AFM phase, peaks at momentum , while for the collinear phase it peaks at momentum and . In the CSS phase, there are 4 main peaks located at and and 4 satellite peaks sitting at huang_coexistence_2022 . We use as a disguising moment for the CSS phase to separate it from the collinear phase.
The dimer order parameter is defined as
| (5) |
where , , , and .
All four local order parameters are computed using the ground state in the sector, and their color contour plots are illustrated in Fig. 3. We observe that the contours of local order parameters are roughly consistent with various phase boundaries of the ground state phase diagram.
IV Topological nature of the CSL phase
To uncover the topological nature of the CSL phase, we compute the modular matrix, which is defined as the overlap matrix between the minimally entangled states (MES) along cuts in and directions. Here the MES along a cut in () direction is numerically optimized by minimizing its entanglement entropy (EE) with respect to superimposing parameters and (defined below) of the two quasi degenerate ground states.
Referring to a winding direction () on a torus, we name the two topological ground states as and respectively ( for vacuum and for semion). ED calculation does not produce and directly. The quasi degenerate eigenstates obtained via ED, say from the sector and from the sector, are combinations of and , as
| (6) |
By definition, minimizing the EE of can settle the two parameters () for a given . Once having and , we define two two-component vectors . The modular matrix is formally written as .
Indeed, through the minimization procedure of we find two EE minima (refer to , respectively), as in Fig. 4(a). Their relative positions on axis square-sum to 1, and their superimposing phase difference is . For the other pair of MES , we take advantage of the rotation symmetry, and find and . We thus identify the matrix within the CSL phase at parameters and as
| (7) |
This result confirms the expected semion mutual statistics with total quantum dimension of zhu_minimal_2013 .
To inspect edge physics, we study the CSL phase on a cylinder with perimeter using an symmetric DMRG algorithm Wbaum12 with open and periodic boundaries in the and directions, respectively. Imagining a vertical line cutting in the middle of the cylinder, when there is an even number of sites on both sides, the ground state will converge to the vacuum sector . On the other hand, when taking away one spin on each side from the above case, the ground state will converge to the semion sector . Fig. 5 demonstrates the bipartite entanglement spectra computed for states (a) and (b) respectively at and with . Each eigenvalue of the reduced density matrix is associated with a total spin quantum number of the left half system and a momentum quantum number with respect to acting the translation operator on the corresponding eigenvector of . Both ES clearly display a degeneracy sequence of (1,1,2,3,5,8,), consistent with the tower of Kac-Moody descendants of the identity and spin- primary fields.
V Nature of the NSL phase
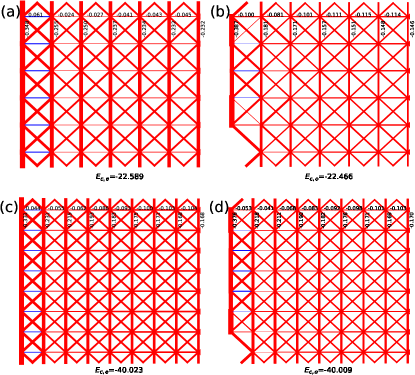
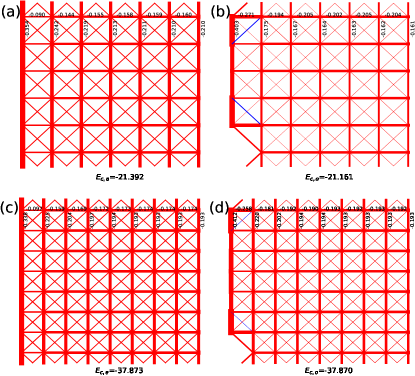
To demonstrate the nature of the NSL phase, we first check the bond energy landscape for both even and odd sectors on a cylinder of various sizes and inspect its anisotropy tendency in the thermodynamic limit. We find that there exists a strong bond anisotropy within the NSL phase. In the even (odd) sector near the center of a cylinder, we find and ( and ). Their bond energy differences defined as
| (8) |
are and for even and odd respectively, as in Fig. 6(a,b). This nematicity tendency enhances on the odd cylinder. We observe that and ( and ). Their bond energy differences are and for even and odd, respectively, as in Fig. 6(c,d). On the other hand, in the CSL phase, the bond energy anisotropy are and at , and and at as in Fig. 7. We find in the CSL phase, the bond anisotropy due to cylinder boundary effect quickly diminishes with the system size , in contrast with that of the NSL behavior. We further measure the total energy of the center area within the even and odd cylinders for both the NSL and CSL phases, and mark them as in Fig. 6 and Fig. 7 respectively. Within the NSL phase, we find that at , and for even and odd respectively; while at , and for even and odd, respectively. It clearly demonstrates that the energy splitting between even and odd sectors of the NSL on a cylinder vanishes exponentially with . A similar behavior is also seen on the CSL phase, as in Fig. 7. We expect the ground state manifold to double (four-fold) on a torus for the NSL phase.
To compare the NSL with the CSL phase, we present the edge ES on a cylinder with a perimeter of , measured at , in Fig. 8. The ES in the even sector exhibits the same chiral edge modes as those observed in the CSL. However, the odd sector displays a degeneracy counting discrepancy compared to its CSL counterpart, providing additional evidence of entering a new phase.
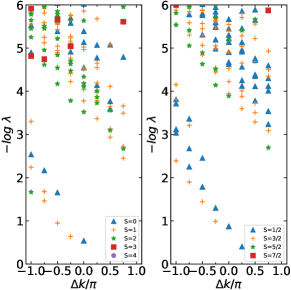
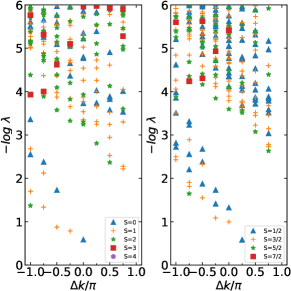
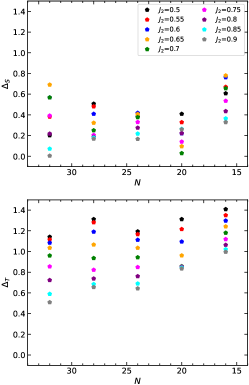
To elucidate the ground state degeneracy on a torus geometry and the persistent triplet gap within the CSL and NSL phases, we introduce as the energy splitting between the lowest two singlets across all sectors, and and as the gap between the stripe triplet and the lowest singlet. These values and are presented at with a step size of for periodic clusters of sizes in Fig. 9. Our observations indicate that the singlet consistently resides below the stripe triplet for all considered values, and the triplet gaps tend to stabilize as deviates from the transition coupling , which demarcates the magnetic stripe phase from the left at . This reaffirms that the triplet gaps within both the CSL and NSL phases remain finite.
An insightful comment about the ground state degeneracy on a 32-site torus within the NSL region follows. From Fig. 2(c), it appears that the two singlets in orange diamonds and red pentagons are positioned above the lowest triplet state; however, this is attributed to finite size effects. The four quasi-degenerate singlets will eventually descend below the gapped triplet excitations, as the energy splitting within the ground state manifold becomes exponentially small with increasing size .
VI Conclusions
We investigate the ground state phase diagram of the spin- -- model on a square lattice. Our analysis reveals a complex two-parameter phase diagram. For small and fixed , the one-parameter phase diagram of the - model Wang18 ; Ferrari20 ; Nomura20 naturally extends to , encompassing four well-known phases, though these are not the primary focus of our study. At intermediate values, a topological chiral spin liquid (CSL) state and a nematic spin liquid (NSL) state emerge concurrently, situated between a valence bond solid (VBS) and a collinear magnetic state. Further, a chiral spin solid (CSS) magnetic state envelops the two spin liquid phases at higher values. The boundaries between these phases are determined using critical level crossing arguments between magnetic and non-magnetic phases, or through peaks in fidelity susceptibility (FS) accompanied by avoided ground state level crossings.
Our phase diagram for the region where the CSL exists aligns closely with an earlier ED study on a cluster Nielsen13 , although the authors of that study overlooked the NSL phase and the CSS magnetic phase. Within the proposed NSL phase, level spectroscopy reveals a quasi four-fold ground state degeneracy on a torus, consistent with rotation symmetry breaking in the bond energy landscape and the two-fold ground state manifold on a cylinder. When comparing entanglement spectra (ES) of the NSL and the CSL on a cylinder, we observe similar edge modes in the even topological sector, but differences in the odd sector. Our findings offer a concrete example of a nematic spin liquid state arising from a realistic lattice Hamiltonian.
Acknowledgements.
Note added. Recently, we became aware of an article by zhang el al., who studied the same model by DMRG. Both of the two works consistently show the AFM, stripe, CSL, and the NSL (named disordered phase in their study) phases. However their DMRG finite size extrapolation doesn’t support the surviving of the CSS order in the thermodynamic limit. While our work doesn’t focus on the finite size extrapolation of the CSS order though. This discrepency shall deserve further inceasing of the cylinder size in the furture. We would like to thank S.-S. Gong for discussion and manuscript sharing, and C. Xu for pointing to us the possibility of a NSL phase, and W. Zhu, G. M. Zhang for enlightening discussion. Z.L. is supported by the National Key Research and Development Program of China (2020YFA0309200). L.W. is supported by the National Natural Science Foundation of China, Grants No. NSFC-12374150 and No. NSFC-11874080 .References
- (1) R. B. Laughlin, Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations, Phys. Rev. Lett. 50 1395 (1983).
- (2) F. D. M. Haldane, Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the ”Parity Anomaly”, Phys. Rev. Lett. 61 2015 (1988).
- (3) G. Moore and N. Read, Nonabelians in the Fractional Quantum Hall Effect, Nucl. Phys. B 360, 362 (1991).
- (4) D. N. Sheng, Z.-C. Gu, K. Sun, L. Sheng, Fractional quantum Hall effect in the absence of Landau levels, Nat Commun 2, 389 (2011).
- (5) Y.-F. Wang, Z.-C. Gu, C.-D. Gong, D. N. Sheng, Fractional Quantum Hall Effect of Hard-Core Bosons in Topological Flat Bands, Phys. Rev. Lett. 107 146803 (2011).
- (6) Bauer, B., Cincio, L., Keller, B. et al. Chiral spin liquid and emergent anyons in a Kagome lattice Mott insulator. Nat Commun 5, 5137 (2014).
- (7) A. Wietek and A. Lauchli, Chiral spin liquid and quantum criticality in extended Heisenberg models on the triangular lattice, Phys. Rev. B 95, 035141 (2017).
- (8) Nielsen, A., Sierra, G. and Cirac, J. Local models of fractional quantum Hall states in lattices and physical implementation. Nat Commun 4, 2864 (2013).
- (9) Y. Huang, W. Zhu, S.-S. Gong, H.-C. Jiang, D. N. Sheng, Coexistence of non-Abelian chiral spin liquid and magnetic order in a spin-1 antiferromagnet, Phys. Rev. B 105,155104 (2022).
- (10) S. Yan, D. A. Huse, and S. R. White, Spin-Liquid Ground State of the S = 1/2 Kagome Heisenberg Antiferromagnet, Science 332, 1173 (2011).
- (11) H. J. Liao, Z. Y. Xie, J. Chen, Z. Y. Liu, H. D Xie, R. Z Huang, B. Normand, and T. Xiang, Gapless Spin-Liquid Ground State in the Kagome Antiferromagnet, Phys. Rev. Lett. 118 137202 (2017).
- (12) Y.-C. He, M. P. Zaletel, M. Oshikawa, and F. Pollmann, Signatures of Dirac Cones in a DMRG Study of the Kagome Heisenberg Model, Phys. Rev. X 7, 031020 (2017).
- (13) Z. Zhu and S. R. White, Spin liquid phase of the - Heisenberg model on the triangular lattice, Phys. Rev. B 92, 041105(R) (2015).
- (14) W.-J. Hu, S.-S. Gong, W. Zhu, and D. N. Sheng, Competing spin-liquid states in the spin- Heisenberg model on the triangular lattice, Phys. Rev. B 92, 140403(R) (2015).
- (15) S. N. Saadatmand, B. J. Powell, and I. P. McCulloch, Phase diagram of the spin- triangular - Heisenberg model on a three-leg cylinder, Phys. Rev. B 91, 245119 (2015).
- (16) Z. Zhu, P. A. Maksimov, S. R. White, and A. L. Chernyshev, Topography of Spin Liquid on a Triangular Lattice, Phys. Rev. Lett. 120, 207203 (2018).
- (17) S.-S. Gong, W. Zhu, D. N. Sheng, O. I. Motrunich, and M. P. A. Fisher, Plaquette Ordered Phase and Quantum Phase Diagram in the Spin- - Square Heisenberg Model, Phys. Rev. Lett. 113, 027201 (2014).
- (18) S. Morita, R. Kaneko, and M. Imada, Quantum spin liquid in spin - Heisenberg model on square lattice: Many-variable variational Monte Carlo study combined with quantum-number projections, J. Phys. Soc. Jpn. 84, 024720 (2015).
- (19) L. Wang and A. W. Sandvik, Critical Level Crossings and Gapless Spin Liquid in the Square-Lattice Spin- - Heisenberg Antiferromagnet, Phys. Rev. Lett. 121, 107202 (2018).
- (20) F. Ferrari and F. Becca, Gapless spin liquid and valence-bond solid in the - Heisenberg model on the square lattice: Insights from singlet and triplet excitations, Phys. Rev. B 102, 014417 (2020).
- (21) Y. Nomura and M. Imada, Dirac-type nodal spin liquid revealed by machine learning, Phys. Rev. X 11, 031034 (2021).
- (22) H. Shackleton, A. Thomson, and S. Sachdev, Deconfined criticality and a gapless spin liquid in the square lattice antiferromagnet, Phys. Rev. B 104, 045110 (2021).
- (23) G. Grissonnanche, A. Legros, S. Badoux, E. Lefrancois, V. Zatko, M. Lizaire, F. Laliberte, A. Gourgout, J.-S. Zhou, S. Pyon, t. takayama, H. takagi, S. Ono, N. Doiron-Leyraud, and L. taillefer, Giant thermal Hall conductivity in the pseudogap phase of cuprate superconductors, Nature 571, 376 (2019).
- (24) R. Samajdar, M. S. Scheurer, S. Chatterjee, H. Guo, C. Xu, and S. Sachdev, Nat. Phys. 15, 1290 (2019).
- (25) V. Kalmeyer, and R.B. Laughlin, Equivalence of the resonating-valence-bond and fractional quantum Hall states. Phys. Rev. Lett. 59, 2095 (1987).
- (26) A. Nielsen, J. I. Cirac, and G. Sierra, Laughlin Spin-Liquid States on Lattices Obtained from Conformal Field Theory, Phys. Rev. Lett. 108, 257206 (2012).
- (27) H. Li and F. D. M. Haldane, Entanglement spectrum as a generalization of entanglement entropy: Identification of topological order in non-abelian fractional quantum hall effect states. Phys. Rev. Lett. 101, 010504 (2008).
- (28) Qi, X.-L., H. Katsura, and A. W. W. Ludwig, General relationship between the entanglement spectrum and the edge state spectrum of topological quantum states. Phys. Rev. Lett. 108, 196402 (2012).
- (29) N. Laflorencie and D. Poilblanc, Simulations of pure and doped low-dimensional spin- gapped systems, Lecture Notes in Physics 645, 227 (2004).
- (30) R.M. Noack and S. Manmana, Diagonalization and Numerical Renormalization-Group-Based Methods for Interacting Quantum Systems, AIP Conf. Proc. 789, 93 (2005).
- (31) A. Weisse, H. Fehske, Exact Diagonalization Techniques, Lecture Notes in Physics 739, 529 (2008).
- (32) A. Lauchli, Numerical Simulations of Frustrated Systems, Springer Ser. Solid-State Sci. 164, 481-511 (2011).
- (33) A. W. Sandvik, Computational Studies of Quantum Spin Systems, AIP Conf. Proc. 1297, 135 (2010).
- (34) S.-J. Gu, Fidelity approach to quantum phase transitions, Int. J. Mod. Phys. B 24, 4371 (2010).
- (35) W.-L. You and Y.-L. Dong, Fidelity susceptibility in two-dimensional spin-orbit models, Phys. Rev. B 84, 174426 (2011).
- (36) B. Wang, M. Feng, and Z.-Q. Chen, Berezinskii-Kosterlitz-Thouless transition uncovered by the fidelity susceptibility in the XXZ model, Phys. Rev. A 81, 064301 (2010).
- (37) W. Zhu, D. N. Sheng, F. D. M. Haldane, Minimal entangled states and modular matrix for fractional quantum Hall effect in topological flat bands, Phys. Rev. B 88,035122 (2013).
- (38) D. A. Rabson and S. A. Trugman, A spin model for investigating chirality, J. Phys: Cond. Matt. 7, 9005 (1995).
- (39) L. Wang, Y. Zhang, and A. W. Sandvik, Quantum spin liquid phase in the Shastry-Sutherland model detected by an improved level spectroscopic method, arXiv:2205.02476
- (40) A. Weichselbaum, Non-abelian symmetries in tensor networks: A quantum symmetry space approach, Ann. Phys. (Amsterdam) 327, 2972 (2012).